Influence of Specimen Preparation and Test Methods on the Flexural Strength Results of Monolithic Zirconia Materials
Abstract
:1. Introduction
2. Material and Methods
2.1. Specimen Preparation
2.2. Flexural Strength Testing
2.3. Profilometry
2.4. Scanning Electron Microscopy (SEM)
2.5. X-ray Diffraction (XRD)
2.6. Statistical Analysis and Methods
3. Results
3.1. Influence of Test Method
3.2. Influence of Specimen Preparation
3.3. Influence of Tested Zirconia Materials
3.4. Surface Roughness (Profilometer) and Surface Topography (SEM)
3.5. Characterization of Monoclinic Phase Transformation (X-ray Diffraction)
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Christel, P.; Meunier, A.; Heller, M.; Torre, J.P.; Peille, C.N. Mechanical properties and short-term in vivo evaluation of yttrium-oxide-partially-stabilized zirconia. J. Biomed. Mater. Res. Part A 1989, 23, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Garvie, R.C.; Hannink, R.H.; Pascoe, R.T. Ceramic steel? Nature 1975, 258, 703–704. [Google Scholar] [CrossRef]
- Pecho, O.E.; Ghinea, R.; Ionescu, A.M.; Cardona, J.D.L.C.; Paravina, R.D.; Pérez, M.D.M. Color and translucency of zirconia ceramics, human dentine and bovine dentine. J. Dent. 2012, 40, e34–e40. [Google Scholar] [CrossRef] [PubMed]
- Aboushelib, M.N.; de Jager, N.; Kleverlaan, C.J.; Feilzer, A.J. Microtensile bond strength of different components of core veneered all-ceramic restorations. Dent. Mater. 2005, 21, 984–991. [Google Scholar] [CrossRef] [PubMed]
- Conrad, H.J.; Seong, W.-J.; Pesun, I.J. Current ceramic materials and systems with clinical recommendations: A systematic review. J. Prosthet. Dent. 2007, 98, 389–404. [Google Scholar] [CrossRef]
- Al-Amleh, B.; Lyons, K.; Swain, M. Clinical trials in zirconia: A systematic review. J. Oral Rehabil. 2010, 37, 641–652. [Google Scholar] [CrossRef] [PubMed]
- Sax, C.; Hammerle, C.H.; Sailer, I. 10-year clinical outcomes of fixed dental prostheses with zirconia frameworks. Int. J. Comput. Dent. 2011, 14, 183–202. [Google Scholar] [PubMed]
- Johansson, C.; Kmet, G.; Rivera, J.; Larsson, C.; Vult Von Steyern, P. Fracture strength of monolithic all-ceramic crowns made of high translucent yttrium oxide-stabilized zirconium dioxide compared to porcelain-veneered crowns and lithium disilicate crowns. Acta Odontol. Scand. 2013, 72, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Beuer, F.; Stimmelmayr, M.; Gueth, J.-F.; Edelhoff, D.; Naumann, M. In vitro performance of full-contour zirconia single crowns. Dent. Mater. 2012, 28, 449–456. [Google Scholar] [CrossRef] [PubMed]
- Quinn, G.D.; Morrell, R. Design data for engineering ceramics: A review of the flexure test. J. Am. Ceram. Soc. 1991, 74, 2037–2066. [Google Scholar] [CrossRef]
- Shetty, D.K.; Rosenfield, A.R.; Duckworth, W.H.; Held, P.R. A biaxial-flexure test for evaluating ceramic strengths. J. Am. Ceram. Soc. 1983, 66, 36–42. [Google Scholar] [CrossRef]
- Quinn, J.B.; Quinn, G.D. A practical and systematic review of Weibull statistics for reporting strengths of dental materials. Dent. Mater. 2010, 26, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Bhamra, G.; Palin, W.M.; Fleming, G.J.P. The effect of surface roughness on the flexure strength of an alumina reinforced all-ceramic crown material. J. Dent. 2002, 30, 153–160. [Google Scholar] [CrossRef]
- Curtis, A.R.; Wright, A.J.; Fleming, G.J.P. The influence of surface modification techniques on the performance of a Y-TZP dental ceramic. J. Dent. 2006, 34, 195–206. [Google Scholar] [CrossRef] [PubMed]
- de Castro, H.L.; Corazza, P.H.; Paes-Junior, T.D.A.; Della Bona, A. Influence of Y-TZP ceramic treatment and different resin cements on bond strength to dentin. Dent. Mater. 2012, 28, 1191–1197. [Google Scholar] [CrossRef] [PubMed]
- Della Bona, A.; Donassollo, T.A.; Demarco, F.F.; Barrett, A.A.; Mecholsky, J.J., Jr. Characterization and surface treatment effects on topography of a glass-infiltrated alumina/zirconia-reinforced ceramic. Dent. Mater. 2007, 23, 769–775. [Google Scholar] [CrossRef] [PubMed]
- Guazzato, M.; Albakry, M.; Quach, L.; Swain, M.V. Influence of surface and heat treatments on the flexural strength of a glass-infiltrated alumina/zirconia-reinforced dental ceramic. Dent. Mater. 2005, 21, 454–463. [Google Scholar] [CrossRef] [PubMed]
- Kosmač, T.; Oblak, C.; Jevnikar, P.; Funduk, N.; Marion, L. The effect of surface grinding and sandblasting on flexural strength and reliability of Y-TZP zirconia ceramic. Dent. Mater. 1999, 15, 426–433. [Google Scholar] [CrossRef]
- Stawarczyk, B.; Frevert, K.; Ender, A.; Roos, M.; Sener, B.; Wimmer, T. Comparison of four monolithic zirconia materials with conventional ones: Contrast ratio, grain size, four-point flexural strength and two-body wear. J. Mech. Behav. Biomed. Mater. 2016, 59, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Dentistry—Ceramic Materials; ISO 6872; International Organizatino for Standardization: Geneva, Switzerland, 2008.
- Toraya, H.; Yoshimura, M.; Somiya, S. Calibration curve for quantitative analysis of the monoclinic-tetragonal ZrO2 system by X-ray diffraction. J. Am. Ceram. Soc. 1984, 67. [Google Scholar] [CrossRef]
- Roos, M.; Stawarczyk, B. Evaluation of bond strength of resin cements using different general-purpose statistical software packages for two-parameter Weibull statistics. Dent. Mater. 2012, 28, e76–e88. [Google Scholar] [CrossRef] [PubMed]
- Stawarczyk, B.; Özcan, M.; Hämmerle, C.H.F.; Roos, M. The fracture load and failure types of veneered anterior zirconia crowns: An analysis of normal and Weibull distribution of complete and censored data. Dent. Mater. 2012, 28, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Bütikofer, L.; Stawarczyk, B.; Roos, M. Two regression methods for estimation of a two-parameter Weibull distribution for reliability of dental materials. Dent. Mater. 2015, 31, e33–e50. [Google Scholar] [CrossRef] [PubMed]
- Stawarczyk, B.; Özcan, M.; Trottmann, A.; Hämmerle, C.H.F.; Roos, M. Evaluation of flexural strength of hipped and presintered zirconia using different estimation methods of Weibull statistics. J. Mech. Behav. Biomed. Mater. 2012, 10, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Fischer, J.; Stawarczyk, B.; Hämmerle, C.H.F. Flexural strength of veneering ceramics for zirconia. J. Dent. 2008, 36, 316–321. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.; Chu, F.C.; Chow, T.W.; Liang, B.M. Chemical solubility and flexural strength of zirconia-based ceramics. Int. J. Prosthodont. 2007, 20, 587–595. [Google Scholar] [PubMed]
- Anusavice, K.J.; Kakar, K.; Ferree, N. Which mechanical and physical testing methods are relevant for predicting the clinical performance of ceramic-based dental prostheses? Clin. Oral Implants Res. 2007, 18, 218–231. [Google Scholar] [CrossRef] [PubMed]
- Ban, S.; Anusavice, K.J. Influence of test method on failure stress of brittle dental materials. J. Dent. Res. 1990, 69, 1791–1799. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Takahashi, H.; Iwasaki, N. Effect of test method on flexural strength of recent dental ceramics. Dent. Mater. J. 2004, 23, 490–496. [Google Scholar] [CrossRef] [PubMed]
- Danzer, R.; Lube, T.; Supancic, P.; Damani, R. Fracture of ceramics. Adv. Eng. Mater. 2008, 10, 275–298. [Google Scholar] [CrossRef]
- Papanagiotou, H.P.; Morgano, S.M.; Giordano, R.A.; Pober, R. In vitro evaluation of low-temperature aging effects and finishing procedures on the flexural strength and structural stability of Y-TZP dental ceramics. J. Prosthet. Dent. 2006, 96, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Kosmač, T.; Oblak, Č.; Jevnikar, P.; Funduk, N.; Marion, L. Strength and reliability of surface treated Y-TZP dental ceramics. J. Biomed. Mater. Res. 2000, 53, 304–313. [Google Scholar] [CrossRef]
- Luthardt, R.G.; Holzhüter, M.; Sandkuhl, O.; Herold, V.; Schnapp, J.D.; Kuhlisch, E.; Walter, M. Reliability and properties of ground Y-TZP-zirconia ceramics. J. Dent. Res. 2002, 81, 487–491. [Google Scholar] [CrossRef] [PubMed]
- Denry, I.L.; Holloway, J.A. Microstructural and crystallographic surface changes after grinding zirconia-based dental ceramics. J. Biomed. Mater. Res. Part B Appl. Biomater. 2006, 76, 440–448. [Google Scholar] [CrossRef] [PubMed]
- Qeblawi, D.M.; Muñoz, C.A.; Brewer, J.D.; Monaco, E.A., Jr. The effect of zirconia surface treatment on flexural strength and shear bond strength to a resin cement. J. Prosthet. Dent. 2010, 103, 210–220. [Google Scholar] [CrossRef]
- Karakoca, S.; Yilmaz, H. Influence of surface treatments on surface roughness, phase transformation, and biaxial flexural strength of Y-TZP ceramics. J. Biomed. Mater. Res. Part B Appl. Biomater. 2009, 91, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Gupta, T.K. Strengthening by surface damage in metastable tetragonal zirconia. J. Am. Ceram. Soc. 1980, 63, 117–117. [Google Scholar] [CrossRef]
- Hannink, R.H.J.; Kelly, P.M.; Muddle, B.C. Transformation toughening in zirconia-containing ceramics. J. Am. Ceram. Soc. 2000, 83, 461–487. [Google Scholar] [CrossRef]
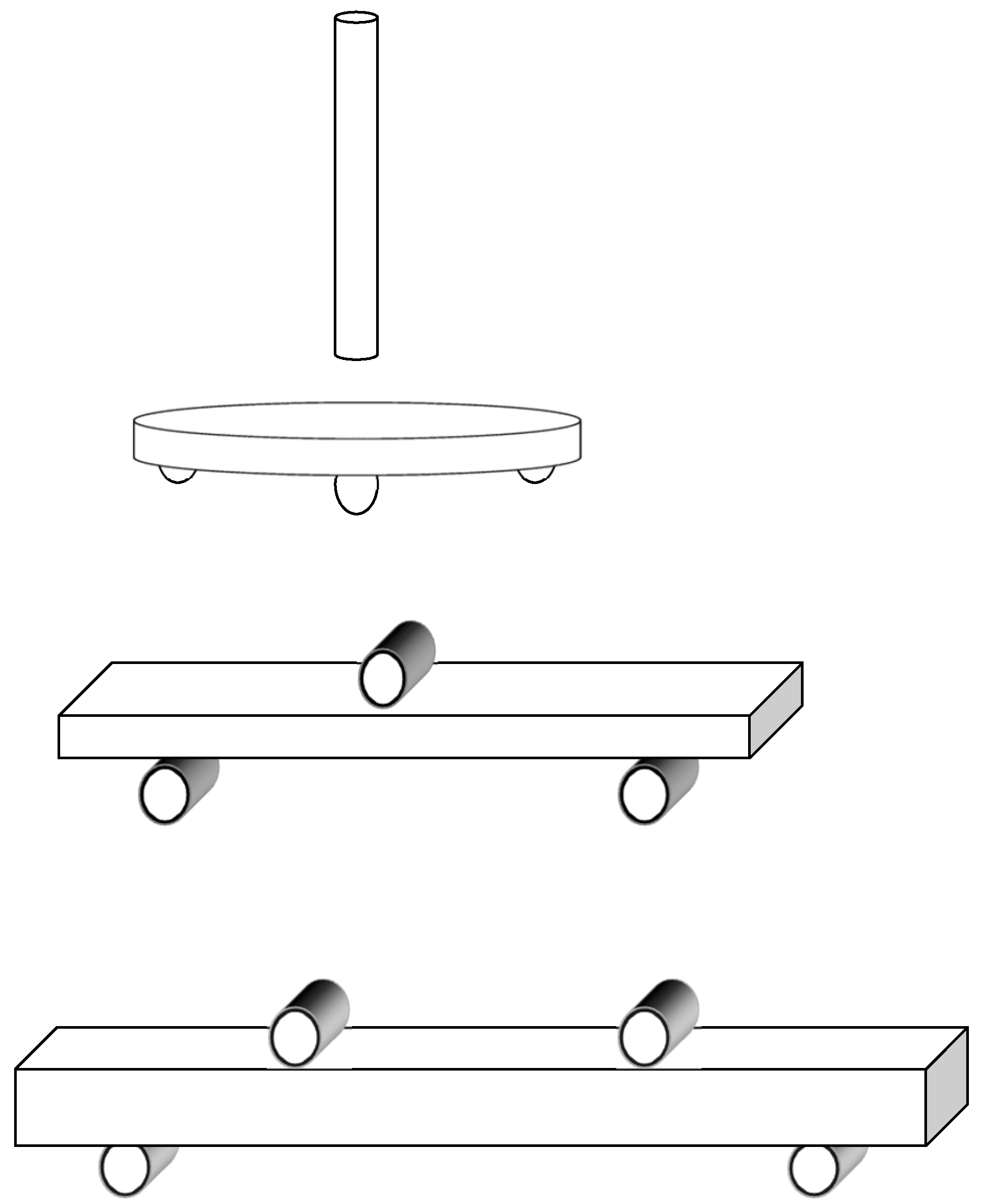
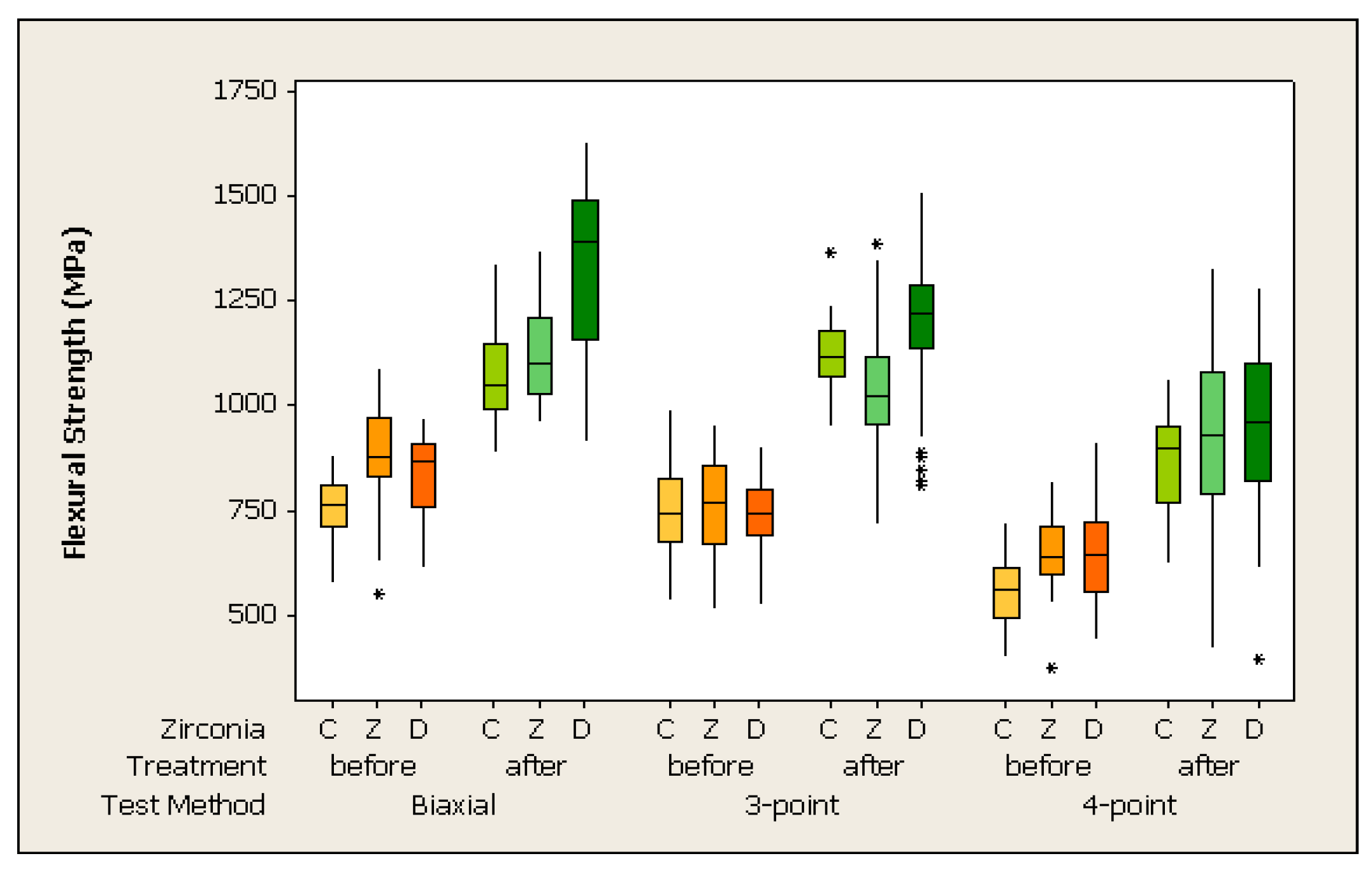

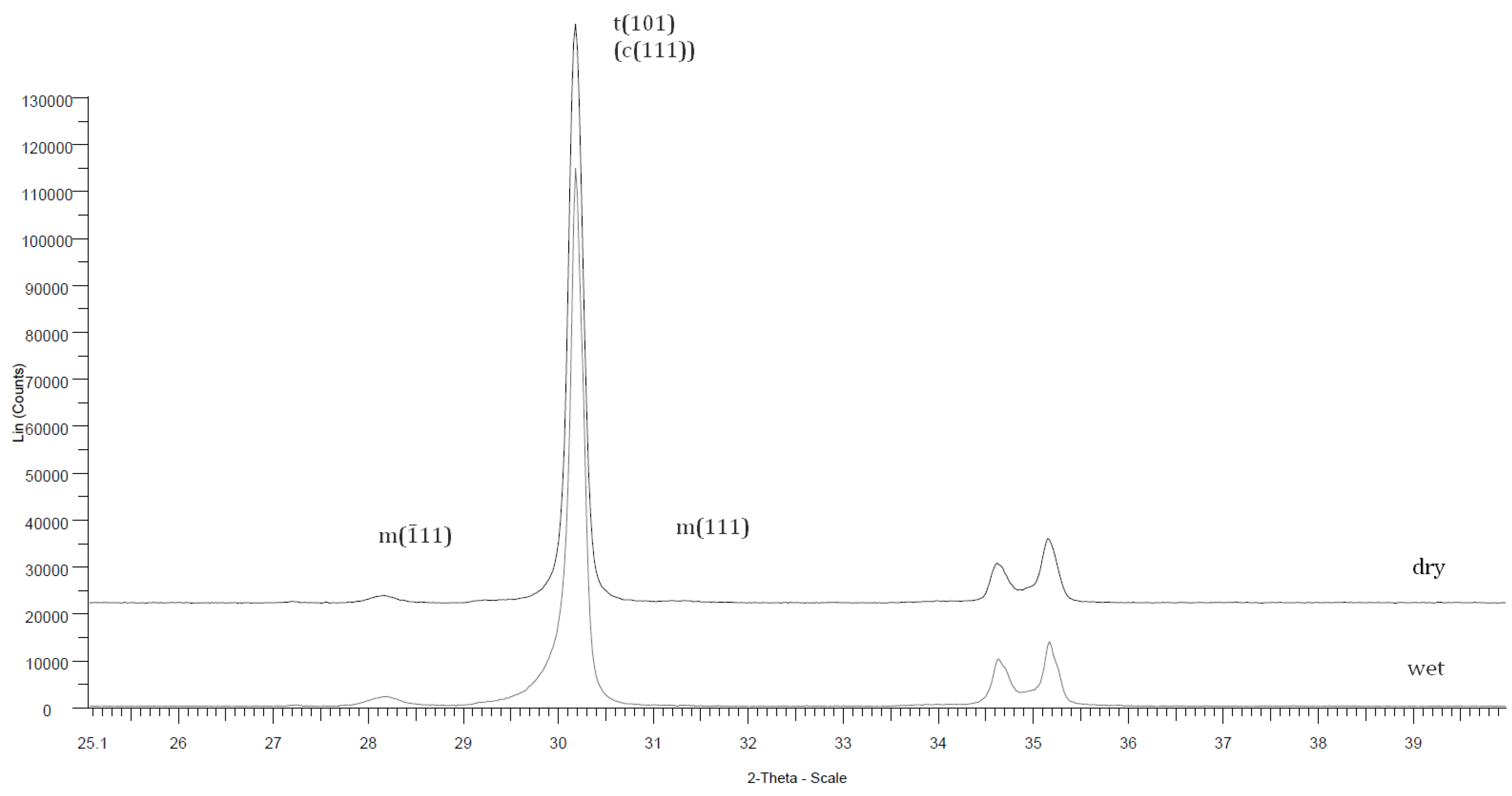
| Abbreviations | Zirconia Materials | Manufacturers | LOT Number | Chemical Components (%) | Grain Size (μm2) Mean ± SD [19] |
|---|---|---|---|---|---|
| C | Ceramill Zolid | Amann Girrbach, Koblach, Austria | 1111813 | ZrO2 + HfO2 + Y2O3 > 99; Y2O3: 4.5–5.6; HfO2 < 5; Al2O3 < 0.5 | 0.088 ± 0.004 a |
| Z | Zenostar Zr Translucent | Wieland+Dental, Pforzheim, Germany | 20120306-27 | ZrO2 + HfO2 + Y2O3 > 99; 4,5 < Y2O3 ≤ 6; HfO2 ≤ 5; Al2O3 + other oxides ≤ 1 | 0.092 ± 0.003 a |
| D | DD Bio zx2 | Dental Direkt, Spenge, Germany | 30712803 | ZrO2 + HfO2 + Y2O3 > 99; Al2O3 < 0.5; other oxides ≤ 1 | 0.124 ± 0.006 b |
| Total | ZM | TM | SP | Subgroup |
|---|---|---|---|---|
| N = 720 | C, D, Z n = 240 | biaxial | dry-polished before sintering | n = 40 |
| n = 80 | wet-polished after sintering | n = 40 | ||
| 3-point | dry-polished before sintering | n = 40 | ||
| n = 80 | wet-polished after sintering | n = 40 | ||
| 4-point | dry-polished before sintering | n = 40 | ||
| n = 80 | wet-polished after sintering | n = 40 |
| ZM | Heat Rate (°C/h) | Holding Temperature and Time (°C, h) | Final Temperature (°C) | Holding Time (h) | Cooling Rate (°C/h) |
|---|---|---|---|---|---|
| C | 480 | - | 1450 | 2 | 300 |
| Z | 600 | 900; 0.5 h; further with 200 °C/h | 1450 | 2 | 600 |
| D | 480 | 900; 0.5 h; further with 200 °C/h | 1450 | 2 | 600 |
| TM | SP | ZM | Weibull | Normal | Optimal Fit | Optimal Fit Distribution |
|---|---|---|---|---|---|---|
| Biaxial | before | C | 0.637 | 0.702 | 0.611 | 3-par Weibull |
| Z | 0.793 | 0.821 | 0.726 | Logistic | ||
| D | 1.102 | 1.735 | 0.947 | SEV | ||
| after | C | 2.405 | 0.799 | 0.482 | 3-par Log normal | |
| Z | 2.070 | 0.713 | 0.593 | 3-par Log normal | ||
| D | 1.111 | 1.589 | 0.940 | SEV | ||
| 3-point | before | C | 0.916 | 0.455 | 0.434 | 3-par Log normal |
| Z | 0.613 | 0.594 | 0.536 | 3-par Weibull | ||
| D | 0.577 | 0.508 | 0.480 | 3-par Weibull | ||
| after | C | 1.101 | 0.568 | 0.512 | Logistic | |
| Z | 2.053 | 0.942 | 0.669 | 3-par Log logistic | ||
| D | 0.946 | 1.412 | 0.835 | 3-par Weibull | ||
| 4-point | before | C | 1.024 | 0.488 | 0.472 | 3-par Log normal |
| Z | 0.946 | 0.746 | 0.743 | 3-par Log normal | ||
| D | 0.755 | 0.496 | 0.496 | normal | ||
| after | C | 0.693 | 1.033 | 0.691 | SEV | |
| Z | 0.685 | 0.708 | 0.708 | normal | ||
| D | 0.625 | 0.698 | 0.625 | Weibull |
| TM | SP | ZM | SD | 95% CI (SD) | Mean | 95% CI (Mean) | COV % |
|---|---|---|---|---|---|---|---|
| Biaxial | before | C a/A | 81 a | (64;102) a | 757 A | (731;782) B | 11 |
| Z a/B | 115 a | (91;144) a | 891 A | (855;927) C | 13 | ||
| D a/B | 101 a | (80;126) a | 835 *,A | (803;866) C | 12 | ||
| after | C a/A | 115 a | (91;145) a | 1077 B | (1040;1112) B | 11 | |
| Z ab/A | 116 a | (92;146) a | 1126 B | (1090;1162) B | 10 | ||
| D b/B | 212 b | (170;265) a | 1322 *,B | (1256;1388) B | 16 | ||
| 3-point | before | C a/A | 110 a | (87;139) a | 752 A | (718;787) B | 15 |
| Z a/A | 124 a | (98;156) a | 755 A | (716;793) B | 16 | ||
| D a/A | 97 a | (76;122) a | 743 A | (712;773) B | 13 | ||
| after | C a/AB | 86 a | (68;108) a | 1118 B | (1090;1144) B | 8 | |
| Z ab/A | 156 a | (123;196) a | 1039 B | (990;1087) AB | 15 | ||
| D b/B | 173 a | (138;216) a | 1183 *,B | (1129;1237) B | 15 | ||
| 4-point | before | C a/A | 78 a | (61;99) a | 561 *,A | (536;585) A | 14 |
| Z a/B | 88 a | (69;110) a | 646 A | (618;673) A | 14 | ||
| D a/AB | 112 a | (88;141)a | 637 A | (602;672) A | 18 | ||
| after | C a/A | 122 a | (97;153)a | 873 B | (834;911) A | 14 | |
| Z a/A | 206 b | (163;260) a | 922 B | (858;987) A | 22 | ||
| D a/A | 182 a | (144;228) a | 947 B | (890;1004) A | 19 |
| TM | SP | ZM | m | 95%CI (m) | s | 95%CI (s) |
|---|---|---|---|---|---|---|
| Biaxial | before | C a/A | 11.2 a | (8.7;14.4) a | 791 A | (768;814) A |
| Z a/B | 9.0 a | (6.9;11.6) a | 940 A | (906;975) C | ||
| D a/B | 9.6 a | (7.1;13.1) a | 878 A | (848;908) C | ||
| after | C a/A | 12.4 a | (10.5;14.6) a,b | 1120 B | (1090;1152) B | |
| Z a/A | 12.8 a | (10.7;15.2) b | 1170 B | (1139;1202) B | ||
| D a/B | 7.3 a | (5.4;9.8) a | 1408 B | (1346;1472) B | ||
| 3-point | before | C a/A | 8.5 a | (7.0;10.4) a | 795 A | (764;827) A |
| Z a/A | 7.3 a | (5.7;9.5) a | 804 A | (768;841) B | ||
| D a/A | 9.3 a | (7.3;11.8) a | 782 A | (755;811) B | ||
| after | C b/AB | 16.5 b | (14.1;19.1) b | 1153 B | (1129;1177) B | |
| Z a/A | 8.5 a | (7.1;10.2) a,b | 1097 B | (1055;1142) A,B | ||
| D a/B | 7.9 a | (6.0;10.4) a | 1255 B | (1204:1308) B | ||
| 4-point | before | C a/A | 9.1 a | (7.4;11.1) a | 591 A | (570;614) B |
| Z a/B | 8.8 a | (7.0;11.0) a | 681 A | (656;708) A | ||
| D a/B | 7.1 a | (5.8;8.6) a | 679 A | (648;712) A | ||
| after | C a/A | 8.4 a | (6.4;11.1) a | 923 B | (888;959) A | |
| Z a/A | 5.1 a | (3.9;6.7) a | 1002 B | (940;1069) A | ||
| D a/A | 5.7 a | (4.2;7.7) a | 1023 B | (965;1084) A |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schatz, C.; Strickstrock, M.; Roos, M.; Edelhoff, D.; Eichberger, M.; Zylla, I.-M.; Stawarczyk, B. Influence of Specimen Preparation and Test Methods on the Flexural Strength Results of Monolithic Zirconia Materials. Materials 2016, 9, 180. https://doi.org/10.3390/ma9030180
Schatz C, Strickstrock M, Roos M, Edelhoff D, Eichberger M, Zylla I-M, Stawarczyk B. Influence of Specimen Preparation and Test Methods on the Flexural Strength Results of Monolithic Zirconia Materials. Materials. 2016; 9(3):180. https://doi.org/10.3390/ma9030180
Chicago/Turabian StyleSchatz, Christine, Monika Strickstrock, Malgorzata Roos, Daniel Edelhoff, Marlis Eichberger, Isabella-Maria Zylla, and Bogna Stawarczyk. 2016. "Influence of Specimen Preparation and Test Methods on the Flexural Strength Results of Monolithic Zirconia Materials" Materials 9, no. 3: 180. https://doi.org/10.3390/ma9030180
APA StyleSchatz, C., Strickstrock, M., Roos, M., Edelhoff, D., Eichberger, M., Zylla, I.-M., & Stawarczyk, B. (2016). Influence of Specimen Preparation and Test Methods on the Flexural Strength Results of Monolithic Zirconia Materials. Materials, 9(3), 180. https://doi.org/10.3390/ma9030180







