Transition Behaviors of Configurations of Colloidal Particles at a Curved Oil-Water Interface
Abstract
:1. Introduction
2. Results and Discussion
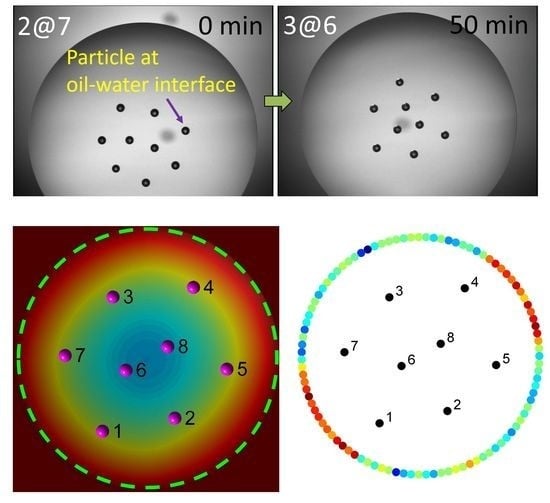
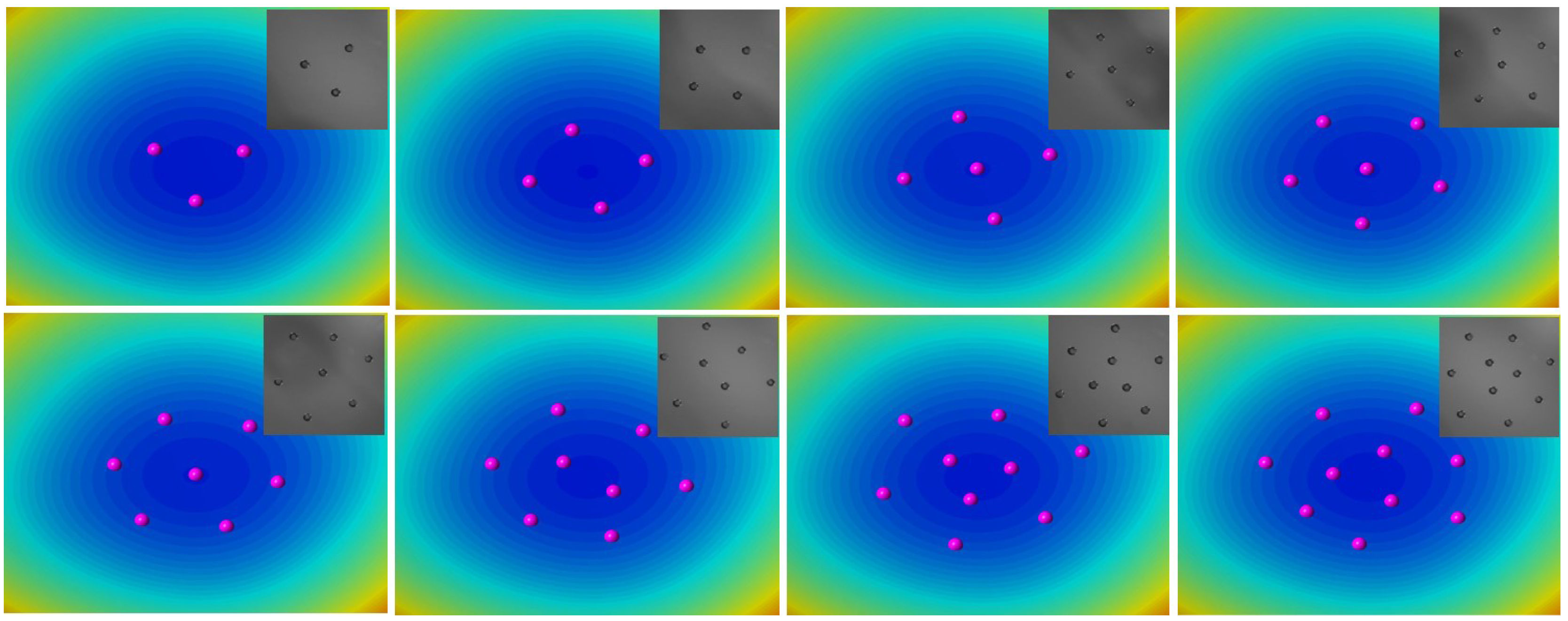
2.1. Experimental Observations of Assembly Configurations
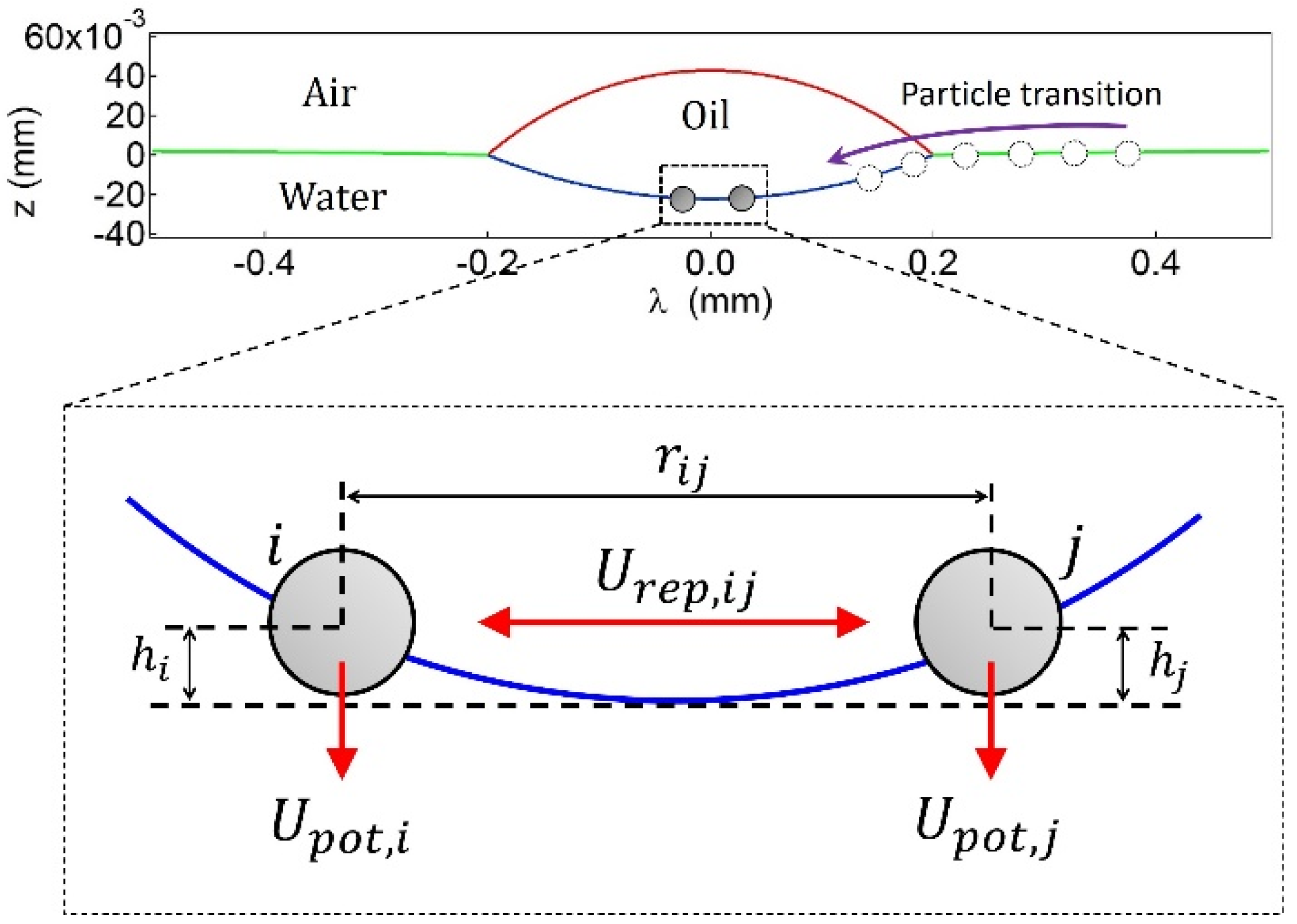
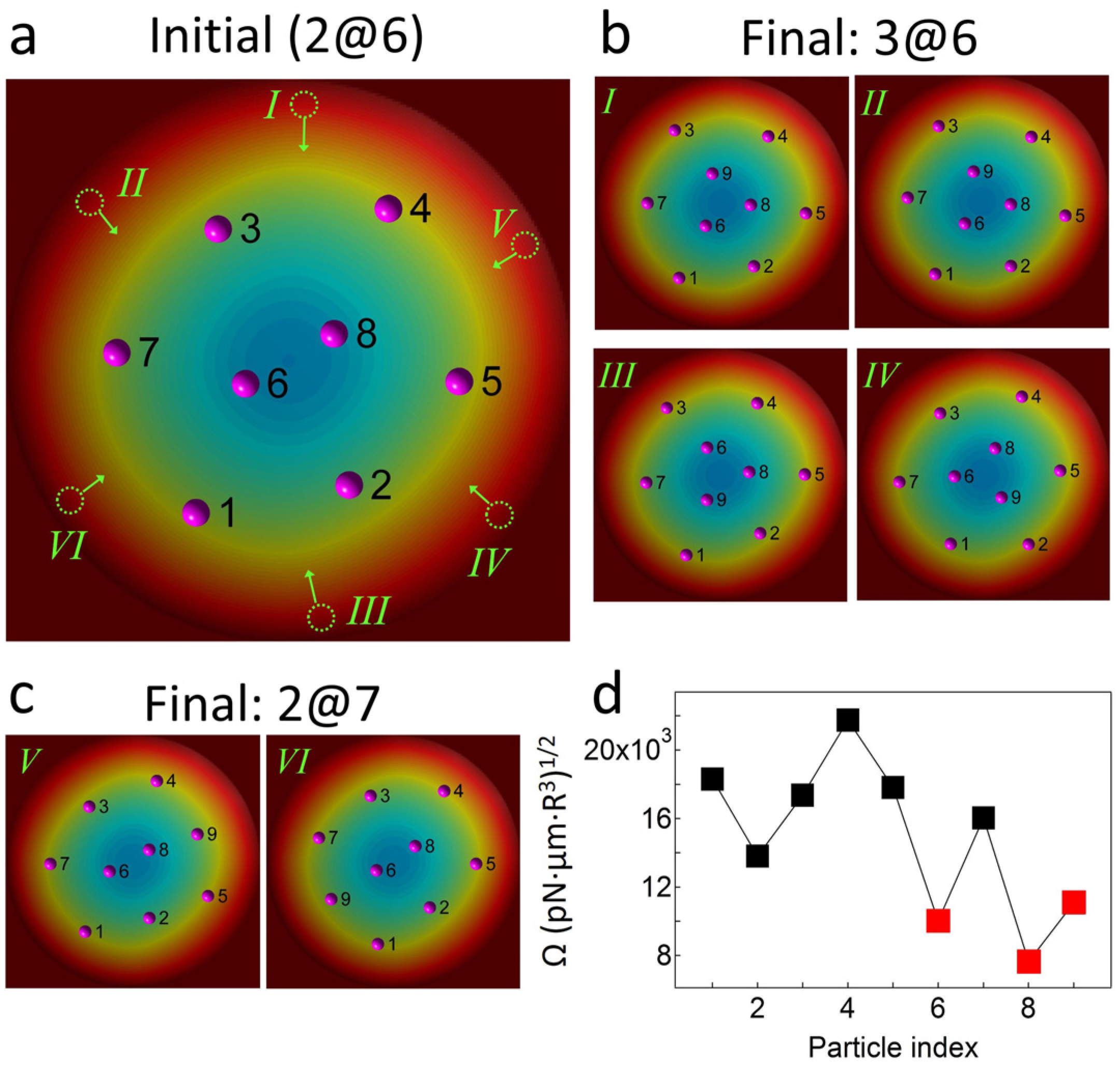
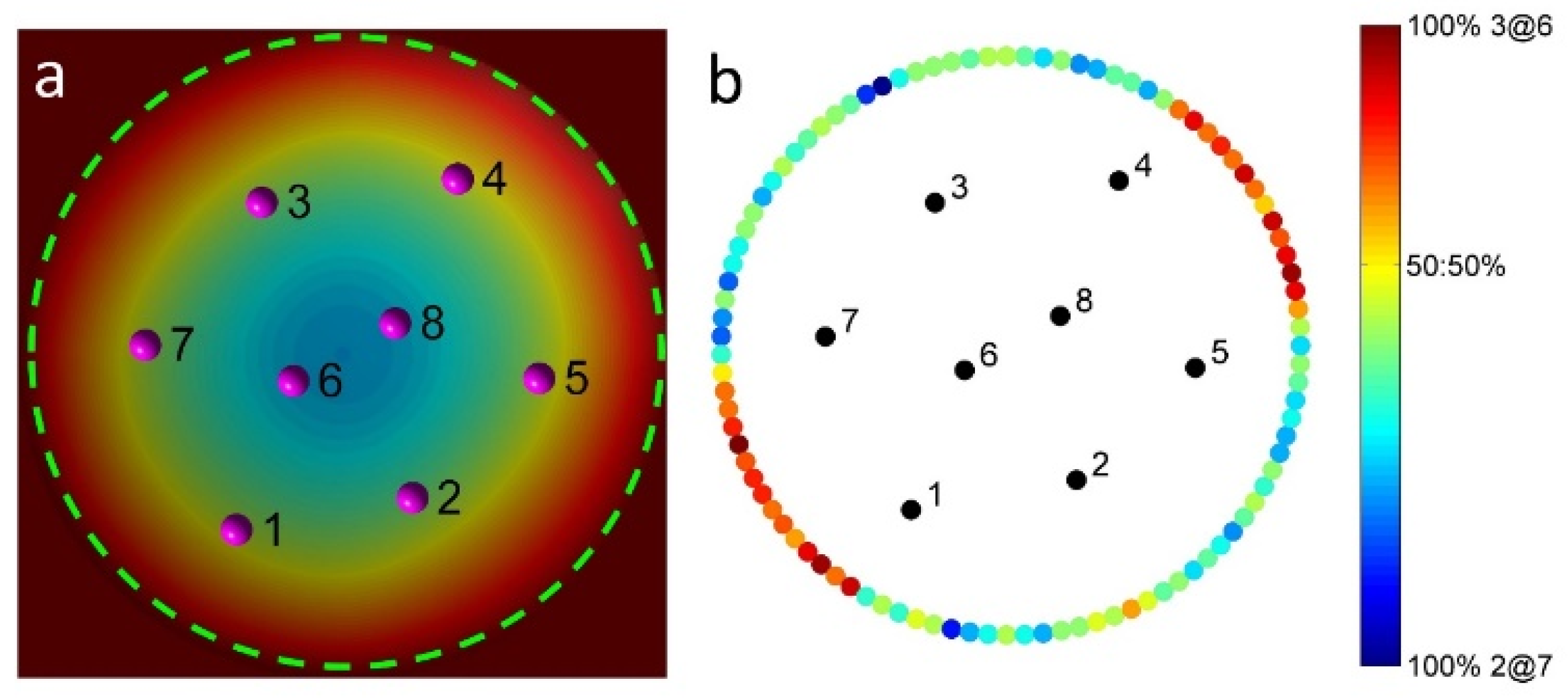
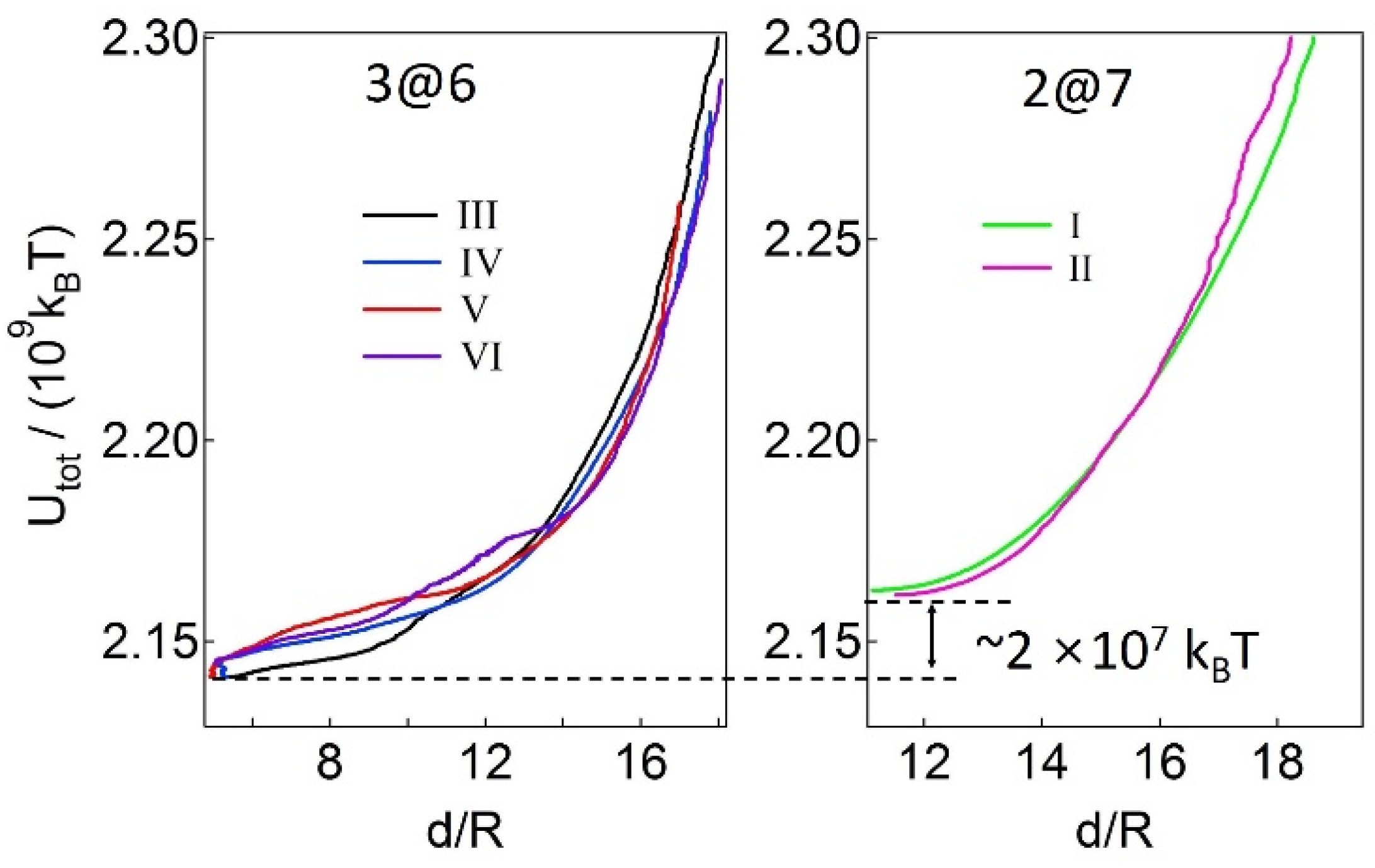
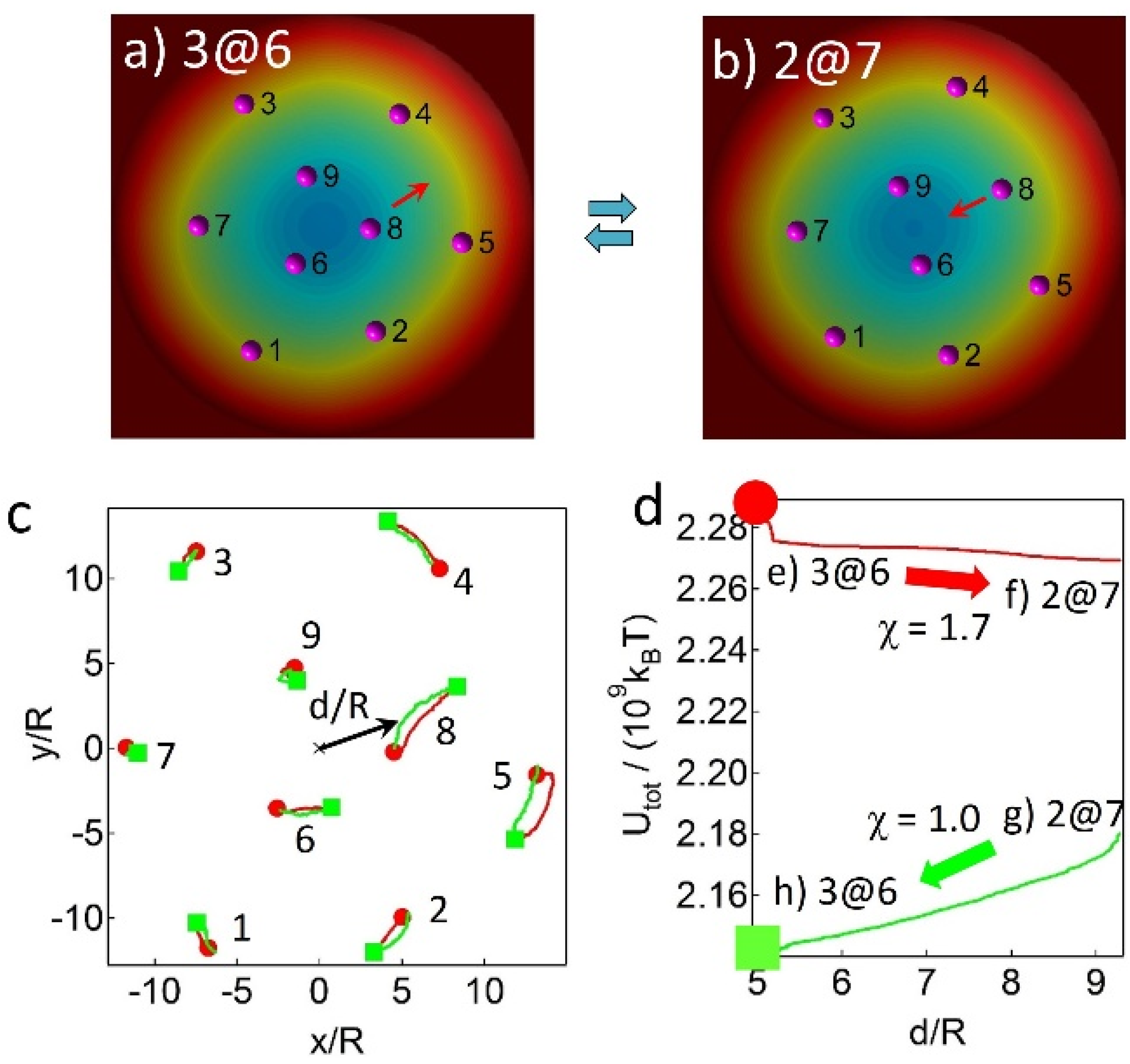
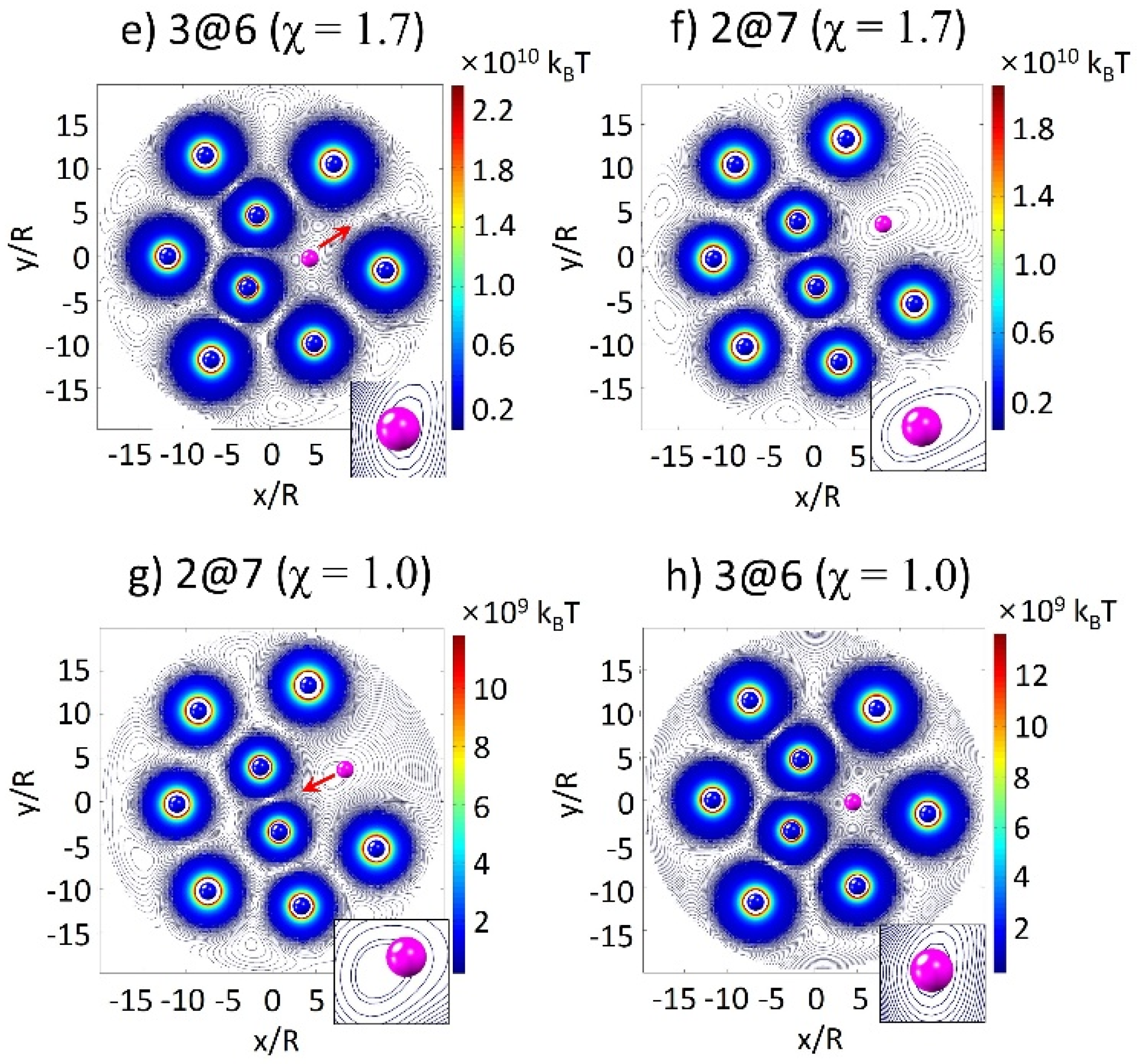
2.2. Assembly Behaviors via MC Simulations
3. Materials and Methods
3.1. Preparation of Particles
3.2. Formation of Convex Oil Lens
3.3. Particle Adsorption to the Curved Oil-Water Interface
3.4. Monte Carlo Simulation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Binks, B.P.; Horozov, T.S. Colloidal Particles at Liquid Interfaces; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Park, B.J.; Lee, D. Particles at fluid-fluid interfaces: From single-particle behavior to hierarchical assembly of materials. MRS Bulletin 2014, 39, 1089–1098. [Google Scholar] [CrossRef]
- Aveyard, R. Can Janus particles give thermodynamically stable Pickering emulsions? Soft Matter 2012, 8, 5233–5240. [Google Scholar] [CrossRef]
- Binks, B.P. Particles as surfactants-similarities and differences. Curr. Opin. Colloid Interface Sci. 2002, 7, 21–41. [Google Scholar] [CrossRef]
- Pieranski, P. Two-dimensional interfacial colloidal crystals. Phys. Rev. Lett. 1980, 45, 569–572. [Google Scholar] [CrossRef]
- Hurd, A.J. The electrostatic interaction between interfacial colloidal particles. J. Phys. A Math. Gen. 1985, 18. [Google Scholar] [CrossRef]
- Oettel, M.; Dietrich, S. Colloidal interactions at fluid interfaces. Langmuir 2008, 24, 1425–1441. [Google Scholar] [CrossRef] [PubMed]
- Aveyard, R.; Binks, B.P.; Clint, J.H.; Fletcher, P.D.; Horozov, T.S.; Neumann, B.; Paunov, V.N.; Annesley, J.; Botchway, S.W.; Nees, D.; et al. Measurement of long-range repulsive forces between charged particles at an oil-water interface. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Aveyard, R.; Clint, J.H.; Nees, D.; Paunov, V.N. Compression and structure of monolayers of charged latex particles at air/water and octane/water interfaces. Langmuir 2000, 16, 1969–1979. [Google Scholar] [CrossRef]
- Botto, L.; Lewandowski, E.P.; Cavallaro, M.; Stebe, K.J. Capillary interactions between anisotropic particles. Soft Matter 2012, 8, 9957–9971. [Google Scholar] [CrossRef]
- Cavallaro, M., Jr.; Botto, L.; Lewandowski, E.P.; Wang, M.; Stebe, K.J. Curvature-driven capillary migration and assembly of rod-like particles. Proc. Natl. Acad. Sci. USA 2011, 108, 20923–20928. [Google Scholar] [CrossRef] [PubMed]
- Danov, K.D.; Kralchevsky, P.A.; Naydenov, B.N.; Brenn, G. Interactions between particles with an undulated contact line at a fluid interface: Capillary multipoles of arbitrary order. J. Colloid Interface Sci. 2005, 287, 121–134. [Google Scholar] [CrossRef] [PubMed]
- Kralchevsky, P.A.; Nagayama, K. Capillary forces between colloidal particles. Langmuir 1994, 10, 23–36. [Google Scholar] [CrossRef]
- Lewandowski, E.P.; Cavallaro, M.; Botto, L.; Bernate, J.C.; Garbin, V.; Stebe, K.J. Orientation and self-assembly of cylindrical particles by anisotropic capillary interactions. Langmuir 2010, 26, 15142–15154. [Google Scholar] [CrossRef] [PubMed]
- Loudet, J.C.; Alsayed, A.M.; Zhang, J.; Yodh, A.G. Capillary interactions between anisotropic colloidal particles. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Madivala, B.; Fransaer, J.; Vermant, J. Self-assembly and rheology of ellipsoidal particles at interfaces. Langmuir 2009, 25, 2718–2728. [Google Scholar] [CrossRef] [PubMed]
- Park, B.J.; Lee, B.; Yu, T. Pairwise interactions of colloids in two-dimensional geometric confinement. Soft Matter 2014, 10, 9675–9680. [Google Scholar] [CrossRef] [PubMed]
- Park, B.J.; Pantina, J.P.; Furst, E.M.; Oettel, M.; Reynaert, S.; Vermant, J. Direct measurements of the effects of salt and surfactant on interaction forces between colloidal particles at water-oil interfaces. Langmuir 2008, 24, 1686–1694. [Google Scholar] [CrossRef] [PubMed]
- Ballard, N.; Bon, S.A.F. Hybrid biological spores wrapped in a mesh composed of interpenetrating polymer nanoparticles as “patchy” Pickering stabilizers. Polym. Chem. 2011, 2, 823–827. [Google Scholar] [CrossRef]
- Dinsmore, A.D.; Hsu, M.F.; Nikolaides, M.G.; Marquez, M.; Bausch, A.R.; Weitz, D.A. Colloidosomes: Selectively permeable capsules composed of colloidal particles. Science 2002, 298, 1006–1009. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-W.; Larsen, R.J.; Weitz, D.A. Synthesis of nonspherical colloidal particles with anisotropic properties. J. Am. Chem. Soc. 2006, 128, 14374–14377. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-W.; Lee, D.; Shum, H.C.; Weitz, D.A. Colloid surfactants for emulsion stabilization. Adv. Mater. 2008, 20, 3239–3243. [Google Scholar] [CrossRef]
- Park, B.J.; Lee, D. Spontaneous particle transport through a triple-fluid phase boundary. Langmuir 2013, 29, 9662–9667. [Google Scholar] [CrossRef] [PubMed]
- Pickering, S.U. Emulsions. J. Chem. Soc. Trans. 1907, 91, 2001–2021. [Google Scholar] [CrossRef]
- Ramsden, W. Separation of solids in the surface-layers of solutions and ‘suspensions’ (observations on surface-membranes, bubbles, emulsions, and mechanical coagulation).—Preliminary account. Proc. R. Soc. London 1903, 72, 156–164. [Google Scholar] [CrossRef]
- Reynaert, S.; Moldenaers, P.; Vermant, J. Control over colloidal aggregation in monolayers of latex particles at the oil-water interface. Langmuir 2006, 22, 4936–4945. [Google Scholar] [CrossRef] [PubMed]
- Stancik, E.J.; Widenbrant, M.J.O.; Laschitsch, A.T.; Vermant, J.; Fuller, G.G. Structure and dynamics of particle monolayers at a liquid-liquid interface subjected to extensional flow. Langmuir 2002, 18, 4372–4375. [Google Scholar] [CrossRef]
- Crossley, S.; Faria, J.; Shen, M.; Resasco, D.E. Solid nanoparticles that catalyze biofuel upgrade reactions at the water/oil interface. Science 2010, 327, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Park, B.J.; Vermant, J.; Furst, E.M. Heterogeneity of the electrostatic repulsion between colloids at the oil-water interface. Soft Matter 2010, 6, 5327–5333. [Google Scholar] [CrossRef]
- Lee, M.; Lee, D.; Park, B.J. Effect of interaction heterogeneity on colloidal arrangements at a curved oil-water interface. Soft Matter 2015, 11, 318–323. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Park, B.J. Heterogeneity of single-colloid self-potentials at an oil-water interface. Soft Matter 2015, 11, 8812–8817. [Google Scholar] [CrossRef] [PubMed]
- Burton, J.C.; Huisman, F.M.; Alison, P.; Rogerson, D.; Taborek, P. Experimental and numerical investigation of the equilibrium geometry of liquid lenses. Langmuir 2010, 26, 15316–15324. [Google Scholar] [CrossRef] [PubMed]
- Park, B.J.; Furst, E.M. Optical trapping forces for colloids at the oil-water interface. Langmuir 2008, 24, 13383–13392. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Meth. 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Paunov, V.N. Novel method for determining the three-phase contact angle of colloid particles adsorbed at air-water and oil-water interfaces. Langmuir 2003, 19, 7970–7976. [Google Scholar] [CrossRef]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Xia, M.; Park, B.J. Transition Behaviors of Configurations of Colloidal Particles at a Curved Oil-Water Interface. Materials 2016, 9, 138. https://doi.org/10.3390/ma9030138
Lee M, Xia M, Park BJ. Transition Behaviors of Configurations of Colloidal Particles at a Curved Oil-Water Interface. Materials. 2016; 9(3):138. https://doi.org/10.3390/ma9030138
Chicago/Turabian StyleLee, Mina, Ming Xia, and Bum Jun Park. 2016. "Transition Behaviors of Configurations of Colloidal Particles at a Curved Oil-Water Interface" Materials 9, no. 3: 138. https://doi.org/10.3390/ma9030138
APA StyleLee, M., Xia, M., & Park, B. J. (2016). Transition Behaviors of Configurations of Colloidal Particles at a Curved Oil-Water Interface. Materials, 9(3), 138. https://doi.org/10.3390/ma9030138