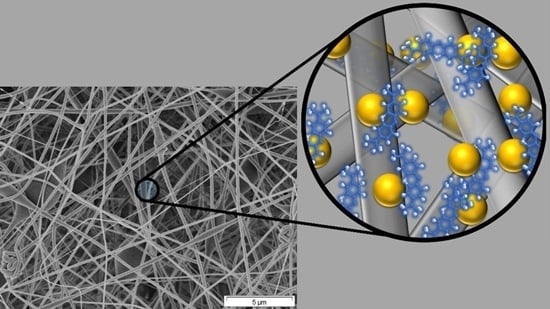
A Novel Nanohybrid Nanofibrous Adsorbent for Water Purification from Dye Pollutants
Abstract
:1. Introduction
2. Results and Discussion
2.1. Physicochemical Characteristics of the Nanofibrous Adsorbents
2.2. Structural Characteristics of the Nanofibrous Adsorbents
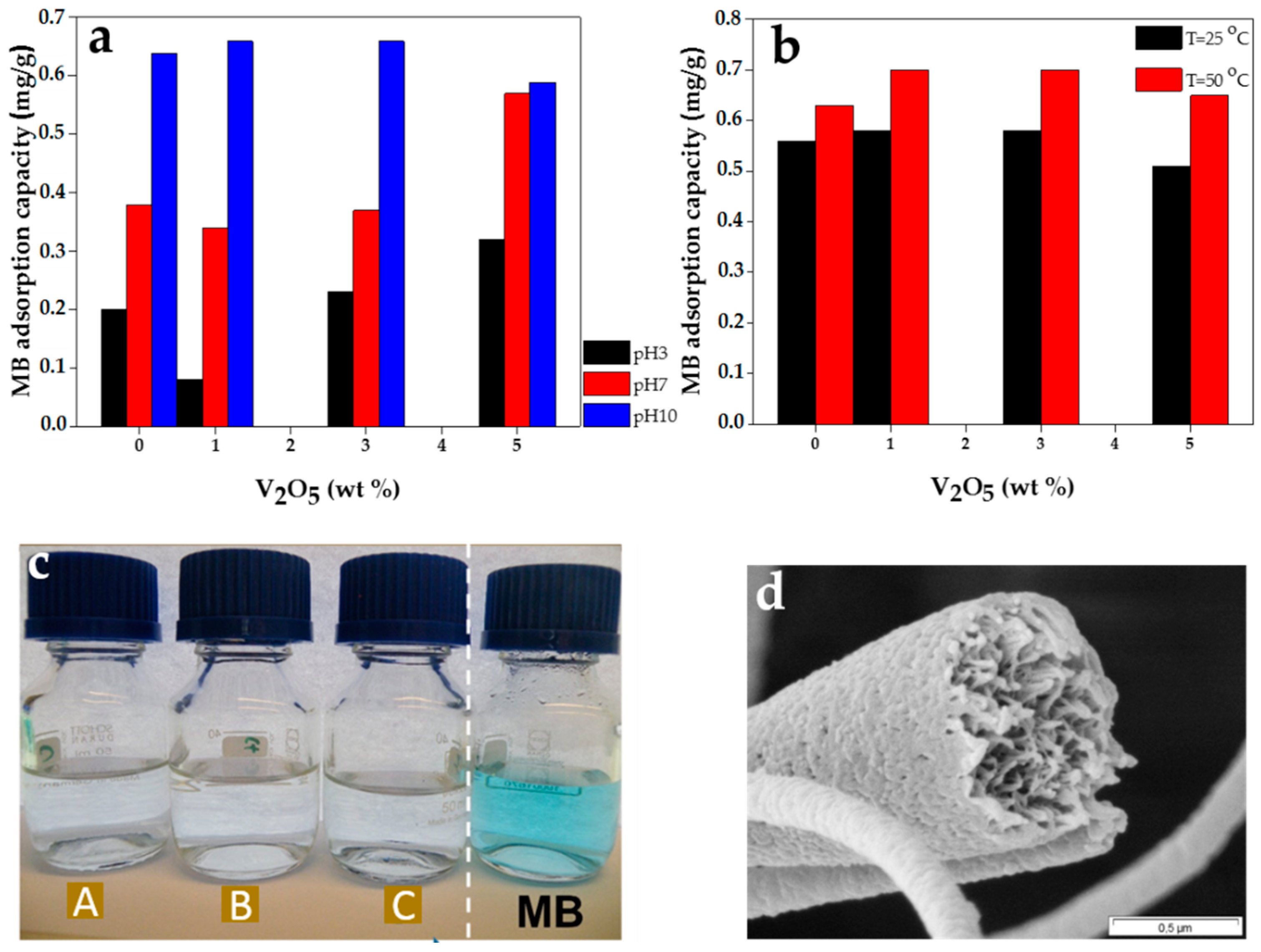
2.3. Dye Removal Capacity of The Nanofibrous Adsorbent
2.3.1. Effect of pH on Dye Removal
2.3.2. Effect of Filler Concentration on Dye Removal
2.3.3. Effect of Temperature on Dye Removal
2.4. Adsorption Thermodynamics
2.5. Adsorption Kinetics
2.6. Adsorption Isotherms
3. Materials and Methods
3.1. Materials
3.2. Preparation of the Nanofibrous Adsorbents
3.3. Characterization of the Physicochemical Properties
3.4. Characterization of the Structural Properties
3.5. Characterization of the Dye Removal Efficiency
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saravanan, R.; Karthikeyan, N.; Gupta, V.K.; Thirumal, E.; Thangadurai, P.; Narayanan, V.; Stephen, A. ZnO/Ag nanocomposite: An efficient catalyst for degradation studies of textile effluents under visible light. Mater. Sci. Eng. C 2013, 33, 2235–2244. [Google Scholar] [CrossRef] [PubMed]
- Homaeigohar, S.; Dai, T.; Elbahri, M. Biofunctionalized nanofibrous membranes as super separators of protein and enzyme from water. J.Colloid Interface Sci. 2013, 406, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Janaki, V.; Oh, B.-T.; Shanthi, K.; Lee, K.-J.; Ramasamy, A.K.; Kamala-Kannan, S. Polyaniline/chitosan composite: An eco-friendly polymer for enhanced removal of dyes from aqueous solution. Synth. Met. 2012, 162, 974–980. [Google Scholar] [CrossRef]
- Raghuvanshi, S.; Singh, R.; Kaushik, C.; Raghav, A. Kinetics study of methylene blue dye bioadsorption on baggase. Appl. Ecol. Environ. Res. 2004, 2, 35–43. [Google Scholar] [CrossRef]
- Konstantinou, I.K.; Albanis, T.A. TiO2-assisted photocatalytic degradation of azo dyes in aqueous solution: Kinetic and mechanistic investigations: A review. Appl. Catal. B Environ. 2004, 49, 1–14. [Google Scholar] [CrossRef]
- Gupta, V.K.; Suhas. Application of low-cost adsorbents for dye removal—A review. J. Environ. Manag. 2009, 90, 2313–2342. [Google Scholar] [CrossRef] [PubMed]
- Scalese, S.; Nicotera, I.; D’Angelo, D.; Filice, S.; Libertino, S.; Simari, C.; Dimos, K.; Privitera, V. Cationic and anionic azo-dye removal from water by sulfonated graphene oxide nanosheets in Nafion membranes. New J. Chem. 2016, 40, 3654–3663. [Google Scholar] [CrossRef]
- Xiao, J.; Lv, W.; Xie, Z.; Tan, Y.; Song, Y.; Zheng, Q. Environmentally friendly reduced graphene oxide as a broad-spectrum adsorbent for anionic and cationic dyes via π-π interactions. J. Mater. Chem. A 2016, 4, 12126–12135. [Google Scholar] [CrossRef]
- Umoren, S.; Etim, U.; Israel, A. Adsorption of methylene blue from industrial effluent using poly (vinyl alcohol). J. Mater. Environ. Sci. 2013, 4, 75–86. [Google Scholar]
- Valderrama, C.; Gamisans, X.; De las Heras, F.; Cortina, J.; Farran, A. Kinetics of polycyclic aromatic hydrocarbons removal using hyper-cross-linked polymeric sorbents Macronet Hypersol MN200. React. Funct. Polym. 2007, 67, 1515–1529. [Google Scholar] [CrossRef]
- Gezici, O.; Küçükosmanoğlu, M.; Ayar, A. The adsorption behavior of crystal violet in functionalized sporopollenin-mediated column arrangements. J. Colloid Interface Sci. 2006, 304, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Malana, M.A.; Ijaz, S.; Ashiq, M.N. Removal of various dyes from aqueous media onto polymeric gels by adsorption process: Their kinetics and thermodynamics. Desalination 2010, 263, 249–257. [Google Scholar] [CrossRef]
- Crini, G. Kinetic and equilibrium studies on the removal of cationic dyes from aqueous solution by adsorption onto a cyclodextrin polymer. Dyes Pigments 2008, 77, 415–426. [Google Scholar] [CrossRef]
- Dhodapkar, R.; Rao, N.; Pande, S.; Kaul, S. Removal of basic dyes from aqueous medium using a novel polymer: Jalshakti. Bioresour. Technol. 2006, 97, 877–885. [Google Scholar] [CrossRef] [PubMed]
- Homaeigohar, S.; Buhr, K.; Ebert, K. Polyethersulfone electrsopun nanofibrous composite membrane for liquid filtration. J. Membr. Sci. 2010, 365, 68–77. [Google Scholar] [CrossRef]
- Pontié, M.; Chasseray, X.; Lemordant, D.; Laine, J. The streaming potential method for the characterization of ultrafiltration organic membranes and the control of cleaning treatments. J. Membr. Sci. 1997, 129, 125–133. [Google Scholar] [CrossRef]
- Ricq, L.; Pierre, A.; Bayle, S.; Reggiani, J.-C. Electrokinetic characterization of polyethersulfone UF membranes. Desalination 1997, 109, 253–261. [Google Scholar] [CrossRef]
- Krishnamoorthy, R.; Sagadevan, V. Polyethylene glycol and iron oxide nanoparticles blended polyethersulfone ultrafiltration membrane for enhanced performance in dye removal studies. e-Polymers 2015, 15, 151–159. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Sun, C.; Ji, H.; Zhao, W.; Sun, S.; Zhao, C. Graphene oxide-based polymeric membranes for broad water pollutant removal. RSC Adv. 2015, 5, 100651–100662. [Google Scholar] [CrossRef]
- Lin, C.-H.; Gung, C.-H.; Sun, J.-J.; Suen, S.-Y. Preparation of polyethersulfone/plant-waste-particles mixed matrix membranes for adsorptive removal of cationic dyes from water. J. Membr. Sci. 2014, 471, 285–298. [Google Scholar] [CrossRef]
- Lala, N.L.; Jose, R.; Yusoff, M.M.; Ramakrishna, S. Continuous tubular nanofibers of vanadium pentoxide by electrospinning for energy storage devices. J. Nanopart. Res. 2012, 14, 1–9. [Google Scholar] [CrossRef]
- Im, J.S.; Kwon, O.; Kim, Y.H.; Park, S.-J.; Lee, Y.-S. The effect of embedded vanadium catalyst on activated electrospun CFs for hydrogen storage. Microporous Mesoporous Mater. 2008, 115, 514–521. [Google Scholar] [CrossRef]
- Huang, J.-S.; Chou, C.-Y.; Liu, M.-Y.; Tsai, K.-H.; Lin, W.-H.; Lin, C.-F. Solution-processed vanadium oxide as an anode interlayer for inverted polymer solar cells hybridized with ZnO nanorods. Org. Electron. 2009, 10, 1060–1065. [Google Scholar] [CrossRef]
- Dhayal Raj, A.; Pazhanivel, T.; Suresh Kumar, P.; Mangalaraj, D.; Nataraj, D.; Ponpandian, N. Self assembled V2O5 nanorods for gas sensors. Curr. Appl. Phys. 2010, 10, 531–537. [Google Scholar] [CrossRef]
- Ban, C.; Chernova, N.A.; Whittingham, M.S. Electrospun nano-vanadium pentoxide cathode. Electrochem. Commun. 2009, 11, 522–525. [Google Scholar] [CrossRef]
- Jin, A.; Chen, W.; Zhu, Q.; Jian, Z. Multi-electrochromism behavior and electrochromic mechanism of electrodeposited molybdenum doped vanadium pentoxide films. Electrochim. Acta 2010, 55, 6408–6414. [Google Scholar] [CrossRef]
- González, G.; Saraiva, S.M.; Aliaga, W. Isoelectric points for niobium and vanadium pentoxides. J. Dispers. Sci. Technol. 1994, 15, 249–249. [Google Scholar] [CrossRef]
- Avansi, W.; de Mendonça, V.R.; Lopes, O.F.; Ribeiro, C. Vanadium pentoxide 1-D nanostructures applied to dye removal from aqueous systems by coupling adsorption and visible-light photodegradation. RSC Adv. 2015, 5, 12000–12006. [Google Scholar] [CrossRef]
- Özer, N. Electrochemical properties of sol-gel deposited vanadium pentoxide films. Thin Solid Films 1997, 305, 80–87. [Google Scholar] [CrossRef]
- Homaeigohar, S.; Mahdavi, H.; Elbahri, M. Extraordinarily water permeable sol gel formed nanocomposite nanofibrous membranes. J. Colloid Interface Sci. 2012, 366, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Banfield, J.F. Kinetics of crystallization and crystal growth of nanocrystalline anatase in nanometer-sized amorphous titania. Chem. Mater. 2002, 14, 4145–4154. [Google Scholar] [CrossRef]
- Homaeigohar, S.S.; Elbahri, M. Novel compaction resistant and ductile nanocomposite nanofibrous microfiltration membranes. J. Colloid Interface Sci. 2012, 372, 6–15. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.M.; Zhang, Y.Z.; Kotaki, M.; Ramakrishna, S. A review on polymer nanofibers by electrospinning and their applications in nanocomposites. Compos. Sci. Technol. 2003, 63, 2223–2253. [Google Scholar] [CrossRef]
- Deitzel, J.; Kleinmeyer, J.; Harris, D.; Beck Tan, N. The effect of processing variables on the morphology of electrospun nanofibers and textiles. Polymer 2001, 42, 261–272. [Google Scholar] [CrossRef]
- Fong, H.; Chun, I.; Reneker, D. Beaded nanofibers formed during electrospinning. Polymer 1999, 40, 4585–4592. [Google Scholar] [CrossRef]
- Yu, D.; Chen, C.; Xie, S.; Liu, Y.; Park, K.; Zhou, X.; Zhang, Q.; Li, J.; Cao, G. Mesoporous vanadium pentoxide nanofibers with significantly enhanced Li-ion storage properties by electrospinning. Energy Environ. Sci. 2011, 4, 858–861. [Google Scholar] [CrossRef]
- Han, T.; Yarin, A.L.; Reneker, D.H. Viscoelastic electrospun jets: Initial stresses and elongational rheometry. Polymer 2008, 49, 1651–1658. [Google Scholar] [CrossRef]
- Belfer, S.; Fainchtain, R.; Purinson, Y.; Kedem, O. Surface characterization by FTIR-ATR spectroscopy of polyethersulfone membranes-unmodified, modified and protein fouled. J. Membr. Sci. 2000, 172, 113–124. [Google Scholar] [CrossRef]
- Luo, M.L.; Tang, W.; Zhao, J.Q.; Pu, C. Hydrophilic modification of poly(ether sulfone) used TiO2 nanoparticles by a sol–gel process. J. Mater. Process. Technol. 2006, 172, 431–436. [Google Scholar] [CrossRef]
- Croce, F.; Persi, L.; Scrosati, B.; Serraino-Fiory, F.; Plichta, E.; Hendrickson, M. Role of the ceramic fillers in enhancing the transport properties of composite polymer electrolytes. Electrochim. Acta 2001, 46, 2457–2461. [Google Scholar] [CrossRef]
- Novak, B.M. Hybrid Nanocomposite Materials—Between inorganic glasses and organic polymers. Adv. Mater. 1993, 5, 422–433. [Google Scholar] [CrossRef]
- Li, J.F.; Xu, Z.L.; Yang, H.; Yu, L.Y.; Liu, M. Effect of TiO2 nanoparticles on the surface morphology and performance of microporous PES membrane. Appl. Surf. Sci. 2009, 255, 4725–4732. [Google Scholar] [CrossRef]
- Meng, X.; Luo, N.; Cao, S.; Zhang, S.; Yang, M.; Hu, X. In-situ growth of titania nanoparticles in electrospun polymer nanofibers at low temperature. Mater. Lett. 2009, 63, 1401–1403. [Google Scholar] [CrossRef]
- Bae, T.H.; Kim, I.C.; Tak, T.M. Preparation and characterization of fouling-resistant TiO2 self-assembled nanocomposite membranes. J. Membr. Sci. 2006, 275, 1–5. [Google Scholar] [CrossRef]
- Wu, G.P.; Gan, S.Y.; Cui, L.Z.; Xu, Y.Y. Preparation and characterization of PES/TiO2 composite membranes. Appl. Surf. Sci. 2008, 254, 7080–7086. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Jose, R.; Archana, P.S.; Nair, A.S.; Balamurugan, R.; Venugopal, J.; Teo, W.E. Science and engineering of electrospun nanofibers for advances in clean energy, water filtration, and regenerative medicine. J. Mater. Sci. 2010, 45, 6283–6312. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Vandecasteele, C.; Van Gestel, T.; Doyen, W.; Leysen, R. A Review of pressure-driven membrane processes in wastewater treatment and drinking water production. Environ. Prog. 2003, 22, 46–56. [Google Scholar] [CrossRef]
- Yoon, K.; Kim, K.; Wang, X.; Fang, D.; Hsiao, B.S.; Chu, B. High flux ultrafiltration membranes based on electrospun nanofibrous PAN scaffolds and chitosan coating. Polymer 2006, 47, 2434–2441. [Google Scholar] [CrossRef]
- Sivakumar, S.; Senthilkumar, P.; Subburam, V. Carbon from cassava peel, an agricultural waste, as an adsorbent in the removal of dyes and metal ions from aqueous solution. Bioresour. Technol. 2001, 80, 233–235. [Google Scholar]
- Doğan, M.; Alkan, M.; Türkyilmaz, A.; Özdemir, Y. Kinetics and mechanism of removal of methylene blue by adsorption onto perlite. J. Hazard. Mater. 2004, 109, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Crini, G.; Peindy, H.N.; Gimbert, F.; Robert, C. Removal of CI Basic Green 4 (Malachite Green) from aqueous solutions by adsorption using cyclodextrin-based adsorbent: Kinetic and equilibrium studies. Sep. Purif. Technol. 2007, 53, 97–110. [Google Scholar] [CrossRef]
- Acemioğlu, B. Adsorption of Congo red from aqueous solution onto calcium-rich fly ash. J. Colloid Interface Sci. 2004, 274, 371–379. [Google Scholar] [CrossRef] [PubMed]
- Asfour, H.; Fadali, O.; Nassar, M.; El-Geundi, M. Equilibrium studies on adsorption of basic dyes on hardwood. J. Chem. Technol. Biotechnol. Chem. Technol. 1985, 35, 21–27. [Google Scholar] [CrossRef]
- Doğan, M.; Alkan, M.; Onganer, Y. Adsorption of methylene blue from aqueous solution onto perlite. Water Air Soil Pollut. 2000, 120, 229–248. [Google Scholar] [CrossRef]
- Uçar, B.; Güvenç, A.; Mehmetoglu, Ü. Use of aluminium hydroxide sludge as adsorbents for the removal of reactive dyes: Equilibrium, thermodynamic, and kinetic studies. Hydrol. Curr. Res. 2011, 112. [Google Scholar] [CrossRef]
- Kothiyal, N.C.; Sharma, S. Study of chromium (VI) adsorption using pterospermumacerifolium fruit capsule activated carbon (FCAC) and commercial activated charcoal (CAC) as a selective adsorbents. Holist. Approach Environ. 2013, 3, 63–82. [Google Scholar]
- Namasivayam, C.; Kavitha, D. Removal of Congo Red from water by adsorption onto activated carbon prepared from coir pith, an agricultural solid waste. Dyes Pigments 2002, 54, 47–58. [Google Scholar] [CrossRef]
- Al-Degs, Y.S.; El-Barghouthi, M.I.; El-Sheikh, A.H.; Walker, G.M. Effect of solution pH, ionic strength, and temperature on adsorption behavior of reactive dyes on activated carbon. Dyes Pigments 2008, 77, 16–23. [Google Scholar] [CrossRef]
- Bulut, Y.; Aydın, H. A kinetics and thermodynamics study of methylene blue adsorption on wheat shells. Desalination 2006, 194, 259–267. [Google Scholar] [CrossRef]
- Ho, Y.; McKay, G. The sorption of lead (II) ions on peat. Water Res. 1999, 33, 578–584. [Google Scholar] [CrossRef]
- Ho, Y.-S.; McKay, G. Pseudo-second order model for sorption processes. Process. Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Aksu, Z.; Tezer, S. Equilibrium and kinetic modelling of biosorption of Remazol Black B by Rhizopus arrhizus in a batch system: Effect of temperature. Process. Biochem. 2000, 36, 431–439. [Google Scholar] [CrossRef]
- Aksu, Z. Biosorption of reactive dyes by dried activated sludge: Equilibrium and kinetic modelling. Biochem. Eng. J. 2001, 7, 79–84. [Google Scholar] [CrossRef]
- Na, H.; Zhao, Y.; Liu, X.; Zhao, C.; Yuan, X. Structure and properties of electrospun poly(vinylidene fluoride)/polycarbonate membranes after hot-press. J. Appl. Polym. Sci. 2011, 122, 774–781. [Google Scholar] [CrossRef]



| The Nanofiller Amount | Thermal Decomposition Temperature (°C) | Residual Mass (%) |
|---|---|---|
| 0 wt % | 466 | 1.7 |
| 1 wt % | 493 | 3.5 |
| 3 wt % | 486 | 4.3 |
| 5 wt % | 478 | 7.4 |
| Temperature (°C) | Kc,25°C | Kc,50°C | ΔG0 (kJ/mol), 25 °C | ΔG0 (kJ/mol), 50 °C | ΔH0 (kJ/mol), 25 °C | ΔH0 (kJ/mol), 50 °C | ΔS0 (kJ/mol), 25 °C | ΔS0 (kJ/mol), 50 °C |
|---|---|---|---|---|---|---|---|---|
| PES (pH3) | 0.267 | 0.31 | 3.27 | 3.14 | 0.005 | 0.005 | 0.005 | 0.005 |
| PES (pH7) | 0.153 | 0.32 | 5.04 | 3.14 | 0.025 | 0.025 | 0.06 | 0.06 |
| PES (pH10) | 1.72 | 3.43 | −1.343 | −3.30 | 0.023 | 0.023 | 0.08 | 0.08 |
| 1 wt % V2O5/PES (pH3) | 0.1 | 0.29 | 5.7 | 3.32 | 0.03 | 0.03 | 0.1 | 0.1 |
| 1 wt % V2O5/PES (pH7) | 0.1 | 0.3 | 5.7 | 3.32 | 0.03 | 0.03 | 0.1 | 0.1 |
| 1 wt % V2O5/PES (pH10) | 1.81 | 4.38 | −1.47 | −3.96 | 0.03 | 0.03 | 0.1 | 0.1 |
| 3 wt % V2O5/PES (pH3) | 0.33 | 0.475 | 2.74 | 2 | 0.01 | 0.01 | 0.03 | 0.03 |
| 3 wt % V2O5/PES (pH7) | 0.135 | 0.184 | 5 | 4.54 | 0.01 | 0.01 | 0.02 | 0.02 |
| 3 wt % V2O5/PES (pH10) | 1.705 | 3.1 | −1.32 | −3.04 | 0.02 | 0.02 | 0.07 | 0.07 |
| 5 wt % V2O5/PES (pH3) | 0.607 | 0.87 | 1.23 | 0.373 | 0.01 | 0.01 | 0.03 | 0.03 |
| 5 wt % V2O5/PES (pH7) | 0.525 | 1.02 | 1.6 | −0.053 | 0.02 | 0.02 | 0.07 | 0.07 |
| 5 wt % V2O5/PES (pH10) | 1.5 | 3.31 | −1 | −3.21 | 0.03 | 0.03 | 0.09 | 0.09 |
| Parameter | 1st Order | Kinetic | Model | 2nd Order | Kinetic | Model | |
|---|---|---|---|---|---|---|---|
| qe (exp) (mg/g) | K1 (1/min) | qe (cal) (mg/g) | r2 | K1 (1/min) | qe (cal) (mg/g) | r2 | |
| PES, pH3, T = 25 °C | 0.19 | 0.002 | 0.145 | −0.38 | 0.014 | 0.24 | 0.93 |
| PES, pH7, T = 25 °C | 0.12 | 0.002 | 0.042 | −0.395 | 0.1 | 0.127 | 0.99 |
| PES, pH10, T = 25 °C | 0.57 | 0 | 0.15 | −1 | 0.02 | 0.61 | 0.98 |
| PES, pH3, T = 50 °C | 0.202 | 0.001 | 0.25 | 0.7 | 0.002 | 0.41 | 0.55 |
| PES, pH7, T = 50 °C | 0.206 | 0.001 | 0.134 | 0.9 | 0.01 | 0.29 | 0.91 |
| PES, pH10, T = 50 °C | 0.658 | 0.002 | 0.4 | 0.98 | 0.008 | 0.75 | 0.99 |
| 1 wt % V2O5/PES, pH3, T = 25 °C | 0.08 | 0 | 0.046 | −0.99 | 0.02 | 0.11 | 0.66 |
| 1 wt % V2O5/PES, pH7, T = 25 °C | 0.08 | 0.009 | 0.09 | 0.56 | 0.1 | 0.08 | 0.98 |
| 1 wt %V2O5/PES, pH10, T = 25 °C | 0.58 | 0.005 | 0.467 | 0.67 | 0.013 | 0.64 | 0.99 |
| 1 wt % V2O5/PES, pH3, T = 50 °C | 0.2 | 0.002 | 0.275 | 0.93 | 0.002 | 0.4 | 0.55 |
| 1 wt % V2O5/PES, pH7, T = 50 °C | 0.196 | 0.002 | 0.144 | 0.99 | 0.016 | 0.245 | 0.99 |
| 1 wt %V2O5/PES, pH10, T = 50 °C | 0.692 | 0.003 | 0.436 | 0.99 | 0.01 | 0.763 | 0.99 |
| 3 wt % V2O5/PES, pH3, T = 25 °C | 0.23 | 0.005 | 0.275 | 0.98 | 0.01 | 0.284 | 0.99 |
| 3 wt % V2O5/PES, pH7, T = 25 °C | 0.11 | 0.008 | 0.206 | 0.95 | 0.027 | 0.14 | 0.87 |
| 3 wt %V2O5/PES, pH10, T = 25 °C | 0.58 | 0.002 | 0.363 | 0.98 | 0.012 | 0.63 | 0.99 |
| 3 wt % V2O5/PES, pH3, T = 50 °C | 0.29 | 0.005 | 0.34 | 0.97 | 0.013 | 0.35 | 0.99 |
| 3 wt % V2O5/PES, pH7, T = 50 °C | 0.14 | 0.001 | 0.151 | 0.7 | - | - | −0.43 |
| 3 wt %V2O5/PES, pH10, T = 50 °C | 0.68 | 0.003 | 0.575 | 0.95 | 0.006 | 0.8 | 0.99 |
| 5 wt % V2O5/PES, pH3, T = 25 °C | 0.34 | 0.002 | 0.267 | 0.182 | 0.012 | 0.4 | 0.98 |
| 5 wt % V2O5/PES, pH7, T = 25 °C | 0.31 | 0.005 | 0.354 | 0.71 | 0.009 | 0.39 | 0.91 |
| 5 wt %V2O5/PES, pH10, T = 25 °C | 0.54 | 0.002 | 0.316 | −0.4 | 0.01 | 0.61 | 0.98 |
| 5 wt % V2O5/PES, pH3, T = 50 °C | 0.4 | 0.002 | 0.301 | 0.98 | 0.008 | 0.5 | 0.98 |
| 5 wt % V2O5/PES, pH7, T = 50 °C | 0.43 | 0.002 | 0.301 | 0.97 | 0.004 | 0.53 | 0.98 |
| 5 wt %V2O5/PES, pH10, T = 50 °C | 0.65 | 0.002 | 0.371 | 0.98 | 0.01 | 0.71 | 0.99 |
| Kf (mg/g) | 1/n (L/g) | r2 | |
|---|---|---|---|
| T = 25 °C, pH3 | 0.05 | 3.70 | 0.82 |
| T = 50 °C, pH3 | 0.1 | 1.75 | 0.80 |
| T = 25 °C, pH7 | 0.05 | 3.70 | 0.94 |
| T = 50 °C, pH7 | 0.1 | 1.85 | 0.99 |
| T = 25 °C, pH10 | 0.3 | 0.6 | 0.57 |
| T = 50 °C, pH10 | 0.6 | 0.1 | 0.21 |
| Electrospinning Conditions | PES | V2O5 Precursor/PVP | V2O5/PES |
|---|---|---|---|
| Voltage (kV) | 20 | 17 | 30 |
| Spinning distance (cm) | 20 | 25 | 20 |
| Collector | Al foil | Al foil | Al foil |
| Feed rate (mL/h) | 0.5 | 0.5 | 3 |
| Polymer concentration (wt %) | 20 | 10 | 21 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Homaeigohar, S.; Zillohu, A.U.; Abdelaziz, R.; Hedayati, M.K.; Elbahri, M. A Novel Nanohybrid Nanofibrous Adsorbent for Water Purification from Dye Pollutants. Materials 2016, 9, 848. https://doi.org/10.3390/ma9100848
Homaeigohar S, Zillohu AU, Abdelaziz R, Hedayati MK, Elbahri M. A Novel Nanohybrid Nanofibrous Adsorbent for Water Purification from Dye Pollutants. Materials. 2016; 9(10):848. https://doi.org/10.3390/ma9100848
Chicago/Turabian StyleHomaeigohar, Shahin, Ahnaf Usman Zillohu, Ramzy Abdelaziz, Mehdi Keshavarz Hedayati, and Mady Elbahri. 2016. "A Novel Nanohybrid Nanofibrous Adsorbent for Water Purification from Dye Pollutants" Materials 9, no. 10: 848. https://doi.org/10.3390/ma9100848
APA StyleHomaeigohar, S., Zillohu, A. U., Abdelaziz, R., Hedayati, M. K., & Elbahri, M. (2016). A Novel Nanohybrid Nanofibrous Adsorbent for Water Purification from Dye Pollutants. Materials, 9(10), 848. https://doi.org/10.3390/ma9100848