Influence of Wind Pressure on the Carbonation of Concrete
Abstract
:1. Introduction
2. Mass Transfer of Carbon Dioxide in Concrete
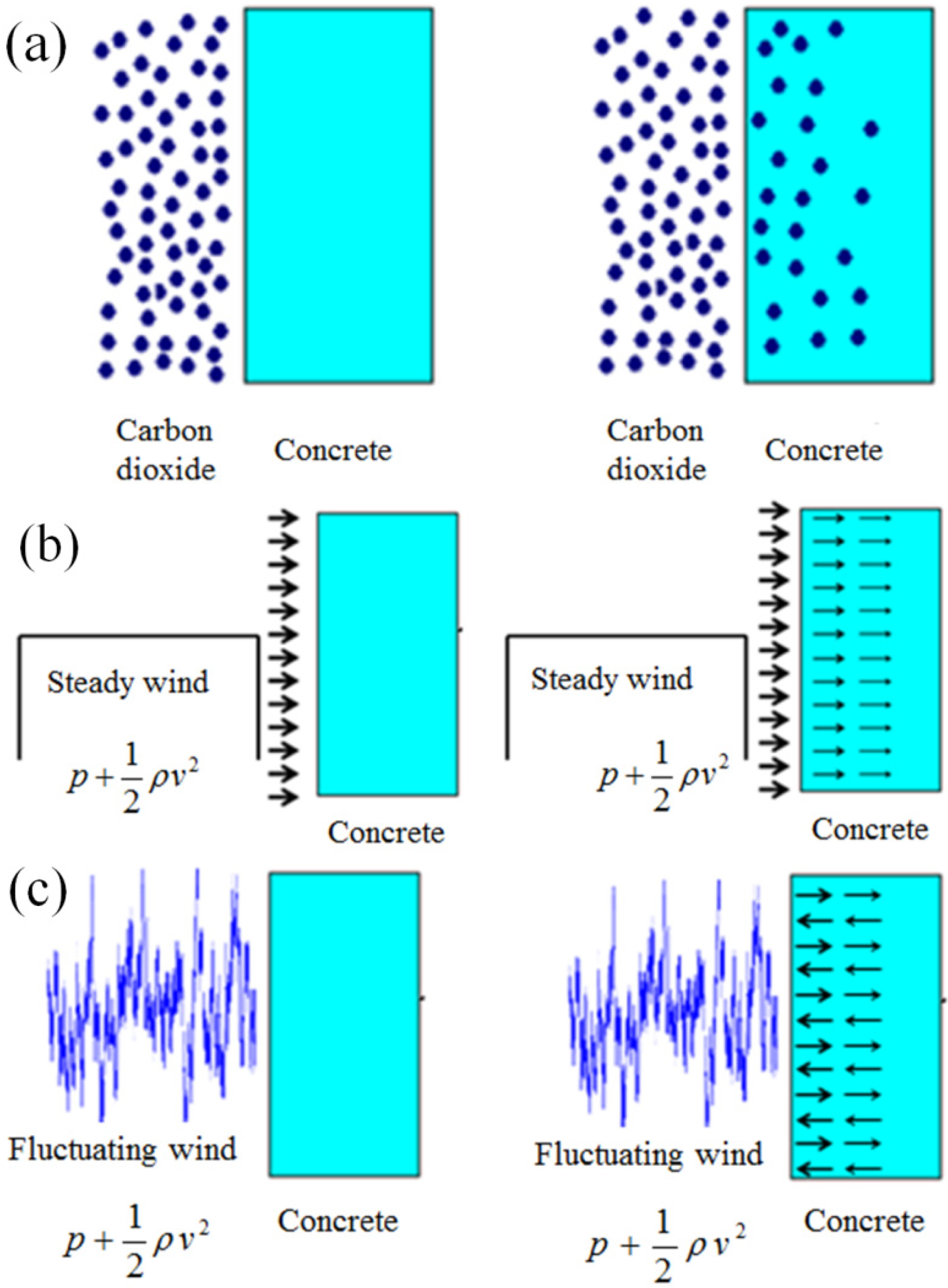
2.1. Carbon Dioxide Diffusion Process
2.2. Carbon Dioxide Penetration Process
2.2.1. Governing Equations of Penetration-Reaction
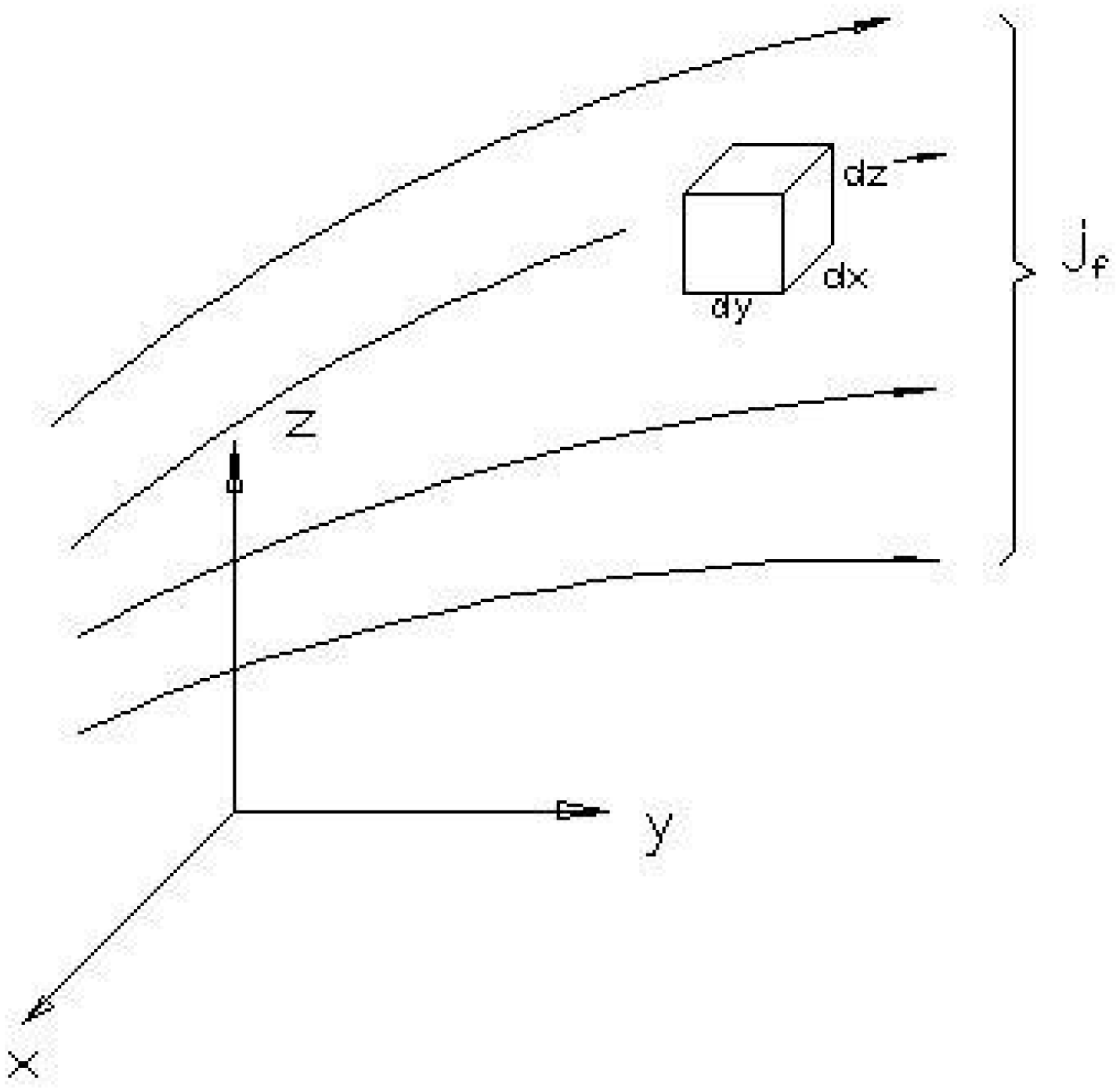
2.2.2. Gas Flow Equation with Klinkenberg Effects
2.3. Penetration-Reaction Carbonation Model
| Temperature | Concentration of CO2 | Relative Humidity | Pressure |
|---|---|---|---|
| 20 °C | 4.70% | 65% | 1 bar above ambient |
| Curing Time (at 100% Relative Humidity with 20 °C) | ||||
|---|---|---|---|---|
| 3 days | 7 days | 28 days | 3 months | |
| Test results (mm) | 9.10 | 7.40 | 4.50 | 3.30 |
| Simulation (mm) | 11.01 | 8.49 | 4.97 | 3.52 |
3. Effect of Wind Pressure on Carbonation
3.1. Initial Conditions and Boundary Conditions
3.2. Numerical Parameters for Concrete and Wind Flow
| w/c | Φ (%) | T (°C) | Cco2 (%) | Dco2 (m2/s) | R (m3/mol/s) | k∞ (m2) | μ (Pa·s) |
|---|---|---|---|---|---|---|---|
| 0.38 | 15.24 | 20 °C | 0.015 | 1 × 10−8 | 5 × 10−5 | 5.59 × 10−17 | 1.84 × 10−5 |
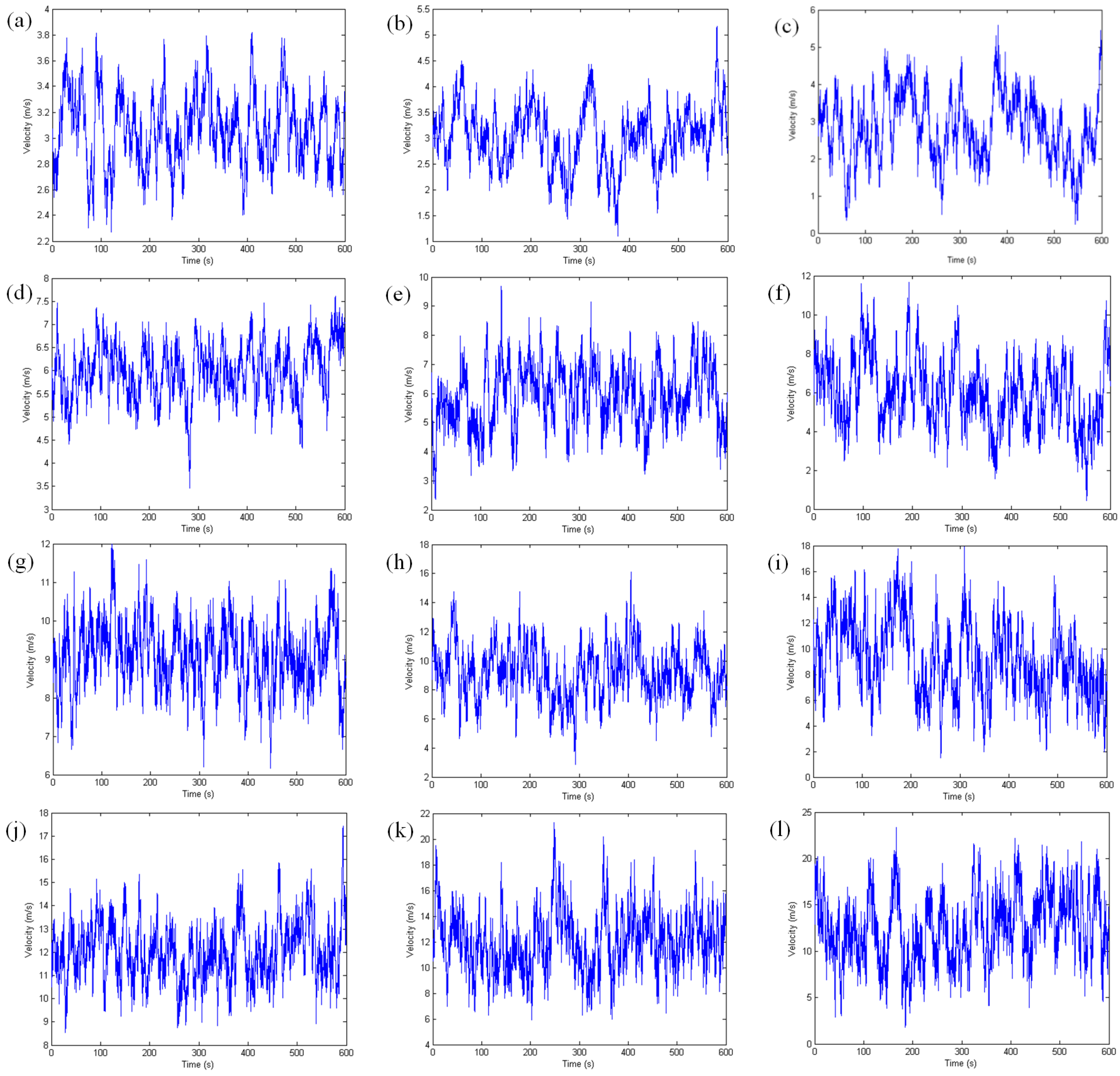
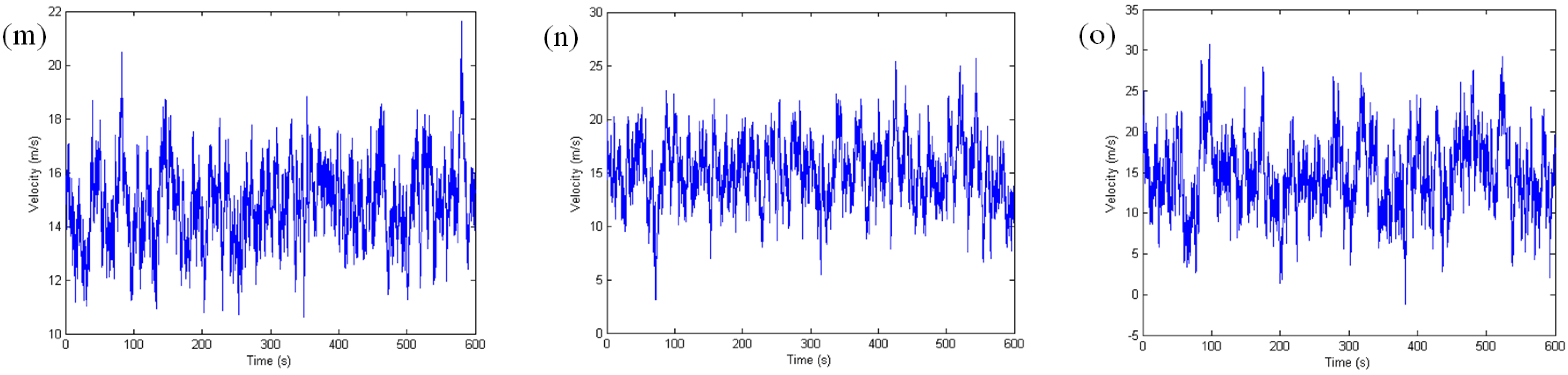
3.3. Results of Numerical Analysis
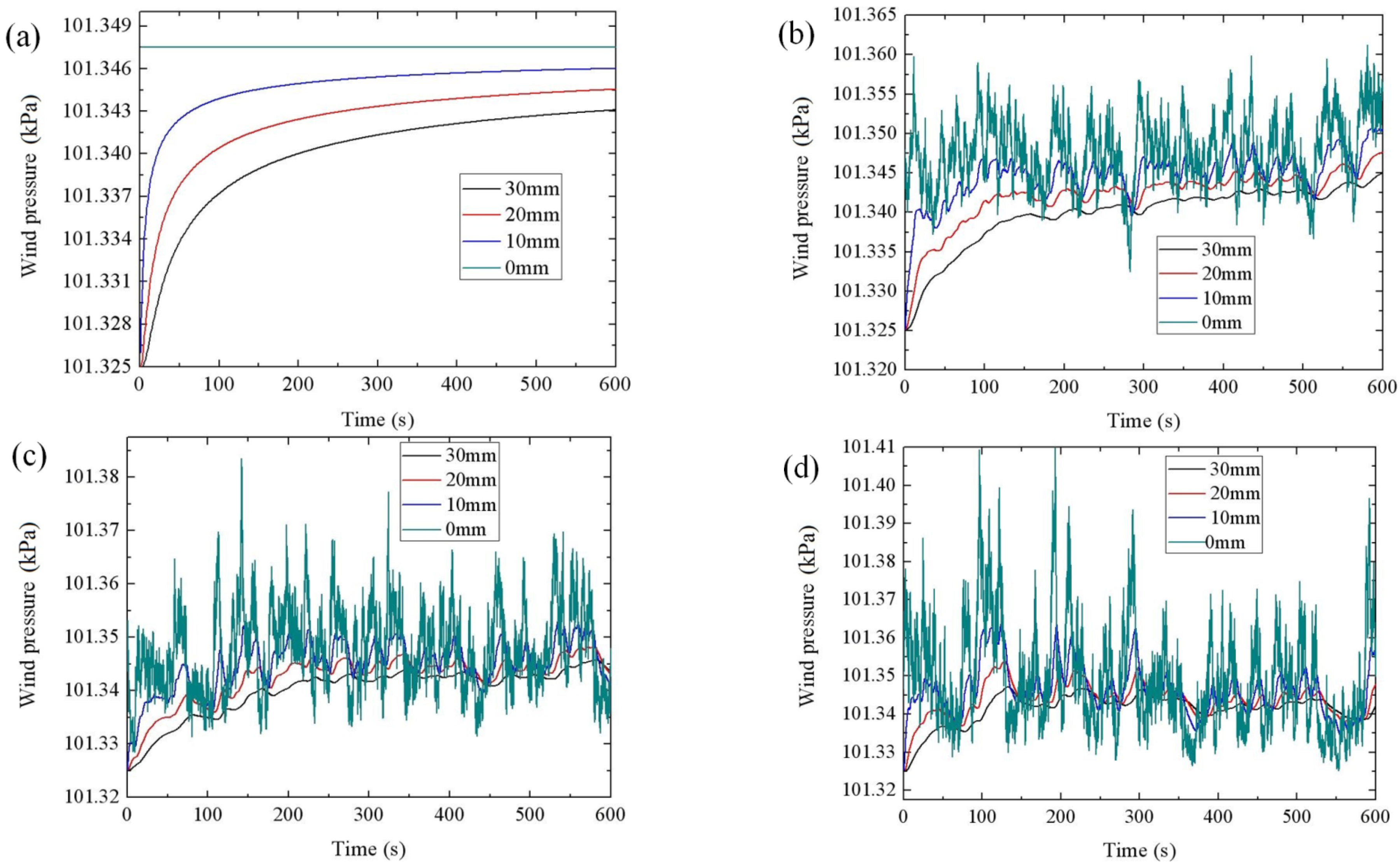
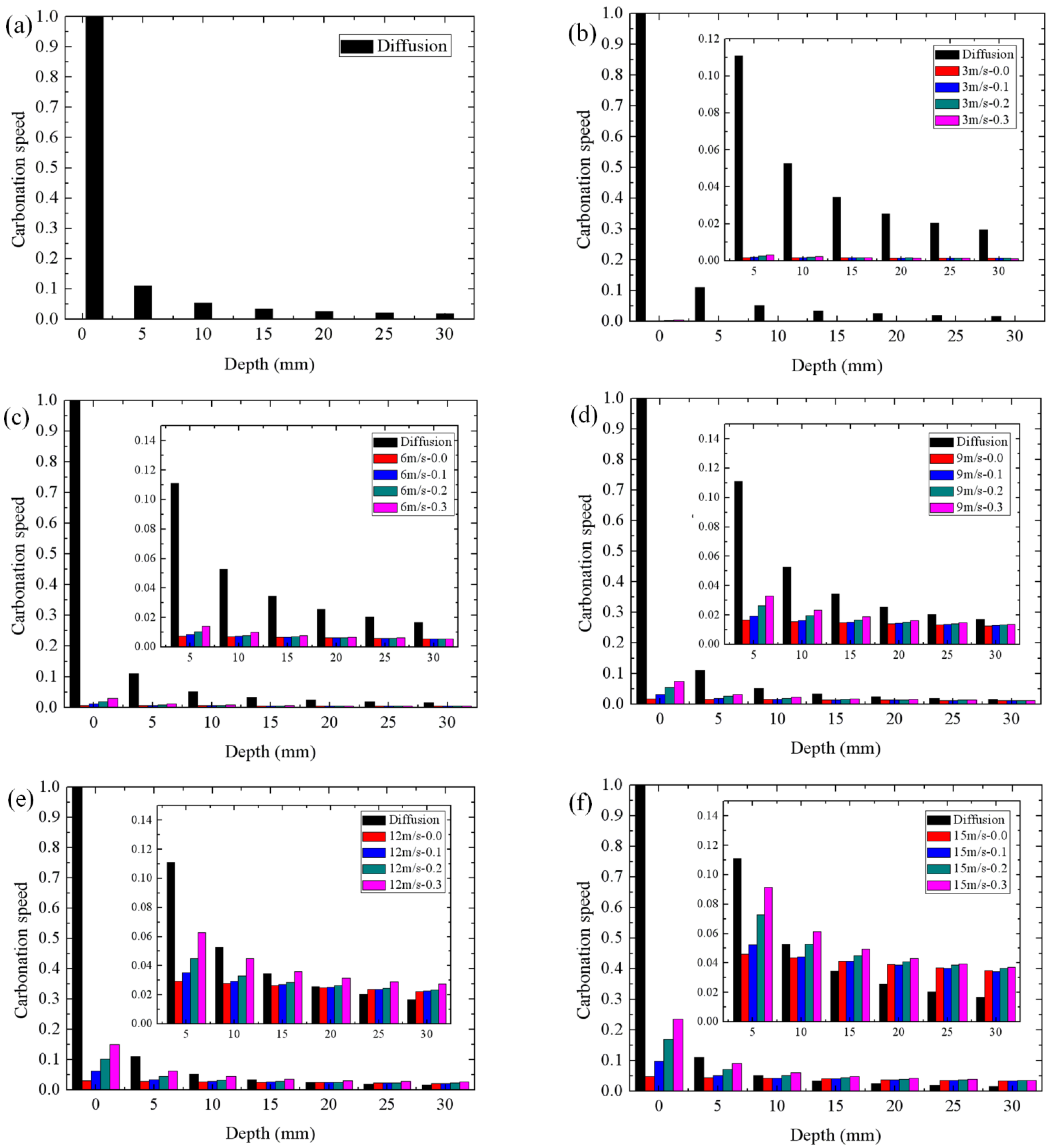
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Diffusion-Reaction Carbonation Model
Notation
concentration of carbon dioxide; | |
concentration of calcium hydroxide, mol/L−1; | |
concentration of calcium carbonica, mol/L−1; | |
diffusion coefficient of carbon dioxide, m2/s; | |
diffusion coefficient of Ca2+, m2/s; | |
| R | rate constant of the reaction, |
| t | time, s. |
References
- BS EN 1992-1-1:2004 Eurocode 2 Design of Concrete Structures Part 1.1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1998-2 Eurocode 8 Design of Structures for Earthquake Resistance Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- EN 1998-2 Eurocode 8 Assessment and Retrofitting of Building Part 3: Design of Structures for Earthquake Resistance; European Committee for Standardization: Brussels, Belgium, 2005.
- Model Code for Service Life Design; International Federation for Structural Concrete: Lausanne, Switzerland, 2006.
- OPCM 3431 Norme teecniche per il progetto, la valutazione e l’adeguamento sismico degli edifice; Ordinance of the Prime Minister: Rome, Italy, 2005.
- Alexander, M.G.; Mackechnie, J.R.; Yam, W. Carbonation of concrete bridge structures in three South African localities. Cem. Concr. Compos. 2007, 29, 750–759. [Google Scholar] [CrossRef]
- Dinakar, P.; Babu, K.G.; Santhanam, M. Corrosion behaviour of blended cements in low and medium strength concretes. Cem. Concr. Compos. 2007, 29, 136–145. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.; Yi, S.; Lee, Y. Effect of carbonation on the rebound number and compressive strength of concrete. Cem. Concr. Compos. 2009, 31, 139–144. [Google Scholar] [CrossRef]
- Younsi, A.; Turcry, P.; Rozière, E.; Aït-Mokhtar, A.; Loukili, A. Performance-based design and carbonation of concrete with high fly ash content. Cem. Concr. Compos. 2011, 33, 993–1000. [Google Scholar] [CrossRef] [Green Version]
- Saetta, A.V.; Schrefler, B.A.; Vitaliani, R.V. The carbonation of concrete and the mechanism of moisture, heat and carbon dioxide flow through porous materials. Cem. Concr. Res. 1993, 23, 761–772. [Google Scholar] [CrossRef]
- Saetta, A.V.; Schrefler, B.A.; Vitaliani, R.V. 2D model for carbonation and moisture/heat flow in porous materials. Cem. Concr. Res. 1995, 25, 1703–1712. [Google Scholar] [CrossRef]
- Saetta, A.V.; Vitaliani, R.V. Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures: Part I: Theoretical formulation. Cem. Concr. Res. 2004, 34, 571–579. [Google Scholar] [CrossRef]
- Saetta, A.V.; Vitaliani, R.V. Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures: Part II. Practical applications. Cem. Concr. Res. 2005, 35, 958–967. [Google Scholar] [CrossRef]
- Bary, B.; Sellier, A. Coupled moisture—carbon dioxide–calcium transfer model for carbonation of concrete. Cem. Concr. Res. 2004, 34, 1859–1872. [Google Scholar] [CrossRef]
- Burkan, I.O.; Razaqpur, A.G. Finite element modeling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos. 2004, 26, 57–73. [Google Scholar] [CrossRef]
- Park, D.C. Carbonation of concrete in relation to CO2 permeability and degradation of coatings. Constr. Build. Mater. 2008, 22, 2260–2268. [Google Scholar] [CrossRef]
- Wang, X.; Lee, H. A model for predicting the carbonation depth of concrete containing low-calcium fly ash. Constr. Build. Mater. 2009, 23, 725–733. [Google Scholar] [CrossRef]
- Khunthongkeaw, J.; Tangtermsirikul, S.; Leelawat, T. A study on carbonation depth prediction for fly ash concrete. Constr. Build. Mater. 2006, 20, 744–753. [Google Scholar] [CrossRef]
- Moskvin, V.M. Corrosion of Concrete and Reinforced Concrete, Methods of Their Protection; Strojizdat: Moscow, Soviet, 1980. (In Russian) [Google Scholar]
- Qu, W.J.; Guo, M. Tentative study on carbonization of T-type beam concrete accelerated by wind pressure. J. Xi’an Univ. Archit. Technol. 2006, 38, 1–4. (In Chinese) [Google Scholar]
- Gardner, D.R.; Jefferson, A.D.; Lark, R.J. An experimental, numerical and analytical investigation of gas flow characteristics in concrete. Cem. Concr. Res. 2008, 38, 360–367. [Google Scholar] [CrossRef]
- Wu, Y.; Pruess, K.; Persoff, P. Gas flow in porous media with Klinkenberg effects. Transp. Porous Media 1998, 32, 117–137. [Google Scholar] [CrossRef]
- Borges, P.H.R.; Costa, J.O.; Milestone, N.B.; Lynsdale, C.J.; Streatfield, R.E. Carbonation of CH and C–S–H in composite cement pastes containing high amounts of BFS. Cem. Concr. Res. 2010, 40, 284–292. [Google Scholar] [CrossRef]
- Morandeau, A.; Thiery, M.; Dangla, P. Investigation of the carbonation mechanism of CH and CSH in terms of kinetics, microstructure changes and moisture properties. Cem. Concr. Res. 2014, 56, 153–170. [Google Scholar] [CrossRef] [Green Version]
- Knopf, F.C.; Roy, A.; Samrow, H.A.; Dooley, K.M. High-pressure molding and carbonation of cementitious materials. Ind. Eng. Chem. Res. 1999, 38, 2641–2649. [Google Scholar] [CrossRef]
- Kashef-Haghighi, S.; Ghoshal, S. Physico-chemical processes limiting CO2 uptake in concrete during accelerated carbonation curing. Ind. Eng. Chem. Res. 2013, 52, 5529–5537. [Google Scholar] [CrossRef]
- Atiş, C.D. Accelerated carbonation and testing of concrete made with fly ash. Constr. Build. Mater. 2003, 17, 147–152. [Google Scholar] [CrossRef]
- Bamforth, P.B. The relationship between permeability coefficients for concrete obtained using liquid and gas. Mag. Concr. Res. 1987, 39, 3–11. [Google Scholar] [CrossRef]
- CEB-FIP. Model Code for Concrete Structures; Comite Euro-International du Beton: Lausanne, Switzerland, 1990. [Google Scholar]
- Fukushima, T. Theoretical Predictive Methods and Numerical Analysis for the Progress of Neutralization of Concrete; Japanese Architectural Institute: Tokyo, Japan, 1991. [Google Scholar]
- Saeki, T.; Ohga, H.; Nagataki, S. Mechanism of carbonation and prediction of carbonation process of concrete. Concr. Lib. JSCE 1991, 17, 23–36. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Rehman, S.; Halawani, T.O. A neural networks approach for wind speed prediction. Renew. Energy 1998, 13, 345–354. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, D.; Liu, T.; Du, C.; Teng, J. Influence of Wind Pressure on the Carbonation of Concrete. Materials 2015, 8, 4652-4667. https://doi.org/10.3390/ma8084652
Zou D, Liu T, Du C, Teng J. Influence of Wind Pressure on the Carbonation of Concrete. Materials. 2015; 8(8):4652-4667. https://doi.org/10.3390/ma8084652
Chicago/Turabian StyleZou, Dujian, Tiejun Liu, Chengcheng Du, and Jun Teng. 2015. "Influence of Wind Pressure on the Carbonation of Concrete" Materials 8, no. 8: 4652-4667. https://doi.org/10.3390/ma8084652
APA StyleZou, D., Liu, T., Du, C., & Teng, J. (2015). Influence of Wind Pressure on the Carbonation of Concrete. Materials, 8(8), 4652-4667. https://doi.org/10.3390/ma8084652





