Semi-Analytic Solution and Stability of a Space Truss Using a High-Order Taylor Series Method
Abstract
:1. Introduction
2. A Discrete Nonlinear Dynamic System and the Taylor Series Method (TSM)
2.1. Formulation of Nonlinear Motion Equations of a Space Truss
2.2. High-Order Taylor Series Method (TSM)
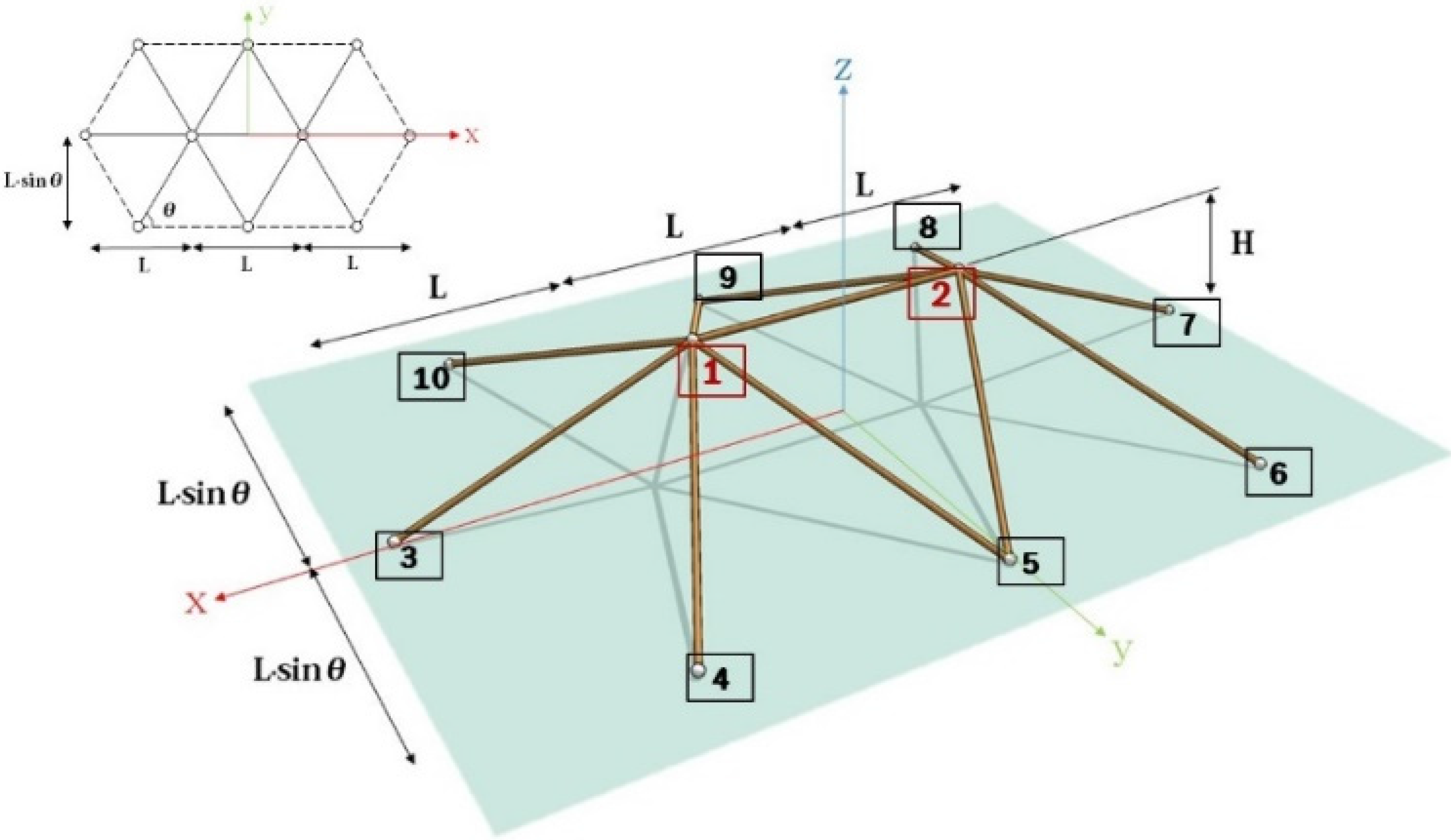
3. A Single-Free-Node (SFN) Steel Space Truss Model
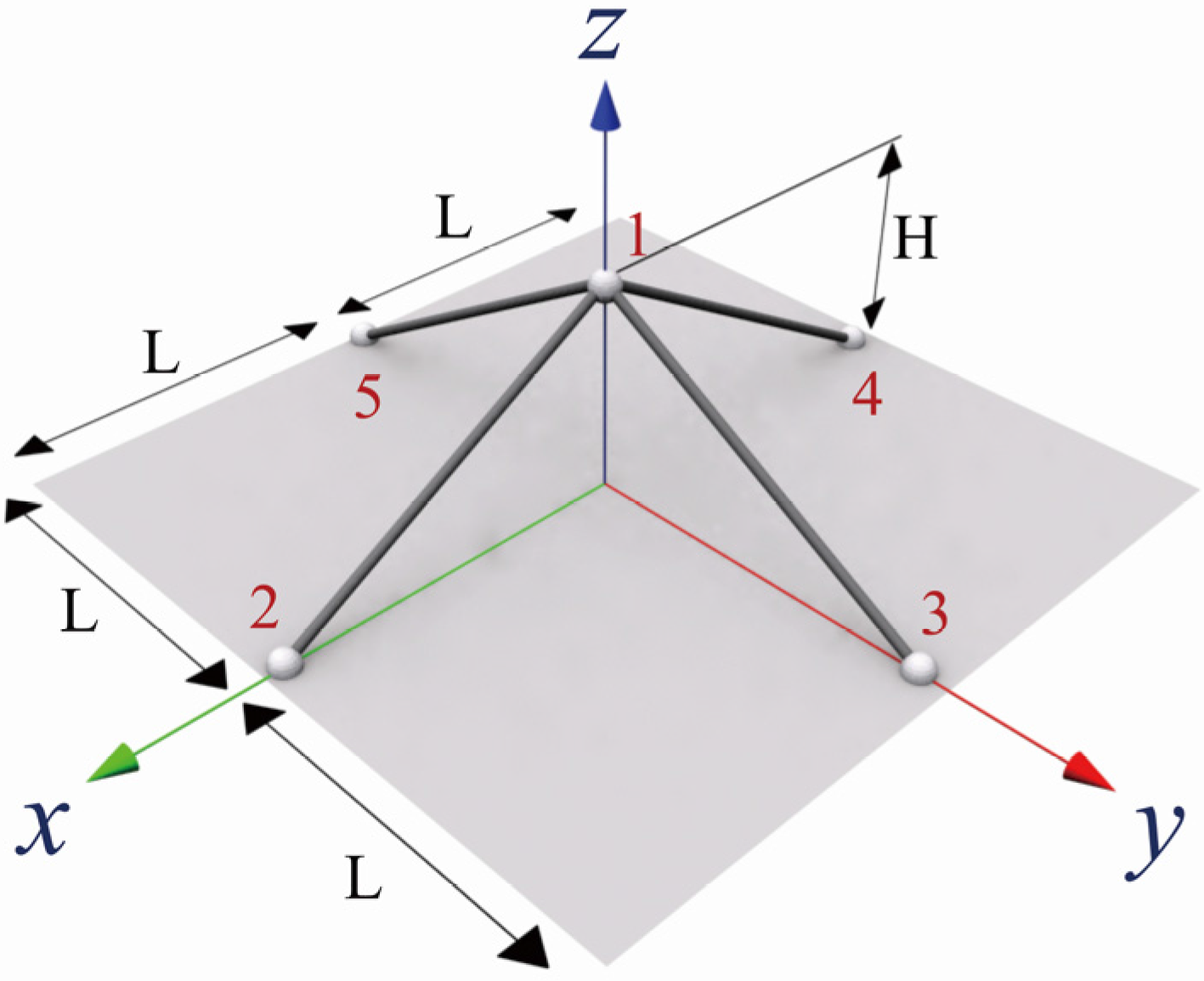
3.1. Dynamic Response under a Step Excitation
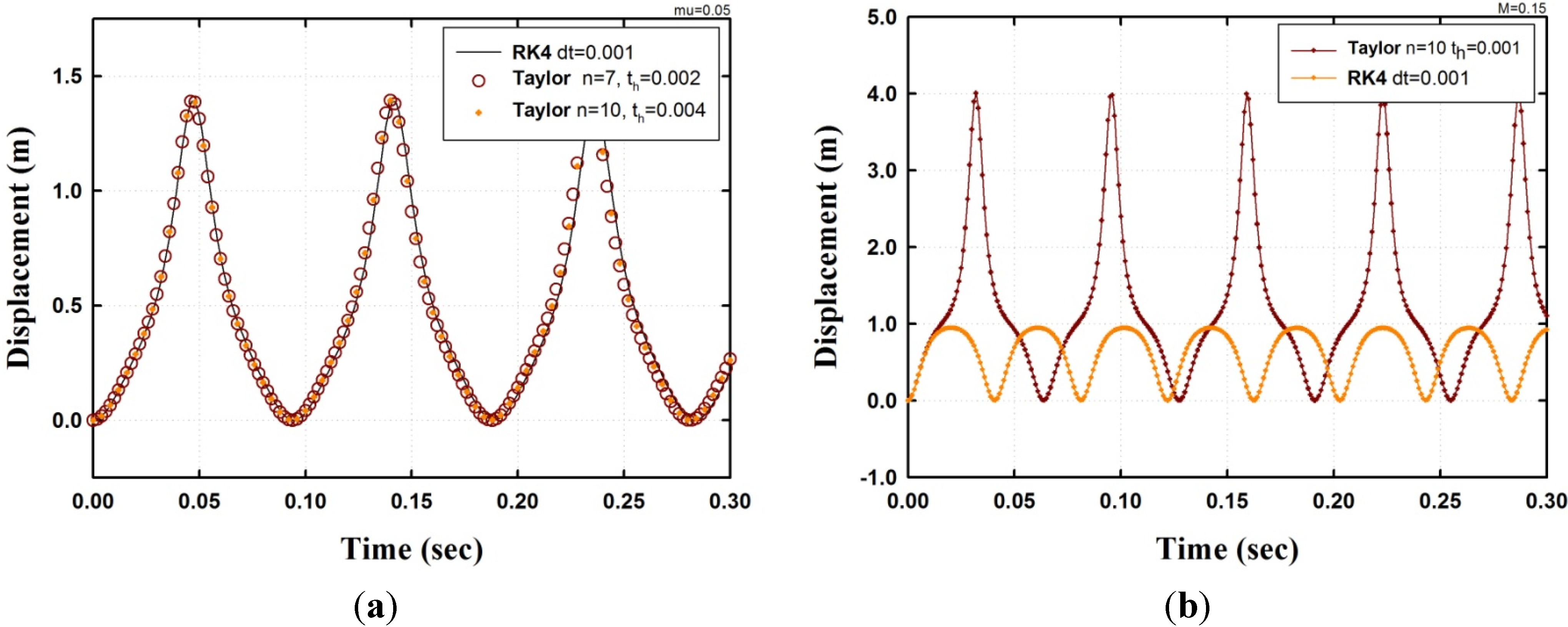


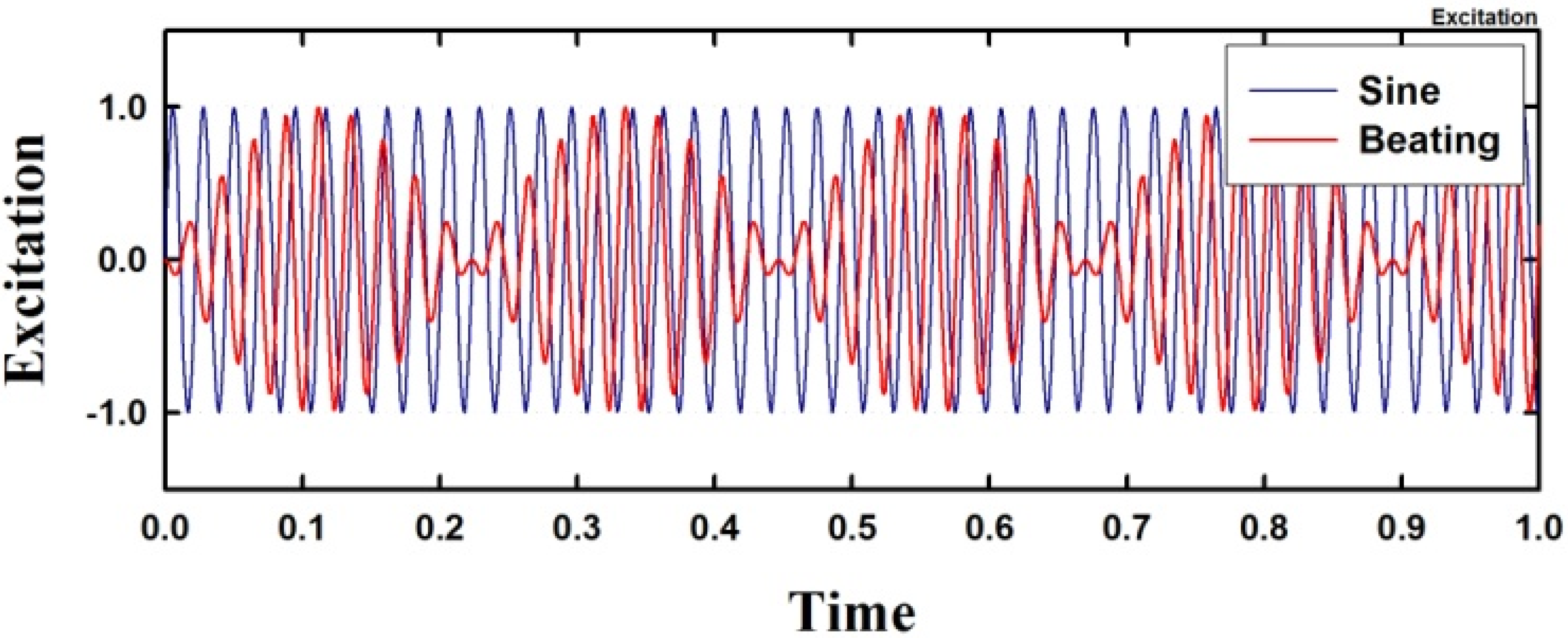
3.2. Dynamic Response under a Periodic Excitation
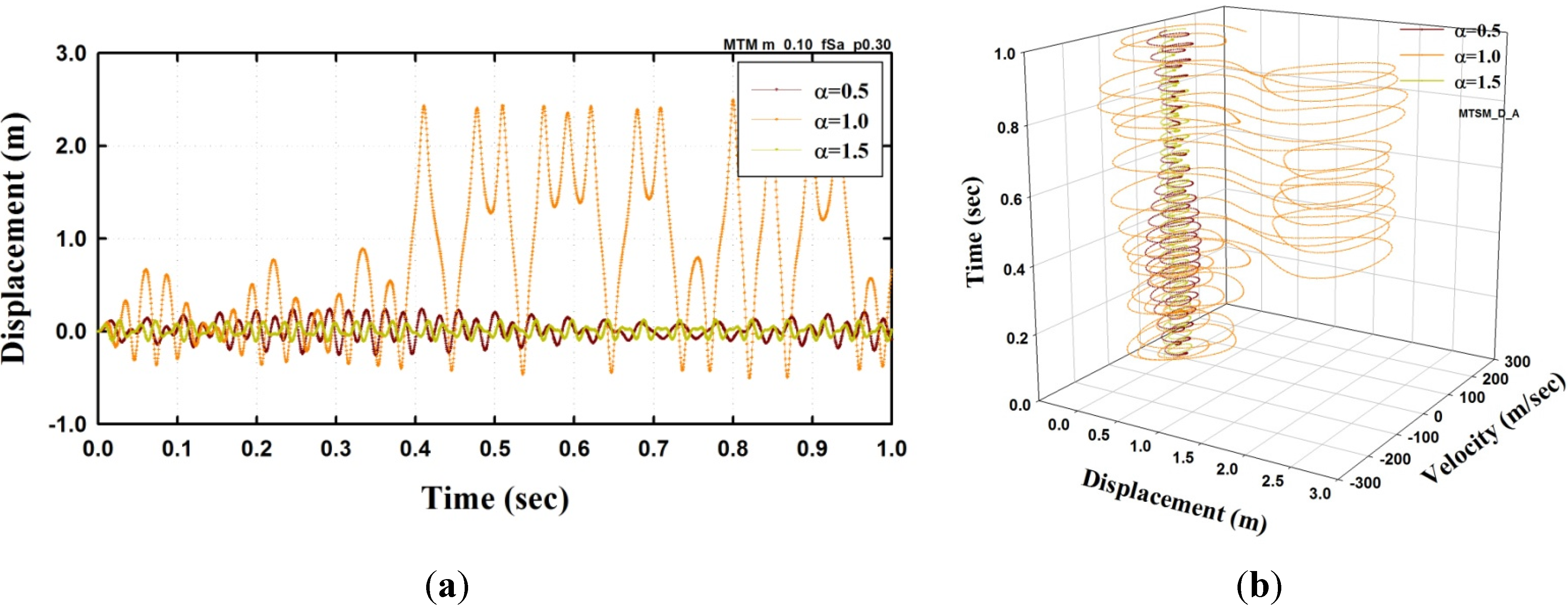
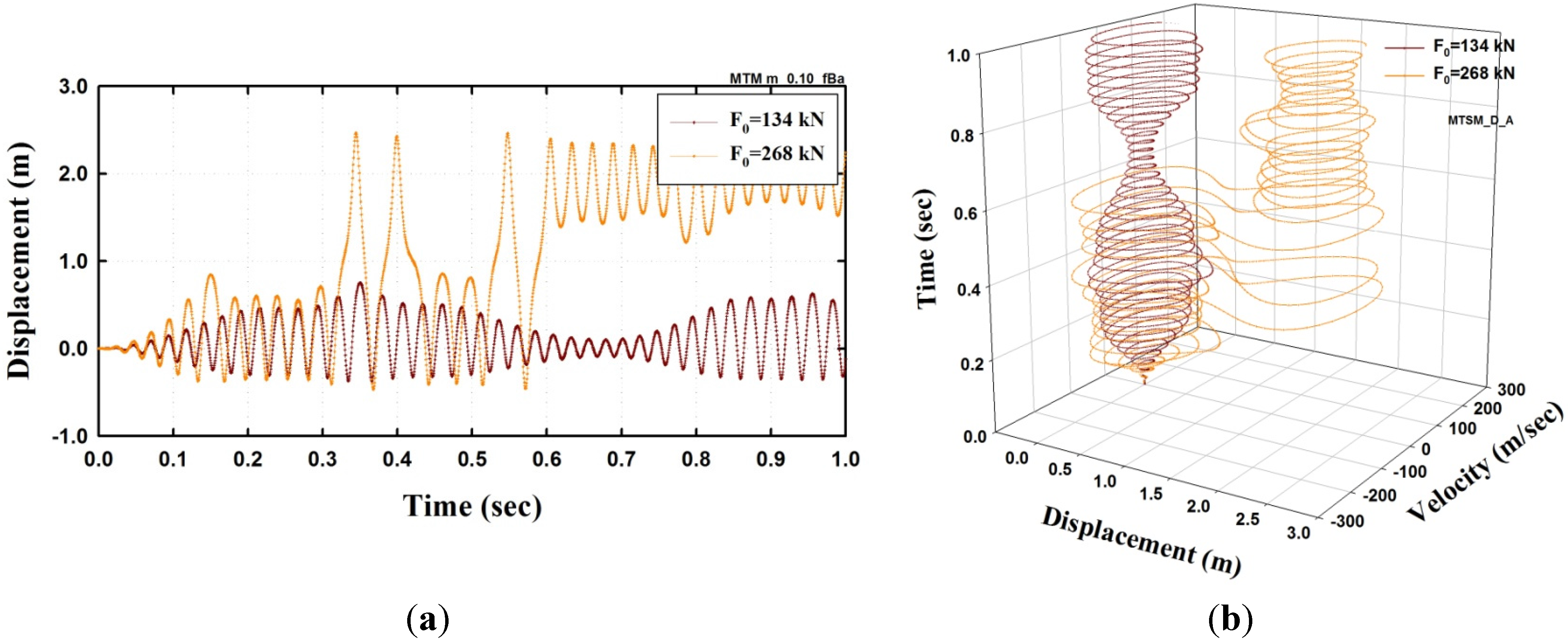
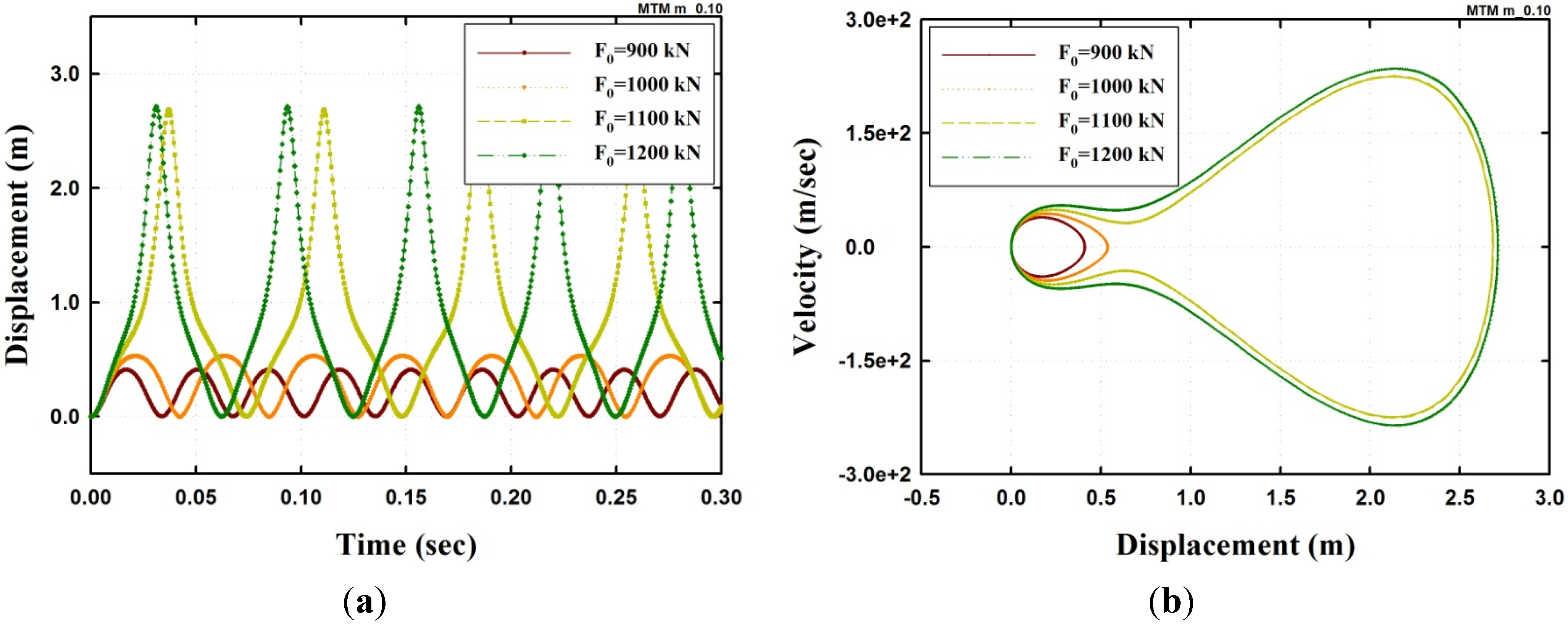
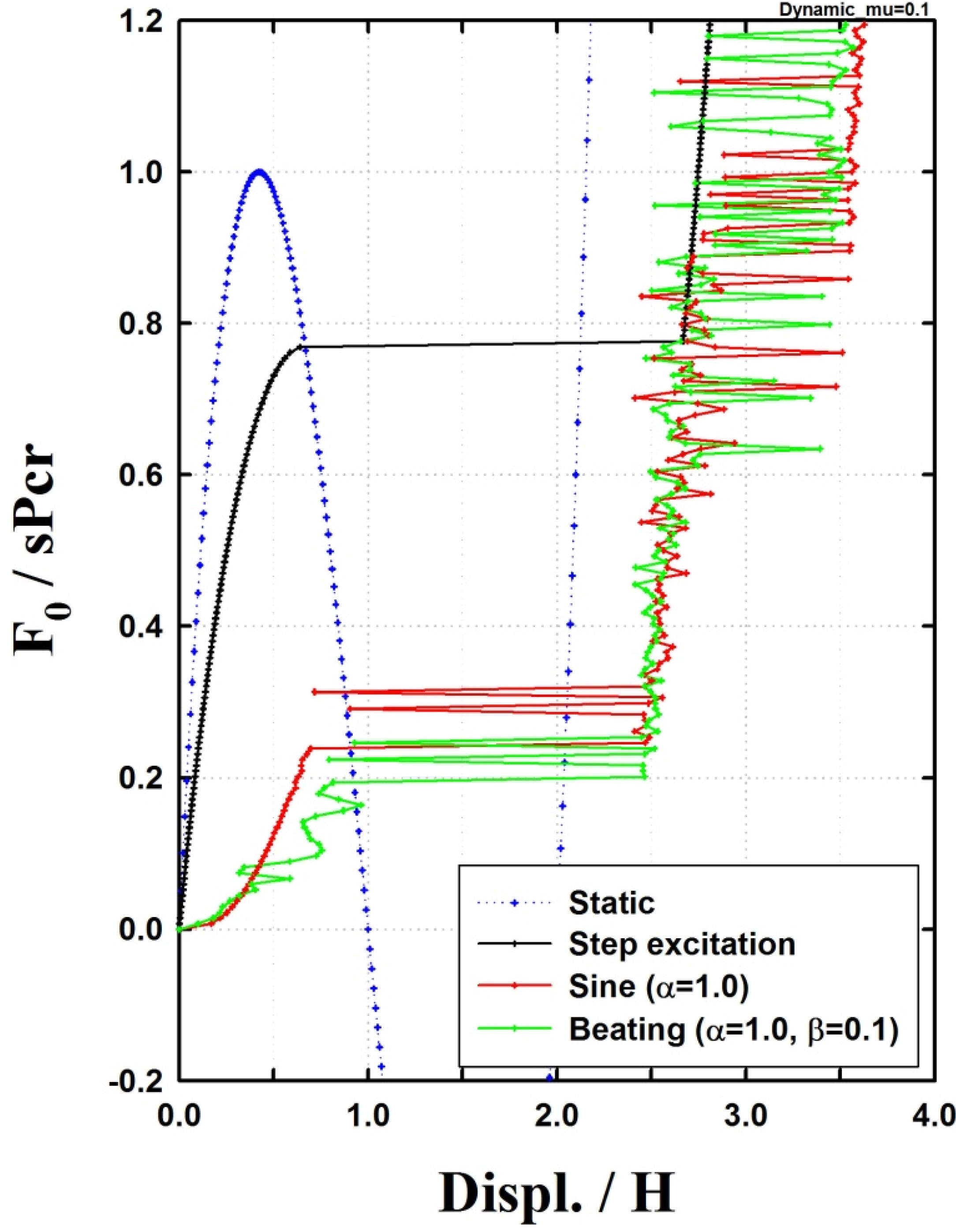
3.3. Dynamic Instability and Buckling Load
| Μ | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 |
| sPcr (kN) | 175 | 1340 | 4214 | 9098 | 15886 |
| Μ | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 |
| dPcr (kN) | 136 | 1032 | 3244 | 7004 | 12229 |
| dPcr/sPcr | 0.7771 | 0.7703 | 0.7698 | 0.7698 | 0.7698 |
| Μ | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 |
| dPcr (kN) | 146 | 1106 | 3479 | 7511 | 13113 |
| dPcr/sPcr | 0.8343 | 0.8256 | 0.8256 | 0.8255 | 0.8255 |
4. Double-Free-Nodes (DFN) Steel Space Truss Model
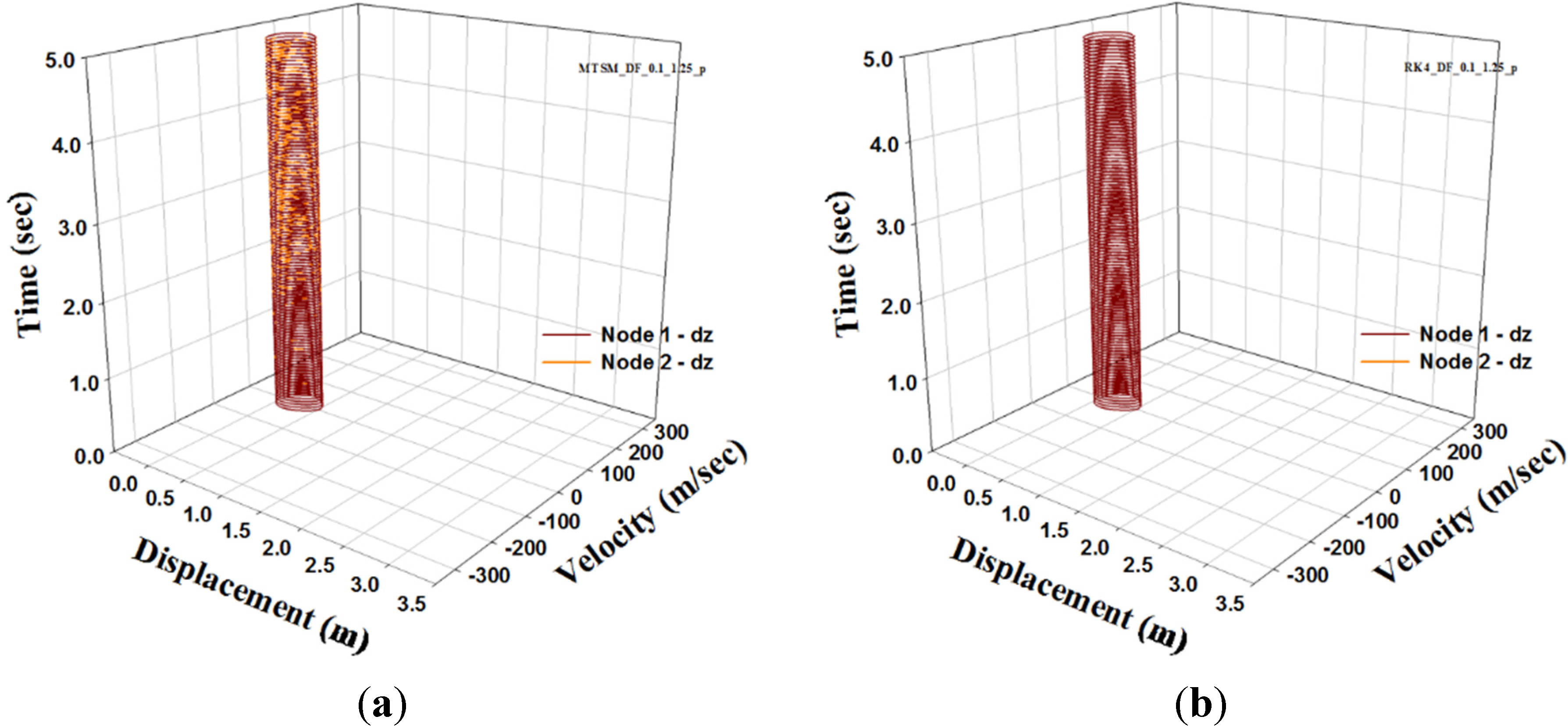
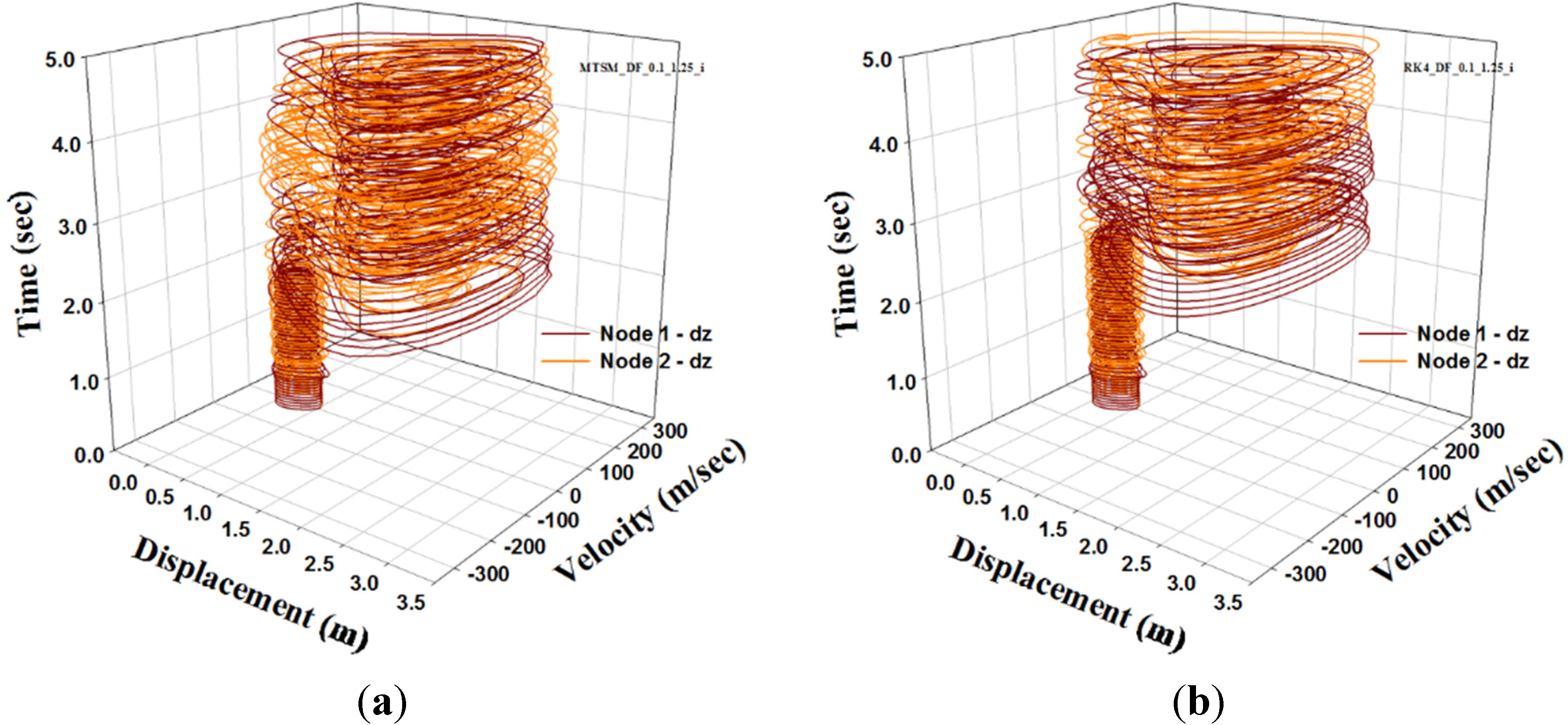
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Budiansky, B.; Roth, R.S. Axisymmetric dynamic buckling of clamped shallow spherical shells. In Collected Papers on Instability of Shells Structures; NASA TN D 1510; The National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1962; pp. 597–606. [Google Scholar]
- Ball, R.E.; Burt, J.A. Dynamic buckling of shallow spherical shells. J. Appl. Mech. 1973, 40, 411–416. [Google Scholar] [CrossRef]
- Akkas, N. Bifurcation and snap-through phenomena in asymmetric dynamic analysis of shallow spherical shells. Comput. Struct. 1976, 6, 241–251. [Google Scholar] [CrossRef]
- Papadrakakis, M. Post-buckling analysis of spatial structures by vector iteration methods. Comput. Struct. 1981, 14, 393–402. [Google Scholar] [CrossRef]
- Hill, C.D.; Blandford, G.E.; Wang, S.T. Post-bucking analysis of steel space trusses. J. Struct. Eng. 1989, 115, 900–919. [Google Scholar] [CrossRef]
- Kong, X.; Wang, B.; Hu, J. Dynamic snap buckling of an elastoplastic shallow arch with elastically supported and clamped ends. Comput. Struct. 1995, 55, 163–166. [Google Scholar] [CrossRef]
- Blair, K.B.; Krousgrill, C.M.; Farris, T.N. Non-linear dynamic response of shallow arches to harmonic forcing. J. Sound Vib. 1996, 194, 353–367. [Google Scholar] [CrossRef]
- Blandford, G.E. Progressive failure analysis of inelastic space truss structures. Comput. Struct. 1996, 58, 981–990. [Google Scholar] [CrossRef]
- Sansour, C.; Wriggers, P.; Sansour, J. Nonlinear dynamics of shells: Theory, finite element formulation, and integration schemes. Nonlinear Dyn. 1997, 13, 279–305. [Google Scholar] [CrossRef]
- Xu, J.X.; Huang, H.; Zhang, P.Z.; Zhou, J.Q. Dynamic stability of shallow arch with elastic supports-application in the dynamic stability analysis of inner winding of transformer during short circuit. Int. J. Non-Linear Mech. 2002, 37, 909–920. [Google Scholar] [CrossRef]
- Kassimali, A.; Bidhendi, E. Stability of trusses under dynamic loads. Comput. Struct. 1988, 29, 381–392. [Google Scholar] [CrossRef]
- Tada, M.; Suito, A. Static and dynamic post-buckling behavior of truss structures. Eng. Struct. 1998, 20, 384–389. [Google Scholar] [CrossRef]
- Ha, J.H.; Gutman, S.; Shon, S.D.; Lee, S.J. Stability of shallow arches under constant load. Int. J. Nonlinear Mech. 2014, 58, 120–127. [Google Scholar] [CrossRef]
- Shon, S.D.; Lee, S.J.; Lee, G.G. Characteristics of bifurcation and buckling load of space truss in consideration of initial imperfection and load mode. J. Zhejiang Univ. Sci. A 2013, 14, 206–218. [Google Scholar] [CrossRef]
- Kim, S.D.; Kang, M.M.; Kwun, T.J.; Hangai, Y. Dynamic instability of shell-like shallow trusses considering damping. Comput. Struct. 1997, 64, 481–489. [Google Scholar] [CrossRef]
- Slaats, P.M.A.; Jongh, J.; Sauren, A.A.H.J. Model reduction tools for nonlinear structural dynamics. Comput. Struct. 1995, 54, 1155–1171. [Google Scholar] [CrossRef]
- Coan, C.H.; Plaut, R.H. Dynamic stability of a lattice dome. Earthq. Eng. Struct. Dyn. 1983, 11, 269–274. [Google Scholar] [CrossRef]
- Belytschko, T. A survey of numerical methods and computer programs for dynamic structural analysis. Nucl. Eng. Des. 1976, 37, 23–34. [Google Scholar] [CrossRef]
- Sadighi, A.; Ganji, D.D.; Ganjavi, B. Travelling wave solutions of the Sine-Gordon and the coupled Sine-Gordon equations using the homotopy perturbation method. Sci. Iran. Trans. B Mech. Eng. 2007, 16, 189–195. [Google Scholar]
- Barrio, R. Performance of the Taylor series method for ODEs/DAEs. Appl. Math. Comput. 2005, 163, 525–545. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Lara, M. VSVO Formulation of the Taylor method for the numerical solution of ODEs. Comput. Math. Appl. 2005, 50, 93–111. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Generalization of adomian polynomials to functions of several variables. Comput. Math. Appl. 1992, 24, 11–24. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Modified adomian polynomials. Math. Comput. Model. 1996, 24, 39–46. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Chowdhury, M.S.H.; Hashim, I.; Momani, S. The multistage homotopy-perturbation method: A powerful scheme for handling the Lorenz system. Chaos Solutions Fractals 2009, 40, 1929–1937. [Google Scholar] [CrossRef]
- Barrio, R.; Rodriguez, M.; Abad, A.; Blesa, F. Breaking the limits: the Taylor series method. Appl. Math. Comput. 2011, 217, 7940–7954. [Google Scholar] [CrossRef]
- Abad, A.; Barrio, R.; Blesa, F.; Rodriguez, M. TIDES: A Taylor series integrator for differential equations. ACM Trans. Math. Softw. TOMS 2012, 39. [Google Scholar] [CrossRef]
- Rodriguez, M.; Barrio, R. Reducing rounding errors and achieving Brouwerʼs law with Taylor Series Method. Appl. Numer. Math. 2012, 62, 1014–1024. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shon, S.; Lee, S.; Ha, J.; Cho, C. Semi-Analytic Solution and Stability of a Space Truss Using a High-Order Taylor Series Method. Materials 2015, 8, 2400-2414. https://doi.org/10.3390/ma8052400
Shon S, Lee S, Ha J, Cho C. Semi-Analytic Solution and Stability of a Space Truss Using a High-Order Taylor Series Method. Materials. 2015; 8(5):2400-2414. https://doi.org/10.3390/ma8052400
Chicago/Turabian StyleShon, Sudeok, Seungjae Lee, Junhong Ha, and Changgeun Cho. 2015. "Semi-Analytic Solution and Stability of a Space Truss Using a High-Order Taylor Series Method" Materials 8, no. 5: 2400-2414. https://doi.org/10.3390/ma8052400
APA StyleShon, S., Lee, S., Ha, J., & Cho, C. (2015). Semi-Analytic Solution and Stability of a Space Truss Using a High-Order Taylor Series Method. Materials, 8(5), 2400-2414. https://doi.org/10.3390/ma8052400






