Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel
Abstract
:1. Introduction
2. Materials and Methods
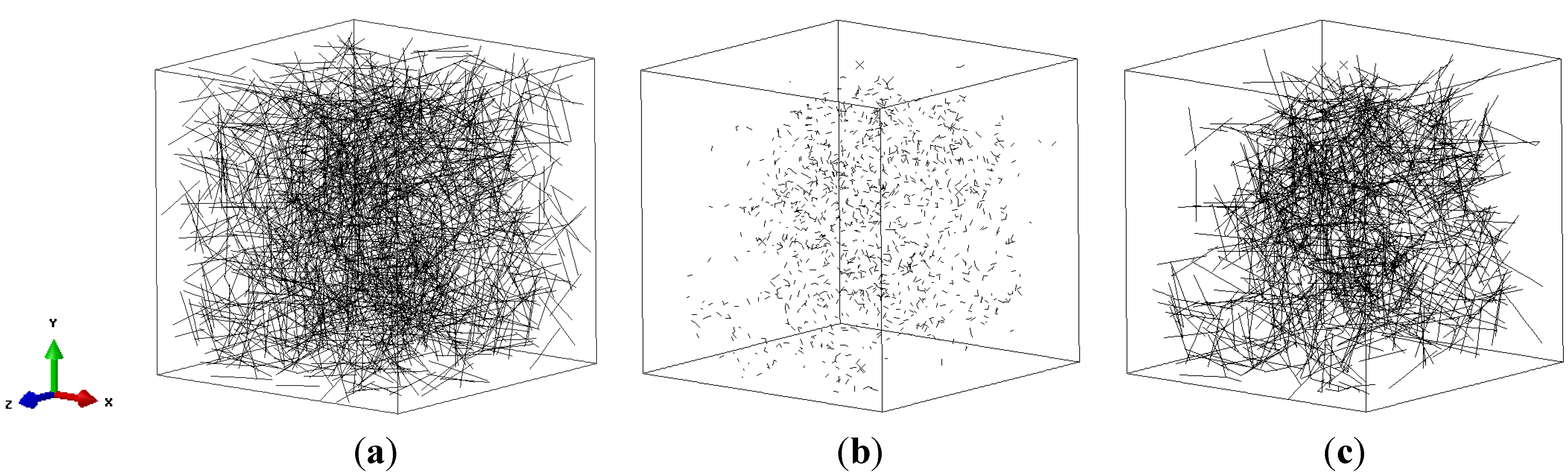
3. Results
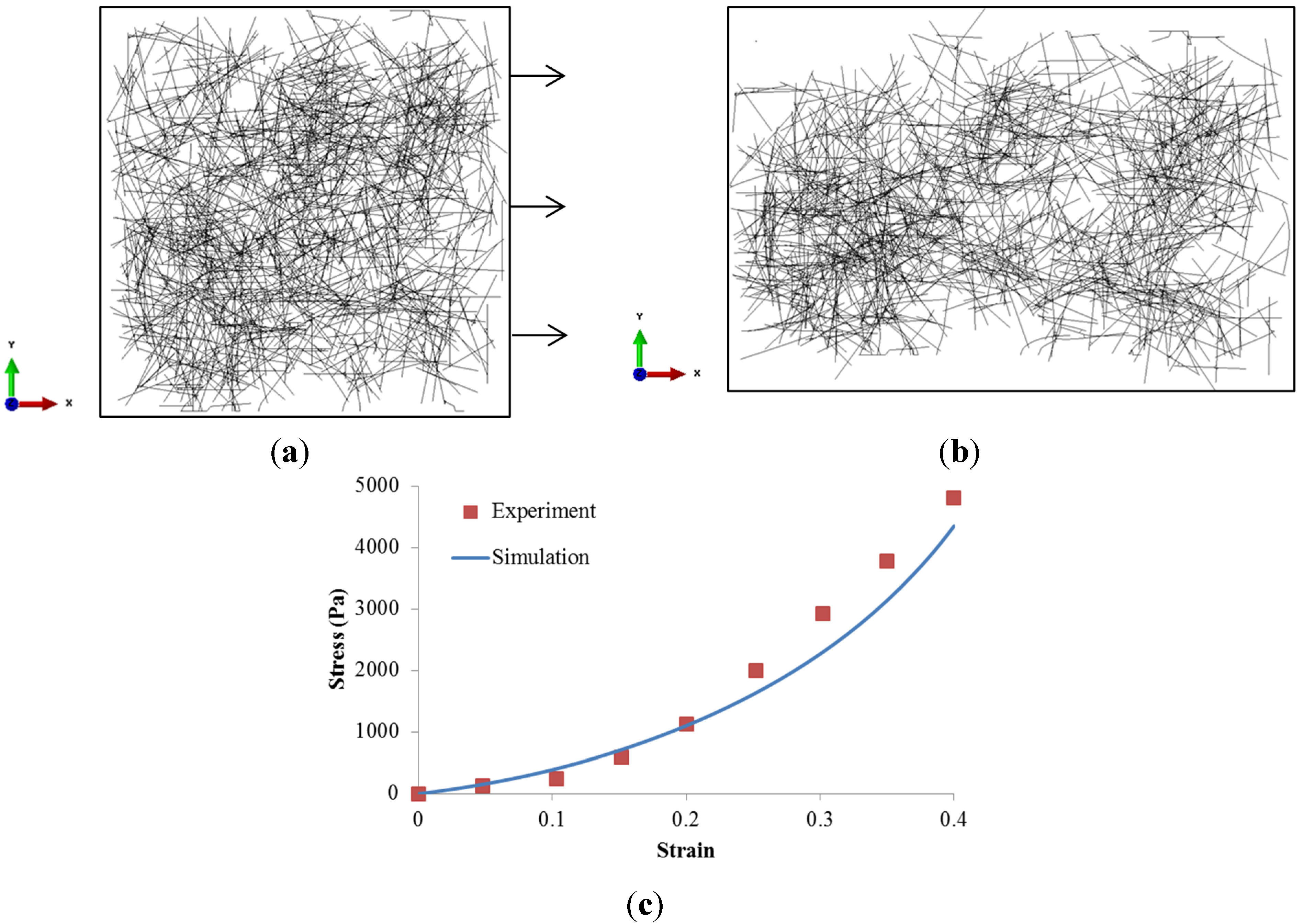
3.1. Model Validation
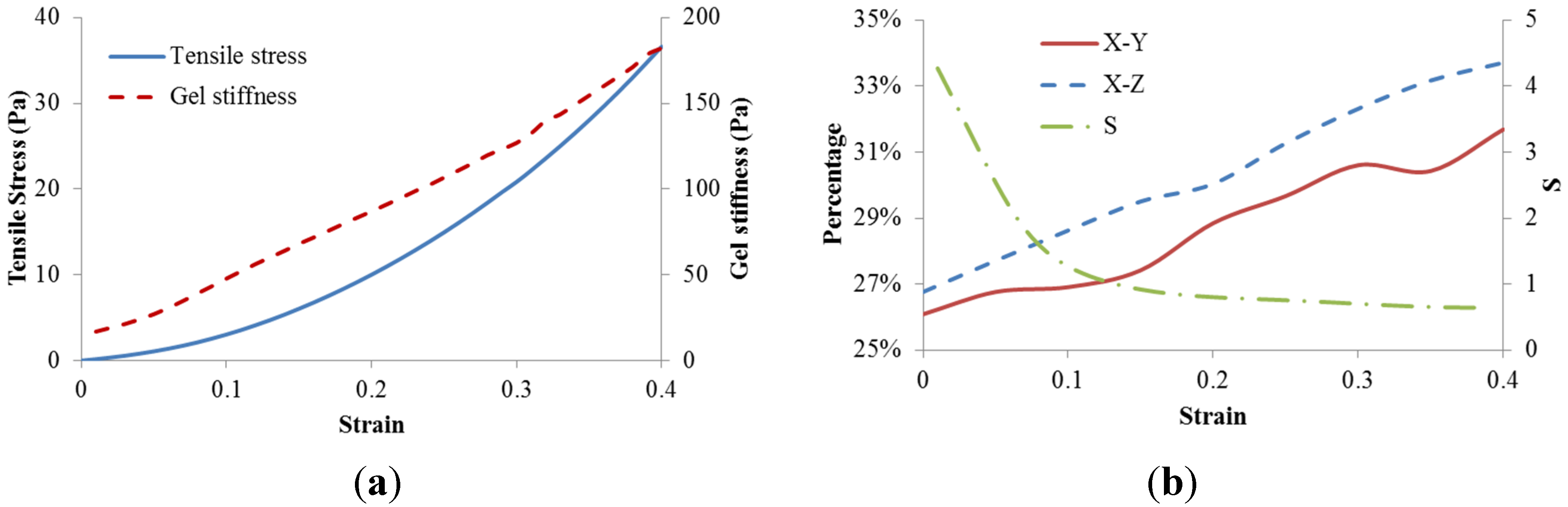
3.2. Strain Stiffening Effect in the Baseline Model
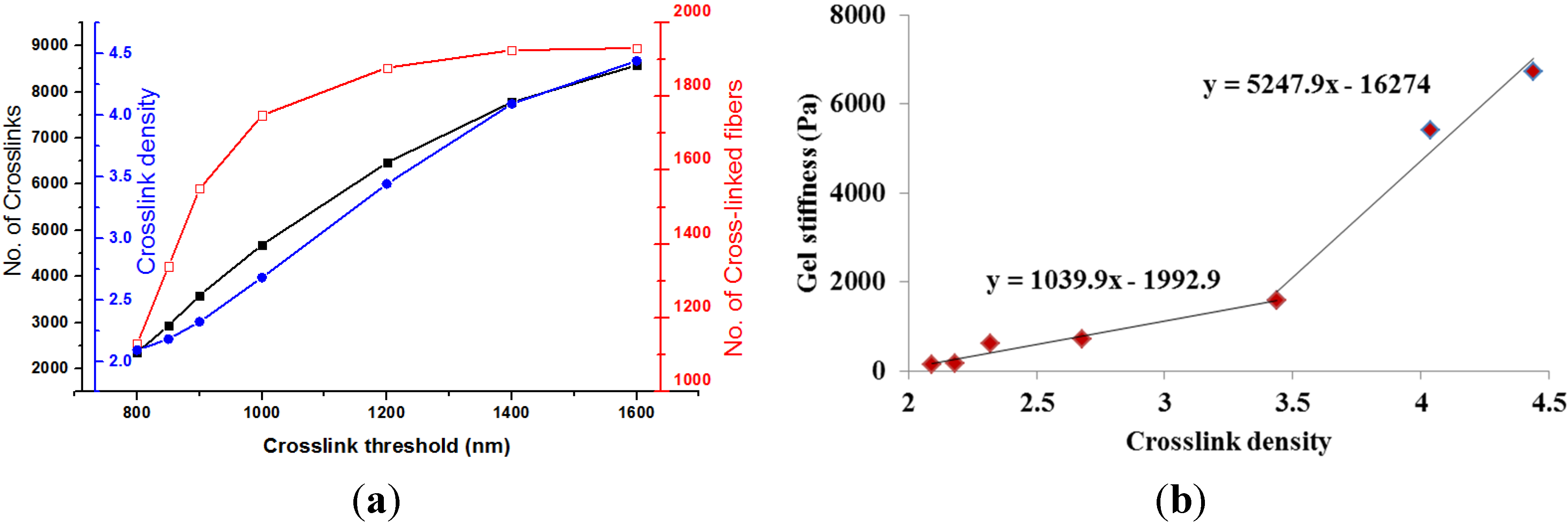
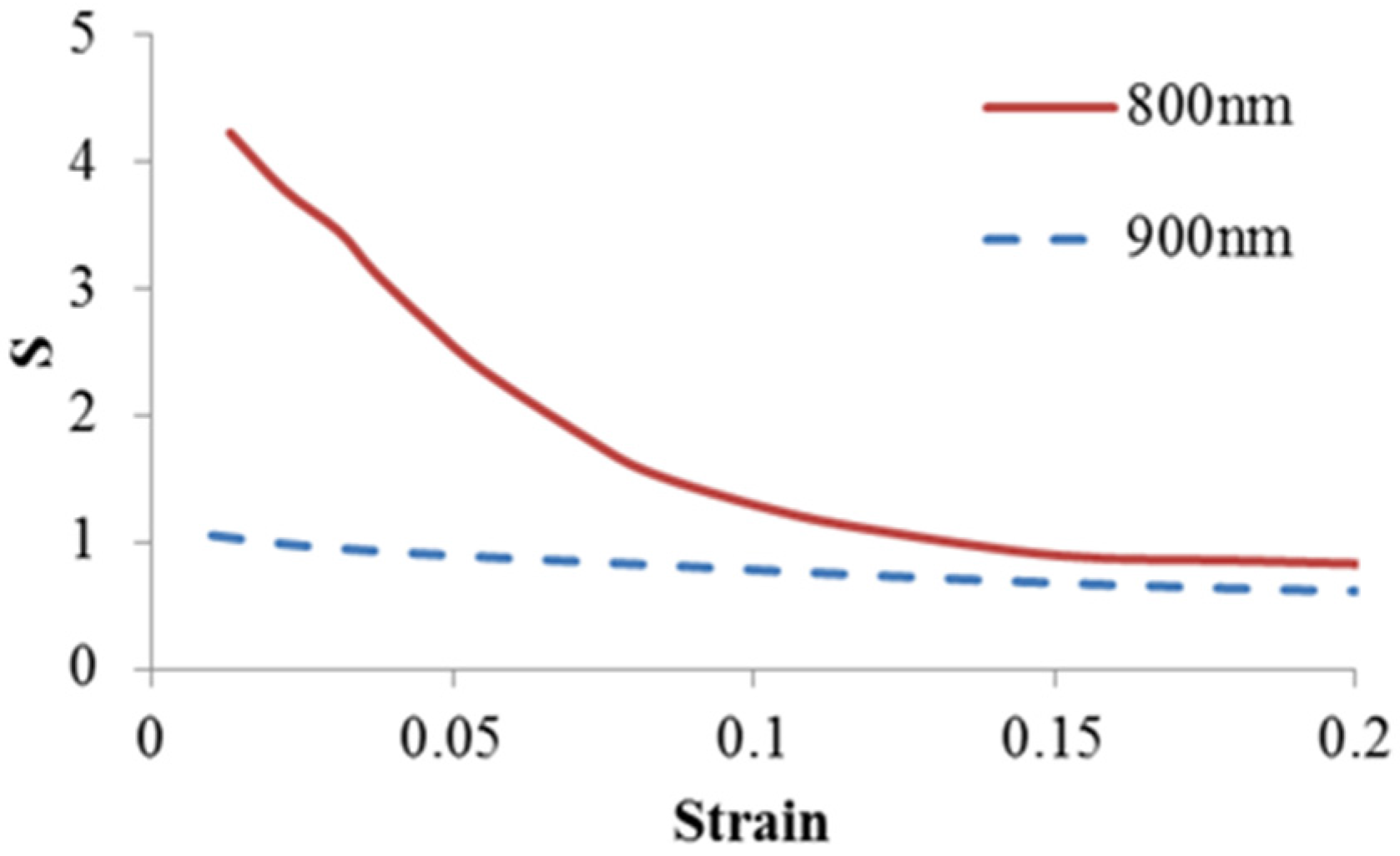
3.3. Effect of Crosslink Density
| Cases | Base | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Crosslink threshold (nm) | 800 | 850 | 900 | 1000 | 1200 | 1400 | 1600 |
| No. of Crosslinks | 2360 | 2933 | 3594 | 4687 | 6467 | 7776 | 8572 |
| No. of Cross-linked fibers | 1130 | 1340 | 1550 | 1749 | 1878 | 1925 | 1931 |
| Crosslink density | 2.09 | 2.18 | 2.32 | 2.68 | 3.44 | 4.039 | 4.439 |
| Gel stiffness (Pa) | 30.02 | 40.823 | 154.27 | 545.3 | 1280.3 | 4379.6 | 5659.1 |
3.4. Effect of Crosslink Stiffness
| Crosslink Stiffness | 25 MPa | 50 MPa | 75 MPa | 100 MPa |
|---|---|---|---|---|
| Gel stiffness | 23.3 Pa | 30.0 Pa | 31.4 Pa | 32.2 Pa |
| Percentage of total load shared by crosslinks | 0.09% | 1.55% | 2.35% | 2.92% |
| Percentage of strain energy shared by crosslinks | 19.3% | 11.9% | 8.7% | 6.9% |
4. Discussion
5. Conclusions
- The strain stiffening effect of the collagen gel was dominated by the fiber alignment.
- The increased crosslink density has much more impact on the gel stiffening than the crosslink stiffness. A positive bilinear correlation between the crosslink density and gel stiffness was predicted.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ingber, D.E. Mechanical and chemical determinants of tissue development. In Principles of Tissue Engineering; Academic Press, Inc.: San Diego, CA, USA, 2000; pp. 101–110. [Google Scholar]
- Vader, D.; Kabla, A.; Weitz, D.; Mahadevan, L. Strain-induced alignment in collagen gels. PLoS One 2009, 4. [Google Scholar] [CrossRef] [PubMed]
- Lieleg, O.; Claessens, M.M.; Bausch, A.R. Structure and dynamics of cross-linked actin networks. Soft Matter 2010, 6, 218–225. [Google Scholar] [CrossRef]
- Bozec, L.; Horton, M. Topography and mechanical properties of single molecules of type I collagen using atomic force microscopy. Biophys. J. 2005, 88, 4223–4231. [Google Scholar] [CrossRef] [PubMed]
- Raub, C.B.; Suresh, V.; Krasieva, T.; Lyubovitsky, J.; Mih, J.D.; Putnam, A.J.; Tromberg, B.J.; George, S.C. Noninvasive assessment of collagen gel microstructure and mechanics using multiphoton microscopy. Biophys. J. 2007, 92, 2212–2222. [Google Scholar] [CrossRef] [PubMed]
- Roeder, B.A.; Kokini, K.; Sturgis, J.E.; Robinson, J.P.; Voytik-Harbin, S.L. Tensile mechanical properties of three-dimensional type I collagen extracellular matrices with varied microstructure. J. Biomech. Eng. 2002, 124, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Motte, S.; Kaufman, L.J. Strain stiffening in collagen I networks. Biopolymers 2013, 99, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Zeugolis, D.I.; Paul, G.R.; Attenburrow, G. Cross‐linking of extruded collagen fibers—A biomimetic three‐dimensional scaffold for tissue engineering applications. J. Biomed. Mater. Res. A 2009, 89, 895–908. [Google Scholar] [CrossRef] [PubMed]
- Sheu, M.-T.; Huang, J.C.; Yeh, G.C.; Ho, H.O. Characterization of collagen gel solutions and collagen matrices for cell culture. Biomaterials 2001, 22, 1713–1719. [Google Scholar] [CrossRef] [PubMed]
- Charulatha, V.; Rajaram, A. Influence of different crosslinking treatments on the physical properties of collagen membranes. Biomaterials 2003, 24, 759–767. [Google Scholar] [CrossRef] [PubMed]
- Stein, A.M.; Vader, D.A.; Weitz, D.A.; Sander, L.M. The micromechanics of three‐dimensional collagen‐I gels. Complexity 2011, 16, 22–28. [Google Scholar] [CrossRef]
- Stylianopoulos, T.; Barocas, V.H. Volume-averaging theory for the study of the mechanics of collagen networks. Comput. Methods Appl. Mechan. Eng. 2007, 196, 2981–2990. [Google Scholar] [CrossRef]
- Head, D.A.; Levine, A.J.; MacKintosh, F.C. Distinct regimes of elastic response and deformation modes of cross-linked cytoskeletal and semiflexible polymer networks. Phys. Rev. E 2003, 68. [Google Scholar] [CrossRef]
- Heussinger, C.; Schaefer, B.; Frey, E. Nonaffine rubber elasticity for stiff polymer networks. Phys. Rev. E 2007, 76. [Google Scholar] [CrossRef]
- Heussinger, C.; Frey, E. Stiff polymers, foams, and fiber networks. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Onck, P.R.; Koeman, T.; van Dillen, T.; van der Giessen, E. Alternative explanation of stiffening in cross-linked semiflexible networks. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Hulmes, D.J.; Miller, A. Quasi-hexagonal molecular packing in collagen fibrils. Nature 1979, 282, 878–880. [Google Scholar] [CrossRef] [PubMed]
- Digimat, A. Software for the Linear and Nonlinear Multi-Scale Modeling of Heterogeneous Materials; e-Xstream Engineering: Louvain-la-Neuve, Belgium, 2011. [Google Scholar]
- Lindström, S.B.; Vader, D.A.; Kulachenko, A.; Weitz, D.A. Biopolymer network geometries: Characterization, regeneration, and elastic properties. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef]
- Rezakhaniha, R.; Agianniotis, A.; Schrauwen, J.T.; Griffa, A.; Sage, D.; Bouten, C.V.; van de Vosse, F.N.; Unser, M.; Stergiopulos, N. Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy. Biomech. Model. Mechanobiol. 2012, 11, 461–473. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Basu, A.; Winer, J.P.; Yodh, A.; Janmey, P.A. Local and global deformations in a strain-stiffening fibrin gel. New J. Phys. 2007, 9. [Google Scholar] [CrossRef]
- Parenteau-Bareil, R.; Gauvin, R.; Berthod, F. Collagen-based biomaterials for tissue engineering applications. Materials 2010, 3, 1863–1887. [Google Scholar] [CrossRef]
- Balguid, A.; Rubbens, M.P.; Mol, A.; Bank, R.A.; Bogers, A.J.; van Kats, J.P.; de Mol, B.A.; Baaijens, F.P.; Bouten, C.V. The role of collagen cross-links in biomechanical behavior of human aortic heart valve leaflets-relevance for tissue engineering. Tissue Eng. 2007, 13, 1501–1511. [Google Scholar] [CrossRef] [PubMed]
- Gardel, M.L.; Shin, J.H.; MacKintosh, F.C.; Mahadevan, L.; Matsudaira, P.; Weitz, D.A. Elastic behavior of cross-linked and bundled actin networks. Science 2004, 304, 1301–1305. [Google Scholar] [CrossRef] [PubMed]
- Gardel, M.L.; Kasza, K.E.; Brangwynne, C.P.; Liu, J.; Weitz, D.A. Mechanical response of cytoskeletal networks. Methods Cell Biol. 2008, 89, 487–519. [Google Scholar] [PubMed]
- Lake, S.P.; Hadi, M.F.; Lai, V.K.; Barocas, V.H. Mechanics of a fiber network within a non-fibrillar matrix: Model and comparison with collagen-agarose co-gels. Ann. Biomed. Eng. 2012, 40, 2111–2121. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Gu, L. Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel. Materials 2015, 8, 551-560. https://doi.org/10.3390/ma8020551
Lin S, Gu L. Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel. Materials. 2015; 8(2):551-560. https://doi.org/10.3390/ma8020551
Chicago/Turabian StyleLin, Shengmao, and Linxia Gu. 2015. "Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel" Materials 8, no. 2: 551-560. https://doi.org/10.3390/ma8020551
APA StyleLin, S., & Gu, L. (2015). Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel. Materials, 8(2), 551-560. https://doi.org/10.3390/ma8020551






