3.1. Laboratory Tests
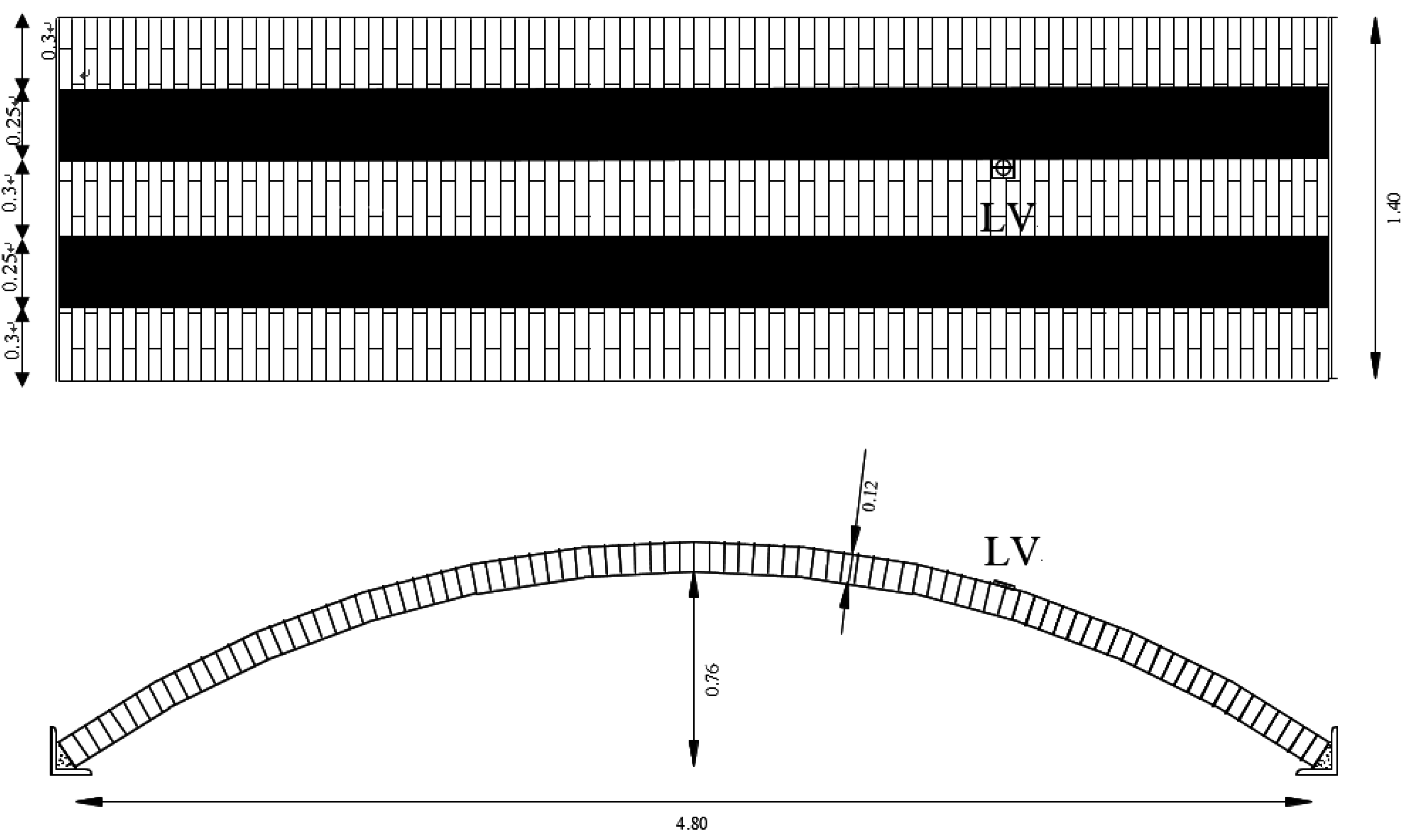
For the laboratory tests, the dynamic excitation is achieved through the use of a sling which allows the “vertical raising” of the vault followed by the release of the sling to enable the vault to vibrate (
Figure 6) until rest. Individual resonance peaks are detected on the Frequency Response Function (FRF) plot and the frequency of maximum response is taken as the mode natural frequency.
Figure 6.
Raising of the vault to allow free vibrations.
Figure 6.
Raising of the vault to allow free vibrations.
In the case of specimen BV1, the sling was applied at left haunch and the excitation method allowed the measurement of the natural modal frequencies, particularly the first mode frequency. Measurement of vibrations of the vaults have been recorded using a Polytec Doppler laser-vibrometer model OFV 3001-OFV 303 (Polytec GmbH, Waldbronn, Germany) with CPU OFV-600 at the center point of the “raised” haunch along a direction with a slope of 40° on the horizontal plane. Results are partially reported in [
25]. From the experimental investigations on specimens BV2 and BV3, with the excitation applied at one haunch, the results are presented in
Table 2.
Table 2.
Natural frequencies under free oscillation.
Table 2.
Natural frequencies under free oscillation.
| Specimen | Undamaged | Damaged | Strengthened |
|---|
| 1st Mode (Hz) | 2nd Mode (Hz) | 1st Mode (Hz) | 2nd Mode (Hz) | 1st Mode (Hz) | 2nd Mode (Hz) |
|---|
| BV1 | 11.25 | – | 10.50 | – | 12.50 | – |
| BV2 | 10.00 | – | 6.25 | 10.62 | 9.37 | 18.75 |
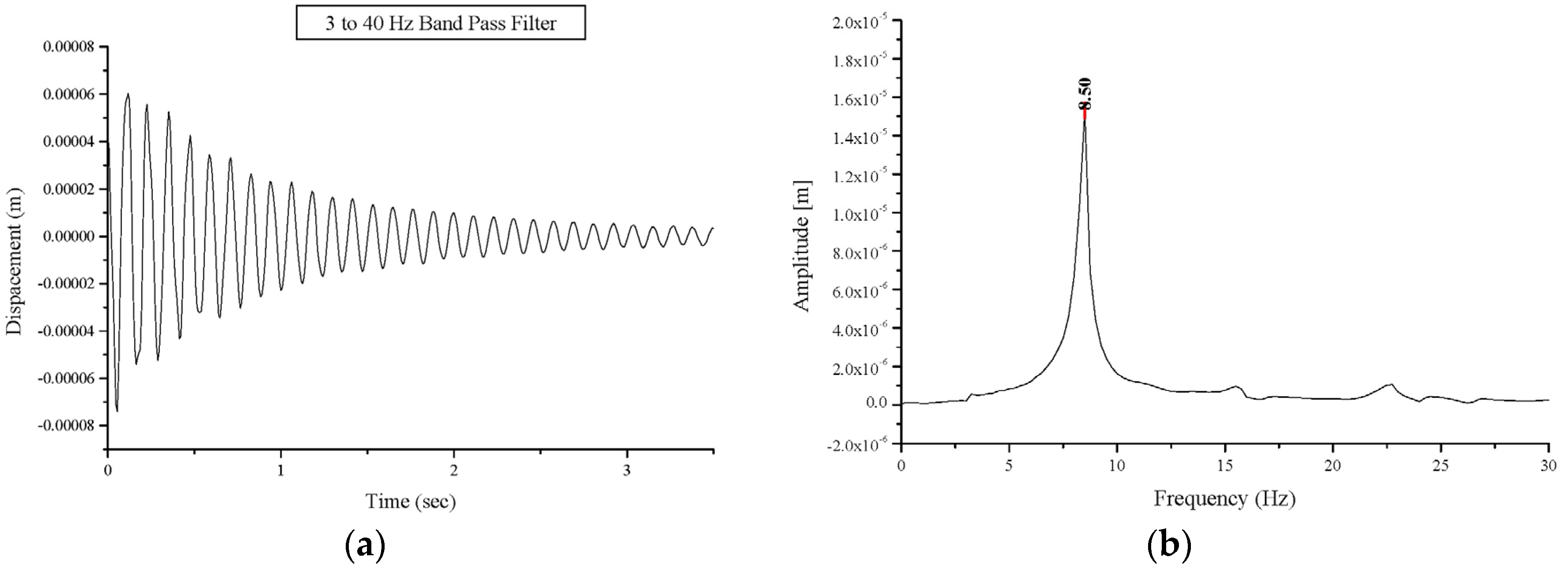
| BV3 | 6.25 | 13.00 | 3.50 | 9.00 | 8.50 | 15.50 |
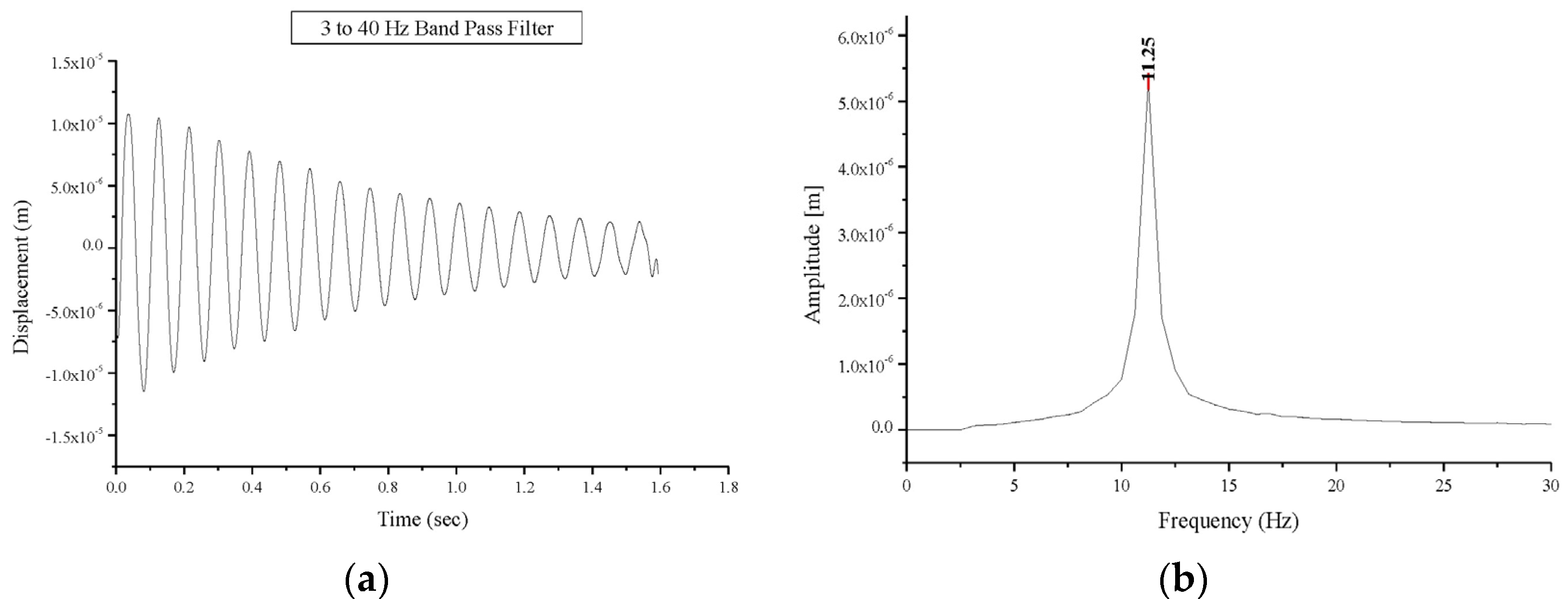
Testing of the masonry vaults occurred 45 days post-construction. The first modal frequencies values of 11.25 Hz and 10.00 Hz were recorded for BV1 and BV2 respectively (
Figure 7) while a much lower natural frequency value, 6.25 Hz, up to 40% lower, was recorded for BV3. These frequency values can be also compared with those obtained from a numerical simulation: frequencies of 10.66 and 9.62 Hz were found from the numerical simulation for BV1- and BV3-type vaults, respectively. For a BV1-type vault, these values are in a very good agreement with experimental ones. The difference in dynamic behavior illustrated by the first-mode natural frequency of BV3 when compared with BV1 and BV2, can be explained by the difference in vault thickness and the presence of the ribs.
Figure 7.
Free oscillations response of the undamaged vault BV1: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
Figure 7.
Free oscillations response of the undamaged vault BV1: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
A simple 3D linear finite element model has been used to deepen the dynamic behaviour of the vault. The geometry is the same of the experimentally tested specimens and the vault body is created by an Ansys [
26] software using Solid 65 elements (three-dimensional eight-node hexahedron isoparametric elements). For the boundary conditions in the finite element model of the vault, all translations are fixed at the vault imposts, but rotations are allowed.
For the sake of simplicity, both elastic and perfectly plastic behavior were adopted: (a) with infinite ductility and (b) with isotropic behavior hypotheses for the material. It must be underlined that such assumptions do not take into account two important aspects of masonry at failure, the first related to the damaging behavior of joints, the latter related to the well-known higher masonry horizontal in-plane strength with respect to the vertical one, essentially due to brick staggering. Nevertheless, these aspects cannot be taken into account easily. On the other hand, the assumption of a zero tensile strength with frictional behavior is widely accepted [
27] for the analysis of masonry constructions. Within this approach, a Mohr–Coulomb type failure criterion with tension cut-off type behavior was assumed for masonry. This failure criterion, initially adopted for concrete, accounts for both cracking and crushing failure modes through a smeared model. In particular, the masonry brittle behavior was here defined by means of only two constants:
ft (uniaxial tensile strength) and
fc (uniaxial compressive strength).
The main aim of this simple model was only to determine the natural frequencies and modes of vibrations.
Figure 8 shows the first two natural modes of vibration of BV3. For undamaged vaults, this analysis demonstrated that the experimental value of first natural frequency is very similar to the numerical one: the first natural frequency from the model was 11.12 Hz (compared to 11.25 and 10 Hz measured for BV1 and BV2, respectively). For damaged vaults, the results of numerical and experimental tests highly differed for the difficulty of modelling the vault damage and the hinges. This difference (in terms of first natural frequency value) reduced for strengthened vaults (numerical 11.84 Hz, average experimental 10.93 Hz) due to the mitigation of non-linear effects.
Figure 8.
Numeric simulation: the first (a) and second (b) mode of vibration (BV3).
Figure 8.
Numeric simulation: the first (a) and second (b) mode of vibration (BV3).
Damping values were also calculated for all the three tested masonry vaults (
Table 3). The value of the damping α, has taken into consideration the time range (
ti+1,
ti) of approximate 0.4 s and also the tests with the sling placed at the left haunch. For an underdamped system:
The value of the damping α is given by:
xi and xi+1 are the peaks of the displacements x(t) respectively within the time range ti+1, ti.
Table 3.
Recorded damping values from free oscillations.
Table 3.
Recorded damping values from free oscillations.
| Specimen | Undamaged (s−1) | Damaged (s−1) | Strengthened (s−1) |
|---|
| BV1 | 1.28 | 1.50 | 1.47 |
| BV2 | 1.25 | 2.08 | 1.75 |
| BV3 | 1.22 | 1.87 | 1.15 |
Free oscillation tests were also performed on the damaged vaults. Damage was caused by a vertical load through the application of two hydraulic cylinders and a spreader beam under one haunch (
Figure 9). The static vertical loading was increased until hinges formed at three locations along the curved length of the vault; one hinge occurred around the vault springing, another hinge formed over the position of the vertical load, and the third hinge formed in the opposite haunch 11 brick lengths from the crown (for BV1-type vault).
Figure 9.
(a) Application of hydraulic cylinders to promote damage; (b) Hinge formation.
Figure 9.
(a) Application of hydraulic cylinders to promote damage; (b) Hinge formation.
The global behavior of the damaged vaults was predominantly elastic allowing for analysis of the vault’s behavior via free oscillation tests, as previously done for the undamaged vault. A decrease in the frequencies of the first natural mode was recorded in all tests carried out on the damaged vaults compared to the values recorded for undamaged vaults. Natural frequencies values of first and second mode for the tested masonry vaults are presented in
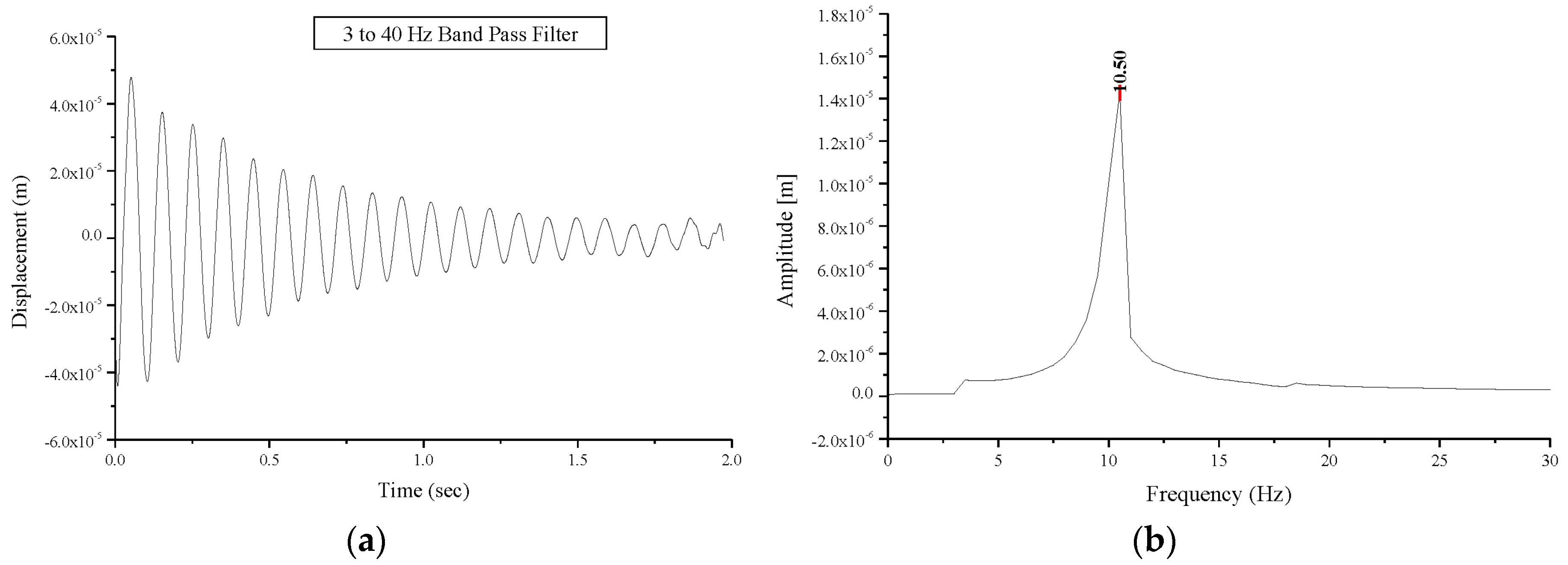
Table 2. The first natural mode frequency value for specimen BV1 experiences a decrease from 11.25 Hz (undamaged vault) to 10.50 Hz (damaged vault) as shown in
Figure 10, while a decrease from 10.00 Hz to 6.25 Hz and from 6.25 Hz to 3.50 Hz was recorded for specimens BV2 and BV3, respectively. The decrease in the first-mode natural frequency is a consequence of the damage sustained. This value depends on the positions of the hinges and the extent of structural damage. This explains the different values (10.50 and 6.25 Hz) recorded for vaults BV1 and BV2. It must be highlighted that if damage does not progress, this value remains constant with time. Similarly, an increase in the damping values was experienced in the damaged vaults compared to the undamaged vaults. The damping values are summarized in
Table 3. Corresponding values were recorded for undamaged vaults (average value 1.25 s
−1). The damage resulted in an increase in the damping value between 17.1% and 66.4%.
Figure 10.
Free oscillations’ response of the damaged vault BV1: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
Figure 10.
Free oscillations’ response of the damaged vault BV1: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
The test procedure, applied to the undamaged and damaged vaults was repeated on strengthened vaults, and the results are presented in
Table 2 and
Table 3. Due to the strengthening, an increase in the frequencies of the first natural mode compared to those for damaged vaults was recorded. The first mode frequency values for the strengthened vaults were almost the same as that of the undamaged vaults. The first natural mode frequency for specimen BV3 after strengthening, reached the value of 8.50 Hz compared the 6.25 Hz and 3.50 Hz for the same vault in the undamaged and the damaged configurations, respectively (
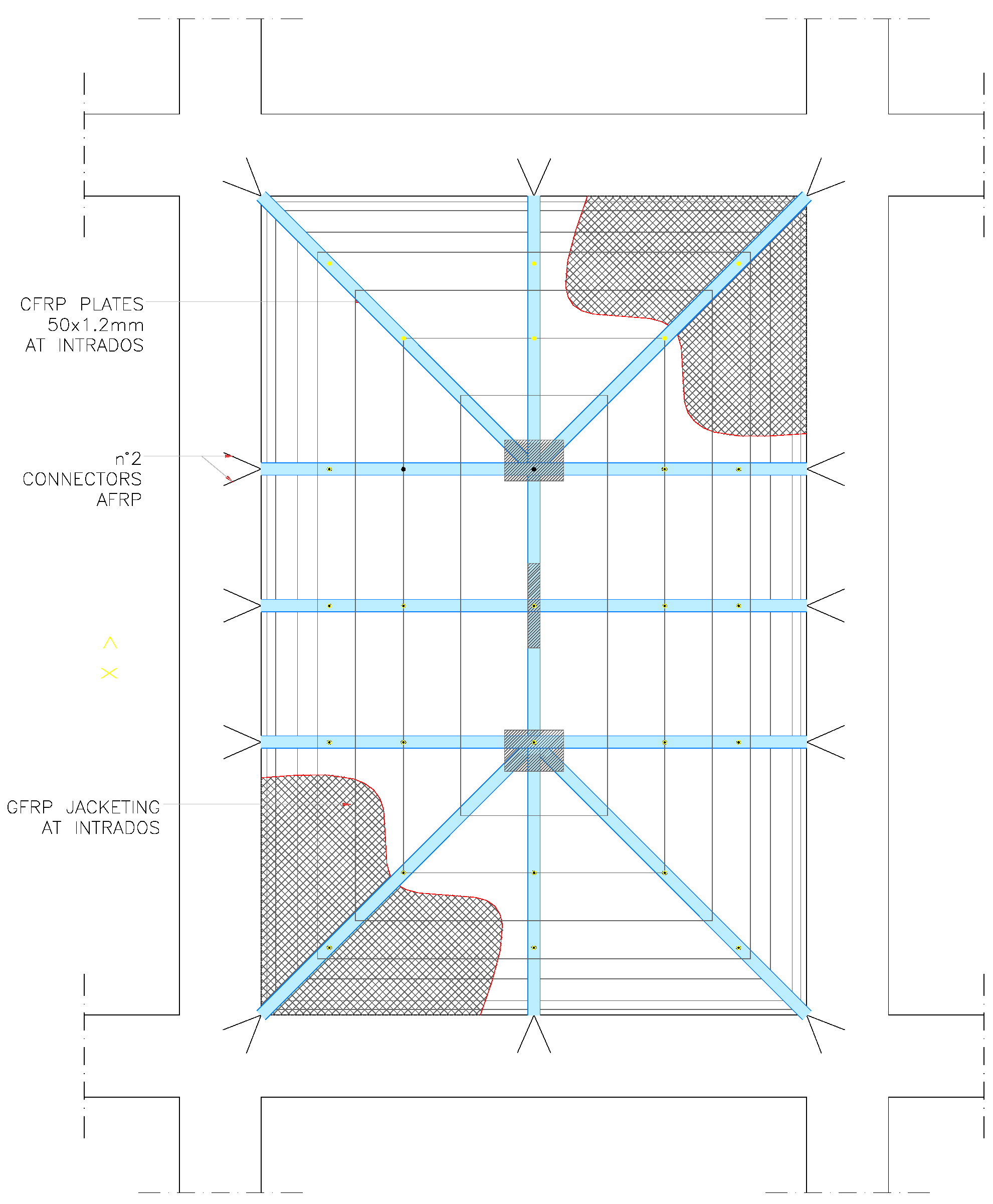
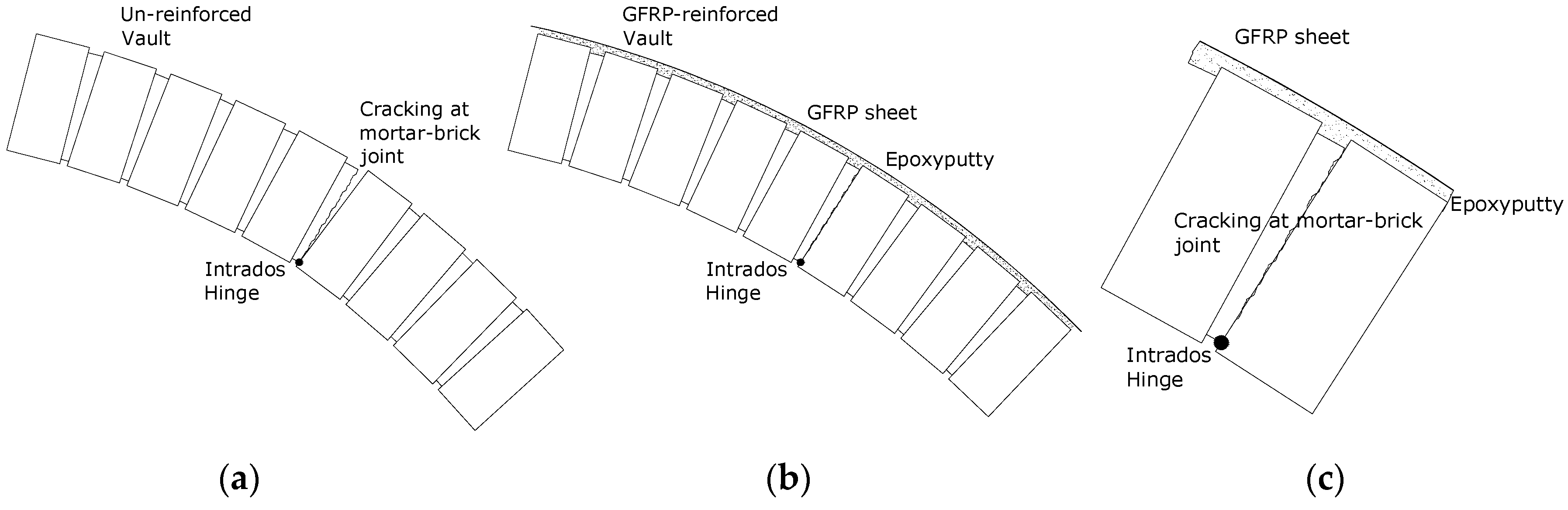
Figure 11). The cracks where the three hinges formed are still present, but tensile stresses are now transferred to the GFRP reinforcements (
Figure 12).
Strengthening with GFRP sheets has resulted in a decrease of the damping value (
Table 3) for the repaired vault compared to the vault that is damaged but has had no strengthening interventions. However, the application of the GFRP at the vault extrados has not re-established the original damping values due to the presence of the mortar joint cracks. This could be considered as an additional advantage to be gained from strengthening. Reinforcement can greatly enhance the tensile strength of masonry while re-establishing the original dynamic response of the undamaged structure.
Figure 11.
Free oscillations’ response of the strengthened vault BV3: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
Figure 11.
Free oscillations’ response of the strengthened vault BV3: (a) displacement versus time; (b) Fourier transform: amplitude versus frequency.
Figure 12.
(a) Hinge opening at intrados for the un-reinforced vault; (b) GFRP reinforced vault; (c) detail at the hinge after the application of the reinforcement.
Figure 12.
(a) Hinge opening at intrados for the un-reinforced vault; (b) GFRP reinforced vault; (c) detail at the hinge after the application of the reinforcement.
Consideration of the behavior of the rib masonry barrel vault illustrates the natural frequency of the strengthened specimen to be higher than in the control undamaged vault. This may be explained by the increased masonry stiffness between the ribs, resulting from the application of fibre strips. A high decrease in damping was suggested in the damping value following the strengthening application.
3.2. On-site Tests
A further dynamic investigation has been carried out on-site on a thin brick vault to validate the efficiency of the reinforcing technique. Dynamic tests were performed on the vault before and after the application of reinforcement at the intrados. Free vault oscillations were induced by a blow from a sledgehammer. The tests were conducted over a period of four days, as a preliminary investigation into the dynamic characteristics of the vault. A full modal survey was not conceived, the study only served to identify the prominent modes of vibration. It was expected that a mildly non-linear response of the masonry vault would be observed due to the presence of cracks at the sides of the un-strengthened damaged vault.
A 2 kg sledgehammer instrumented with a piezoelectric force transducer was used for the forced excitation of the vault. The response of the structure was measured using three low-frequency Monitran MTN/7100 accelerometers with nominal sensitivity of 5.39 mV/g.
Both force and response signals were filtered using a 16th order low-pass Butterworth filter with a cut-off frequency of 200 Hz. Accelerometers mounted on steel blocks were attached to the masonry vault with an adhesive. Hammer excitation was concentrated on the vault key-stone, as it was almost level, and, therefore, easy to balance on (
Figure 13). The magnitude of the accelerations were recorded at the vault haunches on a direction perpendicular to the vault surface at that point. The Frequency Response Function (FRF) for each location was obtained from an average of ten hammer blows for a spectral resolution of 0.0625 Hz.
Figure 13.
Sledge hammer applied to the crown of the vault intrados.
Figure 13.
Sledge hammer applied to the crown of the vault intrados.
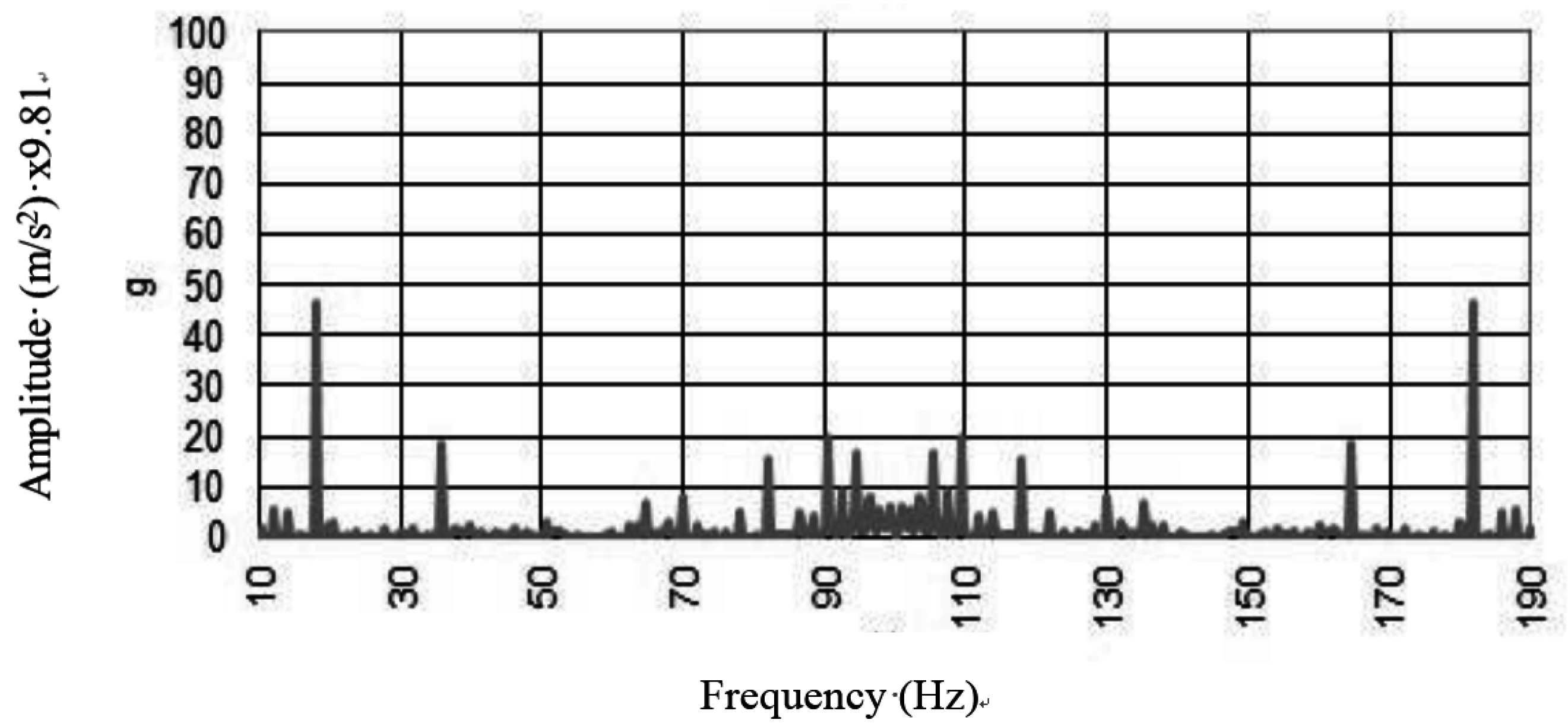
Typical FRF spectra for un-reinforced vault (
Figure 14) are presented showing their component magnitudes. The damage to the vault promoted an inelastic dynamic response and any natural frequency could be recorded for the vault. Dynamic pounding between closely spaced parts of the vault resulted in the recording of high peaks for the amplitude of acceleration, but any dynamic analysis could be executed.
Figure 14.
Free oscillations’ response to the in situ test on the damaged vault.
Figure 14.
Free oscillations’ response to the in situ test on the damaged vault.
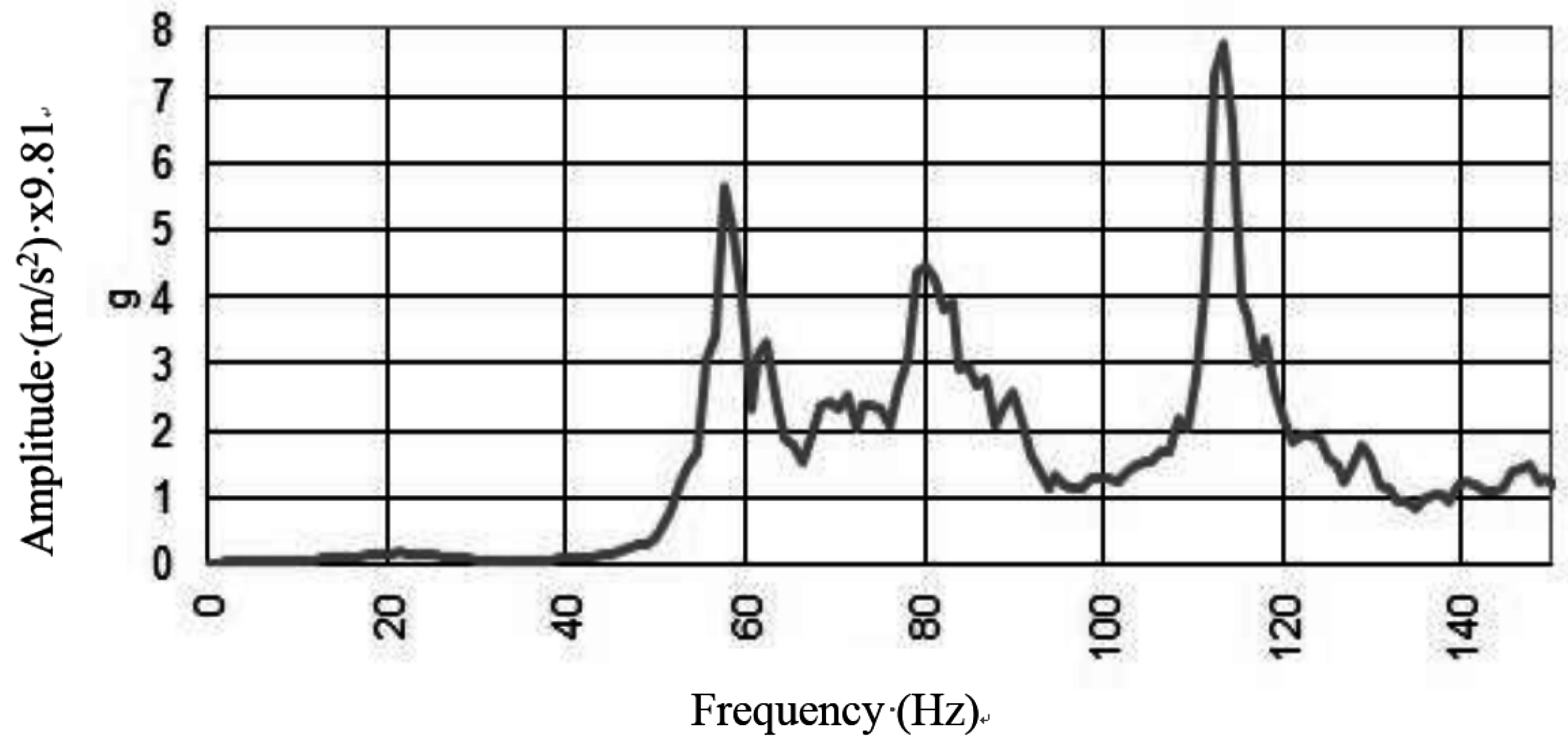
For the reinforced vault, an elastic behavior was restored and the vault exhibited a clear dynamic behavior (
Figure 15). Modal peaks in the spectra indicated the presence of a number of modes of vibration below 120 Hz. The well-defined peaks represent individual modes, and their repeatability across the full spectral set facilitated a modal analysis. Re-establishing the elastic behavior of the vault through application of reinforcement is considered to be a positive result of the investigation.
Figure 15.
Free oscillations response to the in situ test on the reinforced vault.
Figure 15.
Free oscillations response to the in situ test on the reinforced vault.