Investigation of Key Parameters of Rock Cracking Using the Expansion of Vermiculite Materia
Abstract
:1. Introduction
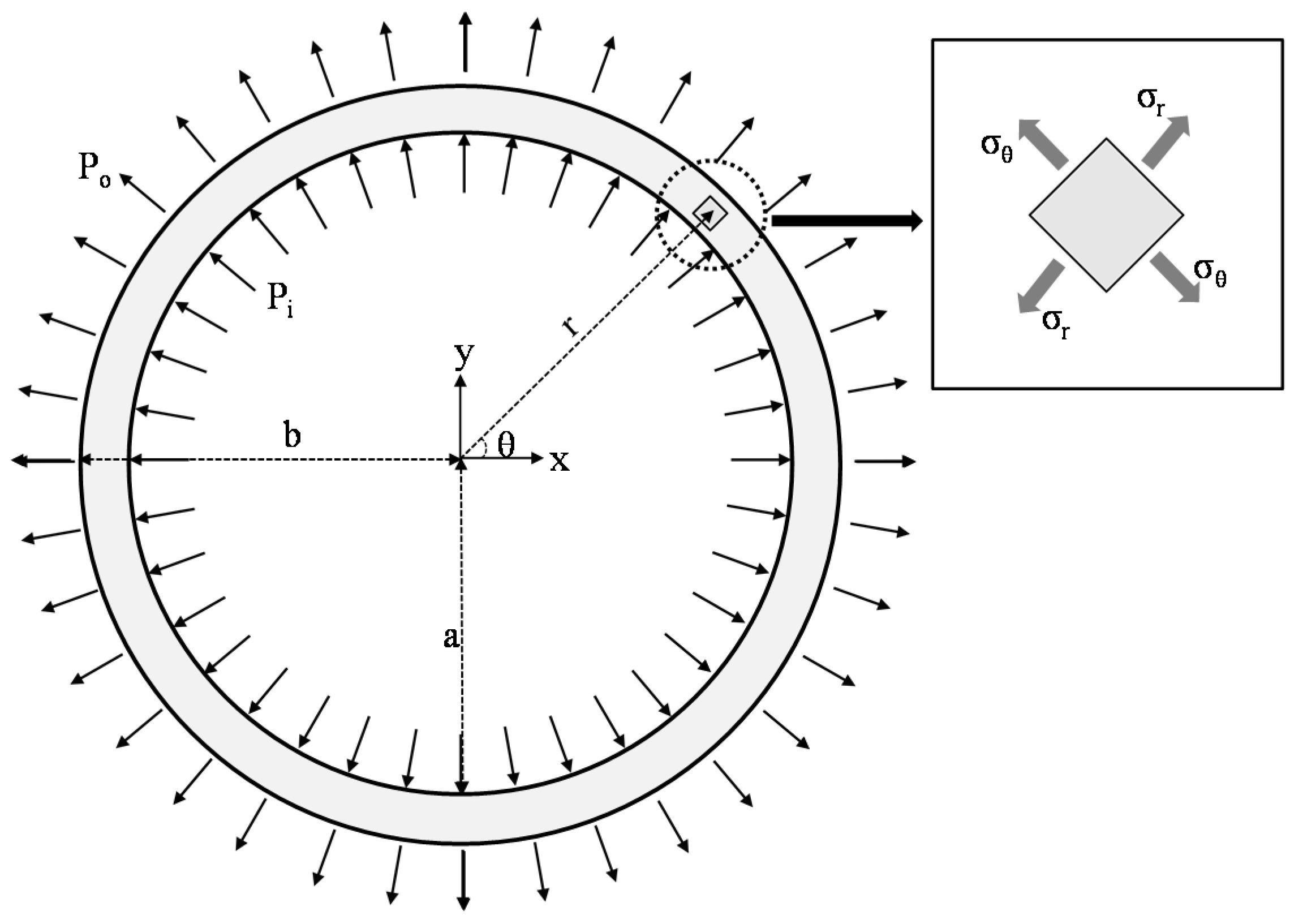
2. Vermiculite Expansion

3. Experimental Tests
3.1. Experimental Setup

| Model ID | Conditions | Other Remarks |
|---|---|---|
| T1-1 | Large Particle Size: LPS (8 mm) | Diameter of Heater (21 mm) **Equal Mixing Ratios |
| T1-2 | Middle Particle Size: MPS (5 mm) | |
| T1-3 | Small Particle Size: SPS (3 mm) | |
| T2-1 | *Particle Mixing Ratio (LPS:MPS = 9:1) | Diameter of Heater (21 mm) **Equal Mixing Ratios |
| T2-2 | *Particle Mixing Ratio (LPS:MPS = 7:3) | |
| T2-3 | *Particle Mixing Ratio (LPS:MPS = 5:5) | |
| T3-1 | Diameter of Heater (24 mm) | *Particle Mixing Ratio (LPS:MPS = 9:1) **Equal Mixing Ratios |
| T3-2 | Diameter of Heater (21 mm) | |
| T3-3 | Diameter of Heater (18 mm) |


3.2. Expansion Measurements
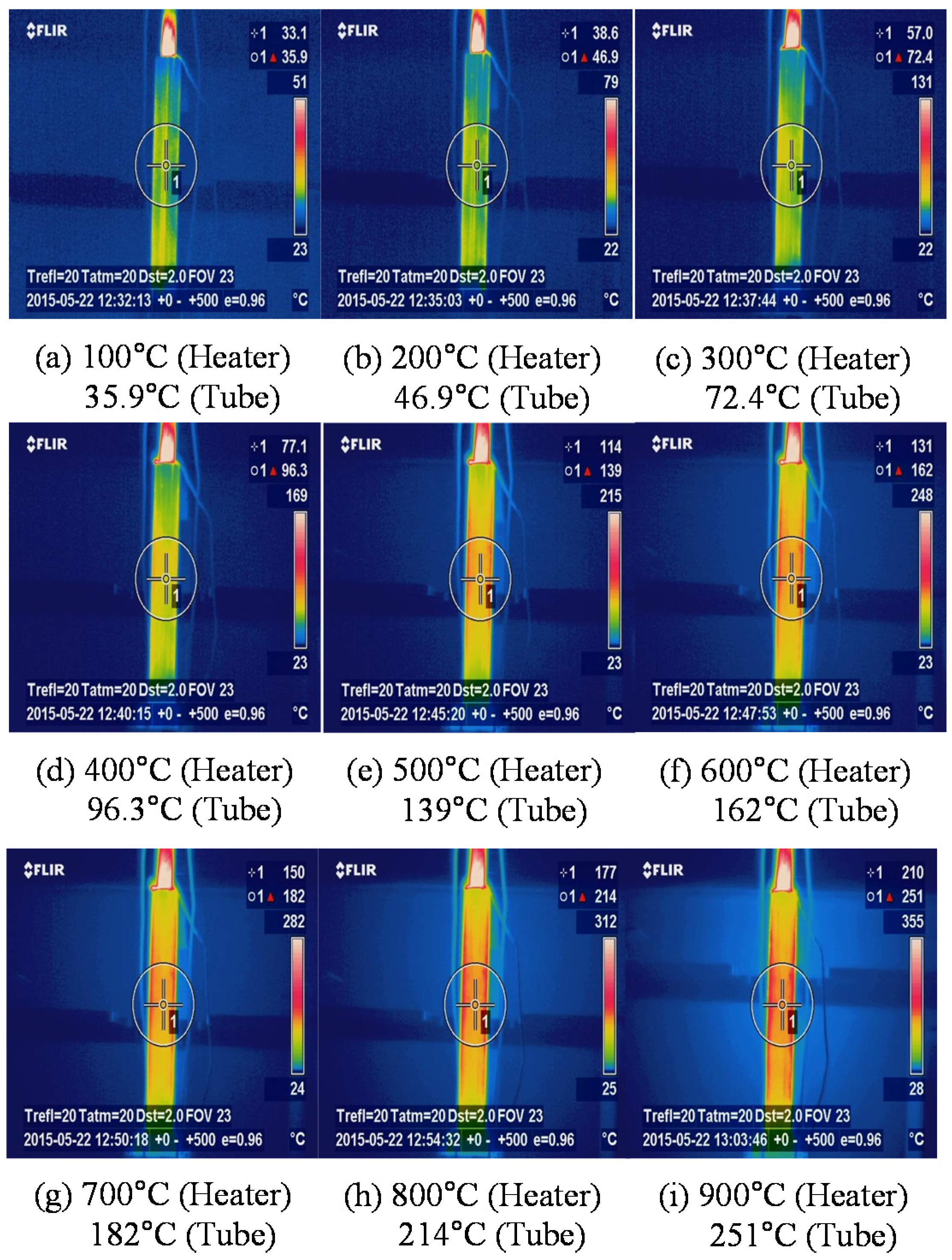
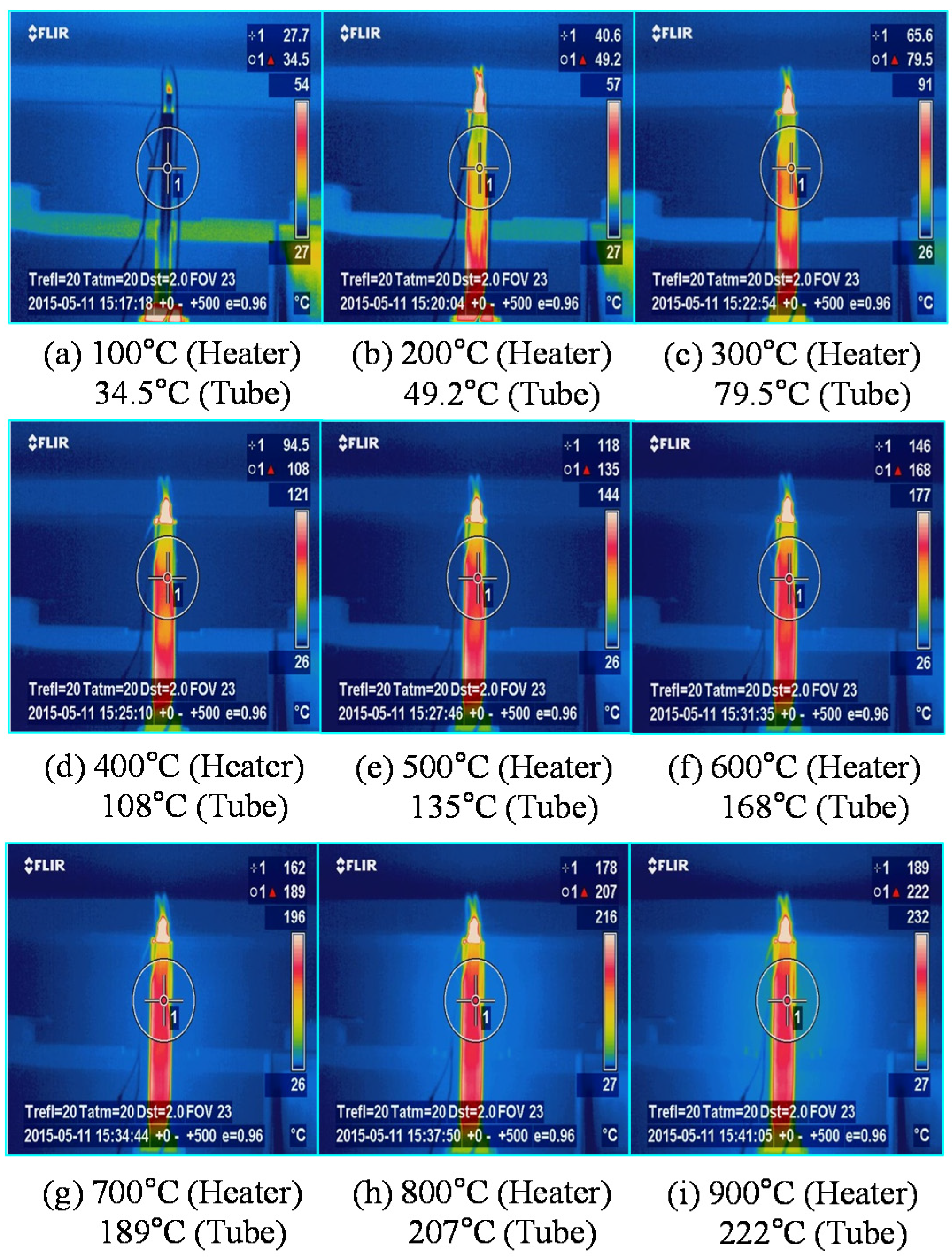
4. Experimental Results
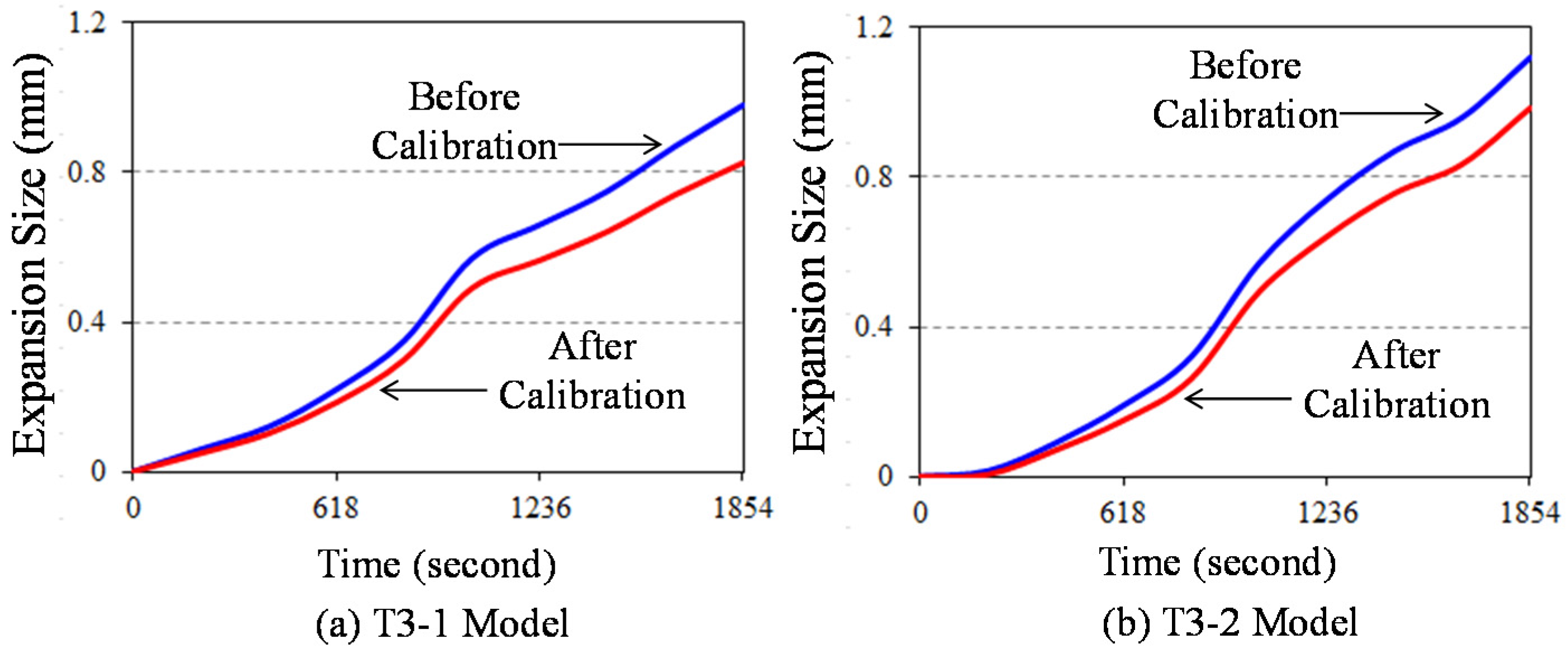
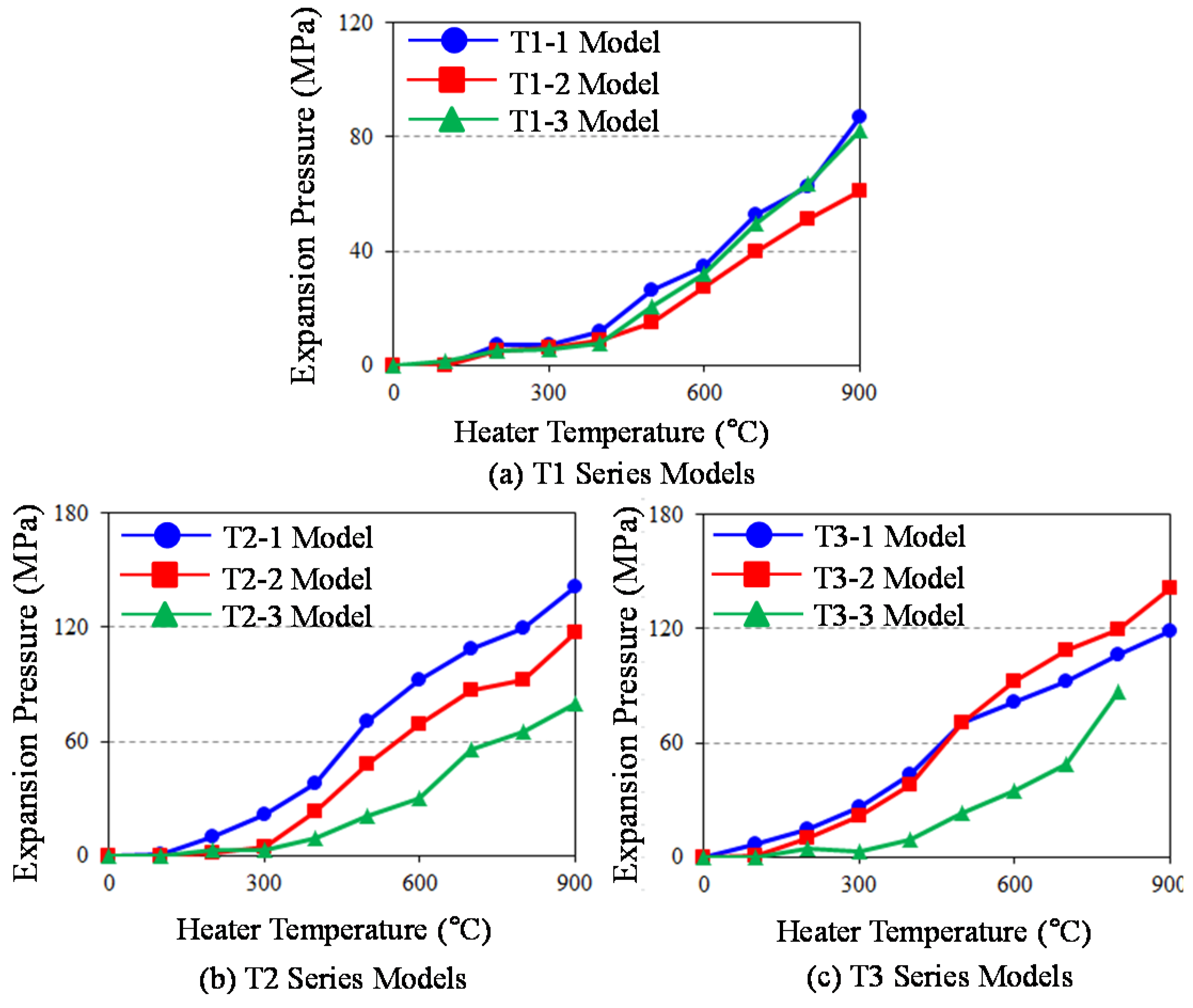
5. Parametric Investigation
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arshadnejad, S.; Goshtasbi, K.; Aghazadeh, J. A model to determine hole spacing in the rock fracture process by non-explosive expansion material. Int. J. Min. Met. Mater. 2011, 18, 509–514. [Google Scholar] [CrossRef]
- Nateghi, R. Prediction of ground vibration level induced by blasting at different rock units. Int. J. Rock Mech. Min. Sci. 2011, 48, 899–908. [Google Scholar] [CrossRef]
- Yagiz, S. Assessment of brittleness using rock strength and density with punch penetration test. Tunnel. Undergr. Space Tech. 2009, 24, 66–74. [Google Scholar] [CrossRef]
- Nateghi, R.; Kiyani, M.; Gholipour, O. Control negative effects of blasting waves on concrete of the structures by analyzing of parameters of ground vibration. Tunnel. Undergr. Space Tech. 2009, 24, 608–616. [Google Scholar] [CrossRef]
- Arshadnejad, S.; Goshtasbi, K.; Aghazadeh, J. Stress concentration analysis between two neighboring circular holes under internal pressure of a non-explosive expansion material. Earth Sci. 2009, 30, 259–270. [Google Scholar]
- Song, K.; Oh, T.; Cho, G. Precutting of tunnel perimeter for reducing blasting-induced vibration and damaged zone—numerical analysis. KSCE J. Civil Eng. 2014, 18, 1165–1175. [Google Scholar] [CrossRef]
- Jeng, F.S.; Huang, T.H.; Hilmersson, S. New development of waterjet technology for tunnel excavation purposes. J. Korean Tunnel. Undergr. Space Assoc. 2004, 19, 438–439. [Google Scholar]
- Oh, T.M.; Cho, G. Effect of abrasive waterjet parameters on rock removal. J. Korean Tunnel. Undergr. Space Assoc. 2012, 14, 421–435. [Google Scholar] [CrossRef]
- Arshadnejad, S.H.; Goshtasbi, K.; Aghazadeh, J. Stress analysis due to time and investigating of crack growth in rock, under non-explosive expansion material’s pressure. J. Geo. Env. 2010, 4, 1–14. [Google Scholar]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behavior of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Hillier, S.; Marwa, E.M.M.; Rice, C.M. On the mechanism of exfoliation of ‘Vermiculite’. Clay Min. 2013, 48, 563–582. [Google Scholar] [CrossRef]
- Brindley, G.W.; Zalba, P.E.; Bethke, C.M. Hydrobiotite, a regular 1:1 interstratification of biotite and vermiculite layers. American Miner. 1983, 68, 420–425. [Google Scholar]
- Douglas, L.A. Vermiculite; Book Series No.1; Soil Science Society of America: Fitchburg, MA, USA, 1989. [Google Scholar]
- Muiambo, H.F.; Focke, W.W.; Atanasova, M.; Westhuizen, I.V.; Tiedt, L.R. Thermal properties of sodium-exchanged palabora vermiculite. Appl. Clay Sci. 2010, 50, 51–57. [Google Scholar] [CrossRef]
- ThermaCAM® S65. Available online: http://yellotec.com/pdf/S65_Datasheet.pdf (accessed on 30 September 2015).
- Ibrahim, A.; Rye, Y.; Saidpour, M. Stress analysis of thin-walled pressure vessels. Modern Mech. Eng. 2015, 5, 1–9. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, C.-H.; Hu, J.W. Investigation of Key Parameters of Rock Cracking Using the Expansion of Vermiculite Materia. Materials 2015, 8, 6950-6961. https://doi.org/10.3390/ma8105351
Ahn C-H, Hu JW. Investigation of Key Parameters of Rock Cracking Using the Expansion of Vermiculite Materia. Materials. 2015; 8(10):6950-6961. https://doi.org/10.3390/ma8105351
Chicago/Turabian StyleAhn, Chi-Hyung, and Jong Wan Hu. 2015. "Investigation of Key Parameters of Rock Cracking Using the Expansion of Vermiculite Materia" Materials 8, no. 10: 6950-6961. https://doi.org/10.3390/ma8105351
APA StyleAhn, C.-H., & Hu, J. W. (2015). Investigation of Key Parameters of Rock Cracking Using the Expansion of Vermiculite Materia. Materials, 8(10), 6950-6961. https://doi.org/10.3390/ma8105351






