Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Surgical Procedures
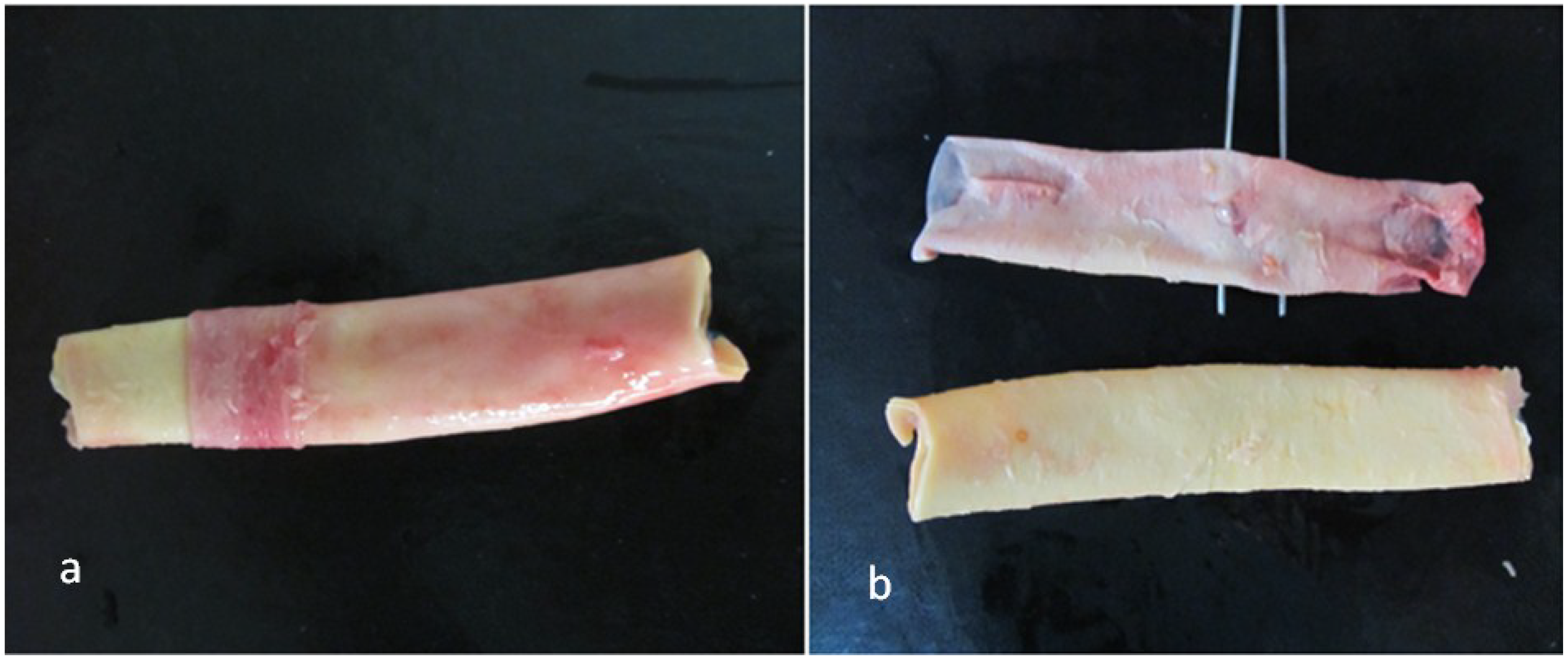
2.2. Tissue Preparation
2.3. Biaxial Testing

2.4. Histological Staining
2.5. Constitutive Equations and Parameter Estimation
2.5.1. Theoretical Framework
2.5.2. Strain Energy Function
2.5.3. Parameter Estimation
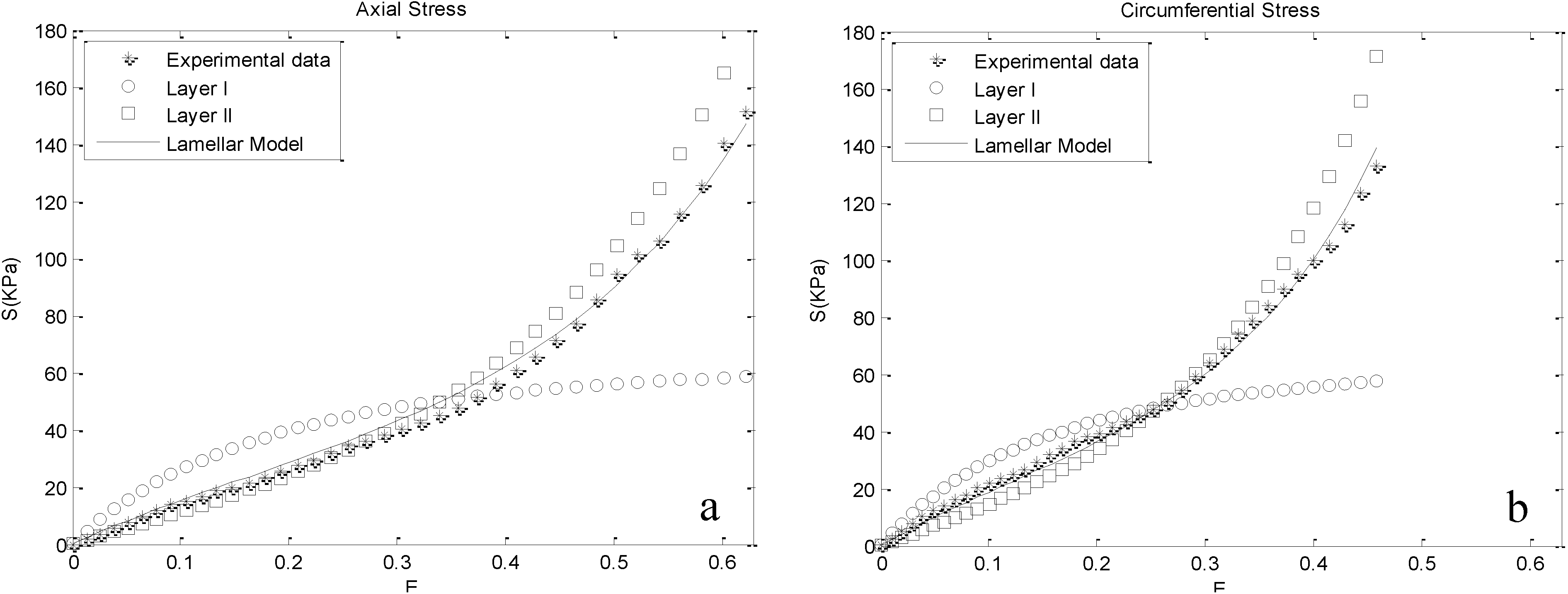
3. Results

| Parameters | Cases | ||
|---|---|---|---|
| M25 | M28 | M42 | |
| fI (-) | 0.2803 ± 0.0113 | 0.2711 ± 0.0100 | 0.2172 ± 0.0067 |
| fII (-) | 0.7197 ± 0.0113 | 0.7289 ± 0.0100 | 0.7828 ± 0.0067 |
| c1 (kPa) | 33.894 | 43.795 | 43.428 |
| c2 (kPa) | 35.877 | 15.692 | 46.627 |
| a1 (-) | 1.4655 | 1.9984 | 1.1188 |
| a2 (-) | 1.85712 | 2.2043 | 1.2865 |
| a3 (-) | 0.0473 | 0.0080 | 0.2265 |
| R2 (-) | 0.9946 | 0.9761 | 0.9959 |
4. Discussion
5. Limitations
6. Conclusions
- Visualizing the contributions of Layers I and II for the range of physiologic and supraphysiological deformations.
- Providing an appropriate fit to biaxial test data of the aortic samples in both the axial and circumferential directions for different functional phases, i.e., initial crimp and gradual activation of collagen fibers. The model predictions were in good agreement with the experimental data in both the circumferential and axial directions.
Author Contributions
Conflicts of Interest
References
- Humphrey, J.D. Mechanics of the arterial wall: Review and directions. Crit. Rev. Biomed. Eng. 1995, 23, 1–162. [Google Scholar] [PubMed]
- Nichols, M.; Townsend, N.; Luengo-Fernandez, R.; Leal, J.; Gray, A.; Scarborough, P.; Rayner, M. European Cardiovascular Disease Statistics 2012; European Society of Cardiology: Brussels, Belgium, 2012. [Google Scholar]
- Takamizawa, K.; Hayashi, K. Strain energy density function and uniform strain hypothesis for arterial mechanics. J. Biomech. 1987, 20, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Bauer, C.A.; Holzapfel, G.A. Determination of constitutive equations for human arteries from clinical data. J. Biomech. 2003, 36, 165–169. [Google Scholar] [CrossRef] [PubMed]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef] [PubMed]
- Haskett, D.; Johnson, G.; Zhou, A.; Utzinger, U.; Vande Geest, J. Microstructural and biomechanical alterations of the human aorta as a function of age and location. Biomech. Model. Mechanobiol. 2010, 9, 725–736. [Google Scholar] [CrossRef] [PubMed]
- Demiray, H.; Vito, R.P. A layered cylindrical–shell model for an aorta. Int. J. Eng. Sci. 1991, 29, 47–54. [Google Scholar] [CrossRef]
- Sommer, G.; Regitnig, P.; Koltringer, L.; Holzapfel, G.A. Biaxial mechanical properties of intact and layer-dissected human carotid arteries at physiological and supraphysiological loadings. Am. J. Physiol. Heart Circ. Physiol. 2010, 298, H898–H912. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Gasser, T.C. A constitutive model for vascular tissue that integrates fibril, fiber and continuum levels with application to the isotropic and passive properties of the infrarenal aorta. J. Biomech. 2011, 44, 2544–2550. [Google Scholar] [CrossRef] [PubMed]
- Zulliger, M.A.; Fridez, P.; Hayashi, K.; Stergiopulos, N. A strain energy function for arteries accounting for wall composition and structure. J. Biomech. 2004, 37, 989–1000. [Google Scholar] [CrossRef] [PubMed]
- Maceri, F.; Marino, M.; Vairo, G. A unified multiscale mechanical model for soft collagenous tissues with regular fiber arrangement. J. Biomech. 2010, 43, 355–363. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Buehler, M.J.; Moran, B. A constitutive model of soft tissue: From nanoscale collagen to tissue continuum. Ann. Biomed. Eng. 2009, 37, 1117–1130. [Google Scholar] [CrossRef] [PubMed]
- Marino, M.; Vairo, G. Multiscale elastic models of collagen bio-structures: From cross-linked molecules to soft tissues. In Multiscale Computer Modeling in Biomechanics and Biomedical Engineering; Springer: Berlin, Germany, 2013; pp. 73–102. [Google Scholar]
- Wagenseil, J.E.; Mecham, R.P. Vascular extracellular matrix and arterial mechanics. Physiol. Rev. 2009, 89, 957–989. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Zhu, Y.; Sun, Z.; Trzeciakowski, J.P.; Gansner, M.; Depre, C.; Resuello, R.R.G.; Natividad, F.F.; Hunter, W.C.; Genin, G.M.; et al. Short communication: Vascular smooth muscle cell stiffness as a mechanism for increased aortic stiffness with aging. Circ. Res. 2010, 107, 615–619. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Lu, X.; Kassab, G. Non-linear micromechanics of soft tissues. Int. J. Non-Linear Mech. 2013, 58, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Bio-viscoelastic solids. In Biomechanics; Springer: New York, NY, USA, 1981; pp. 196–214. [Google Scholar]
- Wolinsky, H.; Glagov, S. A lamellar unit of aortic medial structure and function in mammals. Circ. Res. 1967, 20, 99–111. [Google Scholar] [CrossRef] [PubMed]
- Avolio, A.; Jones, D.; Tafazzoli-Shadpour, M. Quantification of alterations in structure and function of elastin in the arterial media. Hypertension 1998, 32, 170–175. [Google Scholar] [CrossRef] [PubMed]
- Sokolis, D.P.; Kefaloyannis, E.M.; Kouloukoussa, M.; Marinos, E.; Boudoulas, H.; Karayannacos, P.E. A structural basis for the aortic stress–strain relation in uniaxial tension. J. Biomech. 2006, 39, 1651–1662. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.M.; Glagov, S. Transmural organization of the arterial media. The lamellar unit revisited. Arteriosclerosis 1985, 5, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Dingemans, K.P.; Teeling, P.; Lagendijk, J.H.; Becker, A.E. Extracellular matrix of the human aortic media: An ultrastructural histochemical and immunohistochemical study of the adult aortic media. Anat. Rec. 2000, 258, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Rhodin, J.A.G. Architecture of the vessel wall. In Handbook of Physiology, the Cardiovascular System, Vascular Smooth Muscle; American Physiological Society: Bethesda, MD, USA, 1980; Volume 2, pp. 1–31. [Google Scholar]
- O’Connell, M.K.; Murthy, S.; Phan, S.; Xu, C.; Buchanan, J.; Spilker, R.; Dalman, R.L.; Zarins, C.K.; Denk, W.; Taylor, C.A.; et al. The three-dimensional micro- and nanostructure of the aortic medial lamellar unit measured using 3D confocal and electron microscopy imaging. Matrix Biol. 2008, 27, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Weisbecker, H.; Viertler, C.; Pierce, D.M.; Holzapfel, G.A. The role of elastin and collagen in the softening behavior of the human thoracic aortic media. J. Biomech. 2013, 46, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Faghihi, S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater. Sci. Eng. C 2013, 33, 2550–2554. [Google Scholar] [CrossRef]
- Okamoto, R.J.; Wagenseil, J.E.; DeLong, W.R.; Peterson, S.J.; Kouchoukos, N.T.; Sundt, T.M., 3rd. Mechanical properties of dilated human ascending aorta. Ann. Biomed. Eng. 2002, 30, 624–635. [Google Scholar] [CrossRef] [PubMed]
- Limbert, G. A mesostructurally-based anisotropic continuum model for biological soft tissues—Decoupled invariant formulation. J. Mech. Behav. Biomed. Mater. 2011, 4, 1637–1657. [Google Scholar] [CrossRef] [PubMed]
- Wolinsky, H.; Glagov, S. Comparison of abdominal and thoracic aortic medial structure in mammals. Deviation of man from the usual pattern. Circ. Res. 1969, 25, 677–686. [Google Scholar] [CrossRef] [PubMed]
- Yosibash, Z.; Manor, I.; Gilad, I.; Willentz, U. Experimental evidence of the compressibility of arteries. J. Mech. Behav. Biomed. Mater. 2014, 39, 339–354. [Google Scholar] [CrossRef] [PubMed]
- Chuong, C.J.; Fung, Y.C. Three-dimensional stress distribution in arteries. J. Biomech. Eng. 1983, 105, 268–274. [Google Scholar] [CrossRef] [PubMed]
- Delfino, A.; Stergiopulos, N.; Moore, J.E., Jr.; Meister, J.J. Residual strain effects on the stress field in a thick wall finite element model of the human carotid bifurcation. J. Biomech. 1997, 30, 777–786. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Nonlinear solid mechanics: A continuum approach for engineering science. Meccanica 2002, 37, 489–490. [Google Scholar] [CrossRef]
- Agrawal, V.; Kollimada, S.A.; Byju, A.G.; Gundiah, N. Regional variations in the nonlinearity and anisotropy of bovine aortic elastin. Biomech. Model. Mechanobiol. 2013, 12, 1181–1194. [Google Scholar] [CrossRef] [PubMed]
- Hollander, Y.; Durban, D.; Lu, X.; Kassab, G.S.; Lanir, Y. Constitutive modeling of coronary arterial media—Comparison of three model classes. J. Biomech. Eng. 2011, 133. [Google Scholar] [CrossRef]
- Driessen, N.J.; Bouten, C.V.; Baaijens, F.P. A structural constitutive model for collagenous cardiovascular tissues incorporating the angular fiber distribution. J. Biomech. Eng. 2005, 127, 494–503. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C.; Fronek, K.; Patitucci, P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am. J. Physiol. 1979, 237, H620–H631. [Google Scholar] [PubMed]
- Holzapfel, G.A.; Weizsacker, H.W. Biomechanical behavior of the arterial wall and its numerical characterization. Comput. Biol. Med. 1998, 28, 377–392. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Boss, C.; Rezakhaniha, R.; Stergiopulos, N. Experimental characterization of the distribution of collagen fiber recruitment. J. Biorheol. 2011, 24, 84–93. [Google Scholar] [CrossRef]
- Fleenor, B.S. Large elastic artery stiffness with aging: Novel translational mechanisms and interventions. Aging Dis. 2013, 4, 76–83. [Google Scholar] [PubMed]
- Sherratt, M.J. Tissue elasticity and the ageing elastic fibre. Age 2009, 31, 305–325. [Google Scholar] [CrossRef] [PubMed]
- Maceri, F.; Marino, M.; Vairo, G. Age-dependent arterial mechanics via a multiscale elastic approach. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 141–151. [Google Scholar] [CrossRef]
- Roach, M.R.; Burton, A.C. The reason for the shape of the distensibility curves of arteries. Can. J. Biochem. Physiol. 1957, 35, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Lillie, M.A.; Shadwick, R.E.; Gosline, J.M. Mechanical anisotropy of inflated elastic tissue from the pig aorta. J. Biomech. 2010, 43, 2070–2078. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Gasser, T.C. Turnover of fibrillar collagen in soft biological tissue with application to the expansion of abdominal aortic aneurysms. J. R. Soc. Interface 2012, 9, 3366–3377. [Google Scholar] [CrossRef] [PubMed]
- Schriefl, A.J.; Zeindlinger, G.; Pierce, D.M.; Regitnig, P.; Holzapfel, G.A. Determination of the layer-specific distributed collagen fibre orientations in human thoracic and abdominal aortas and common iliac arteries. J. R. Soc. Interface 2012, 9, 1275–1286. [Google Scholar] [CrossRef] [PubMed]
- Debes, J.C.; Fung, Y.C. Biaxial mechanics of excised canine pulmonary arteries. Am. J. Physiol. 1995, 269, H433–H442. [Google Scholar] [PubMed]
- Hill, M.R.; Duan, X.; Gibson, G.A.; Watkins, S.; Robertson, A.M. A theoretical and non-destructive experimental approach for direct inclusion of measured collagen orientation and recruitment into mechanical models of the artery wall. J. Biomech. 2012, 45, 762–771. [Google Scholar] [CrossRef] [PubMed]
- Tsamis, A.; Krawiec, J.T.; Vorp, D.A. Elastin and collagen fibre microstructure of the human aorta in ageing and disease: A review. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Schriefl, A.J.; Wolinski, H.; Regitnig, P.; Kohlwein, S.D.; Holzapfel, G.A. An automated approach for three-dimensional quantification of fibrillar structures in optically cleared soft biological tissues. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghizadeh, H.; Tafazzoli-Shadpour, M.; Shadmehr, M.B.; Fatouraee, N. Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure. Materials 2015, 8, 302-316. https://doi.org/10.3390/ma8010302
Taghizadeh H, Tafazzoli-Shadpour M, Shadmehr MB, Fatouraee N. Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure. Materials. 2015; 8(1):302-316. https://doi.org/10.3390/ma8010302
Chicago/Turabian StyleTaghizadeh, Hadi, Mohammad Tafazzoli-Shadpour, Mohammad B. Shadmehr, and Nasser Fatouraee. 2015. "Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure" Materials 8, no. 1: 302-316. https://doi.org/10.3390/ma8010302
APA StyleTaghizadeh, H., Tafazzoli-Shadpour, M., Shadmehr, M. B., & Fatouraee, N. (2015). Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure. Materials, 8(1), 302-316. https://doi.org/10.3390/ma8010302





