Materials Development for Next Generation Optical Fiber
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Materials Physics of Linear and Nonlinear Optical Phenomena
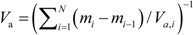 ;
;
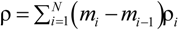 ;
;
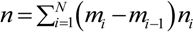 ; and
; and
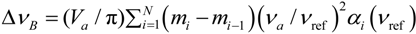
2.2. Materials Solutions
2.2.1. Intrinsically Low Brillouin Gain Glasses and Optical Fibers
| Parameter | Unit | Silica (SiO2) | YAG-Derived Fiber | Al2O3-Derived Fiber | MgO-Derived Fiber | BaO-Derived Fiber | Yb2O3-Derived Fiber | La2O3-Derived Fiber |
|---|---|---|---|---|---|---|---|---|
| Va | m/s | 5970 | 7649 | 9790 | 8731 | 3131 | 4110 | 3979 |
| ρ | kg/m3 | 2200 | 3848 | 3350 | 3322 | 4688 | 8102 | 5676 |
| ΔνB | MHz | 17 | 253 | 274 | † | 178 | 1375 | 181 |
| n | – | 1.444 | 1.868 | 1.653 | 1.810 | 1.792 | 1.881 | 1.877 |
| p12 | – | 0.271 | 0.022 | −0.03 | † | −0.33 | −0.123 | −0.027 |
| Reference | – | 22 | 34 | 22,33 | 36 | 35 | 37 | 49 |
2.2.2. Intrinsically Low Raman Gain Glasses and Optical Fibers
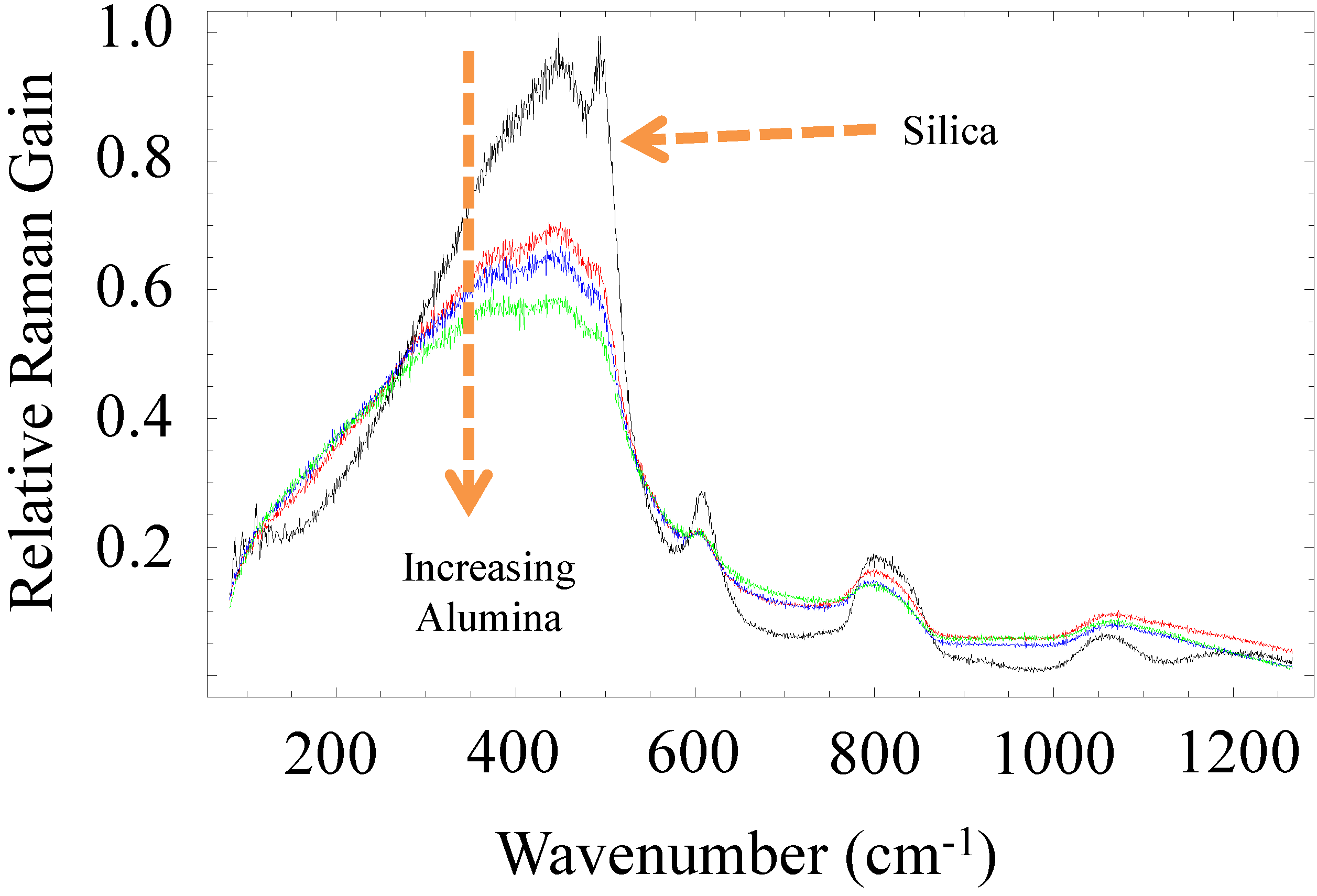
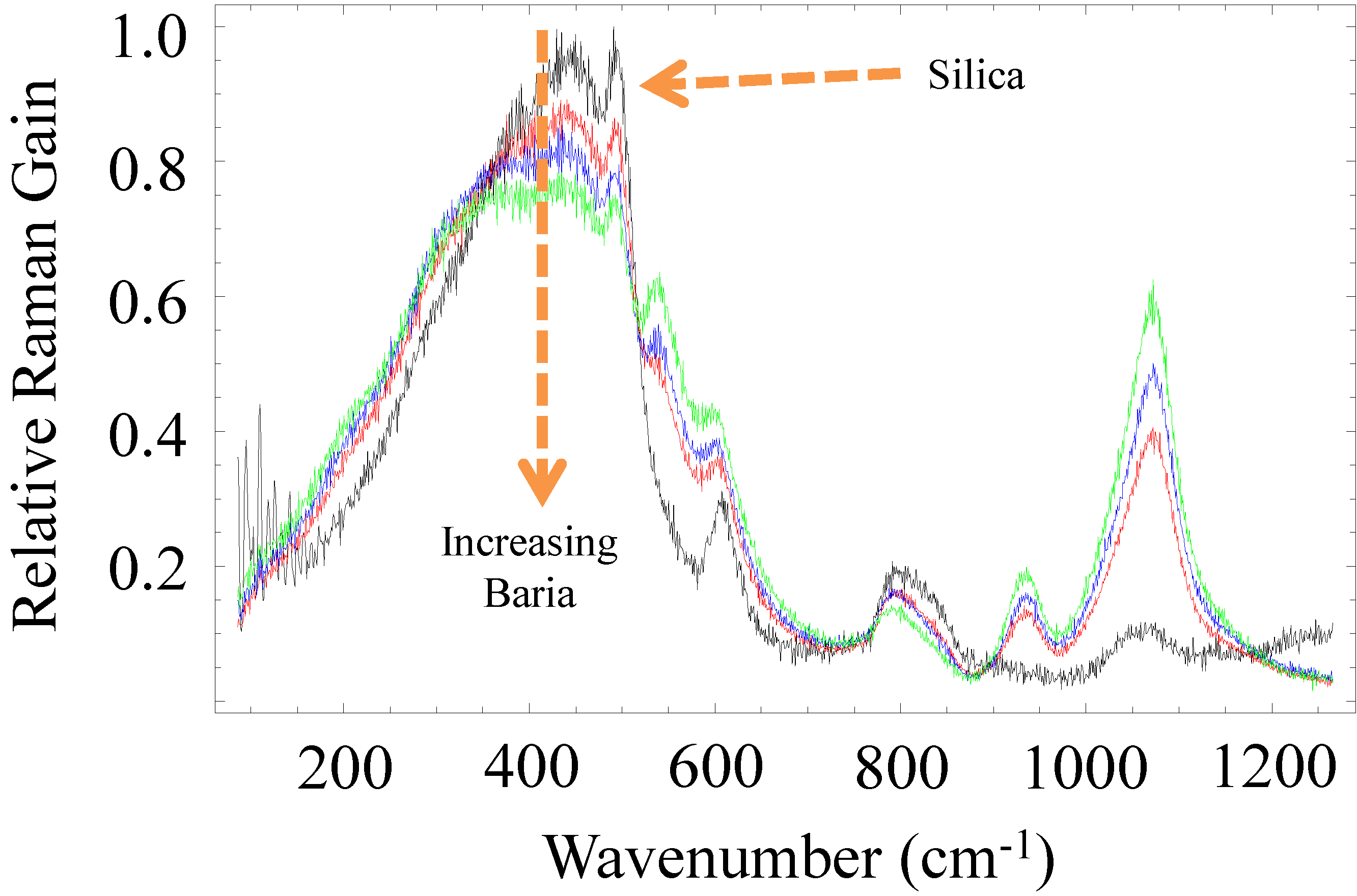
2.2.3. Optical Fibers with Enhanced Thresholds for Higher Order Mode Instabilities (HOMI)
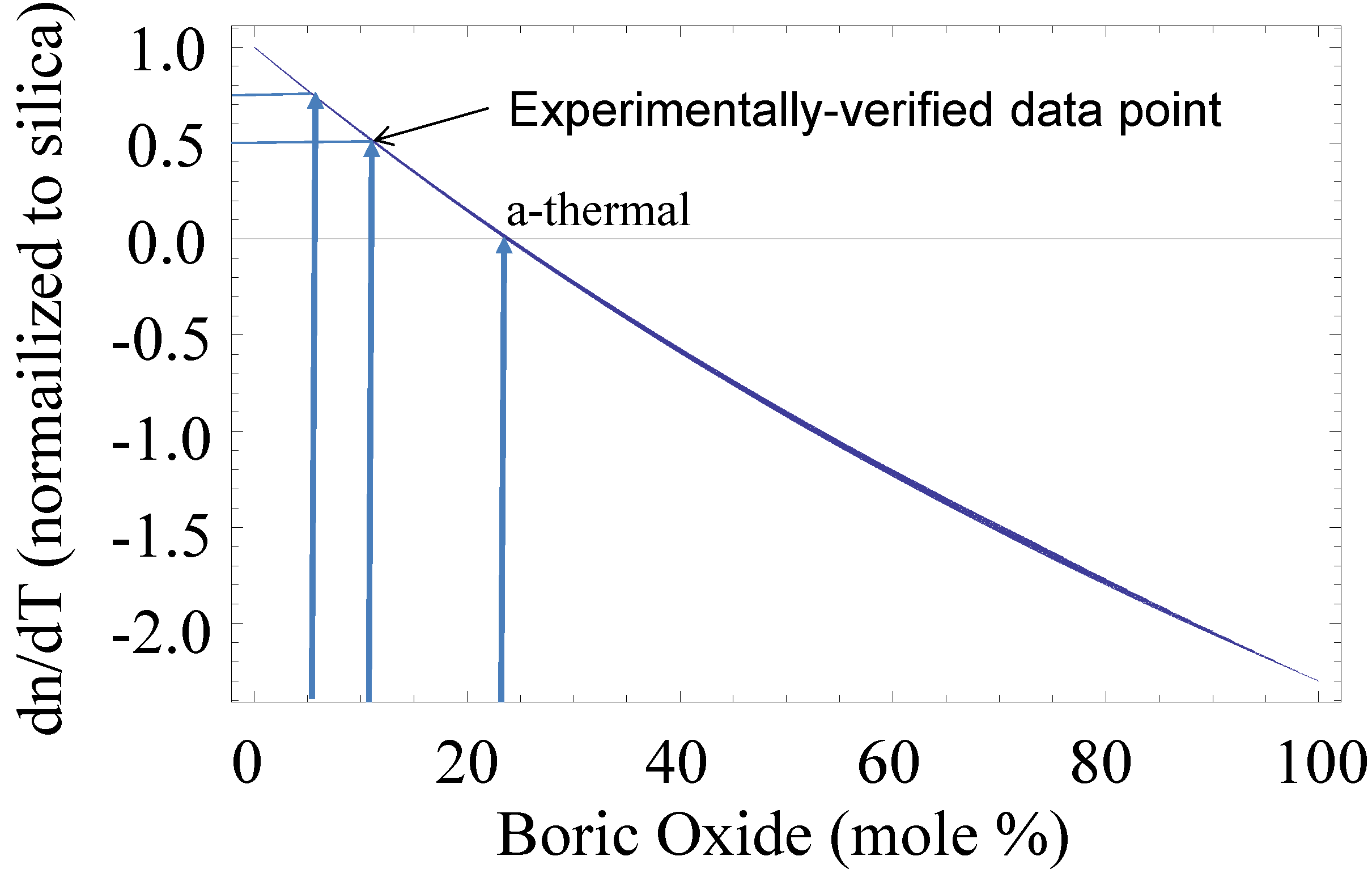
2.2.4. Nonlinear Refractive Index and Parasitics Depending Thereon
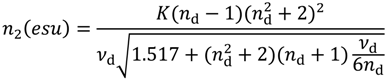
2.3. Limitations
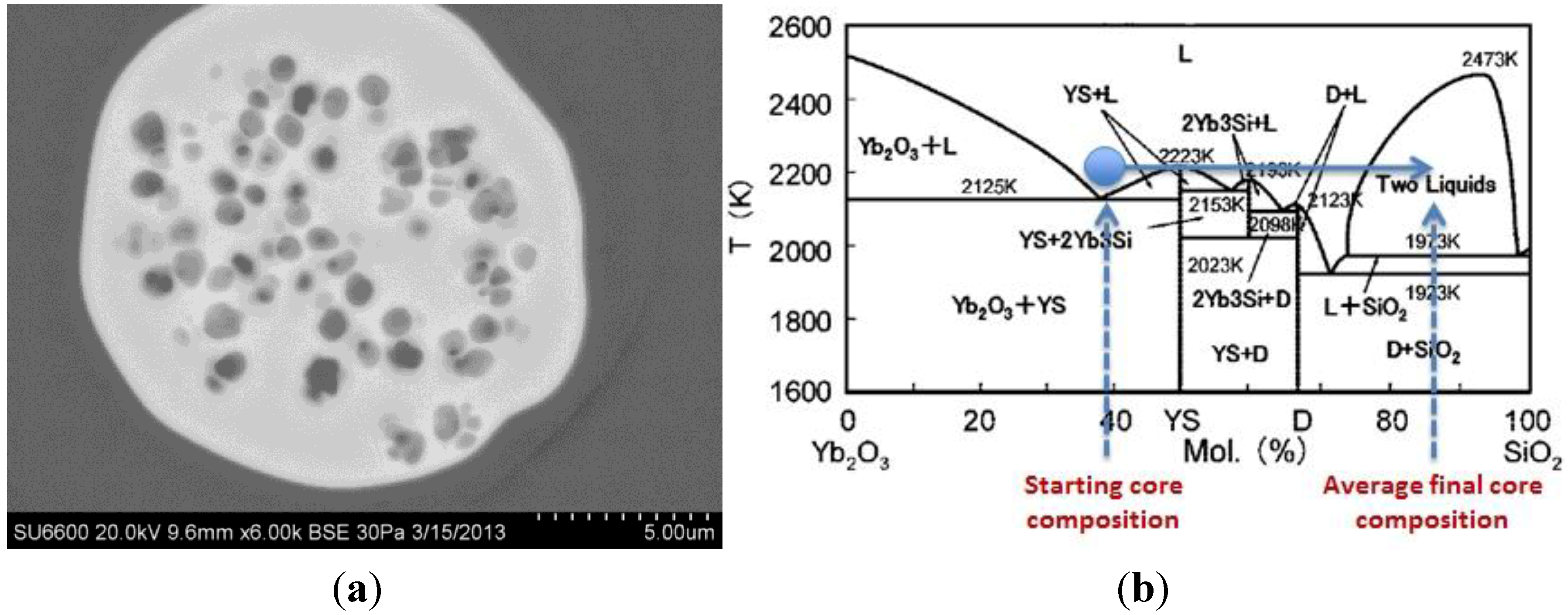
2.4. A Note on Costs
3. Experimental Section
4. Conclusions
Acknowledgments
Author Contribution
Conflicts of Interest
References
- National Research Council. Optics and Photonics: Essential Technologies for Our Nation; The National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Baer, T.; Schlachter, F. Report to the OSTP—Lasers in Science and Technology 2010; Stanford University: Stanford, CA, USA, 2013. [Google Scholar]
- Mazzali, C. The Timing for Specialty Optical Fibers. In Proceedings of the Workshop on Specialty Optical Fibers and their Applications, Optical Society of America Topical Digest, paper T3.3, Sigtuna, Sweden, 28–30 August 2013.
- Ballato, J.; Dragic, P. Rethinking Optical Fiber: New Demands, Old Glasses. J. Am. Ceram. Soc. 2013, 96, 2675–2692. [Google Scholar] [CrossRef]
- Mauro, J.; Philip, C.; Vaughn, D.; Pambianchi, M. Glass Science in the United States: Current Status and Future Directions. Int. J. Appl. Glass Sci. 2014, 4, 1–14. [Google Scholar]
- Stolen, R. The early years of fiber nonlinear optics. J. Light. Technol. 2008, 26, 1021–1031. [Google Scholar] [CrossRef]
- Fermann, M. Single-mode excitation of multimode fibers with ultrashort pulses. Opt. Lett. 1998, 23, 52–54. [Google Scholar] [CrossRef]
- Koplow, J.; Kliner, D.; Goldberg, L. Single-mode operation of a coiled multimode fiber amplifier. Opt. Lett. 2000, 25, 442–444. [Google Scholar]
- Limpert, J.; Schmidt, O.; Rothhardt, J.; Röser, F.; Schreiber, T.; Tünnermann, A.; Ermeneux, S.; Yvernault, P.; Salin, F. Extended single-mode photonic crystal fiber lasers. Opt. Express 2006, 14, 2715–2720. [Google Scholar] [CrossRef]
- Ramachandran, S.; Nicholson, J.; Ghalmi, S.; Yan, M.; Wisk, P.; Monberg, E.; Dimarcello, F. Light propagation with ultralarge modal areas in optical fibers. Opt. Lett. 2006, 31, 1797–1799. [Google Scholar] [CrossRef]
- Sosnowski, T.; Kuznetsov, A.; Maynard, R.; Ma, X.; Zhu, C.; Hu, I.; Galvanauskas, A.; Koponen, J.; McComb, T. 3C Yb-doped Fiber Based High Energy and Power Pulsed Fiber Lasers. In Proceedings of the SPIE 8601, Fiber Lasers X: Technology, Systems, and Applications, Photonics West, San Fancisco, CA, USA, 2 February 2013.
- Gaponov, D.; Février, S.; Devautour, M.; Roy, P.; Likhachev, M.; Aleshkina, S.; Salganskii, M.; Yashkov, M.; Guryanov, A. Management of the high-order mode content in large (40 μm) core photonic bandgap Bragg fiber laser. Opt. Lett. 2010, 35, 2233–2235. [Google Scholar] [CrossRef]
- Kashiwagi, M.; Saitoh, K.; Takenaga, K.; Tanigawa, S.; Matsuo, S.; Fujimaki, M. Effectively single-mode all-solid photonic bandgap fiber with large effective area and low bending loss for compact high-power all-fiber lasers. Opt. Express 2012, 20, 15061–15070. [Google Scholar]
- Dong, L.; Wu, T.; McKay, H.; Fu, L.; Li, J.; Winful, H. All-Glass Large-Core Leakage Channel Fibers. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 47–53. [Google Scholar] [CrossRef]
- Laperle, P.; Paré, C.; Zheng, H.; Croteau, A. Yb-Doped LMA Triple-Clad Fiber for Power Amplifiers. In Proceedings of the SPIE 6453, Fiber Lasers IV: Technology, Systems, and Applications, San Jose, CA, USA, 20 January 2007.
- Otto, H.; Stutzki, F.; Jansen, F.; Eidam, T.; Jauregui, C.; Limpert, J.; Tünnermann, A. Temporal dynamics of mode instabilities in high-power fiber lasers and amplifiers. Opt. Express 2012, 20, 15710–15722. [Google Scholar]
- Jauregui, C.; Eidam, T.; Otto, H.; Stutzki, F.; Jansen, F.; Limpert, J.; Tünnermann, A. Physical origin of mode instabilities in high-power fiber laser systems. Opt. Express 2012, 20, 12912–12925. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 2nd ed.; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Winkelmann, A. Ueber die specifischen Wärmen verschieden zusammengesetzter Gläser [On the specific heats of different composite glasses]. Ann. Phys. Chem. 1893, 49, 401–420. (In German) [Google Scholar] [CrossRef]
- Winkelmann, A.; Schott, O. Über die Elastizität und über die Zugund Druckfestigkeit verschiedener neuer Gläser in ihrer Abhängigkeit von der chemischen Zusammensetzung [On the elasticity and the tensile and compressive strength of several new glasses in their dependence on the chemical composition]. Ann. Phys. Chem. 1894, 51, 697–730. (In German) [Google Scholar] [CrossRef]
- Law, P.; Dragic, P. Wavelength dependence of the Brillouin spectral width of boron doped germanosilicate optical fibers. Opt. Express 2010, 18, 18852–18865. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J.; Morris, S.; Hawkins, T. Pockels’ coefficients of alumina in aluminosilicate optical fiber. J. Opt. Soc. Am. B 2013, 30, 244–250. [Google Scholar] [CrossRef]
- Stolen, R.; Ippen, E. Raman gain in glass optical waveguides. Appl. Phys. Lett. 1973, 22, 276–278. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J. Characterisation of Raman gain spectra in Yb:YAG-derived optical fibres. Electron. Lett. 2013, 49, 895–897. [Google Scholar] [CrossRef]
- Baret, G.; Madar, R.; Bernard, C. Silica-Based Oxide Systems I. Experimental and Calculated Phase Equilibria in Silicon, Boron, Phosphorus, Germanium, and Arsenic Oxide Mixtures. J. Electrochem. Soc. 1991, 138, 2830–2835. [Google Scholar] [CrossRef]
- Tien, T.; Hummel, F. The System SiO2–P2O5. J. Am. Ceram. Soc. 1965, 48, 75–80. [Google Scholar]
- Dragic, P.; Ballato, J. 120 Years of Optical Glass Property Calculations: From the Law of Mixtures and the Birth of Glass Science to Mixing the Unmixable. Opt. Photonics News 2014, in press. [Google Scholar]
- MacDowell, J.; Beall, G. Immiscibility and Crystallization in Al2O3-SiO2 Glasses. J. Am. Ceram. Soc. 1969, 52, 17–25. [Google Scholar] [CrossRef]
- Hyatt, M.; Day, D. Glass Properties in the Yttria-Alumina-Silica System. J. Am. Ceram. Soc. 1987, 70, C283–C287. [Google Scholar]
- Jung, I.; Decterov, S.; Pelton, A. Critical Thermodynamic Evaluation and Optimization of the MgO-Al2O3, CaO-MgO-Al2O3, and MgO-Al2O3-SiO2 Systems. J. Phase Equilibria Diffus. 2004, 25, 329–345. [Google Scholar] [CrossRef]
- Frantz, J.; Mysen, B. Raman Spectra and Structure of BaO-SiO2, SrO-SiO2, and CaO-SiO2 melts at 1600 °C. Chem. Geol. 1995, 121, 155–176. [Google Scholar] [CrossRef]
- Zhang, Y.; Navrotsky, A. Thermochemistry of Glasses in the Y2O3-Al2O3-SiO2 System. J. Am. Ceram. Soc. 2003, 86, 1727–1732. [Google Scholar] [CrossRef]
- Dragic, P.; Hawkins, T.; Morris, S.; Ballato, J. Sapphire-derived all-glass optical fibers. Nat. Photon. 2012, 6, 629–635. [Google Scholar] [CrossRef]
- Dragic, P.; Law, P.; Ballato, J.; Hawkins, T.; Foy, P. Brillouin Spectroscopy of YAG-Derived Optical Fibers. Opt. Express 2010, 18, 10055–10067. [Google Scholar] [CrossRef]
- Dragic, P.; Kucera, C.; Furtick, J.; Guerrier, J.; Hawkins, T.; Ballato, J. Brillouin Spectroscopy of a Novel Baria-doped Silica Glass Optical Fiber. Opt. Express 2013, 21, 10924–10941. [Google Scholar] [CrossRef]
- Mangognia, A.; Kucera, C.; Guerrier, J.; Furtick, J.; Dragic, P.; Ballato, J. Spinel-Derived Single Mode Optical Fiber. Opt. Mater. Express 2013, 3, 511–518. [Google Scholar] [CrossRef]
- Liu, Y.; Galvin, T.; Hawkins, T.; Ballato, J.; Dong, L.; Foy, P.; Eden, J.; Dragic, P. Linkage of Oxygen Deficiency Defects and Rare Earth Concentrations in Glass Optical Fiber Probed by Ultraviolet Absorption and Laser Excitation Spectroscopy. Opt. Express 2012, 20, 14494–14507. [Google Scholar]
- Ballato, J.; Hawkins, T.; Foy, P.; Kokuoz, B.; Stolen, R.; McMillen, C.; Daw, M.; Su, Z.; Tritt, T.; Dubinskii, M.; et al. On the Fabrication of All-Glass Optical Fibers from Crystals. J. Appl. Phys. 2009, 105. [Google Scholar] [CrossRef]
- Shima, K.; Himeno, K.; Sakai, T.; Okude, S.; Wada, A.; Yamauchi, R. A novel temperature-insensitive long-period fiber grating using a boron-doped-germanosilicated-core fiber. In Proceedings of the Conference on Optical Fiber Communication, Dallas, TX, USA, 16–21 February 1997.
- Boling, N.; Glass, A.; Owyoung, A. Empirical Relationships for Predicting Nonlinear Refractive Index Changes in Optical Solids. IEEE J. Quantum Electron. 1978, QE-14, 601–608. [Google Scholar] [CrossRef]
- Fournier, J.; Snitzer, E. The nonlinear refractive index of glass. IEEE J. Quantum Electron 1974, QE-10, 473–475. [Google Scholar] [CrossRef]
- Töpfer, T.; Hein, J.; Philipps, J.; Ehrt, D.; Sauerbrey, E. Tailoring the nonlinear refractive index of fluoride-phosphate glasses for laser applications. Appl. Phys. B 2000, 71, 203–206. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Flytzanis, C. Delocalization and superalternation effects in the nonlinear susceptibilities of one-dimensional systems. Chem. Phys. Lett. 1976, 44, 366–370. [Google Scholar] [CrossRef]
- DiGiovanni, D.J.; MacChesney, J.B.; Kometani, T.Y. Structure and properties of silica containing aluminum and phosphorus near the AlPO4 join. J. NonCryst. Solids 1989, 113, 58–64. [Google Scholar] [CrossRef]
- Yamamoto, H.; Akiyama, K.; Hirata, T.; Murakami, Y. Dependence of Yb2O3/SiO2 Molar Ratio on High temperature Characteristics of Gas Pressure Sintered Si3N4. J. Ceram. Soc. Jpn. 2005, 113, 325–329. [Google Scholar] [CrossRef]
- Karbasi, S.; Hawkins, T.; Ballato, J.; Koch, K.; Mafi, A. Transverse Anderson localization in a disordered glass optical fiber. Opt. Mater. Express 2012, 2, 1496–1503. [Google Scholar] [CrossRef]
- Karbasi, S.; Frazier, R.; Koch, K.; Hawkins, T.; Ballato, J.; Mafi, A. Image Transport through a Disordered Optical Fiber Mediated by Transverse Anderson Localization. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J.; Morris, S.; Hawkins, T. The Brillouin gain coefficient of Yb-doped aluminosilicate glass optical fibers. Opt. Mater. 2013, 35, 1627–1632. [Google Scholar] [CrossRef]
- Dragic, P.; Litzkendorf, D.; Kucera, C.; Ballato, J.; Schuster, K. Brillouin Scattering Properties of Lanthano-Aluminosilicate-Core Optical Fiber. Appl. Opt. 2014. submitted. [Google Scholar]
- MacChesney, J.; DiGiovanni, D. Materials Development of Optical Fiber. J. Am. Ceram. Soc. 1990, 73, 3537–3556. [Google Scholar] [CrossRef]
- Nagel, S.; MacChesney, J.; Walker, K. An Overview of the Modified Chemical Vapor Deposition (MCVD) Process and Performance. IEEE Trans. Microw. Theory Tech. 1982, 30, 305–322. [Google Scholar] [CrossRef]
- Izawa, T. Early days of VAD process. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1220–1227. [Google Scholar] [CrossRef]
- Ballato, J.; Snitzer, E. Fabrication of Fibers with High Rare-Earth Concentrations for Faraday Isolator Applications. Appl. Opt. 1995, 34, 6848–6854. [Google Scholar] [CrossRef]
- Morris, S.; Ballato, J. Molten Core Fabrication of Novel Optical Fibers. Bull. Am. Ceram. Soc. 2013, 92, 24–29. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ballato, J.; Dragic, P. Materials Development for Next Generation Optical Fiber. Materials 2014, 7, 4411-4430. https://doi.org/10.3390/ma7064411
Ballato J, Dragic P. Materials Development for Next Generation Optical Fiber. Materials. 2014; 7(6):4411-4430. https://doi.org/10.3390/ma7064411
Chicago/Turabian StyleBallato, John, and Peter Dragic. 2014. "Materials Development for Next Generation Optical Fiber" Materials 7, no. 6: 4411-4430. https://doi.org/10.3390/ma7064411
APA StyleBallato, J., & Dragic, P. (2014). Materials Development for Next Generation Optical Fiber. Materials, 7(6), 4411-4430. https://doi.org/10.3390/ma7064411




