Surface Stability and Growth Kinetics of Compound Semiconductors: An Ab Initio-Based Approach
Abstract
:1. Introduction
1.1. Scope of Review
1.2. Prior Works in the Field of GaAs MBE
1.3. Issues with III-Nitride MOVPE
2. Methodology
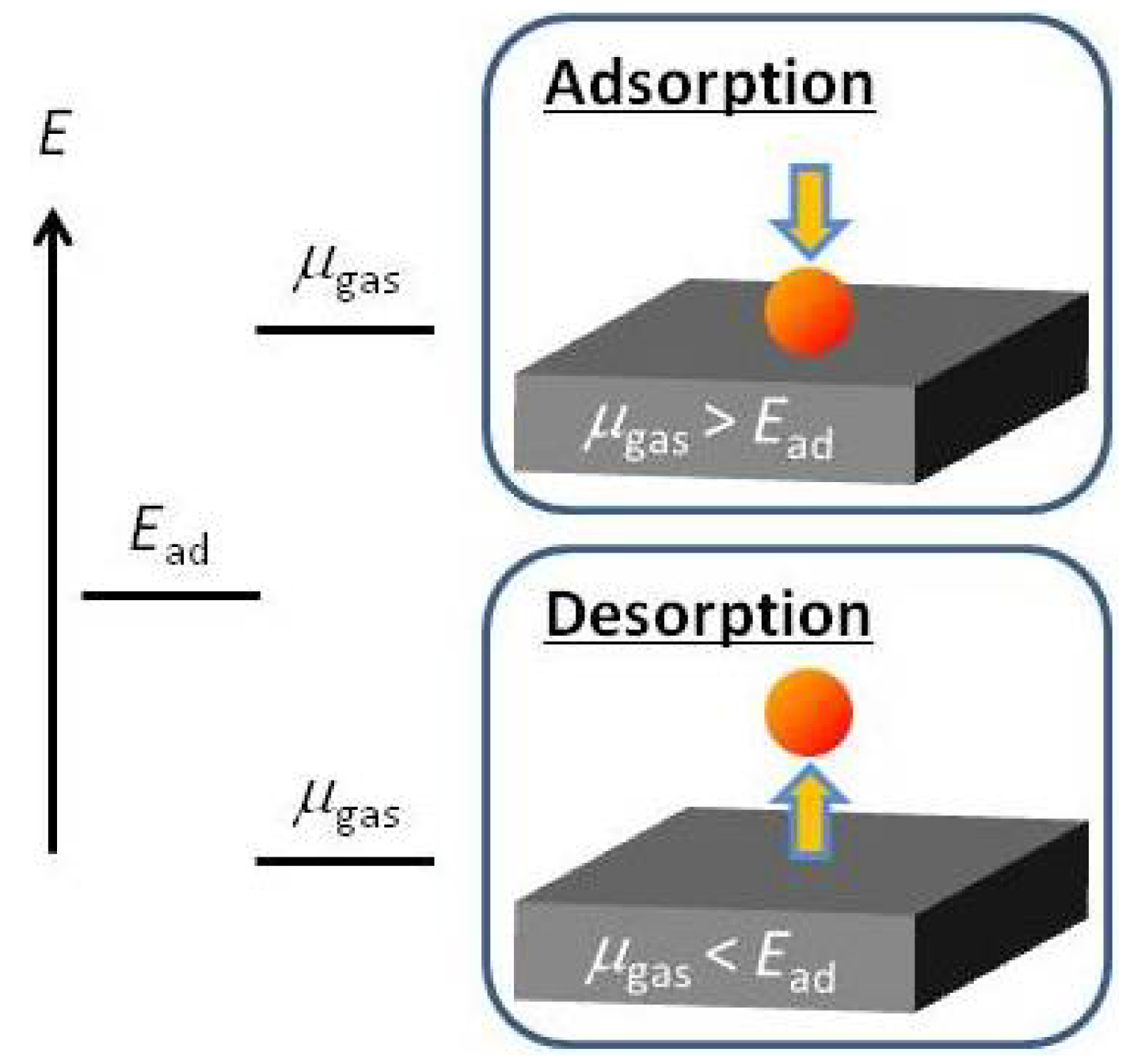
2.1. Ab Initio-based Approach Incorporating Gas-phase Free Energy
| Group | Element | g |
|---|---|---|
| I | H, Li, Na, K, Rb, Cs, Cu, Ag, Au | 2 |
| II | Be, Mg, Ca, Sr, Ba, Zn, Cd, Hg | 1 |
| III | B, Al, Ga, In, Tl | 2 |
| IV | C, Si, Ge, Sn, Pb | 3 |
| V | N, P, As, Sb, Bi | 4 |
| VI | O, S, Se, Te, Po | 3 |
| VII | F, Cl, Br, I | 2 |
| 0 | He, Ne, Ar, Kr, Xe, Rn | 1 |
2.1.1. Computational Approach for GaAs Surfaces
| Molecule | B3LYP | MP2 | Exp. | ||
|---|---|---|---|---|---|
| MIDI-4** | 6-31G** | MIDI-4** | 6-31G** | ||
| H2 | – | 4467 (0.7427) | – | 4609 (0.7338) | 4401 |
| N2 | – | 2458 (1.1055) | – | 2180 (1.1300) | 2360 |
| P2 | 792 (1.9217) | 796 (1.9044) | 696 (1.9648) | 717 (1.9323) | – |
| As2 | 446 (2.1242) | – | 385 (2.1694) | – | – |
2.1.2. Computational Approach for III-nitride Surfaces
2.2. Monte Carlo Simulation
3. Applications to GaAs Surfaces
3.1. Surface Phase Diagram
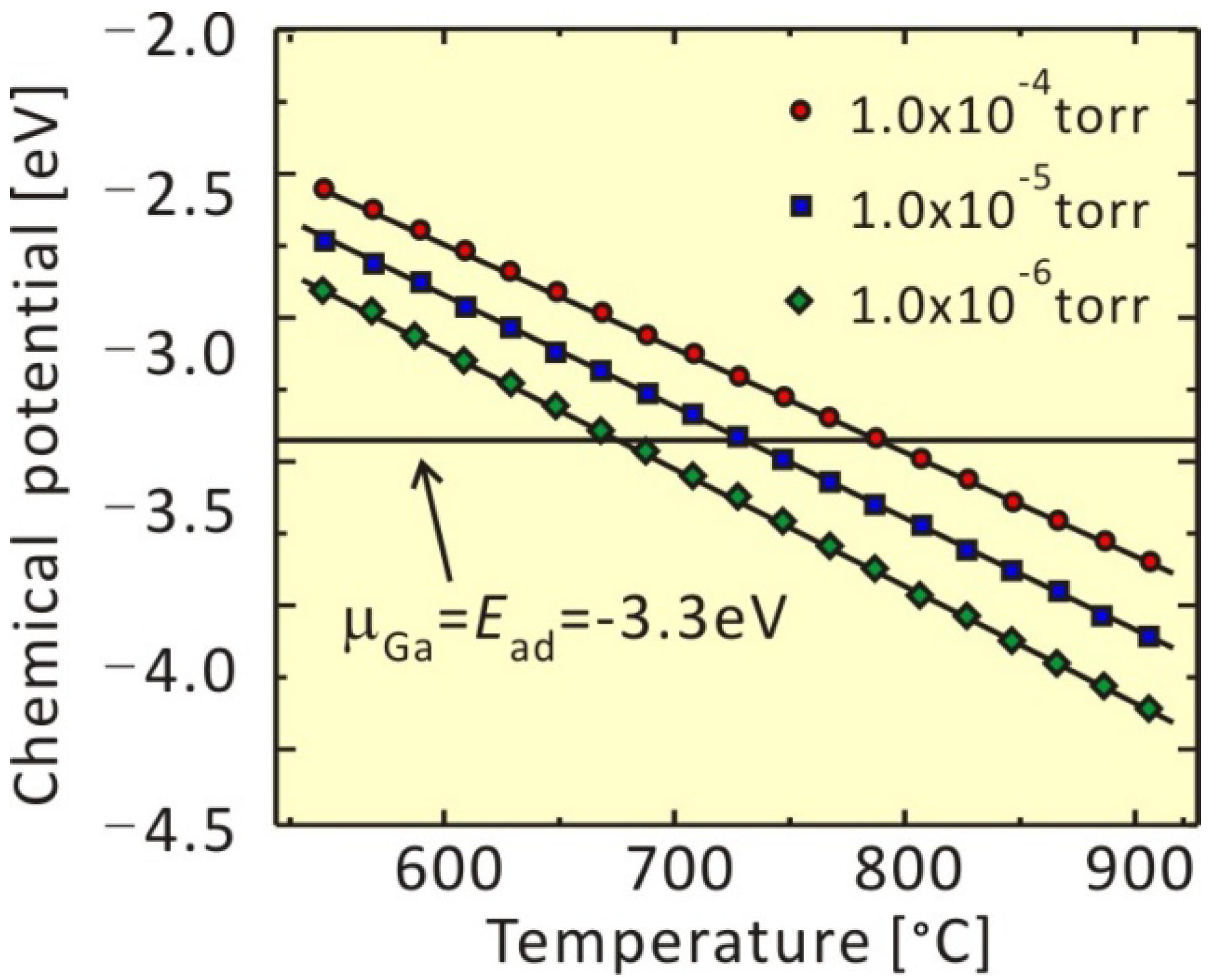
3.1.1. GaAs(001)-(4 × 2)β2
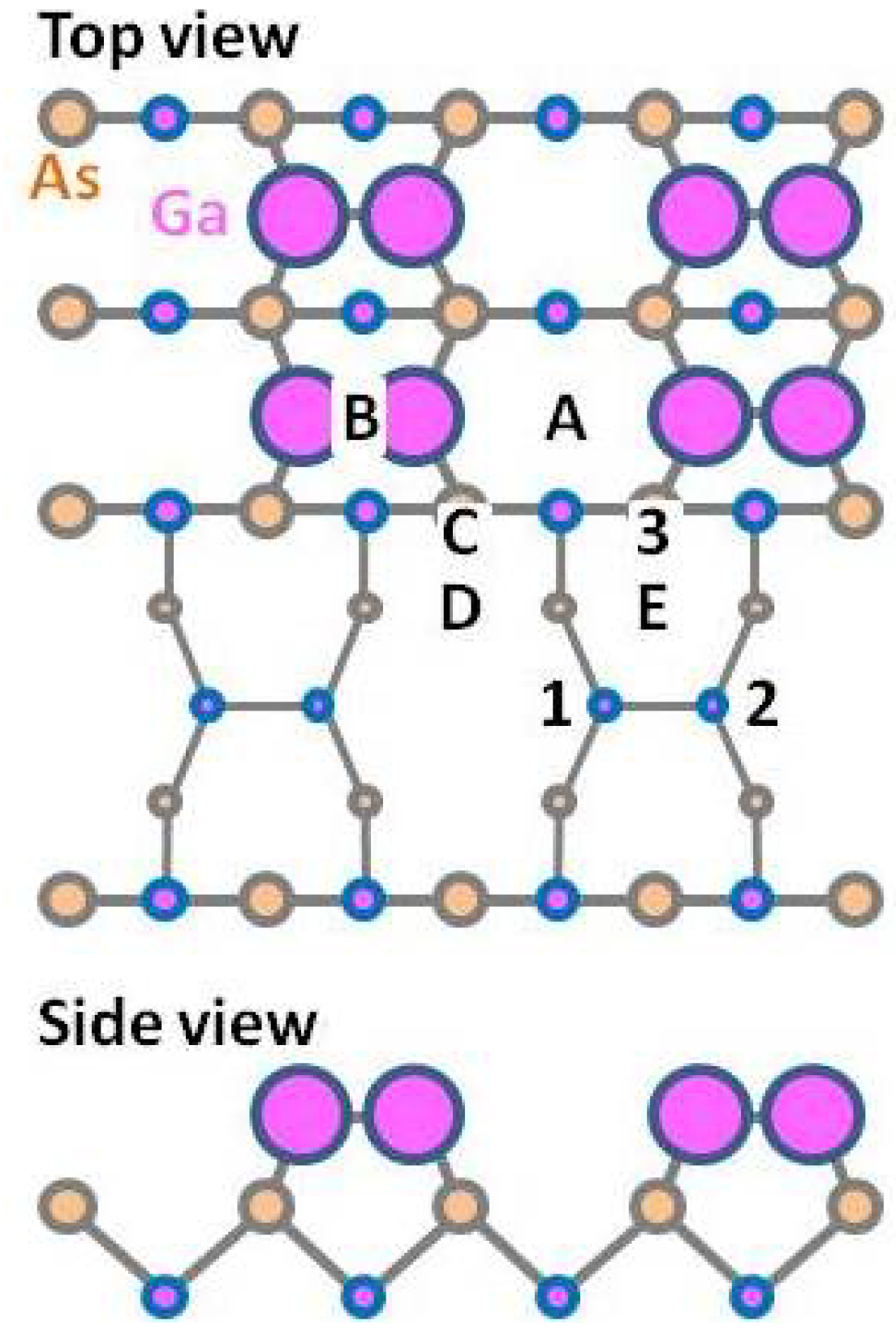

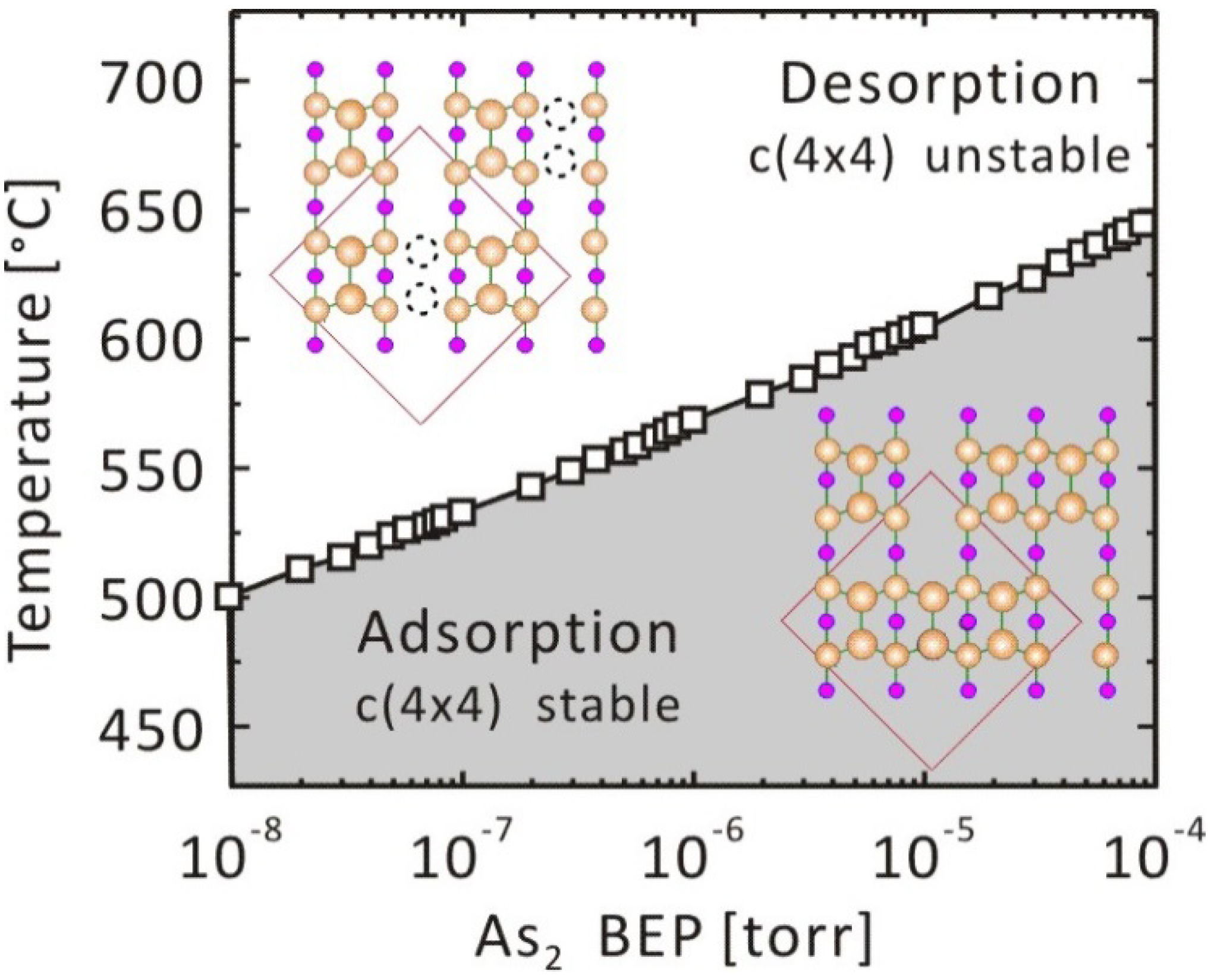
3.1.2. GaAs(001)-c(4 × 4)
3.2. Growth Kinetics
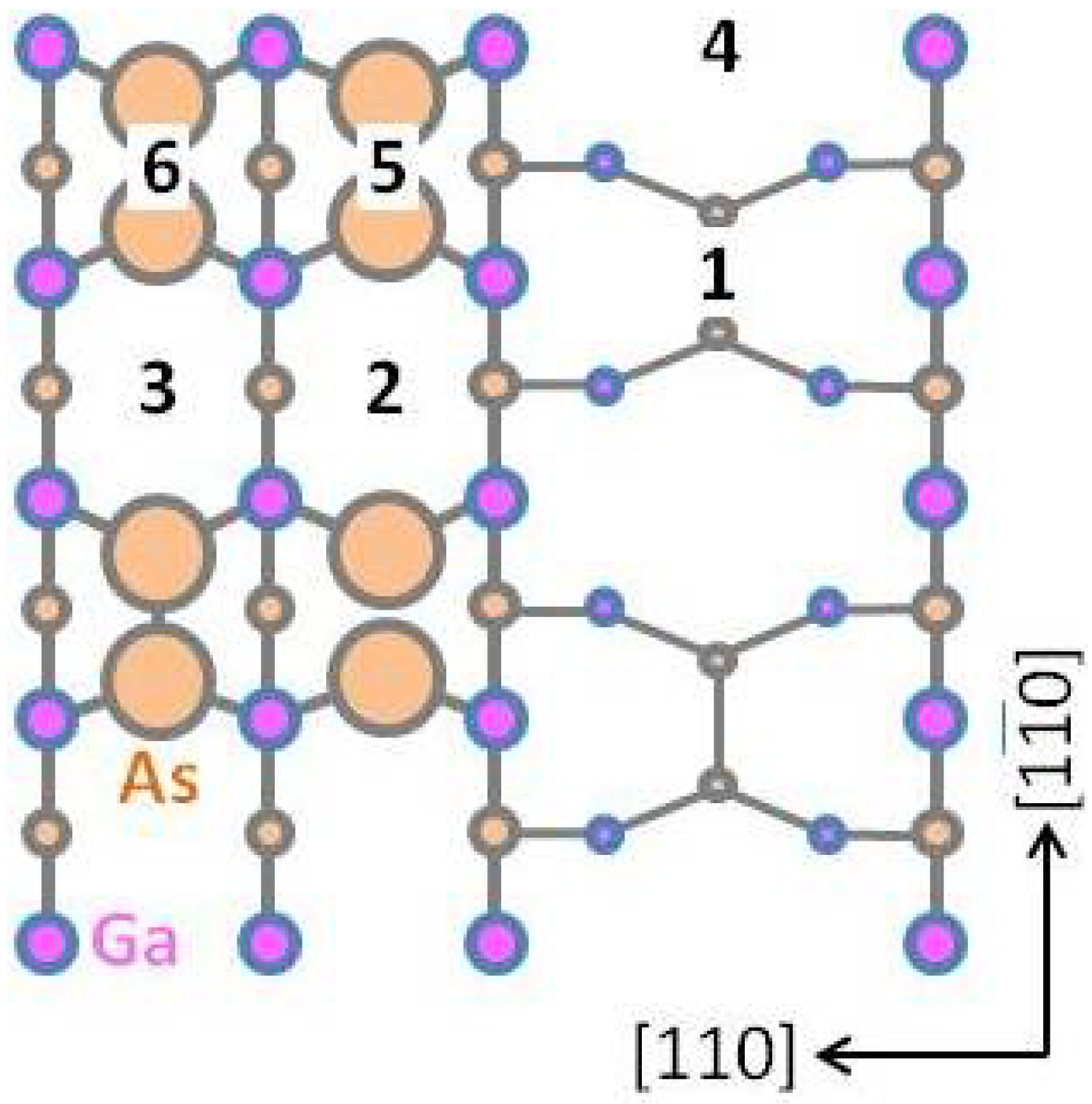
| x′ | 1 | 2 | 3 | 4 | 5 | 6 | Ede | |
|---|---|---|---|---|---|---|---|---|
| x | ||||||||
| 1 | 1.5 | 1.5 | 1.2 | 1.7 | 1.7 | 3.2 | ||
| 2 | 0.5 | 0.4 | 0.5 | 0.75 | – | 2.2 | ||
| 3 | 0.5 | 0.4 | 0.5 | – | 0.75 | 2.2 | ||
| 4 | 0.5 | 0.5 | 0.8 | 1.0 | 1.0 | 2.5 | ||
| 5 | 1.1 | 1.15 | – | 1.1 | 1.0 | 2.6 | ||
| 6 | 1.1 | – | 1.15 | 1.1 | 1.0 | 2.6 | ||
 ) [69] and dashed lines (
) [69] and dashed lines (  ) [65].
) [65].
 ) [69] and dashed lines (
) [69] and dashed lines (  ) [65].
) [65].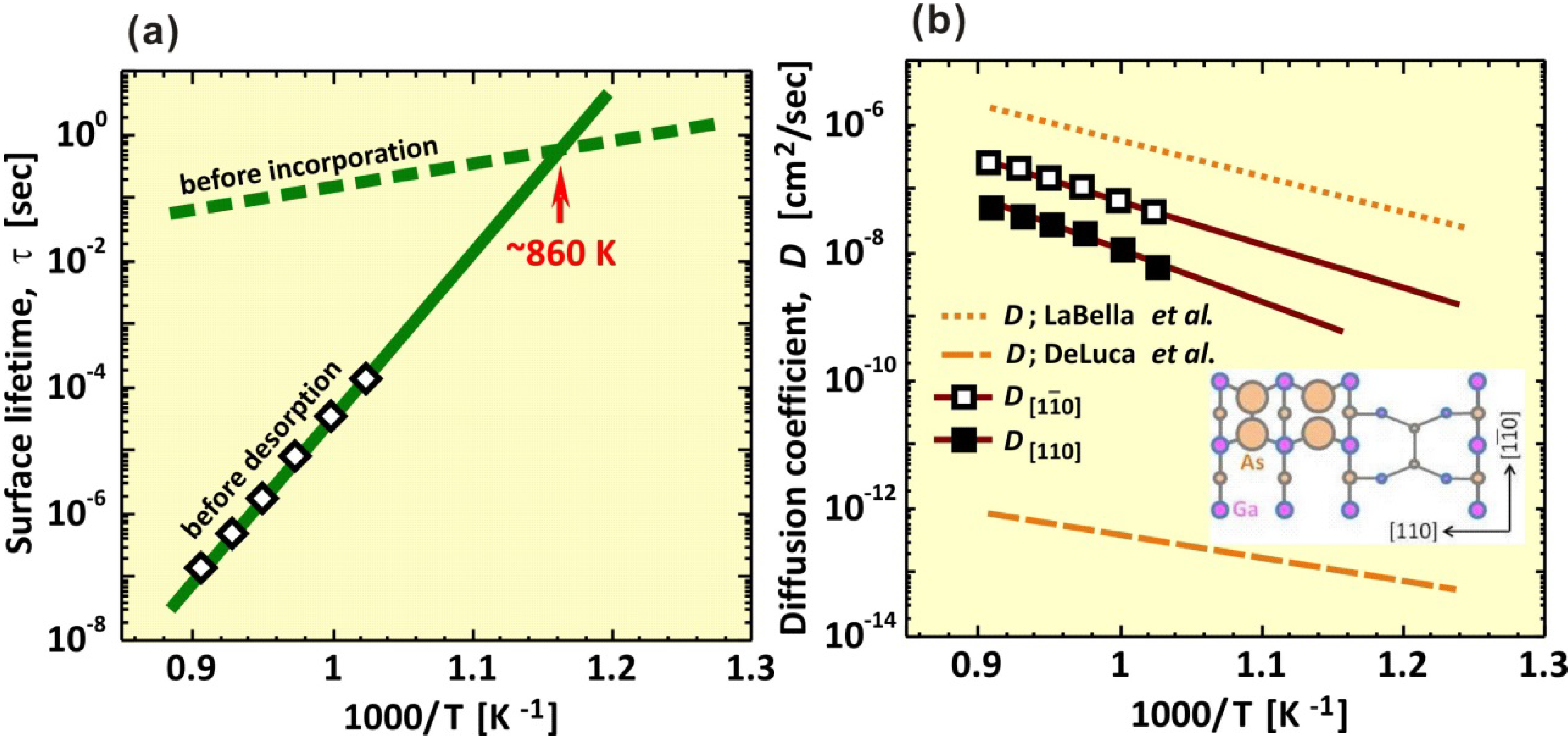
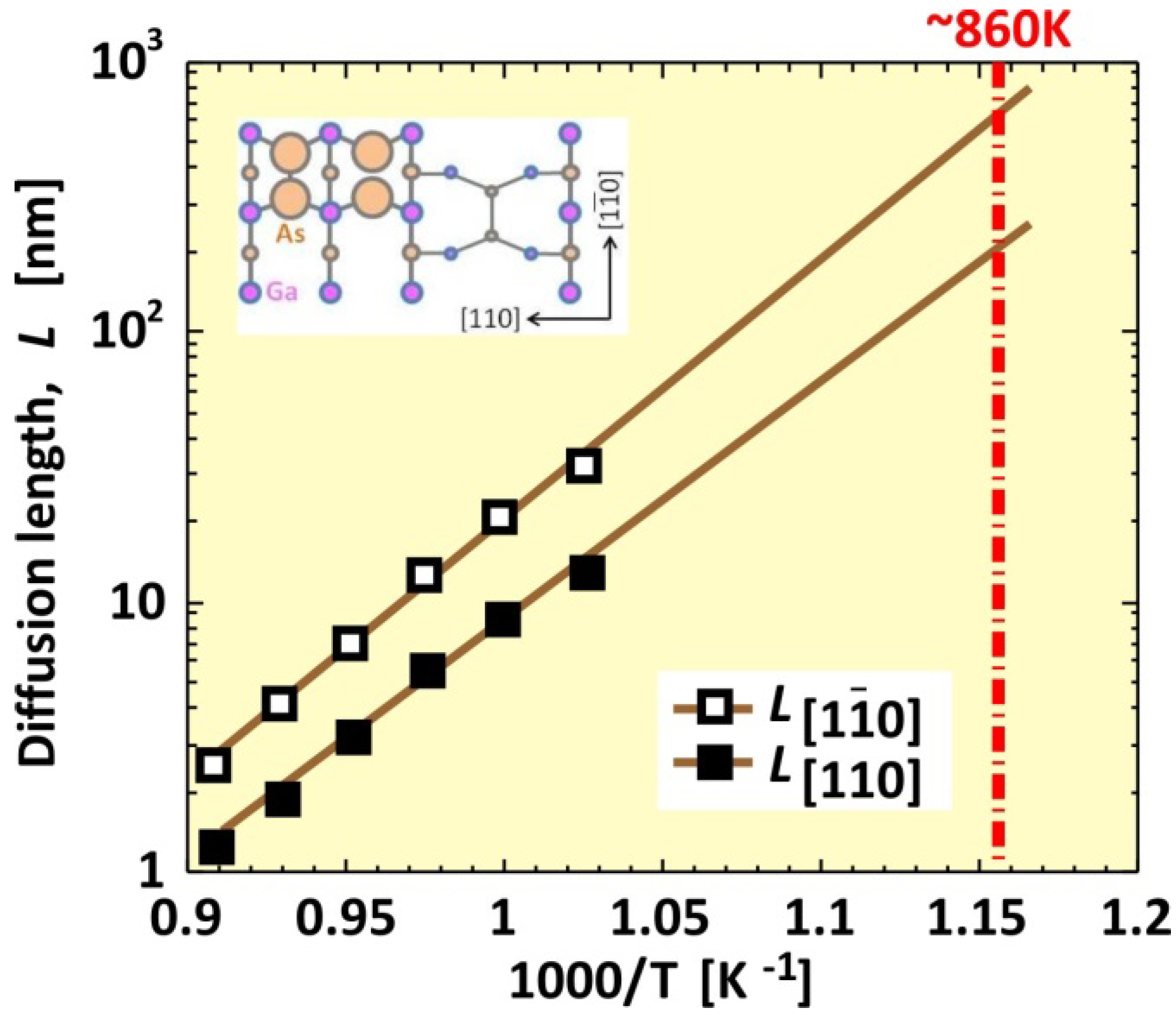
4. Applications to III-Nitride Surfaces
4.1. Surface Phase Diagram
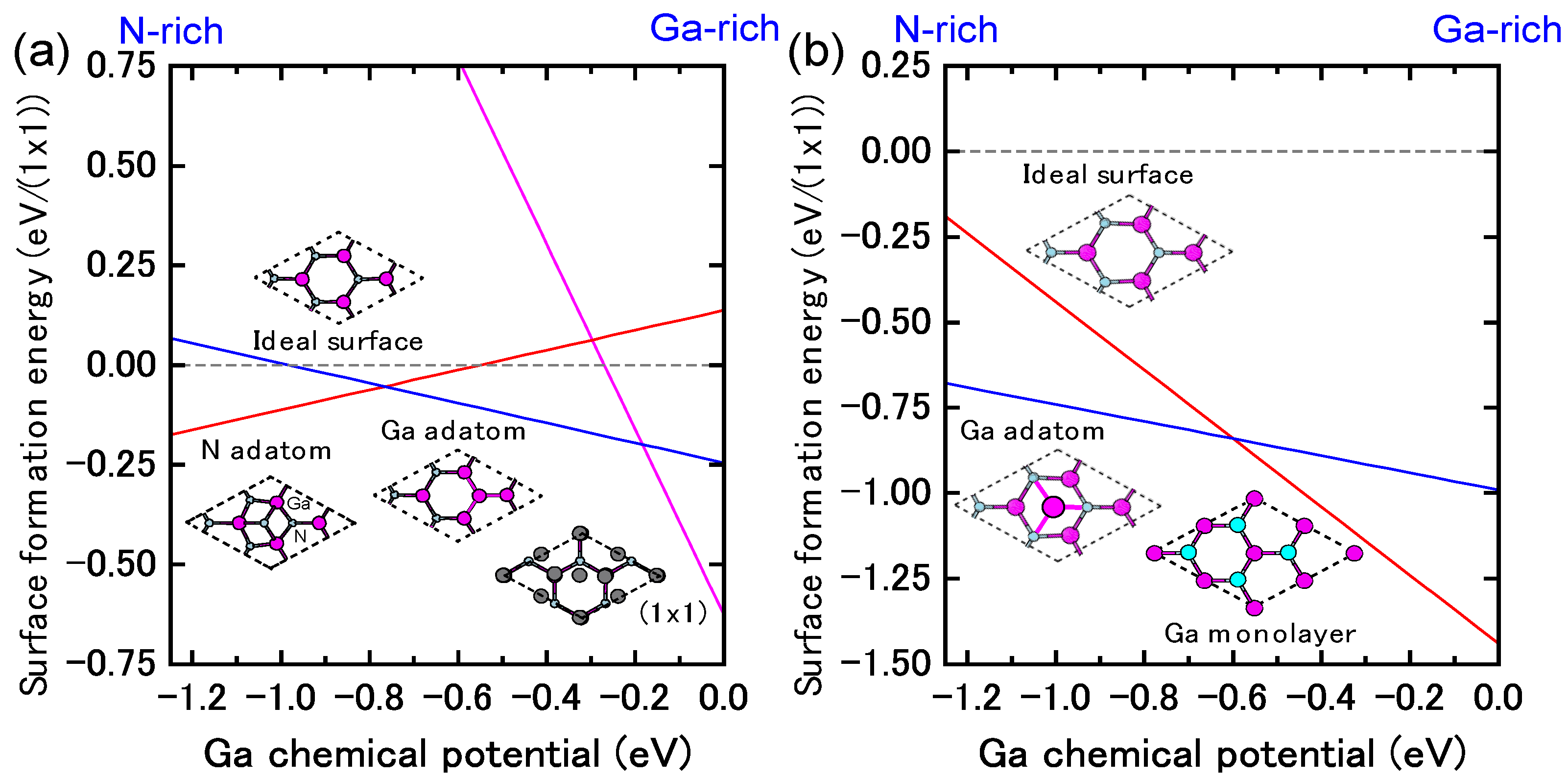
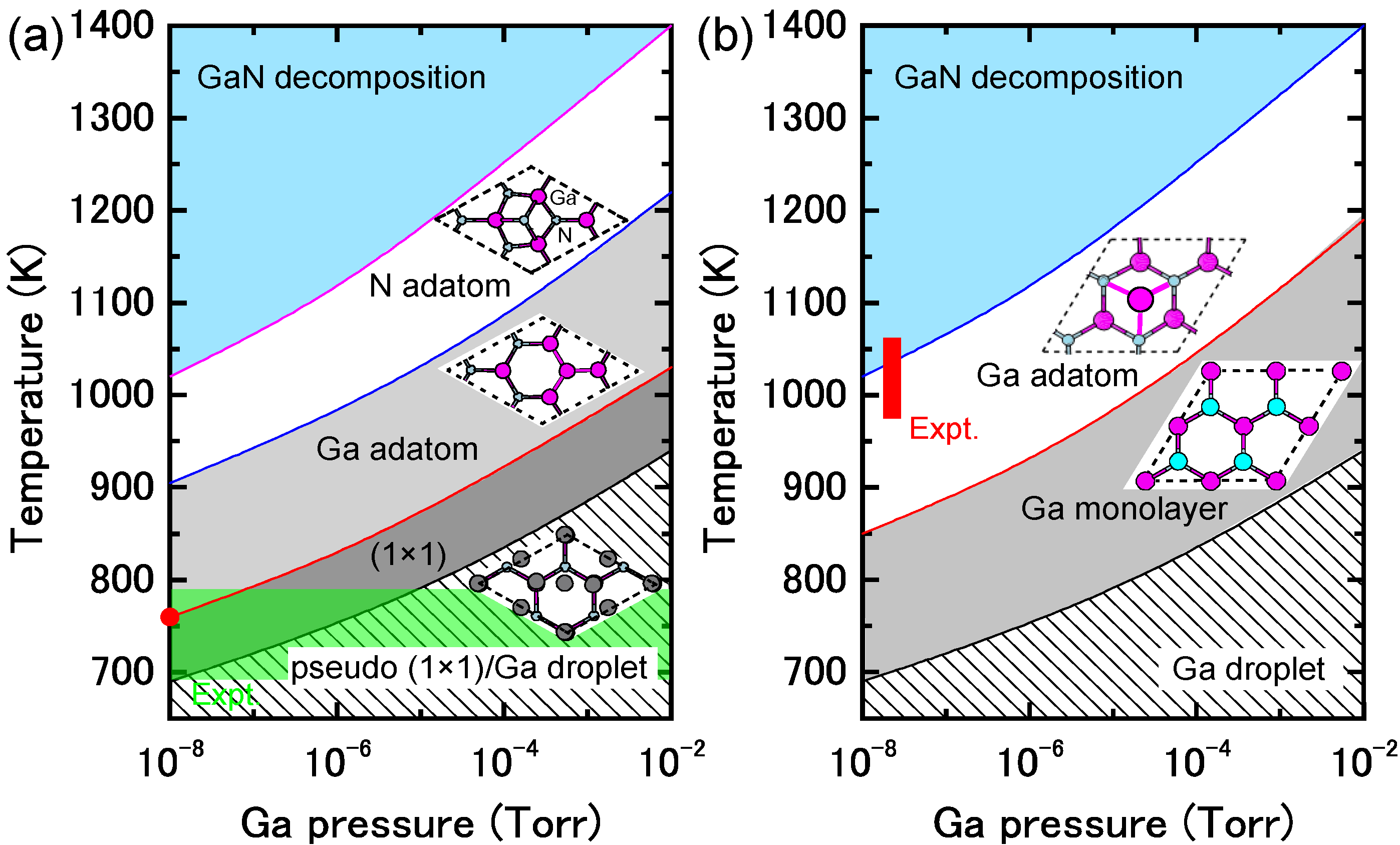
4.1.1. GaN Polar Surfaces
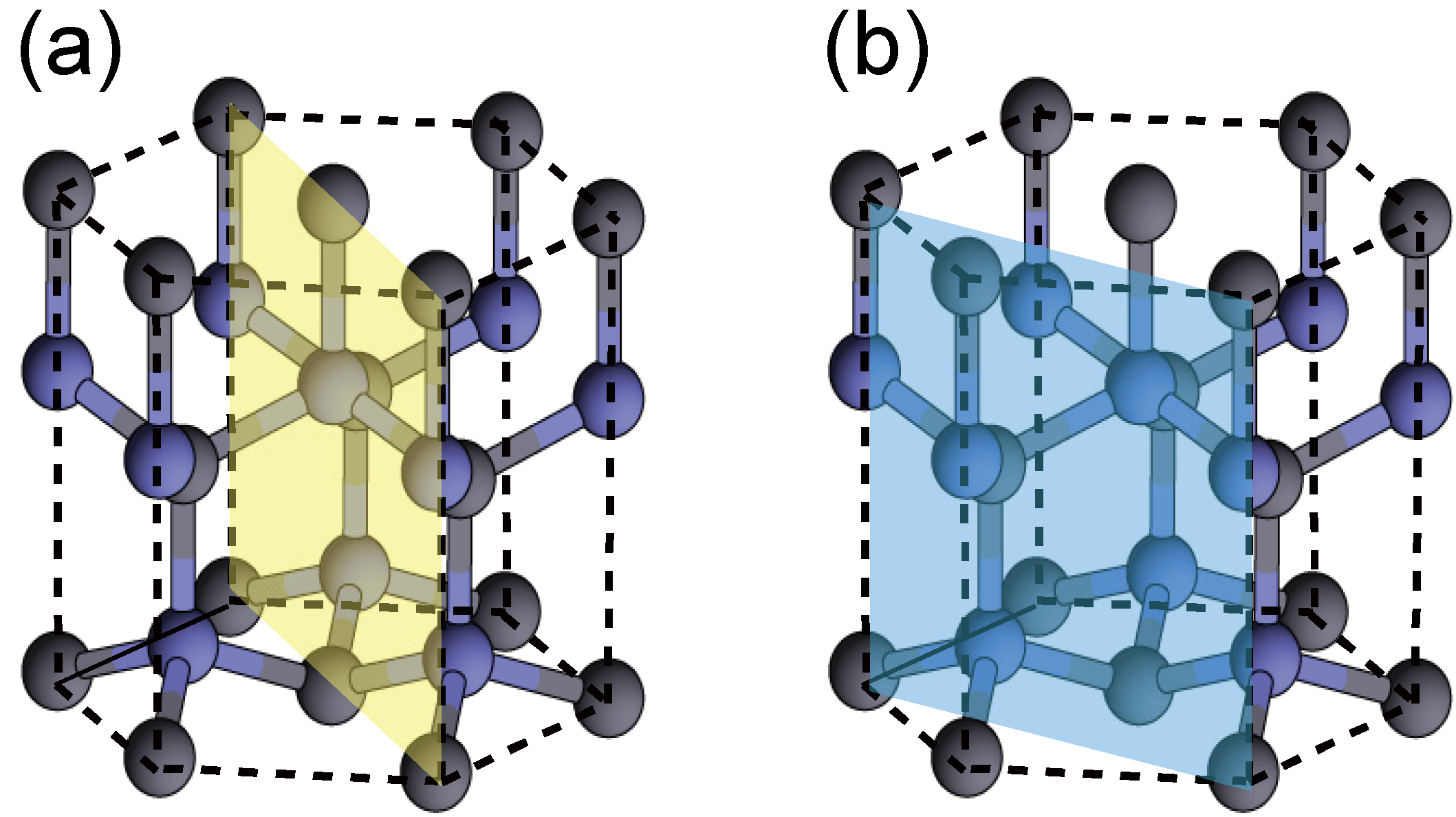
4.1.2. GaN Nonpolar Surfaces

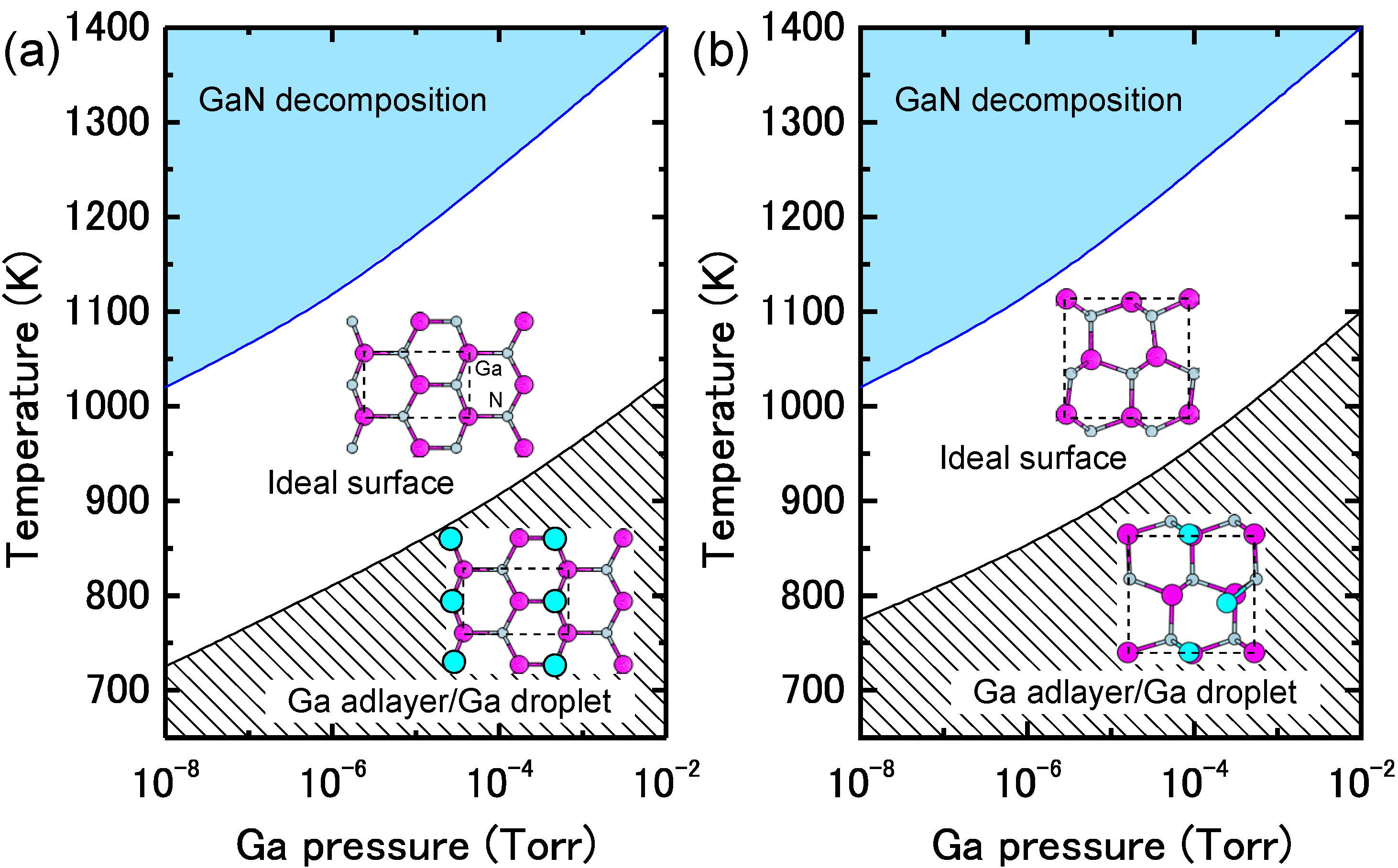
4.1.3. GaN Semipolar Surfaces
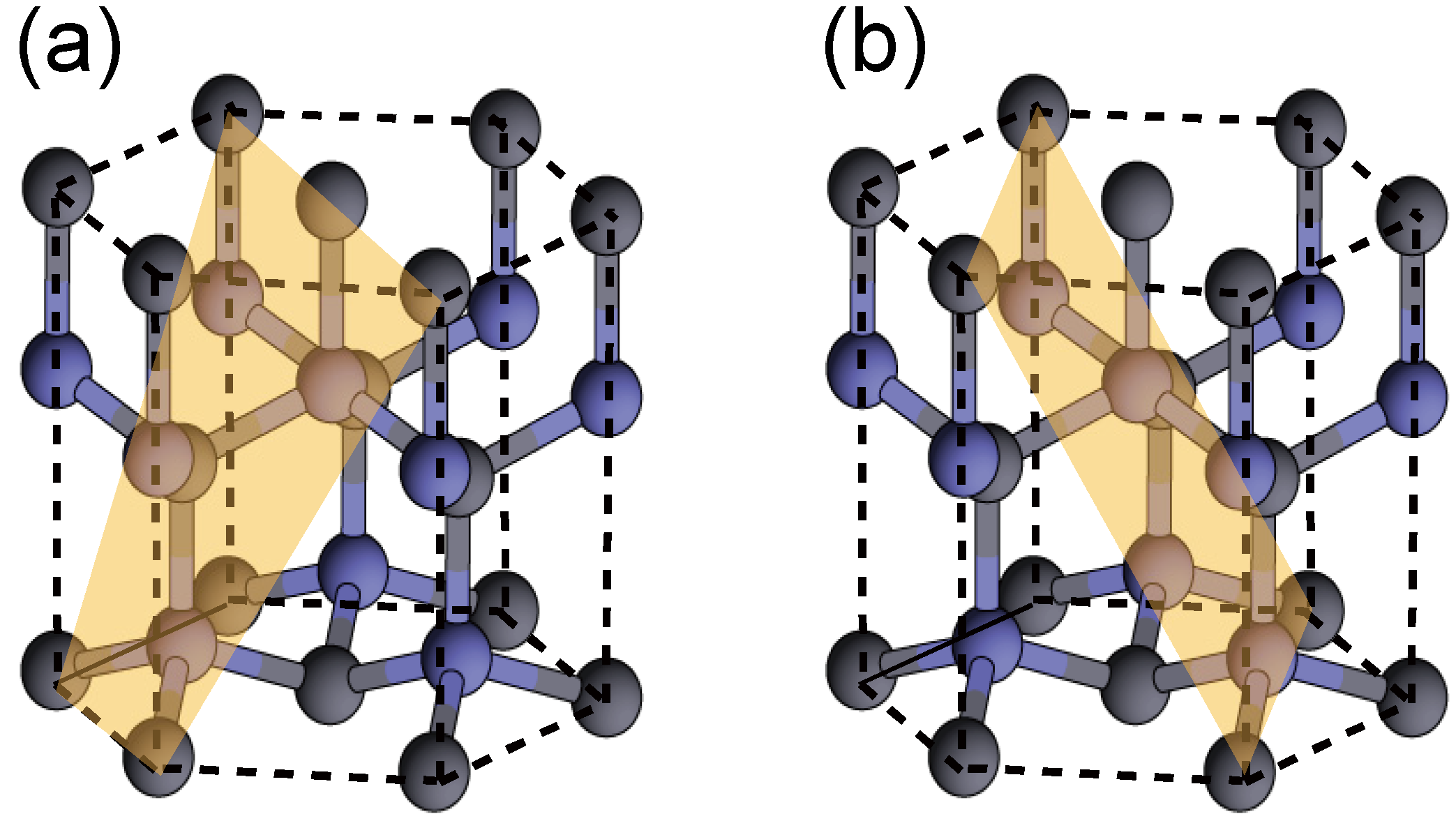
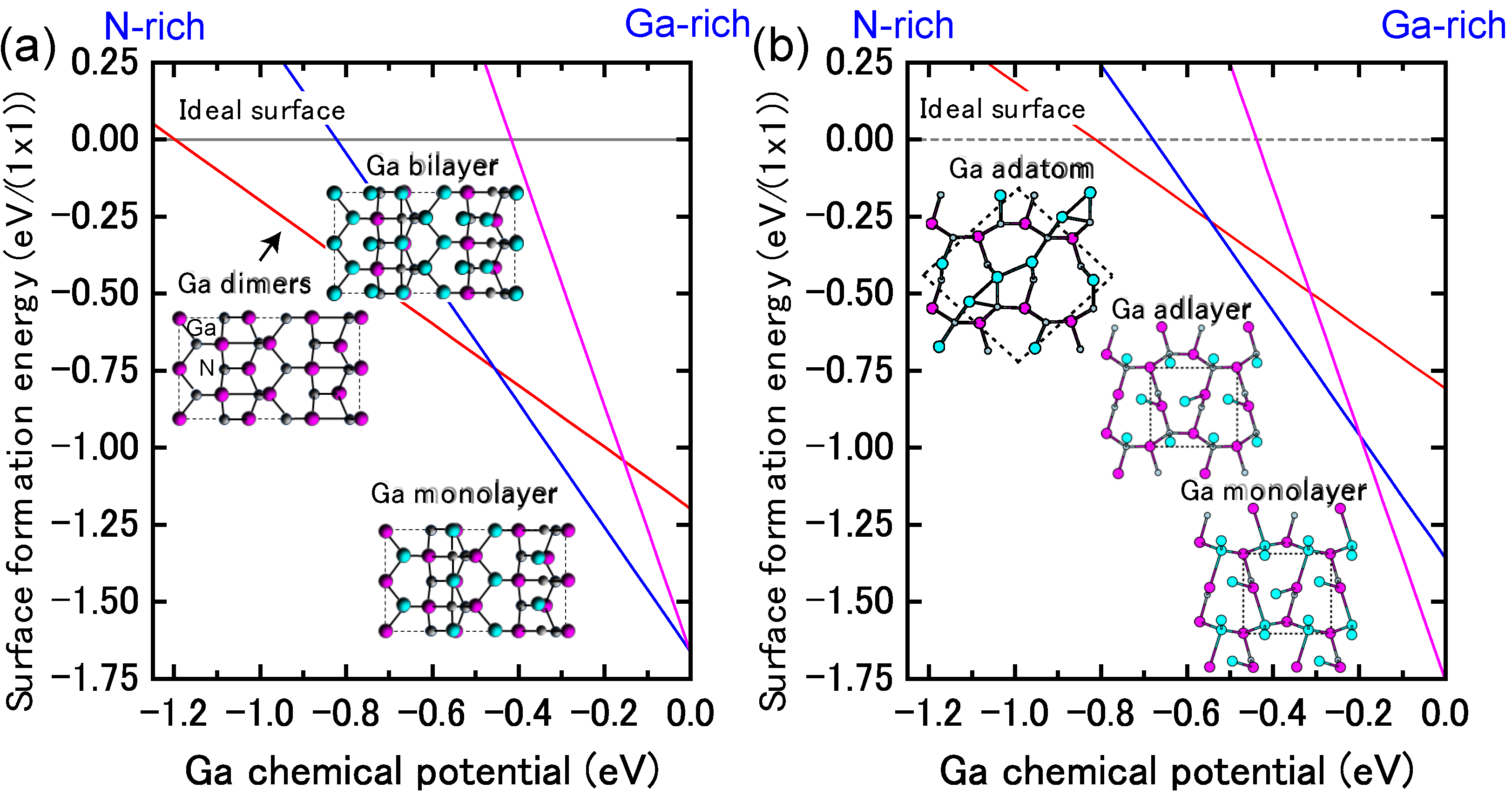
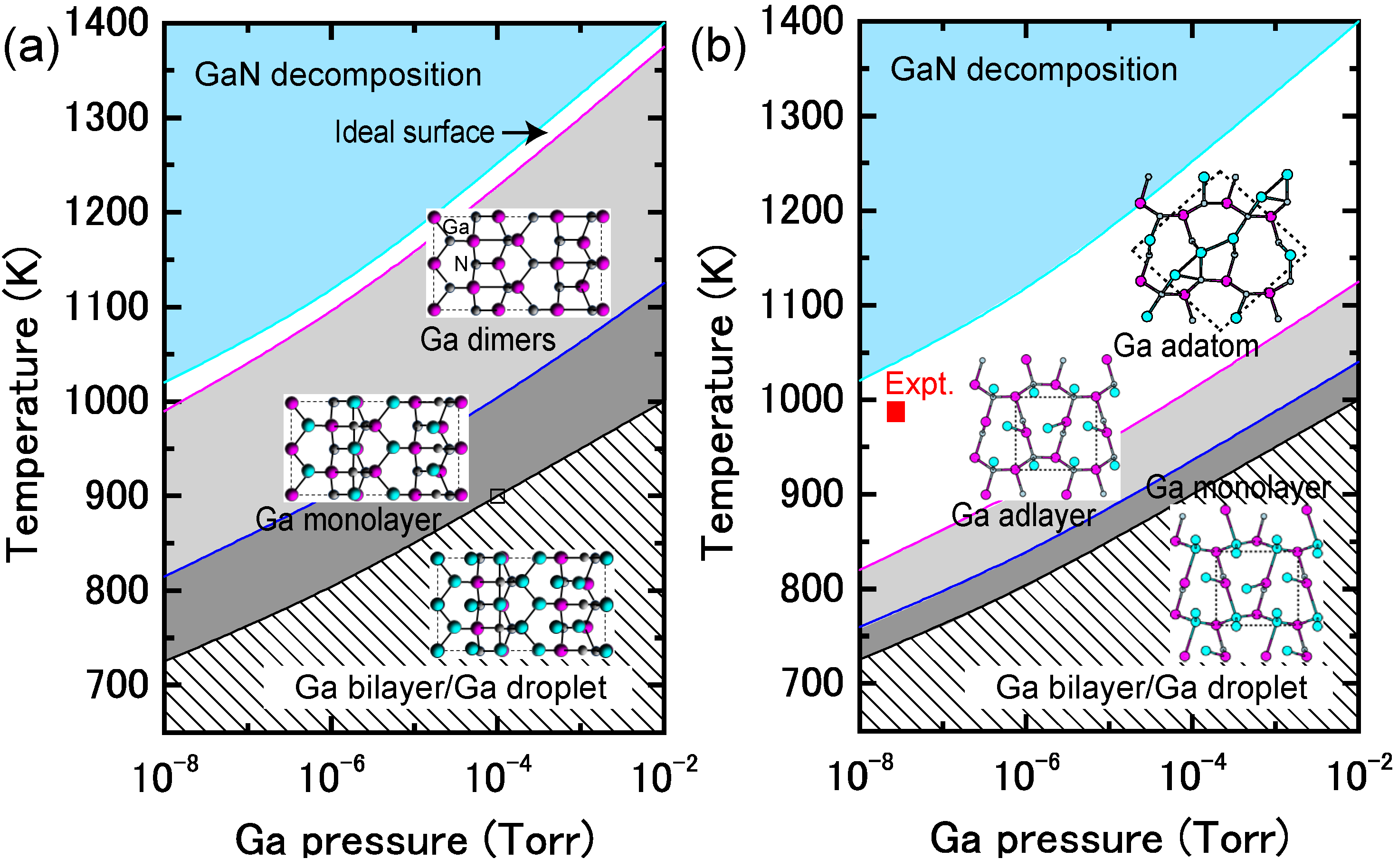
4.1.4. InN Polar Surfaces
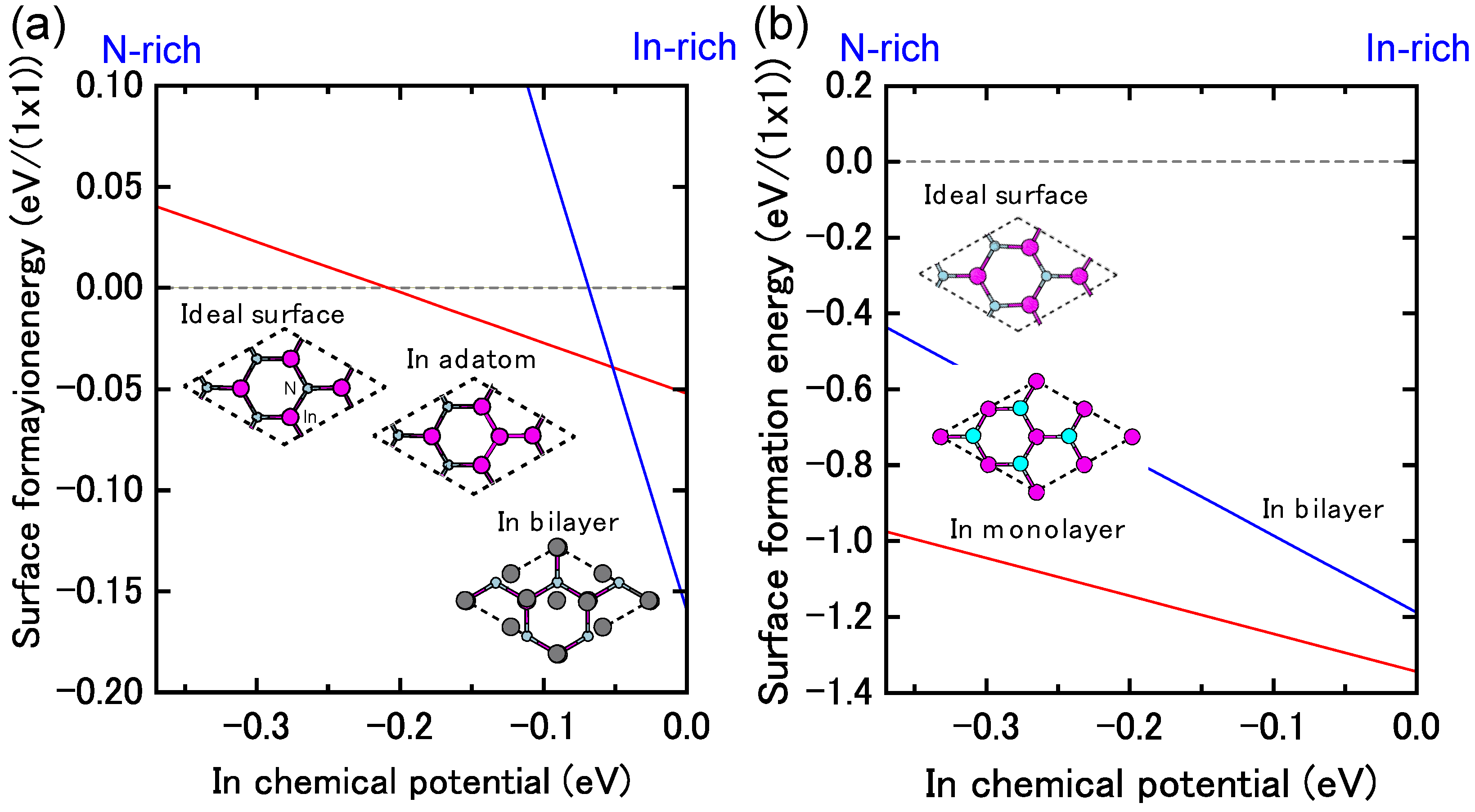
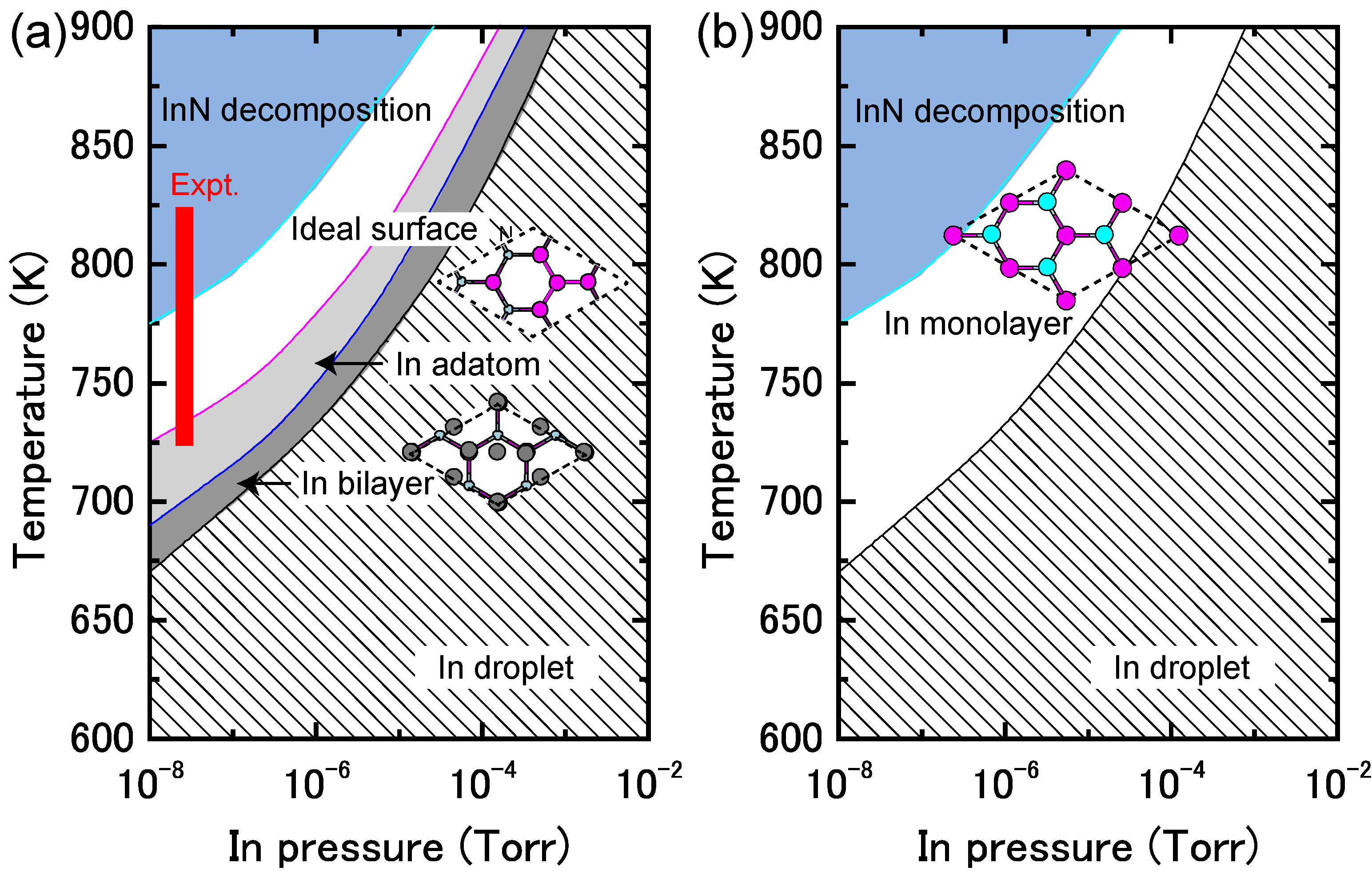
4.1.5. InN Nonpolar Surfaces


4.1.6. InN Semipolar Surfaces


4.1.7. AlN Polar Surfaces

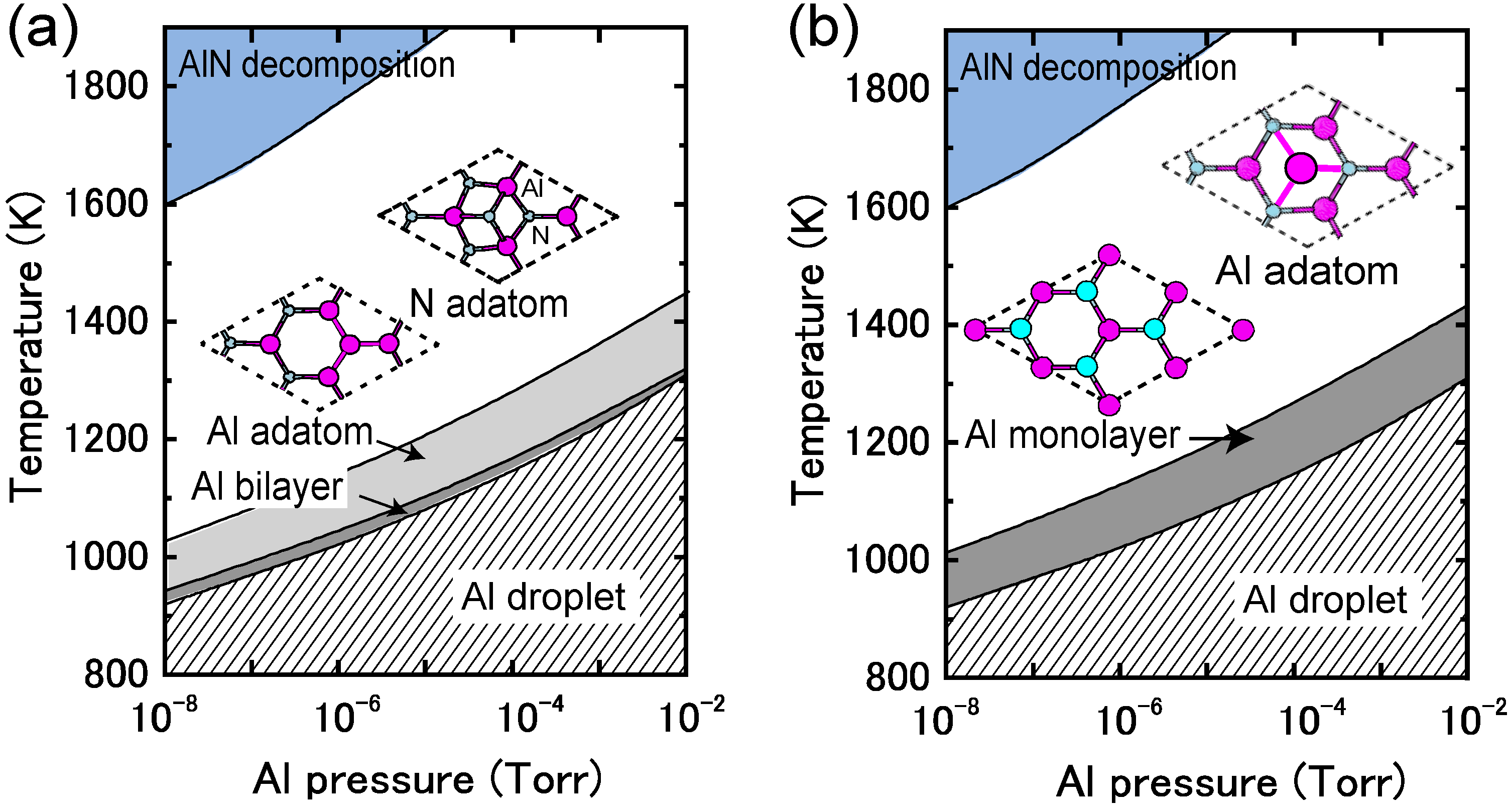
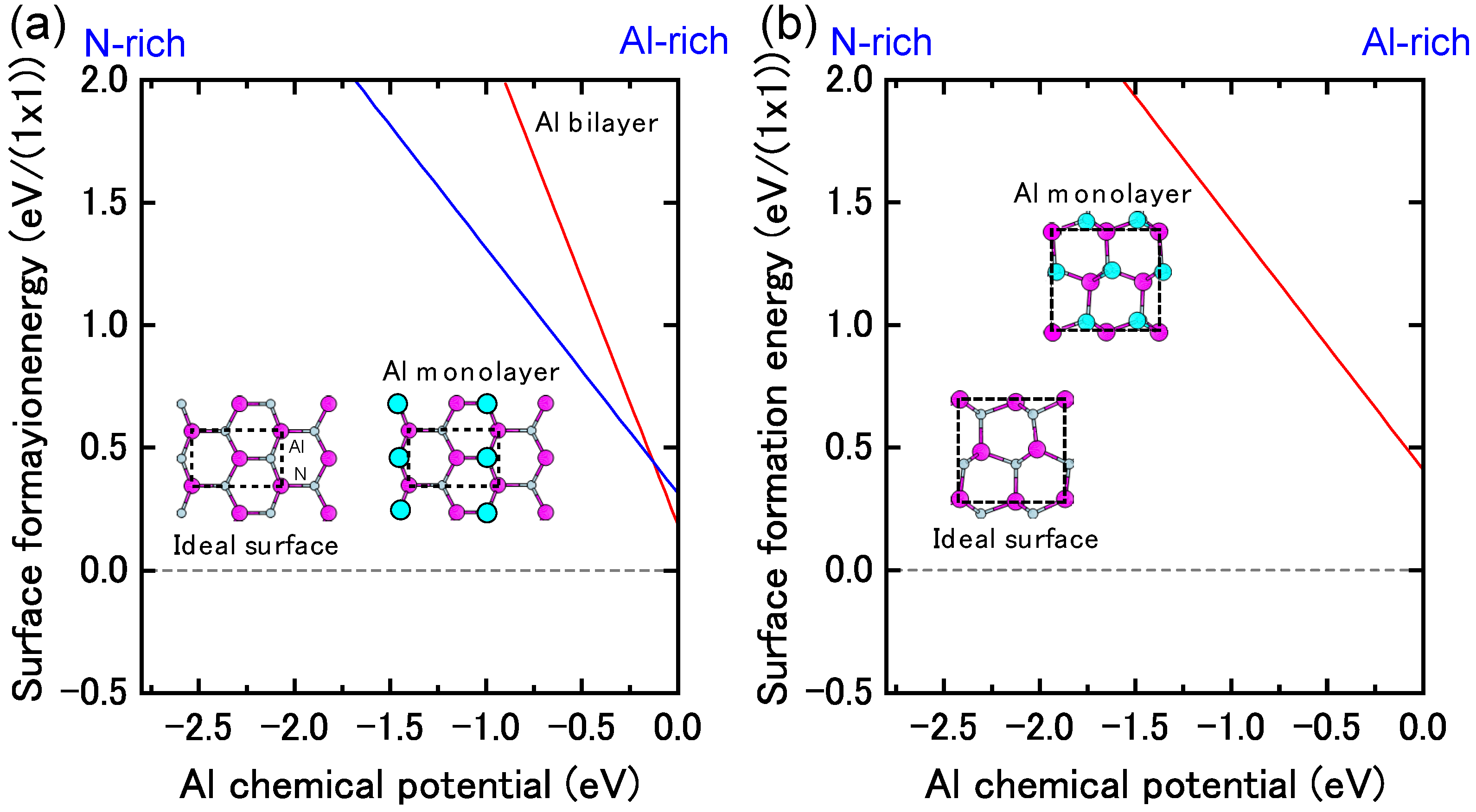
4.1.8. AlN Non-polar Surfaces
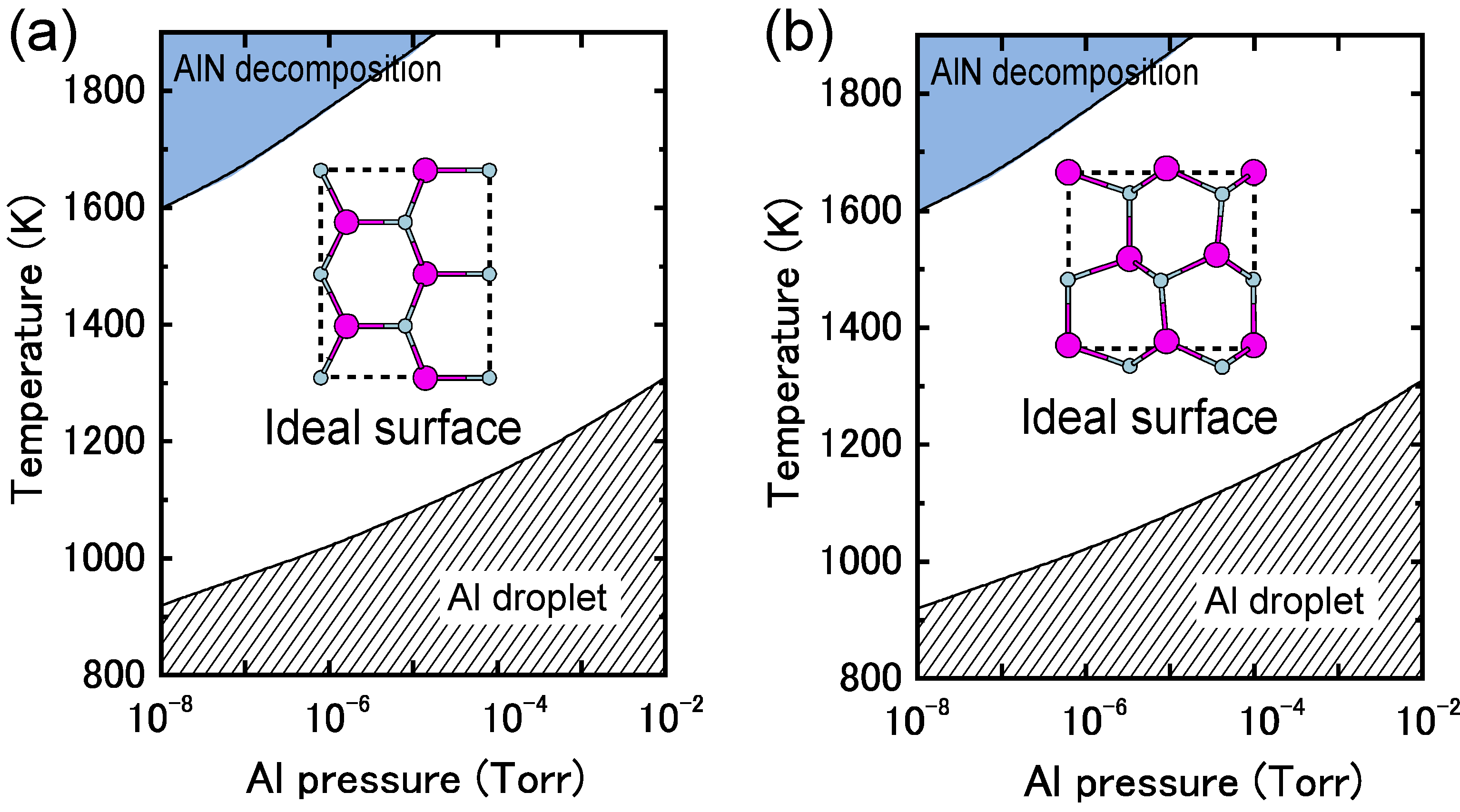
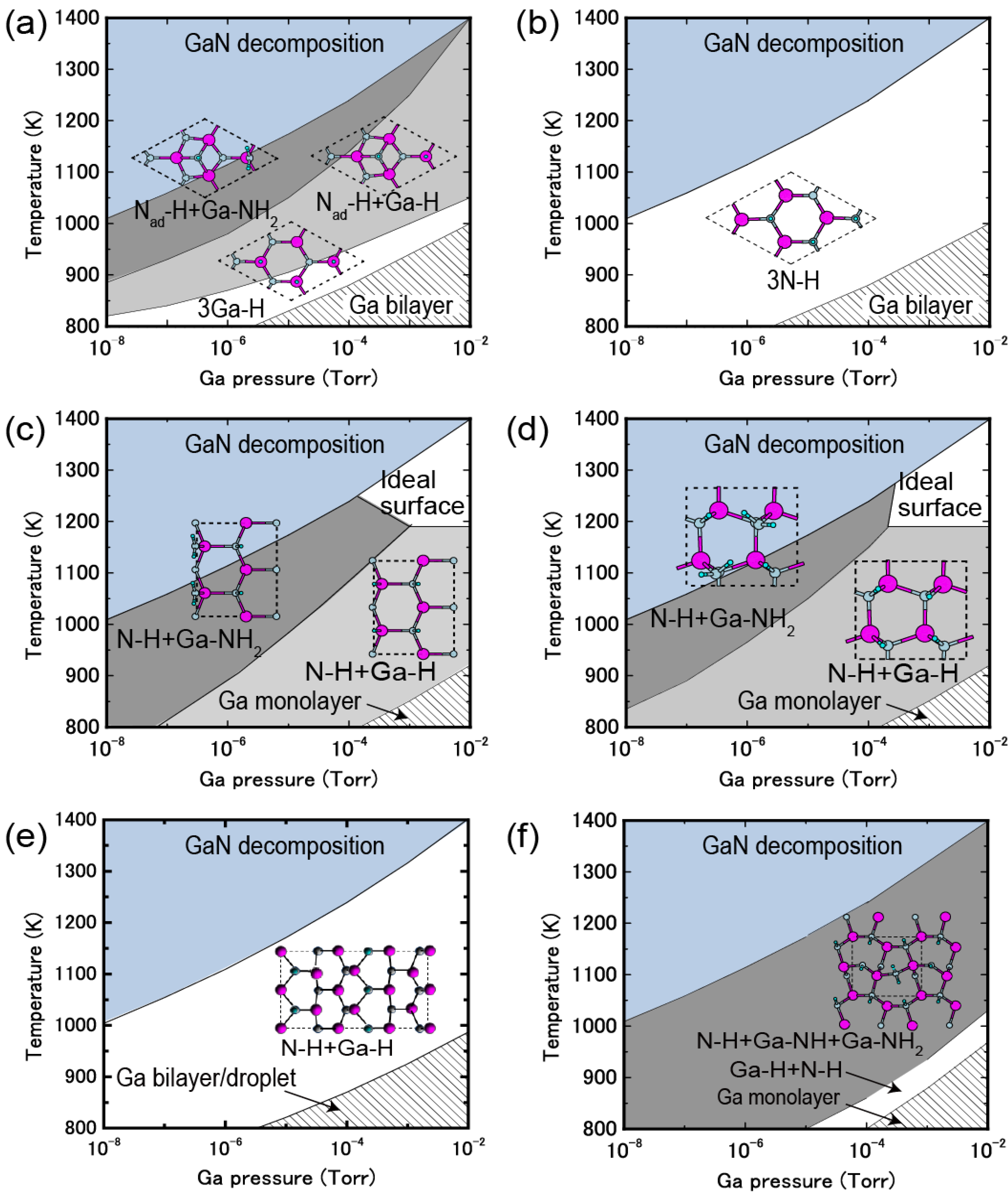
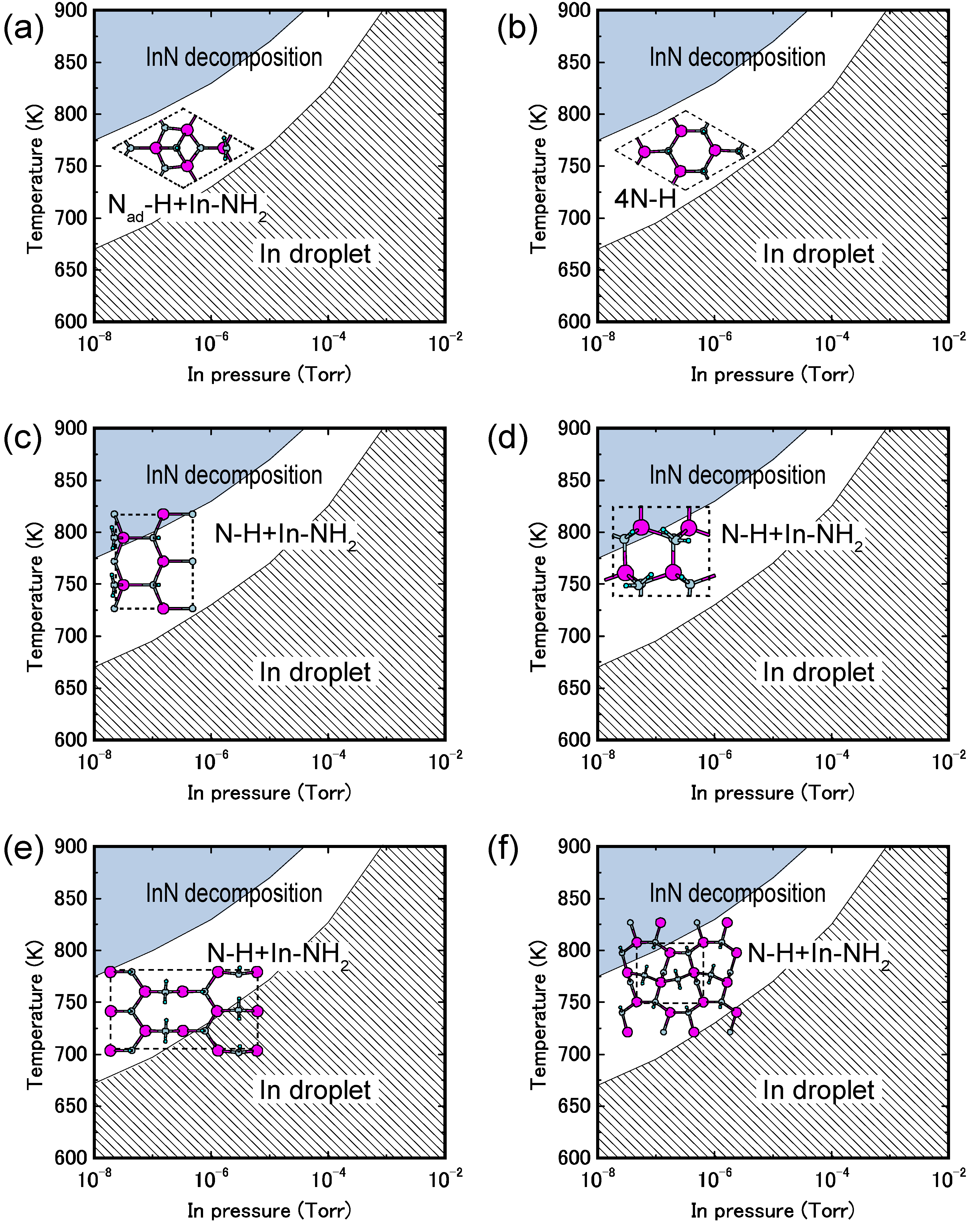
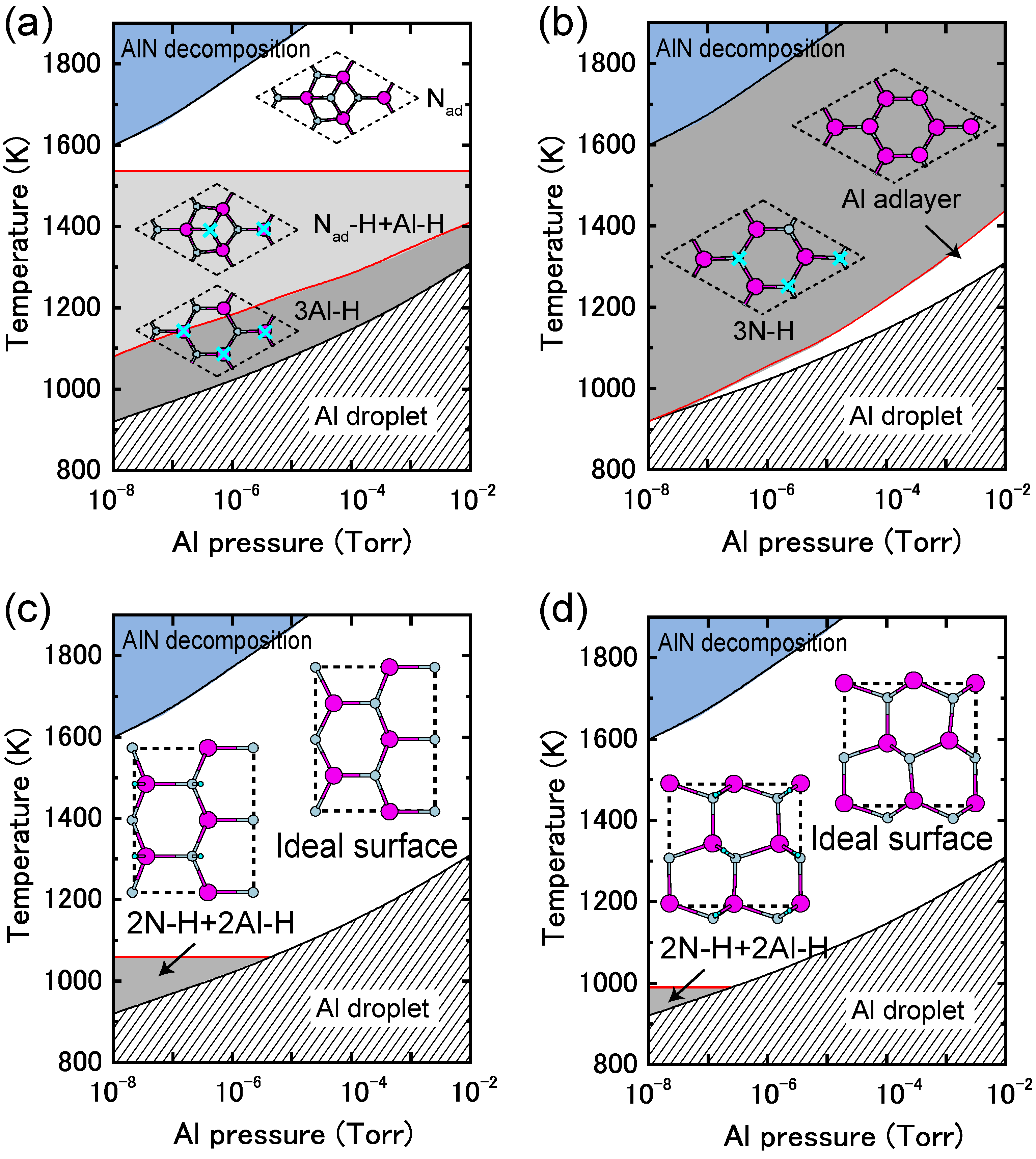
4.2. Hydrogen Adsorption
4.2.1. GaN Surfaces
4.2.2. InN Surfaces
4.2.3. AlN Surfaces
4.3. Growth Kinetics
4.3.1. Adatom Kinetics on Semipolar GaN Surfaces
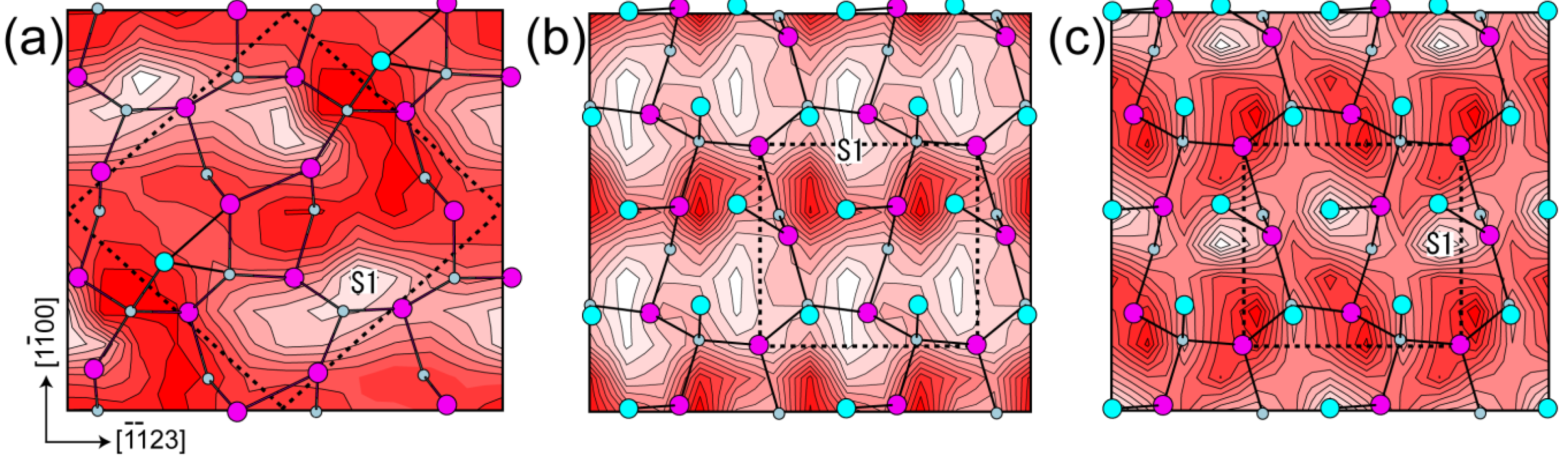
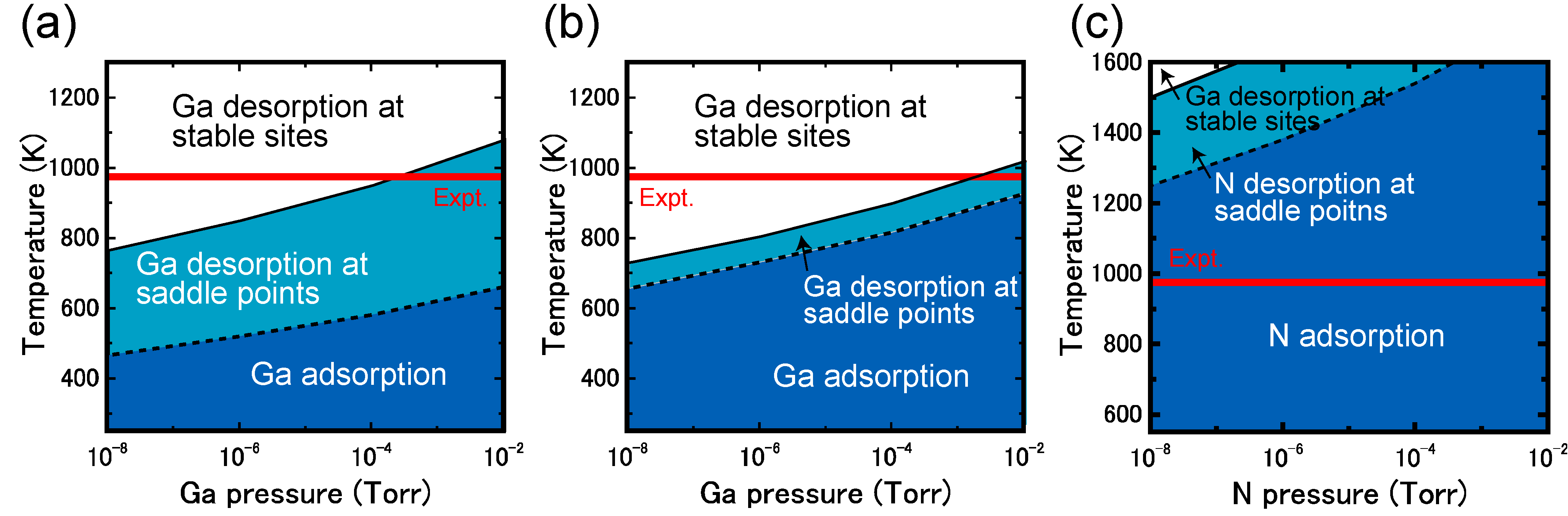
4.3.2. Cubic GaN Growth Conditions
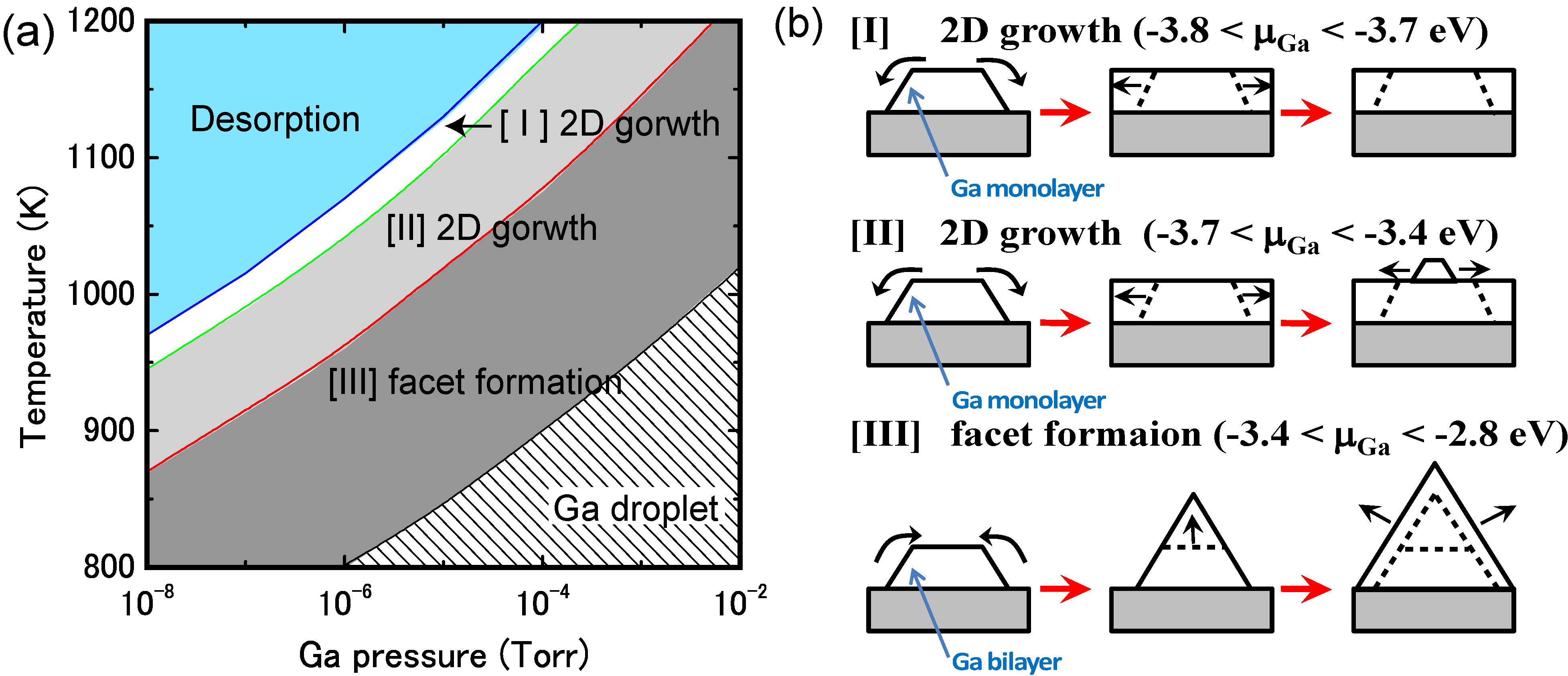
4.3.3. Adatom Kinetics on Polar AlN Surfaces

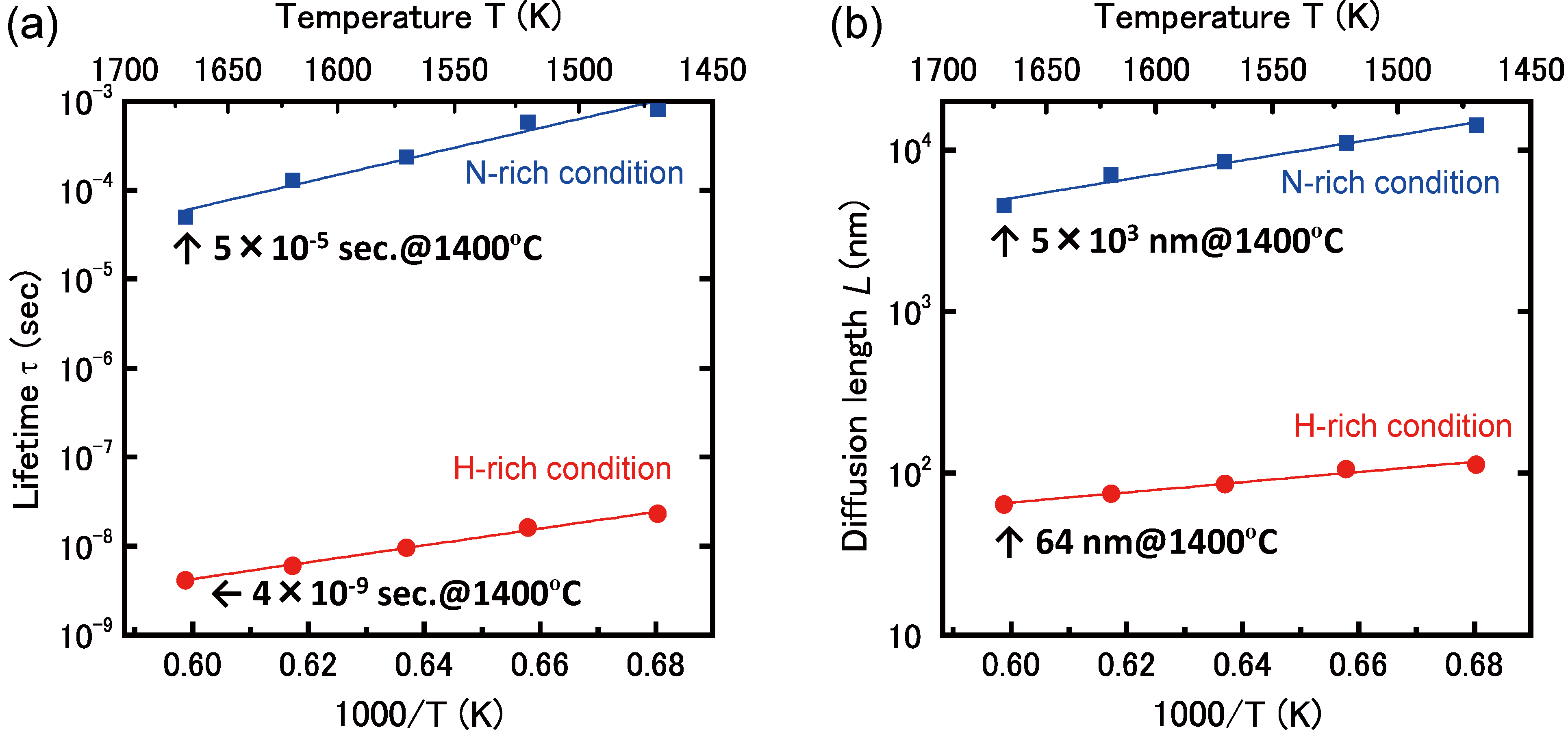
4.4. Impurity Incorporation
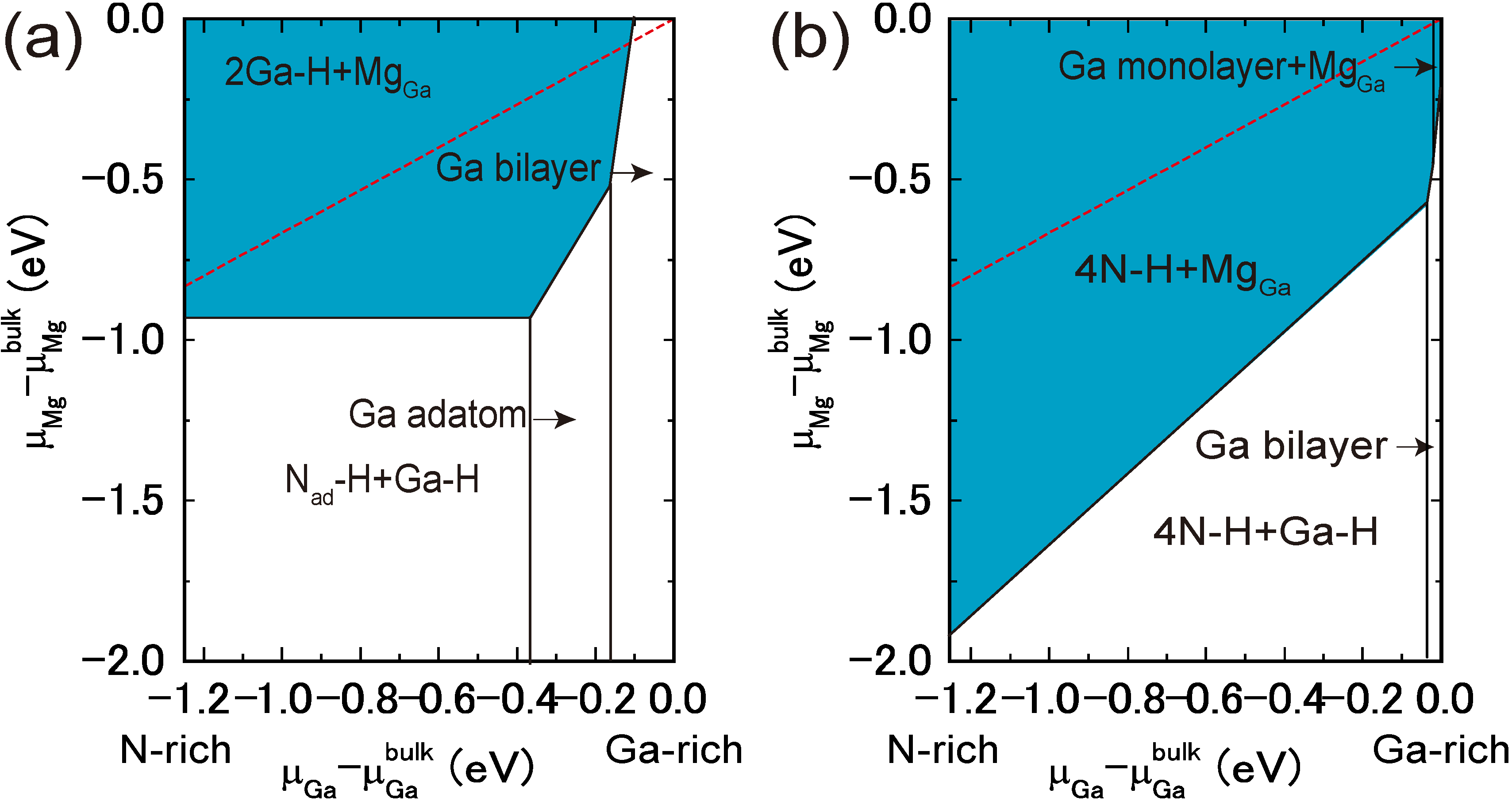
4.4.1. Mg Incorporation on GaN Surfaces
4.4.2. C Incorporation on GaN Surfaces

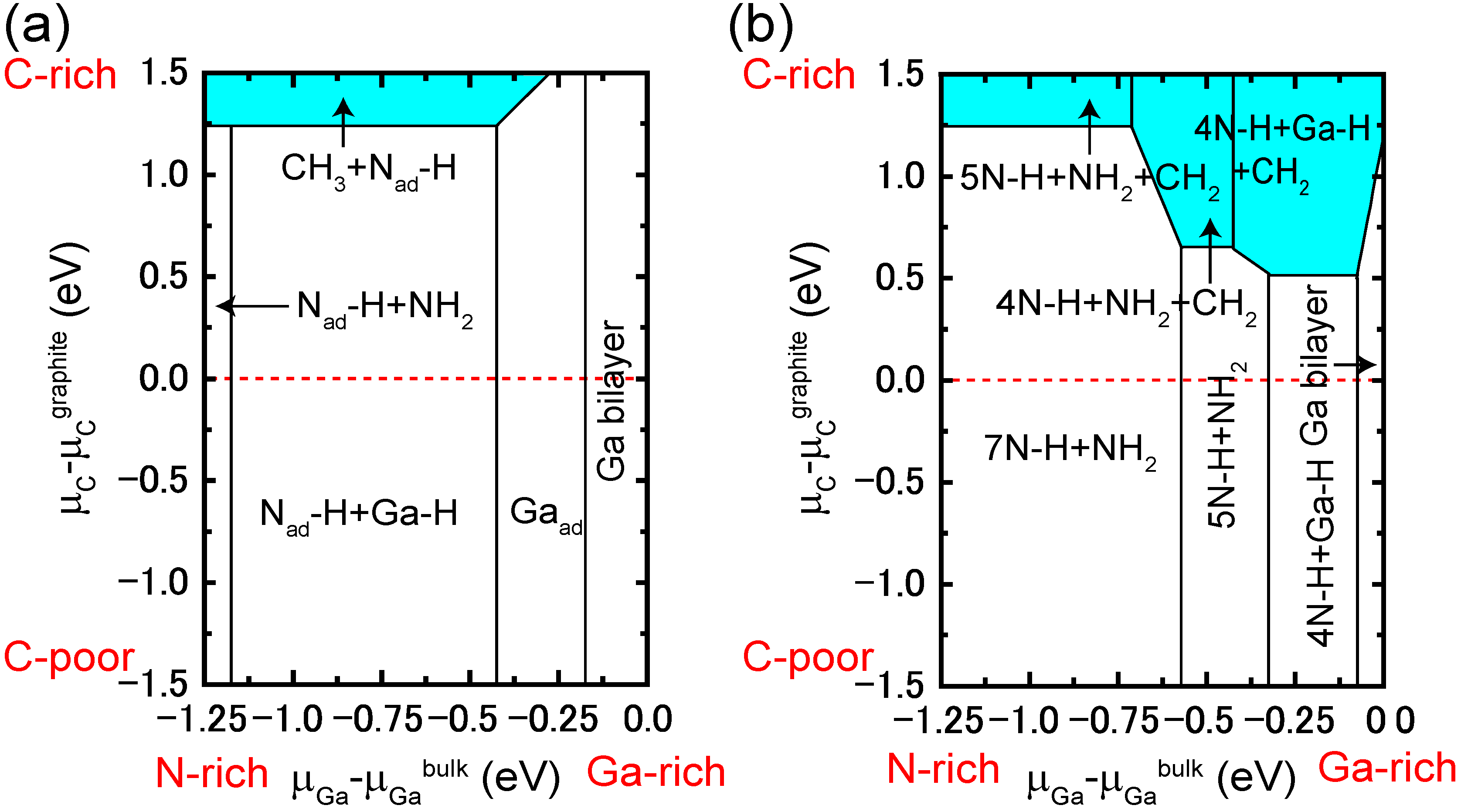
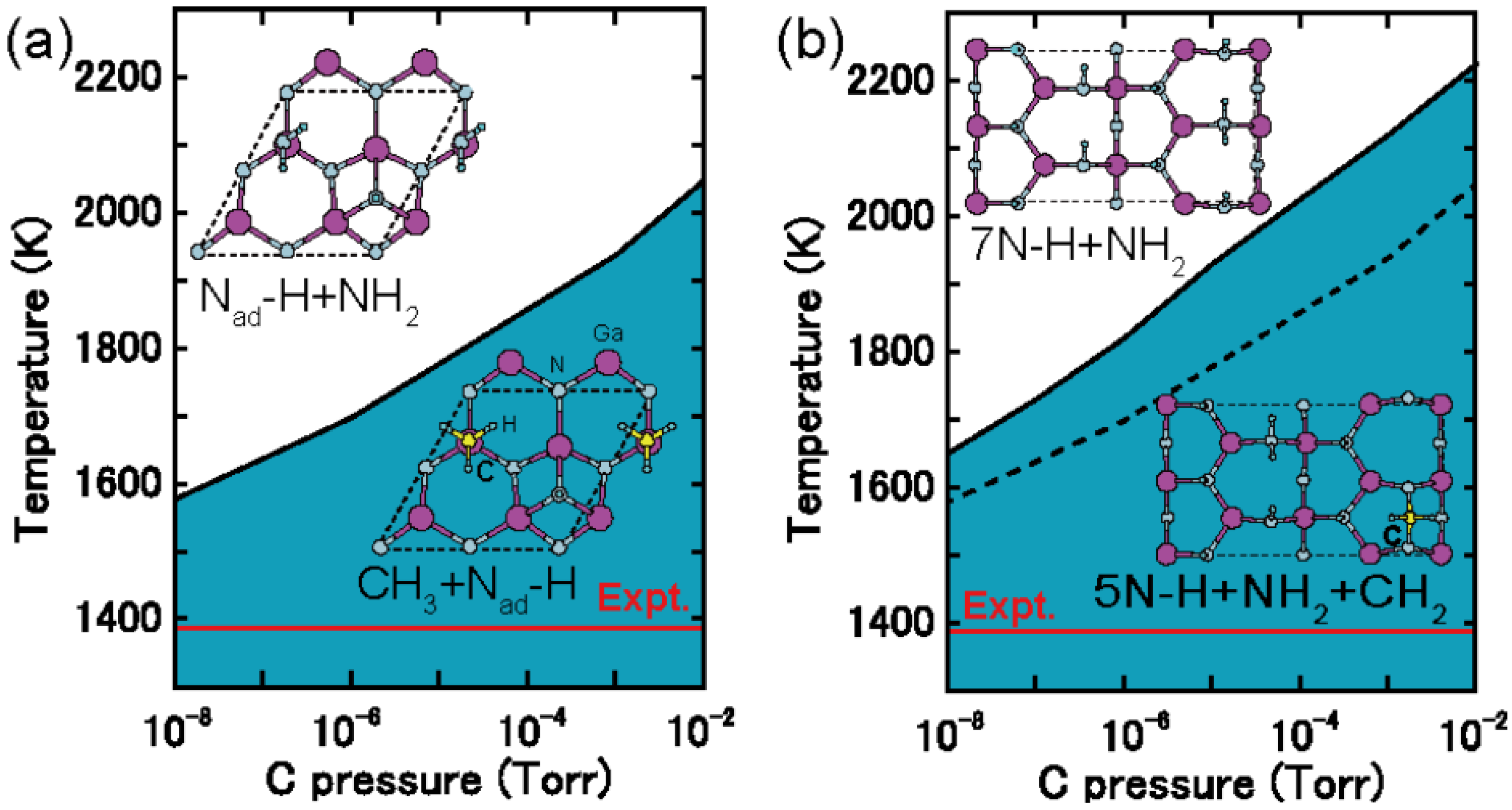
5. Conclusions
Acknowledgements
Conflict of Interest
References
- Däweritz, L.; Hey, R. Reconstruction and defect structure of vicinal GaAs(001) and AlxGa1−xAs(001) surfaces during MBE growth. Surf. Sci. 1990, 236, 15–22. [Google Scholar] [CrossRef]
- Kaxiras, E.; Bar-Yam, Y.; Joannopoulos, J.D.; Pandey, K.C. Ab initio theory of polar semiconductor surfaces. II. (2 × 2) reconstructions and related phase transitions of GaAs(). Phys. Rev. B 1987, 35, 9625–9643. [Google Scholar] [CrossRef]
- Qian, G.X.; Martin, R.M.; Chadi, D.J. Stoichiometry and surface reconstruction: An Ab Initio study of GaAs(100) surfaces. Phys. Rev. Lett. 1988, 60, 1962–1965. [Google Scholar] [CrossRef] [PubMed]
- Northrup, J.E. Structure of Si(100)H: Dependence on the H chemical potential. Phys. Rev. B 1991, 44, 1419–1422. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Taguchi, A.; Shiraishi, K.; Ohachi, T. A new theoretical approach to adsorption–desorption behavior of Ga on GaAs surfaces. Surf. Sci. 2001, 493, 178–181. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Hiraoka, Y.S.; Taguchi, A.; Shiraishi, K.; Ohachi, T. Theoretical approach to influence of As2 pressure on GaAs growth kinetics. Surf. Sci. 2002, 507, 285–289. [Google Scholar] [CrossRef]
- Van de Walle, C.G.; Neugebauer, J. First-principles surface phase diagram for hydrogen on GaN surfaces. Phys. Rev. Lett. 2002, 88, 066103:1–066103:4. [Google Scholar]
- Shu, H.; Chen, X.; Dong, R.; Wang, X.; Lu, W. Thermodynamic phase diagram for hydrogen on polar InP(111)B surfaces. J. Appl. Phys. 2010, 107, 063516:1–063516:5. [Google Scholar] [CrossRef]
- Cho, A.Y.; Arthur, J.R. Molecular beam epitaxy. Prog. Solid State Chem. 1975, 10, 157–191. [Google Scholar] [CrossRef]
- Harris, J.J.; Joyce, B.A.; Dobson, P.J. Oscillations in the surface structure of Sn-doped GaAs during growth by MBE. Surf. Sci. Lett. 1981, 103, L90–L96. [Google Scholar]
- Neave, J.H.; Joyce, B.A.; Dobson, P.J.; Norton, N. Dynamics of film growth of GaAs by MBE from RHEED observations. Appl. Phys. A 1983, 31, 1–8. [Google Scholar] [CrossRef]
- Neave, J.H.; Joyce, B.A. Structure and stoichiometry of {100} GaAs surfaces during molecular beam epitaxy. J. Cryst. Growth 1978, 44, 387–397. [Google Scholar] [CrossRef]
- Shiraishi, K.; Ito, T. Theoretical investigation of adsorption behavior during molecular beam epitaxy growth of GaAs: Ab initio based microscopic calculation. J. Cryst. Growth 1995, 150, 158–162. [Google Scholar] [CrossRef]
- Ito, T. Recent progress in computer-aided materials design for compound semiconductors. J. Appl. Phys. 1995, 77, 4845–4887. [Google Scholar] [CrossRef]
- Ito, M.; Bell, G.R.; Avey, A.R.; Jones, T.S.; Joyce, B.A.; Vvedensky, D.D. Island Nucleation and Growth on Reconstructed GaAs(001) Surfaces. Phys. Rev. Lett. 1998, 81, 633–636. [Google Scholar] [CrossRef]
- Nishinaga, T.; Shen, X.Q.; Kishimoto, D. Surface diffusion length of cation incorporation studied by microprobe-RHEED/SEM MBE. J. Cryst. Growth 1996, 163, 60–66. [Google Scholar] [CrossRef]
- Amano, H.; Sawaki, N.; Akasaki, I.; Toyoda, Y. Metalorganic vapor phase epitaxial growth of a high quality GaN film using an AlN buffer layer. Appl. Phys. Lett. 1986, 48, 353–356. [Google Scholar] [CrossRef]
- Nakamura, S.; Harada, Y.; Seno, M. Novel metalorganic chemical vapor deposition system for GaN growth. Appl. Phys. Lett. 1991, 58, 2021–2024. [Google Scholar] [CrossRef]
- Nakamura, S.; Mukai, T.; Senoh, M. Candela-class high-brightness InGaN/AlGaN double-heterostructure blue-light-emitting diodes. Appl. Phys. Lett. 1994, 64, 1687–1690. [Google Scholar] [CrossRef]
- Takeuchi, T.; Lester, S.; Basile, D.; Girolami, G.; Twist, R.; Mertz, F.; Wong, M.; Schneider, R.; Amano, H.; Akasaki, I. Polarization control in nitride-based semiconductor. Proc. Int. Workshop Nitride Semicond. 2000, 1, 137–140. [Google Scholar]
- Glasstone, S.; Laidler, K.J.; Eyring, H.E. The Theory of Rate Processes; McGraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1941. [Google Scholar]
- Hamman, D.R.; Schluter, M.; Chiang, C. Norm-conserving pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. [Google Scholar] [CrossRef]
- Ohno, T. Energetics of As dimers on GaAs(001) As-rich surfaces. Phys. Rev. Lett. 1993, 70, 631–634. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; et al. Gaussian 98; Revision A. 9; Gaussian Inc.: Pitsburgh, PA, USA, 1998. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5653. [Google Scholar] [CrossRef]
- Andzelm, J.; Huzinaga, S.; Klobukowski, M.; RadzioAndzelm, E.; Sakai, Y.; Takewaki, H. Gaussian Basis Sets for Molecular Calculations; Physical Sciences Data 16; Elsevier: Amsterdam, the Netherland, 1984. [Google Scholar]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure, Constants of Diatomic Molecules; Van Nostrand-Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Louie, S.G.; Froyen, S.; Cohen, M.L. Nonlinear ionic pseudopotentials in spin-density-functional calculations. Phys. Rev. B 1982, 26, 1738–1742. [Google Scholar] [CrossRef]
- Yamauchi, J.; Tsukada, M.; Watanabe, S.; Sugino, O. First-principles study on energetics of c-BN(001) reconstructed surfaces. Phys. Rev. B 1996, 54, 5586–5603. [Google Scholar] [CrossRef]
- Kageshima, H.; Shiraishi, K. Momentum-matrix-element calculation using pseudopotentials. Phys. Rev. B 1997, 56, 14985–14992. [Google Scholar] [CrossRef]
- Kangawa, Y.; Matsuo, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Kakimoto, K. Theoretical approach to initial growth kinetics of GaN on GaN(001). J. Cryst. Growth 2007, 300, 62–65. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to structural change of compound semiconductor surfaces during MBE growth. J. Cryst. Growth 2009, 311, 698–701. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. An ab initio-based approach to the stability of GaN(0001) surfaces under Ga-rich conditions. J. Cryst. Growth 2009, 311, 3093–3096. [Google Scholar] [CrossRef]
- Kangawa, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Kakimoto, K. Theoretical approach to structural stability of GaN: How to grow cubic GaN. J. Cryst. Growth 2009, 311, 3106–3109. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T.; Song, J.-H.; Freeman, A.J. Structures and electronic states of Mg incorporated into InN surfaces: First-principles pseudopotential calculations. Phys. Rev. B 2009, 80, 075316:1–075316:5. [Google Scholar]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Reconstructions of GaN and InN Semipolar (10) Surfaces. Jpn. J. Appl. Phys. 2009, 48, 100201:1–100201:3. [Google Scholar]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Stability of Magnesium-Incorporated Semipolar GaN(10) Surfaces. Jpn. J. Appl. Phys. 2009, 48, 110202:1–110202:3. [Google Scholar]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Surface reconstructions on GaN and InN semipolar (1122) surfaces. Jpn. J. Appl. Phys. 2009, 48, 120201:1–120201:3. [Google Scholar]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Ab initio-based Study for Adatom Kinetics on Semipolar GaN(1122) Surfaces. Jpn. J. Appl. Phys. 2009, 48, 120218:1–120218:3. [Google Scholar]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Stability and indium incorporation processes on In0.25Ga0.75N surfaces under growth conditions: First-principles calculations. Jpn. J. Appl. Phys. 2010, 49, 030212:1–030212:3. [Google Scholar]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Surface reconstruction and magnesium incorporation on semipolar GaN(1101) surfaces. Phys. Rev. B 2010, 81, 245317:1–245317:6. [Google Scholar]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Stability of hydrogen on nonpolar and semipolar nitride surfaces: Role of surface orientation. J. Cryst. Growth 2011, 318, 79–83. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Stability of carbon incorpoated semipolar GaN(1101) surface. Jpn. J. Appl. Phys. 2011, 50, 080216:1–080216:3. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to reconstruction, adsorption and incorporation on GaN surfaces. Semicond. Sci. Technol. 2012, 27, 024010:1–024010:9. [Google Scholar] [CrossRef]
- Akiyama, T.; Obara, D.; Nakamura, K.; Ito, T. Reconstructions on AlN Polar Surfaces under Hydrogen Rich Conditions. Jpn. J. Appl. Phys. 2012, 51, 018001:1–018001:2. [Google Scholar] [CrossRef]
- Akiyama, T.; Saito, Y.; Nakamura, K.; Ito, T. Reconstructions on AlN Nonpolar Surfaces in the Presence of Hydrogen. Jpn. J. Appl. Phys. 2012, 51, 048002:1–048002:2. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based study for adatom kinetics on AlN(0001) surfaces during metal-organic vapor-phase epitaxy growth. Appl. Phys. Lett. 2012, 100, 251601:1–251601:3. [Google Scholar] [CrossRef]
- Northrup, J.E. Effect of magnesium on the structure and growth of GaN(0001). Appl. Phys. Lett. 2005, 86, 122108:1–122108:3. [Google Scholar]
- Sun, Q.; Selloni, A.; Myers, T.H.; Doolittle, W.A. Energetics of Mg incorporation at GaN(0001) and GaN(0001) surfaces. Phys. Rev. B 2006, 73, 155337:1–155337:9. [Google Scholar]
- Kangawa, Y.; Ito, T.; Taguchi, A.; Shiraishi, K.; Irisawa, T.; Ohachi, T. Monte Carlo simulation for temperature dependence of Ga diffusion length on GaAs(001). Appl. Surf. Sci. 2002, 190, 517–520. [Google Scholar] [CrossRef]
- Clarke, S.; Vvedensky, D.D. Origin of reflection high-energy electron-diffraction intensity oscillations during molecular-beam epitaxy: A computational modeling approach. Phys. Rev. Lett. 1987, 58, 2235–2238. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Moritz, W.; Scheffler, M. GaAs(001) surface under conditions of low As pressure: Evidence for a novel surface geometry. Phys. Rev. Lett. 2000, 85, 3890–3893. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.; Modine, N.A.; Millunchick, J.M.; van der Ven, A. Systematic approach for determination of equilibrium atomic surface structure. Phys. Rev. B 2010, 82, 165434:1–165434:13. [Google Scholar] [CrossRef]
- Yamada, K.; Inoue, N.; Osaka, J.; Wada, K. In situ observation of molecular beam epitaxy of GaAs and AlGaAs under deficient As4 flux by scanning reflection electron microscopy. Appl. Phys. Lett. 1989, 55, 622–624. [Google Scholar] [CrossRef]
- Kojima, T.; Kawai, N.J.; Nakagawa, T.; Ohta, K.; Sakamoto, T.; Kawashma, M. Layer-by-layer sublimation observed by reflection high-energy electron diffraction intensity oscillation in a molecular beam epitaxy system. Appl. Phys. Lett. 1985, 47, 286–289. [Google Scholar] [CrossRef]
- Gibson, E.M.; Foxon, C.T.; Zhang, J.; Joyce, B.A. Gallium desorption from GaAs and (Al,Ga)As during molecular beam epitaxy growth at high temperatures. Appl. Phys. Lett. 1990, 57, 1203–1206. [Google Scholar] [CrossRef]
- Shiraishi, K.; Ito, T. Ga-adatom-induced As rearrangement during GaAs epitaxial growth: Self-surfactant effect. Phys. Rev. B 1998, 57, 6301–6304. [Google Scholar] [CrossRef]
- Bell, G.R.; Belk, J.G.; McConvile, C.F.; Jones, T.S. Species intermixing and phase transitions on the reconstructed (001) surfaces of GaAs and InAs. Phys. Rev. B 1999, 59, 2947–2955. [Google Scholar] [CrossRef]
- Ishizaki, H.; Akiyama, T.; Nakamura, K.; Shiraishi, K.; Taguchi, A.; Ito, T. Theoretical investigation of phase transition on GaAs(001)-c(4×4) surface. Appl. Surf. Sci. 2005, 244, 186–189. [Google Scholar] [CrossRef]
- Ito, T.; Tsutsumida, K.; Nakamura, K.; Kangawa, Y.; Shiraishi, K.; Taguchi, A.; Kageshima, H. Systematic theoretical investigations of adsorption behavior on the GaAs(001)-c(4×4) surfaces. Appl. Surf. Sci. 2004, 237, 194–199. [Google Scholar] [CrossRef]
- Fichthorn, K.; Tiwary, Y.; Hammerschmidt, T.; Kratzer, P.; Scheffler, M. Analytic many-body potential for GaAs(001) homoepitaxy: Bulk and surface properties. Phys. Rev. B 2011, 83, 195328:1–195328:11. [Google Scholar] [CrossRef]
- DeLuca, P.M.; Labanda, J.G.C.; Barnet, S.A. An ion-beam technique for measuring surface diffusion coefficients. Appl. Phys. Lett. 1999, 74, 1719–1722. [Google Scholar] [CrossRef]
- Suzuki, T.; Ichimura, I.; Nishinaga, T. Dependence of Ga desorption rate upon the step density in molecular beam epitaxy of GaAs. Jpn. J. Appl. Phys. 1991, 30, L1612–L1615. [Google Scholar] [CrossRef]
- Kley, A.; Ruggerone, P.; Scheffler, M. Novel diffusion mechanism on the GaAs(001) surface: The role of adatom-dimer interaction. Phys. Rev. Lett. 1977, 79, 5278–5281. [Google Scholar] [CrossRef]
- Ohta, K.; Kojima, T.; Nakagawa, T. Anisotropic surface migration of Ga atoms on GaAs(001). J. Cryst. Growth 1989, 95, 71–74. [Google Scholar] [CrossRef]
- LaBella, V.P.; Bullock, D.W.; Ding, Z.; Emery, C.; Harter, W.G.; Thibado, P.M. Monte Carlo derived diffusion parameters for Ga on the GaAs(001)-(2 × 4) surface: A molecular beam epitaxy–scanning tunneling microscopy study. J. Vac. Sci. Technol. A 2000, 18, 1526–1532. [Google Scholar] [CrossRef]
- Shen, X.-Q.; Nishinaga, T. Arsenic pressure dependence of the surface diffusion in molecular beam epitaxy on (111)B-(001) mesa-etched GaAs substrates studied by in situ scanning microprobe reflection high-energy electron diffraction. Jpn. J. Appl. Phys. 1993, 32, L1117–L1119. [Google Scholar] [CrossRef]
- Biegelsen, D.K.; Bringans, R.D.; Northrup, J.E.; Swartz, L.-E. Reconstructions of GaAs(-1-1-1) surfaces observed by scanning tunneling microscopy. Phys. Rev. Lett. 1990, 65, 452–455. [Google Scholar] [CrossRef] [PubMed]
- Northrup, J.E.; Froyen, S. Energetics of GaAs(100)-(2×4) and -(4×2) reconstructions. Phys. Rev. Lett. 1993, 71, 2276–2279. [Google Scholar] [CrossRef] [PubMed]
- Kley, A.; Moll, N.; Pehlke, E.; Scheffler, M. GaAs equilibrium crystal shape from first principles. Phys. Rev. B 1996, 54, 8844–8855. [Google Scholar] [CrossRef]
- Northrup, J.E.; Neugebauer, J.; Feenstra, R.M.; Smith, A.R. Structure of GaN(0001): The laterally contracted Ga bilayer model. Phys. Rev. B 2000, 61, 9932–9935. [Google Scholar] [CrossRef]
- Ishii, A. First-principles study for molecular beam epitaxial growth of GaN(0001). Appl. Surf. Sci. 2003, 216, 447–452. [Google Scholar] [CrossRef]
- Xue, Q.K.; Xue, Q.Z.; Bakhtizin, R.Z.; Hasegawa, Y.; Tsong, I.S.T.; Sakurai, T.; Ohno, T. Structures of GaN(0001)-(2×2), -(4×4), and -(5×5) surface reconstructions. Phys. Rev. Lett. 1999, 82, 3074–3077. [Google Scholar] [CrossRef]
- Smith, A.R.; Feenstra, R.M.; Greve, D.W.; Shin, M.-S.; Skowronski, M.; Neugebauer, J.; Northrup, J.E. GaN(0001) surface structures studied using scanning tunneling microscopy and first-principles total energy calculations. Surf. Sci. 1999, 423, 70–84. [Google Scholar] [CrossRef]
- Xie, M.H.; Zheng, L.X.; Dai, X.Q.; Wu, H.S.; Tong, S.Y. A model for GaN “ghost” islands. Surf. Sci. 2004, 558, 195–200. [Google Scholar] [CrossRef]
- Pashley, M.D.; Haberern, K.W.; Friday, W.; Woodall, J.M.; Kirchner, P.D. Structure of GaAs(001) (2×4)-c(2×8) Determined by Scanning Tunneling Microscopy. Phys. Rev. Lett. 1988, 60, 2176–2179. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, V.; Lee, C.D.; Feenstra, R.M.; Smith, A.R.; Northrup, J.E.; Greve, D.W. Structure of clean and arsenic-covered GaN(0001) surfaces. J. Cryst. Growth 2000, 209, 355–363. [Google Scholar] [CrossRef]
- Vézian, S.; Semond, F.; Massies, J.; Bullock, D.W.; Ding, Z.; Thibado, P.M. Origins of GaN(0001) surface reconstructions. Surf. Sci. 2003, 541, 242–251. [Google Scholar] [CrossRef]
- Feenstra, R.M.; Northrup, J.E.; Neuegbauer, J. Review of structure of bare and adsorbate-covered GaN(0001) surfaces. MRS Internet J. Nitride Semicond. Res. 2002, 7, 1–27. [Google Scholar]
- Smith, A.R.; Feenstra, R.M.; Greve, D.W.; Neugebauer, J.; Northrup, J.E. Reconstructions of the GaN(0001) surface. Phys. Rev. Lett. 1997, 79, 3934–1937. [Google Scholar] [CrossRef]
- Bernardini, F.; Fiorentini, V. Macroscopic polarization and band offsets at nitride heterojunctions. Phys. Rev. B 1998, 57, R9427–R9430. [Google Scholar] [CrossRef]
- Waltereit, P.; Brandt, O.; Trampert, A.; Grahn, H.T.; Menniger, J.; Ramsteiner, M.; Reiche, M.; Ploog, K.H. Nitride semiconductors free of electrostatic fields for efficient white light-emitting diodes. Nature 2000, 406, 865–868. [Google Scholar] [CrossRef] [PubMed]
- McLaurin, M.; Haskell, B.; Nakamura, S.; Speck, J.S. Gallium adsorption onto (1120) gallium nitride surfaces. J. Appl. Phys. 2004, 96, 327–335. [Google Scholar] [CrossRef]
- Segev, D.; van de Walle, C.G. Surface reconstructions on InN and GaN polar and nonpolar surfaces. Surf. Sci. 2007, 601, L15–L18. [Google Scholar] [CrossRef]
- Northrup, J.E.; Neugebauer, J. Theory of GaN(1010) and (1120) surfaces. Phys. Rev. B 1996, 53, R10477–R10480. [Google Scholar] [CrossRef]
- Nishizuka, K.; Funato, M.; Kawakami, Y.; Fujita, S.; Narukawa, Y.; Mukai, T. Efficient radiative recombination from <1122>-oriented InxGa1−xN multiple quantum wells fabricated by the regrowth technique. Appl. Phys. Lett. 2004, 85, 3122–3127. [Google Scholar] [CrossRef]
- Nishizuka, K.; Funato, M.; Kawakami, Y.; Narukawa, Y.; Mukai, T. Efficient rainbow color luminescence from InxGa1−xN single quantum wells fabricated on {1122} microfacets. Appl. Phys. Lett. 2005, 87, 231901:1–231901:3. [Google Scholar] [CrossRef]
- Sharma, R.; Pattison, P.M.; Masui, H.; Farrel, R.M.; Baker, T.J.; Haskell, B.A.; Wu, F.; DenBaars, S.P.; Speck, J.S.; Nakamura, S. Demonstration of a semipolar (10) InGaN/GaN green light emitting diode. Appl. Phys. Lett. 2005, 87, 231110:1–231110:3. [Google Scholar]
- Baker, T.J.; Haskell, B.A.; Wu, F.; Fini, P.T.; Speck, J.S.; Nakamura, S. Characterization of planar semipolar gallium nitride films on spinel substrates. Jpn. J. Appl. Phys. 2005, 44, L920–L922. [Google Scholar] [CrossRef]
- Chakraborty, A.; Baker, T.J.; Haskell, B.A.; Wu, F.; Speck, J.S.; DenBaars, S.P.; Nakamura, S.; Mishra, U.K. Milliwatt power blue InGaN/GaN light-emitting diodes on semipolar GaN templates. Jpn. J. Appl. Phys. 2005, 44, L945–L947. [Google Scholar] [CrossRef]
- Funato, M.; Kotani, T.; Kondou, T.; Kawakami, Y.; Narukawa, Y.; Mukai, T. Tailored emission color synthesis using microfacet quantum wells consisting of nitride semiconductors without phosphors. Appl. Phys. Lett. 2006, 88, 261920:1–261920:3. [Google Scholar] [CrossRef]
- Ueda, M.; Kojima, K.; Funato, M.; Kawakami, Y.; Narukawa, Y.; Mukai, T. Epitaxial growth and optical properties of semipolar (1122) GaN and InGaN/GaN quantum wells on GaN bulk substrates. Appl. Phys. Lett. 2006, 89, 211907:1–211907:3. [Google Scholar] [CrossRef]
- Lahourcade, L.; Renard, J.; Gayral, B.; Monroy, E.; Chaivat, M.P.; Ruterana, P. Ga kinetics in plasma-assisted molecular-beam epitaxy of GaN(1122): Effect on the structural and optical properties. J. Appl. Phys. 2008, 103, 93514:1–93514:10. [Google Scholar] [CrossRef]
- MacChesney, J.B.; Bridenbaugh, P.M.; O’Connor, P.B. Thermal stability of indium nitride at elevated temperatures and nitrogen pressures. Mater. Res. Bull. 1970, 5, 783–791. [Google Scholar] [CrossRef]
- Ambacher, O.; Brandt, M.S.; Dimitrov, R.; Metzger, T.; Stutzmann, M.; Fischer, R.A.; Miehr, A.; Bergmaier, A.; Dollinger, G. Thermal stability and desorption of Group III nitrides prepared by metal organic chemical vapor deposition. J. Vac. Sci. Technol. B 1996, 14, 3532–3542. [Google Scholar] [CrossRef]
- Davydov, V.Y.; Klochikhin, A.A.; Seisyan, R.P.; Emptsev, V.V.; Ivanov, S.V.; Bechstedt, F.; Furthmüller, J.; Harima, H.; Mudryi, A.V.; Aderhold, J.; et al. Absorption and Emission of Hexagonal InN. Evidence of narrow fundamental band gap. Phys. Status Solidi B 2002, 229, R1–R3. [Google Scholar] [CrossRef]
- Wu, J.; Walukiewicz, W.; Yu, K.M.; Ager, J.W.; Haller, E.E.; Lu, H.; Schaff, W.J.; Saito, Y.; Nanishi, Y. Unusual properties of the fundamental band gap of InN. Appl. Phys. Lett. 2002, 80, 3967–3969. [Google Scholar] [CrossRef]
- Nanishi, Y.; Saito, Y.; Yamaguchi, T. RF-molecular beam epitaxy growth and properties of InN and related alloys. Jpn. J. Appl. Phys. 2003, 42, 2549–2559. [Google Scholar] [CrossRef]
- Saito, Y.; Tanabe, Y.; Yamaguchi, T.; Teraguchi, N.; Suzuki, A.; Araki, T.; Nanishi, Y. Polarity of High-Quality Indium Nitride Grown by RF Molecular Beam Epitaxy. Phys. Status Solidi B 2001, 228, 13–16. [Google Scholar] [CrossRef]
- Gan, C.K.; Srolovitz, D.J. First-principles study of wurtzite InN (0001) and (0001) surfaces. Phys. Rev. B 2006, 74, 115319:1–115319:5. [Google Scholar]
- Johnson, M.A.L.; Fujita, S.; Rowland, W.H.; Bowers, K.A.; Hughes, W.C.; He, Y.W.; El-Masry, N.A.; Cook, J.W.; Schetzina, J.F.; Ren, J.; et al. Molecular beam epitaxy growth and properties of GaN, AlxGa1−xN, and AlN on GaN/SiC substrates. J. Vac. Sci. Technol. B 1996, 14, 2349–2353. [Google Scholar] [CrossRef]
- Lee, C.D.; Dong, Y.; Feenstra, R.M.; Northrup, J.E.; Neugebauer, J. Reconstructions of the AlN(0001) surface. Phys. Rev. B 2003, 68, 205317:1–205317:11. [Google Scholar]
- Dasgupta, S.; Wu, F.; Speck, J.S.; Mishra, U.K. Growth of high quality N-polar AlN(0001) on Si(111) by plasma assisted molecular beam epitaxy. Appl. Phys. Lett. 2009, 94, 151906:1–151906:3. [Google Scholar] [CrossRef]
- Ohba, Y.; Yoshida, H.; Sato, R. Growth of High-Quality AlN, GaN and AlGaN with atomically smooth surfaces on sapphire substrates. Jpn. J. Appl. Phys. 1997, 36, L1565–L1567. [Google Scholar] [CrossRef]
- Fujimoto, N.; Kitano, T.; Narita, G.; Okada, N.; Balakrishnan, K.; Iwaya, M.; Kamiyama, S.; Amano, H.; Akasaki, I.; Shimono, K.; et al. Growth of high-quality AlN at high growth rate by high-temperature MOVPE. Phys. Status Solidi C 2006, 3, 1617–1619. [Google Scholar] [CrossRef]
- Okada, N.; Kato, N.; Sato, S.; Sumii, T.; Nagai, T.; Fujimoto, N.; Imura, M.; Balakrishnan, K.; Iwaya, M.; Kamiyama, S.; et al. Growth of high-quality and crack free AlN layers on sapphire substrate by multi-growth mode modification. J. Cryst. Growth 2007, 298, 349–353. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Tanabe, T.; Miyake, H.; Hiramatsu, K.; Shibata, T.; Tanaka, M.; Masa, Y. Growth of thick AlN layer by hydride vapor phase epitaxy. Jpn. J. Appl. Phys. 2005, 44, L505–L507. [Google Scholar]
- Kumagai, Y.; Yamane, T.; Koukitu, A. Growth of thick AlN layers by hydride vapor-phase epitaxy. J. Cryst. Growth 2005, 281, 62–67. [Google Scholar] [CrossRef]
- Kadas, K.; Alvarez, S.; Ruiz, E.; Alemany, P. Structure of the non-polar (1010) surfaces of AlN and α-SiC: A periodic Hartree-Fock study. Surf. Sci. 1996, 355, 167–176. [Google Scholar] [CrossRef]
- Northrup, J.E.; DiFelice, R.; Neugebauer, J. Atomic structure and stability of AlN(0001) and (0001) surfaces. Phys. Rev. B 1997, 55, 13878–13883. [Google Scholar] [CrossRef]
- Fritsch, J.; Sankey, O.F.; Schmidt, K.E.; Page, J.B. Ab initio calculation of the stoichiometry and structure of the (0001) surfaces of GaN and AlN. Phys. Rev. B 1998, 57, 15360–15371. [Google Scholar] [CrossRef]
- Suzuki, H.; Togashi, R.; Murakami, H.; Kumagai, Y.; Koukitu, A. Theoretical analysis for surface reconstruction of AlN and InN in the presence of hydrogen. Jpn. J. Appl. Phys. 2007, 46, 5112–5115. [Google Scholar] [CrossRef]
- Miao, M.S.; Janotti, A.; van de Walle, C.G. Reconstructions and origin of surface states on AlN polar and nonpolar surfaces. Phys. Rev. B 2009, 80, 155319:1–155319:9. [Google Scholar] [CrossRef]
- Koukitsu, A.; Taki, T.; Takahashi, N.; Seki, H. Thermodynamic study on the role of hydrogen during the MOVPE growth of group III nitrides. J. Cryst. Growth 1999, 197, 99–105. [Google Scholar]
- Marchand, H.; Ibbetson, J.P.; Fini, P.T.; Keller, S.; DenBaars, S.P.; Speck, J.S.; Mishra, U.K. Mechanisms of lateral epitaxial overgrowth of gallium nitride by metalorganic chemical vapor deposition. J. Cryst. Growth 1998, 195, 328–332. [Google Scholar] [CrossRef]
- Hiramatsu, K.; Nishiyama, K.; Motogaito, A.; Miyake, H.; Iyechika, Y.; Maeda, T. Recent Progress in Selective Area Growth and Epitaxial Lateral Overgrowth of III-Nitrides: Effects of Reactor Pressure in MOVPE Growth. Phys. Status Solidi A 1999, 176, 535–543. [Google Scholar] [CrossRef]
- Hiramatsu, K.; Nishiyama, K.; Onishi, M.; Mizutani, H.; Narukawa, M.; Motogaito, A.; Miyake, H.; Iyechika, Y.; Maeda, T. Fabrication and characterization of low defect density GaN using facet-controlled epitaxial lateral overgrowth (FACELO). J. Cryst. Growth 2000, 221, 316–326. [Google Scholar] [CrossRef]
- Zywietz, T.; Neugebauer, J.; Scheffler, M. Adatom diffusion at GaN (0001) and (0001) surfaces. Appl. Phys. Lett. 1998, 73, 487–489. [Google Scholar] [CrossRef]
- Lymperakis, L.; Neugebauer, J. Large anisotropic adatom kinetics on nonpolar GaN surfaces: Consequences for surface morphologies and nanowire growth. Phys. Rev. B 2009, 79, 241308R:1–241308R:4. [Google Scholar] [CrossRef]
- Kimura, R.; Suzuki, T.; Ouchi, M.; Ishida, K.; Takahashi, K. Thick cubic GaN film growth using ultra-thin low-temperature buffer layer by RF–MBE. J. Cryst. Growth 2005, 278, 411–414. [Google Scholar] [CrossRef]
- Okumura, H.; Ohta, K.; Feuillet, G.; Balakrishnan, K.; Chichibu, S.; Hamaguchi, H.; Hacke, P.; Yoshida, S. Growth and characterization of cubic GaN. J. Cryst. Growth 1997, 178, 113–133. [Google Scholar]
- Neugebauer, J.; Zywietz, T.; Scheffler, M.; Northrup, J.E.; van de Walle, C.G. Clean and As-covered zinc-blende GaN (001) surfaces: Novel surface structures and surfactant behavior. Phys. Rev. Lett. 1998, 80, 3097–3100. [Google Scholar] [CrossRef]
- Adeimann, C.; Braut, J.; Jalabert, D.; Gentile, P.; Mariette, H.; Mula, G.; Daudin, B. Dynamically stable gallium surface coverages during plasma-assisted molecular-beam epitaxy of (0001) GaN. J. Appl. Phys. 2002, 91, 9638:1–9638:8. [Google Scholar]
- Miyagawa, R.; Yang, S.; Miyake, H.; Hiramatsu, K. Effects of carrier gas ratio and growth temperature on MOVPE growth of AlN. Phys. Status Solidi C 2012, 9, 499–502. [Google Scholar] [CrossRef]
- Rice, A.; Collazo, R.; Tweedie, J.; Dalmau, R.; Mita, S.; Xie, J.; Sitar, Z. Surface preparation and homoepitaxial deposition of AlN on (0001)-oriented AlN substrates by metalorganic chemical vapor deposition. J. Appl. Phys. 2010, 108, 043510:1–043510:8. [Google Scholar] [CrossRef]
- Amano, H.; Kito, M.; Hiramatsu, K.; Akasaki, I. P-type conduction in Mg-doped GaN treated with low-energy electron beam irradiation (LEEBI). Jpn. J. Appl. Phys. 1989, 28, L2112–L2114. [Google Scholar] [CrossRef]
- Nakamura, S.; Iwasa, N.; Senoh, M.; Mukai, T. Hole compensation mechanism of P-type GaN films. Jpn. J. Appl. Phys. 1992, 31, 1258–1266. [Google Scholar] [CrossRef]
- Hikosaka, T.; Koide, N.; Honda, Y.; Yamaguchi, M.; Sawaki, N. Mg doping in (1101)GaN grown on a 7° off-axis (001)Si substrate by selective MOVPE. J. Cryst. Growth 2007, 298, 207–210. [Google Scholar] [CrossRef]
- Tomita, K.; Hikosaka, T.; Kachi, T.; Sawaki, N. Mg segregation in a (1101) GaN grown on a 7° off-axis (001) Si substrate by MOVPE. J. Cryst. Growth 2009, 311, 2883–2886. [Google Scholar] [CrossRef]
- Li, L.K.; Jurkovic, M.J.; Wang, W.I. Surface polarity dependence of Mg doping in GaN grown by molecular-beam epitaxy. Appl. Phys. Lett. 2000, 76, 1740–1742. [Google Scholar] [CrossRef]
- Monroy, E.; Andreev, T.; Holliger, P.; Bellet-Amalric, E.; Shibata, T.; Tanaka, M.; Daudin, B. Modification of GaN(0001) growth kinetics by Mg doping. Appl. Phys. Lett. 2004, 84, 2554:1–2554:3. [Google Scholar]
- Northrup, J.E. Hydrogen and magnesium incorporation on c-plane and m-plane GaN surfaces. Phys. Rev. B 2008, 77, 045313:1–045313:7. [Google Scholar] [CrossRef]
- Zhong, H.; Tyagi, A.; Fellows, N.N.; Wu, F.; Chung, R.B.; Saito, M.; Fujito, K.; Speck, J.S.; DenBaars, S.P.; Nakamura, S. High power and high efficiency blue light emitting diode on freestanding semipolar (10) bulk GaN substrate. Appl. Phys. Lett. 2007, 90, 233504:1–233504:3. [Google Scholar]
- Boguslawski, P.; Briggs, E.L.; Bernholc, J. Amphoteric properties of substitutional carbon impurity in GaN and AlN. Appl. Phys. Lett. 1996, 69, 233–235. [Google Scholar] [CrossRef]
- Tang, H.; Webb, J.B.; Bardwell, J.A.; Raymond, S.; Salzman, J.; Uzan-Saguy, C. Properties of carbon-doped GaN. Appl. Phys. Lett. 2001, 78, 757–759. [Google Scholar] [CrossRef]
- Hikosaka, T.; Koide, N.; Honda, Y.; Yamaguchi, M.; Sawaki, N. p-type conduction in a C-doped (1101)GaN grown on a 7-degree-off oriented (001)Si substrate by selective MOVPE. Phys. Status Solidi C 2006, 3, 1425–1428. [Google Scholar] [CrossRef]
- Sawaki, N.; Hikosaka, T.; Koide, N.; Tanaka, S.; Honda, Y.; Yamaguchi, M. Growth and properties of semi-polar GaN on a patterned silicon substrate. J. Cryst. Growth 2009, 311, 2867–2874. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kangawa, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Nakayama, T. Surface Stability and Growth Kinetics of Compound Semiconductors: An Ab Initio-Based Approach. Materials 2013, 6, 3309-3360. https://doi.org/10.3390/ma6083309
Kangawa Y, Akiyama T, Ito T, Shiraishi K, Nakayama T. Surface Stability and Growth Kinetics of Compound Semiconductors: An Ab Initio-Based Approach. Materials. 2013; 6(8):3309-3360. https://doi.org/10.3390/ma6083309
Chicago/Turabian StyleKangawa, Yoshihiro, Toru Akiyama, Tomonori Ito, Kenji Shiraishi, and Takashi Nakayama. 2013. "Surface Stability and Growth Kinetics of Compound Semiconductors: An Ab Initio-Based Approach" Materials 6, no. 8: 3309-3360. https://doi.org/10.3390/ma6083309
APA StyleKangawa, Y., Akiyama, T., Ito, T., Shiraishi, K., & Nakayama, T. (2013). Surface Stability and Growth Kinetics of Compound Semiconductors: An Ab Initio-Based Approach. Materials, 6(8), 3309-3360. https://doi.org/10.3390/ma6083309





