The Role Played by Computation in Understanding Hard Materials
Abstract
:1. Introduction
2. Computational Approaches
3. Boron Carbon Nitrogen Structures
3.1. Graphitic Precursor Structures
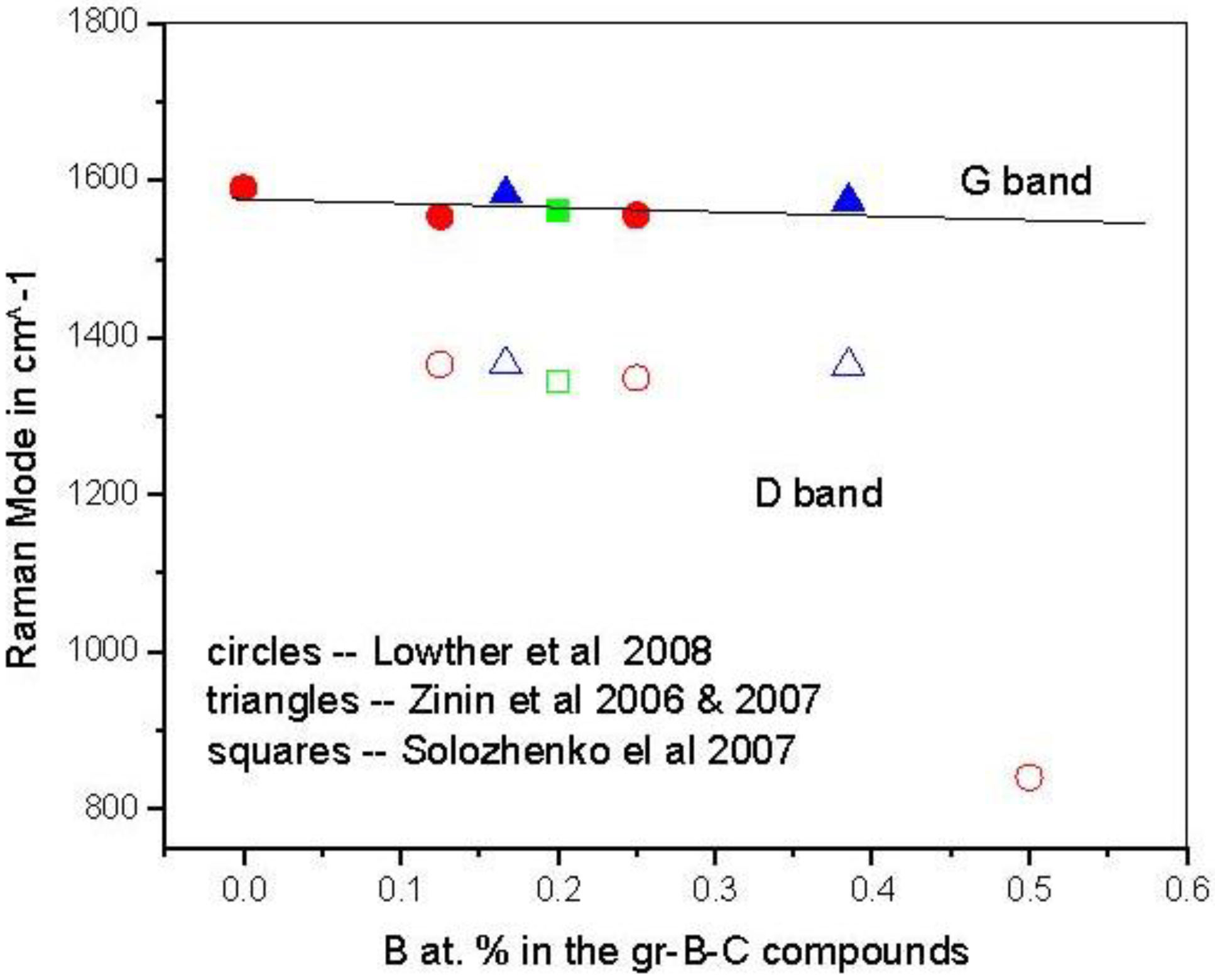
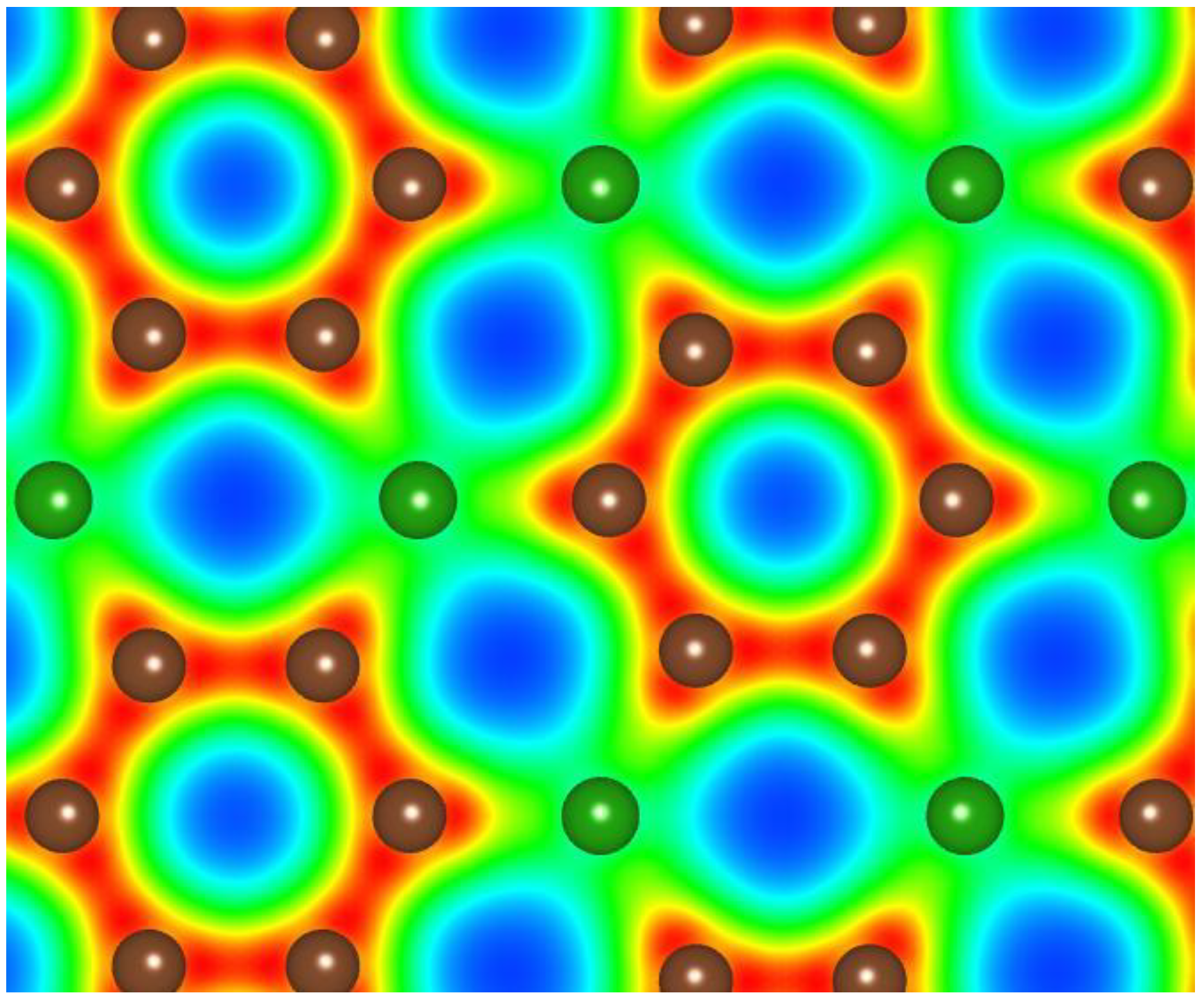
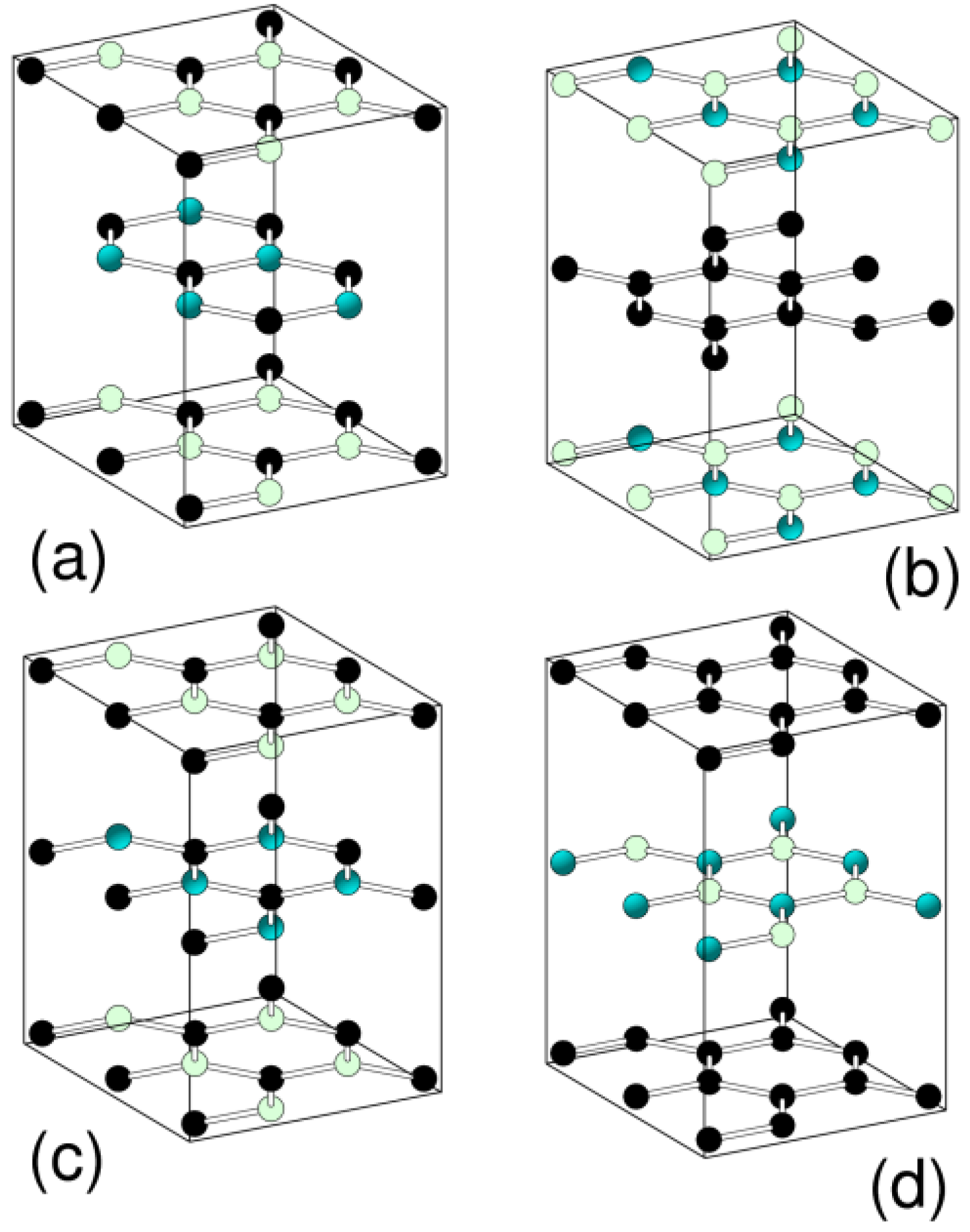
| a (A) | c (A) | Etot (eV/atom) | |
|---|---|---|---|
| h-BC2N (a) | 2.50 | 5.74 | −8.456 |
| h-BC2N (b) | 2.47 | 6.41 | −9.880 |
| h-BC2N (c) | 2.50 | 5.89 | −8.440 |
| h-BC2N (d) | 2.47 | 6.82 | −9.868 |
| Expt. | 2.42 | 7.25 |
3.2. Superhard Structures
| Stoichiometry | hexagonal phase | Diamond-like phase | Energy difference (eV/atom) |
|---|---|---|---|
| BC2N | h-BC2N | BC2N | −0.397 |
| BC3 | BC3 | BC3 | +0.058 |
| C | graphite | diamond | −0.003 |
| BN | h-BN | c-BN | +0.056 |
4. Advanced Nitrides
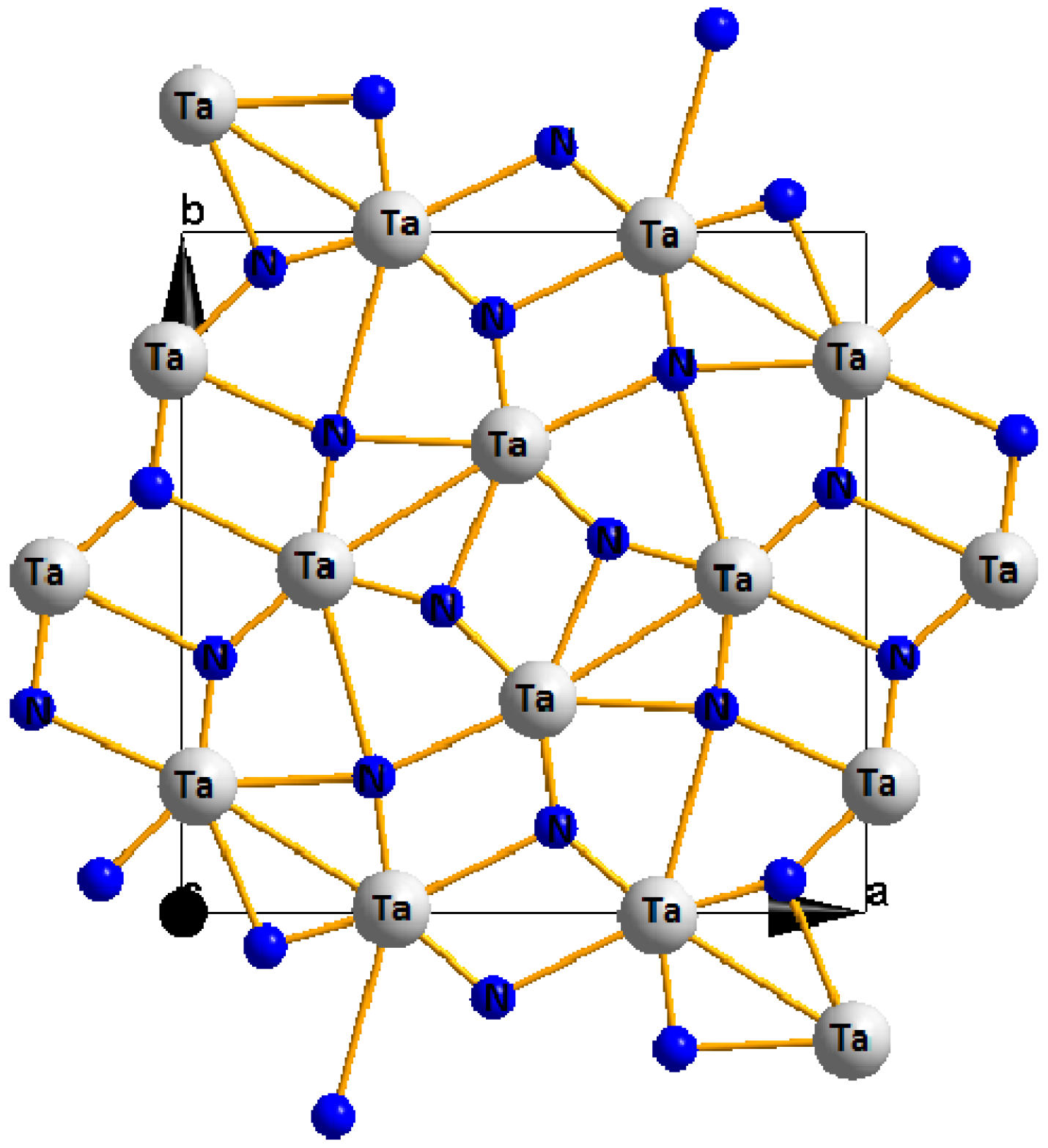
5. Strong Metallic Alloys

6. Conclusions
Acknowledgements
References
- Haines, J.; Leger, J.M.; Bocquillon, G. Synthesis and design of superhard materials. Ann. Rev. Mater. Res. 2001, 31, 1–18. [Google Scholar] [CrossRef]
- Brazhkin, W.; Lyapin, A.G.; Hemley, R.J.; Hemley, R.J. Harder than diamond: Dreams and reality. Philos. Mag. A Phys. Condens. 2002, 82, 231–241. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Superhard Materials; Naukova Dumka: Kiev, Ukraine, 1980. [Google Scholar]
- Oganov, A.R.; Lyakhov, A.O. Towards the theory of hardness of materials. J. Superhard Mater. 2010, 32, 143–147. [Google Scholar] [CrossRef]
- Li, Q.; Wang, H.; Ma, Y.M. Predicting new superhard phases. J. Superhard Mater. 2010, 32, 192–204. [Google Scholar] [CrossRef]
- Joubert, D. Density functionals: Theory and application. Lect. N. Phys. 1997, 500, 47–48. [Google Scholar]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joanopoulos, J.D. Joanopoulos, electronic structure of materials. Rev. Mod. Phys. 1992, 64, 1045–1051. [Google Scholar] [CrossRef]
- Martin, R. Electronic Structure Basic Theory and Practical Methods; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Hong, S.; Seung-Hoon, J.; Roundy, D.; Cohen, M.L.; Louie, S.G. Structural forms of cubic BC2N. Phys. Rev. B 2003, 64, 094108:1–094108:6. [Google Scholar]
- Lowther, J.E. Potential super-hard phases and the stability of diamond-like boron-carbon structures. J. Phys. Condens. Matter 2005, 17, 3221–3229. [Google Scholar] [CrossRef]
- Kim, E.; Pang, T.; Utsumi, W.; Solozhenko, V.L.; Zhao, Y.S. Cubic phases of BC2N: A first-principles study. Phys. Rev. B 2007, 75, 184115:1–184115:4. [Google Scholar]
- Hubble, H.W.; Kudryashov, I.; Solozhenko, V.L.; Zinin, P.V.; Sharma, S.K.; Ming, L.C. Raman studies of cubic BC2N, a new superhard phase. J. Raman Spectrosc. 2004, 35, 822–825. [Google Scholar] [CrossRef]
- Solozhenko, V.L. High-pressure synthesis of novel superhard phases in the B-C-N system: Recent achievements. High Pressure Res. 2009, 29, 612–617. [Google Scholar] [CrossRef]
- Tkachev, S.N.; Solozhenko, V.L.; Zinin, P.V.; Manghnani, M.H.; Ming, L.C. Elastic moduli of the superhard cubic BC2N phase by Brillouin scattering. Phys. Rev. B 2003, 68, 052104:1–052104:3. [Google Scholar] [CrossRef]
- Haines, J.; Cambon, O.; Le Parc, R.; Levelut, C. The effect of static disorder on pressure-induced phase transitions and amorphization in alpha-quartz-type solid solutions. Phase Transit. 2007, 80, 1039–1049. [Google Scholar] [CrossRef]
- Teter, D.M.; Hemley, R.J.; Kresse, G.; Hafner, J. High pressure polymorphism in silica. Phys. Rev. Lett. 1998, 80, 2145–2151. [Google Scholar] [CrossRef]
- Munetoh, S.; Motooka, T.; Moriguchi, K.; Shintani, A. potential for Si-O systems using Tersoff parameterization. Computat. Mater. Sci. 2007, 39, 334–339. [Google Scholar] [CrossRef]
- Dubrovinskaia, N.A.; Dubrovinsky, L.S. High-pressure silica polymorphs as hardest known oxides. Mater. Chem. Phys. 2001, 68, 77–83. [Google Scholar] [CrossRef]
- Dewhurst, J.K.; Lowther, J.E.; Madzwara, L.T. High-pressure phases of SiO2 using local-density and generalized-gradient approximations. Phys. Rev. B 1997, 55, 11003–11005. [Google Scholar] [CrossRef]
- Grimsditch, M.; Popova, S.; Brazhkin, V.V.; Voloshin, R.N. Temperate induced amorphization of SiO2 Stishovite. Phys. Rev. B 1994, 50, 12984–12992. [Google Scholar] [CrossRef]
- Tsuchida, Y.; Yagi, T. A new post-stishovite high pressure phase polymorph of silica. Nature 1989, 340, 217–219. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Swamy, V.; Muscat, J.; Harrison, N.M.; Ahuja, R.; Holm, B.; Johansson, B. Materials science—The hardest known oxide. Nature 2001, 410, 653–654. [Google Scholar] [CrossRef] [PubMed]
- Haines, J.; Leger, J.M.; Atouf, A. Crystal-structure and equation of state of cotunnite-type zirconia. J. Amer. Ceram. Soc. 1995, 78, 445–448. [Google Scholar] [CrossRef]
- Lowther, J.E.; Dewhurst, J.K.; Leger, J.M.; Haines, J. Relative stability of ZrO2 and HfO2 structural phases. Phys. Rev. B 1999, 60, 14485–14488. [Google Scholar] [CrossRef]
- Desgreniers, S.; Lagarec, K. High-density ZrO2 and HfO2: Crystalline structures and equations of state. Phys. Rev. B 1999, 59, 8467–8472. [Google Scholar] [CrossRef]
- Yang, J.W.; Chen, X.R.; Luo, F.; Ji, G.F. First-principles calculations for elastic properties of OsB2 under pressure. Phys. B Condens. Matter 2009, 404, 3608–3613. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.J. Mechanical and electronic properties of 5d transition metal diborides MB2 (M = Re, W, Os, Ru). J. Appl. Phys. 2009, 105, 122–131. [Google Scholar]
- Chung, H.Y.; Weinberger, M.B.; Yang, J.M.; Tolbert, S.H.; Kaner, R.B. Correlation between hardness and elastic moduli of the ultracompressible transition metal diborides RuB2, OsB2, and ReB2. Appl. Phys. Lett. 2008, 92, 98–103. [Google Scholar]
- Gregoryanz, E.; Sanloup, C.; Somayazulu, M.; Badroi, J.; Fiquet, G.; Mao, H.-K.; Hemley, R.J. Synthesis and characterization of a binary noble metal nitride. Nature 2004, 3, 294–297. [Google Scholar] [CrossRef]
- Dey, G.K.; Sekhar, J.A. Physical metallurgy of nickel aluminides. Metall. Mater. Trans. B. 1987, 28, 905–909. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566–568. [Google Scholar] [CrossRef]
- Perdew, J.P.; Kurth, S. Density Functionals: Theory and Applications; Theoretical Physics Held at Meerensee: Cape Town, South Africa, 1997; Volume 8. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–563. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Quantum Espresso. Available online: http://www.quantum-espresso.org/contacts.php (accessed on 11 May 2009).
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–1997. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D.P. From Ultrasoft Pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1762. [Google Scholar] [CrossRef]
- Joubert, D.P. Density Functional Theory; Springer: Heidelberg, Germany, 1998. [Google Scholar]
- Smith, W.; Forester, T. DLPOLY code for molecular dynamics. J. Mol. Graph. 1996, 14, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D. Gulp: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 1, 629–641. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermodynamics of Crystals; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Oganov, A.R.; Chen, J.-H.; Gatti, C.; Ma, Y.-Zh.; Yuan, Y.M.; Glass, C.W.; Liu, Zh.X.; Tony-Yu, O.O.K.; Solozhenk, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–865. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Solozhenko, V.L. Boron: A hunt for superhard polymorphs. J. Superhard Mater. 2009, 31, 285–291. [Google Scholar] [CrossRef]
- Letsoalo, T.; Lowther, J.E. Systematic trends in boron icosahedral structured materials. J. Phys. B Condens. Matter 2008, 403, 2760–2767. [Google Scholar] [CrossRef]
- Johnson, O.T.; Sigalas, I.; Ogunmuyiwa, E.N.; Kleebe, H.J.; Muller, M.M.; Herrmann, M. Boron suboxide materials with Co sintering additives. Ceram. Int. 2010, 36, 1762–1771. [Google Scholar]
- Fahy, S.; Louie, S.G.; Cohen, M.L. Aproach to graphite to diamond transitions. Phys. Rev. B 1987, 35, 7623–7629. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Petrusha, I.A. On the kinetic boundary of the rBN to wBN transformation at high static pressure. Sverkhtverdye Materialy 1996, 62, 67–71. [Google Scholar]
- Albe, K.; Moller, W. Modelling of boron nitride: Atomic scale simulations on thin film growth. Comput. Mater. Sci. 1998, 10, 111–115. [Google Scholar] [CrossRef]
- Lowther, J.E.; Zinin, P.V.; Ming, L.C. Vibrational energies of graphene and hexagonal structured planar B–C complexes. Phys. Rev. B 2009, 79, 033401:1–033401:4. [Google Scholar] [CrossRef]
- Zinin, P.V.; Ming, L.C.; Kudryashov, I.; Konishi, N.; Manghnani, M.H.; Sharma, S.K. Pressure- and temperature-induced phase transition in the B–C system. J. Appl. Phys. 2006, 100, 013516:1–013516:6. [Google Scholar] [CrossRef]
- Zinin, P.V.; Ming, L.C.; Kudryashov, I.; Konishi, N.; Sharma, S.K. Raman spectroscopy of the BC3 phase obtained under high pressure and high temperature. J. Raman Spectrosc. 2007, 38, 1362–1367. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Kuznetsov, A.Y. Raman scattering from turbostratic graphitelike BC4 under pressure. J. Appl. Phys. 2007, 102, 5–12. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Andrault, D.; Fiquet, G.; Mezouar, M.; Rubie, D.C. Synthesis of superhard cubic BC2N. Appl. Phys. Lett. 2001, 78, 1385–1389. [Google Scholar] [CrossRef]
- Sun, H.; Jhi, S.H.; Roundy, D.; Cohen, M.L.; Louie, S.G. Structural forms of cubic BC2N. Phys. Rev. B 2001, 64, 094108:1–094108:6. [Google Scholar]
- Lowther, J.E. Elastic and Vibrational Properties of Boron-Carbon Ultra Hard Materials. In Sensors, Ultra High Temperature Ceramics, Thermoelectrics, Armor; Lugovy, N.O.A.M., Ed.; Springer: Aalborg, Denmark, 2010. [Google Scholar]
- Abdel-Mottaleb, M.M.S.; Van der Auweraer, M.; Abdel-Mottaleb, M.S.A. Photostability of J-aggregates adsorbed on TiO2 nanoparticles and AFM imaging of J-aggregates on a glass surface. Int. J. Photoenergy 2004, 6, 29–33. [Google Scholar] [CrossRef]
- Nkambule, S.M.; Lowther, J.E. Crystalline and random “diamond-like” boron-carbon structures. Solid State Commun. 2010, 150, 133–136. [Google Scholar] [CrossRef]
- Ma, X.Y.; He, D.Y.; Chen, G.H. Synthesis and mechanism of BC2N thin films in stalk-like growth. Acta Phys. Sin. 2001, 50, 2023–2027. [Google Scholar]
- Mattesini, A.; Matar, S.F. Search for ultra-hard materials: Theoretical characterisation of novel orthorhombic BC2N crystals. Int. J. Inorg. Mater. 2001, 3, 943–947. [Google Scholar] [CrossRef]
- Huang, J.Y.; Zhu, Y.T.; Mori, H. Structure and phase characteristics of amorphous boron-carbon-nitrogen under high pressure and high temperature. J. Mater. Res. 2001, 16, 1178–1184. [Google Scholar] [CrossRef]
- He, J.L.; Tian, Y.J.; Yu, D.L.; Wang, T.S.; Liu, S.M.; Guo, L.C.; Li, D.C.; Jia, X.P.; Chen, L.X.; Zou, G.T.; Yanagisawa, O. Orthorhombic BC2N crystal synthesized by high pressure and temperature. Chem. Phys. Lett. 2001, 340, 431–436. [Google Scholar] [CrossRef]
- Kohler-Redlich, P.; Terrones, M.; Manteca-Diego, C.; Hsu, W.K.; Terrones, H.; Ruhle, M.; Kroto, H.W.; Walton, D.R.M. Stable BC2N nanostructures: Low-temperature production of segregated C/BN layered materials. Chem. Phys. Lett. 1999, 310, 459–465. [Google Scholar] [CrossRef]
- Widany, J.; Verwoerd, W.S.; Frauenheim, T. Density-functional based tight-binding calculations on zinc-blende type BC2N-crystals. Diam. Relat. Mater. 1998, 7, 1633–1638. [Google Scholar] [CrossRef]
- Tateyama, Y.; Ogitsu, T.; Kusakabe, K.; Tsuneyuki, S.; Itoh, S. Proposed synthesis path for heterodiamond BC2N. Phys. Rev. B 1997, 55, R10161–R10164. [Google Scholar] [CrossRef]
- Zerr, A.; Riedel, R.; Sekine, T.; Lowther, J.E.; Ching, W.-Y.; Tanaka, I. Recent advances in new hard high-pressure nitrides. Adv. Mater. 2006, 18, 2933–2953. [Google Scholar] [CrossRef]
- McMillan, P.F. New materials from high-pressure experiments. Nat. Mater. 2002, 1, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Kroll, P.; Schroter, T.; Peters, M. Prediction of novel phases of tantalum(V) nitride and tungsten(VI) nitride that can be synthesized under high pressure and high temperature. Angew. Chem. Int. Ed. 2005, 44, 4249–4254. [Google Scholar] [CrossRef]
- Crowhurst, J.; Goncharov, A.; Sadigh, B.; Zaug, J.; Meng, Y.; Prakapenka, V. Synthesis and characterization of nitrides of iridium and palladium. Mater. Res. High Pressure 2007, 987, 3–9. [Google Scholar]
- Young, A.F.; Sanloup, C.; Gregoryanz, E.; Scandolo, S.; Hemley, R.J.; Mao, H.K. Synthesis of novel transition metal nitrides IrN2 and OsN2. Phys. Rev. Lett. 2006, 96, 155501:1–155501:4. [Google Scholar] [CrossRef]
- Young, A.F.; Montoya, J.A.; Sanloup, C.; Lazzeri, M.; Gregoryanz, E.; Scandolo, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 1566–1577. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev B 2006, 73, 104118:1–104118:8. [Google Scholar]
- Jamal, U.; Scuseria, G.E. Structures and electronic properties of platinum nitride by density functional theory. Phys. Rev. B 2005, 72, 035101:1–035101:6. [Google Scholar]
- Young, A.F.; Montoya, J.A.; Sanloup, C.; Lazzeri, M.; Gregoryanz, E.; Scandolo, S. Interstitial dinitrogen makes PtN2 an insulating hard solid. Phys. Rev. B 2006, 73, 153102:1–153102:4. [Google Scholar] [CrossRef]
- Fan, C.Z.; Zeng, S.Y.; Li, L.X.; Zhan, Z.J.; Liu, R.P.; Wang, W.K.; Zhang, P.; Yao, Y.G. Potential superhard osmium dinitride with fluorite and pyrite structure: First-principles calculations. Phys. Rev. B 2006, 74, 1088–1092. [Google Scholar]
- Friedrich, A.; Winkler, B.; Bayarjargal, L.; Juarez Arellano, E.A.; Morgenroth, W.; Biehler, J.; Schröder, F.; Yan, J.; Clark, S.M. In situ observation of the reaction of tantalum with nitrogen in a laser heated diamond anvil cell. J. Alloys Compounds 2010, 502, 5–12. [Google Scholar] [CrossRef]
- Jiang, Ch.; Lin, Zh.J.; Zhao, Y.Sh. Thermodynamic and mechanical stabilities of tantalum nitride. Phys. Rev. Lett. 2009, 103, 185501:1–185501:4. [Google Scholar]
- Banejee, D.; Gogia, K.K.; Nandy, T.K.; Uraleedharan, K.M.; Mishra, R.S. Structural Intermetallics. In Proceedings of International Symposium on Structural Intermetallics, Champion, PA, USA, 26–30 September 1993; pp. 19–23.
- Dey, G.K.; Sekhar, J.A. Micropyretic synthesis of tough NiAl alloys. Metall. Mater. Trans. 1997, 28, 905–908. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Gu, Y.; Huang, C.; Volki, R.; Harada, H. Platinum-group-metal-based intermetallics as high-temperature structural materials. J. Mater. Chem. 2004, 56, 34–42. [Google Scholar]
- Zangwill, A.; Redfield, A.C. Structural selectivity in aluminium-transition-metal alloys. J. Phys. F. Met. Phys 1988, 18, 1–10. [Google Scholar] [CrossRef]
- Peng, P.; Soh, A.K.; Yang, R.; Hu, Z.Q. First-principles study of alloying effect of Re on properties of Ni/Ni3Al interface. Comput. Mater. Sci. 2006, 38, 354–361. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.K.; Chen, L.-Q. Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations. Acta Mater. 2004, 52, 2665–2668. [Google Scholar] [CrossRef]
- H Kart, H.H.; Tomak, M.; Agin, T.C. Molecular dynamics study of thermal properties of intermetallic alloys. Turk. J. Phys. 2006, 30, 311–318. [Google Scholar]
- Mekhrabov, A.O.; Akdeniz, M.V. Modelling and monte carlo simulation of the atomic ordering processes in Ni3Al intermetallics. Model. Simul. Mater. Sci. Eng. 2007, 15, 1–12. [Google Scholar] [CrossRef]
- Sutton, A.P.; Chen, J. Long-range Finnis-Sinclair potentials. Phil. Mag. Lett. 1990, 61, 139–145. [Google Scholar] [CrossRef]
- Phasha, M. J.; Ngoepe, P. E.; Chauke, H.R.; Pettifor, D.G.; Nguyen-Mann, D. Link between structural and mechanical stability of fee- And bcc-based ordered Mg-Li alloys. Intermetalics 2010, 18, 2083–2089. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Chen, J.; Du, Y.; Yu, J.; Zhou, R. Stability, thermal and mechanical properties of PtxAly compounds. Mater. Design 2011, 32, 3231–3239. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lowther, J.E. The Role Played by Computation in Understanding Hard Materials. Materials 2011, 4, 1104-1116. https://doi.org/10.3390/ma4061104
Lowther JE. The Role Played by Computation in Understanding Hard Materials. Materials. 2011; 4(6):1104-1116. https://doi.org/10.3390/ma4061104
Chicago/Turabian StyleLowther, John Edward. 2011. "The Role Played by Computation in Understanding Hard Materials" Materials 4, no. 6: 1104-1116. https://doi.org/10.3390/ma4061104
APA StyleLowther, J. E. (2011). The Role Played by Computation in Understanding Hard Materials. Materials, 4(6), 1104-1116. https://doi.org/10.3390/ma4061104




