Abstract
In the last decade, computation has played a valuable role in the understanding of materials. Hard materials, in particular, are only part of the application. Although materials involving B, C, N or O remain the most valued atomic component of hard materials, with diamond retaining its distinct superiority as the hardest, other materials involving a wide variety of metals are proving important. In the present work the importance of both ab-initio approaches and molecular dynamics aspects will be discussed with application to quite different systems. On one hand, ab-initio methods are applied to lightweight systems and advanced nitrides. Following, the use of molecular dynamics will be considered with application to strong metals that are used for high temperature applications.
1. Introduction
There have been many reviews of superhardness dealing with understanding new materials [1,2,3,4,5]. Several new materials have been suggested, some synthesized and others not. The search for new materials is considerably aided through theory and especially ab-initio modeling procedures. Density functional theory [6,7,8] in particular has played an important role here. This “ab-initio” approach is applied at various levels and has been shown to lead to some significant results regarding the prediction of structural, elastic and often thermodynamic properties. There are differing opinions as to which of the approaches is best, but in general; trends are often independent of the fundamental formalism.
Properties of diamond are well known—it is the hardest material and synthesized from graphitic precursors. Cubic boron nitride is another commercially used material likewise synthesized from a similar graphitic structured material as diamond. More recent superhard materials exploiting the properties of boron, carbon and nitrogen have been examined at both theoretical [9,10,11] and experimental [12,13,14] levels. In general, the calculational insight has afforded a good interpretation of the materials synthesized although mysteries still remain.
Quartz has many different polytypes depending upon the relative orientation of SiO2 tetrahdrea [15,16,17,18]. Under pressure, a superhard phase of SiO2 named stishovite is created, consisting of octahedral SiO2 units [16,19]. However, this material has not been stabilized and as such rapidly reverts back to a quartz related amorphous structure [20]. There is also a very high pressure transformation of stishovite into a CaCl2 form [21] with some related enhancement of elastic properties. Thereafter enhancement of the coordination has required metals which involve d states. In this way the near nine-fold coordinated TiO2 cotunnite phase has now been suggested to be the hardest known oxide [22]. However, synthesis of this material needs very high pressures (in excess of 50 GPa) while similar cotunnite phases of ZrO2 or HfO2 are synthesized at lower pressures between 12–18 GPa [23,24,25] and could also show superhard features.
Other hard materials that have been identified from computation [26,27] have been based upon some heavy metals such as Os, Re or Rh [28] forming nitrides [29]. The noble metals in themselves are also proving quite important in the formation of hard superalloys. Nickel-based superalloys are highly efficient materials for engines because of interactions between component phases. Exceptional high-temperature properties of the nickel superalloys have been attributed to its microstructure. Despite the success of such alloys, they are presently at the limit of their high-temperature and here the incorporation of noble metals has been suggested [30].
The purpose of this paper is to consider some examples of novel materials where computation has provided some insight and possibly even prediction. Computation aspects will extend from the “ab-initio” level to the more empirical aspect as used in molecular dynamics.
2. Computational Approaches
There are now various very efficient computer algorithms available that can evaluate the total energy of a system using density functional approaches. Choice is often associated with available resources and notably computer power. This paper does not wish to cover the fundamental aspects of the density functional approach other than to remind the reader that effectively the theory is still under development and that many problems, e.g., the application to excited states, energy gaps, etc., are still being studied. However, so saying for ground state properties of a particular ensemble of atoms, two choices of density functional theory are especially significant. These are the local density approximation (LDA) [31] and the Generalized Gradient Approximation (GGA) [32]. Several computations—namely VASP [33], SIESTA [34], ESPRESSO [35] among others—are proving useful. One useful aspect of the codes is the use of pseudopotentials [36,37] and the plane wave approach [38].
Other approaches that involve molecular dynamics can handle far larger systems of atoms than the ab-initio approaches. However, this comes at some cost, namely in the description of the inter-atomic potentials and these tend to take some kind of analytical form. Of the various codes that can implement such techniques, DLPOLY [39] and GULP [40] are examples. Various thermodynamic conditions can be imposed in the simulations of extended systems and usually many thousands of atoms can be involved.
Using such approaches it is possible to deduce a total electronic energy of the system, Etot, and from variation of this with a unit cell distortion the elastic constants (cij) and thereafter an effective Voigt isotropic bulk (Bv) and shear elastic moduli (Gv) through an expression of the form:
It is often thought the both moduli—or better the shear—relate to hardness but this has to be treated carefully especially when anisotropic materials are concerned. A mechanical stability can also be established for a specified system—where the shape of the system will sustain an external force. In the case of a simple cubic system where there are only three elastic constants, namely c11, c12 and c33, the stability criteria is [41]:
(c11 − c12) > 0; c44 > 0; (c11 + 2c12) > 0
The requirement of mechanical stability for orthorhombic crystals with nine elastic constants are as follows:
Theory can only give an approximate estimate of the transition pressures between phases as the precise mechanism of the transition often requires some subtle dynamic processes. However, the relative energy between the phases is an important indicator with very small differences implying low transition pressures needed between different phases. In fact, the region where one material transforms to another can involve the existence of a highly metastable system where very little is understood.
It has often been noted that although the GGA gives a good description of the lattice geometry, LDA may be better for elastic constants and moduli. However, use of the fundamental approach gives results that still need caution in a predictive modeling context.
3. Boron Carbon Nitrogen Structures
There are many boron related structures composed of elemental boron icosahedra formed from 12 boron atoms [42,43] and similar boron structures are found in important hard materials like B4C, B6O or MgAlB4 etc. [44]. Some of the latter materials are established for application or are under research for further improvement [45]. Other structures based on B–C or B–C–N are under intense investigation for their potential to rival the properties of diamond because of chemical differences and to produce new application. Of importance to the synthesis of these materials are the precursor phases. As with diamond, graphitic structures are considered to be the most likely possibilities here. However, in this respect, it is noted that there are differences in the relative energetics of the diamond-graphite systems as compared with the cubic BN-hexagonal BN system. In the case of the diamond-graphite system, the energy of diamond lies above that of graphite [46] whereas for the c-BN-hBN system it is the reverse [47,48].
3.1. Graphitic Precursor Structures
Precursor phases to either a B–C or a B–C–N related structure are graphitic [13]. In the case of the B–C graphitic system, Raman measurements of BCn graphitic structures have now been obtained and the frequencies are somewhat consistent with theory [49] as shown in Figure 1. The theory assumed flat graphitic related BCn sheets as indicated in Figure 2, but it likely that these will slightly buckle and this could account for the very marginal differences between theory and experiment.
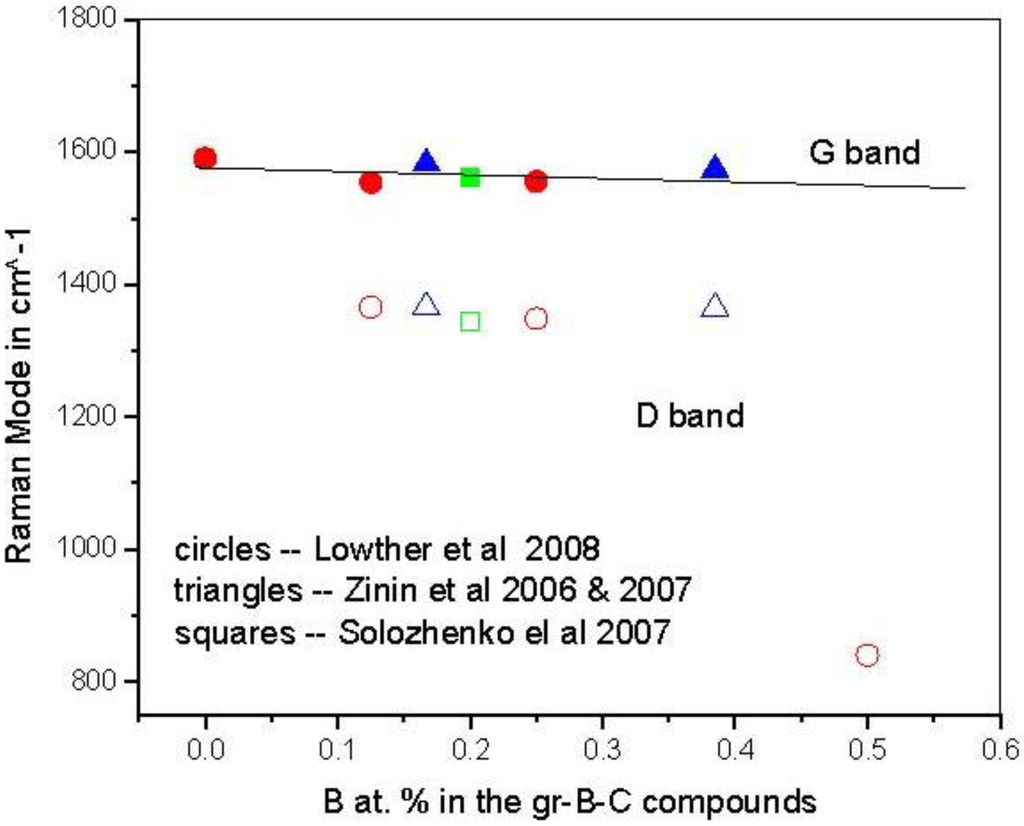
Figure 1.
Comparison of vibration energies of the G and D Raman bands in various B–C graphitic structures. Circles are calculations [49], triangles from Zinin et al. [50,51] and squares from Solozhenko et al. [52].
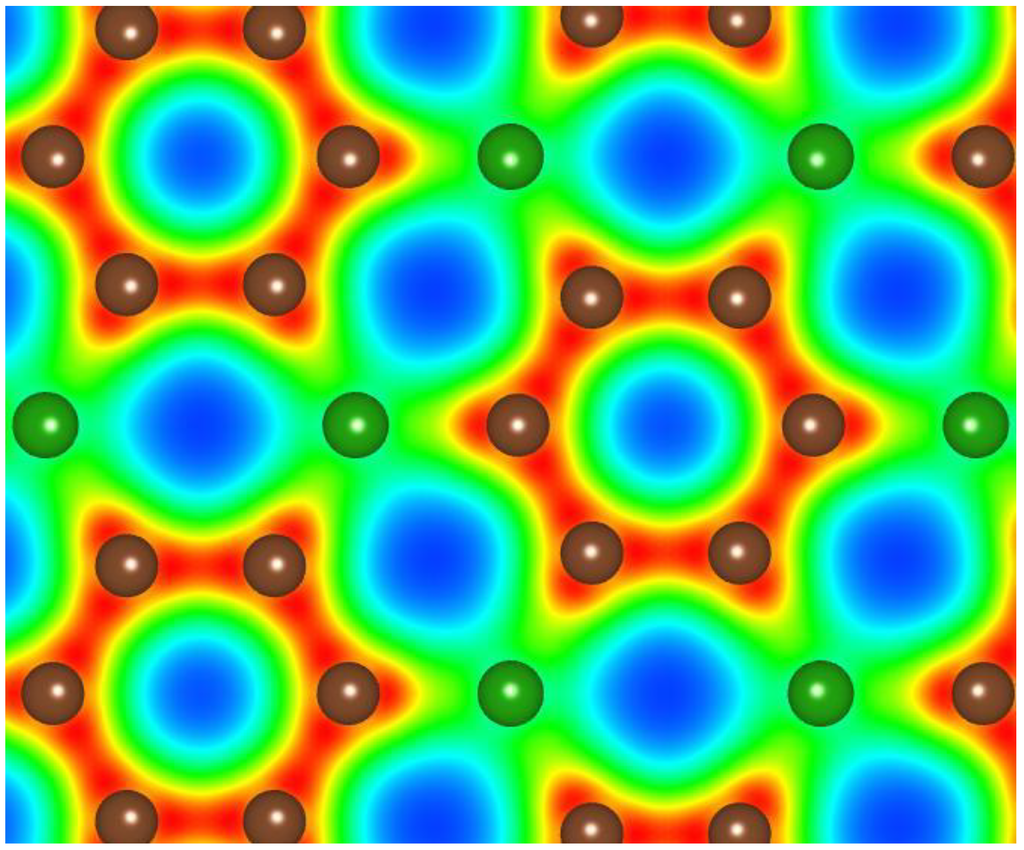
Figure 2.
Calculated electronic structure of g-BC3 (adapted from [49]).
On the contrary, with B-C-N graphic phases, there is some suggestion that there is a separation of the sheets into C and B-N structures [53]. Calculations have been performed on the graphitic structures shown in Figure 3.
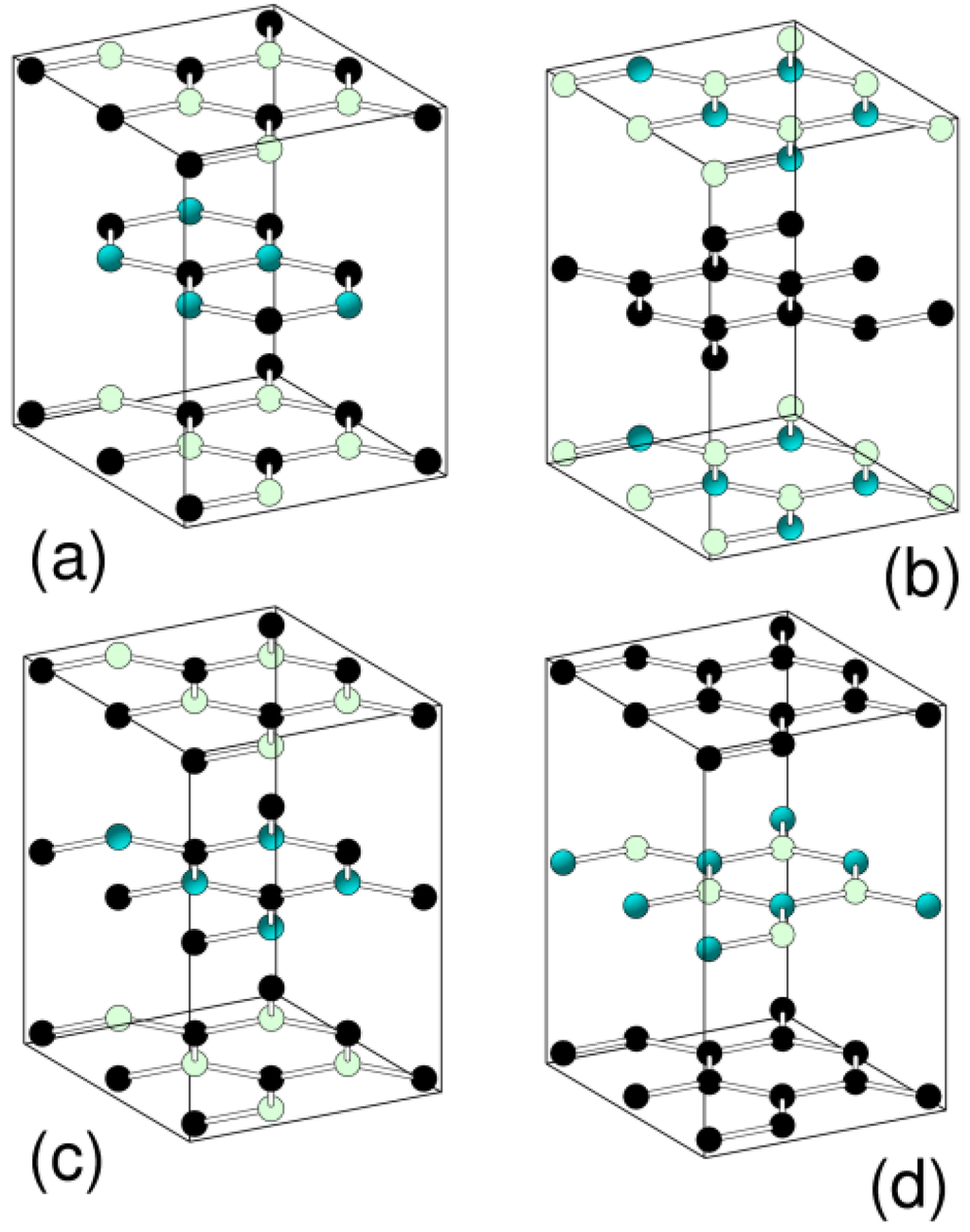
Figure 3.
Various graphitic structures considered for hexagonal BC2N. Structures (a) and (c) follow stacking as for graphite, structures (b) and (d) as for h-BN. The shading of spheres is white B, black C and grey N.
From Table 1, it is clear that the h-BC2N structures (b) and (d) have the lowest energy, consistent with a sheet phase separation in this material. This phase separation could be somewhat disappointing from the superhard synthesis of a crystalline diamond-like superhard phase of BC2N. In fact, suggested crystalline structures of diamond-like BC2N have been studied using ab-initio approaches [54] with several forms having large elastic moduli again consistent to that being found. But the superhardness of such a material is likely to relate mainly to the number of C-C bonds in the material. Calculations have also suggested that large amounts of B in diamond would lead to graphitization [55].

Table 1.
Cell structure and calculated total energy of hexagonal BC2N structures. Experimental values from [53].
| a (A) | c (A) | Etot (eV/atom) | |
|---|---|---|---|
| h-BC2N (a) | 2.50 | 5.74 | −8.456 |
| h-BC2N (b) | 2.47 | 6.41 | −9.880 |
| h-BC2N (c) | 2.50 | 5.89 | −8.440 |
| h-BC2N (d) | 2.47 | 6.82 | −9.868 |
| Expt. | 2.42 | 7.25 |
The transition pressure from the various graphitic phases of both BCn and BC2N structures appear to be quite similar around P = 18 GPa and around 2000 K. Although the structures are metastable relative to diamond/graphite or phases of BN, this is a difficulty that will be overcome [56].
3.2. Superhard Structures
There are many attempts to understand the nature of the superhard structures of the B-C-N system but most are based upon the structure of diamond. Simple modification in the case of either a BCn [10] or BC2N [54] structure has been used. Relative to diamond and graphite, all of these structures are metastable from the point of view of the relative energies and this will be a problem to overcome in a satisfactory synthesis. The essential conclusion that is emerging in the case of the superhard BC structures is that the number of C-C bonds will dictate the ultimate strength of the material [57]. Although there is still some uncertainty as to how much boron can actually be incorporated into a diamond structure, recent calculations suggest that a very heavily B-doped material will easily graphitize [55].
The situation for a material like BC2N is not as straightforward as the BCn system obviously because of the presence of both B-N and C-C bonds. Although various structures have been speculated for this material [58,59,60,61,62,63,64], as yet a precise structure is not determined. However, there is some indication that the relative energies of these structures are quite close.
As with diamond-graphite and cBN–h–BN, it is interesting to compare similar phases of BC3 and BC2N. Results of LDA calculations are shown in Table 2—the results suggest that N concentration dramatically affects the relative energy and may possibly affect the transition pressure.

Table 2.
Local density approximation (LDA) calculated relative energies of precursor graphitic and super-hard diamond-like structures. A positive value indicates that the precursor phase is higher in energy that the diamond-like phase. The estimated calculational uncertainty is 10 meV/atom.
| Stoichiometry | hexagonal phase | Diamond-like phase | Energy difference (eV/atom) |
|---|---|---|---|
| BC2N | h-BC2N | BC2N | −0.397 |
| BC3 | BC3 | BC3 | +0.058 |
| C | graphite | diamond | −0.003 |
| BN | h-BN | c-BN | +0.056 |
4. Advanced Nitrides
Binary nitrides of transition metals constitute a diverse class of materials with technological and fundamental importance because of their strength and durability as well as their optical, electronic and magnetic properties [65,66]. Oxidation states of the binary nitrides of transition metals are limited by the metal even if the number of available valence electrons is high [67]. For these reasons three metal dinitrides—PtN2 [68], InN2 and OsN2 [69]—have successfully been synthesized under extreme conditions of pressure and temperature. There have been several studies of the crystal structure of these nitrides [70,71,72], some pointing to an enhanced bulk modulus of the nitride over the metal with a rock-salt structure being the most stable structure [72] or a pyrite structure [73] and this arises due to strong hybridization between the metal d and N 2p states [74].
More recently, nitrides of tantalum have become a rapidly growing field of interest. The binary Ta-N system display rich compounds with well defined variable stoichiometry [67,75]. This crystal chemistry ranges from Ta3N6, Ta4N5 up to Ta3N5—three polymorphs of the mononitride TaN and two phases of Ta2N. High pressure δ-TaN having a NaCl structure and orthorhombic Ta3N5 have outstanding properties among the Ta-N system and are said to be superconducting.
Very recently, Zerr et al. [65] synthesized the novel tantalum nitride having an orthorhombic U2S3 structure (space group Pbnm) at high pressure and temperature conditions with the aim of obtaining the high pressure phase. The structure is shown in Figure 4.
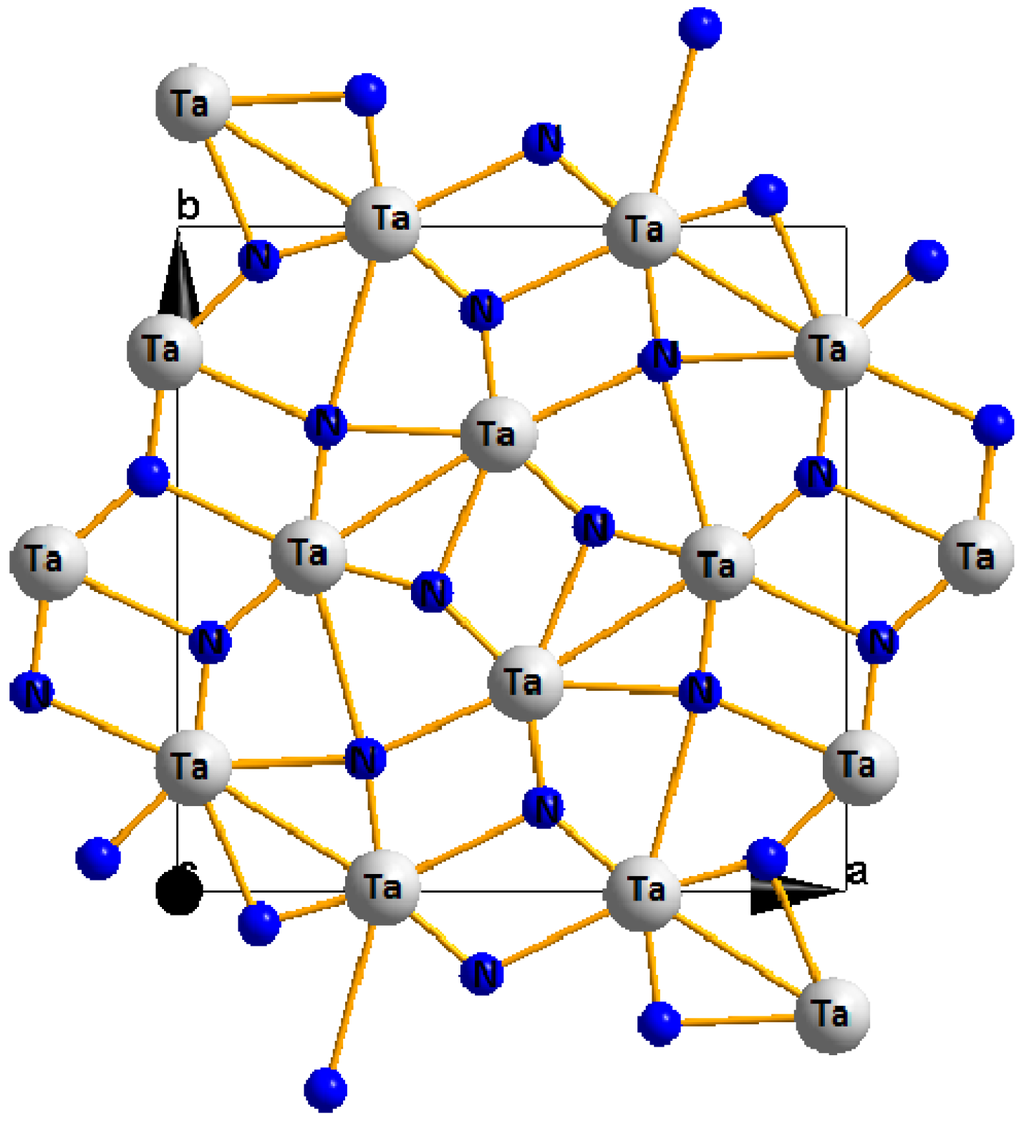
Figure 4.
Crystal structure of orthrhombic Ta2N3.
From the experimental findings of Zerr et. al., the orthorhombic Ta2N3 displays high hardness and a unique texture and this makes it a potential superhard material for industrial applications.
Recent compuational studies using the GGA approach [76], however, have suggested the Ta2N3 is unstable as one of the elastic moduli (c66) is less tha zero and contravenes the Born criteria for orthrhombic systems. This is so despite the other moduli—buk or shear are quite large and indicators of a superhard material. However, more recent calculations using LDA are not consistent with this interpretation and, in fact, predict all elastic constants that are consistent with the Born criteria, thus indicating the stability of the orthorhombic structure of Ta2N3.
5. Strong Metallic Alloys
Nickel-based superalloys (NBSAs) are presently used for engines primarily because of highly efficient material properties including resistance to oxidation and corrosion, elevated temperature strength, relatively low density and high melting points. Unlike most intermetallics, NBSAs also have excellent ductility both at room and elevated temperatures, even though they are not often considered as being hard materials at room temperature. NBSAs are either solid solution or precipitation strengthened. The exceptional high-temperature properties of NBSAs have been attributed to an interplay between two microstructures—a f.c.c phase and a more elaborate one. This latter type of micro-structure has been found to demonstrate exceptional structural stability and best characteristics of high temperature strength, resulting in their usage in aircraft engines. Despite the success of NBSAs, they are presently at the limit of their high-temperature capability [77]. Due to increased demand for system efficiency, other alloys capable of higher temperature operation are required. Advantages gained with higher system efficiency are high throughput and less environmental pollution and alloys based on the noble metals are therefore currently being investigated as material for high temperature alloy design [78,79]. Although, noble metals offer the hope of developing exceptional alloys capable of high temperature applications, considerable effort is also required to understand the fundamental factors that control their mechanical properties as they also exhibit a variety of phases [80].
Ni3Al has proven an interesting material for both ab-initio [81,82] and molecular dynamic simulation [83,84]. Sutton-Chen potentials [85] seem quite good in simulating this phase with calculations of the melting temperatures being in quite good agreement with experimental. Such calculations show the distribution of atoms at various temperatures—a typical result is shown in Figure 5 for the cubic structure of Ni3Al. As can be seen, initially the cubic lattice has only slightly deformed but at very higher temperatures there is no sign of a cubic lattice, showing that the material essentially has melted. A more quantitative analysis of the behavior is based upon the behavior of the diffusion coefficient of the various component atoms which increases dramatically at the melting temperature.

Figure 5.
Molecular Dynamics results for the melting of Ni3Al [83]. Top: T = 0 K; bottom left T = 1000 K and bottom right T = 2000 K.
The use of platinum in a Pt3Al alloy has been considered as a possible alternative to Ni3Al as a high temperature strong material but is currently hampered by its weight and high cost. However these factors are expected to be counterbalanced by platinum’s exceptional chemical stability, oxidation resistance, ductility, thermal-shock resistance, and electrical or thermal conductivity, which makes it desirable for the design of next generation of super-alloys [86,87].
6. Conclusions
There are two regions of computational materials modeling that are proving useful in not only understanding materials but also, and more important, predicting new ones. The ab-initio approach is quite reliable for ground state properties—elastic constants and lattice geometries—albeit the various density functional approaches do not agree even though similar trends are suggested. On the other hand, very large systems can be examined using various forms of rigid potential molecular dynamics. At this stage in the theoretical development, it is not really clear how the ab-initio methods will be able to be extended into the same region as the rigid potential molecular dynamics but despite this rather major shortcoming there have been many achievements in materials modeling and this will continue.
Acknowledgements
The NRF (South Africa) is thanked for supporting this work. Discussions with Vinit Sharma, Esther Orisakwe and Isaac Popoola are duly acknowledged.
References
- Haines, J.; Leger, J.M.; Bocquillon, G. Synthesis and design of superhard materials. Ann. Rev. Mater. Res. 2001, 31, 1–18. [Google Scholar] [CrossRef]
- Brazhkin, W.; Lyapin, A.G.; Hemley, R.J.; Hemley, R.J. Harder than diamond: Dreams and reality. Philos. Mag. A Phys. Condens. 2002, 82, 231–241. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Superhard Materials; Naukova Dumka: Kiev, Ukraine, 1980. [Google Scholar]
- Oganov, A.R.; Lyakhov, A.O. Towards the theory of hardness of materials. J. Superhard Mater. 2010, 32, 143–147. [Google Scholar] [CrossRef]
- Li, Q.; Wang, H.; Ma, Y.M. Predicting new superhard phases. J. Superhard Mater. 2010, 32, 192–204. [Google Scholar] [CrossRef]
- Joubert, D. Density functionals: Theory and application. Lect. N. Phys. 1997, 500, 47–48. [Google Scholar]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joanopoulos, J.D. Joanopoulos, electronic structure of materials. Rev. Mod. Phys. 1992, 64, 1045–1051. [Google Scholar] [CrossRef]
- Martin, R. Electronic Structure Basic Theory and Practical Methods; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Hong, S.; Seung-Hoon, J.; Roundy, D.; Cohen, M.L.; Louie, S.G. Structural forms of cubic BC2N. Phys. Rev. B 2003, 64, 094108:1–094108:6. [Google Scholar]
- Lowther, J.E. Potential super-hard phases and the stability of diamond-like boron-carbon structures. J. Phys. Condens. Matter 2005, 17, 3221–3229. [Google Scholar] [CrossRef]
- Kim, E.; Pang, T.; Utsumi, W.; Solozhenko, V.L.; Zhao, Y.S. Cubic phases of BC2N: A first-principles study. Phys. Rev. B 2007, 75, 184115:1–184115:4. [Google Scholar]
- Hubble, H.W.; Kudryashov, I.; Solozhenko, V.L.; Zinin, P.V.; Sharma, S.K.; Ming, L.C. Raman studies of cubic BC2N, a new superhard phase. J. Raman Spectrosc. 2004, 35, 822–825. [Google Scholar] [CrossRef]
- Solozhenko, V.L. High-pressure synthesis of novel superhard phases in the B-C-N system: Recent achievements. High Pressure Res. 2009, 29, 612–617. [Google Scholar] [CrossRef]
- Tkachev, S.N.; Solozhenko, V.L.; Zinin, P.V.; Manghnani, M.H.; Ming, L.C. Elastic moduli of the superhard cubic BC2N phase by Brillouin scattering. Phys. Rev. B 2003, 68, 052104:1–052104:3. [Google Scholar] [CrossRef]
- Haines, J.; Cambon, O.; Le Parc, R.; Levelut, C. The effect of static disorder on pressure-induced phase transitions and amorphization in alpha-quartz-type solid solutions. Phase Transit. 2007, 80, 1039–1049. [Google Scholar] [CrossRef]
- Teter, D.M.; Hemley, R.J.; Kresse, G.; Hafner, J. High pressure polymorphism in silica. Phys. Rev. Lett. 1998, 80, 2145–2151. [Google Scholar] [CrossRef]
- Munetoh, S.; Motooka, T.; Moriguchi, K.; Shintani, A. potential for Si-O systems using Tersoff parameterization. Computat. Mater. Sci. 2007, 39, 334–339. [Google Scholar] [CrossRef]
- Dubrovinskaia, N.A.; Dubrovinsky, L.S. High-pressure silica polymorphs as hardest known oxides. Mater. Chem. Phys. 2001, 68, 77–83. [Google Scholar] [CrossRef]
- Dewhurst, J.K.; Lowther, J.E.; Madzwara, L.T. High-pressure phases of SiO2 using local-density and generalized-gradient approximations. Phys. Rev. B 1997, 55, 11003–11005. [Google Scholar] [CrossRef]
- Grimsditch, M.; Popova, S.; Brazhkin, V.V.; Voloshin, R.N. Temperate induced amorphization of SiO2 Stishovite. Phys. Rev. B 1994, 50, 12984–12992. [Google Scholar] [CrossRef]
- Tsuchida, Y.; Yagi, T. A new post-stishovite high pressure phase polymorph of silica. Nature 1989, 340, 217–219. [Google Scholar] [CrossRef]
- Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Swamy, V.; Muscat, J.; Harrison, N.M.; Ahuja, R.; Holm, B.; Johansson, B. Materials science—The hardest known oxide. Nature 2001, 410, 653–654. [Google Scholar] [CrossRef] [PubMed]
- Haines, J.; Leger, J.M.; Atouf, A. Crystal-structure and equation of state of cotunnite-type zirconia. J. Amer. Ceram. Soc. 1995, 78, 445–448. [Google Scholar] [CrossRef]
- Lowther, J.E.; Dewhurst, J.K.; Leger, J.M.; Haines, J. Relative stability of ZrO2 and HfO2 structural phases. Phys. Rev. B 1999, 60, 14485–14488. [Google Scholar] [CrossRef]
- Desgreniers, S.; Lagarec, K. High-density ZrO2 and HfO2: Crystalline structures and equations of state. Phys. Rev. B 1999, 59, 8467–8472. [Google Scholar] [CrossRef]
- Yang, J.W.; Chen, X.R.; Luo, F.; Ji, G.F. First-principles calculations for elastic properties of OsB2 under pressure. Phys. B Condens. Matter 2009, 404, 3608–3613. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.J. Mechanical and electronic properties of 5d transition metal diborides MB2 (M = Re, W, Os, Ru). J. Appl. Phys. 2009, 105, 122–131. [Google Scholar]
- Chung, H.Y.; Weinberger, M.B.; Yang, J.M.; Tolbert, S.H.; Kaner, R.B. Correlation between hardness and elastic moduli of the ultracompressible transition metal diborides RuB2, OsB2, and ReB2. Appl. Phys. Lett. 2008, 92, 98–103. [Google Scholar]
- Gregoryanz, E.; Sanloup, C.; Somayazulu, M.; Badroi, J.; Fiquet, G.; Mao, H.-K.; Hemley, R.J. Synthesis and characterization of a binary noble metal nitride. Nature 2004, 3, 294–297. [Google Scholar] [CrossRef]
- Dey, G.K.; Sekhar, J.A. Physical metallurgy of nickel aluminides. Metall. Mater. Trans. B. 1987, 28, 905–909. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566–568. [Google Scholar] [CrossRef]
- Perdew, J.P.; Kurth, S. Density Functionals: Theory and Applications; Theoretical Physics Held at Meerensee: Cape Town, South Africa, 1997; Volume 8. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–563. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Quantum Espresso. Available online: http://www.quantum-espresso.org/contacts.php (accessed on 11 May 2009).
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–1997. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D.P. From Ultrasoft Pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1762. [Google Scholar] [CrossRef]
- Joubert, D.P. Density Functional Theory; Springer: Heidelberg, Germany, 1998. [Google Scholar]
- Smith, W.; Forester, T. DLPOLY code for molecular dynamics. J. Mol. Graph. 1996, 14, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D. Gulp: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 1, 629–641. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermodynamics of Crystals; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Oganov, A.R.; Chen, J.-H.; Gatti, C.; Ma, Y.-Zh.; Yuan, Y.M.; Glass, C.W.; Liu, Zh.X.; Tony-Yu, O.O.K.; Solozhenk, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–865. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Solozhenko, V.L. Boron: A hunt for superhard polymorphs. J. Superhard Mater. 2009, 31, 285–291. [Google Scholar] [CrossRef]
- Letsoalo, T.; Lowther, J.E. Systematic trends in boron icosahedral structured materials. J. Phys. B Condens. Matter 2008, 403, 2760–2767. [Google Scholar] [CrossRef]
- Johnson, O.T.; Sigalas, I.; Ogunmuyiwa, E.N.; Kleebe, H.J.; Muller, M.M.; Herrmann, M. Boron suboxide materials with Co sintering additives. Ceram. Int. 2010, 36, 1762–1771. [Google Scholar]
- Fahy, S.; Louie, S.G.; Cohen, M.L. Aproach to graphite to diamond transitions. Phys. Rev. B 1987, 35, 7623–7629. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Petrusha, I.A. On the kinetic boundary of the rBN to wBN transformation at high static pressure. Sverkhtverdye Materialy 1996, 62, 67–71. [Google Scholar]
- Albe, K.; Moller, W. Modelling of boron nitride: Atomic scale simulations on thin film growth. Comput. Mater. Sci. 1998, 10, 111–115. [Google Scholar] [CrossRef]
- Lowther, J.E.; Zinin, P.V.; Ming, L.C. Vibrational energies of graphene and hexagonal structured planar B–C complexes. Phys. Rev. B 2009, 79, 033401:1–033401:4. [Google Scholar] [CrossRef]
- Zinin, P.V.; Ming, L.C.; Kudryashov, I.; Konishi, N.; Manghnani, M.H.; Sharma, S.K. Pressure- and temperature-induced phase transition in the B–C system. J. Appl. Phys. 2006, 100, 013516:1–013516:6. [Google Scholar] [CrossRef]
- Zinin, P.V.; Ming, L.C.; Kudryashov, I.; Konishi, N.; Sharma, S.K. Raman spectroscopy of the BC3 phase obtained under high pressure and high temperature. J. Raman Spectrosc. 2007, 38, 1362–1367. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Kuznetsov, A.Y. Raman scattering from turbostratic graphitelike BC4 under pressure. J. Appl. Phys. 2007, 102, 5–12. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Andrault, D.; Fiquet, G.; Mezouar, M.; Rubie, D.C. Synthesis of superhard cubic BC2N. Appl. Phys. Lett. 2001, 78, 1385–1389. [Google Scholar] [CrossRef]
- Sun, H.; Jhi, S.H.; Roundy, D.; Cohen, M.L.; Louie, S.G. Structural forms of cubic BC2N. Phys. Rev. B 2001, 64, 094108:1–094108:6. [Google Scholar]
- Lowther, J.E. Elastic and Vibrational Properties of Boron-Carbon Ultra Hard Materials. In Sensors, Ultra High Temperature Ceramics, Thermoelectrics, Armor; Lugovy, N.O.A.M., Ed.; Springer: Aalborg, Denmark, 2010. [Google Scholar]
- Abdel-Mottaleb, M.M.S.; Van der Auweraer, M.; Abdel-Mottaleb, M.S.A. Photostability of J-aggregates adsorbed on TiO2 nanoparticles and AFM imaging of J-aggregates on a glass surface. Int. J. Photoenergy 2004, 6, 29–33. [Google Scholar] [CrossRef]
- Nkambule, S.M.; Lowther, J.E. Crystalline and random “diamond-like” boron-carbon structures. Solid State Commun. 2010, 150, 133–136. [Google Scholar] [CrossRef]
- Ma, X.Y.; He, D.Y.; Chen, G.H. Synthesis and mechanism of BC2N thin films in stalk-like growth. Acta Phys. Sin. 2001, 50, 2023–2027. [Google Scholar]
- Mattesini, A.; Matar, S.F. Search for ultra-hard materials: Theoretical characterisation of novel orthorhombic BC2N crystals. Int. J. Inorg. Mater. 2001, 3, 943–947. [Google Scholar] [CrossRef]
- Huang, J.Y.; Zhu, Y.T.; Mori, H. Structure and phase characteristics of amorphous boron-carbon-nitrogen under high pressure and high temperature. J. Mater. Res. 2001, 16, 1178–1184. [Google Scholar] [CrossRef]
- He, J.L.; Tian, Y.J.; Yu, D.L.; Wang, T.S.; Liu, S.M.; Guo, L.C.; Li, D.C.; Jia, X.P.; Chen, L.X.; Zou, G.T.; Yanagisawa, O. Orthorhombic BC2N crystal synthesized by high pressure and temperature. Chem. Phys. Lett. 2001, 340, 431–436. [Google Scholar] [CrossRef]
- Kohler-Redlich, P.; Terrones, M.; Manteca-Diego, C.; Hsu, W.K.; Terrones, H.; Ruhle, M.; Kroto, H.W.; Walton, D.R.M. Stable BC2N nanostructures: Low-temperature production of segregated C/BN layered materials. Chem. Phys. Lett. 1999, 310, 459–465. [Google Scholar] [CrossRef]
- Widany, J.; Verwoerd, W.S.; Frauenheim, T. Density-functional based tight-binding calculations on zinc-blende type BC2N-crystals. Diam. Relat. Mater. 1998, 7, 1633–1638. [Google Scholar] [CrossRef]
- Tateyama, Y.; Ogitsu, T.; Kusakabe, K.; Tsuneyuki, S.; Itoh, S. Proposed synthesis path for heterodiamond BC2N. Phys. Rev. B 1997, 55, R10161–R10164. [Google Scholar] [CrossRef]
- Zerr, A.; Riedel, R.; Sekine, T.; Lowther, J.E.; Ching, W.-Y.; Tanaka, I. Recent advances in new hard high-pressure nitrides. Adv. Mater. 2006, 18, 2933–2953. [Google Scholar] [CrossRef]
- McMillan, P.F. New materials from high-pressure experiments. Nat. Mater. 2002, 1, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Kroll, P.; Schroter, T.; Peters, M. Prediction of novel phases of tantalum(V) nitride and tungsten(VI) nitride that can be synthesized under high pressure and high temperature. Angew. Chem. Int. Ed. 2005, 44, 4249–4254. [Google Scholar] [CrossRef]
- Crowhurst, J.; Goncharov, A.; Sadigh, B.; Zaug, J.; Meng, Y.; Prakapenka, V. Synthesis and characterization of nitrides of iridium and palladium. Mater. Res. High Pressure 2007, 987, 3–9. [Google Scholar]
- Young, A.F.; Sanloup, C.; Gregoryanz, E.; Scandolo, S.; Hemley, R.J.; Mao, H.K. Synthesis of novel transition metal nitrides IrN2 and OsN2. Phys. Rev. Lett. 2006, 96, 155501:1–155501:4. [Google Scholar] [CrossRef]
- Young, A.F.; Montoya, J.A.; Sanloup, C.; Lazzeri, M.; Gregoryanz, E.; Scandolo, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 1566–1577. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev B 2006, 73, 104118:1–104118:8. [Google Scholar]
- Jamal, U.; Scuseria, G.E. Structures and electronic properties of platinum nitride by density functional theory. Phys. Rev. B 2005, 72, 035101:1–035101:6. [Google Scholar]
- Young, A.F.; Montoya, J.A.; Sanloup, C.; Lazzeri, M.; Gregoryanz, E.; Scandolo, S. Interstitial dinitrogen makes PtN2 an insulating hard solid. Phys. Rev. B 2006, 73, 153102:1–153102:4. [Google Scholar] [CrossRef]
- Fan, C.Z.; Zeng, S.Y.; Li, L.X.; Zhan, Z.J.; Liu, R.P.; Wang, W.K.; Zhang, P.; Yao, Y.G. Potential superhard osmium dinitride with fluorite and pyrite structure: First-principles calculations. Phys. Rev. B 2006, 74, 1088–1092. [Google Scholar]
- Friedrich, A.; Winkler, B.; Bayarjargal, L.; Juarez Arellano, E.A.; Morgenroth, W.; Biehler, J.; Schröder, F.; Yan, J.; Clark, S.M. In situ observation of the reaction of tantalum with nitrogen in a laser heated diamond anvil cell. J. Alloys Compounds 2010, 502, 5–12. [Google Scholar] [CrossRef]
- Jiang, Ch.; Lin, Zh.J.; Zhao, Y.Sh. Thermodynamic and mechanical stabilities of tantalum nitride. Phys. Rev. Lett. 2009, 103, 185501:1–185501:4. [Google Scholar]
- Banejee, D.; Gogia, K.K.; Nandy, T.K.; Uraleedharan, K.M.; Mishra, R.S. Structural Intermetallics. In Proceedings of International Symposium on Structural Intermetallics, Champion, PA, USA, 26–30 September 1993; pp. 19–23.
- Dey, G.K.; Sekhar, J.A. Micropyretic synthesis of tough NiAl alloys. Metall. Mater. Trans. 1997, 28, 905–908. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Gu, Y.; Huang, C.; Volki, R.; Harada, H. Platinum-group-metal-based intermetallics as high-temperature structural materials. J. Mater. Chem. 2004, 56, 34–42. [Google Scholar]
- Zangwill, A.; Redfield, A.C. Structural selectivity in aluminium-transition-metal alloys. J. Phys. F. Met. Phys 1988, 18, 1–10. [Google Scholar] [CrossRef]
- Peng, P.; Soh, A.K.; Yang, R.; Hu, Z.Q. First-principles study of alloying effect of Re on properties of Ni/Ni3Al interface. Comput. Mater. Sci. 2006, 38, 354–361. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.K.; Chen, L.-Q. Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations. Acta Mater. 2004, 52, 2665–2668. [Google Scholar] [CrossRef]
- H Kart, H.H.; Tomak, M.; Agin, T.C. Molecular dynamics study of thermal properties of intermetallic alloys. Turk. J. Phys. 2006, 30, 311–318. [Google Scholar]
- Mekhrabov, A.O.; Akdeniz, M.V. Modelling and monte carlo simulation of the atomic ordering processes in Ni3Al intermetallics. Model. Simul. Mater. Sci. Eng. 2007, 15, 1–12. [Google Scholar] [CrossRef]
- Sutton, A.P.; Chen, J. Long-range Finnis-Sinclair potentials. Phil. Mag. Lett. 1990, 61, 139–145. [Google Scholar] [CrossRef]
- Phasha, M. J.; Ngoepe, P. E.; Chauke, H.R.; Pettifor, D.G.; Nguyen-Mann, D. Link between structural and mechanical stability of fee- And bcc-based ordered Mg-Li alloys. Intermetalics 2010, 18, 2083–2089. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Chen, J.; Du, Y.; Yu, J.; Zhou, R. Stability, thermal and mechanical properties of PtxAly compounds. Mater. Design 2011, 32, 3231–3239. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).