Persistent Luminescence in Eu2+-Doped Compounds: A Review
Abstract
:1. Introduction
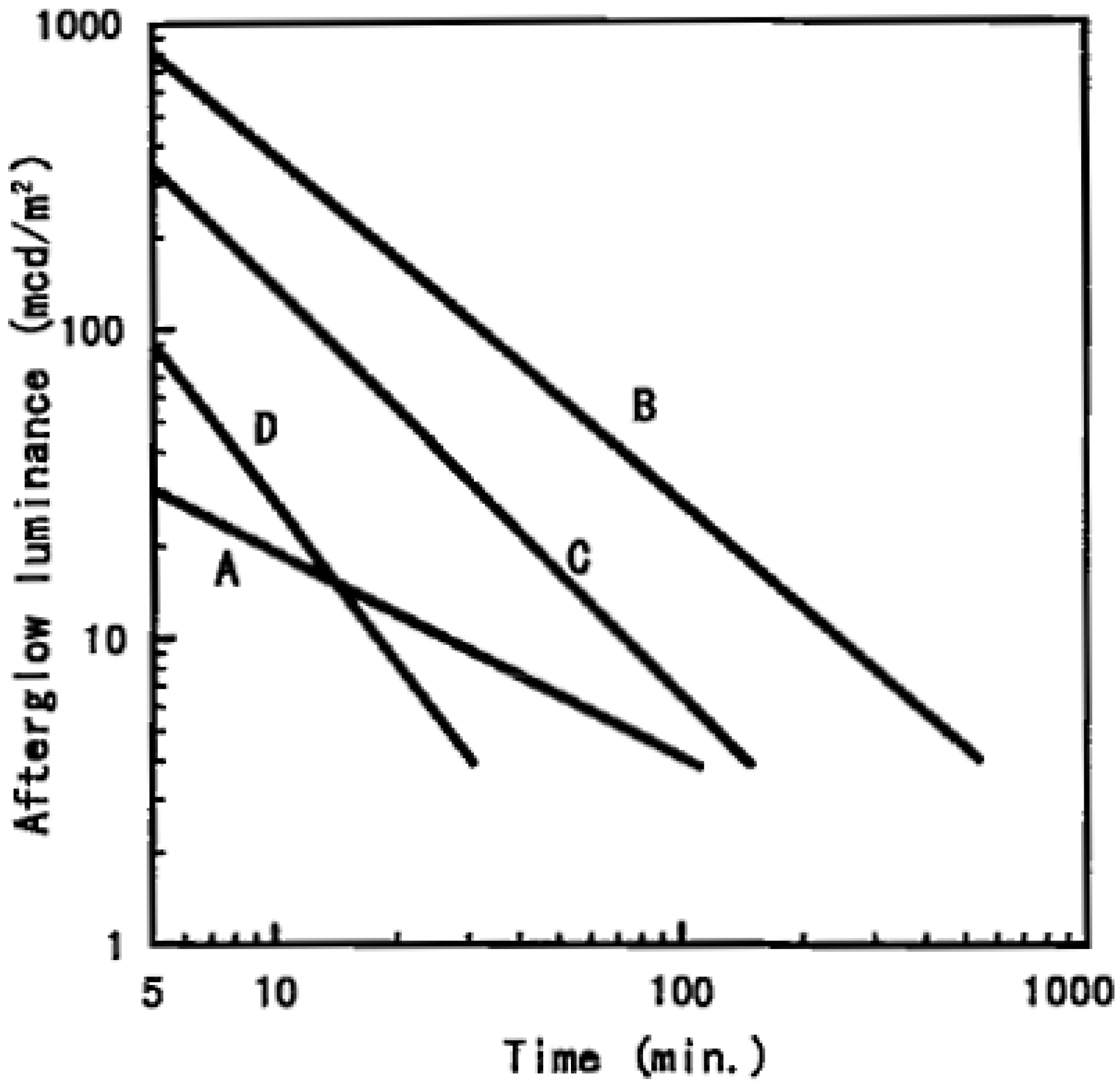
2. Known Compounds
2.1. Aluminates
| Host material | Dopants | Fluorescence maximum (nm) | Afterglow maximum (nm) | Afterglow duration | References |
|---|---|---|---|---|---|
| SrAl2O4 | Eu2+,Dy3+ | 520 (green) | idem | >30 h | [5,17] |
| CaAl2O4 | Eu2+,Nd3+ | 440 (blue) | 430 (blue) | >5 h | [18,19,20] |
| BaAl2O4 | Eu2+,Dy3+ | 500 (green) | idem | >2 h | [21,22] |
| Sr4Al14O25 | Eu2+,Dy3+ | 490 (blue) | idem | >20 h | [23,24,25] |
| SrAl4O7 | Eu2+,Dy3+ | 480 (blue) | idem | >3 h | [26,27] |
| SrAl12O19 | Eu2+,Dy3+ | 400 (blue) | idem | >3 h | [26] |
| Ca12Al14O33 | Eu2+,Nd3+ | 440 (indigo) | idem | >10 min | [28] |
| Sr3Al2O6 | Eu2+,Dy3+ | 510/610 (disputed) | idem | (disputed) | [29,30] |
| SrMgAl10O17 | Eu2+,Dy3+ | 460 (blue) | 515 (green) | >3 min | [31] |
| BaMgAl10O17 | Eu2+,Co3+ | 450 (blue) | idem | >5 min | [32] |
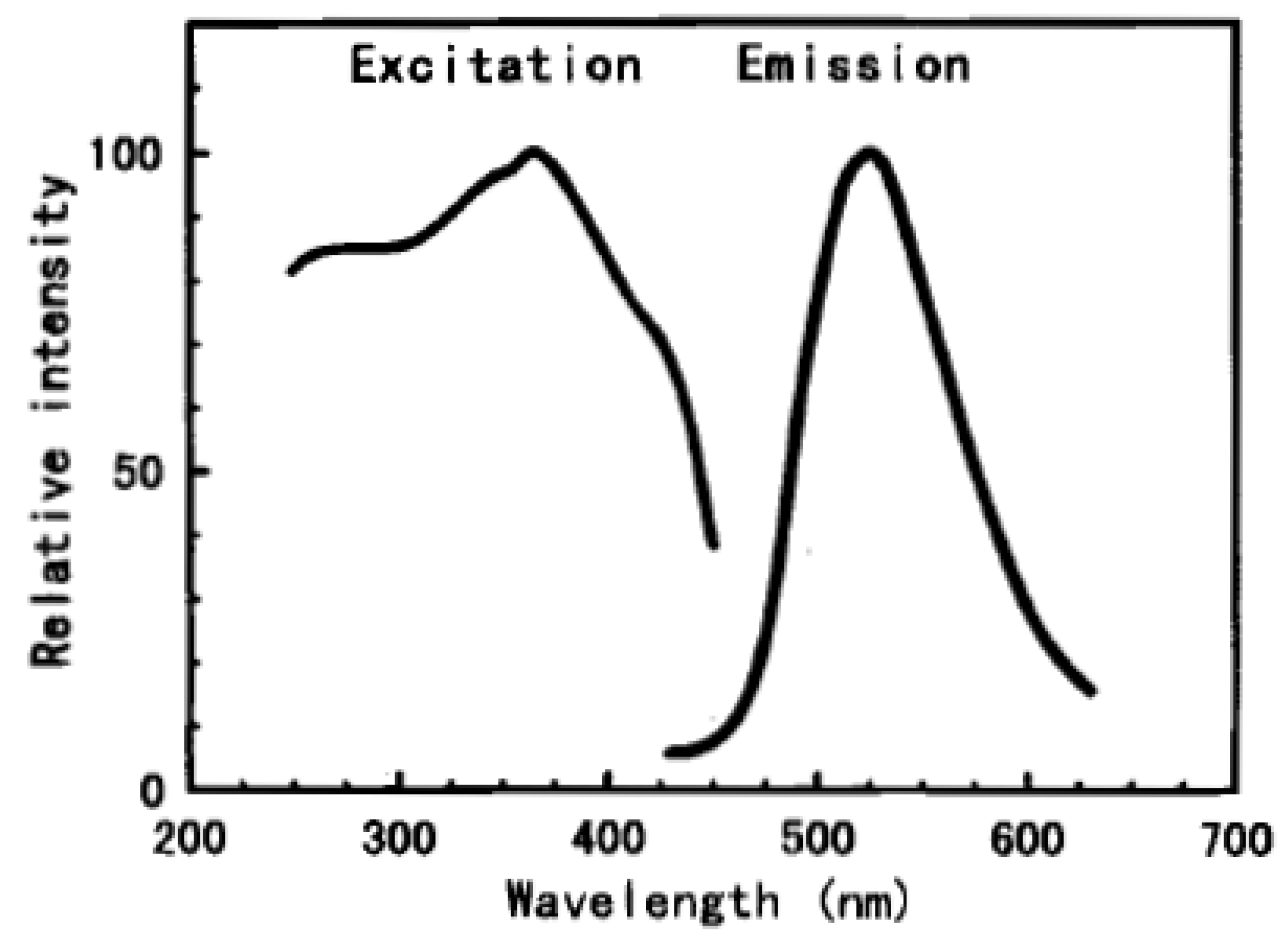
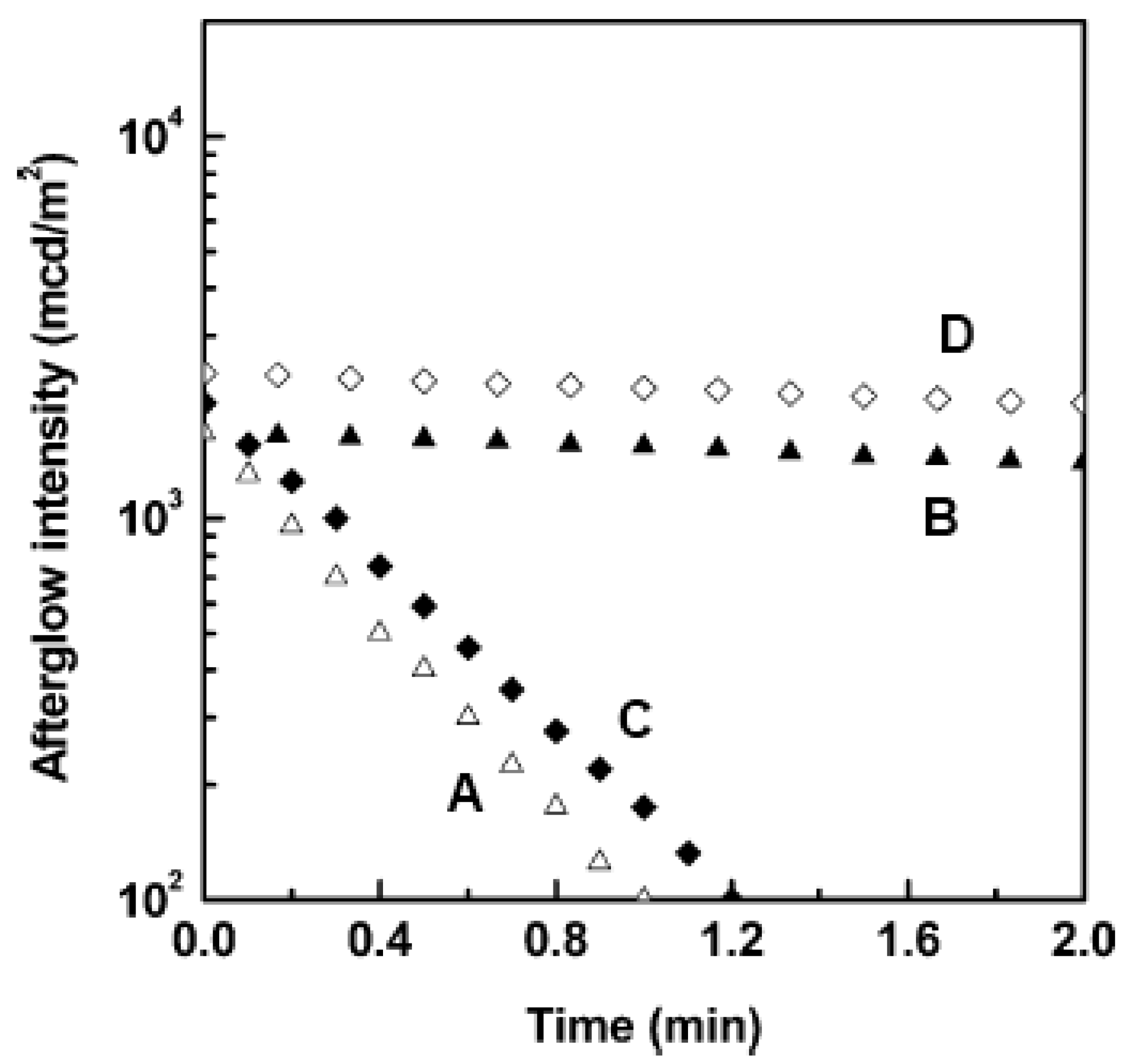
2.2. Silicates
| Host material | Dopants | Fluorescence maximum (nm) | Afterglow maximum (nm) | Afterglow duration | References |
|---|---|---|---|---|---|
| Sr2MgSi2O7 | Eu2+,Dy3+ | 470 (blue) | idem | >10 h | [8,50,51] |
| Ca2MgSi2O7 | Eu2+(,Tb3+) | 515/535 (green) | idem | >5 h | [52,53,54] |
| Ba2MgSi2O7 | Eu2+,Tm3+ | 505 (green) | idem | >5 h | [55,56] |
| Sr3MgSi2O8 | Eu2+,Dy3+ | 460 (blue) | idem | >10 h | [57,58] |
| Ca3MgSi2O8 | Eu2+,Dy3+ | 470 (blue) | idem | >5 h | [57,59] |
| Ba3MgSi2O8 | Eu2+,Dy3+ | 440 (blue) | idem | >1 h | [57] |
| CaMgSi2O6 | Eu2+,Dy3+ | 445 (blue) | idem | >4 h | [54,60] |
| Sr3Al10SiO20 | Eu2+,Ho3+ | 465 (blue) | idem | >6 h | [61,62] |
| CaAl2Si2O8 | Eu2+,Dy3+ or Pr3+ | 435 (blue) | 435/510 (blue) | >3 h | [63,64] |
| Sr2Al2SiO7 | Eu2+,Dy3+ | 485 (blue/green) | idem | >2 h | [65] |
| Sr2ZnSi2O7 | Eu2+,Dy3+ | 460 (blue) | idem | >5 min | [66,67] |
| Sr2SiO4 | Eu2+,Dy3+ | 480 (green) | idem | >5 min | [68] |
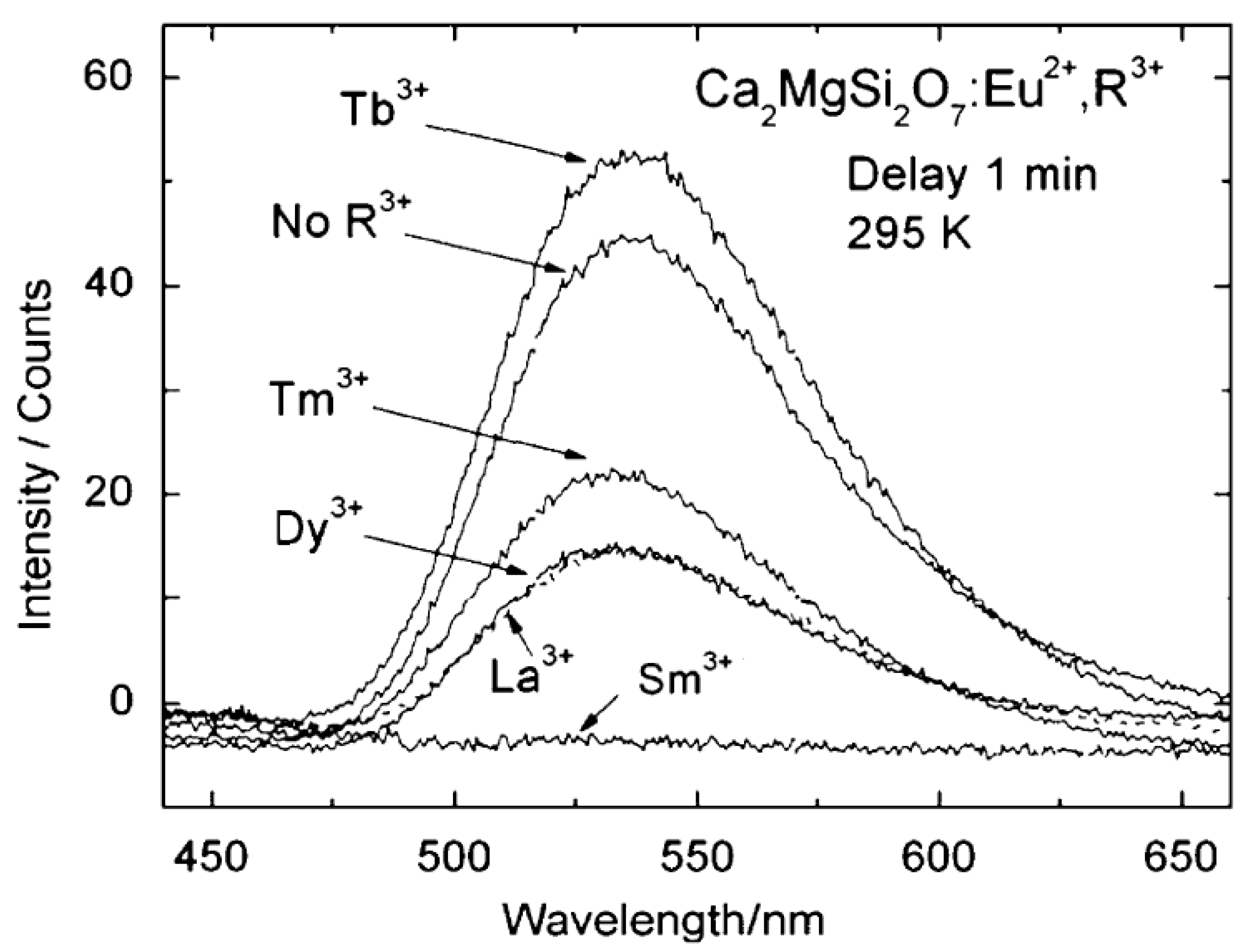
2.3. Other compounds
| Host material | Dopants | Fluorescence maximum (nm) | Afterglow maximum (nm) | Afterglow duration | References |
|---|---|---|---|---|---|
| CaS | Eu2+,Tm3+(,Ce3+) | 650 (red) | idem | >1 h | [78,79,80] |
| CaGa2S4 | Eu2+,Ho3+ or Ce3+ | 555 (yellow) | idem | >30 min | [81,82,83] |
| Ca2SiS4 | Eu2+,Nd3+ | 660 (red) | idem | >30 min | [84] |
| Sr2P2O7 | Eu2+,Y3+ | 420 (blue) | idem | >8 h | [85] |
| Ca2P2O7 | Eu2+,Y3+ | 415 (blue) | idem | >6 h | [86] |
| SrMg2P2O8 | Eu2+,Ce3+ | 400 (blue) | idem | >2 h | [87] |
| Ca2Si5N8 | Eu2+,Tm3+ | 610 (orange) | 620 (orange) | >1 h | [88,89] |
| CaAl2B2O7 | Eu2+,Nd3+ | 465 (blue) | idem | >1 h | [90] |
| SrB2O4 | Eu2+ | 430 (blue) | idem | unknown | [91] |
2.4. Dopant and codopant concentrations
3. Estimating Trap Depths
3.1. Thermoluminescence
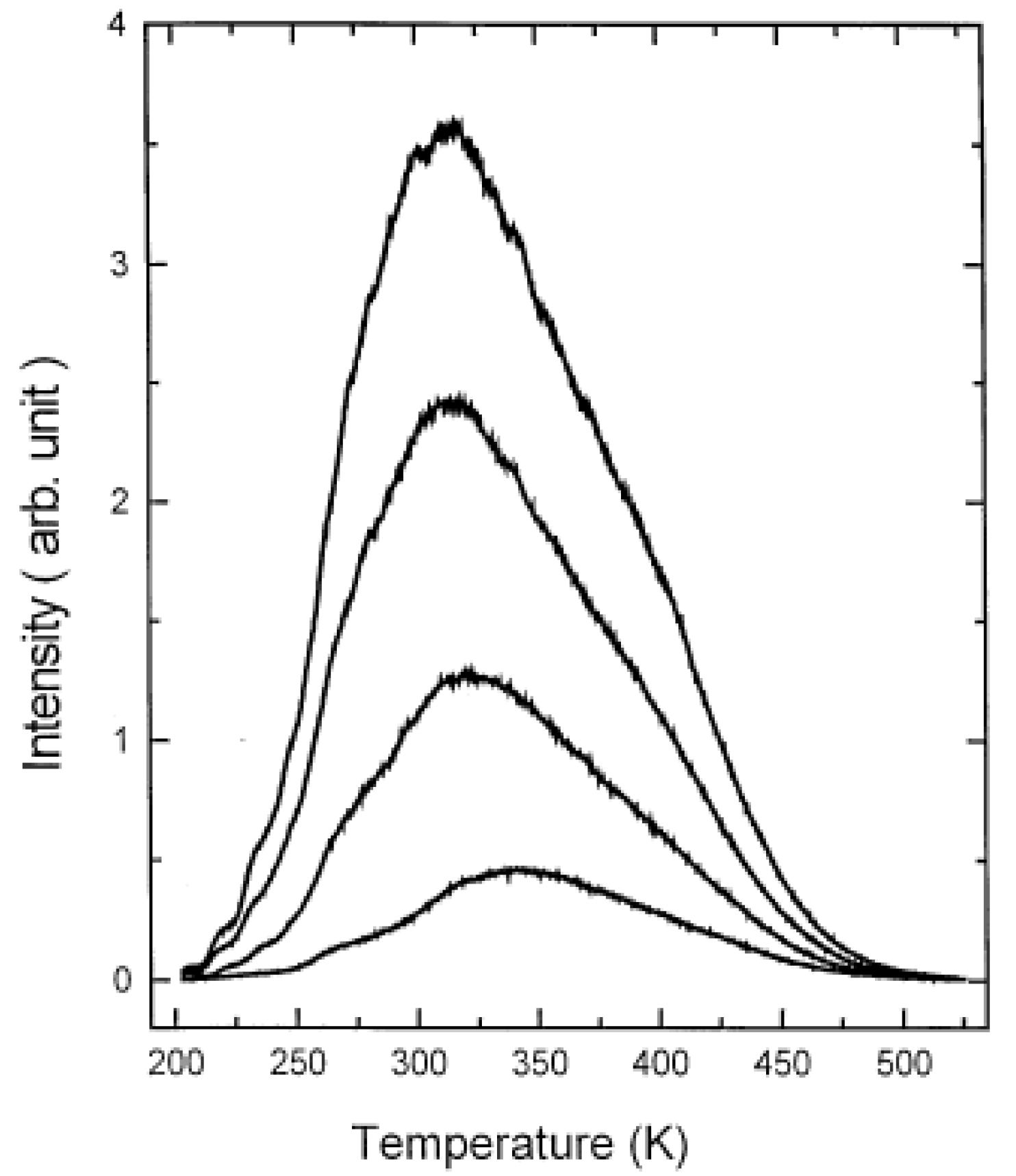
3.2. Other methods
| Phosphor | Method | Trap depths (eV) | Reference |
|---|---|---|---|
| SrAl2O4:Eu2+,Dy3+ | initial rise | 0.55/0.60/0.65/0.75 | [111] |
| Chen | 0.30/0.65/0.95/1.20/1.40 | [112] | |
| Hoogenstraaten | 0.65 | [5] | |
| TTL | 1.1 | [113] | |
| CaAl2O4:Eu2+,Nd3+ | initial rise | 0.55/0.65 | [114] |
| Sr4Al14O25:Eu2+,Dy3+ | Chen | 0.72 | [47] |
| Chen | 0.49 | [46] | |
| TTL | 0.91 | [25] | |
| Sr2MgSi2O7:Eu2+,Dy3+ | Chen | 0.75 | [51] |
| Sr2MgSi2O7:Eu2+,Nd3+ | Hoogenstraaten | 0.08/0.18/0.29/0.23 | [115] |
| Ca2MgSi2O7:Eu2+,Tm3+ | Chen | 0.56 | [52] |
4. Suggested Persistent Luminescence Mechanisms
4.1. The Matsuzawa model
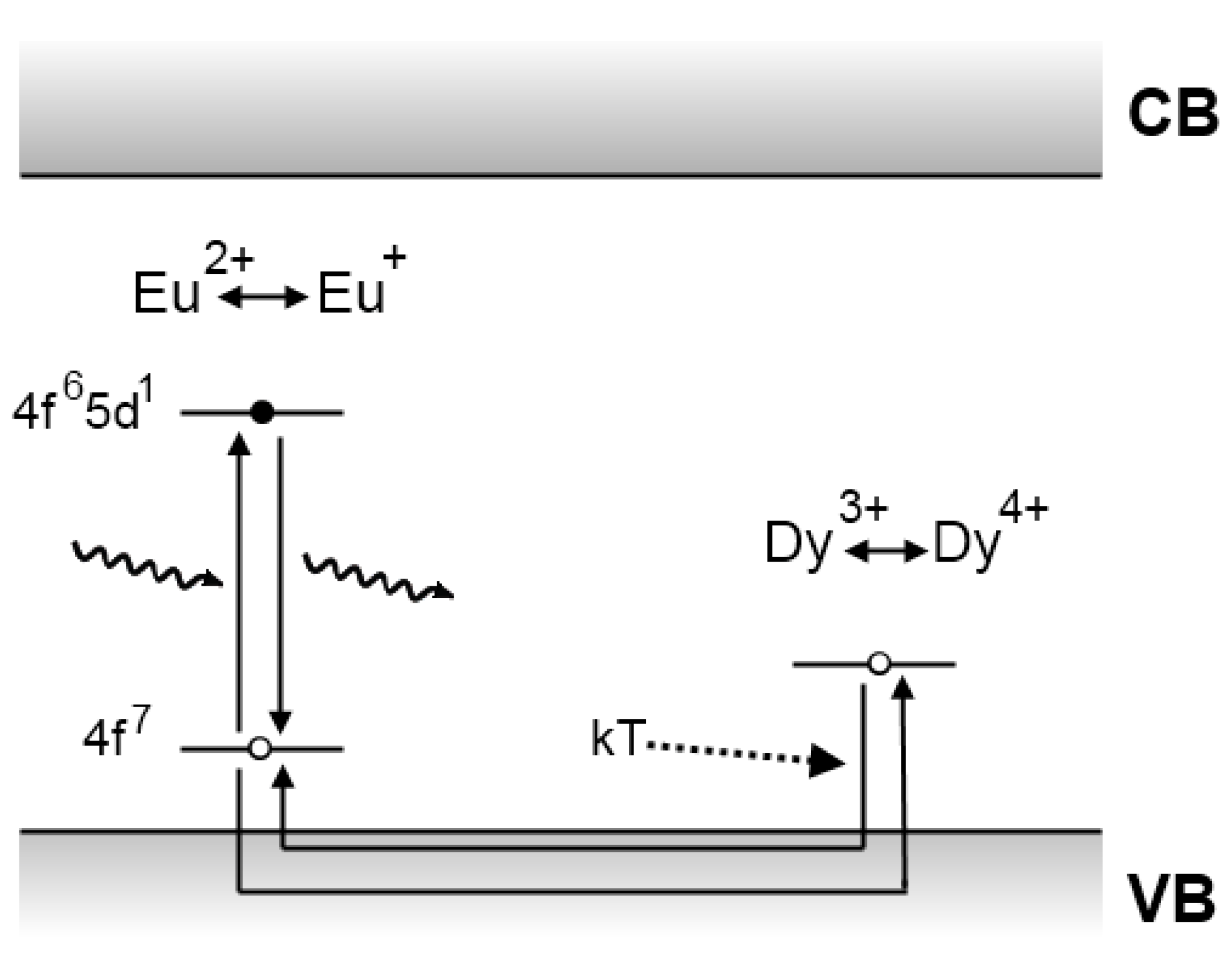
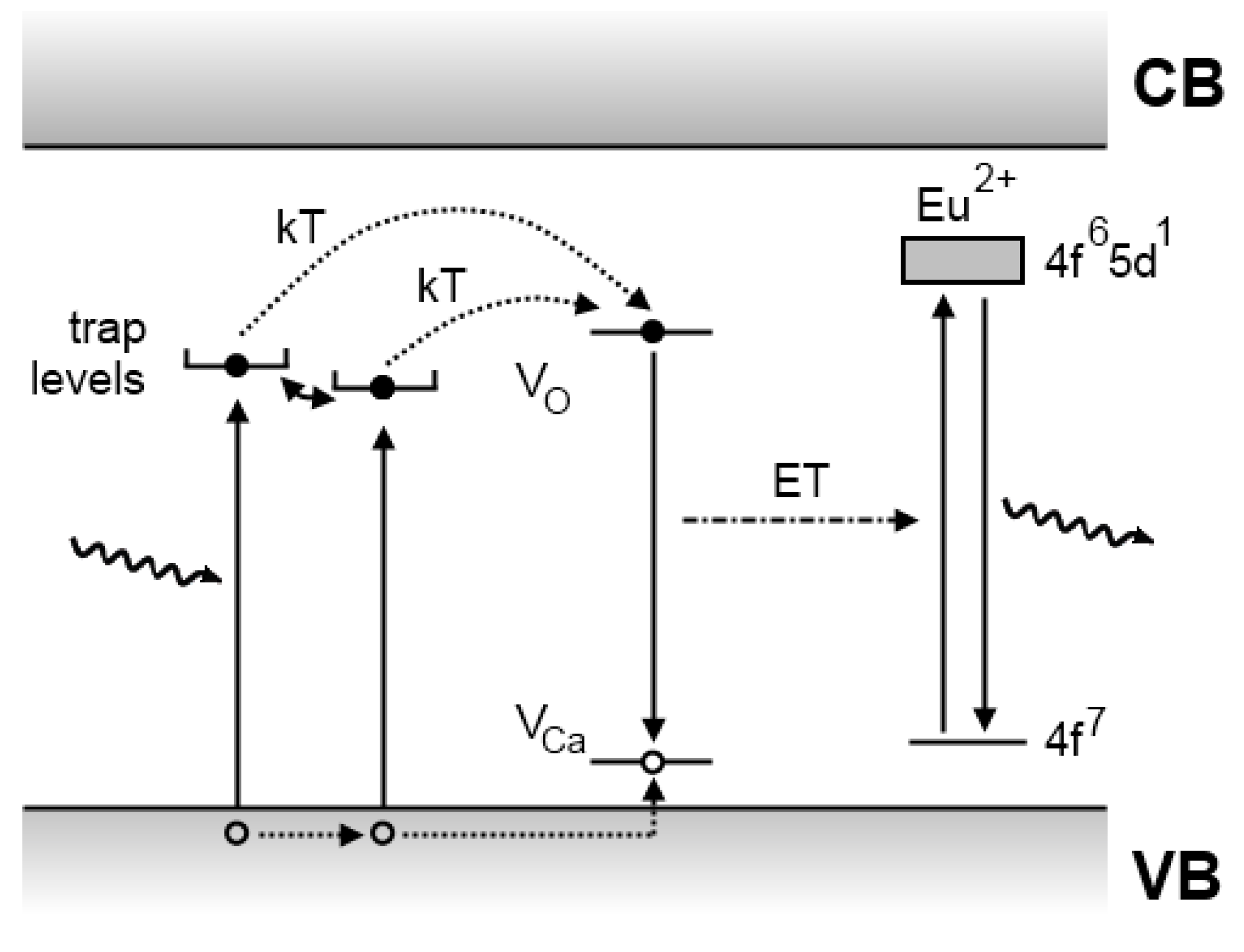
4.2. The Aitasalo model
4.3. The Dorenbos model
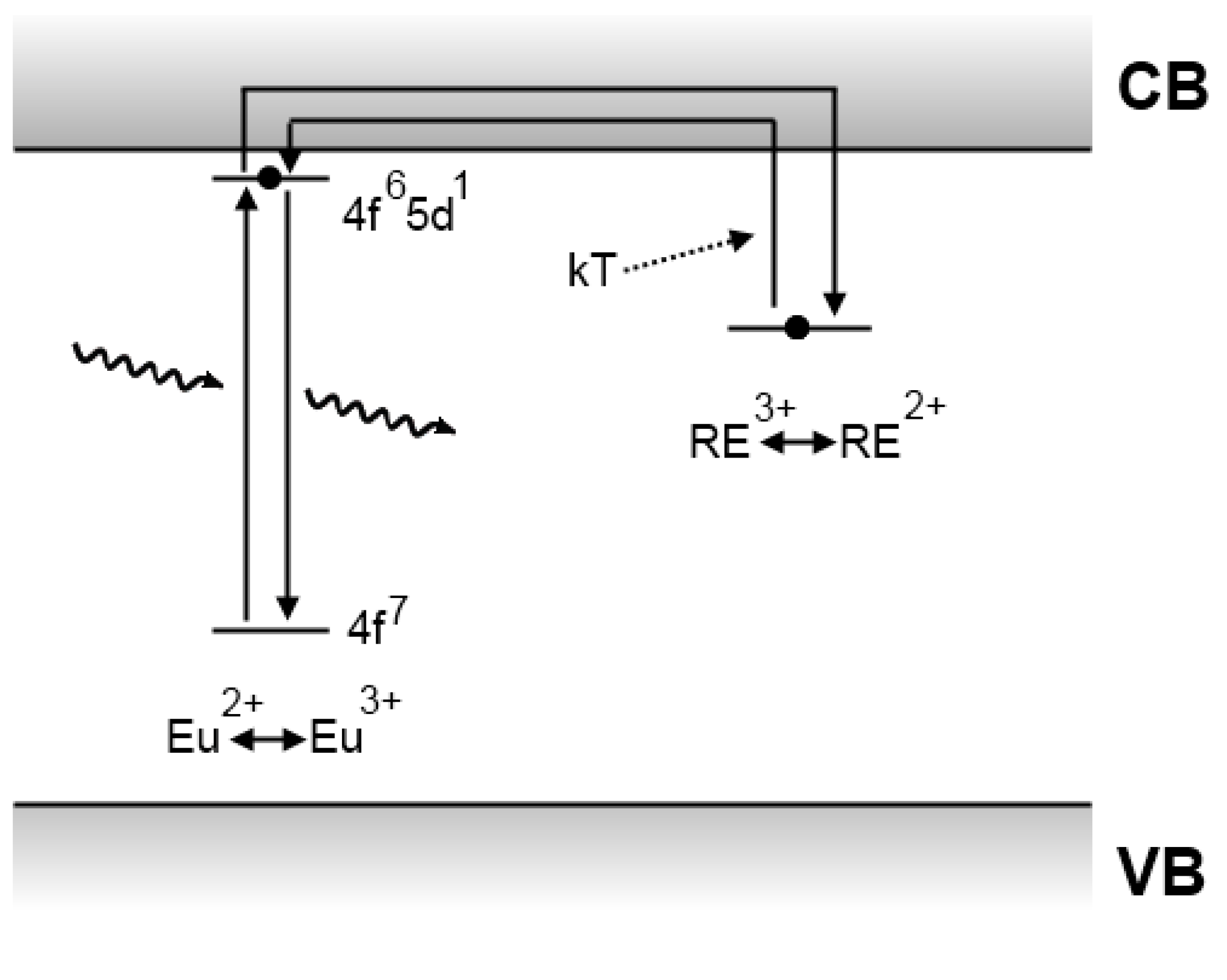
4.4. The Clabau model
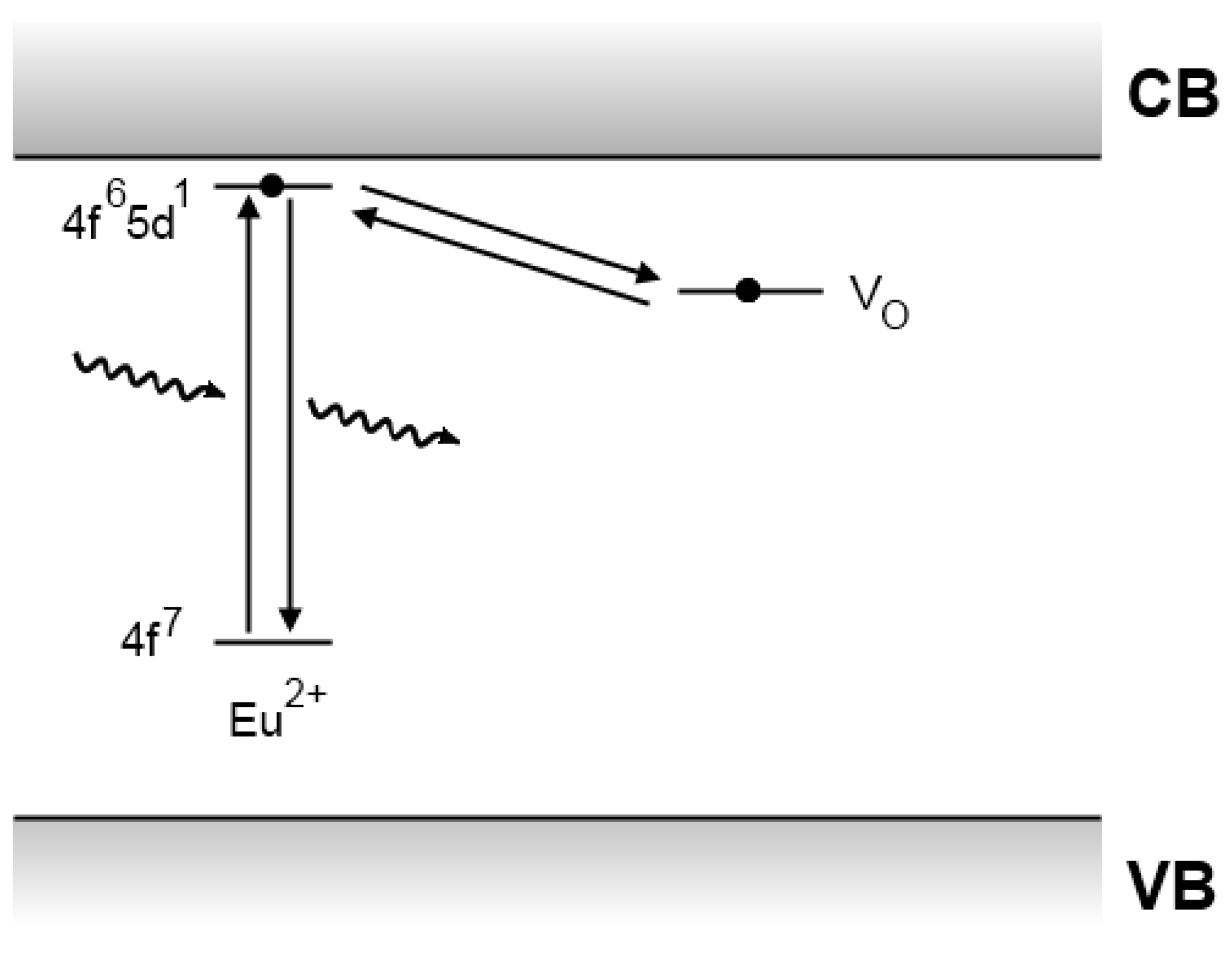
4.5. Recent developments

4.6. Experimental evidence
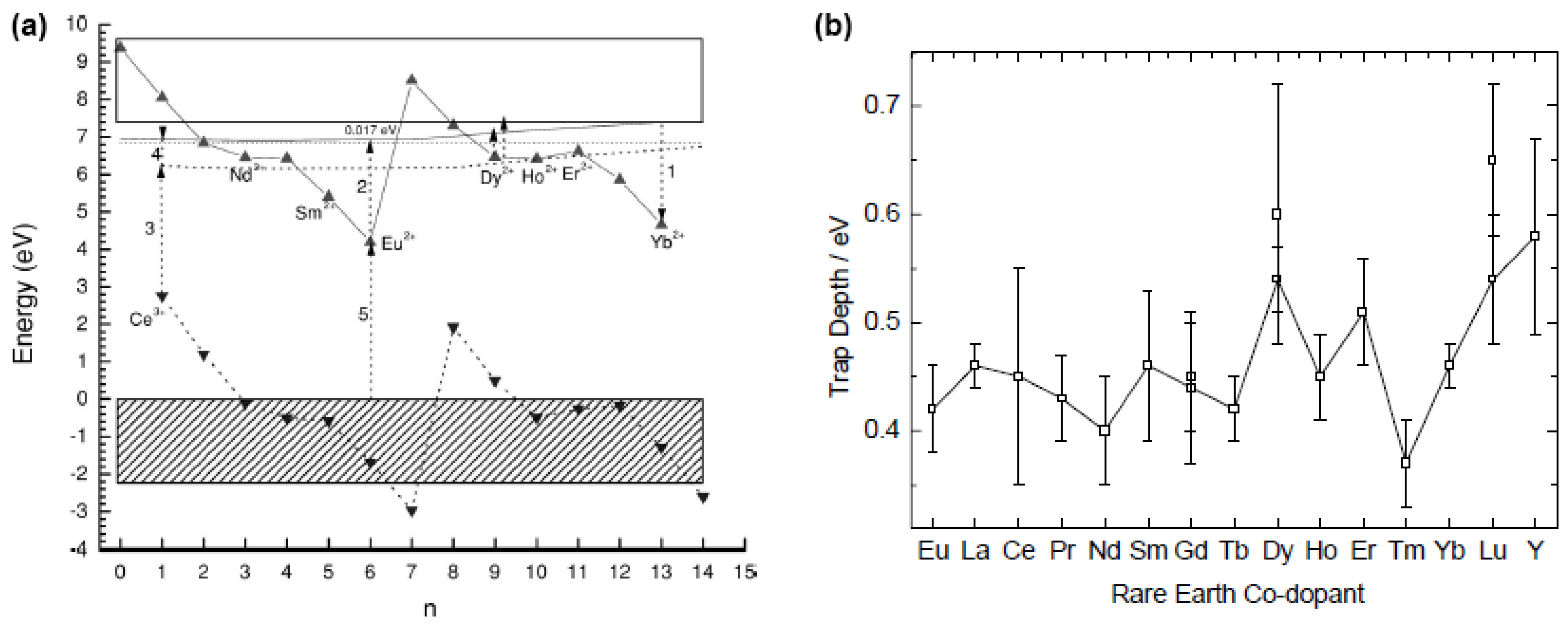
4.7. Concluding remarks
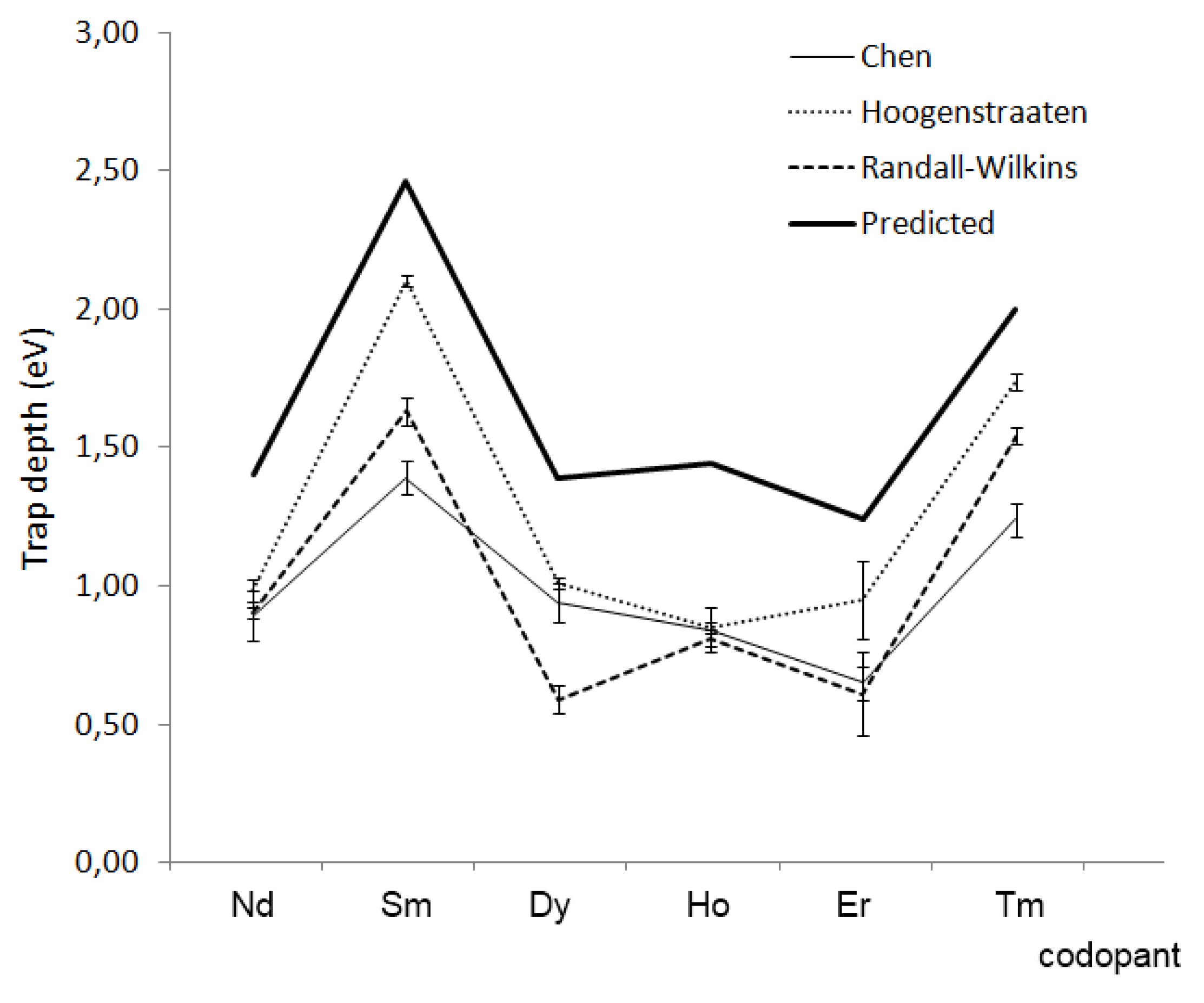
5. Challenges and Perspectives
Acknowledgements
References
- Harvey, E.N. A History of Luminescence from the Earliest Times until 1900; American Philosophical Society: Philadelphia, PA, USA, 1957. [Google Scholar]
- Hoogenstraaten, W.; Klasens, H.A. Some properties of zinc sulfide activated with copper and cobalt. J. Electrochem. Soc. 1953, 100, 366–375. [Google Scholar] [CrossRef]
- Yen, W.M.; Shionoya, S.; Yamamoto, H. Phosphor Handbook, 2nd ed.; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Wang, D.; Yin, Q.; Li, Y.; Wang, M. Concentration quenching of Eu2+ in SrO·Al2O3:Eu2+ phosphor. J. Lumines. 2002, 97, 1–6. [Google Scholar] [CrossRef]
- Matsuzawa, T.; Aoki, Y.; Takeuchi, N.; Murayama, Y. A new long phosphorescent phosphor with high brightness, SrAl2O4:Eu2+,Dy3+. J. Electrochem. Soc. 1996, 143, 2670–2673. [Google Scholar] [CrossRef]
- Abbruscato, V. Optical and electrical properties of SrAl2O4:Eu2+. J. Electrochem. Soc. 1971, 118, 930–933. [Google Scholar] [CrossRef]
- Takasaki, H.; Tanabe, S.; Hanada, T. Long-lasting afterglow characteristics of Eu, Dy codoped SrO-Al2O3 phosphor. J. Ceram. Soc. Jpn. 1996, 104, 322–326. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, Z.; Zhang, Z.; Wang, X.; Zhang, J. Preparation of a new long afterglow blue-emitting Sr2MgSi2O7-based photoluminescent phosphor. J. Mater. Sci. Lett. 2001, 20, 1505–1506. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Lastusaari, M.; Niittykoski, J. Mechanisms of persistent luminescence in Eu2+, RE3+ doped alkaline earth aluminates. J. Lumines. 2001, 94–95, 59–63. [Google Scholar] [CrossRef]
- Dorenbos, P. Mechanism of persistent luminescence in Eu2+ and Dy3+ codoped aluminate and silicate compounds. J. Electrochem. Soc. 2005, 152, H107–H110. [Google Scholar] [CrossRef]
- Blasse, G.; Grabmaier, B.C. Luminescent Materials; Springer-Verlag: Berlin, Germany, 1994. [Google Scholar]
- Poelman, D.; Avci, N.; Smet, P.F. Measured luminance and visual appearance of multi-color persistent phosphors. Opt. Express 2009, 17, 358–364. [Google Scholar] [CrossRef] [PubMed]
- Clabau, F.; Rocquefelte, X.; Jobic, S.; Deniard, P.; Whangbo, M.H.; Garcia, A.; Le Mercier, T. On the phosphorescence mechanism in SrAl2O4:Eu2+ and its codoped derivatives. Solid State Sci. 2007, 9, 608–612. [Google Scholar] [CrossRef]
- Schulze, A.R.; Buschbaum, H.M. Zur Verbindungsbildung von MeO: M2O3. IV. Zur Struktur von monoklinem SrAl2O4. Z. Anorg. Allg. Chem. 1981, 475, 205–210. [Google Scholar] [CrossRef]
- Lange, H. Luminescent Europium Activated Strontium Aluminate. US patent 3,294,699, 1966. [Google Scholar]
- Blasse, G.; Bril, A. Fluorescence of Eu2+-activated alkaline-earth aluminates. Philips Res. Rep. 1968, 23, 201–206. [Google Scholar]
- Katsumata, T.; Nabae, T.; Sasajima, K.; Komuro, S.; Morikawa, T. Effects of composition on the long phosphorescent SrAl2O4:Eu2+, Dy3+ phosphor crystals. J. Electrochem. Soc. 1997, 144, L243–L245. [Google Scholar] [CrossRef]
- Hölsä, J.; Jungner, H.; Lastusaari, M.; Niittykoski, J. Persistent luminescence of Eu2+ doped alkaline earth aluminates, MAl2O4:Eu2+. J. Alloy. Compd. 2001, 323–324, 326–330. [Google Scholar] [CrossRef]
- Katsumata, T.; Nabae, T.; Sasajima, K.; Matsuzawa, T. Growth and characteristics of long persistent SrAl2O4- and CaAl2O4-based phosphor crystals by a floating zone technique. J. Cryst. Growth 1998, 183, 361–365. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, Z.; Zhang, Z.; Nan, C. Influence of co-doping different rare earth ions on the luminescence of CaAl2O4-based phosphors. J. Eur. Ceram. Soc. 2003, 23, 175–178. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, Z.; Tang, Z.; Zhang, J.; Zheng, Z.; Lu, X. The characterization and mechanism of long afterglow in alkaline earth aluminates phosphors co-doped by Eu2O3 and Dy2O3. Mater. Chem. Phys. 2001, 70, 156–159. [Google Scholar] [CrossRef]
- Sakai, R.; Katsumata, T.; Komuro, S.; Morikawa, T. Effect of composition on the phosphorescence from BaAl2O4: Eu2+, Dy3+ crystals. J. Lumines. 1999, 85, 149–154. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, Z.; Zhang, Z. Preparation of long-afterglow Sr4Al14O25-based luminescent material and its optical properties. Mater. Lett. 2001, 51, 14–18. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, Z.; Zhang, Z.; Nan, C.W. Anomalous luminescence in Sr4Al14O25:Eu, Dy phosphors. Appl. Phys. Lett. 2002, 81, 996–998. [Google Scholar] [CrossRef]
- Nakazawa, E.; Murazaki, Y.; Saito, S. Mechanism of the persistent phosphorescence in Sr4Al14O25:Eu and SrAl2O4:Eu codoped with rare earth ions. J. Appl. Phys. 2006, 100, 113113. [Google Scholar] [CrossRef]
- Katsumata, T.; Sasajima, K.; Nabae, T.; Komuro, S.; Morikawa, T. Characteristics of strontium aluminate crystals used for long-duration phosphors. J. Am. Ceram. Soc. 1998, 81, 413–416. [Google Scholar] [CrossRef]
- Preethi, K.R.S.; Lu, C.H.; Thirumalai, J.; Jagannathan, R.; Natarajan, T.S.; Nayak, N.U.; Radhakrishna, I.; Jayachandran, M.; Trivedi, D.C. SrAl4O7:Eu2+ nanocrystals: synthesis and fluorescence properties. J. Phys. D-Appl. Phys. 2004, 37, 2664–2669. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Wang, T.; Hao, W. Preparation and characterization of a new long afterglow indigo phosphor Ca12Al14O33:Nd,Eu. Mater. Lett. 2003, 57, 4315–4318. [Google Scholar] [CrossRef]
- Chang, C.; Li, W.; Huang, X.; Wang, Z.; Chen, X.; Qian, X.; Guo, R.; Ding, Y.; Mao, D. Photoluminescence and afterglow behavior of Eu2+, Dy3+ and Eu3+, Dy3+ in Sr3Al2O6 matrix. J. Lumines. 2010, 130, 347–350. [Google Scholar] [CrossRef]
- Zhang, P.; Xu, M.; Zheng, Z.; Sun, B.; Zhang, Y. Rapid formation of red long afterglow phosphor Sr3Al2O6:Eu2+, Dy3+ by microwave irradiation. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2007, 136, 159–164. [Google Scholar] [CrossRef]
- Wanjun, T.; Donghua, C.; Ming, W. Luminescence studies on SrMgAl10O17:Eu,Dy phosphor crystals. Opt. Laser Technol. 2009, 41, 81–84. [Google Scholar] [CrossRef]
- Jüstel, T.; Bechtel, H.; Mayr, W.; Wiechert, D.U. Blue emitting BaMgAl10O17:Eu with a blue body color. J. Lumines. 2003, 104, 137–143. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Lastusaari, M.; Niittykoski, J.; Parkkinen, M.; Valtonen, R. Eu2+ doped calcium aluminates prepared by alternative low temperature routes. Opt. Mater. 2004, 26, 113–116. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Y.; Hu, Y.; Hu, Z.; Liu, C. Modification on luminescent properties of SrAl2O4:Eu2+,Dy3+ phosphor by Yb3+ ions doping. J. Lumines. 2008, 128, 1180–1184. [Google Scholar] [CrossRef]
- Peng, T.; Yang, H.; Pu, X.; Hu, B.; Jiang, Z.; Yan, C. Combustion synthesis and photoluminescence of SrAl2O4:Eu,Dy phosphor nanoparticles. Mater. Lett. 2004, 58, 352–356. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhou, Y.; Lü, M.; Zhang, A.; Ma, Q. Combustion synthesis of long-persistent luminescent MAl2O4: Eu2+, R3+ (M = Sr, Ba, Ca, R = Dy, Nd and La) nanoparticles and luminescence mechanism research. Acta Mater. 2007, 55, 2615–2620. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, D. Synthesis of CaAl2O4:Eu,Nd long persistent phosphor by combustion processes and its optical properties. Mater. Lett. 2007, 61, 3673–3675. [Google Scholar] [CrossRef]
- Geng, J.; Wu, Z. Synthesis of long afterglow SrAl2O4: Eu2+, Dy3+ phosphors through microwave route. J. Mater. Synth. Proces. 2002, 10, 245–248. [Google Scholar] [CrossRef]
- Jia, W.; Yuan, H.; Lu, L.; Liu, H.; Yen, W.M. Crystal growth and characterization of Eu2+, Dy3+ : SrAl2O4 and Eu2+, Nd3+ : CaAl2O4 by the LHPG method. J. Cryst. Growth 1999, 200, 179–184. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Lastusaari, M.; Niittykoski, J. Sol-gel processed Eu2+-doped alkaline earth aluminates. J. Alloy. Compd. 2002, 341, 76–78. [Google Scholar] [CrossRef]
- Chen, I.C.; Chen, T.M. Sol-gel synthesis and the effect of boron addition on the phosphorescent properties of SrAl2O4:Eu2+,Dy3+ phosphors. J. Mater. Res. 2001, 16, 644–651. [Google Scholar] [CrossRef]
- Peng, T.; Huajun, L.; Yang, H.; Yan, C. Synthesis of SrAl2O4:Eu, Dy phosphor nanometer powders by sol-gel processes and its optical properties. Mater. Chem. Phys. 2004, 85, 68–72. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, F.; Zhang, Z.; Huang, C.; Lin, Y. Luminescent properties of SrAl2O4: Eu, Dy material prepared by the gel method. J. Eur. Ceram. Soc. 2000, 20, 2129–2132. [Google Scholar] [CrossRef]
- Nag, A.; Kutty, T.R.N. The mechanism of long phosphorescence of SrAl2-xBxO4 (0 <x <0.2) and Sr4Al14-xBxO25 (0.1 <x <0.4) co-doped with Eu2+ and Dy3+. Mater. Res. Bull. 2004, 39, 331–342. [Google Scholar] [CrossRef]
- Nag, A.; Kutty, T.R.N. Role of B2O3 on the phase stability and long phosphorescence of SrAl2O4:Eu, Dy. J. Alloy. Compd. 2003, 354, 221–231. [Google Scholar] [CrossRef]
- Suriyamurthy, N.; Panigrahi, B.S. Effects of non-stoichiometry and substitution on photoluminescence and afterglow luminescence of Sr4Al14O25:Eu2+, Dy3+ phosphor. J. Lumines. 2008, 128, 1809–1814. [Google Scholar] [CrossRef]
- Yuan, Z.; Chang, C.; Mao, D.; Ying, W. Effect of composition on the luminescent properties of Sr4Al14O25: Eu2+, Dy3+ phosphors. J. Alloy. Compd. 2004, 377, 268–271. [Google Scholar] [CrossRef]
- Akiyama, M.; Xu, C.; Nonaka, K.; Watanabe, T. Intense visible light emission from Sr3Al2O6:Eu,Dy. Appl. Phys. Lett. 1998, 73, 3046–3048. [Google Scholar] [CrossRef]
- Zhang, P.; Li, L.; Xu, M.; Liu, L. The new red luminescent Sr3Al2O6:Eu2+ phosphor powders synthesized via sol-gel route by microwave-assisted. J. Alloy. Compd. 2008, 456, 216–219. [Google Scholar] [CrossRef]
- Lin, Y.; Nan, C.W.; Zhou, X.; Wu, J.; Wang, H.; Chen, D.; Xu, S. Preparation and characterization of long afterglow M2MgSi2O7-based (M: Ca, Sr, Ba) photoluminescent phosphors. Mater. Chem. Phys. 2003, 82, 860–863. [Google Scholar] [CrossRef]
- Liu, B.; Shi, C.; Yin, M.; Dong, L.; Xiao, Z. The trap states in the Sr2MgSi2O7 and (Sr,Ca)MgSi2O7 long afterglow phosphor activated by Eu2+ and Dy3+. J. Alloy. Compd. 2005, 387, 65–69. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Kirm, M.; Laamanen, T.; Lastusaari, M.; Niittykoski, J.; Raud, J.; Valtonen, R. Persistent luminescence and synchrotron radiation study of the Ca2MgSi2O7:Eu2+,R3+ materials. Radiat. Meas. 2007, 42, 644–647. [Google Scholar] [CrossRef]
- Blasse, G.; Wanmaker, W.L.; ter Vrugt, J.W.; Bril, A. Fluorescence of Eu2+-activated silicates. Philips Res. Rep. 1968, 23, 189–200. [Google Scholar]
- Jiang, L.; Chang, C.; Mao, D. Luminescent properties of CaMgSi2O6 and Ca2MgSi2O7 phosphors activated by Eu2+, Dy3+ and Nd3+. J. Alloy. Compd. 2003, 360, 193–197. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Laamanen, T.; Lastusaari, M.; Lehto, L.; Niittykoski, J.; Pellé, F. Luminescence properties of Eu2+ doped dibarium magnesium disilicate, Ba2MgSi2O7:Eu2+. Ceram.-Silikáty 2005, 49, 58–62. [Google Scholar]
- Aitasalo, T.; Hreniak, D.; Hölsä, J.; Laamanen, T.; Lastusaari, M.; Niittykoski, J.; Pellé, F.; Strek, W. Persistent luminescence of Ba2MgSi2O7:Eu2+. J. Lumines. 2007, 122–123, 110–112. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, Z.; Zhang, Z.; Nan, C.W. Luminescence of Eu2+ and Dy3+ activated R3MgSi2O8-based (R = Ca, Sr, Ba) phosphors. J. Alloy. Compd. 2003, 348, 76–79. [Google Scholar] [CrossRef]
- Sabbagh Alvani, A.A.; Moztarzadeh, F.; Sarabi, A.A. Effects of dopant concentrations on phosphorescence properties of Eu/Dy-doped Sr3MgSi2O8. J. Lumines. 2005, 114, 131–136. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, Z.; Tang, Z.; Wang, X.; Zhang, J.; Zheng, Z. Luminescent properties of a new long afterglow Eu2+ and Dy3+ activated Ca3MgSi2O8 phosphor. J. Eur. Ceram. Soc. 2001, 21, 683–685. [Google Scholar] [CrossRef]
- Jiang, L.; Chang, C.; Mao, D.; Feng, C. Luminescent properties of CaMgSi2O6-based phosphors co-doped with different rare earth ions. J. Alloy. Compd. 2004, 377, 211–215. [Google Scholar] [CrossRef]
- Kuang, J.; Liu, Y.; Zhang, J.; Huang, L.; Rong, J.; Yuan, D. Blue-emitting long-lasting phosphor, Sr3Al10SiO20:Eu2+,Ho3+. Solid State Commun. 2005, 136, 6–10. [Google Scholar] [CrossRef]
- Kuang, J.Y.; Liu, Y.L.; Zhang, J.X. Effects of RE3+ as a co-dopant in blue-emitting long-lasting phosphors, Sr3Al10SiO20 : Eu2+. J. Mater. Sci. 2006, 41, 5500–5503. [Google Scholar] [CrossRef]
- Clabau, F.; Garcia, A.; Bonville, P.; Gonbeau, D.; Le Mercier, T.; Deniard, P.; Jobic, S. Fluorescence and phosphorescence properties of the low temperature forms of the MAl2Si2O8:Eu2+ (M = Ca, Sr, Ba) compounds. J. Solid State Chem. 2008, 181, 1456–1461. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zhang, P.; Hong, Z.; Fan, X.; Qian, G. Preparation of Eu2+ and Dy3+ co-activated CaAl2Si2O8-based phosphor and its optical properties. Mater. Lett. 2004, 58, 3308–3311. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Y.; Wang, Z.; Li, W.; Mao, D.; Han, H.; Chang, C. Photoluminescence of Eu single doped and Eu/Dy codoped Sr2Al2SiO7 phosphors with long persistence. J. Lumines. 2009, 129, 294–299. [Google Scholar] [CrossRef]
- Jiang, L.; Chang, C.; Mao, D.; Zhang, B. A new long persistent blue-emitting Sr2ZnSi2O7:Eu2+,Dy3+ prepared by sol-gel method. Mater. Lett. 2004, 58, 1825–1829. [Google Scholar] [CrossRef]
- Wang, X.J.; He, Z.Y.; Jia, D.; Strek, W.; Pazik, R.; Hreniak, D.; Yen, W.M. Crystal size dependence of the persistent phosphorescence in Sr2ZnSi2O7:Eu2+,Dy3+. Microelectron. J. 2005, 36, 546–548. [Google Scholar] [CrossRef]
- Lakshminarasimhan, N.; Varadaraju, U.V. Luminescence and afterglow in Sr2SiO4:Eu2+,RE3+ [RE = Ce, Nd, Sm and Dy] phosphors—Role of co-dopants in search for afterglow. Mater. Res. Bull. 2008, 43, 2946–2953. [Google Scholar] [CrossRef]
- Ji, H.; Xie, G.; Lv, Y.; Lu, H. A new phosphor with flower-like structure and luminescent properties of Sr2MgSi2O7:Eu2+,Dy3+ long afterglow materials by sol–gel method. J. Sol-Gel Sci. Technol. 2007, 44, 133–137. [Google Scholar] [CrossRef]
- Pan, W.; Ning, G.; Zhang, X.; Wang, J.; Lin, Y.; Ye, J. Enhanced luminescent properties of long-persistent Sr2MgSi2O7:Eu2+, Dy3+ phosphor prepared by the co-precipitation method. J. Lumines. 2008, 128, 1975–1979. [Google Scholar] [CrossRef]
- Song, F.; Donghua, C.; Yuan, Y. Synthesis of Sr2MgSi2O7:Eu, Dy and Sr2MgSi2O7:Eu, Dy, Nd by a modified solid-state reaction and their luminescent properties. J. Alloy. Compd. 2008, 458, 564–568. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, D. Combustion synthesis and photoluminescence of Sr2MgSi2O7:Eu,Dy long lasting phosphor nanoparticles. Ceram. Int. 2008, 34, 2117–2120. [Google Scholar] [CrossRef]
- Toda, K.; Imanari, Y.; Nonogawa, T.; Miyoshi, J.; Uematsu, K.; Sato, M. Synthesis and characterization of new long persistent phosphor. J. Ceram. Soc. Jpn. 2002, 110, 283–288. [Google Scholar] [CrossRef]
- Fei, Q.; Chang, C.; Mao, D. Luminescent properties of Sr2MgSi2O7 and Ca2MgSi2O7 long lasting phosphors activated by Eu2+, Dy3+. J. Alloy. Compd. 2005, 390, 133–137. [Google Scholar] [CrossRef]
- Jiang, L.; Chang, C.; Mao, D.; Feng, C. Luminescent properties of Ca2MgSi2O7 phosphor activated by Eu2+, Dy3+ and Nd3+. Opt. Mater. 2004, 27, 51–55. [Google Scholar] [CrossRef]
- Dorenbos, P. Energy of the first 4f7-->4f65d transition of Eu2+ in inorganic compounds. J. Lumines. 2003, 104, 239–260. [Google Scholar] [CrossRef]
- Jia, D.; Zhu, J.; Wu, B. Improvement of persistent phosphorescence of Ca0.9Sr0.1S : Bi3+ by codoping Tm3+. J. Lumines. 2000, 91, 59–65. [Google Scholar] [CrossRef]
- Jia, D.; Jia, W.; Evans, D.R.; Dennis, W.M.; Liu, H.; Zhu, J.; Yen, W.M. Trapping processes in CaS:Eu2+, Tm3+. J. Appl. Phys. 2000, 88, 3402–3407. [Google Scholar] [CrossRef]
- Jia, D.; Zhu, J.; Wu, B. Trapping Centers in CaS:Bi3+ and CaS:Eu2+,Tm3+. J. Electrochem. Soc. 2000, 147, 386–389. [Google Scholar] [CrossRef]
- Jia, D. Enhancement of long-persistence by Ce co-doping in CaS:Eu2+,Tm3+ red phosphor. J. Electrochem. Soc. 2006, 153, H198–H201. [Google Scholar] [CrossRef]
- Guo, C.; Tang, Q.; Huang, D.; Zhang, C.; Su, Q. Influence of co-doping different rare earth ions on CaGa2S4: Eu2+, RE3+ (RE = Ln) phosphors. J. Phys. Chem. Solids 2007, 68, 217–223. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, C.; Lü, Y.; Tang, Q.; Su, Q. Luminescent properties of Eu2+ and Ho3+ co-doped CaGa2S4 phosphor. Phys. Status Solidi A-Appl. Mat. 2004, 201, 1588–1593. [Google Scholar] [CrossRef]
- Najafov, H.; Kato, A.; Toyota, H.; Iwai, K.; Bayramov, A.; Iida, S. Effect of Ce co-doping on CaGa2S4:Eu phosphor: II. Thermoluminescence. Jpn. J. Appl. Phys. 2002, 41, 2058–2065. [Google Scholar] [CrossRef]
- Smet, P.F.; Avci, N.; Poelman, D. Red persistent luminescence in Ca2SiS4:Eu,Nd. J. Electrochem. Soc. 2009, 156, H243–H248. [Google Scholar] [CrossRef]
- Pang, R.; Li, C.; Shi, L.; Su, Q. A novel blue-emitting long-lasting proyphosphate phosphor Sr2P2O7:Eu2+,Y3+. J. Phys. Chem. Solids 2009, 70, 303–306. [Google Scholar] [CrossRef]
- Pang, R.; Li, C.; Zhang, S.; Su, Q. Luminescent properties of a new blue long-lasting phosphor Ca2P2O7:Eu2+,Y3+. Mater. Chem. Phys. 2009, 113, 215–218. [Google Scholar] [CrossRef]
- Liu, L.; Li, C.; Wang, S.; Su, Q. Redshift phenomenon of the excitation light of long life emission phosphor. Appl. Phys. Lett. 2006, 88, 241107. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kato, H.; Honna, Y.; Yamamoto, H.; Ohmi, K. An orange-emitting, long-persistent phosphor, Ca2Si5N8:Eu2+,Tm3+. J. Electrochem. Soc. 2009, 156, J235–J241. [Google Scholar] [CrossRef]
- Van den Eeckhout, K.; Smet, P.F.; Poelman, D. Persistent luminescence in rare-earth codoped Ca2Si5N8:Eu2+. J. Lumines. 2009, 129, 1140–1143. [Google Scholar] [CrossRef]
- Li, C.; Su, Q. A new blue phosphorescent glass-ceramic: Rare-earth-doped calcium aluminoborate. J. Alloy. Compd. 2006, 408–412, 875–878. [Google Scholar] [CrossRef]
- Zhang, L.; Li, C.; Su, Q. Long lasting phosphorescence in Eu2+ and Ce3+ co-doped strontium borate glasses. J. Rare Earths 2006, 24, 196–198. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, J.; Zhang, X.; Sun, X.; Luo, Y.; Lu, S.; Wang, X. White light emitting diode by using α-Ca2P2O7:Eu2+,Mn2+ phosphor. Appl. Phys. Lett. 2007, 90, 261113. [Google Scholar] [CrossRef]
- Li, Y.Q.; van Steen, J.E.J.; van Krevel, J.W.H.; Botty, G.; Delsing, A.C.A.; DiSalvo, F.J.; de With, G.; Hintzen, H.T. Luminescence properties of red-emitting M2Si5N8:Eu2+ (M = Ca, Sr, Ba) LED conversion phosphors. J. Alloy. Compd. 2006, 417, 273–279. [Google Scholar] [CrossRef]
- Chen, R.; McKeever, S.W.S. Theory of Thermoluminescence and Related Phenomena; World Scientific: Singapore, 1997; Volume xiii, p. 559. [Google Scholar]
- McKeever, S.W.S. Thermoluminescence of Solids; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- McKeever, S.W.S.; Moscovitch, M.; Townsend, P.D. Thermoluminescence Dosimetry Materials: Properties and Uses; Nuclear Technology Pub.: Ashford, UK, 1995. [Google Scholar]
- Urbach, F. Zur Lumineszenz der Alkalihalogenide: II. Messungmethoden. Sitzungsberichte Akademie der Wissenshaften in Wien 1930, 139, 363. [Google Scholar]
- Randall, J.T.; Wilkins, M.H.F. Phosphorescence and electron traps. I. The study of trap distributions. P. Roy. Soc. Lond. A 1945, 184, 365–389. [Google Scholar] [CrossRef]
- Randall, J.T.; Wilkins, M.H.F. Phosphorescence and electron traps. II. The interpretation of long-period phosphorescence. P. Roy. Soc. Lond. A 1945, 184, 390–407. [Google Scholar] [CrossRef]
- Garlick, G.F.J.; Gibson, A.F. The electron trap mechanism of luminescence in sulphide and silicate phosphors. Proc. Phys. Soc. 1948, 60, 574–590. [Google Scholar] [CrossRef]
- Bos, A.J.J. Theory of thermoluminescence. Radiat. Meas. 2006, 41, S45–S56. [Google Scholar] [CrossRef]
- Chen, R. On the calculation of activation energies and frequency factors from glow curves. J. Appl. Phys. 1969, 40, 570–585. [Google Scholar] [CrossRef]
- Hoogenstraaten, W. Electron traps in ZnS phosphors. Philips Res. Rep. 1958, 13, 515–693. [Google Scholar]
- Chen, R. Glow curves with general order kinetics. J. Electrochem. Soc. 1969, 116, 1254–1257. [Google Scholar] [CrossRef]
- Chung, K.S. TL Glow Curve Analyzer v0.9.6; Korea Atomic Energy Research Institute and Gyeongsang National University: Daejeon, Korea, 2003. [Google Scholar]
- Chung, K.S.; Choe, H.S.; Lee, J.I.; Kim, J.L.; Chang, S.Y. A computer program for the deconvolution of thermoluminescence glow curves. Radiat. Prot. Dosim. 2005, 115, 343–349. [Google Scholar] [CrossRef]
- Thomas, R.; Nampoori, V.P.N. On the luminescence characteristics of cerium and copper doped barium sulfide phosphor. Solid State Commun. 1988, 68, 821–824. [Google Scholar] [CrossRef]
- Bube, R.H. Luminescence and trapping in zinc sulfide phosphors with and without copper activator. Phys. Rev. 1950, 80, 655–666. [Google Scholar] [CrossRef]
- Paulose, P.I.; Joseph, J.; Rudra Warrier, M.K.; Jose, G.; Unnikrishnan, N.V. Relaxation kinetics of Sm: Ce-doped CaS phosphors. J. Lumines. 2007, 127, 583–588. [Google Scholar] [CrossRef]
- Nakazawa, E. A new method for the characterization of traps in luminescent materials. Jpn. J. Appl. Phys. - Lett. 1984, 23, L755–L757. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Krupa, J.C.; Lastusaari, M.; Legendziewicz, J.; Niittykoski, J. Effect of temperature on the luminescence processes of SrAl2O4:Eu2+. Radiat. Meas. 2004, 38, 727–730. [Google Scholar] [CrossRef]
- Arellano-Tánori, O.; Meléndrez, R.; Pedroza-Montero, M.; Castañeda, B.; Chernov, V.; Yen, W.M.; Barboza-Flores, M. Persistent luminescence dosimetric properties of UV-irradiated SrAl2O4:Eu2+, Dy3+ phosphor. J. Lumines. 2008, 128, 173–184. [Google Scholar] [CrossRef]
- Nakazawa, E.; Mochida, T. Traps in SrAl2O4:Eu2+ phosphor with rare-earth ion doping. J. Lumines. 1997, 72–74, 236–237. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Lastusaari, M.; Niittykoski, J. Thermoluminescence study of persistent luminescence materials: Eu2+- and R3+-doped calcium aluminates, CaAl2O4:Eu2+,R3+. J. Phys. Chem. B 2006, 110, 4589–4598. [Google Scholar] [CrossRef] [PubMed]
- Jia, D.; Jia, W.Y.; Jia, Y. Long persistent alkali-earth silicate phosphors doped with Eu2+,Nd3+. J. Appl. Phys. 2007, 101, 023520. [Google Scholar] [CrossRef]
- Jia, W.; Yuan, H.; Holmstrom, S.; Liu, H.; Yen, W.M. Photo-stimulated luminescence in SrAl2O4 : Eu2+,Dy3+ single crystal fibers. J. Lumines. 1999, 83–84, 465–469. [Google Scholar] [CrossRef]
- Jia, W.; Yuan, H.; Lu, L.; Liu, H.; Yen, W.M. Phosphorescent dynamics in SrAl2O4: Eu2+, Dy3+ single crystal fibers. J. Lumines. 1998, 76–77, 424–428. [Google Scholar] [CrossRef]
- Yuan, H.B.; Jia, W.; Basun, S.A.; Lu, L.; Meltzer, R.S.; Yen, W.M. The long-persistent photoconductivity of SrAl2O4:Eu2+, Dy3+ single crystals. J. Electrochem. Soc. 2000, 147, 3154–3156. [Google Scholar] [CrossRef]
- Kato, K.; Tsutai, I.; Kamimura, T.; Kaneko, F.; Shinbo, K.; Ohta, M.; Kawakami, T. Thermoluminescence properties of SrAl2O4:Eu sputtered films with long phosphorescence. J. Lumines. 1999, 82, 213–220. [Google Scholar] [CrossRef]
- Yamamoto, H.; Matsuzawa, T. Mechanism of long phosphorescence of SrAl2O4:Eu2+, Dy3+ and CaAl2O4:Eu2+, Nd3+. J. Lumines. 1997, 72–74, 287–289. [Google Scholar] [CrossRef]
- Nakamura, T.; Kaiya, K.; Takahashi, N.; Matsuzawa, T.; Ohta, M.; Rowlands, C.C.; Smith, G.M.; Riedi, P.C. High frequency EPR investigations of gadolinium(III)-doped strontium aluminates. Phys. Chem. Chem. Phys. 2001, 3, 1721–1723. [Google Scholar] [CrossRef]
- Aitasalo, T.; Deren, P.; Hölsä, J.; Jungner, H.; Krupa, J.C.; Lastusaari, M.; Legendziewicz, J.; Niittykoski, J.; Strek, W. Persistent luminescence phenomena in materials doped with rare earth ions. J. Solid State Chem. 2003, 171, 114–122. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.H. Relations between the concentrations of imperfections in crystalline solids. In Solid State Phys.; Sietz, F., Turnbull, D., Eds.; Academic Press: San Diego, CA, USA, 1956. [Google Scholar]
- Palilla, F.C.; Levine, A.K.; Tomkus, M.R. Fluorescent properties of alkaline earth aluminates of the type MAl2O4 activated by divalent europium. J. Electrochem. Soc. 1968, 115, 642–644. [Google Scholar] [CrossRef]
- Dorenbos, P. Locating lanthanide impurity levels in the forbidden band of host crystals. J. Lumines. 2004, 108, 301–305. [Google Scholar] [CrossRef]
- Dorenbos, P. Mechanism of persistent luminescence in Sr2MgSi2O7:Eu2+;Dy3+. Phys. Status Solidi B-Basic Solid State Phys. 2005, 242, R7–R9. [Google Scholar] [CrossRef]
- Dorenbos, P. Systematic behaviour in trivalent lanthanide charge transfer energies. J. Phys.-Condens. Matter 2003, 15, 8417–8434. [Google Scholar] [CrossRef]
- Clabau, F.; Rocquefelte, X.; Jobic, S.; Deniard, P.; Whangbo, M.H.; Garcia, A.; Le Mercier, T. Mechanism of phosphorescence appropriate for the long-lasting phosphors Eu2+-doped SrAl2O4 with codopants Dy3+ and B3+. Chem. Mat. 2005, 17, 3904–3912. [Google Scholar] [CrossRef]
- Clabau, F.; Rocquefelte, X.; Le Mercier, T.; Deniard, P.; Jobic, S.; Whangbo, M.H. Formulation of phosphorescence mechanisms in inorganic solids based on a new model of defect conglomeration. Chem. Mater. 2006, 18, 3212–3220. [Google Scholar] [CrossRef]
- Qiu, J.; Kawasaki, M.; Tanaka, K.; Shimizugawa, Y.; Hirao, K. Phenomenon and mechanism of long-lasting phosphorescence in Eu2+-doped aluminosilicate glasses. J. Phys. Chem. Solids 1998, 59, 1521–1525. [Google Scholar] [CrossRef]
- Qi, Z.; Shi, C.; Liu, M.; Zhou, D.; Luo, X.; Zhang, J.; Xie, Y. The valence of rare earth ions in R2MgSi2O7:Eu, Dy (R = Ca, Sr) long-afterglow phosphors. Phys. Status Solidi A-Appl. Mat. 2004, 201, 3109–3112. [Google Scholar] [CrossRef]
- Carlson, S.; Hölsä, J.; Laamanen, T.; Lastusaari, M.; Malkamäki, M.; Niittykoski, J.; Valtonen, R. X-ray absorption study of rare earth ions in Sr2MgSi2O7:Eu2+,R3+ persistent luminescence materials. Opt. Mater. 2009, 31, 1877–1879. [Google Scholar] [CrossRef]
- Hölsä, J.; Aitasalo, T.; Jungner, H.; Lastusaari, M.; Niittykoski, J.; Spano, G. Role of defect states in persistent luminescence materials. J. Alloy. Compd. 2004, 374, 56–59. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Dorenbos, P.; Bessière, A.; Viana, B. Lanthanide energy levels in YPO4. Radiat. Meas. 2008, 43, 222–226. [Google Scholar] [CrossRef]
- Jia, D. Charging curves and excitation spectrum of long persistent phosphor SrAl2O4:Eu2+, Dy3+. Opt. Mater. 2003, 22, 65–69. [Google Scholar] [CrossRef]
- Höppe, H.A. Recent developments in the field of inorganic phosphors. Angew. Chem. Int. Ed. 2009, 48, 3572–3582. [Google Scholar] [CrossRef]
- Schubert, E.F. Light-Emitting Diodes, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hong, Z.; Zhang, P.; Fan, X.; Wang, M. Eu3+ red long afterglow in Y2O2S:Ti, Eu phosphor through afterglow energy transfer. J. Lumines. 2007, 124, 127–132. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z.; Tang, Z.; Lin, Y. Characterization and properties of a red and orange Y2O2S-based long afterglow phosphor. Mater. Chem. Phys. 2003, 80, 1–5. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, J.; Zhang, X.; Wang, X. Mn2+ activated red long persistent phosphors in BaMg2Si2O7. J. Lumines. 2007, 122–123, 914–916. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Electromagnetic Theory of Propagation, Interference, and Diffraction of Light, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rea, M.S.; Bullough, J.D.; Freyssinier-Nova, J.P.; Bierman, A. A proposed unified system of photometry. Lighting Res. Technol. 2004, 36, 85–109. [Google Scholar] [CrossRef]
- Stockman, A.; Sharpe, L.T. Into the twilight zone: the complexities of mesopic vision and luminous efficiency. Opht. Phys. Opt. 2006, 26, 225–239. [Google Scholar] [CrossRef]
- Saito, M.; Adachi, N.; Kondo, H. Full-color illumination that needs no electric power. Opt. Express 2007, 15, 1621–1626. [Google Scholar] [CrossRef] [PubMed]
- le Masne de Chermont, Q.; Chanéac, C.; Seguin, J.; Pellé, F.; Maîtrejean, S.; Jolivet, J.P.; Gourier, D.; Bessodes, M.; Scherman, D. Nanoprobes with near-infrared persistent luminescence for in vivo imaging. Proc. Nat. Acad. Sci. USA 2007, 104, 9266–9271. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Van den Eeckhout, K.; Smet, P.F.; Poelman, D. Persistent Luminescence in Eu2+-Doped Compounds: A Review. Materials 2010, 3, 2536-2566. https://doi.org/10.3390/ma3042536
Van den Eeckhout K, Smet PF, Poelman D. Persistent Luminescence in Eu2+-Doped Compounds: A Review. Materials. 2010; 3(4):2536-2566. https://doi.org/10.3390/ma3042536
Chicago/Turabian StyleVan den Eeckhout, Koen, Philippe F. Smet, and Dirk Poelman. 2010. "Persistent Luminescence in Eu2+-Doped Compounds: A Review" Materials 3, no. 4: 2536-2566. https://doi.org/10.3390/ma3042536
APA StyleVan den Eeckhout, K., Smet, P. F., & Poelman, D. (2010). Persistent Luminescence in Eu2+-Doped Compounds: A Review. Materials, 3(4), 2536-2566. https://doi.org/10.3390/ma3042536






