Predicting New Materials for Hydrogen Storage Application
Abstract
:1. Introduction
2. Prediction of Hydride Crystal Structures
2.1. Structural complexity
2.2. Tailor made complex hydrides
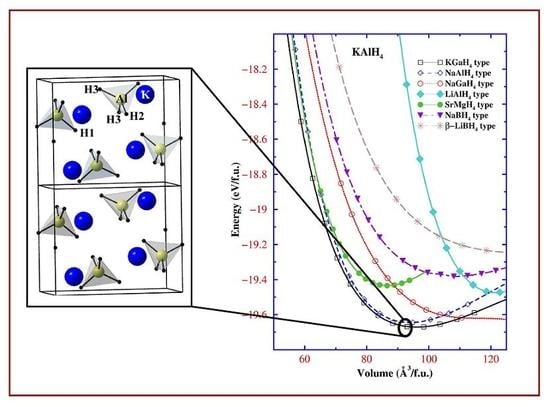
3. Structural Investigation: A Challenging Task
| Unit-cell dimensions (Å) | Positional parameters | |
| Theory | Experiment | |
| KGaH type: | K () : 0.1778, 1/4, 0.1621 | K () : 0.1775(7), 1/4, 0.1598(9) |
| a = 9.009 (8.814; 8.736) | Al () : 0.5663, 1/4, 0.8184 | Al () : 0.5659(6), 1/4, 0.8201(7) |
| b = 5.767 (5.819; 5.725) | H1 () : 0.4034, 1/4, 0.9184 | D1 () : 0.4063(5), 1/4, 0.9250(4) |
| c = 7.399 (7.331; 7.260) | H2 () : 0.7055, 1/4, 0.9623 | D2 () : 0.7153(5), 1/4, 0.9611(6) |
| H3 () : 0.4194, 0.9810, 0.3127 | D3 () : 0.4181(3), 0.9791(4), 0.3137(4) | |
| ICSD formula | Example | Number of entries | Independent structures |
| LiH | 3710 | 58 | |
| MgH | 3375 | 98 | |
| KSbZn | 391 | 69 | |
| AgInTe | 17 | 7 | |
| NaMgH | 6639 | 30 | |
| LiAlH | 2015 | 103 | |
| CaAlH | 317 | 45 | |
| GaBH | 377 | 32 | |
| MgCsH | 4790 | 131 | |
| AgPO | 226 | 26 | |
| MgCsH | 173 | 34 | |
| RuSrH | 1344 | 36 | |
| LiAlH | 465 | 43 | |
| SrAlH | 243 | 34 | |
| Ca(BH) | 271 | 50 | |
| MgCsD | 6 | 3 | |
| BaMgD | 62 | 12 | |
| TiTaKO | 127 | 12 | |
| LiMgAlH | 158 | 18 | |
| LiAlKH | 1957 | 23 | |
| CaLi(BH) | 18 | 8 | |
| CaLi(BH) | 27 | 9 |
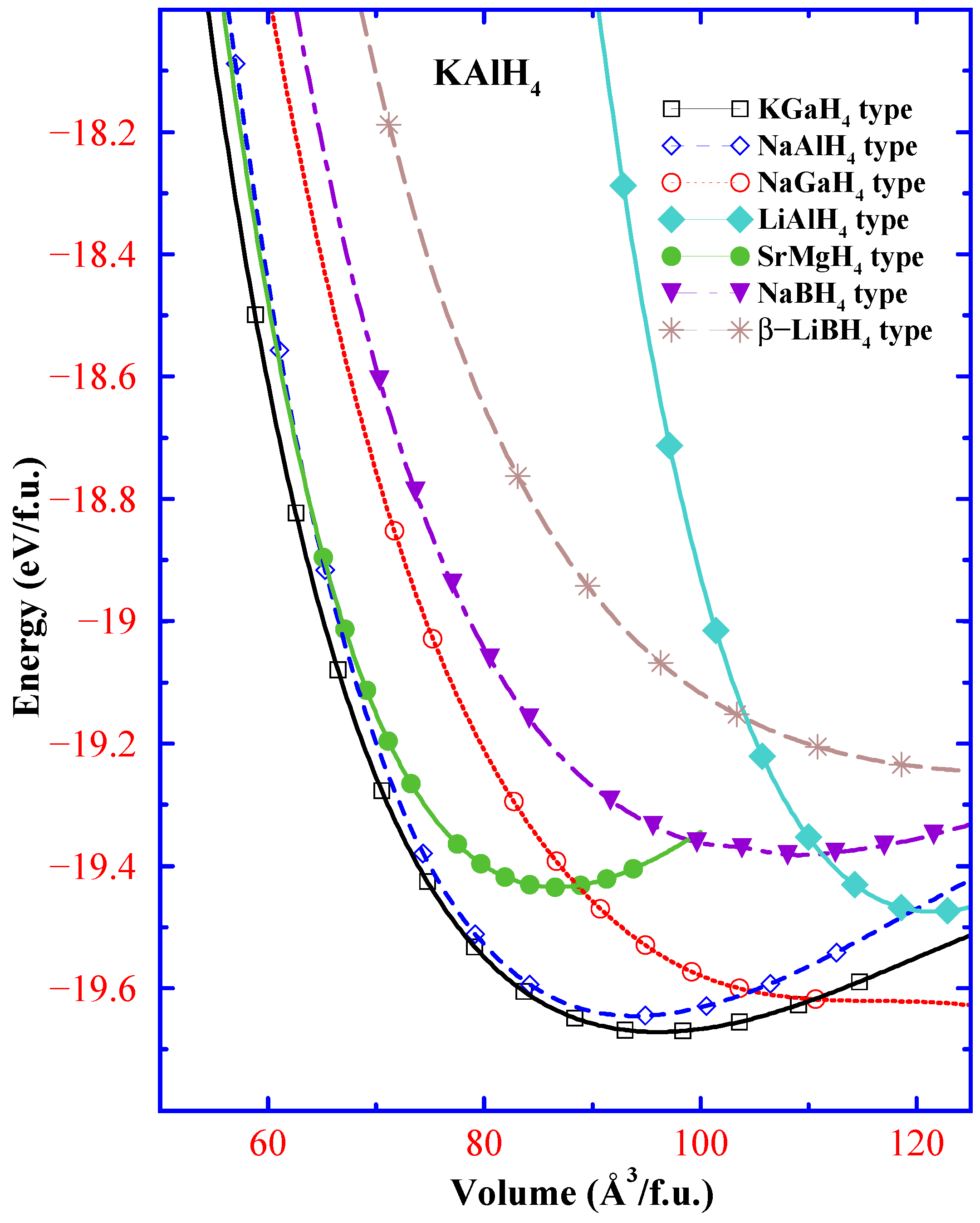
Magnesium borohydride Mg(BH): A challenging case
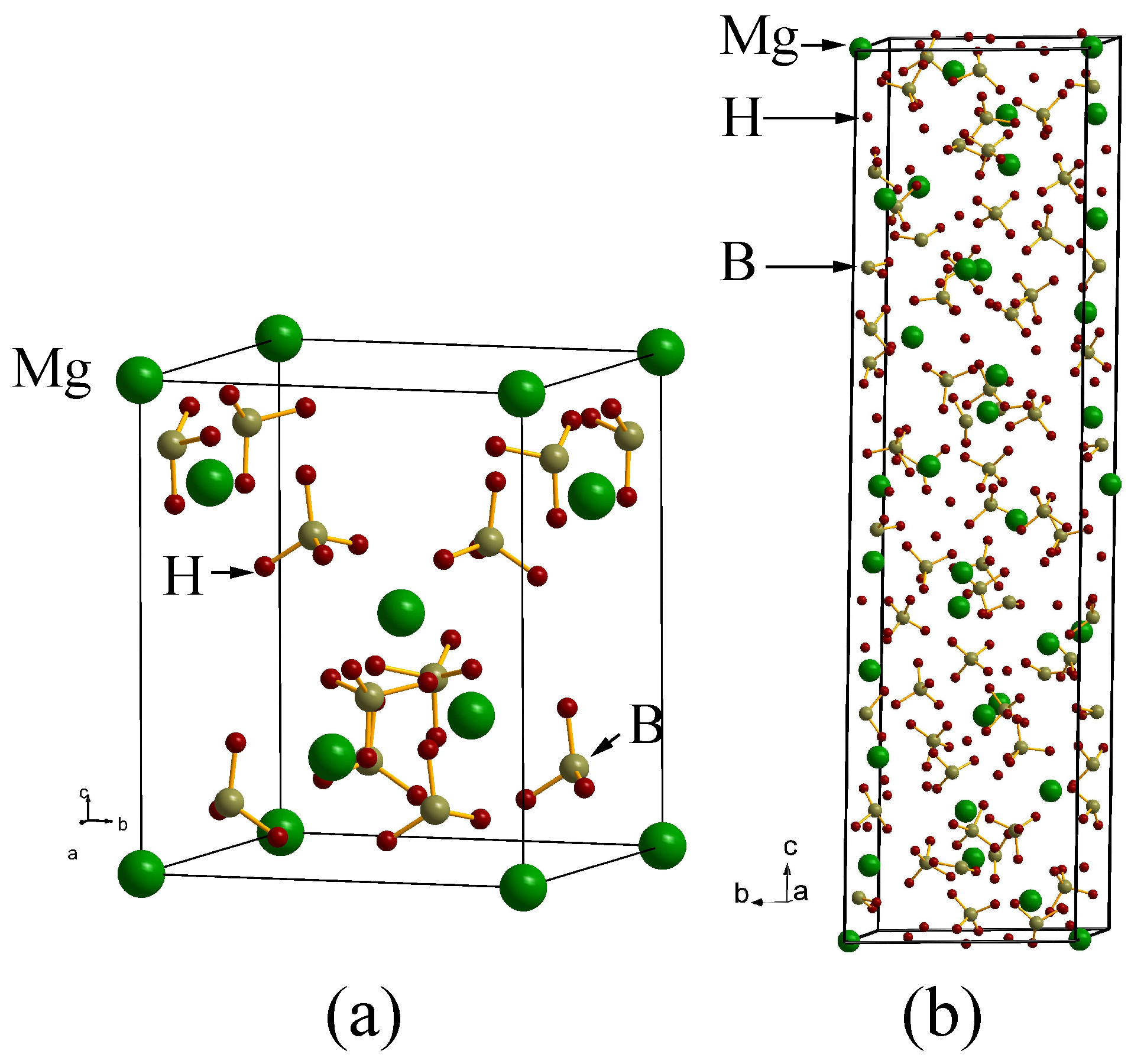
4. Search for Potential Metastable Phases
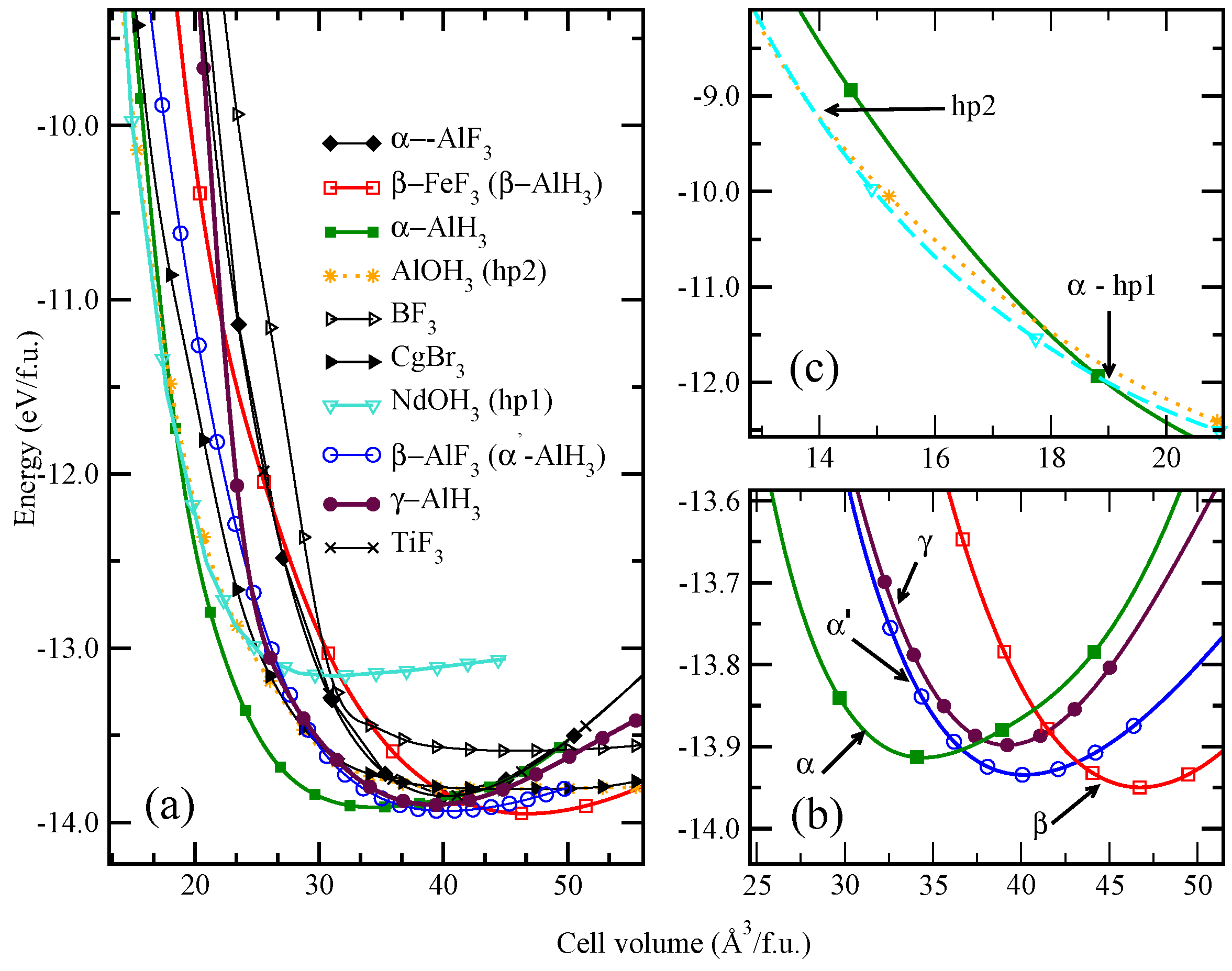
5. Stabilizing Meta-Stable Phases by Substitution
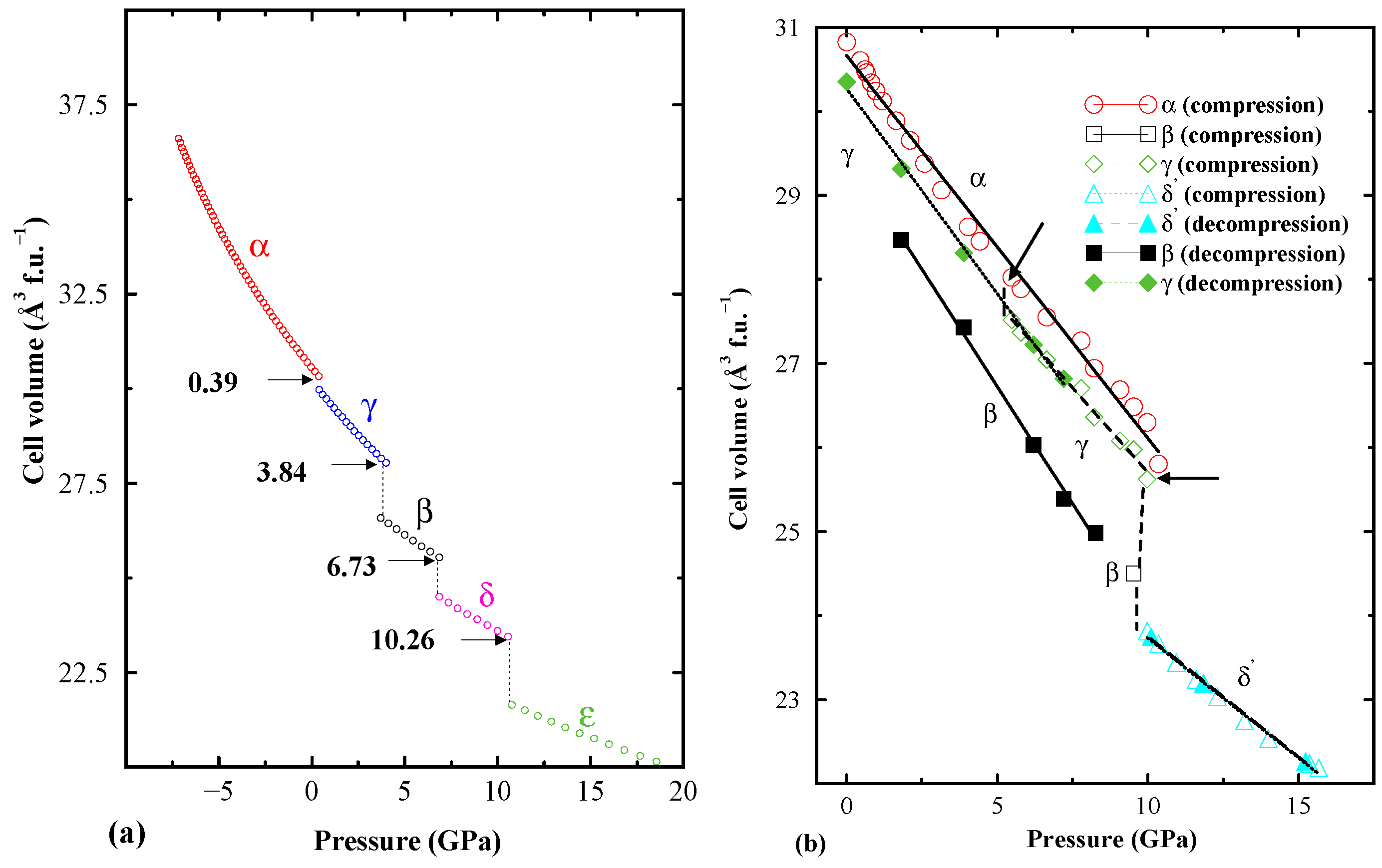
6. Conclusions
Acknowledgements
References
- Block, J.; Gray, A.P. Thermal decomposition of lithium aluminum hydride. Inorg. Chem. 1965, 4, 304–305. [Google Scholar] [CrossRef]
- Dilts, J.A.; Ashby, E.C. Thermal decomposition of complex metal hydrides. Inorg. Chem. 1972, 11, 1230–1236. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Schwickardi, M. Ti-doped alkali metal aluminium hydrides as potential novel reversible hydrogen storage materials. J. Alloys Compd. 1997, 253, 1–9. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Brand, R.A.; Marjanovic, A.; Schwikardi, M.; Tölle. Metal-doped sodium aluminium hydrides as potential new hydrogen storage materials. J. Alloys Compd. 2000, 302, 36–58. [Google Scholar] [CrossRef]
- Brinks, H.W.; Hauback, B.C.; Norby, P.; Fjellvåg, H. The decomposition of LiAlD4 studied by in situ x-ray and neutron diffraction. J. Alloys Compd. 2003, 351, 222–227. [Google Scholar] [CrossRef]
- Jensen, C.M.; Gross, K. Development of catalytically enhanced sodium aluminum hydride as a hydrogen-storage material. J. Appl. Phys. A: Mater. Sci. Process. 2001, 72, 213–219. [Google Scholar] [CrossRef]
- Morioka, H.; Kakizaki, K.; Chung, S.C.; Yamada, A. Reversible hydrogen decomposition of KAlH4. J. Alloys Compd. 2003, 353, 310–314. [Google Scholar] [CrossRef]
- Pinkerton, F.E.; Meisner, G.P.; Meyer, M.S.; Balogh, M.P.; Kundrat, M.D. Hydrogen desorption exceeding ten weight percent from the new quaternary hydride Li3BN2H8. J. Phys. Chem. B 2005, 109, 6–8. [Google Scholar] [CrossRef] [PubMed]
- Orimo, S.; Fujii, H.; Ikeda, K. Notable hydriding properties of a nanostructured composite material of the Mg2Ni-H system synthesized by reactive mechanical grinding. Acta Mater. 1997, 45, 331–341. [Google Scholar] [CrossRef]
- Zaluska, A.; Zaluski, L.; Strom-Olsen, J.O. Nanocrystalline magnesium for hydrogen storage. J. Alloys Compd. 1999, 288, 217–225. [Google Scholar] [CrossRef]
- Huot, J.; Liang, G.; Schultz, R. Mechanically alloyed metal hydride systems. Appl. Phys. A: Mater. Sci. Process. 2001, 72, 187–195. [Google Scholar] [CrossRef]
- Huot, J.; Pelletier, J.F.; Lurio, L.B.; Sutton, M.; Schulz, R. Investigation of dehydrogenation mechanism of MgH2Nb nanocomposites. J. Alloys Compd. 2003, 348, 319–324. [Google Scholar] [CrossRef]
- Multi-Year Research, Development and Demonstration Plan: Planned Program Activities for 2003: Technical Plan. U.S. Department of Energy. Energy Efficiency and Renewable Energy. Available online at http://www.eere.energy.gov/hydrogenandfuelcells/mypp/pdfs/storage.pdf/ accessed 14 December 2009.
- Service, R.F. Hydrogen Cars: Fad or the Future? Science 2009, 324, 1257–1259. [Google Scholar] [CrossRef] [PubMed]
- Yvon, K.; Fischer, P. Hydrogen in Intermetallic Compounds, Topics in Applied Physics; Schlapbach, L., Ed.; Springer: Berlin, Germany, 1988; p. 87. [Google Scholar]
- Sørby, M.H.; Brinks, H.W.; Fossdal, A.; Thorshaug, K.; Hauback, B.C. The crystal structure and stability of K2NaAlH6. J. Alloys Compd. 2006, 415, 284–287. [Google Scholar] [CrossRef]
- Grove, H.; Brinks, H.W.; Heyn, R.H.; Wu, F.-J.; Opalka, S.M.; Tang, X.; Laube, B.L.; Hauback, B.C. The structure of LiMg(AlD4)3. J. Alloys Compd. 2008, 455, 249–254. [Google Scholar] [CrossRef]
- Ravnsbæk, D.; Filinchuk, Y.; Cerenius, Y.; Jakobsen, H.J.; Besenbacher, F.; Skibsted, J.; Jensen, T.R. A series of mixed-metal borohydrides. Angew. Chem. Int. Ed. 2009, 48, 6659–6663. [Google Scholar] [CrossRef] [PubMed]
- Yvon, K. Encyclopedia of Inorganic Chemistry; King, R.B., Ed.; Wiley: New York, NY, USA, 1994; Volume 3, p. 1401. [Google Scholar]
- Zhang, Q.A.; Nakamura, Y.; Oikawa, K.; Kamiyama, T.; Akiba, E. New alkaline earth aluminum hydride with one-dimensional zigzag chains of [AlH6]: Synthesis and crystal structure of BaAlH5. Inorg. Chem. 2002, 41, 6941–6943. [Google Scholar] [CrossRef] [PubMed]
- Bertheville, B.; Fischer, P.; Yvon, K. High-pressure synthesis and crystal structures of new ternary caesium magnesium hydrides, CsMgH3, Cs4Mg3H10 and Cs2MgH4. J. Alloys Compd. 2002, 330-332, 152–156. [Google Scholar] [CrossRef]
- Zaluska, A.; Zaluski, L. New catalytic complexes for metal hydride systems. J. Alloys Compds. 2005, 404-406, 706–711. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database; Gmelin Institut.: Germany, February 2006.
- Hector, L.G., Jr.; Herbst, J.F. Density functional theory for hydrogen storage materials: Successes and opportunities. J. Phys: Condens. Matter 2008, 20, 064229. [Google Scholar] [CrossRef]
- Skriver, H.L. Crystal structure from one-electron theory. Phys. Rev. B 1985, 31, 1909–1923. [Google Scholar] [CrossRef]
- Söderlind, P.; Eriksson, O.; Johansson, B.; Wills, J.M.; Boring, A.M. A unified picture of the crystal structures of metals. Nature 1995, 374, 524–525. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Fjellvåg, H.; Kjekshus, A. Crystal structure of KAlH4 from first princible calculation. J. Alloys Compd. 2003, 363, L7–L11. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, R558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, S.; Ernzerhof, M. Generalized gradient approximation made simple Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Hauback, B.C.; Brinks, H.W.; Fjellvåg, H. Accurate structure of LiAlD4 studied by combined powder neutron and x-ray diffraction. J. Alloys Comp. 2002, 346, 184–189. [Google Scholar] [CrossRef]
- Belskii, V.K.; Bulychev, B.M.; Golubeva, A.V. The repeated definition of the structure NaAlH4. Acta Crystallogr. Sec. B 1979, 35, 1454–1456. [Google Scholar]
- Vajeeston, P.; Ravindran, P.; Vidya, R.; Fjellvåg, H.; Kjekshus, A. Pressure-induced phase of NaAlH4 : A potential candidate for hydrogen storage? Appl. Phys. Lett. 2003, 82, 2257–2259. [Google Scholar] [CrossRef]
- Soulié, J.P.; Renaudin, G.; Eerny, R.; Yvon, K. Lithium boro-hydride LiBH4: I. Crystal structure. J. Alloys Comp. 2002, 346, 200–205. [Google Scholar] [CrossRef]
- Irodova, A.V.; Somenkov, V.A.; Kurchatovy, I.V.; Bakum, S.I.; Kuznetsova, S.F.; Kurnakov, N.S. Structure of NaGaH4 (D4). Z. Phys. Chem. 1989, 163, 239–242. [Google Scholar] [CrossRef]
- Davis, R.L.; Kennardy, C.H.L. Structure of sodium tetradeuteroborate, NaBD4. J. Solid State Chem. 1985, 59, 393–396. [Google Scholar] [CrossRef]
- Gingl, F.; Yvon, K.; Fischer, P. Strontium magnesium tetrahydride (SrMgH4): A new ternary alkaline earth hydride. J. Alloys Comp. 1992, 187, 105–111. [Google Scholar] [CrossRef]
- Backum, S.I.; Irodova, A.V.; Kuznetsova, S.F.; Lyakhovitskaya, O.I.; Nozik, Y.Z.; Somenkov, V.A. Crystal structure of KGaH4. Russ. J. Coord. Chem. 1990, 16, 1210–1214. [Google Scholar]
- Hauback, B.C.; Brinks, H.W.; Heyn, R.H.; Blom, R.; Fjellvåg, H. The crystal structure of KAlD4. J. Alloys Compd. 2005, 394, 35–38. [Google Scholar] [CrossRef]
- Bastide, J.-P.; Claudy, P.; Letoffe, J.-M.; Hajri, J.E. Preparation and characterization of potassium tetrahydroaluminate (KAlH4). Rev. Chim. Mineral. 1987, 24, 248–263. [Google Scholar]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Crystal structure and high-pressure study of BeH2 from First Princible Calculation. Appl. Phys. Lett. 2004, 84, 34–36. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Pressure-induced structural transitions in MgH2. Phys. Rev. Lett. 2002, 89, 175506. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Ahuja, R. Ab initio prediction of high-pressure structural phase transition in BaH2. J. Alloys Compd. 2007, 446-447, 405–408. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Fjellvåg, H. Novel high pressure phases of β-AlH3 : A density-functional study. Chem. Matt. 2008, 20, 5997–6002. [Google Scholar] [CrossRef]
- Ke, X.; Kuwabara, A.; Tanaka, I. Cubic and orthorhombic structures of aluminum hydride AlH3 predicted by a first-principles study. Phys. Rev. B 2005, 71, 184107. [Google Scholar] [CrossRef]
- Chung, S.; Morioka, H. Thermochemistry and crystal structures of lithium, sodium and potassium alanates as determined by ab initio simulations. J. Alloys Compd. 2004, 372, 92–96. [Google Scholar] [CrossRef]
- Scheicher, R.H.; Kim, D.Y.; Lebègue, S.; Arnaud, B.; Alouani, M.; Ahuja, R. Cubic metallic phase of aluminum hydride showing improved hydrogen desorption. Appl. Phys. Lett. 2008, 92, 201903. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Metallization of aluminum hydride at high pressures: A first-principles study. Phys. Rev. B 2007, 76, 144114. [Google Scholar] [CrossRef]
- Kim, D.Y.; Scheicher, R.H.; Ahuja, R. Dynamical stability of the cubic metallic phase of AlH3 at ambient pressure: Density functional calculations. Phys. Rev. B 2008, 78, 100102(R). [Google Scholar] [CrossRef]
- Kim, E.; Kumar, R.; Weck, P.F.; Cornelius, A.L.; Nicol, M.; Vogel, S.C.; Zhang, J.; Hartl, M.; Stowe, A.C.; Daemen, L.; Zhao, Y. Pressure-driven phase transitions in NaBH4: Theory and experiments. J. Phys. Chem. B 2007, 111, 13873–13876. [Google Scholar] [CrossRef] [PubMed]
- Chellappa, R.S.; Chandra, D.; Somayazulu, M.; Gramsch, S.A.; Hemley, R.J. Pressure-induced phase transitions in LiNH2. J. Phys. Chem. B 2007, 111, 10785–10789. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.; Chen, C.F. Thermodynamic functions and pressure-temperature phase diagram of lithium alanates by ab initio calculations. Phys. Rev. B 2007, 76, 024112. [Google Scholar] [CrossRef]
- Hu, C.H.; Chen, D.M.; Wang, Y.M.; Xu, D.S.; Yang, K. First-principles investigations of the pressure-induced structural transitions in Mg(AlH4)2. J. Phys.: Condens. Matter 2007, 19, 176205. [Google Scholar] [CrossRef] [PubMed]
- Pitt, M.P.; Blanchard, D.; Hauback, B.C.; Fjellvåg, H.; Marshall, W.G. Pressure-induced phase transitions of the LiAlD4 system. Phys. Rev. B 2005, 72, 214113. [Google Scholar] [CrossRef]
- Araujo, C.M.; Ahuja, R.; Talyzin, A.V.; Sundqvist, B. Pressure-induced structural phase transition in NaBH4. Phys. Rev. B 2005, 72, 054125. [Google Scholar] [CrossRef]
- Goncharenko, I.; Eremets, M.I.; Hanfland, M.; Tse, J.S.; Amboage, M.; Yao, Y.; Trojan, I.A. Pressure-induced hydrogen-dominant metallic state in aluminum hydride. Phys. Rev. Lett. 2008, 100, 045504. [Google Scholar] [CrossRef] [PubMed]
- Vajeeston, P.; Ravindran, P.; Vidya, R.; Fjellvåg, H.; Kjekshus, A. Design of potential hydrogen-storage material using first-principle density-functional calculations. Cry. Growth Design 2004, 4, 471–477. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. A huge pressure-induced volume collapse in LiAlH4 and its implications to hydrogen storage. Phys. Rev. B 2003, 68, 212101. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Structural phase stability in Alkali boro-tetrahydrides ABH4 (A = Li, Na, K, Rb, Cs) from first principle calculation. J. Alloys Compd. 2005, 387, 97–104. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. First-principles investigations of aluminum hydrides: M3AlH6 (M = Na, K). Phys. Rev. B 2005, 71, 092103. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. A new series of high hydrogen content complex hydrides predicted from density functional calculations. Appl. Phys. Lett. 2006, 89, 071906. [Google Scholar] [CrossRef]
- Klaveness, A.; Vajeeston, P.; Ravindran, P.; Fjellvåg, H.; Kjekshus, A. Structural prediction and bonding of BAlH5 (B = Be, Ca, Sr) from first-principle calculations. J. Alloys Compd. 2007, 433, 225–232. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Fjellvåg, H. Structural phase stability studies on MBeH3 (M = Li, Na, K, Rb, Cs) from density functional calculations. Inorg. Chem. 2008, 47, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Tse, J.S.; Klug, D.D.; Desgreniers, S.; Smith, J.S.; Flacau, R.; Liu, Z.; Hu, J.; Chen, N.; Jiang, D.T. Structural phase transition in CaH2 at high pressures. Phys. Rev. B 2007, 75, 134108. [Google Scholar] [CrossRef]
- Nakamori, Y.; Miwa, K.; Ninomiya, A.; Li, H.; Ohba, N.; Towata, S.; ZKttel, A.; Orimo, V. Correlation between thermodynamical stabilities of metal borohydrides and cation electronegativites: First-principles calculations and experiments. Phys. Rev. B 2006, 74, 045126. [Google Scholar] [CrossRef]
- Wolverton, C.; Ozolins, V. Hydrogen storage in calcium alanate: First-principles thermodynamics and crystal structures. Phys. Rev. B 2007, 75, 064101. [Google Scholar] [CrossRef]
- Majzoub, E.H.; Ozolin, V. Prototype electrostatic ground state approach to predicting crystal structures of ionic compounds: Application to hydrogen storage materials. Phys. Rev. B 2008, 77, 104115. [Google Scholar] [CrossRef]
- Løvvik, O.M. Crystal structure of Ca(AlH4)2 predicted from density-functional band-structure calculations. Phys. Rev. B 2005, 71, 144111. [Google Scholar] [CrossRef]
- Løvvik, O.M.; Swang, O. Structure and stability of possible new alanates. Europhys. Lett. 2004, 67, 607–613. [Google Scholar] [CrossRef]
- Lodziana, Z.; Vegge, T. Structural stability of complex hydrides: LiBH4 revisited. Phys. Rev. Lett. 2004, 93, 145501. [Google Scholar] [CrossRef] [PubMed]
- Alapati, S.V.; Johnson, J.K.; Sholl, D.S. Identification of destabilized metal hydrides for hydrogen storage using first principles calculations. J. Phys. Chem. B 2006, 110, 8769–8776. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.H.; Oganov, A.R.; Wang, Y.M.; Zhou, H.Y.; Lyakhov, A.; Hafner, J. Crystal structure prediction of LiBeH3 using ab initio total-energy calculations and evolutionary simulations. J. Chem. Phys. 2008, 129, 234105. [Google Scholar] [CrossRef] [PubMed]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. First principles investigations on MMgH3 (M = Li, Na, K, Rb, Cs) hydrides. J. Alloys Compd. 2008, 450, 327–337. [Google Scholar] [CrossRef]
- Blum, V.; Zunger, A. Prediction of ordered structures in the bcc binary systems of Mo, Nb, Ta, and W from first-principles search of approximately 3,000,000 possible configurations. Phys. Rev. B 2005, 72, 020104(R). [Google Scholar] [CrossRef]
- Bush, T.S.; Catlow, C.R.A.; Battle, P.D. Evolutionary programming techniques for predicting inorganic crystal structures. J. Mater. Chem. 1995, 5, 1269–1272. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
- Woodley, S.M. Prediction of crystal structures using evolutionary algorithms and related techniques. Struct. Bonding (Berlin) 2004, 110, 95–132. [Google Scholar]
- Martonak, R.; Laio, A.; Parrinello, M. Predicting crystal structures: The Parrinello-Rahman method revisited. Phys. Rev. Lett. 2003, 90, 075503. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J.; Doye, J.P.K. Global optimization by Basin-Hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Li, Z.; Scheraga, H.A. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef] [PubMed]
- Pannetier, J.; Bassasalsina, J.; Rodriguez-Carvajal, J.; Caignaert, V. Prediction of crystal structures from crystal chemistry rules by simulated annealing. Nature (London) 1990, 346, 343–345. [Google Scholar] [CrossRef]
- Schön, J.C.; Jansen, M. First step towards planning of syntheses in solid-state chemistry: Determination of promising structure candidates by global optimization. Angew. Chem. 1996, 35, 1286–1304. [Google Scholar] [CrossRef]
- Le Bail, A. Inorganic structure prediction with GRINSP. J. Appl. Crystallogr. 2005, 38, 389–395. [Google Scholar] [CrossRef]
- Godecker, S. Minima hopping: An efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys. 2004, 120, 9911–9917. [Google Scholar] [CrossRef] [PubMed]
- Konoplev, V.N.; Bakulina, V.M. Some properties of magnesium borohydride. Izv. Akad. Nauk SSSR Ser. Khim. 1971, 1, 159–161. [Google Scholar] [CrossRef]
- Plešek, J.; Heřmánek, S. Chemistry of boranes IV. Preparation, properties and behavior of magnesium borohydride towards Lewis bases. Collect. Czech. Chem. Commun. 1966, 31, 3845–3858. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Dymova, T.N. Evaluation of the standard enthalpies and isobaric potentials of the formation of certain complex hydrides. Russ. Chem. Bull. 1971, 20, 204–208. [Google Scholar] [CrossRef]
- Sarner, S.F. Propellant Chemistry, 1st ed.; Reinhold Publishing Corporation: New York, NY, USA, 1966. [Google Scholar]
- Charkin, O.P.; Bonaccorsi, R.; Tomasi, J.; Zyubin, A. S.; Gorbik, A.A. Nonempirical calculation of the structure and stability of magnesium borohydride molecules with consideration of the electronic correlation in the Moeller-Plesset 4/6-31G**. Zh. Neorg. Khim. 1987, 32, 2644–2648. [Google Scholar]
- Majzoub, E.H.; Ozolins, V. International Symposium on MetalHydrogen Systems, Maui, HI, USA, October 1-6, 2006; Abstract in MH-2006. p. 12.
- Bonaccorsi, R.; Charkin, O.P.; Tomasi, J. Nonempirical study of the structure and stability of beryllium, magnesium, and calcium borohydrides. Inorg. Chem. 1991, 30, 2964–2969. [Google Scholar] [CrossRef]
- Ozolins, V.; Majzoub, E.H.; Wolverton, C. First-principles prediction of a ground state crystal structure of magnesium borohydride. Phys. Rev. Lett. 2008, 100, 135501. [Google Scholar] [CrossRef] [PubMed]
- Her, J.H.; Stephens, P.W.; Gao, Y.; Soloveichik, G.L.; Rijssenbeek, J.; Andrusb, M.; Zhaob, J.C. Structure of unsolvated magnesium borohydride Mg(BH4)2. Acta Crystallogr. Sect. B 2007, 63, 561–568. [Google Scholar] [CrossRef] [PubMed]
- Cerny, R.; Filinchuk, Y.; Hagemann, H.; Yvon, K. Magnesium borohydride: Synthesis and crystal structure. Angew. Chem. Int. Ed. 2007, 46, 5765–5767. [Google Scholar] [CrossRef] [PubMed]
- Filinchuk, Y.; Černý, R.; Hagemann, H. Insight into Mg(BH4)2 with synchrotron x-ray diffraction: structure revision, crystal chemistry, and anomalous thermal expansion. Chem. Mater. 2009, 21, 925–933. [Google Scholar] [CrossRef]
- Zhou, X.F.; Quan, A.R.; Zhou, J.; Xu, B.; Tian, Y.; Wang, H.R. Crystal structure and stability of magnesium borohydride from first principles. Phys. Rev. B 2009, 79, 212102. [Google Scholar] [CrossRef]
- Brower, F.M.; Matzek, N.E.; Reigler, P.F.; Rinn, H.W.; Roberts, C.B.; Schmidt, D.L.; Snover, J.A.; Terada, K. Preparation and properties of aluminum hydride. J. Am. Chem. Soc. 1976, 98, 2450–2453. [Google Scholar] [CrossRef]
- Schlapbach, L.; Züttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef] [PubMed]
- Turley, J.W.; Rinn, H.W. Crystal structure of aluminum hydride. Inorg. Chem. 1969, 8, 18–22. [Google Scholar] [CrossRef]
- Brinks, H.W.; Istad-Lem, A.; Hauback, B.C. Mechanochemical synthesis and crystal structure of α’-AlD3 and α-AlD3. Phys. Chem. B 2006, 110, 25833–25837. [Google Scholar] [CrossRef] [PubMed]
- Brinks, H.W.; Langley, W.; Jensen, C.M.; Graetz, J.; Reilly, J.J.; Hauback, B.C. Synthesis and crystal structure of β-AlD3. J. Alloys Compd. 2006, 433, 180–183. [Google Scholar] [CrossRef]
- Yartys, V.A.; Denys, R.V.; Maehlen, J.P.; Frommen, C.; Fichtner, M.; Bulychev, B.M.; Emerich, H. Double-bridge bonding of aluminium and hydrogen in the crystal structure of γ-AlH3. Inorg. Chem. 2007, 46, 1051–1055. [Google Scholar] [CrossRef] [PubMed]
- Zogal, O.J.; Vajda, P.; Beuneu, F.; Pietraszko, A. Lattice damage and Al-metal precipitation in 2.5 MeV-electron-irradiated AlH3. Eur. Phys. J. B 1998, 2, 451–456. [Google Scholar] [CrossRef]
- Aguayo, A.; Singh, D.J. Electronic structure of the complex hydride NaAlH4. Phys. Rev. B 2004, 69, 155103. [Google Scholar] [CrossRef]
- Wolverton, C.; Ozolins, V.; Asta, M. Hydrogen in aluminum: First-principles calculations of structure and thermodynamics. Phys. Rev. B 2004, 69, 144109. [Google Scholar] [CrossRef]
- Graetz, J.; Chaudhuri, S.; Lee, Y.; Vogt, T.; Muckerman, J.T.; Reilly, J. Pressure-induced structural and electronic changes in α-AlH3. Phys. Rev. B 2006, 74, 214114. [Google Scholar] [CrossRef]
- Baranowski, B.; Hochheimer, H.D.; Strossner, K.; Honle, W. High pressure x-ray investigation of AlH3 and Al at room temperature. J. Less-Common Met. 1985, 113, 341–347. [Google Scholar] [CrossRef]
- Goncharenko, I.N.; Glazkov, V.P.; Irodova, A.V.; Somenkov, V.A. Neutron diffraction study of crystal structure and equation of state AlD3 up to the pressure of 7.2 GPa. Physica B 1991, 174, 117–120. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Lattice dynamic study on AlH3 polymorphs. Unpublished work.
- Dubrovinsky, L.S.; Dubrovinskaia, N.A.; Swamy, V.; Muscat, J.; Harrison, N.M.; Ahuja, R.; Holm, B.; Johansson, B. Materials science: The hardest known oxide. Nature 2001, 410, 653–654. [Google Scholar] [CrossRef] [PubMed]
- Dubrovinskaia, N.A.; Dubrovinsky, L.S.; Ahuja, R.; Prokopenko, V.B.; Dmitriev, V.; Weber, J.P.; Osirio- Guillen, J.M.; Johanson, B. Experimental and theoretical identification of a new high-pressure TiO2 polymorph. Phys. Rev. Lett. 2001, 87, 275501. [Google Scholar] [CrossRef] [PubMed]
- The Metal-Hydrogen System—Basic Bulk Properties; Fukai, Y. (Ed.) Springer-Verlag: Berlin, Germany, 1993.
- Griessen, R.; Riesterer, T. Hydrogen in Intermetallic Compounds I; Schlapbach, L., Ed.; Springer: Berlin, Germany, 1988; Volume 63, Topics Appl. Phys.; p. 219. [Google Scholar]
- Bogdanovic, B.; Bohmhammel, K.; Christ, B.; Reiser, A.; Schlichte, K.; Vehlen, R.; Wolf, U. Thermodynamic investigation of the magnesiumhydrogen system. J. Alloys Compd. 1999, 282, 84–82. [Google Scholar] [CrossRef]
- Liang, G.; Huot, J.; Boily, S.; Van Neste, A.; Schulz, R. Catalytic effect of transition metals on hydrogen sorption in nanocrystalline ball milled MgH2 Tm (Tm = Ti, V, Mn, Fe and Ni) systems. J. Alloys Compd. 1999, 292, 247–252. [Google Scholar] [CrossRef]
- Khrussanova, M.; Grigorova, E.; Mitov, I.; Radev, D.; Peshev, P. Hydrogen sorption properties of an MgTiVFe nanocomposite obtained by mechanical alloying. J. Alloys Compd. 2001, 327, 230–334. [Google Scholar] [CrossRef]
- Robert, S.; Strom-Olsen, J.; Zaluski, L.; Alicja, Z. Nanocrystalline Mg or Be-based materials and use thereof for the transportation and storage of hydrogen. U.S. Pat. 5,964,965, 12 October 1999. [Google Scholar]
- NIST-JANAF Thermochemical Tables; Chase, M.W. (Ed.) American Institute of Physics: Woodbury, NY, USA, 1998; J. Phys. Chem. Ref. Data Monogr., No. 9.
- Zaluska, A.; Zaluski, L.; Ström-Olsen, J.O. Structure, catalysis and atomic reactions on the nano-scale: A systematic approach to metal hydrides for hydrogen storage. Appl. Phys. A: Mater. Sci. Process. 2001, 72, 157–165. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Hauback, B.C.; Fjellvåg, H.; Kjekshus, A.; Furuseth, S.; Hanfland, M. Structural stability and pressure-induced phase transitions in MgH2. Phys. Rev. B 2006, 73, 224102. [Google Scholar] [CrossRef]
- Bastide, J.P.; Bonnetot, B.; Letoffe, J.M.; Claudy, P. Polymorphisme de l’hydrure de magnesium sous haute pression. Mat. Res. Bull. 1980, 15, 1215–1224. [Google Scholar] [CrossRef]
- Zachariasen, W.H.; Holley, C.E.; Stamper, J.F. The crystal and molecular structure of bis-biuret-zinc chloride. Acta Cryst. A 1963, 16, 352. [Google Scholar] [CrossRef]
- Bortz, M.; Bertheville, B.; Bøttger, G.; Yvon, K. Structure of the high pressure phase γ-MgH2 by neutron powder diffraction. J. Alloys Compd. 1999, 287, L4–L6. [Google Scholar] [CrossRef]
- Kyoi, D.; Sato, T.; Rönnebro, E.; Kitamura, N.; Ueda, A.; Ito, M.; Katsuyama, S.; Hara, S.; Noréus, D.; Sakai, T. A new ternary magnesiumtitanium hydride Mg7TiHx with hydrogen desorption properties better than both binary magnesium and titanium hydrides. J. Alloys Compd. 2004, 372, 213–217. [Google Scholar] [CrossRef]
- Kyoi, D.; Sato, T.; Rönnebro, E.; Tsuji, Y.; Kitamura, N.; Ueda, A.; Ito, M.; Katsuyama, S.; Hara, S.; Noréus, D.; Sakai, T. A novel magnesiumvanadium hydride synthesized by a gigapascal-high-pressure technique. J. Alloys Compd. 2004, 375, 253. [Google Scholar] [CrossRef]
- Kyoi, D.; Kitamura, N.; Tanaka, H.; Ueda, A.; Tanase, S.; Sakai, T. Hydrogen desorption properties of FCC super-lattice hydride Mg7NbHx prepared by ultra-high pressure techniques. J. Alloys Compd. 2007, 428, 268–273. [Google Scholar] [CrossRef]
- Kyoi, D.; Sakai, T.; Kitamura, N.; Tanaka, H.; Ueda, A.; Tanase, S. Synthesis of FCC MgTa hydrides using GPa hydrogen pressure method and their hydrogen-desorption properties. J. Alloys Compd. 2008, 463, 306–310. [Google Scholar] [CrossRef]
- Rönnebro, E.; Kyoi, D.; Kitano, A.; Kitano, Y.; Sakai, T. Hydrogen sites analysed by x-ray synchrotron diffraction, in Mg7TiH1316 made at gigapascal high-pressures. J. Alloys Compd. 2005, 404-406, 68–72. [Google Scholar] [CrossRef]
- Sato, T.; Kyoi, D.; Rönnebro, E.; Kitamura, N.; Sakai, T.; Noréus, D. Structural investigations of two new ternary magnesiumniobium hydrides, Mg6.5NbH∼14 and MgNb2H∼4. J. Alloys Compd. 2006, 417, 230–234. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an-open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vajeeston, P.; Ravindran, P.; Fjellvåg, H. Predicting New Materials for Hydrogen Storage Application. Materials 2009, 2, 2296-2318. https://doi.org/10.3390/ma2042296
Vajeeston P, Ravindran P, Fjellvåg H. Predicting New Materials for Hydrogen Storage Application. Materials. 2009; 2(4):2296-2318. https://doi.org/10.3390/ma2042296
Chicago/Turabian StyleVajeeston, Ponniah, Ponniah Ravindran, and Helmer Fjellvåg. 2009. "Predicting New Materials for Hydrogen Storage Application" Materials 2, no. 4: 2296-2318. https://doi.org/10.3390/ma2042296
APA StyleVajeeston, P., Ravindran, P., & Fjellvåg, H. (2009). Predicting New Materials for Hydrogen Storage Application. Materials, 2(4), 2296-2318. https://doi.org/10.3390/ma2042296