Flexural Behavior of Engineered Cementitious Composites (ECC) Slabs with Different Strength Grades
Abstract
1. Introduction
2. Experimental Program
2.1. Slab Specimen Design
2.2. Test Specimen Casting and Instrumentation
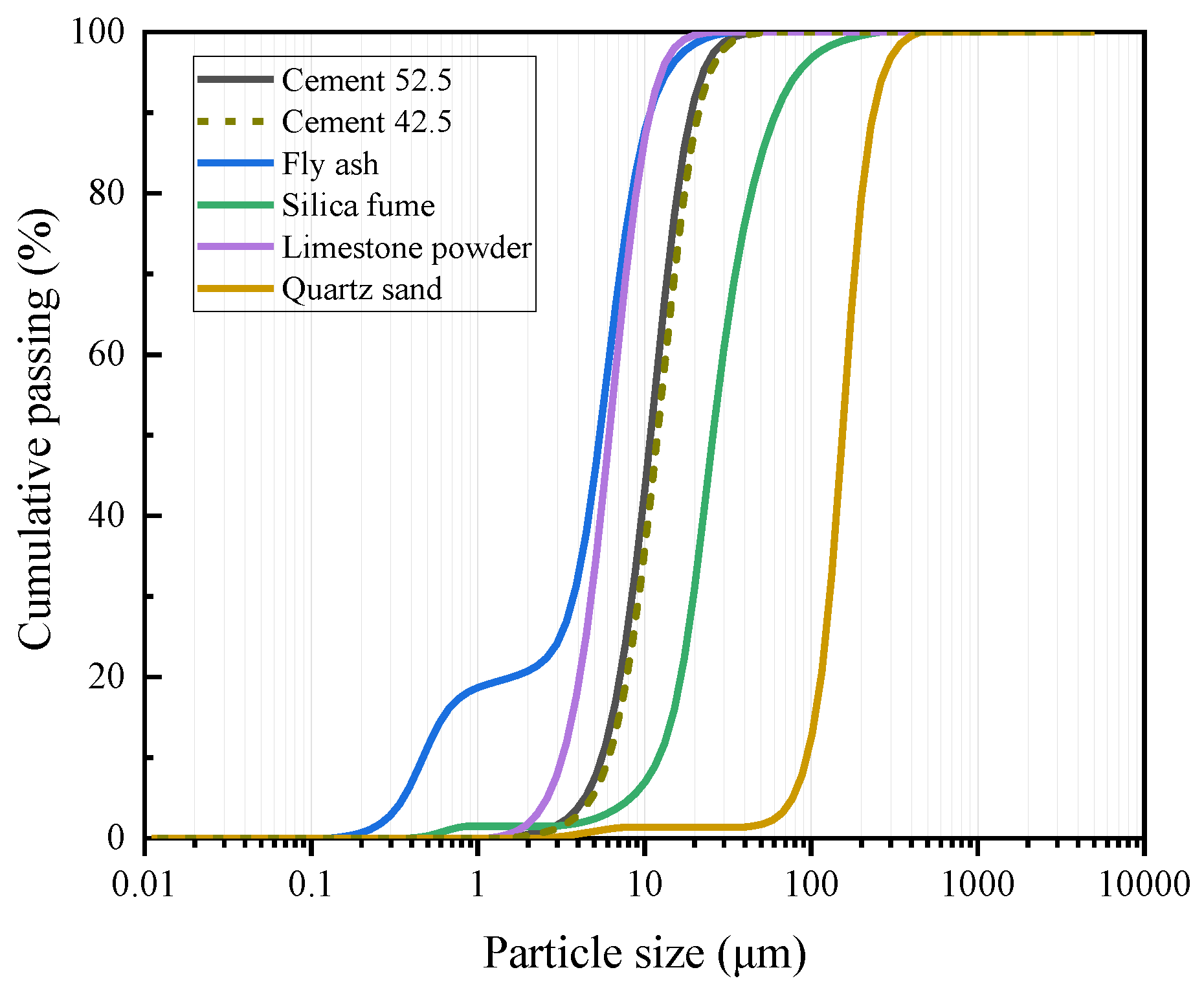
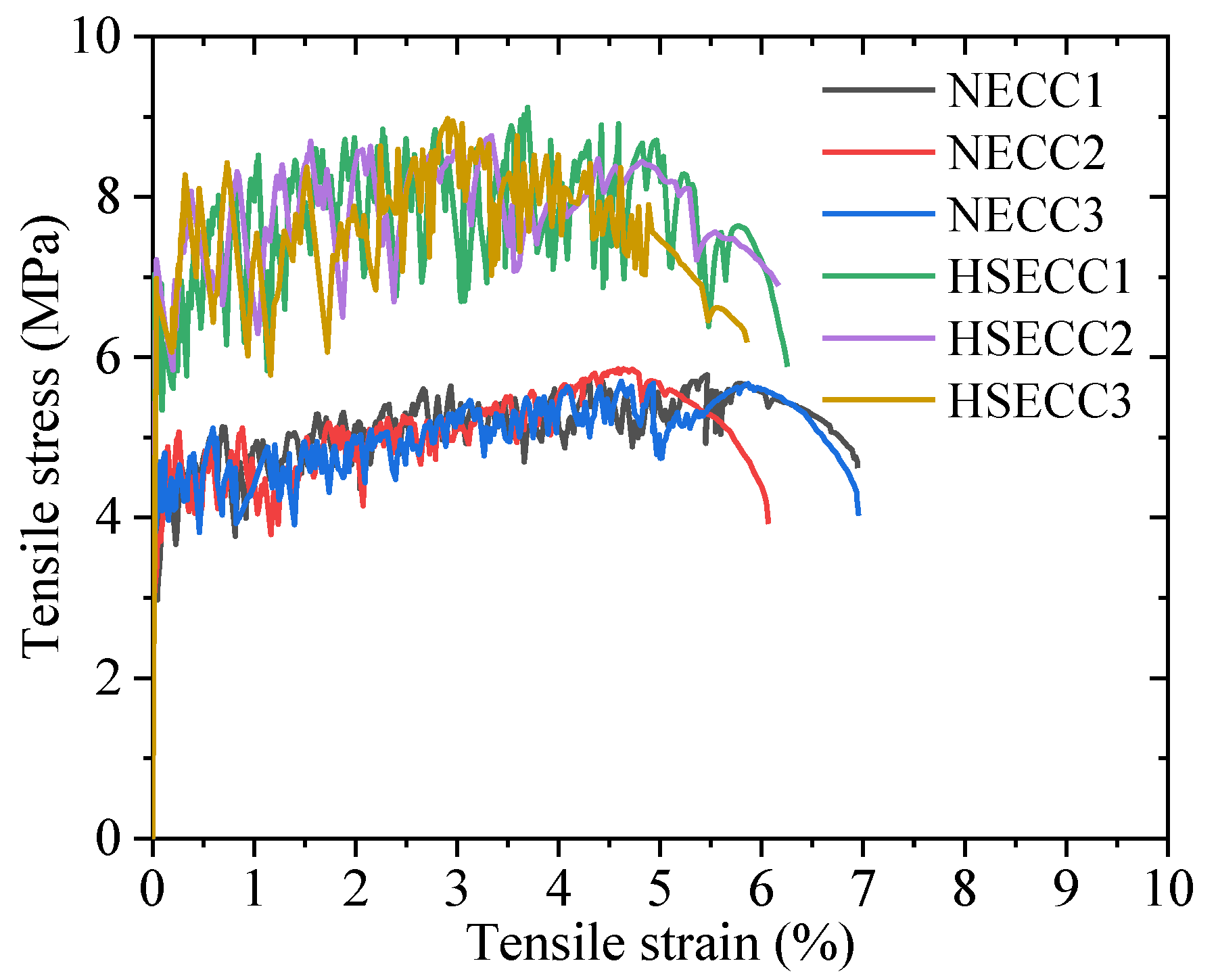
2.3. Material Properties
3. Experimental Results and Discussion
3.1. Crack Distribution and Failure Mode
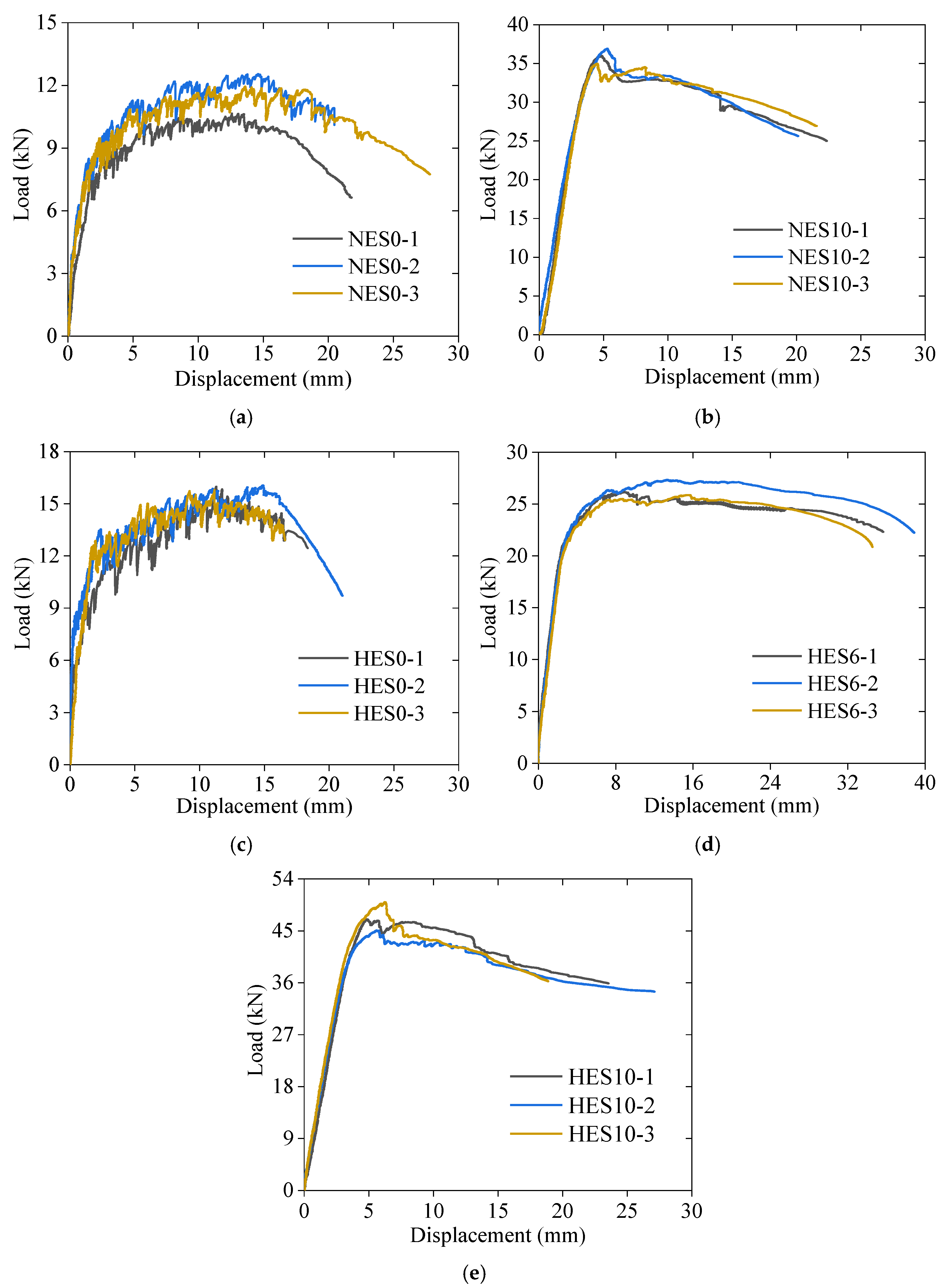
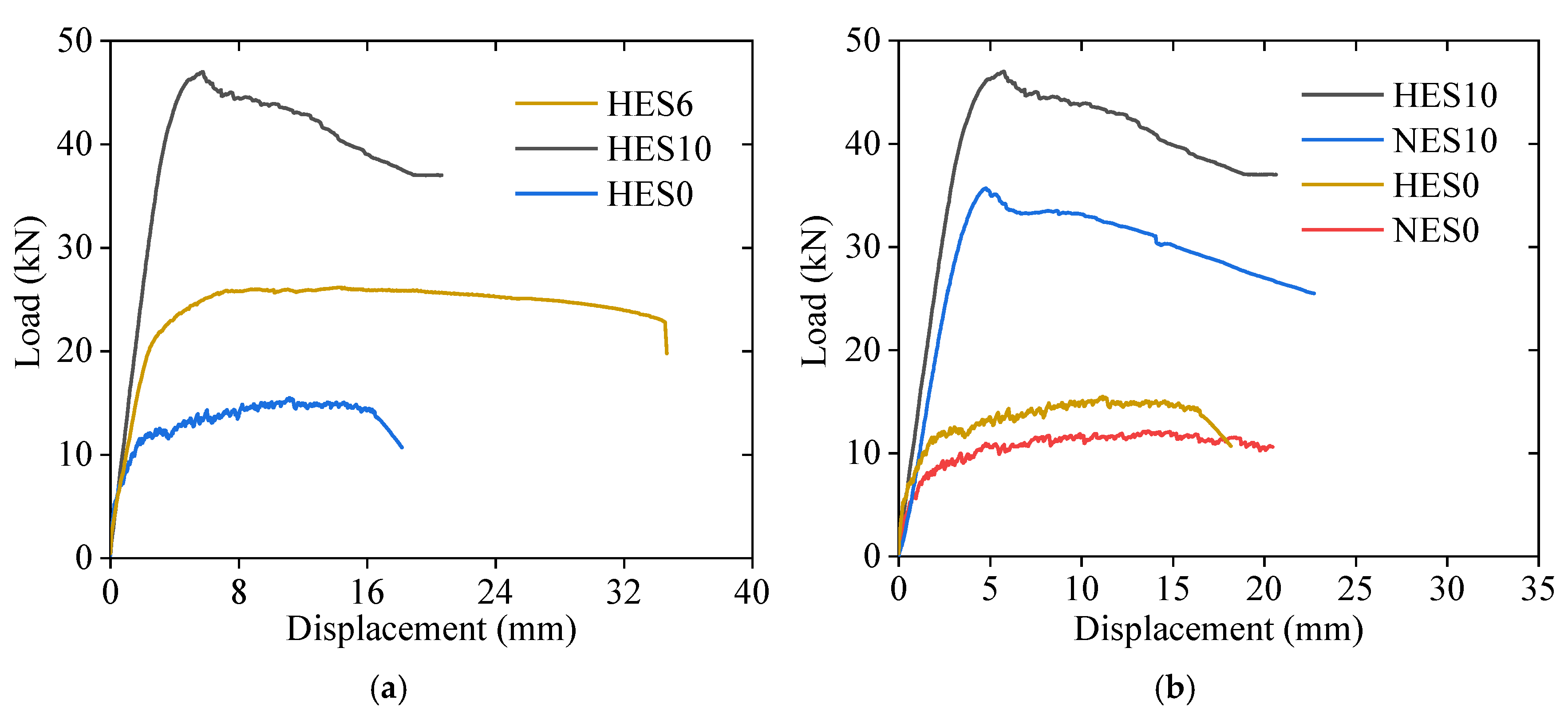
3.2. Load–Displacement Relationship
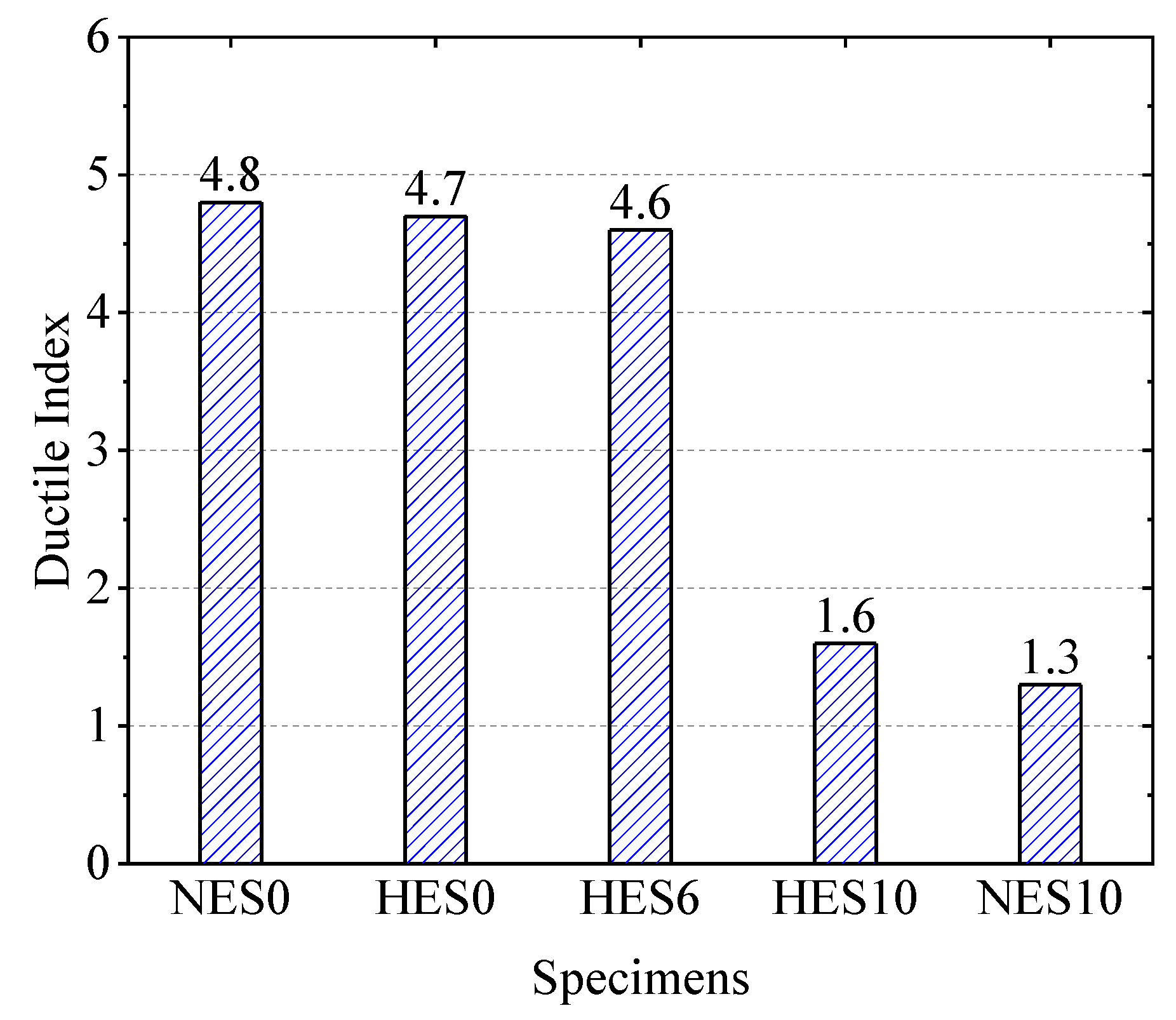
3.3. Ductility Analysis of Slabs
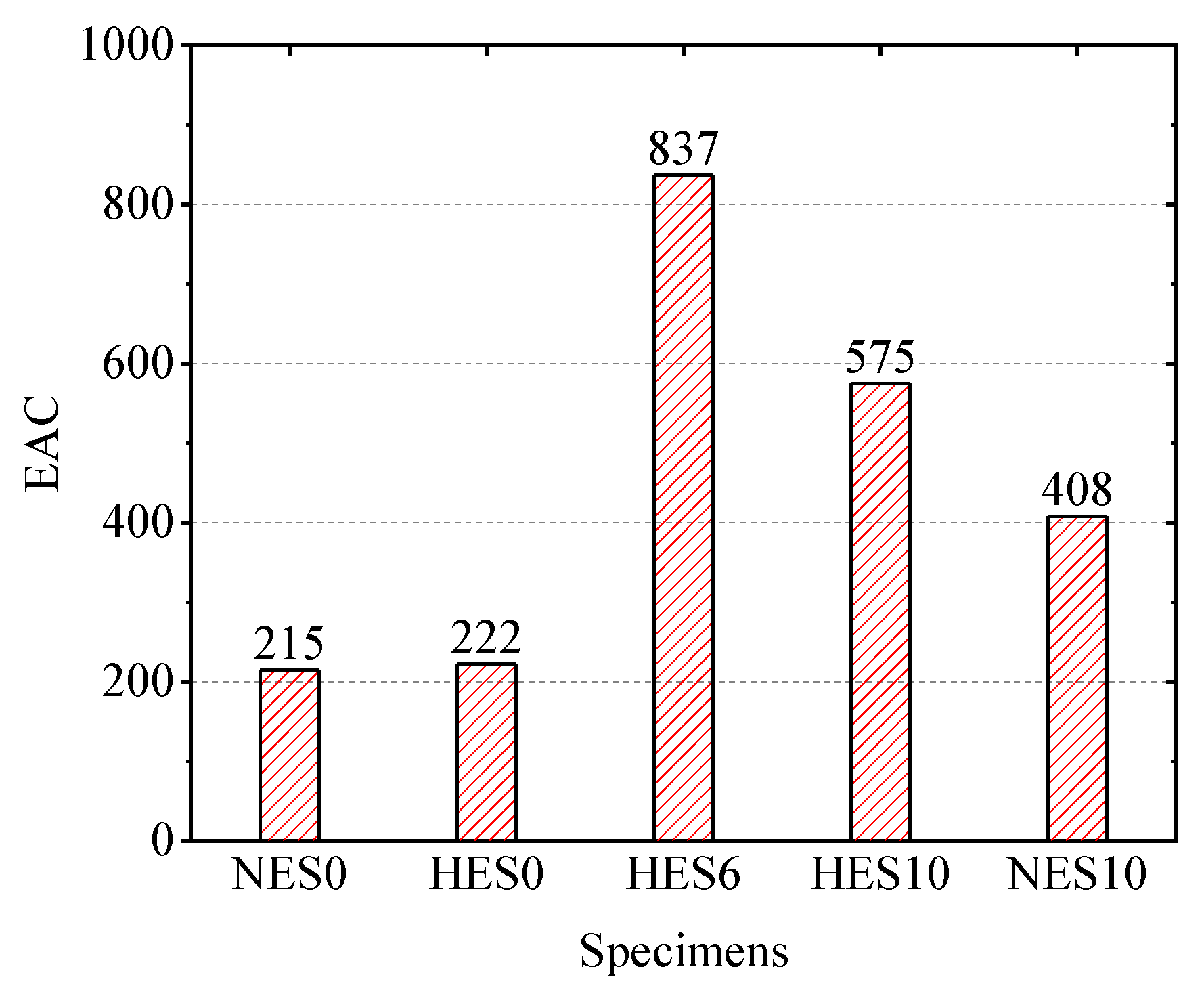
3.4. Energy Absorption Capacity
3.5. Load–Strain Relationship
4. Simplified Method for Prediction of Flexural Capacity
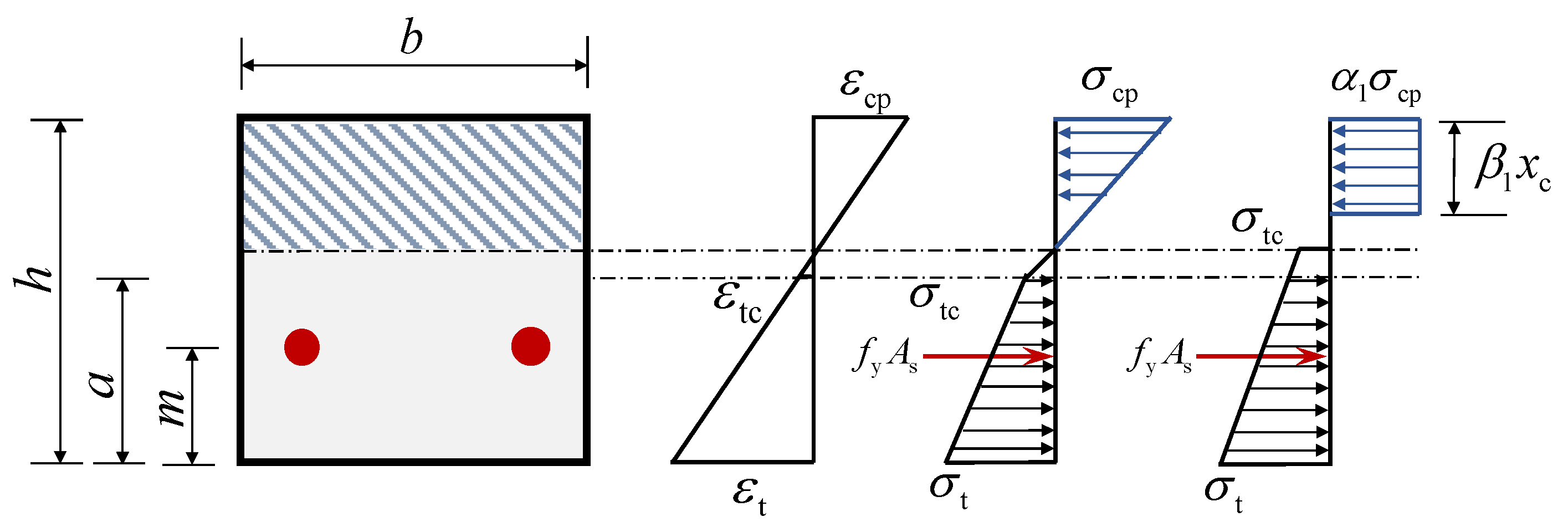
4.1. Fundamental Assumptions
- Cross-sections perpendicular to the axis of the ECC slab, which remain planar after flexural deformation and are perpendicular to the axis of the deformed slab;
- Deformation coordination (a good bond between the ECC slab and reinforcement during loading);
- Considering the strain-hardening behavior of ECC after cracking, i.e., the ECC in the cracked area can still withstand a certain amount of tension;
- Not considering the effect of shrinkage creep of the ECC material.
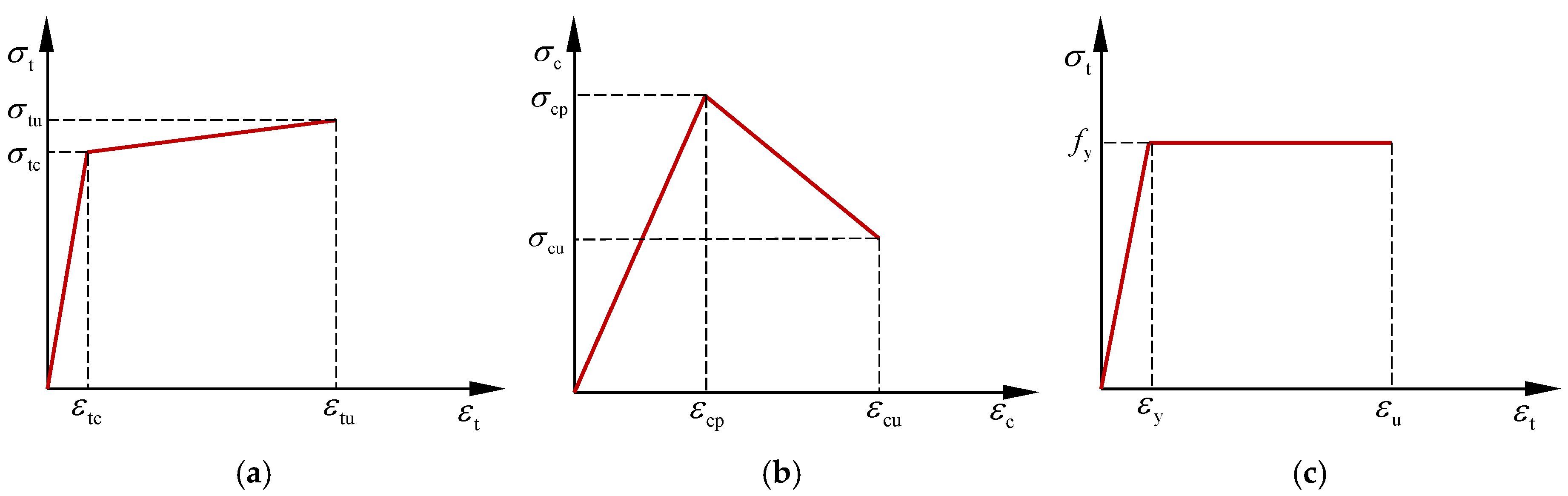
4.2. Material Constitutive Model
4.3. Simplified Calculation Method
5. Conclusions
- 1.
- ECC slabs subjected to flexural deformation are characterized by multi-seam cracking and large displacement before the loss of the load-carrying capacity, which can improve the safety of the structure. In addition, harmful cracks in ECC slabs can be reduced because ECC can control the crack width well. This advantage helps to prevent the corrosion of steel bars in ECC slabs, thus improving the durability of steel-reinforced ECC members.
- 2.
- ECC slabs reinforced with steel bars can significantly improve their flexural capacity and EAC, but the ductility decreases as the reinforcement ratio increases. The flexural capacity of HES6 and HES10 is 69% and 203% higher than that of HES0, respectively. However, the ductility of HES10 is only 34% of that of HES0. Therefore, when designing ECC slabs, an appropriate reinforcement ratio should be chosen to fully leverage the combined performance of the ECC and reinforcement.
- 3.
- With the increase in the ECC strength, the bearing capacity of the ECC slab also increases, but the ductility is almost unaffected. The HSECC has higher compressive and tensile strength compared with the NECC, so it can improve the load-carrying capacity of ECC slabs. The load-carrying capacity of HES0 slabs increases by 28% compared with NES0 slabs, and the load-carrying capacity of HES10 slabs increases by 32% compared with NES10 slabs.
- 4.
- Using the equilibrium condition between the axial force and flexural moment, a simplified method for the prediction of the flexural capacity of ECC slabs is developed. The average predicted-to-experimental ratio is 1.003, with a coefficient of variation of 0.08. This method can serve as a guide for the bending design of ECC slabs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo-strain-hardening fibre reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). Mater. J. 2001, 98, 483–492. [Google Scholar] [CrossRef]
- Men, P.; Chen, F.; Qin, F.; Peng, X.; Di, J.; Jiao, H. Behavior of composite beams with UHPC-concrete composite slabs under negative bending moment. J. Constr. Steel Res. 2025, 227, 109415. [Google Scholar] [CrossRef]
- Men, P.; Ho, H.; Li, T.; Wang, X.; Chung, K.; Zhou, X. Experimental assessment on structural behaviour of short concrete-filled S690 steel tubes. J. Constr. Steel Res. 2025, 227, 109325. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Z.; Wang, S.; Abdalla, J.A.; Hawileh, R.A.; Zhong, J.; Zeng, G. Microstructure and mechanical properties of engineered cementitious composites (ECC) with recycling extracted titanium tailing slag (ETTS). J. Build. Eng. 2024, 98, 111282. [Google Scholar] [CrossRef]
- Men, P.; Wang, X.M.; Liu, D.; Zhang, Z.; Zhang, Q.; Lu, Y. On use of polyvinylpyrrolidone to modify polyethylene fibers for improving tensile properties of high strength ECC. Constr. Build. Mater. 2024, 417, 135354. [Google Scholar] [CrossRef]
- Li, V.C.; Wu, C.; Wang, S.; Ogawa, A.; Saito, T. Interface tailoring for strain-hardening polyvinyl alcohol-engineered cementitious composite (PVA-ECC). Mater. J. 2002, 99, 463–472. [Google Scholar]
- Zhang, Z.; Abdalla, J.A.; Yu, J.Q.; Chen, Y.C.; Hawileh, R.A.; Mahmoudi, F. Use of polypropylene fibers to mitigate spalling in high strength PE-ECC under elevated temperature. Case Stud. Constr. Mater. 2025, 22, e04381. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Li, V.; Su, H.; Gu, C. Durability study on engineered cementitious composites (ECC) under sulfate and chloride environment. Constr. Build. Mater. 2017, 133, 171–181. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Li, V.C. Multiple-scale investigations on self-healing induced mechanical property recovery of ECC. Cem. Concr. Compos. 2019, 103, 293–302. [Google Scholar] [CrossRef]
- Qin, F.; Zhang, Z.; Yin, Z.; Di, J.; Xu, L.; Xu, X. Use of high strength, high ductility engineered cementitious composites (ECC) to enhance the flexural performance of reinforced concrete beams. J. Build. Eng. 2020, 32, 101746. [Google Scholar] [CrossRef]
- Qin, F.; Wei, X.; Lu, Y.; Zhang, Z.; Di, J.; Yin, Z. Flexural behaviour of high strength engineered cementitious composites (ECC)-reinforced concrete composite beams. Case Stud. Constr. Mater. 2023, 18, e02002. [Google Scholar] [CrossRef]
- Wei, X.; Li, X.; Di, J.; Qin, F.; Zhang, Z.; Liang, F. Flexural performance of U-shaped high-strength ECC permanent formwork-concrete composite beams. Structures 2025, 74, 108641. [Google Scholar] [CrossRef]
- Singh, S.B.; Sivasubramanian, M.V. Flexural response of ECC strengthened reinforced concrete beams. Indian Concr. J. 2013, 87, 35–44. [Google Scholar]
- Yang, X.; Gao, W.Y.; Dai, J.G.; Lu, Z.D.; Yu, K.Q. Flexural strengthening of RC beams with CFRP grid-reinforced ECC matrix. Compos. Struct. 2018, 189, 9–26. [Google Scholar] [CrossRef]
- Ismail, M.K.; Abdelaleem, B.H.; Hassan, A.A. Effect of fiber type on the behavior of cementitious composite beam-column joints under reversed cyclic loading. Constr. Build. Mater. 2018, 186, 969–977. [Google Scholar] [CrossRef]
- Gencturk, B.; Elnashai, A.S.; Lepech, M.D.; Billington, S. Behavior of concrete and ECC structures under simulated earthquake motion. J. Struct. Eng. 2013, 139, 389–399. [Google Scholar] [CrossRef]
- Fan, J.; Gou, S.; Ding, R.; Zhang, J.; Shi, Z. Experimental and analytical research on the flexural behaviour of steel–ECC composite beams under negative bending moments. Eng. Struct. 2020, 210, 110309. [Google Scholar] [CrossRef]
- Guan, Y.; Wu, J.; Sun, R.; Zhang, H.; Hu, Y.; Wang, F. Transverse flexural behaviour of steel-engineering cementitious composites (ECC) composite deck under negative and positive bending forces. KSCE J. Civ. Eng. 2021, 25, 2962–2973. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Qian, W.; Chen, Y.; Li, K.; Zhu, J. Flexural behaviour of ECC slabs reinforced with high-strength stainless steel wire rope. Proc. Inst. Civ. Eng.-Struct. Build. 2023, 177, 410–426. [Google Scholar] [CrossRef]
- Ding, Y.; Yu, K.Q.; Yu, J.T.; Xu, S.L. Structural behaviors of ultra-high performance engineered cementitious composites (UHP-ECC) beams subjected to bending-experimental study. Constr. Build. Mater. 2018, 177, 102–115. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Flexural performance of steel-reinforced engineered cementitious composites with different reinforcing ratios and steel types. Constr. Build. Mater. 2020, 231, 117159. [Google Scholar] [CrossRef]
- Xu, S.; Hou, L.; Zhang, X. Flexural and shear behaviors of reinforced ultrahigh toughness cementitious composite beams without web reinforcement under concentrated load. Eng. Struct. 2012, 39, 176–186. [Google Scholar] [CrossRef]
- Yuan, F.; Pan, J.; Wu, Y. Numerical study on flexural behaviors of steel reinforced engineered cementitious composite (ECC) and ECC/concrete composite beams. Sci. China Technol. Sci. 2014, 57, 637–645. [Google Scholar] [CrossRef]
- Liao, Q.; Li, L.; Li, B.; Yu, J. Prediction on the flexural deflection of ultra-high strength rebar reinforced ECC beams at service loads. Structures 2021, 33, 246–258. [Google Scholar] [CrossRef]
- Georgiou, A.V.; Pantazopoulou, S.J. Flexural capacity of reinforced strain-hardening cementitious composite beams: Experimental results and analysis. J. Struct. Eng. 2018, 144, 04018214. [Google Scholar] [CrossRef]
- Ge, W.; Song, W.; Ashour, A.F.; Lu, W.; Cao, D. Flexural performance of FRP/steel hybrid reinforced engineered cementitious composite beams. J. Build. Eng. 2020, 31, 101329. [Google Scholar] [CrossRef]
- Shanour, A.S.; Said, M.; Arafa, A.I.; Maher, A. Flexural performance of concrete beams containing engineered cementitious composites. Constr. Build. Mater. 2018, 180, 23–34. [Google Scholar] [CrossRef]
- Meng, D.; Huang, T.; Zhang, Y.X.; Lee, C.K. Mechanical behaviour of a polyvinyl alcohol fibre reinforced engineered cementitious composite (PVA-ECC) using local ingredients. Constr. Build. Mater. 2017, 141, 259–270. [Google Scholar] [CrossRef]
- Li, V.C.; Lepech, M.D.; Li, M. Field Demonstration of Durable Link Slabs for Jointless Bridge DECKS Based on Strain-Hardening Cementitious Composites Research Report No. RC-1471; Michigan State University: East Lansing, MI, USA, 2005. [Google Scholar]
- Lepech, M.D.; Li, V.C. Application of ECC for bridge deck link slabs. Mater. Struct. 2009, 42, 1185–1195. [Google Scholar] [CrossRef]
- Chu, K.; Hossain, K.M.A.; Lachemi, M. Static and fatigue behaviour of ECC link slabs in reinforced concrete girder joint-free bridges. Structures 2022, 41, 1301–1310. [Google Scholar] [CrossRef]
- Ghatrehsamani, S.G. Structural Performance of Link Slabs Subjected to Monotonic and Fatigue Loading Incorporating Engineered Cementitious Composites; Civil Engineering Department, Ryerson University: Toronto, ON, Canada, 2015. [Google Scholar]
- Anwar Hossain, K.M.; Chu, K.; Lachemi, M. Fatigue performance of ECC link slab incorporated full RC girder joint-free bridges. Adv. Bridge Eng. 2024, 5, 5. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Zhang, Z.; Liu, D.; Abdalla, J.A.; Hawileh, R.A.; Qin, F.; Xu, X. Flexural behavior of reinforced concrete beams externally strengthened with ECC and FRP grid reinforcement. Constr. Build. Mater. 2024, 446, 137964. [Google Scholar] [CrossRef]
- Frías, M.; Moreno de los Reyes, A.M.; Villar-Cociña, E.; García, R.; Vigil de la Villa, R.; Vasić, M.V. New eco-cements made with marabou weed biomass ash. Materials 2024, 17, 5012. [Google Scholar] [CrossRef] [PubMed]
- Said, S.H.; Razak, H.A.; Othman, I. Flexural behavior of engineered cementitious composite (ECC) slabs with polyvinyl alcohol fibers. Constr. Build. Mater. 2015, 75, 176–188. [Google Scholar] [CrossRef]
- Feng, P.; Qiang, H.L.; Ye, L.P. Definition and discussion of “yield point” for materials, members and structures. Eng. Mech. 2017, 34, 36–46. (In Chinese) [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Gopalaratnam, V.S.; Gettu, R. On the characterization of flexural toughness in fiber reinforced concretes. Cem. Concr. Compos. 1995, 17, 239–254. [Google Scholar] [CrossRef]
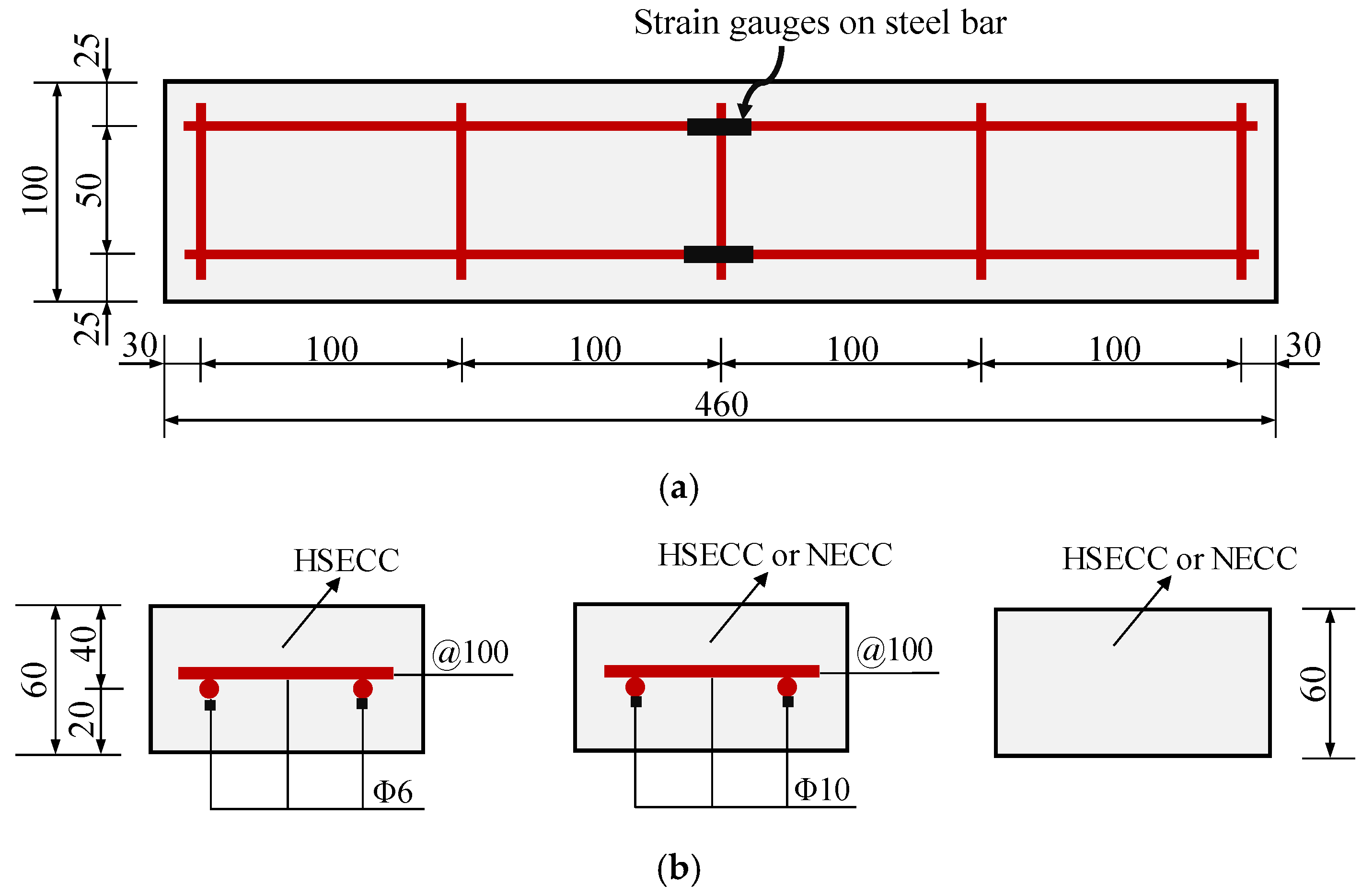
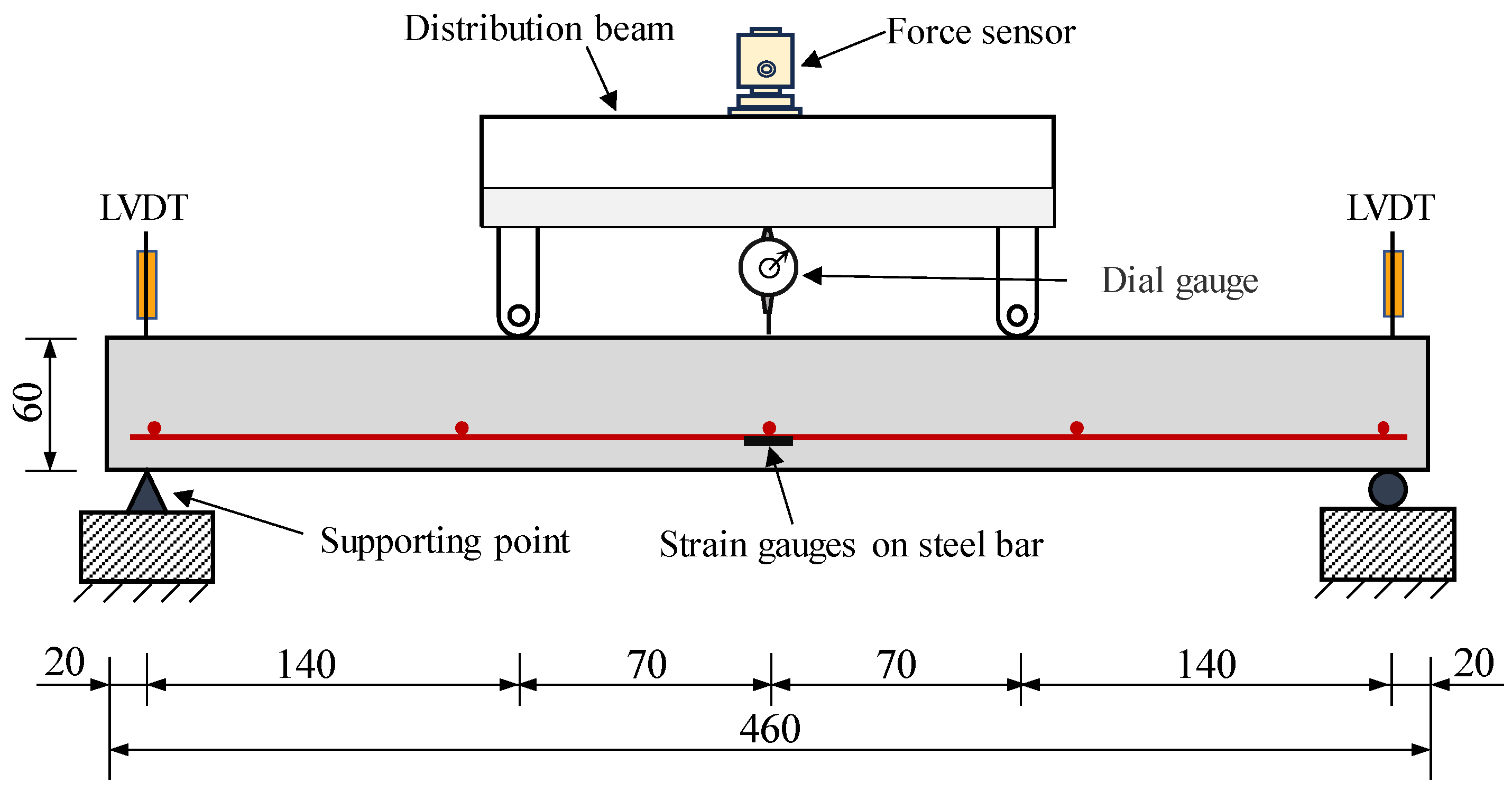






| Specimen | Type of ECC | Main Steel Bars | Reinforcement Ratio | Specimen Number |
|---|---|---|---|---|
| NES0 | N-ECC | / | 0 | 3 |
| NES10 | N-ECC | 2Φ10 | 2.85% | 3 |
| HES0 | HS-ECC | / | 0 | 3 |
| HES6 | HS-ECC | 2Φ6 | 1.02% | 3 |
| HES10 | HS-ECC | 2Φ10 | 2.85% | 3 |
| Mix Ratio | CEM-52.5 | CEM-42.5 | Fly Ash | Silica Fume | Limestone Powder | Quartz Sand | Water | Water Reducer | Fiber |
|---|---|---|---|---|---|---|---|---|---|
| NECC | 0 | 475 | 827 | 0 | 0 | 384 | 354 | 6 | 18 |
| HSECC | 750.4 | 0 | 401.2 | 84.9 | 194.5 | 461 | 260 | 17 | 22 |
| Length (mm) | Fiber Diameter (µm) | Modulus (GPa) | Density (g/cm3) | Elongation (%) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| 12 | 26 | 100 | 0.97 | 2.4 | 3000 |
| Material | CaO | Al2O3 | SiO2 | SO3 | Fe2O3 | MgO | CaCO3 | LOI |
|---|---|---|---|---|---|---|---|---|
| Cement 52.5 | 64.78 | 5.29 | 18.86 | 3.05 | 2.01 | 3.05 | 0.00 | 2.96 |
| Cement 42.5 | 62.6 | 5.76 | 20.57 | 3.02 | 2.05 | 3.00 | 0.00 | 3.00 |
| SF | 0.52 | 0.36 | 97.28 | 0.38 | 0.12 | 0.37 | 0.00 | 0.97 |
| FA | 9.19 | 25.78 | 42.30 | 2.06 | 9.14 | 3.79 | 0.00 | 7.74 |
| LP | 0.00 | 0.00 | 2.31 | 0.00 | 0.00 | 0.00 | 97.61 | 0.00 |
| Material | Elasticity Modulus | Compressive Strength | Crack Strength | Tensile Strength | Ultimate Tensile Strain |
|---|---|---|---|---|---|
| NECC | 22,200 | 56.2 | 4.3 | 5.6 | 0.06 |
| HSECC | 26,100 | 73.1 | 6.9 | 8.3 | 0.04 |
| Material | Diameter (mm) | Elasticity Modulus | Yield Strength | Tensile Strength |
|---|---|---|---|---|
| HRB400 | 6 | 206,000 | 454 | 665 |
| HRB400 | 10 | 206,000 | 463 | 673 |
| Specimen | (kN) | (kN) | (mm) | (kN) | (mm) | μ | EAC |
|---|---|---|---|---|---|---|---|
| HES0 | 5.85 | 11.8 | 2.4 | 15.5 | 11.2 | 4.7 | 222 |
| HES6 | 5.11 | 21.9 | 3.1 | 26.2 | 14.3 | 4.6 | 837 |
| HES10 | 5.57 | 41.9 | 3.7 | 47 | 5.8 | 1.6 | 575 |
| NES0 | 3.51 | 9.2 | 3.1 | 12.1 | 14.8 | 4.8 | 215 |
| NES10 | 3.98 | 32.8 | 3.8 | 35.6 | 4.8 | 1.3 | 408 |
| Material | (10−6) | (10−8) | ||||||
|---|---|---|---|---|---|---|---|---|
| HSECC | 26,100 | 6.9 | 8.3 | 0.04 | 73.1 | 2832 | 36.6 | 4548 |
| NECC | 22,200 | 4.3 | 5.6 | 0.06 | 52.6 | 2687 | 26.3 | 4931 |
| Specimen | Fu,th | Fu,ex | Fu,th/Fu,ex |
|---|---|---|---|
| HES0 | 16.9 | 15.5 | 1.09 |
| HES6 | 27.4 | 26.2 | 1.05 |
| HES10 | 44.0 | 47.0 | 0.94 |
| NES0 | 11.0 | 12.1 | 0.91 |
| NES10 | 36.0 | 35.6 | 1.01 |
| Average | 0.999 | ||
| COV | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, F.; Han, Y.; Wei, X.; Wang, X.; Zhang, Z.; Zhang, X. Flexural Behavior of Engineered Cementitious Composites (ECC) Slabs with Different Strength Grades. Materials 2025, 18, 2047. https://doi.org/10.3390/ma18092047
Qin F, Han Y, Wei X, Wang X, Zhang Z, Zhang X. Flexural Behavior of Engineered Cementitious Composites (ECC) Slabs with Different Strength Grades. Materials. 2025; 18(9):2047. https://doi.org/10.3390/ma18092047
Chicago/Turabian StyleQin, Fengjiang, Yang Han, Xinyan Wei, Xuejun Wang, Zhigang Zhang, and Xiaoyue Zhang. 2025. "Flexural Behavior of Engineered Cementitious Composites (ECC) Slabs with Different Strength Grades" Materials 18, no. 9: 2047. https://doi.org/10.3390/ma18092047
APA StyleQin, F., Han, Y., Wei, X., Wang, X., Zhang, Z., & Zhang, X. (2025). Flexural Behavior of Engineered Cementitious Composites (ECC) Slabs with Different Strength Grades. Materials, 18(9), 2047. https://doi.org/10.3390/ma18092047








