Co-Doping Effects on the Electronic and Optical Properties of β-Ga2O3: A First-Principles Investigation
Abstract
1. Introduction
2. Theoretical Method
2.1. Structural Model
2.2. Calculated Method
3. Results and Discussion
3.1. Crystal Structure and Formation Energy Analysis
3.2. Electronic Properties
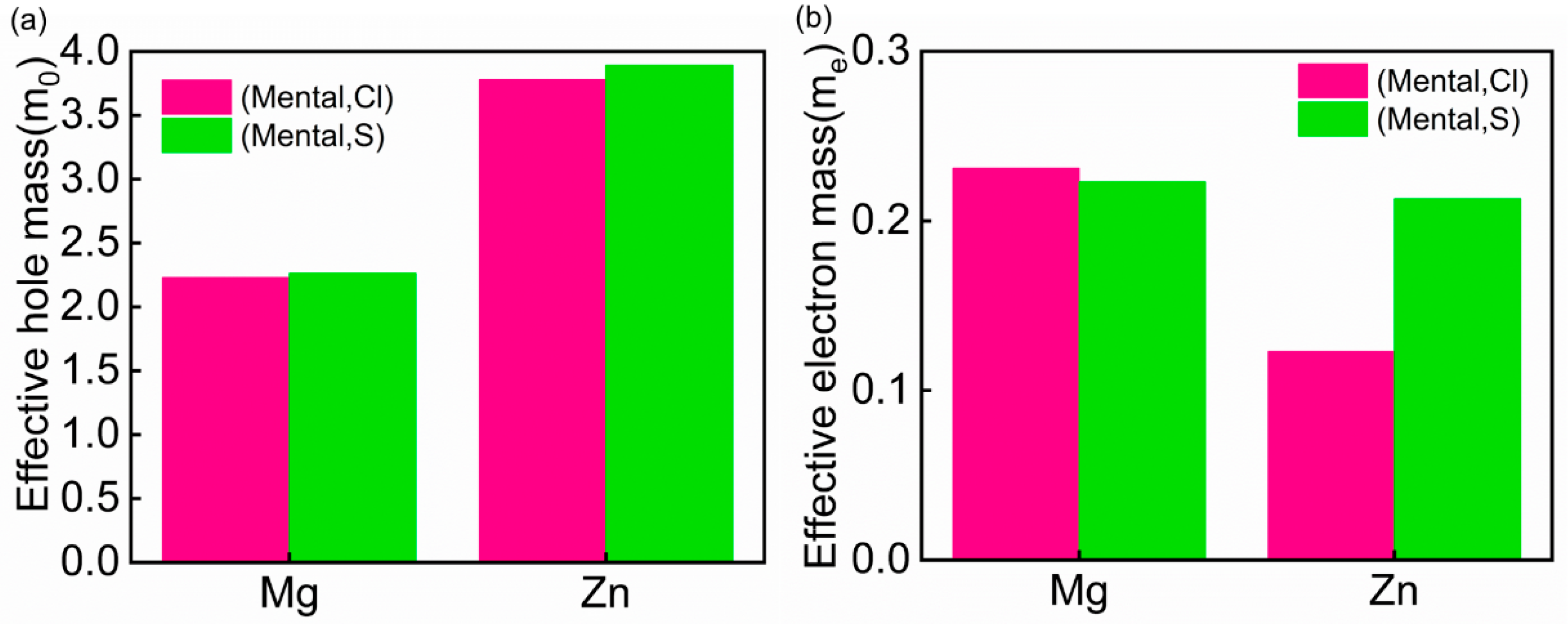
3.3. Effective Mass Analysis
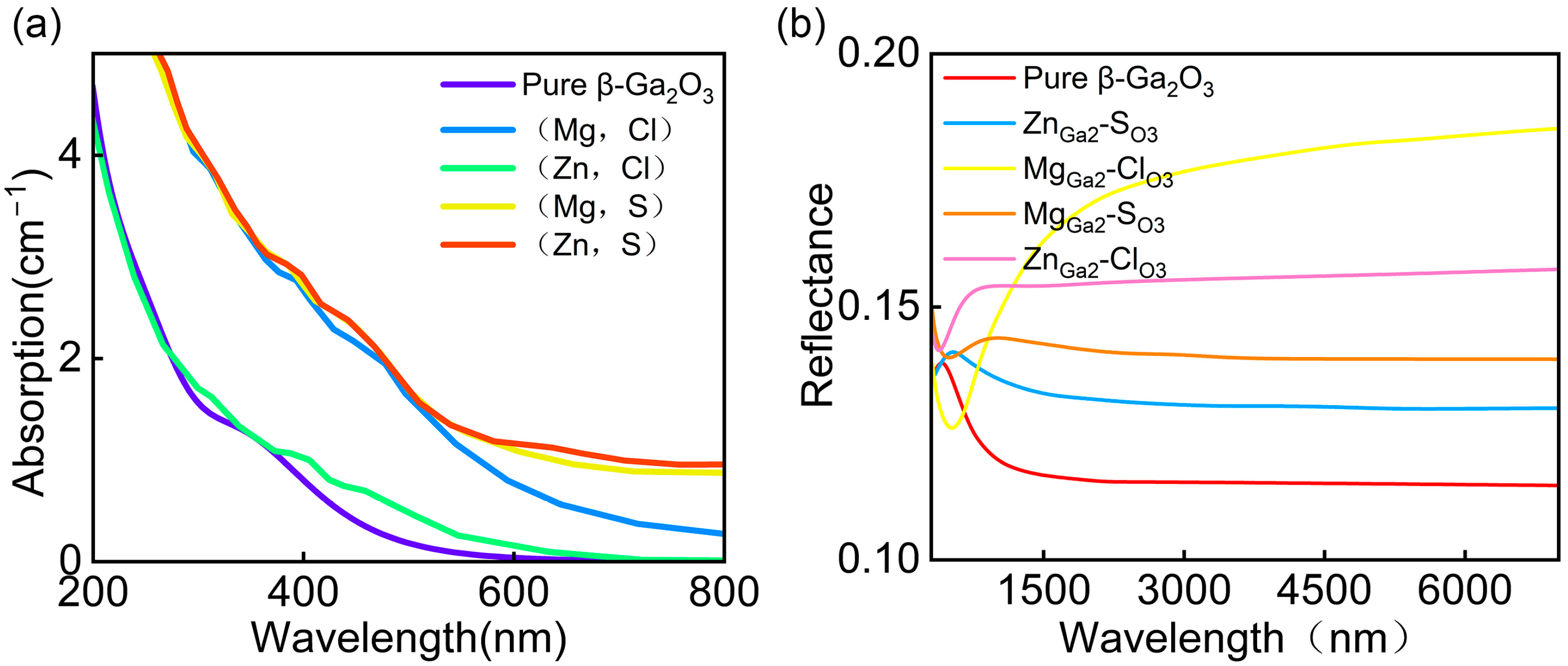
3.4. Optical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nair, M.M.; Iacoban, A.C.; Neaţu, F.; Florea, M.; Neaţu, Ş. A comparative overview of MXenes and metal oxides as cocatalysts in clean energy production through photocatalysis. J. Mater. Chem. A 2023, 11, 12559–12592. [Google Scholar] [CrossRef]
- Liu, D.; Huang, Y.; Zhang, Z.; Li, Z.; Yan, Y.; Chen, D.; Zhao, S.; Feng, Q.; Zhang, J.; Zhang, C.; et al. Strategy to solve the thermal issue of ultra-wide bandgap semiconductor gallium oxide field effect transistor. J. Alloys Compd. 2024, 986, 174143. [Google Scholar] [CrossRef]
- Pan, Y. Prediction of the structural, mechanical, and physical properties of GaC: As a potential third-generation semiconductor material. Inorg. Chem. 2024, 63, 8264–8272. [Google Scholar] [CrossRef]
- Okumuş, E.; Öztürk, S.T.; Gören, S.; Erdem, M.; Şale, Y.; Cengiz, A.; Odrinsky, A.P.; Najafov, A.I.; Mammadov, T.G.; Khaibullin, R.I.; et al. Manganese diluted TlInS2 layered semiconductor: Optical, electronic and magnetic properties. J. Alloys Compd. 2024, 1009, 176898. [Google Scholar] [CrossRef]
- Zhu, J. The influence of Al concentration on the structural stability, electronic and optical properties of InN semiconductor from first-principles study. Comp. Mater. Sci. 2025, 249, 113638. [Google Scholar]
- Choi, W.; Park, T.; Yoo, H.; Hur, J. Vertical asymmetric metal-semiconductor-metal photodiode based on β-Ga2O3 thin films fabricated via solution process for arc discharge detection. J. Alloys Compd. 2023, 953, 170169. [Google Scholar] [CrossRef]
- Yatskiv, R.; Vorochta, M.; Bašinová, N.; Dinhova, T.N.; Maixner, J.; Grym, J. Lowtemperature gas sensing mechanism in β-Ga2O3 nanostructures revealed by nearambient pressure XPS. Appl. Surf. Sci. 2024, 663, 160155. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, D.; Zhao, M.; Han, J.; Hua, Y. Surface plasmon-enhanced ultraviolet photodetectors by using Pt nanoparticles embedded in a-Ga2O3 films. J. Alloys Compd. 2024, 1007, 176357. [Google Scholar] [CrossRef]
- Bae, S.Y.; Kim, D.E.; Kong, M.S.; Kim, S.; Hong, Y.; Heo, K.; Kim, S.; Park, M.S. Heteroepitaxial growth of Ga2O3 thin films on nickel-nanodot-induced buffer layers for solar-blind ultraviolet photodetector applications. J. Alloys Compd. 2024, 995, 174811. [Google Scholar] [CrossRef]
- Chi, Z.; Sartel, C.; Zheng, Y.; Chikoidze, E. Native defects association enabled roomtemperature p-type conductivity in β-Ga2O3. J. Alloys Compd. 2023, 969, 172454. [Google Scholar] [CrossRef]
- Pan, Y. Effects of Cu, Ag and Au on electronic and optical properties of α-Ga2O3 oxide according to first-principles calculations. J. Phys. Chem. Solids 2023, 174, 111152. [Google Scholar] [CrossRef]
- Yuan, H.; Su, J.; Lin, Z.; Zhang, S.; Zhang, J.; Guo, L.; Hao, Y.; Chang, J. Intrinsic polarity extend β-Ga2O3/Janus-XP (X = P, As) heterostructures potential in UV/IR dual-band photodetector: A theoretical study. J. Alloys Compd. 2024, 1003, 175664. [Google Scholar] [CrossRef]
- Harada, T.; Ito, S.; Tsukazaki, A. Electric dipole effect in PdCoO2/β-Ga2O3 Schottky diodes for high-temperature operation. Sci. Adv. 2019, 5, eaax5733. [Google Scholar] [CrossRef]
- Harada, T.; Tsukazaki, A. Dynamic characteristics of PdCoO2/β-Ga2O3 Schottky junctions. Appl. Phys. Lett. 2020, 116, 232104. [Google Scholar] [CrossRef]
- Tang, R.; Li, G.; Li, C.; Li, J.; Zhang, Y.; Huang, K.; Ye, J.; Li, C.; Kang, J.Y.; Zhang, R.; et al. Localized surface plasmon enhanced Ga2O3 solar blind photodetectors. Opt. Express 2020, 28, 5731–5740. [Google Scholar] [CrossRef]
- Jiang, Z.X.; Wu, Z.Y.; Ma, C.C.; Deng, J.N.; Zhang, H.; Xu, Y.; Ye, J.D.; Fang, Z.L.; Zhang, G.Q.; Kang, J.Y.; et al. P-type β-Ga2O3 metal-semiconductor-metal solar-blind photodetectors with extremely high responsivity and gain-bandwidth product. Mater. Today Phys. 2020, 14, 100226. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Hu, H.; Wang, S.; Liu, A.; Guo, D. Review of self-powered solar-blind photodetectors based on Ga2O3. Mater. Today Phys. 2022, 28, 100883. [Google Scholar] [CrossRef]
- Pang, R.; Teramura, K.; Morishita, M.; Asakura, H.; Hosokawa, S.; Tanaka, T. Enhanced CO evolution for photocatalytic conversion of CO2 by H2O over Ca modified Ga2O3. Commun. Chem. 2020, 3, 137. [Google Scholar] [CrossRef]
- Tadjer, M.J. Toward gallium oxide power electronics. Science 2022, 378, 724–725. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, P.; Dang, K.; Zhang, Y.; Yan, Q.; Xiang, H.; Su, J.; Liu, Z.; Si, M.; Gao, J.; et al. Ultrawide bandgap semiconductor Ga2O3 power diodes. Nat. Commun. 2022, 13, 3900. [Google Scholar] [CrossRef]
- He, H.; Wu, C.; Hu, H.; Wang, S.; Zhang, F.; Guo, D.; Wu, F. Bandgap engineering and oxygen vacancy defect electroactivity inhibition in highly crystalline N-alloyed Ga2O3 films through plasma-enhanced technology. J. Phys. Chem. Lett. 2023, 14, 6444–6450. [Google Scholar] [CrossRef]
- Labed, M.; Park, B.I.; Kim, J.; Park, J.H.; Min, J.Y.; Hwang, H.J.; Kim, J.; Rim, Y.S. Ultrahigh photoresponsivity of W/Graphene/β-Ga2O3 Schottky barrier deep ultraviolet photodiodes. ACS Nano 2024, 18, 6558–6569. [Google Scholar] [CrossRef]
- Zhu, J. Tunability of the electronic structure of GaN third generation semiconductor for enhanced band gap: The influence of B concentration. Mater. Sci. Eng. B 2024, 308, 117554. [Google Scholar] [CrossRef]
- Pan, Y. The influence of Ag and Cu on the electronic and optical properties of ZrO from first-principles calculations. Mater. Sci. Semicond. Proc. 2021, 135, 106084. [Google Scholar] [CrossRef]
- Yan, C.; Su, J.; Wang, Y.; Lin, Z.; Zhang, J.; Chang, J.; Hao, Y. Reducing the acceptor levels of p-type β-Ga2O3 by (metal, N) co-doping approach. J. Alloys Compd. 2021, 854, 157247. [Google Scholar] [CrossRef]
- Srivastava, R. Chandiramouli, Electronic and band structure studies on In and N doped β-Ga2O3 nanostructures from first-principles calculations. Mater. Today Proc. 2021, 47, 6418–6428. [Google Scholar] [CrossRef]
- Hong, Y.; Zheng, X.; He, Y.; Liu, K.; Zhang, H.; Wang, X.; Yuan, Z.; Zhang, F.; Wang, Y.; Ma, X.; et al. Enhancing performance of β-Ga2O3 diodes through a NixO/SiNx/Ga2O3 sandwich structure. J. Alloys Compd. 2024, 976, 173062. [Google Scholar] [CrossRef]
- Fang, M.H.; De Guzman, G.N.A.; Bao, Z.; Majewska, N.; Mahlik, S.; Grinberg, M.; Leniec, G.; Kaczmarek, S.M.; Yang, C.W.; Lu, K.M.; et al. Ultra-high-efficiency near-infrared Ga2O3:Cr3+ phosphor and controlling of phytochrome. J. Mater. Chem. C 2020, 8, 11013–11017. [Google Scholar] [CrossRef]
- Ma, J.; Lin, J.; Liu, J.; Li, F.; Liu, Y.; Yang, G. Achieving high conductivity p-type Ga2O3 through Al-N and In-N co-doping. Chem. Phys. Lett. 2020, 746, 137308. [Google Scholar] [CrossRef]
- Gucmann, F.; Nádaždy, P.; Hušeková, K.; Dobročka, E.; Priesol, J.; Egyenes, F.; Šatka, A.; Rosová, A.; Ťapajna, M. Thermal stability of rhombohedral α-and monoclinic β-Ga2O3 grown on sapphire by liquid-injection MOCVD. Mater. Sci. Semicond. Process. 2023, 156, 107289. [Google Scholar] [CrossRef]
- Åhman, J.; Svensson, G.; Albertsson, J. A reinvestigation of β-gallium oxide. Cryst. Struct. Commun. 1996, 52, 1336–1338. [Google Scholar] [CrossRef]
- University of Vienna. Vienna Ab Initio Simulation Package (VASP 6.2.0). 2020. Available online: https://www.vasp.at/ (accessed on 25 January 2025).
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Farmer, W.; Hsiao, C.-L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Ankit, K.; Gueorguiev, G.K. Density functional theory-fed phase field model for semiconductor nanostructures: The case of self-induced core–shell InAlN nanorods. Cryst. Growth Des. 2024, 24, 4717–4727. [Google Scholar] [CrossRef]
- Kresse, G.D. Joubert, From ultrasoft pseudopotentials to the projector augmentedwave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Pu, D. First-principles investigation of equilibrium phase, mechanical and thermodynamic properties of the Nowotny TM5Si3C ternary phase. Ceram. Int. 2022, 48, 20438–20445. [Google Scholar] [CrossRef]
- Xu, L. New insight into the structural, mechanical and thermodynamic properties of Mo2C MXene as the ultrahigh temperature ceramics. Mater. Today Chem. 2024, 42, 102449. [Google Scholar]
- Khandy, S.A.; Alshahrani, T.; Elsaeedy, H.I.; Gupta, D.C. First-principles calculations to investigate structural, electronic, phonon, magnetic and thermal properties of stable halide perovskite semiconductors Cs2GeMnI6 and Cs2GeNiI6. J. Alloys Compd. 2023, 957, 170296. [Google Scholar] [CrossRef]
- Pan, Y. W2AlC: A new layered MAX phase to adjust the balance between strength and ductility. Mater. Today Chem. 2024, 35, 101915. [Google Scholar] [CrossRef]
- Pu, D. First-principles investigation of oxidation behavior of Mo5SiB2. Ceram. Int. 2020, 46, 6698–6702. [Google Scholar]
- Zhang, J.; Feng, W.; Zhang, Y.; Zeng, W.; Zhou, Q. Gas-sensing properties and firstprinciples comparative study of metal (Pd, Pt)-decorated MoSe2 hierarchical nanoflowers for efficient SO2 detection at room temperature. J. Alloys Compd. 2023, 968, 172006. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X. Tailoring the hydrogenated mechanism of Pt3Al from firstprinciples investigation. Vacuum 2023, 212, 112033. [Google Scholar]
- Yang, F.; Zhu, J. Enhanced catalytic activity of noble metal@borophene/WS2 heterojunction for hydrogen evolution reaction. Appl. Surf. Sci. 2025, 680, 161321. [Google Scholar] [CrossRef]
- Pu, D.; Jia, Y. Adjusting the correlation between the oxidation resistance and mechanical properties of Pt-based thermal barrier coating. Vacuum 2020, 172, 109067. [Google Scholar]
- Yu, E. Enhancing the catalytic hydrogen evolution reaction (HER) of the defective borophene@Pt/Pd/MoS2 heterojunction. Int. J. Hydrogen Energy 2024, 50, 920–931. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, Q.; Liao, M.; Xiong, M.; Feng, X.; Zhang, X.; Dong, H.; Zhu, D.; Wu, F.; Mu, Z. Trivalent chromium ions doped fluorides with both broad emission bandwidth and excellent luminescence thermal stability. ACS Appl. Mater. Interfaces 2021, 13, 18274–18282. [Google Scholar] [CrossRef]
- Lorenz, M.R.; Woods, J.F.; Gambino, R.J. Some electrical properties of the semiconductor β-Ga2O3. J. Phys. Chem. Solids 1967, 28, 403–404. [Google Scholar] [CrossRef]
- Kean, L.; Mohamed, M.A.; Mondal, A.K.; Taib, M.F.M.; Samat, M.H.; Berhanuddin, D.D. First-principles studies for electronic structure and optical properties of strontium doped β-Ga2O3. Micromachines 2021, 12, 348. [Google Scholar] [CrossRef]
- Zhong, S.; Wu, M.; Lei, X. First-principle calculations of effective mass of silicon crystal with vacancy defects. Mater. Sci.-Pol. 2016, 34, 916–923. [Google Scholar] [CrossRef]
- Wong, M.H.; Lin, C.H.; Kuramata, A.; Yamakoshi, S.; Murakami, H.; Kumagai, Y.; Higashiwaki, M. Acceptor doping of β-Ga2O3 by Mg and N ion implantations [J/OL]. Appl. Phys. Lett. 2018, 113, 102103. [Google Scholar] [CrossRef]
- Tanaka, T.; Matsunaga, K.; Ikuhara, Y.; Yamamoto, T. First-principles study on structures and energetics of intrinsic vacancies in SrTiO [J/OL]. Phys. Rev. B 2003, 68, 205213. [Google Scholar] [CrossRef]
- Niu, Y.; Wu, F.; Zhang, Q.; Teng, Y.; Huang, Y.; Yang, Z.; Mu, Z. Luminescence and thermometry sensing of Sr2InTaO6: Eu3+, Mn4+ phosphors in a wide temperature range. J. Lumin. 2024, 275, 120748. [Google Scholar] [CrossRef]
- Yang, F. The influence of pressure on the structural stability, mechanical, electronic and optical properties of TiH4 and VH4 tetrahydrides: A first-principles study. Ceram. Int. 2024, 50, 14856–14864. [Google Scholar]
- Mahmood, Q.; Alay-E-Abbas, S.; Hassan, M.; Noor, N.A. First-principles evaluation of Co-doped ZnS and ZnSe ferromagnetic semiconductors. J. Alloys Compd. 2016, 688, 899–907. [Google Scholar] [CrossRef]
- Yang, F. Structural, hydrogen storage capacity, electronic and optical properties of Li-N-H hydrogen storage materials from first-principles investigation. J. Energy Storage 2024, 87, 111492. [Google Scholar]
- Yin, X.; Hou, Q.Y.; Chen, H. First-principles study of the effects of interstitial H and point vacancies on the photocatalytic performance of Be/Mg/Ca-doped GaN. Vacuum 2021, 187, 110119. [Google Scholar] [CrossRef]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
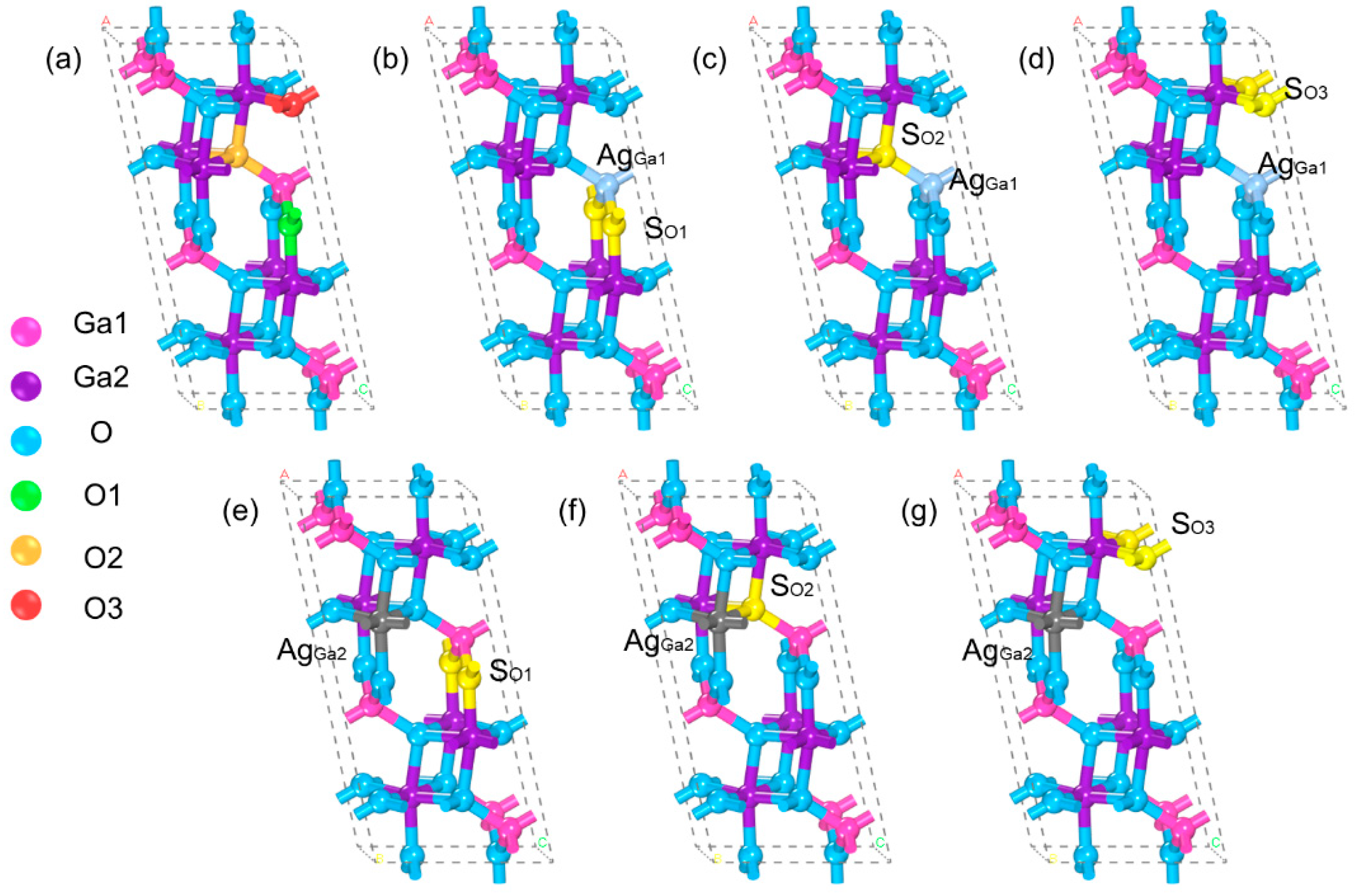
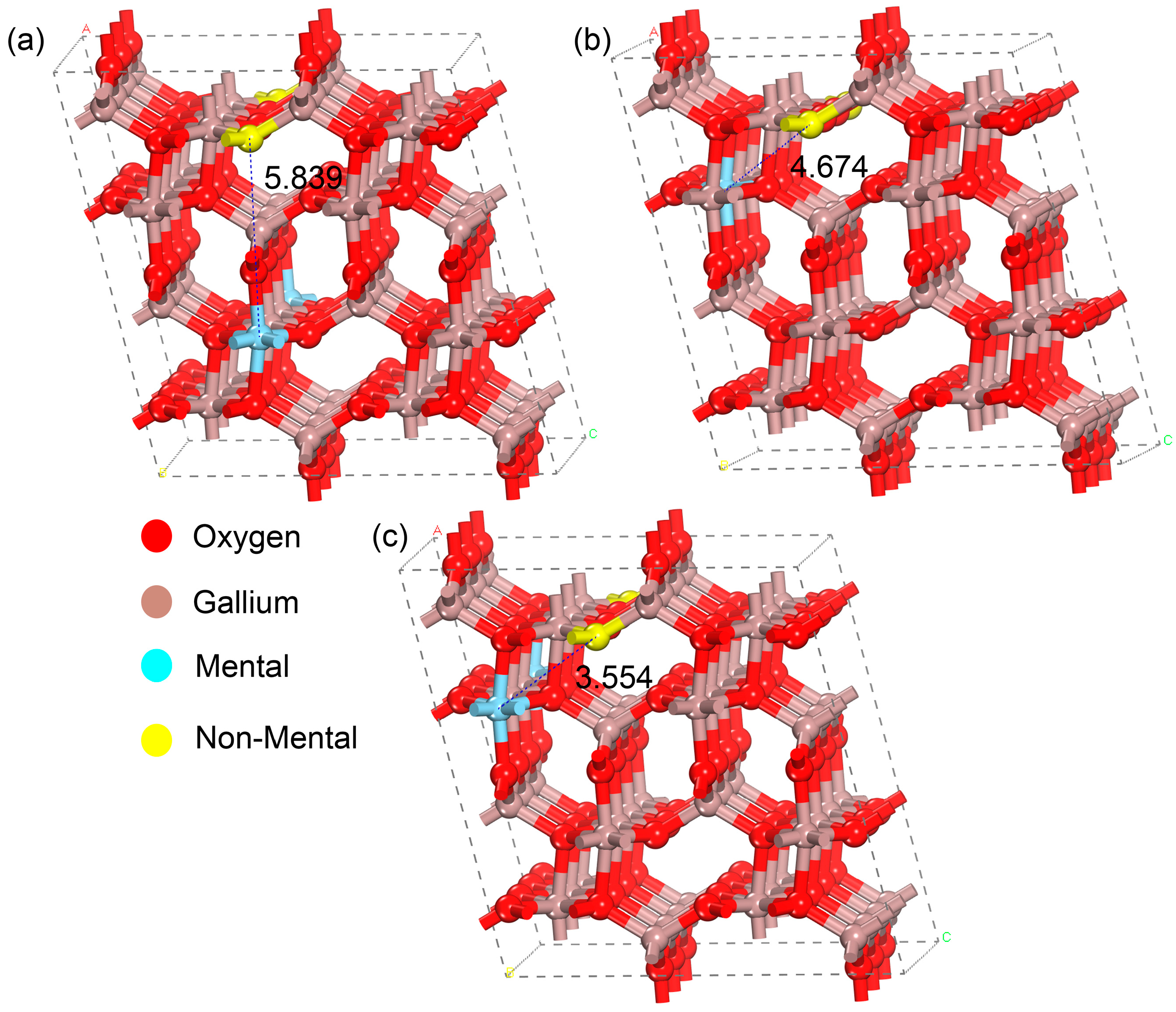
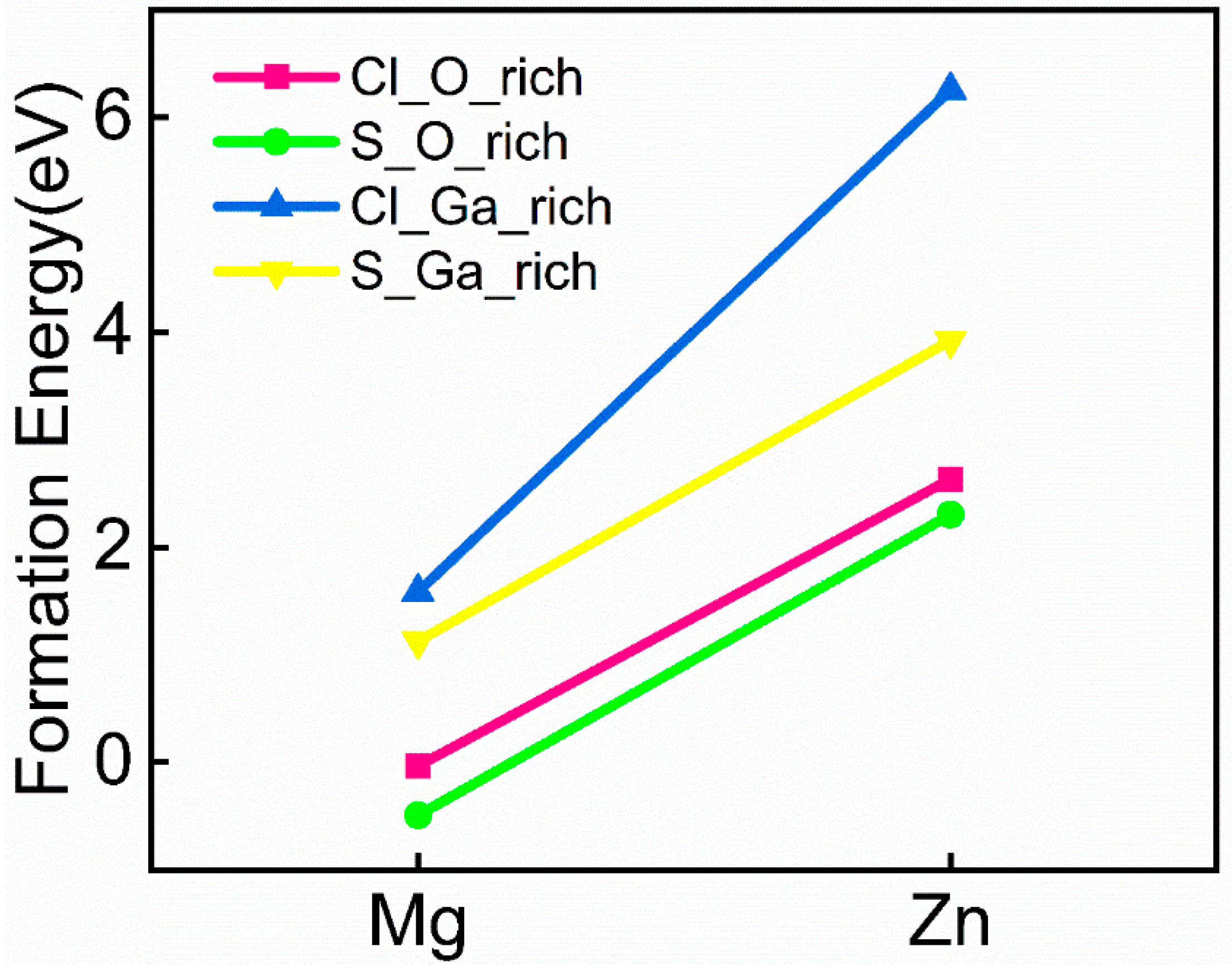

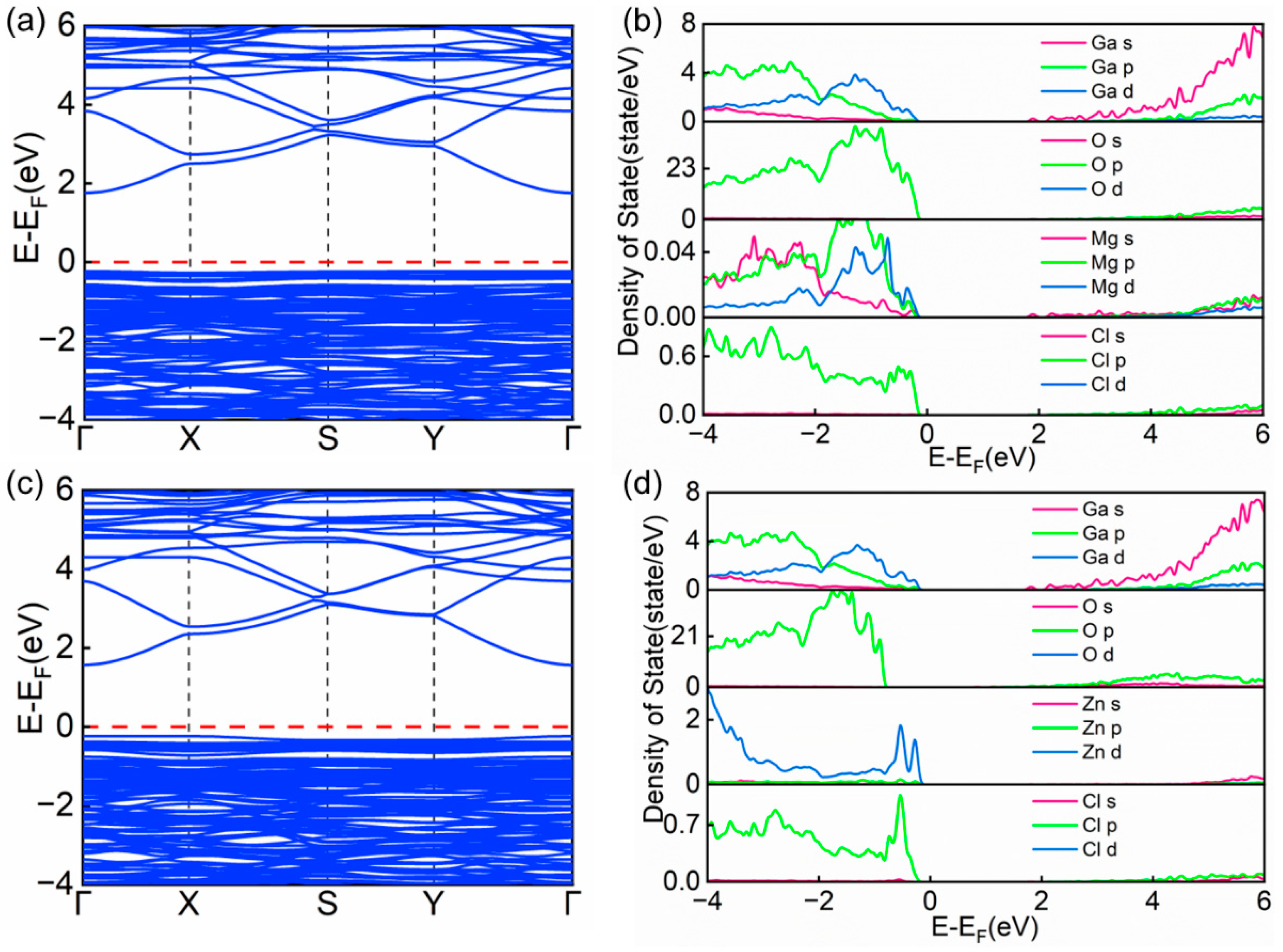

| Structure | a (Å) | b (Å) | c (Å) | β° | V (Å3) | Etot |
|---|---|---|---|---|---|---|
| β-Ga2O3 (This work) | 12.39 | 3.07 | 5.86 | 103.72 | 217.99 | |
| Expt.1 [29] | 12.55 | 3.08 | 5.89 | 103.67 | 222.43 | |
| Expt.2 [30] | 12.27 | 3.05 | 5.82 | 103.82 | 212.14 | |
| AgGa1-SO1 | 13.27 | 3.10 | 5.89 | 105.12 | 234.68 | −108.58 |
| AgGa1-SO2 | 12.95 | 3.10 | 6.05 | 104.23 | 235.87 | −108.92 |
| AgGa1-SO3 | 12.56 | 3.09 | 6.09 | 102.24 | 231.41 | −108.89 |
| AgGa2-SO1 | 12.62 | 3.16 | 5.99 | 102.89 | 234.02 | −109.35 |
| AgGa2-SO2 | 12.83 | 3.15 | 6.06 | 103.72 | 240.53 | −108.89 |
| AgGa2-SO3 | 12.72 | 3.12 | 6.05 | 102.77 | 235.73 | −110.12 |
| AgGa2-ClO1 | 12.61 | 3.14 | 6.12 | 103.32 | 237.34 | −108.81 |
| AgGa2-ClO2 | 12.95 | 3.15 | 6.02 | 102.83 | 240.62 | −108.06 |
| AgGa2-ClO3 | 12.67 | 3.15 | 6.07 | 102.86 | 237.68 | −109.42 |
| Model | CBM (eV) | VBM (eV) | Eg (eV) |
|---|---|---|---|
| Pure | 1.84 | −0.23 | 2.08 |
| Mg-Cl | 1.75 | −0.23 | 1.99 |
| Mg-S | 1.37 | −0.64 | 2.02 |
| Zn-Cl | 1.57 | −0.23 | 1.81 |
| Zn-S | 1.39 | −0.55 | 1.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-R.; Luan, S.-Z. Co-Doping Effects on the Electronic and Optical Properties of β-Ga2O3: A First-Principles Investigation. Materials 2025, 18, 2005. https://doi.org/10.3390/ma18092005
Wang Y-R, Luan S-Z. Co-Doping Effects on the Electronic and Optical Properties of β-Ga2O3: A First-Principles Investigation. Materials. 2025; 18(9):2005. https://doi.org/10.3390/ma18092005
Chicago/Turabian StyleWang, Ya-Rui, and Su-Zhen Luan. 2025. "Co-Doping Effects on the Electronic and Optical Properties of β-Ga2O3: A First-Principles Investigation" Materials 18, no. 9: 2005. https://doi.org/10.3390/ma18092005
APA StyleWang, Y.-R., & Luan, S.-Z. (2025). Co-Doping Effects on the Electronic and Optical Properties of β-Ga2O3: A First-Principles Investigation. Materials, 18(9), 2005. https://doi.org/10.3390/ma18092005





