The Formation of an Interface and Its Energy Levels Inside a Band Gap in InAs/GaSb/AlSb/GaSb M-Structures
Abstract
1. Introduction
2. Materials and Methods
- (a)
- M-structure with an infinite number of periods:
- -
- The material layers were designed in a zinc blende structure.
- -
- The GaSb substrate’s orientation was set to = [100] and = [010].
- -
- The simulation grid size for the x growth direction was set to 0.1 nm.
- -
- For dispersion, with respect to the grid size of the vector (for the direction perpendicular to the growth direction), it was set to about 0.05 nm−1, and for the direction (along the growth direction), it was set to about 0.07 nm−1.
- -
- The temperature dependence of the energy gap and the temperature dependence of the lattice constant were turned on.
- -
- Calculated bands: Gamma, HH, LH, and SO.
- -
- Strain was set as pseudomorphic.
- (b)
- Additional parameters were used for simulations for a 5-period M-structure (for dispersion relation and optical absorption):
- -
- 20 nm thick AlSb buffer (with 0.1 nm grid size).
- -
- 1 μm thick GaSb substrate (with 10 nm grid size).
- (c)
- Additional parameters were used for simulations for a 5-period M-structure (parameters appropriate for optical absorption):
- -
- 0.5 size of the -space (relative to the Brillouin zone) for the computation of optical transitions.
- -
- 16 points (along the y and z axes) where optical transitions intensities were evaluated.
- -
- 8 points between points where optical transitions intensities were interpolated.
- -
- Photon energy steps were set to 0.0001 eV.
- -
- The Gaussian broadening of energy levels for optical transitions was set to 1.0 × eV.
3. Results and Discussion
3.1. HRXRD Measurements
3.2. Nextnano++ Computer Simulations
4. Conclusions
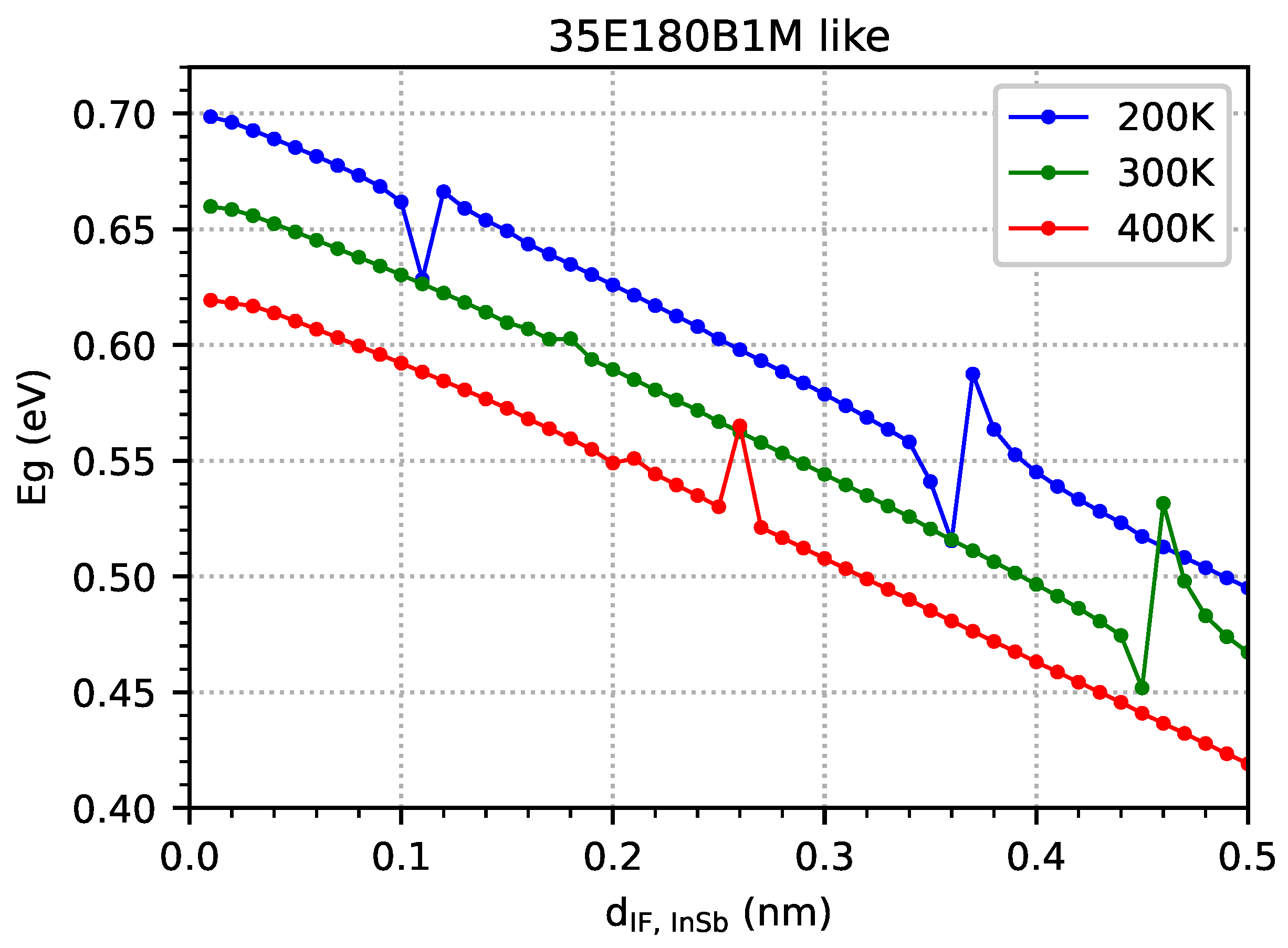
- EGIF levels form within a specific temperature range and a specific range of IF InSb widths. The specific width of IF InSb for EGIF is higher at higher temperatures. The specific temperature for EGIF is higher for higher IF InSb widths.
- In simulations with an infinite number of M-structure periods, the number of EGIF levels is equal to two. In simulations with a five-period M-structure, the number of EGIF levels is equal to 10. The results of the dispersion relation and the EGIF are comparable between these two types of simulations.
- The values of the calculated Fermi velocity for the EGIF levels for the direction are as follows: for , they range from slightly below 0 to about 500 km/s (average about 200 km/s) depending on the temperature and M-structure parameters. For in the range of 0–0.2…0.5 nm−1, it increases almost linearly for a maximum value of approximately 450…800 km/s (for lower temperatures, the maximum value of is higher and is achieved for smaller values of ). For the value of in the range of 0.2–1.0 nm−1, velocity reaches a relatively constant level corresponding to linear dependence —with a slight decrease in the value of with an increase in the value of .
- The EGIF manifests as the maxima of for electrons located in the IF InSb layer. At specific temperatures, EGIF exists for an odd multiplication of the smallest IF InSb base’s width when the first EGIF occurs at this temperature. For the ‘first’ EGIF, there is only one maximum for the EGIF function. For the ‘second’ EGIF, there are two maxima, and for the ‘third’ EGIF, there are three maxima. The amplitudes of the ‘second’/’third’ maxima are approximately two/three times lower than the ‘first’ maxima.
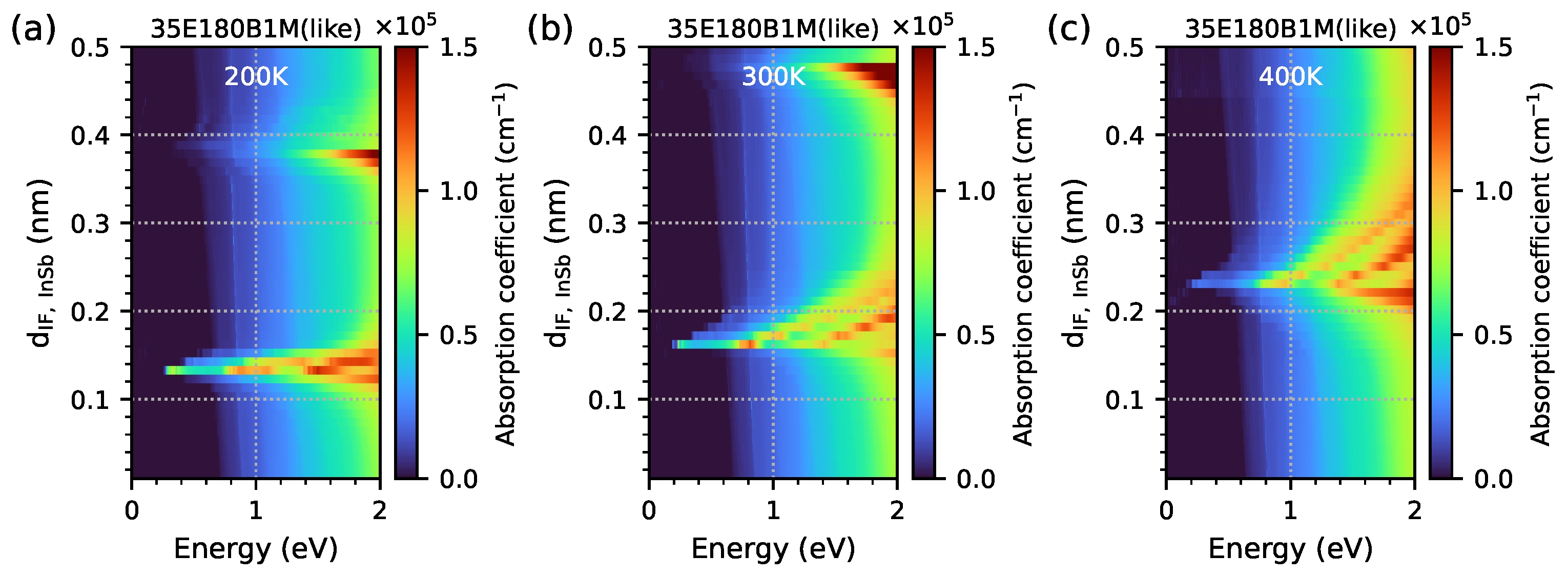
- The computed optical absorption coefficient indicates the optical absorption edge corresponding to the computed . The maxima of absorption versus temperature at specific widths of the IF InSb correspond to the computed EGIF—a high increase in optical absorption at the lowest temperature (and also at lower temperatures) and the middle temperature where EGIF is present. The increase in optical absorption within this temperature range is mainly due to the transitions from EGIF to other electron levels (at the highest temperature where EGIF still exists, the main contribution to optical absorption is from transitions from hole levels to the EGIF).
- The absorption maxima as a function of the IF InSb’s width at specific temperatures correspond to the calculated EGIF. At temperatures of 200 K and 300 K, two optical absorption maxima occur for the IF InSb width within the range of 0.01–0.50 nm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, B.M.; Razeghi, M.; Nathan, V.; Brown, G.J. Type-II M structure photodiodes: An alternative material design for mid-wave to long wavelength infrared regimes. In Proceedings of the Quantum Sensing and Nanophotonic Devices IV; Razeghi, M., Brown, G.J., Eds.; SPIE: Bellingham, WA, USA, 2007; Volume 6479, p. 64790S. [Google Scholar] [CrossRef]
- Lang, X.L.; Xia, J.B. Electronic structure and optical properties of InAs/GaSb/AlSb/GaSb superlattice. J. Appl. Phys. 2013, 113, 043715. [Google Scholar] [CrossRef]
- Nguyen, B.M.; Hoffman, D.; Huang, E.K.w.; Delaunay, P.Y.; Razeghi, M. Background limited long wavelength infrared type-II InAs/GaSb superlattice photodiodes operating at 110 K. Appl. Phys. Lett. 2008, 93, 123502. [Google Scholar] [CrossRef]
- Razeghi, M.; Nguyen, B.M. Band gap tunability of Type II Antimonide-based superlattices. Phys. Procedia 2010, 3, 1207–1212. [Google Scholar] [CrossRef]
- Du, Y.n.; Xu, Y.; Song, G.f. Theoretical analysis on the energy band properties of N- and M-structure type-II superlattices. Superlattices Microstruct. 2020, 145, 106590. [Google Scholar] [CrossRef]
- Tang, B.; Xu, Y.Q.; Zhou, Z.Q.; Hao, R.T.; Wang, G.W.; Ren, Z.W.; Zhi-Chuan, N. GaAs Based InAs/GaSb Superlattice Short Wavelength Infrared Detectors Grown by Molecular Beam Epitaxy. Chin. Phys. Lett. 2009, 26, 028102. [Google Scholar] [CrossRef]
- Guo, J.; Hao, R.T.; Zhao, Q.R.; Man, S.Q. Band-Tailored InAs/GaSb Superlattice in Infrared Application. Adv. Mater. Res. 2013, 750–752, 936–940. [Google Scholar] [CrossRef]
- Razeghi, M.; Haddadi, A.; Hoang, A.; Huang, E.; Chen, G.; Bogdanov, S.; Darvish, S.; Callewaert, F.; McClintock, R. Advances in antimonide-based Type-II superlattices for infrared detection and imaging at center for quantum devices. Infrared Phys. Technol. 2013, 59, 41–52. [Google Scholar] [CrossRef]
- Razeghi, M.; Dehzangi, A.; Li, J. Multi-band SWIR-MWIR-LWIR Type-II superlattice based infrared photodetector. Results Opt. 2021, 2, 100054. [Google Scholar] [CrossRef]
- Hoang, A.M.; Chen, G.; Haddadi, A.; Abdollahi Pour, S.; Razeghi, M. Demonstration of shortwavelength infrared photodiodes based on type-II InAs/GaSb/AlSb superlattices. Appl. Phys. Lett. 2012, 100, 211101. [Google Scholar] [CrossRef]
- Delmas, M.; Rossignol, R.; Rodriguez, J.; Christol, P. Design of InAs/GaSb superlattice infrared barrier detectors. Superlattices Microstruct. 2017, 104, 402–414. [Google Scholar] [CrossRef]
- Krishtopenko, S.S.; Desrat, W.; Spirin, K.E.; Consejo, C.; Ruffenach, S.; Gonzalez-Posada, F.; Jouault, B.; Knap, W.; Maremyanin, K.V.; Gavrilenko, V.I.; et al. Massless Dirac fermions in III-V semiconductor quantum wells. Phys. Rev. B 2019, 99, 121405. [Google Scholar] [CrossRef]
- Krishtopenko, S.S.; Teppe, F. Quantum spin Hall insulator with a large bandgap, Dirac fermions, and bilayer graphene analog. Sci. Adv. 2018, 4, eaap7529. [Google Scholar] [CrossRef]
- Li, C.A.; Zhang, S.B.; Shen, S.Q. Hidden edge Dirac point and robust quantum edge transport in InAs/GaSb quantum wells. Phys. Rev. B 2018, 97, 045420. [Google Scholar] [CrossRef]
- Ermolaev, M.; Suchalkin, S.; Belenky, G.; Kipshidze, G.; Laikhtman, B.; Moon, S.; Ozerov, M.; Smirnov, D.; Svensson, S.P.; Sarney, W.L. Metamorphic narrow-gap InSb/InAsSb superlattices with ultra-thin layers. Appl. Phys. Lett. 2018, 113, 213104. [Google Scholar] [CrossRef]
- Suchalkin, S.; Ermolaev, M.; Valla, T.; Kipshidze, G.; Smirnov, D.; Moon, S.; Ozerov, M.; Jiang, Z.; Jiang, Y.; Svensson, S.P.; et al. Dirac energy spectrum and inverted bandgap in metamorphic InAsSb/InSb superlattices. Appl. Phys. Lett. 2020, 116, 032101. [Google Scholar] [CrossRef]
- Marchewka, M. Finite-difference method applied for eight-band kp model for Hg1−xCdxTe/HgTe quantum well. Int. J. Mod. Phys. B 2017, 31, 1750137. [Google Scholar] [CrossRef]
- Marchewka, M.; Jarosz, D.; Ruszała, M.; Juś, A.; Krzemiński, P.; Bobko, E.; Trzyna-Sowa, M.; Wojnarowska-Nowak, R.; Śliż, P.; Rygała, M.; et al. Interfaces-engineered M-structure for infrared detectors. Opto-Electron. Rev. 2024, 32, 150183. [Google Scholar] [CrossRef]
- Qiao, P.F.; Mou, S.; Chuang, S.L. Electronic band structures and optical properties of type-II superlattice photodetectors with interfacial effect. Opt. Express 2012, 20, 2319. [Google Scholar] [CrossRef] [PubMed]
- Birner, S.; Zibold, T.; Andlauer, T.; Kubis, T.; Sabathil, M.; Trellakis, A.; Vogl, P. nextnano: General Purpose 3-D Simulations. IEEE Trans. Electron. Devices 2007, 54, 2137–2142. [Google Scholar] [CrossRef]
- Birner, S. Modeling of Semiconductor Nanostructures and Semiconductor-Electrolyte Interfaces; Universität München: Garching bei München, Germany, 2011; Volume 135. [Google Scholar]
- Bahder, T.B. Eight-band k·p model of strained zinc-blende crystals. Phys. Rev. B 1990, 41, 11992–12001. [Google Scholar] [CrossRef] [PubMed]
- Sato, T. Optical Absorption for Interband and Intersubband Transitions. Available online: https://www.nextnano.com/documentation/tools/nextnanoplus/tutorials/1D_optics_tutorial.html (accessed on 20 July 2024).
- Nextnano GmbH. HTCondor. Available online: https://www.nextnano.com/documentation/cloud_computing/HTCondor.html (accessed on 20 July 2024).
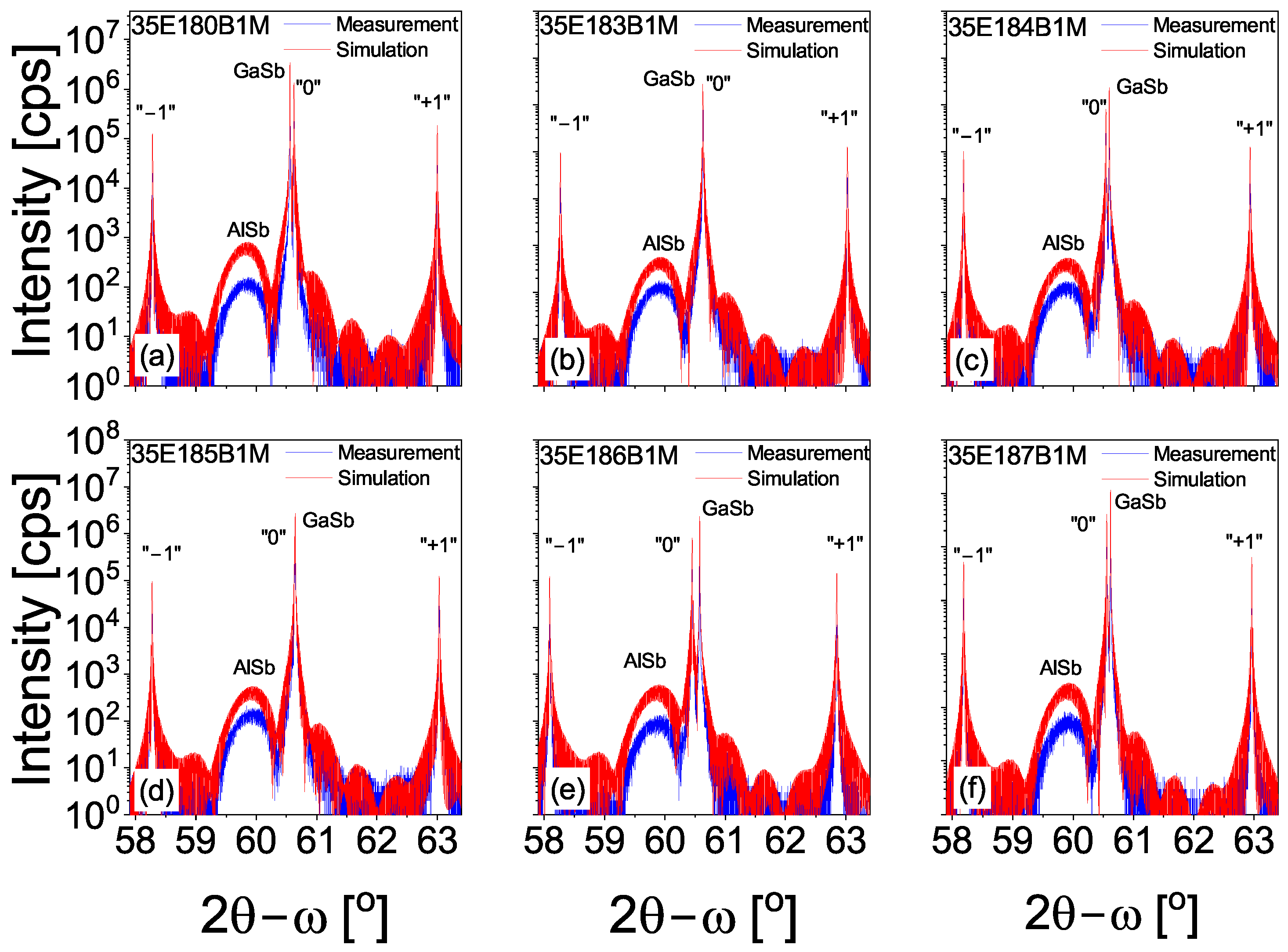

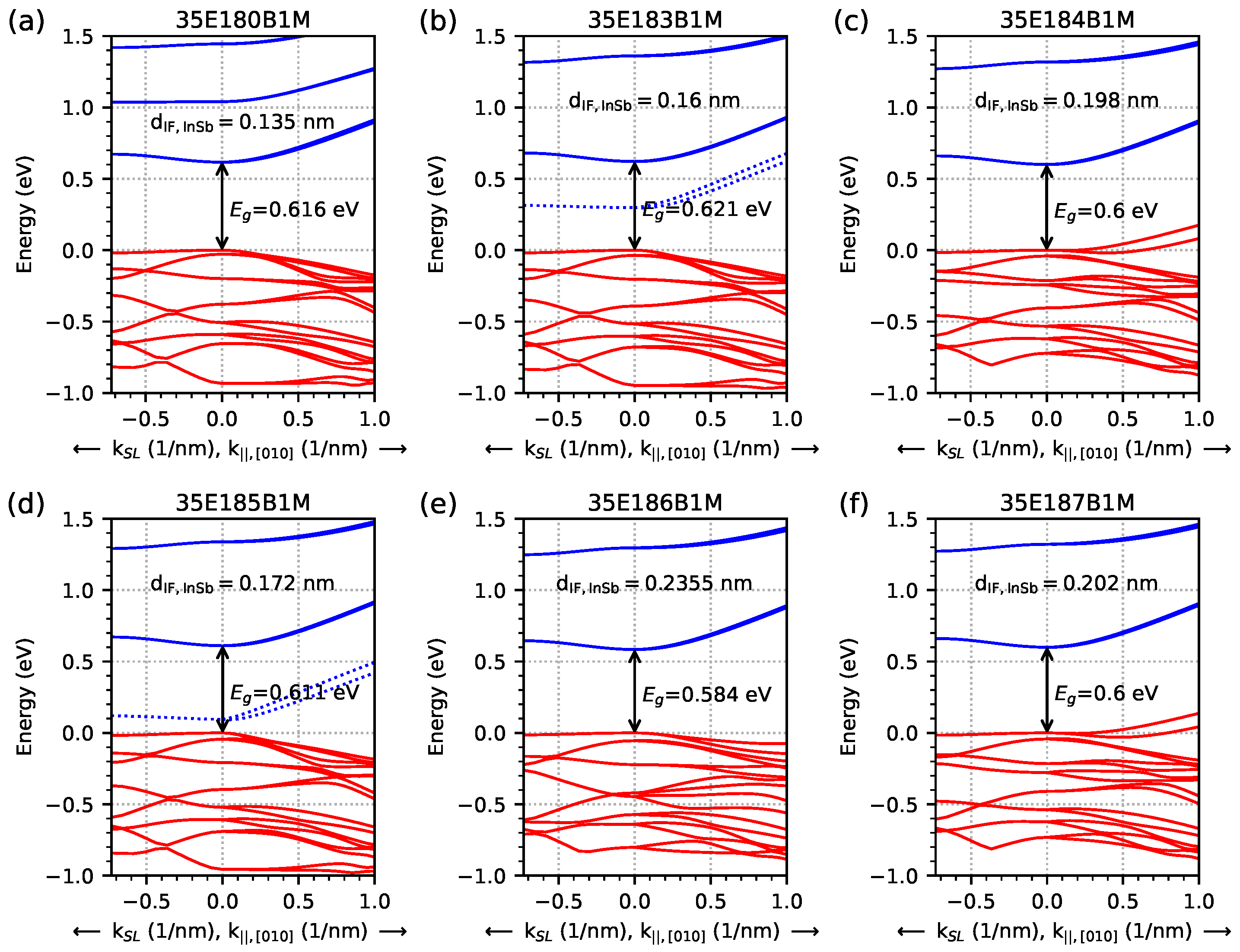
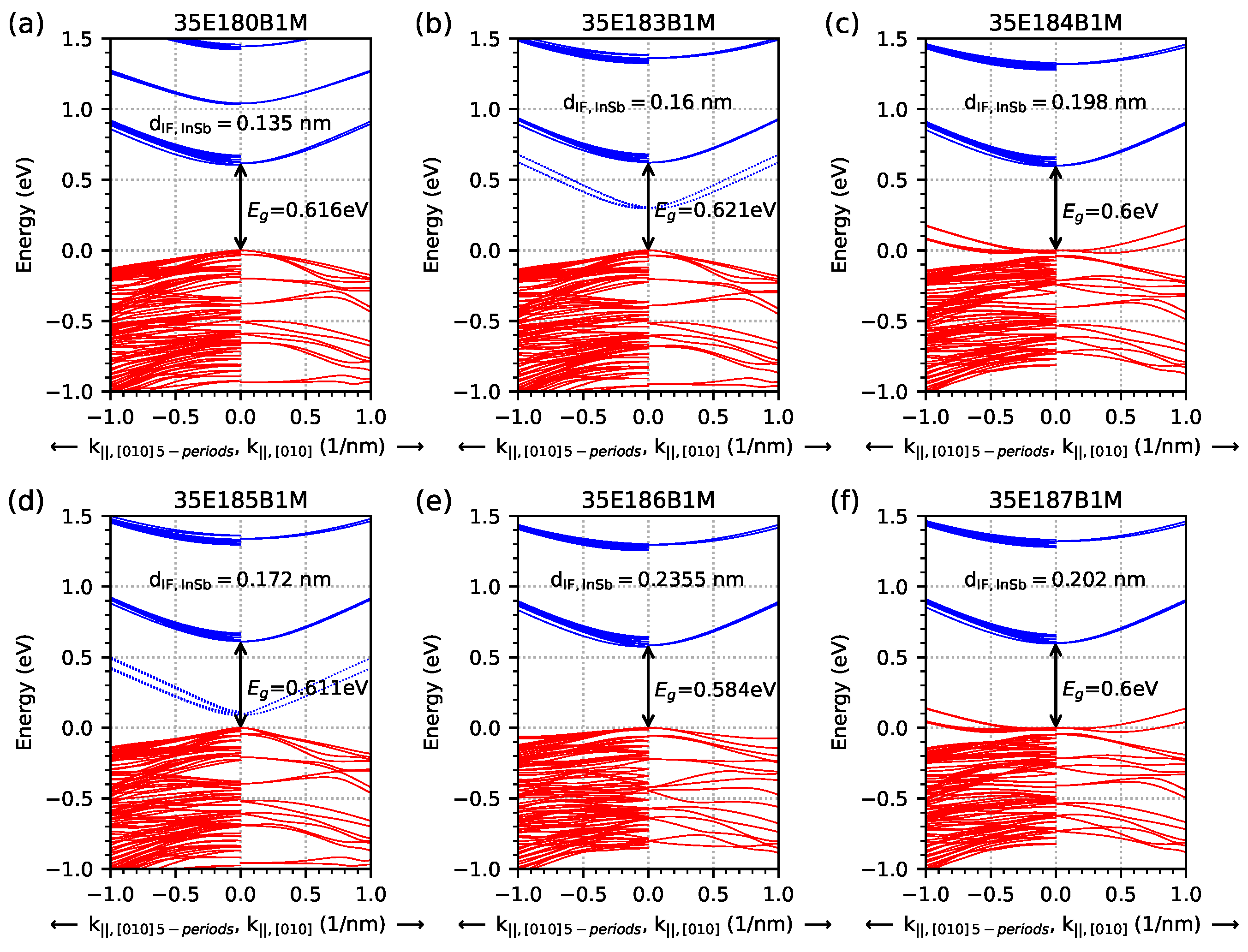
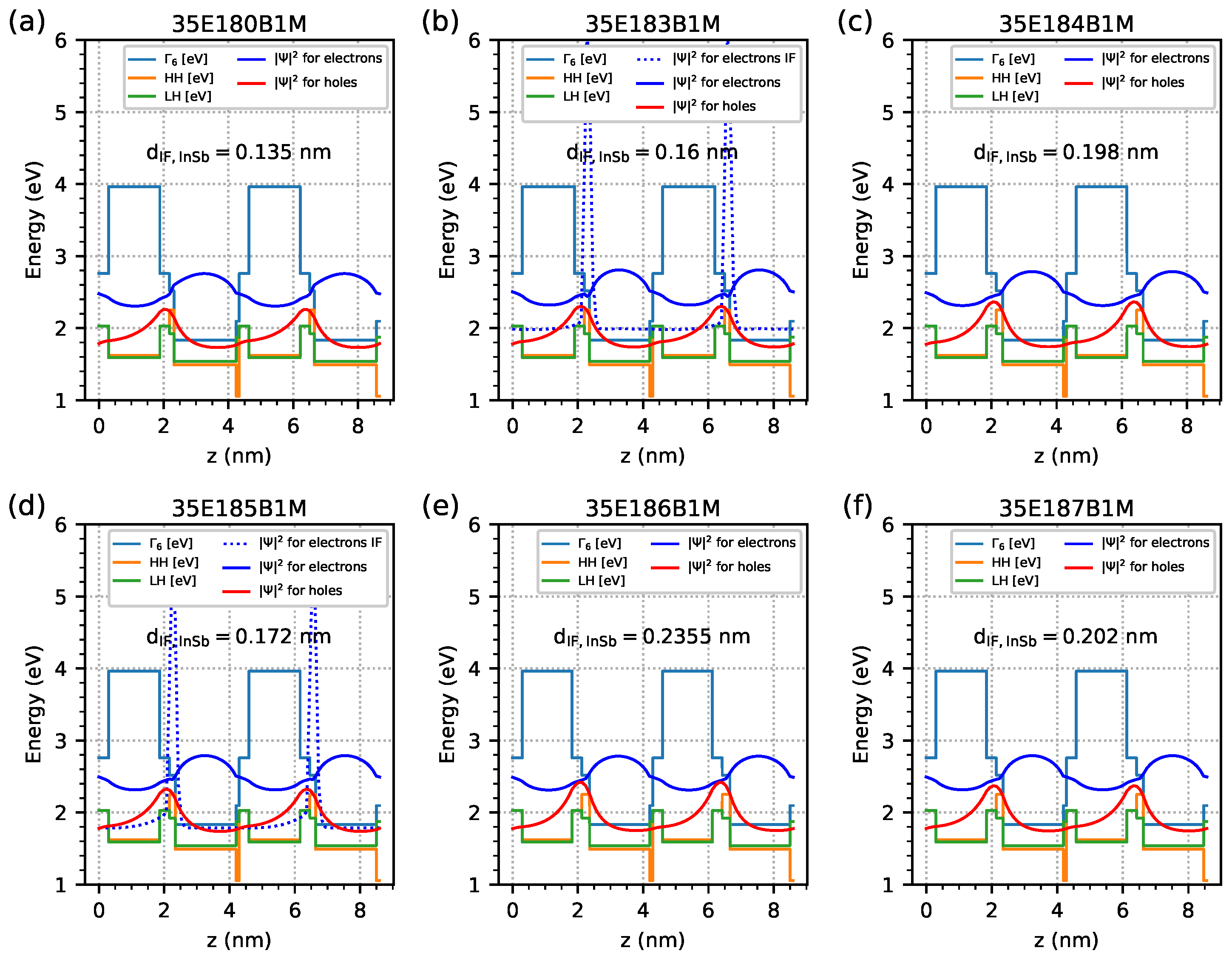

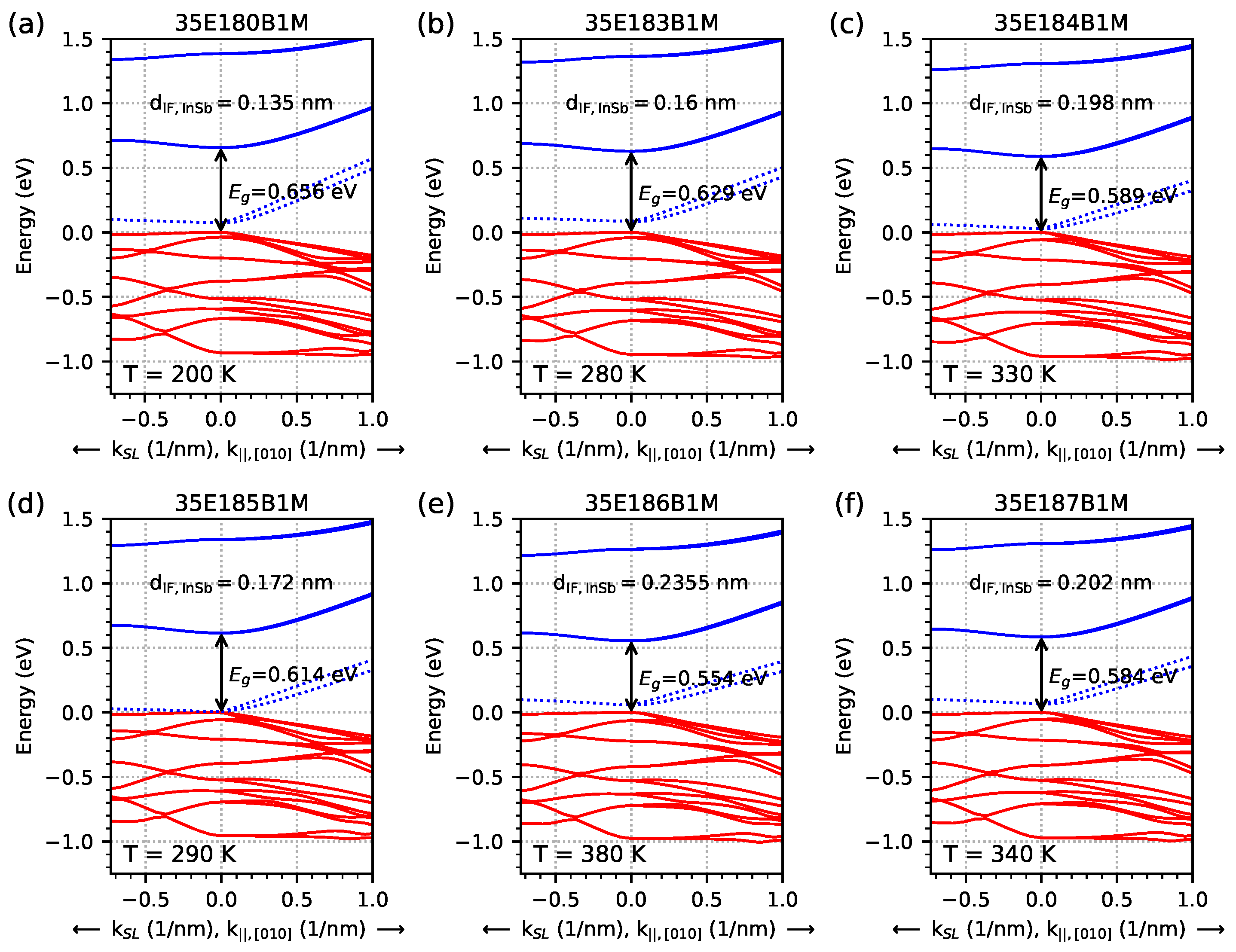
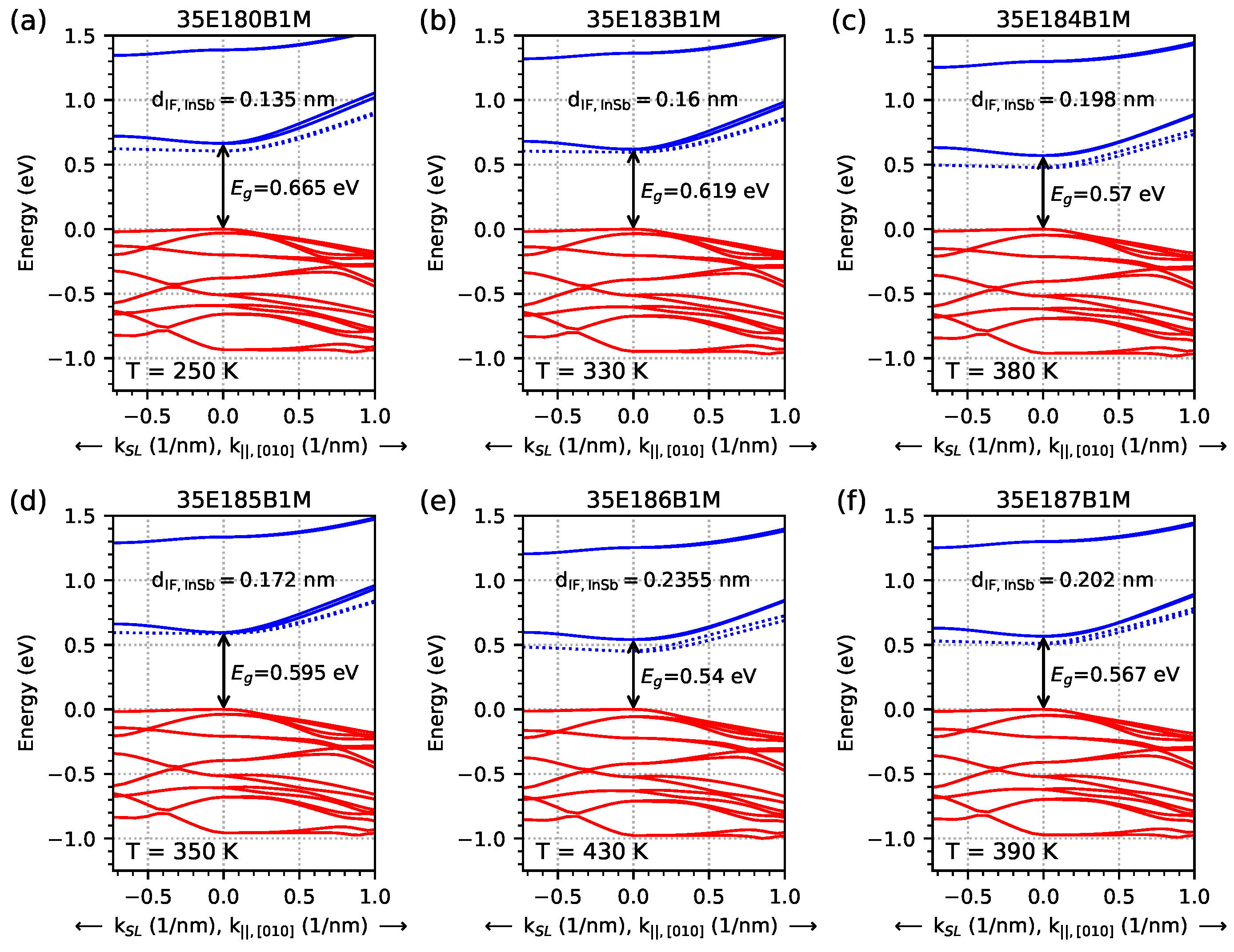
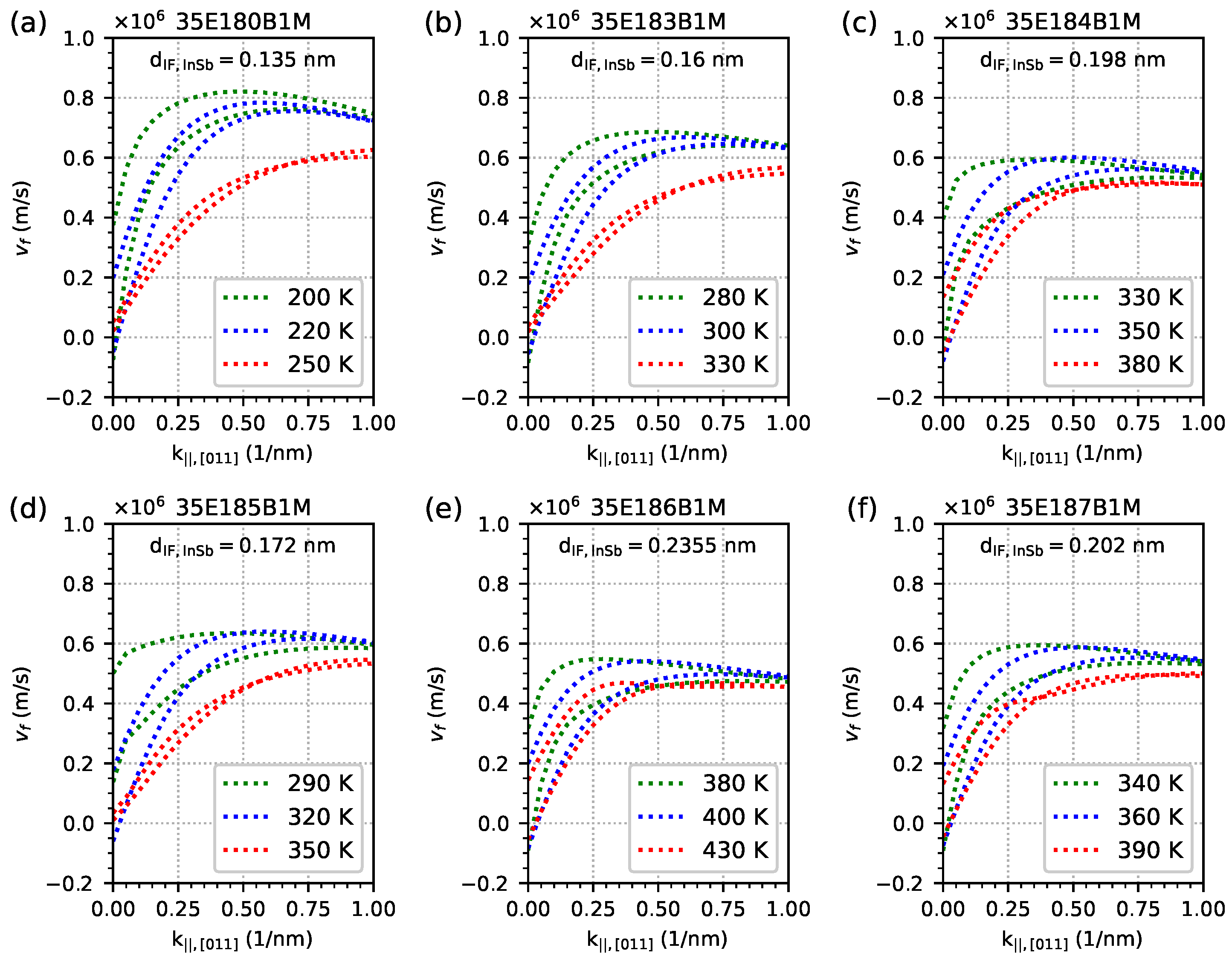
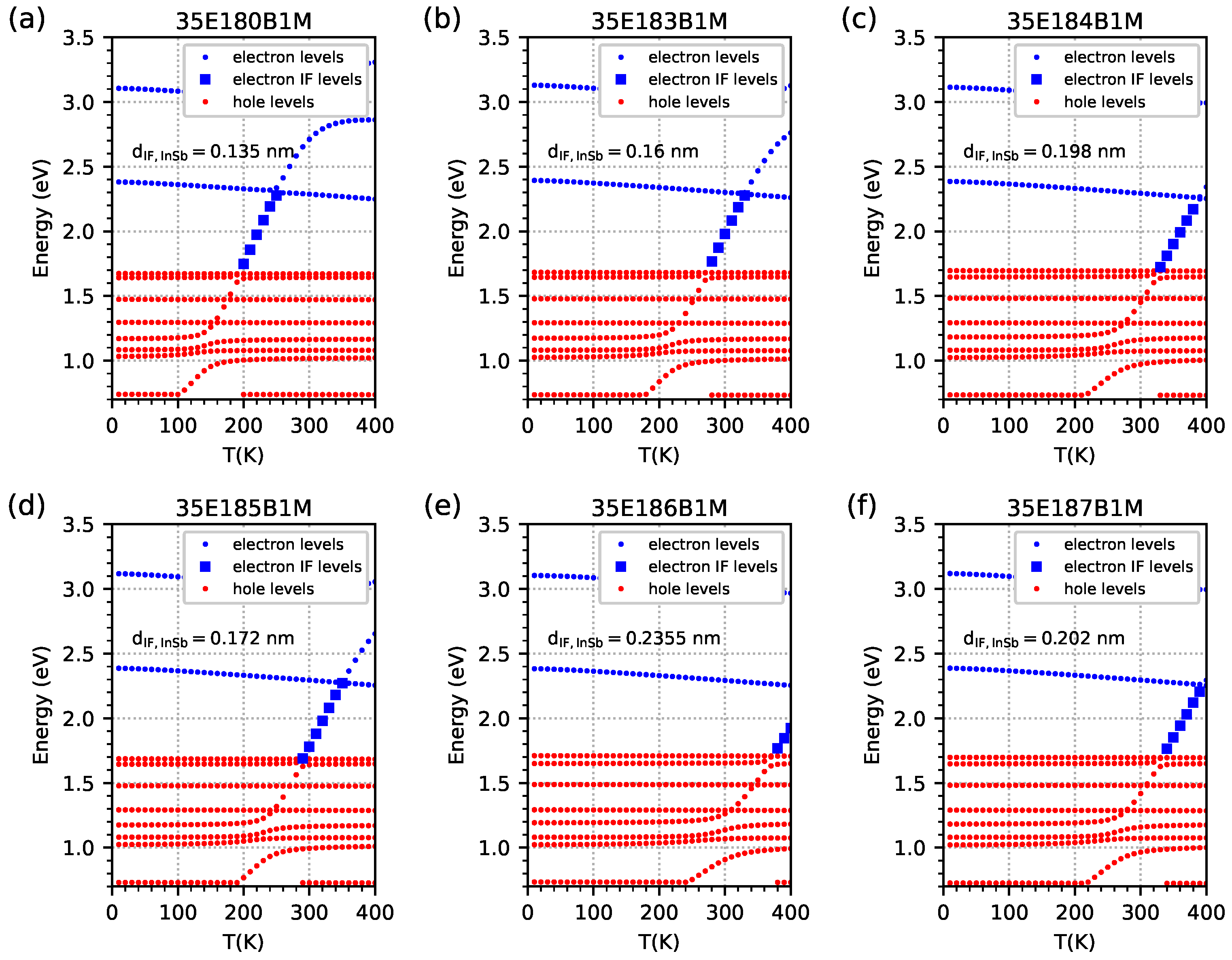



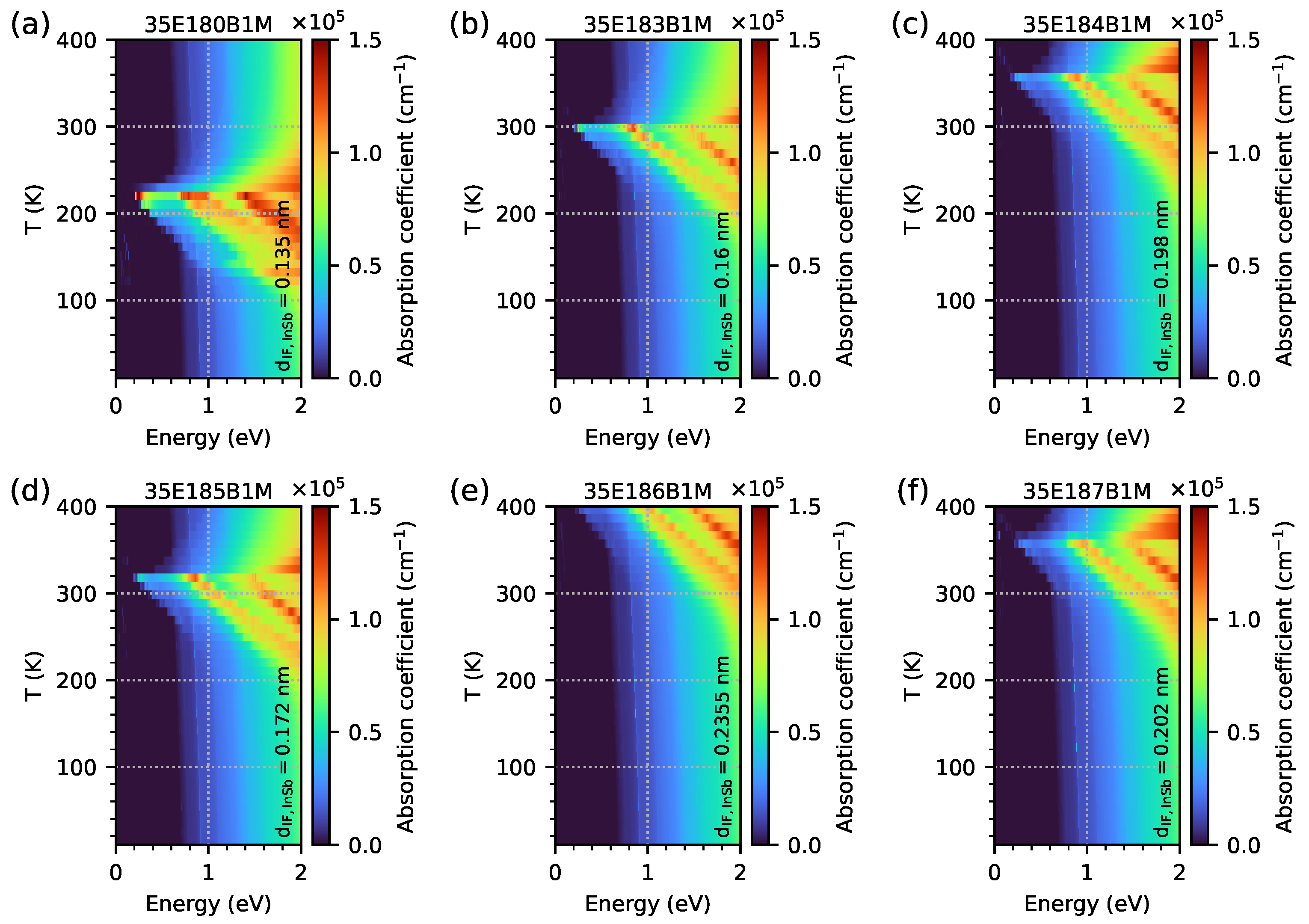


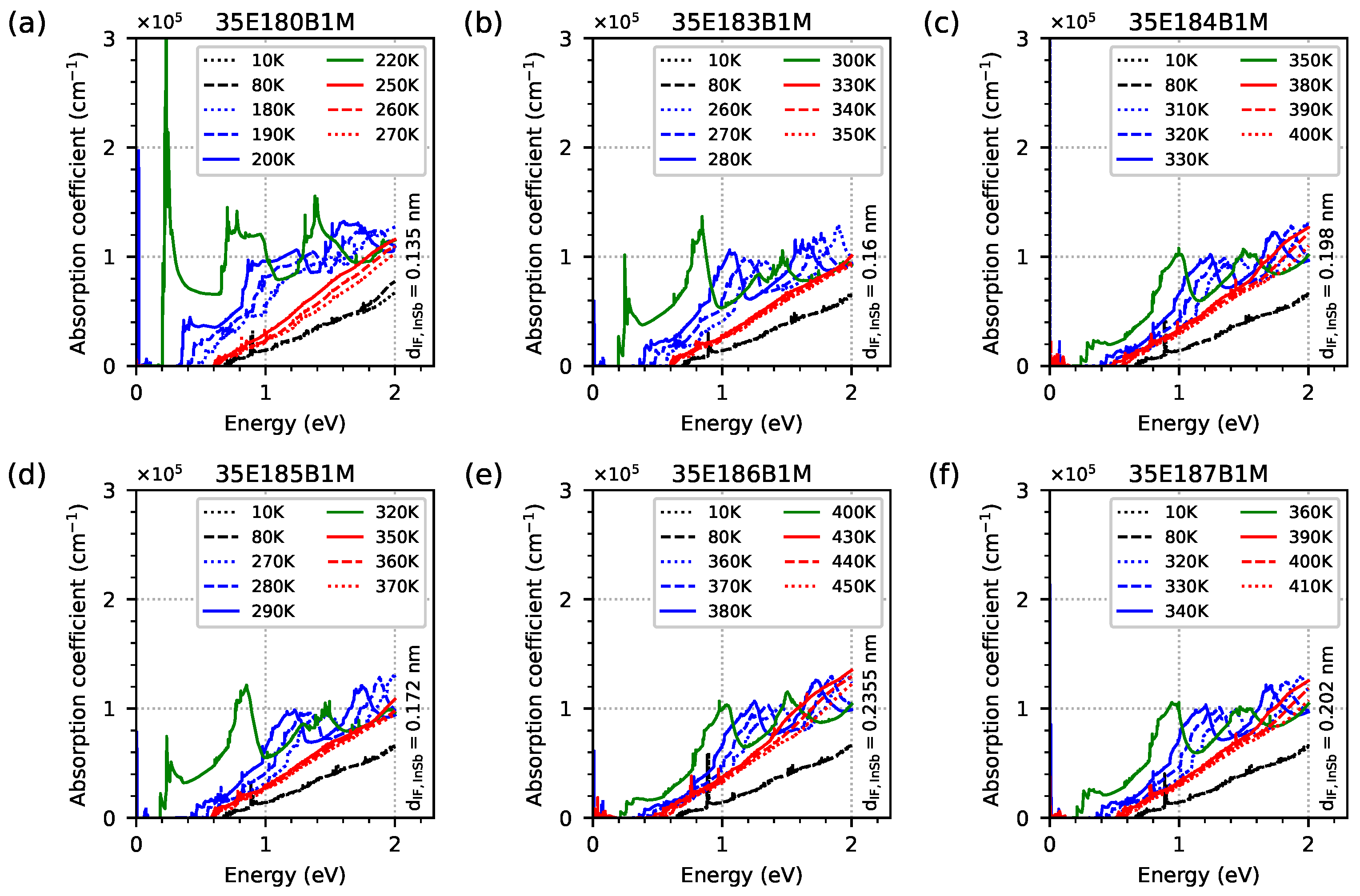

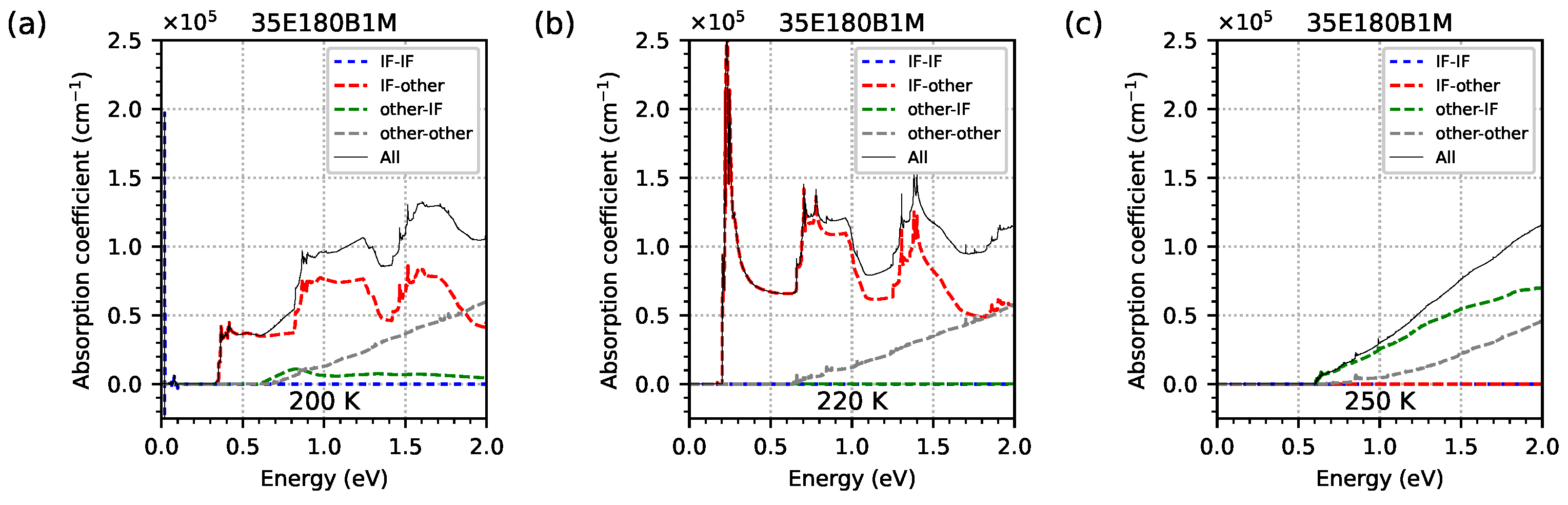
| Sample | InAs | InSb-IF | GaSb | AlSb | GaSb | GaAs-IF | Δa/a |
|---|---|---|---|---|---|---|---|
| No. | (ML) | (ML) | (ML) | (ML) | (ML) | (ML) | 10−3 |
| 35E180B1M | 6.40 | 0.45 | 1 | 5.27 | 1 | 0.33 | −0.93 |
| 35E183B1M | 6.14 | 0.53 | 1 | 5.33 | 1 | 0.33 | −0.13 |
| 35E184B1M | 6.18 | 0.66 | 1 | 5.19 | 1 | 0.33 | 0.83 |
| 35E185B1M | 6.21 | 0.57 | 1 | 5.22 | 1 | 0.33 | 0.13 |
| 35E186B1M | 6.13 | 0.79 | 1 | 5.08 | 1 | 0.33 | 1.80 |
| 35E187B1M | 6.13 | 0.67 | 1 | 5.14 | 1 | 0.33 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śliż, P.; Jarosz, D.; Pasternak, M.; Marchewka, M. The Formation of an Interface and Its Energy Levels Inside a Band Gap in InAs/GaSb/AlSb/GaSb M-Structures. Materials 2025, 18, 991. https://doi.org/10.3390/ma18050991
Śliż P, Jarosz D, Pasternak M, Marchewka M. The Formation of an Interface and Its Energy Levels Inside a Band Gap in InAs/GaSb/AlSb/GaSb M-Structures. Materials. 2025; 18(5):991. https://doi.org/10.3390/ma18050991
Chicago/Turabian StyleŚliż, Paweł, Dawid Jarosz, Marta Pasternak, and Michał Marchewka. 2025. "The Formation of an Interface and Its Energy Levels Inside a Band Gap in InAs/GaSb/AlSb/GaSb M-Structures" Materials 18, no. 5: 991. https://doi.org/10.3390/ma18050991
APA StyleŚliż, P., Jarosz, D., Pasternak, M., & Marchewka, M. (2025). The Formation of an Interface and Its Energy Levels Inside a Band Gap in InAs/GaSb/AlSb/GaSb M-Structures. Materials, 18(5), 991. https://doi.org/10.3390/ma18050991






