On the Prediction and Optimisation of Processing Parameters in Directed Energy Deposition of SS316L via Finite Element Simulation and Machine Learning
Abstract
1. Introduction
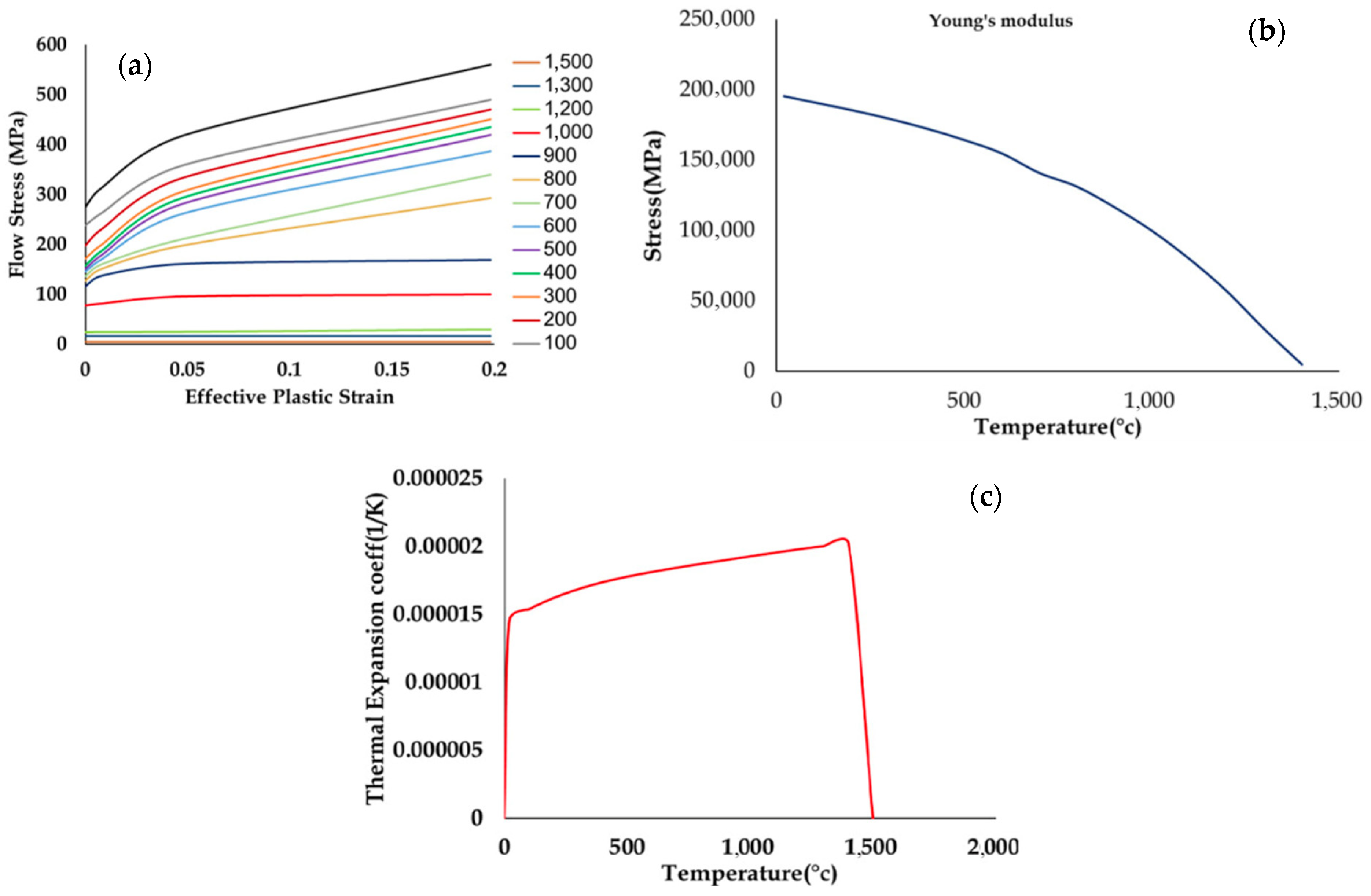
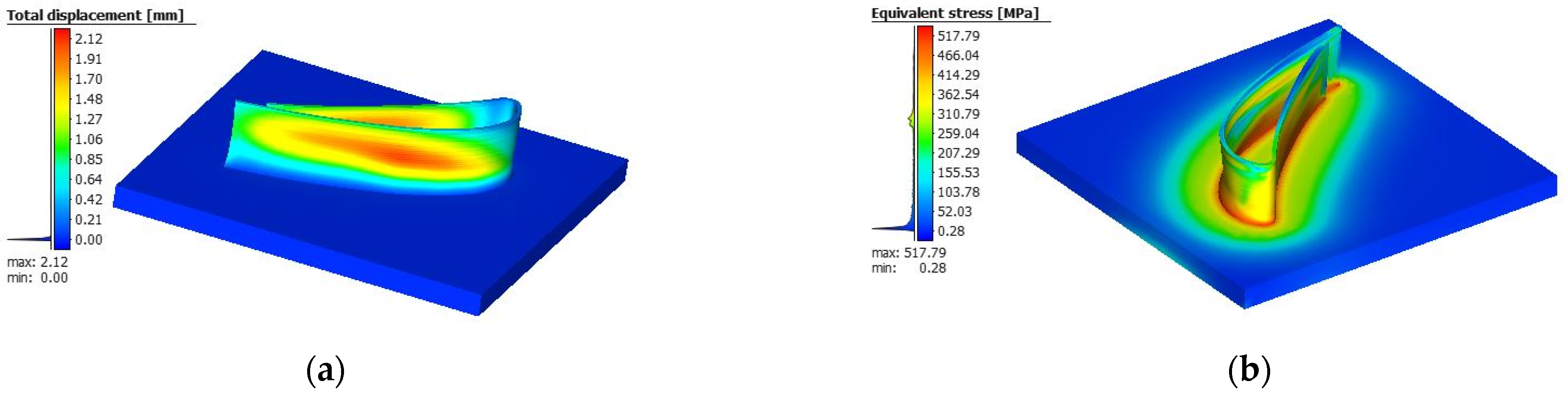
2. Finite Element Simulation and Validation
| Grade | C | Mn | Si | P | S | Cr | Mo | Ni | N |
|---|---|---|---|---|---|---|---|---|---|
| min | - | - | - | - | - | 16.0 | 2.00 | 10.0 | - |
| max | 0.03 | 2.0 | 0.75 | 0.045 | 0.03 | 18.0 | 3.00 | 14.0 | 0.10 |
| Parameter | Value |
|---|---|
| Solidus temperature | 1279 °C |
| Melting temperature | 1450 °C |
| Density | 7966 Kg/m3 |
| Latent heat for melting | 25,400 J/Kg |
| Poison ratio | 0.3 |
| Convective heat transfer for first and remaining layers | 10, 30 (W/m2K) |
| Emissivity for first and remaining layers | 0.6, 0.6 |
| Elastic module | 200 GPa |
| Ultimate Tensile Strength | 580 MPa |
| Yield Strength | 290 MPa |
| Specific heat | 2051.531 J/kg. °C |
| Thermal conduction | 0.225 W/cm. °C |
| Parameter | Value |
|---|---|
| Laser power | 400–800 W |
| Scanning speed | 10–20 mm/s |
| Laser beam diameter | 0.6–0.8 mm |
| Powder feed rate | 7.5 g/min |
| Powder size | 45–90 µm |
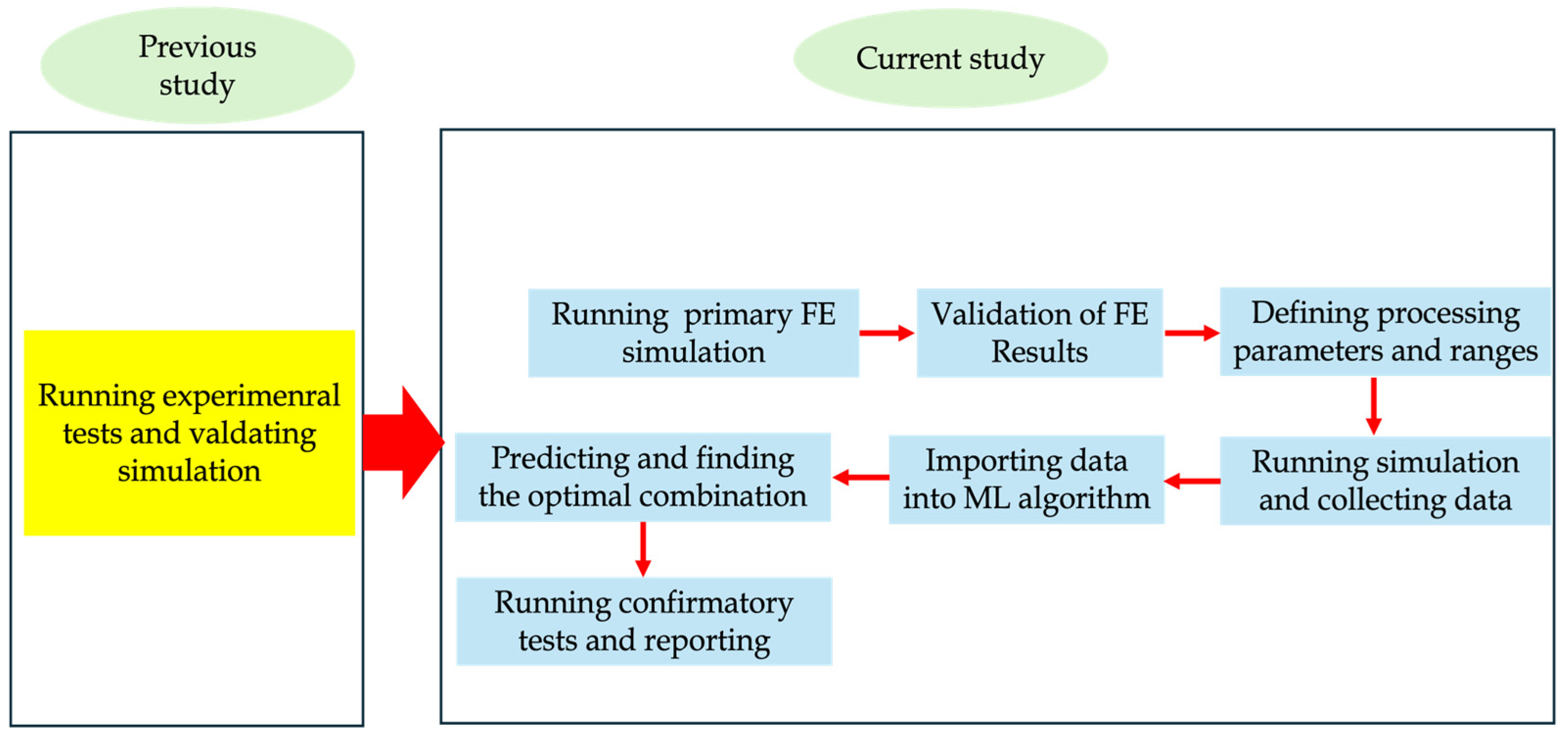
3. Machine Learning Procedure
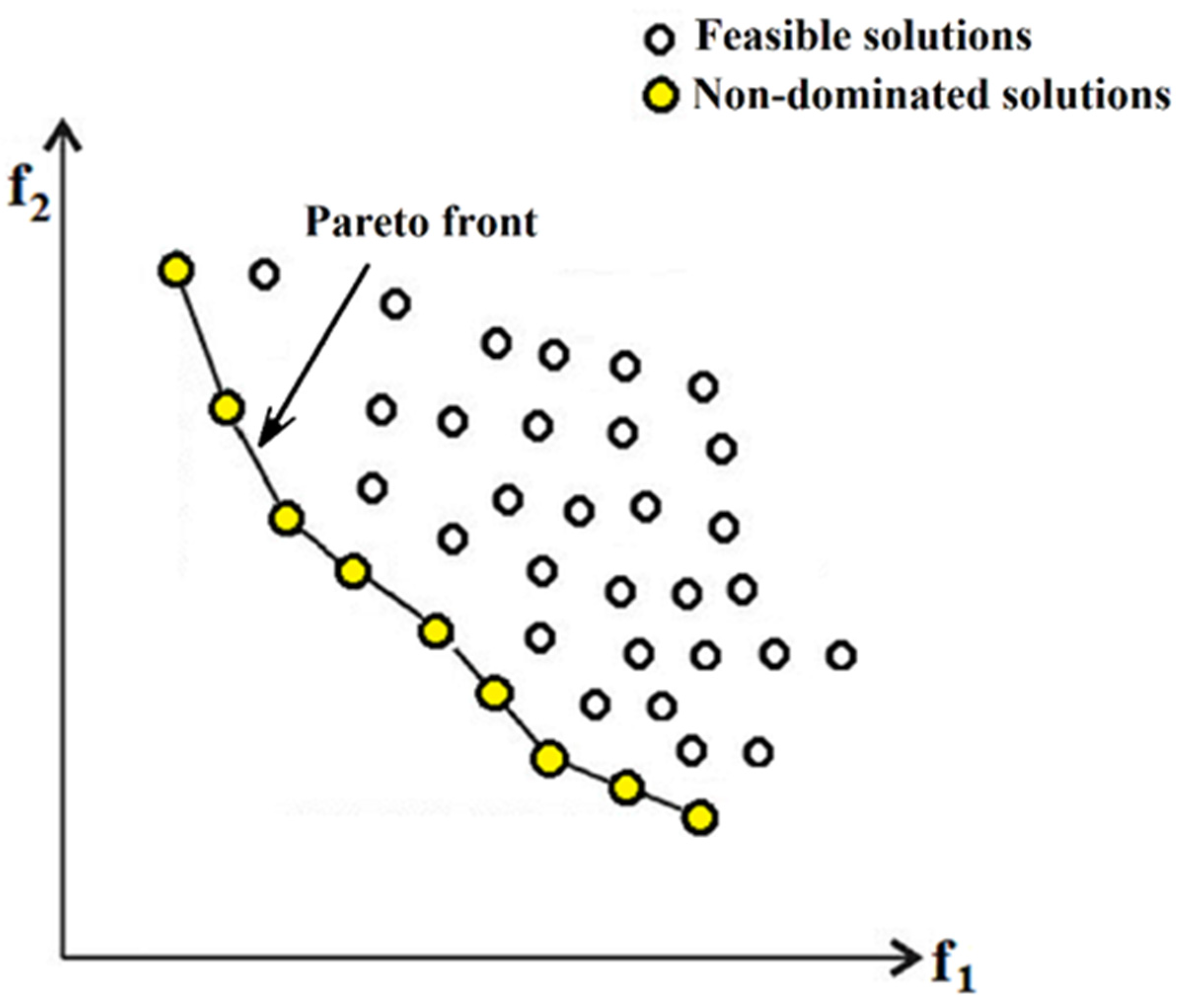
4. Multi-Objective Optimization of Processing via ML
5. Artificial Neural Network (ANN)
6. Data-Driven Multi-Objective Optimization of Artificial Neural Network
7. Multi-Objective Optimization of Processing Parameters in DED
8. Conclusions
- Key findings: Firstly, the validation process was successfully implemented and then a series of tests were carried out to create the data for ANN and NSGA to find the optimal combination of laser power, scanning speed and laser beam radius to reduce the residual stress and displacement. The application of ANN and NSGA enabled the identification of an optimal combination of processing parameters
- Main Advantages: The achievement from the current study illustrated significant enhancement in controlling residual stress and geometrical deviation. This highlights the potential of combining FE simulation with ML algorithms to enhance the efficiency and precision of the DED process, offering a more accurate approach to process optimization.
- Implications for Future Research: The obtained results serve as an applicable reference for further process validation and refinement, particularly when compared to experimental data. This research contributes to a deeper understanding of how different processing parameters affect the overall thermo-mechanical behavior of the DED process, providing insight for future advancements in additive manufacturing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Directed Energy Deposition | DED | Non-dominated Sorting Genetic Algorithm | NSGA |
| Machine Learning | ML | Laser Metal Deposition | LMD |
| Finite Element | FE | Direct Laser Metal Deposition | DLMD |
| Artificial Neural Network | ANN | Particle Swarm Optimization | PSO |
| Multilayer Perceptron | MLP | Wire Laser Metal Deposition | WLMD |
| Artificial Intelligence | AI | Back Propagation | BP |
References
- Ghasempour-Mouziraji, M.; Lagarinhos, J.; Afonso, D. A review study on metal powder materials and processing parameters in Laser Metal Deposition. Opt. Laser Technol. 2024, 170, 110226. [Google Scholar] [CrossRef]
- Shah, K.; Pinkerton, A.J.; Salman, A.; Li, L. Effects of melt pool variables and process parameters in laser direct metal deposition of aerospace alloys. Mater. Manuf. Process. 2010, 25, 1372–1380. [Google Scholar] [CrossRef]
- Kulkarni, M.; Mazare, A.; Schmuki, P.; Iglič, A. Biomaterial surface modification of titanium and titanium alloys for medical applications. In Nanomedicine; One Central Press: Manchester, UK, 2014; pp. 111–615. [Google Scholar]
- Miguel, F.; Ramalho, Q. Study of the Laser Metal Deposition (LMD) Technology in the Automotive Industry. Master’s Thesis, Instituto Politecnico de Leiria, Leiria, Portugal, 2019. [Google Scholar]
- Costa, L.; Vilar, R.; Reti, T.; Deus, A.M. Rapid tooling by laser powder deposition: Process simulation using finite element analysis. Acta Mater. 2005, 53, 3987–3999. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Hao, X. An adaptive machining approach based on in-process inspection of interim machining states for large-scaled and thin-walled complex parts. Int. J. Adv. Manuf. Technol. 2017, 90, 3119–3128. [Google Scholar] [CrossRef]
- Song, L.; Zeng, G.; Xiao, H.; Xiao, X.; Li, S. Repair of 304 stainless steel by laser cladding with 316L stainless steel powders followed by laser surface alloying with WC powders. J. Manuf. Process. 2016, 24, 116–124. [Google Scholar] [CrossRef]
- Rombouts, M.; Maes, G.; Hendrix, W.; Delarbre, E.; Motmans, F. Surface finish after laser metal deposition. Phys. Procedia 2013, 41, 810–814. [Google Scholar] [CrossRef]
- Ghasempour-Mouziraji, M.; Afonso, D.; Hosseinzadeh, S.; Goulas, C.; Najafizadeh, M.; Hosseinzadeh, M.; Ganji, D.; de Sousa, R.A. Modeling the effect of processing parameters on temperature history in Directed Energy Deposition: An analytical and finite element approach. Rapid Prototyp. J. 2023, 30, 338–349. [Google Scholar] [CrossRef]
- Ghasempour, M.; Afonso, D.; Torcato, R. Numerical investigation of deposition strategies on the residual stress and geometrical deviation in Laser Metal Deposition. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 012095. [Google Scholar] [CrossRef]
- Mazzarisi, M.; Angelastro, A.; Latte, M.; Colucci, T.; Palano, F.; Campanelli, S.L. Thermal monitoring of laser metal deposition strategies using infrared thermography. J. Manuf. Process. 2023, 85, 594–611. [Google Scholar] [CrossRef]
- Ghasempour-Mouziraji, M.; Hosseinzadeh, M.; Hajimiri, H.; Najafizadeh, M.; Marzban Shirkharkolaei, E. Machine learning-based optimization of geometrical accuracy in wire cut drilling. Int. J. Adv. Manuf. Technol. 2022, 123, 4265–4276. [Google Scholar] [CrossRef]
- Moradi, M.; Hasani, A.; Pourmand, Z.; Lawrence, J. Direct laser metal deposition additive manufacturing of Inconel 718 superalloy: Statistical modelling and optimization by design of experiments. Opt. Laser Technol. 2021, 144, 107380. [Google Scholar] [CrossRef]
- Pant, P.; Chatterjee, D. Prediction of clad characteristics using ANN and combined PSO-ANN algorithms in laser metal deposition process. Surf. Interfaces 2020, 21, 100699. [Google Scholar] [CrossRef]
- Pellizzari, M.; Zhao, Z.; Bosetti, P.; Perini, M. Optimizing direct laser metal deposition of H13 cladding on CuBe alloy substrate. Surf. Coat. Technol. 2022, 432, 128084. [Google Scholar] [CrossRef]
- Mahamood, R.M.; Akinlabi, E.T. Processing Parameters Optimization for Material Deposition Efficiency in Laser Metal Deposited Titanium Alloy. Lasers Manuf. Mater. Process. 2016, 3, 9–21. [Google Scholar] [CrossRef]
- Li, R.; Ju, G.; Zhao, X.; Zhang, Y.; Li, Y.; Hu, G.; Yan, M.; Wu, Y.; Lin, D. Simulation of residual stress and distortion evolution in dual-robot collaborative wire-arc additive manufactured Al-Cu alloys. Virtual Phys. Prototyp. 2024, 19, e2409390. [Google Scholar] [CrossRef]
- Wu, C.; Wan, B.; Entezari, A.; Fang, J.; Xu, Y.; Li, Q. Machine learning-based design for additive manufacturing in biomedical engineering. Int. J. Mech. Sci. 2024, 266, 108828. [Google Scholar] [CrossRef]
- Mu, H.; He, F.; Yuan, L.; Hatamian, H.; Commins, P.; Pan, Z. Online distortion simulation using generative machine learning models: A step toward digital twin of metallic additive manufacturing. J. Ind. Inf. Integr. 2024, 38, 100563. [Google Scholar] [CrossRef]
- Loreau, T.; Champaney, V.; Hascoet, N.; Lambarri, J.; Madarieta, M.; Garmendia, I.; Chinesta, F. Parametric analysis and machine learning-based parametric modeling of wire laser metal deposition induced porosity. Int. J. Mater. Form. 2022, 15, 33. [Google Scholar] [CrossRef]
- Israr, R.; Buhl, J.; Elze, L.; Bambach, M. Simulation of different path for WAAM with Lagrangian finite element methods. In Proceedings of the 15th LS-DYNA Forum 2018, Bamberg, Germany, 15–17 October 2018. [Google Scholar]
- Lampa, C.; Kaplan, A.F.H.; Powell, J.; Magnusson, C. An analytical thermodynamic model of laser welding. J. Phys. D Appl. Phys. 1997, 30, 1293–1299. [Google Scholar] [CrossRef]
- Alimardani, M.; Toyserkani, E.; Huissoon, J.P. A 3D dynamic numerical approach for temperature and thermal stress distributions in multilayer laser solid freeform fabrication process. Opt. Lasers Eng. 2007, 45, 1115–1130. [Google Scholar] [CrossRef]
- Stainless Steel 316: What Is It? How Is It Made? Grades n.d. Available online: https://www.iqsdirectory.com/articles/stainless-steel/stainless-steel-316.html (accessed on 6 November 2022).
- Kiranmayi, A.V. Characterising High Energy Beam Welding In Structural Steels with Numerical Simulation and Validation. Ph.D. Thesis, University of Bristol, Bristol, UK, 2015. [Google Scholar]
- Biegler, M.; Graf, B.; Rethmeier, M. In-situ distortions in LMD additive manufacturing walls can be measured with digital image correlation and predicted using numerical simulations. Addit. Manuf. 2018, 20, 101–110. [Google Scholar] [CrossRef]
- El Naqa, I.; Murphy, M.J. Machine Learning in Radiation Oncology. In Machine Learning in Radiation Oncology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–11. [Google Scholar] [CrossRef]
- Wiens, J.; Shenoy, E.S. Machine Learning for Healthcare: On the Verge of a Major Shift in Healthcare Epidemiology. Clin. Infect. Dis. 2018, 66, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Wäldchen, J.; Mäder, P. Machine learning for image based species identification. Methods Ecol. Evol. 2018, 9, 2216–2225. [Google Scholar] [CrossRef]
- Thiede, S.; Ghafoorpoor, P.; Sullivan, B.P.; Bienia, S.; Demes, M. Potentials and technical implications of tag based and AI enabled optical real-time location systems (RTLS) for manufacturing use cases. CIRP Ann. 2022, 71, 401–404. [Google Scholar] [CrossRef]
- Nasiri, S.; Khosravani, M.R. Machine learning in predicting mechanical behavior of additively manufactured parts. J. Mater. Res. Technol. 2021, 14, 1137–1153. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Esche, E.; Fischer, A.; Kloft, M.; Repke, J.U.; Sager, S.; Mitsos, A. Machine Learning in Chemical Engineering: A Perspective. Chem.-Ing.-Tech. 2021, 93, 2029–2039. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Multi-Objective Optimization using Evolutionary Algorithms. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Burke, E.K.; Graham, K. Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Yarmohammadi, S.; Mohammadzadeh, K.; Farhadi, M.; Hajimiri, H.; Modir, A. Multi-objective optimization of thermal and flow characteristics of R-404A evaporation through corrugated tubes. J. Energy Storage 2020, 27, 101137. [Google Scholar] [CrossRef]
- Yarmohammadi, S.; Farhadi, M.; Hajimiri, H.; Salimpour, M.R. Multi-Objective Optimization of R-404A Vapor Condensation in Swirling Flow Using Genetic Algorithms. Heat. Transf. Eng. 2017, 38, 137–148. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Fernando, M.; Vieira, G.; Rosanete, A.; Reis, L. Effects of Processing Parameters on Direct Laser Deposited Materials for Industrial Components Repair. Ph.D. Thesis, University of Porto, Porto, Portugal, 2022. [Google Scholar]
- Kusuma, C. The Effect of Laser Power and Scan Speed on Melt Pool Characteristics of Pure Titanium and Ti-6Al-4V Alloy for Selective Laser Melting. Master’s Thesis, Wright State University, Dayton, OH, USA, 2016. [Google Scholar]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Yang, H.; Huang, W. Residual stress and distortion of rectangular and S-shaped Ti-6Al-4V parts by Directed Energy Deposition: Modelling and experimental calibration. Addit. Manuf. 2019, 26, 166–179. [Google Scholar] [CrossRef]
- Woo, S.S.; Lee, K.Y.; Baek, G.Y.; Kim, J.W. Residual stress variations in substrate (AISI D2) during directed energy deposition process of high-speed tool steel (AISI M4) powder. J. Alloy. Metall. Syst. 2024, 6, 100080. [Google Scholar] [CrossRef]
- Xiao, Z.; Chen, C.; Zhu, H.; Hu, Z.; Nagarajan, B.; Guo, L.; Zeng, X. Study of residual stress in selective laser melting of Ti6Al4V. Mater. Des. 2020, 193, 108846. [Google Scholar] [CrossRef]
- Sow, M.C.; De Terris, T.; Castelnau, O.; Hamouche, Z.; Coste, F.; Fabbro, R.; Peyre, P. Influence of beam diameter on Laser Powder Bed Fusion (L-PBF) process. Addit. Manuf. 2020, 36, 101532. [Google Scholar] [CrossRef]

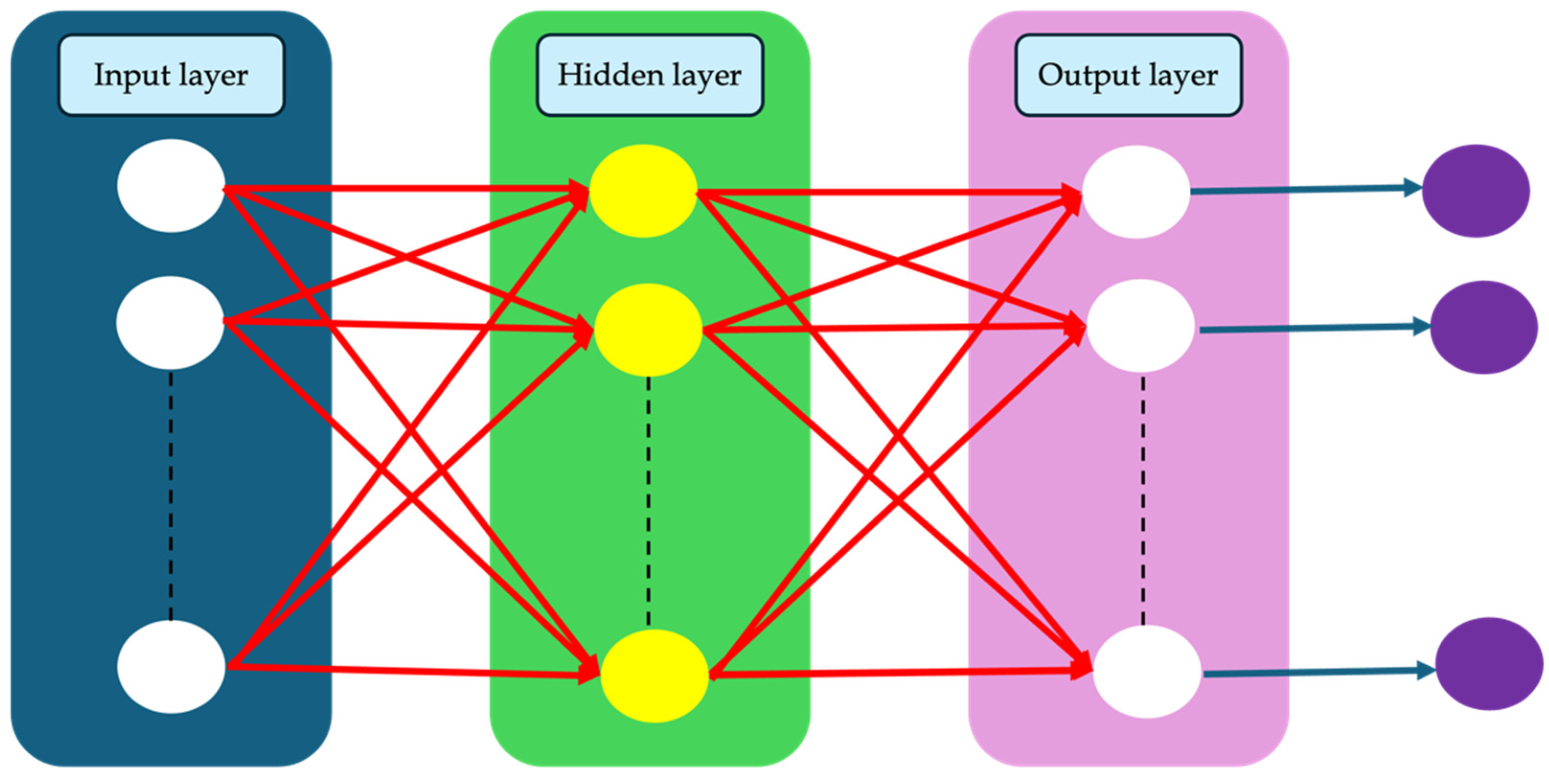
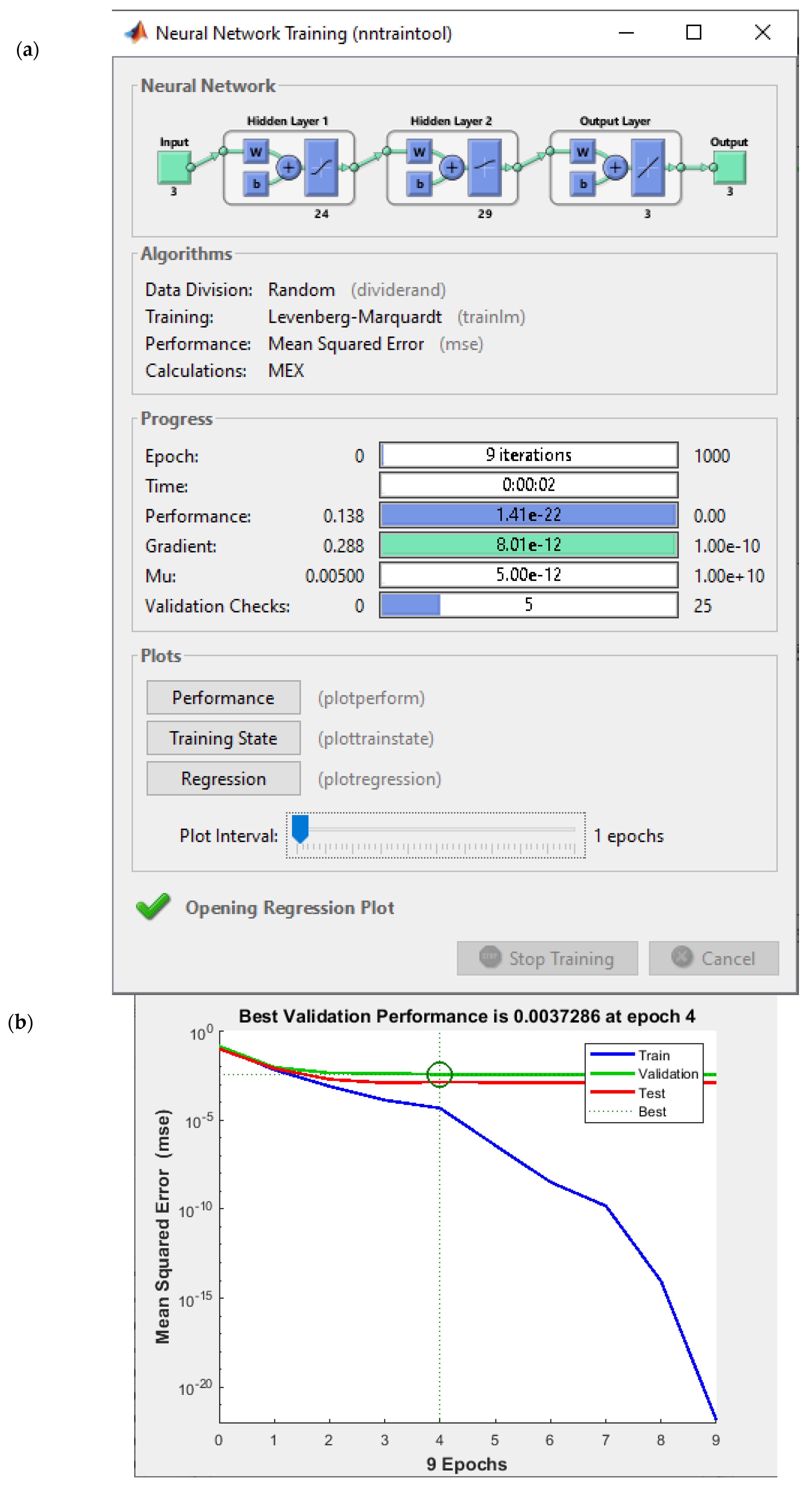
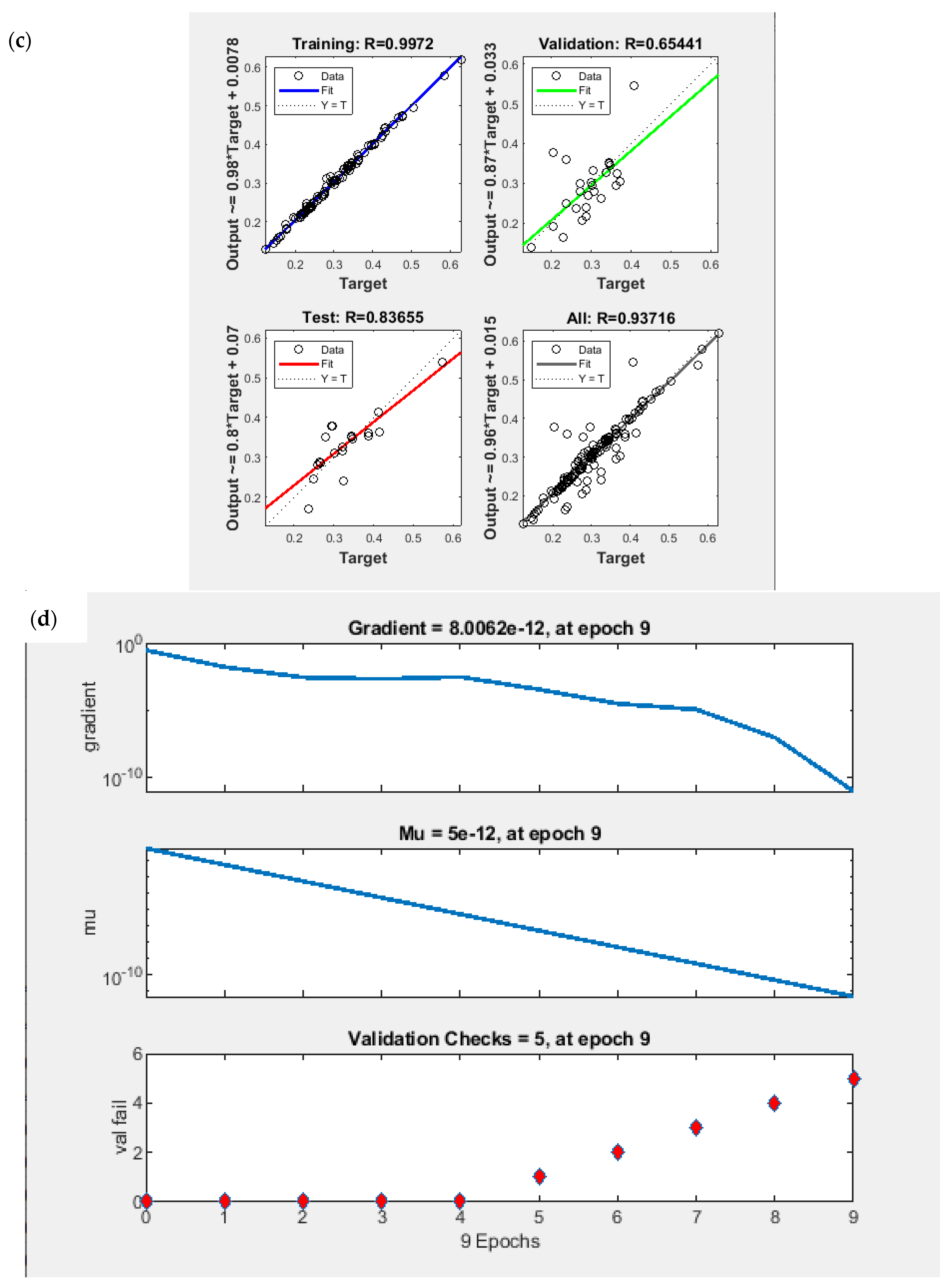
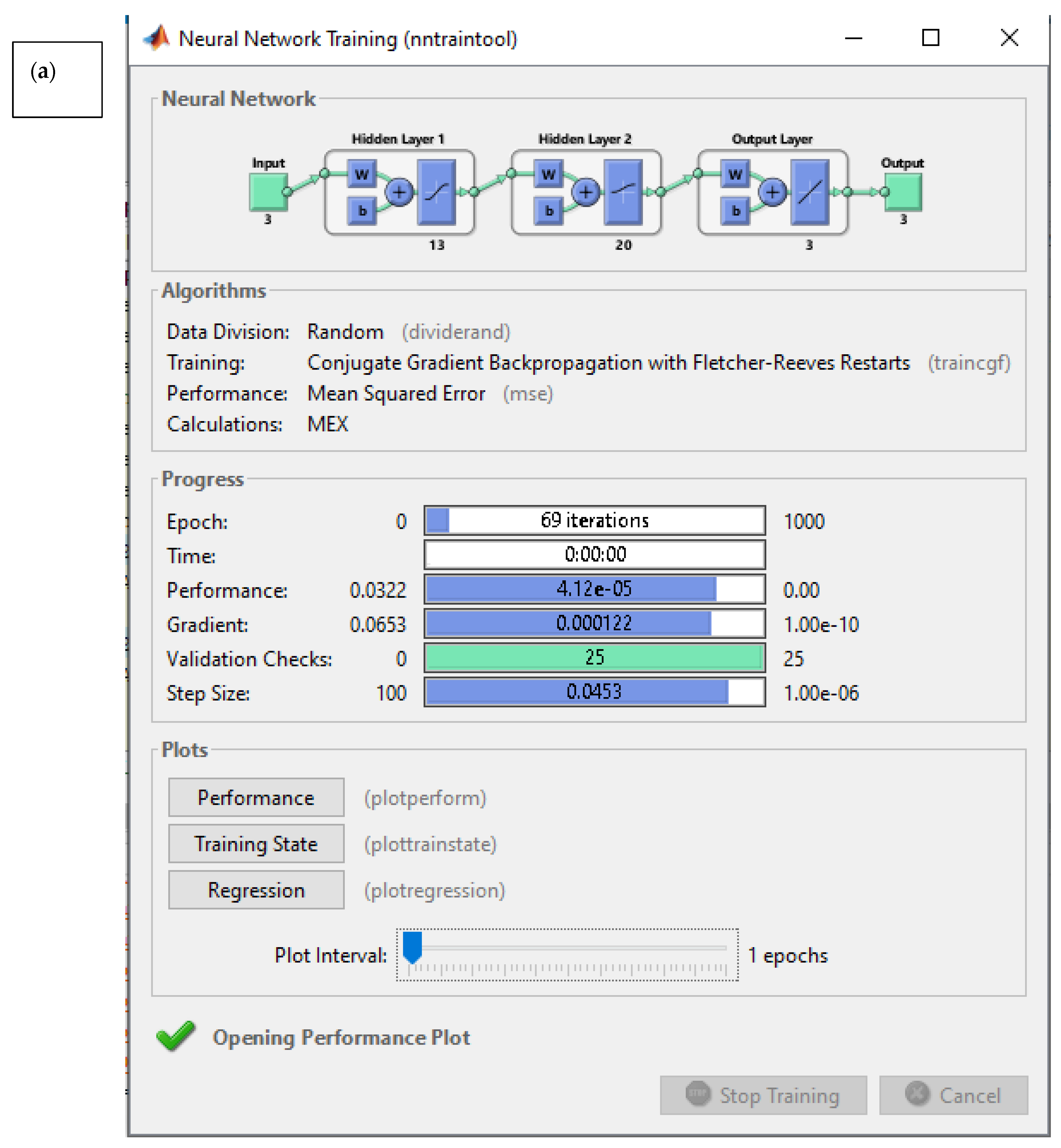
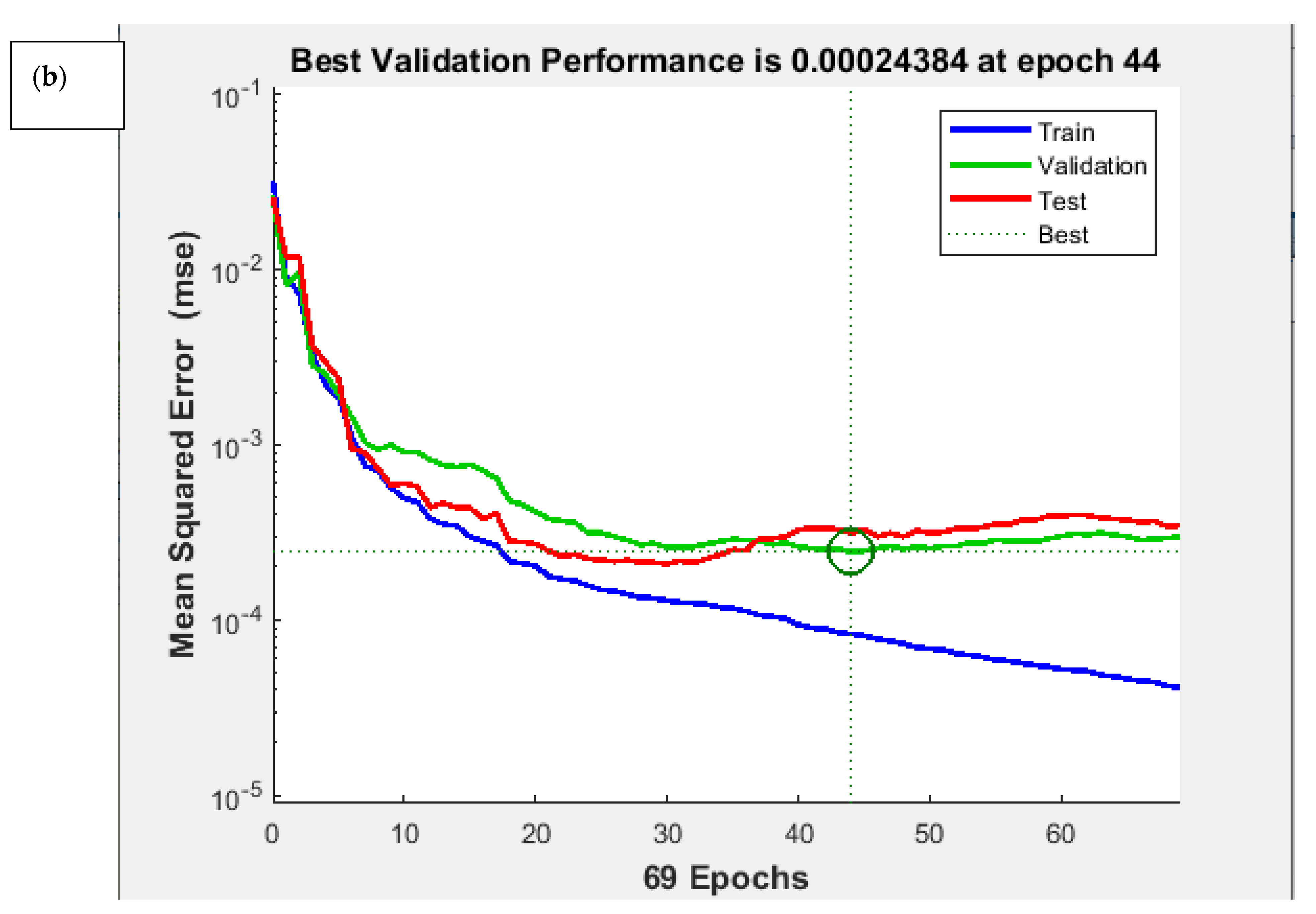
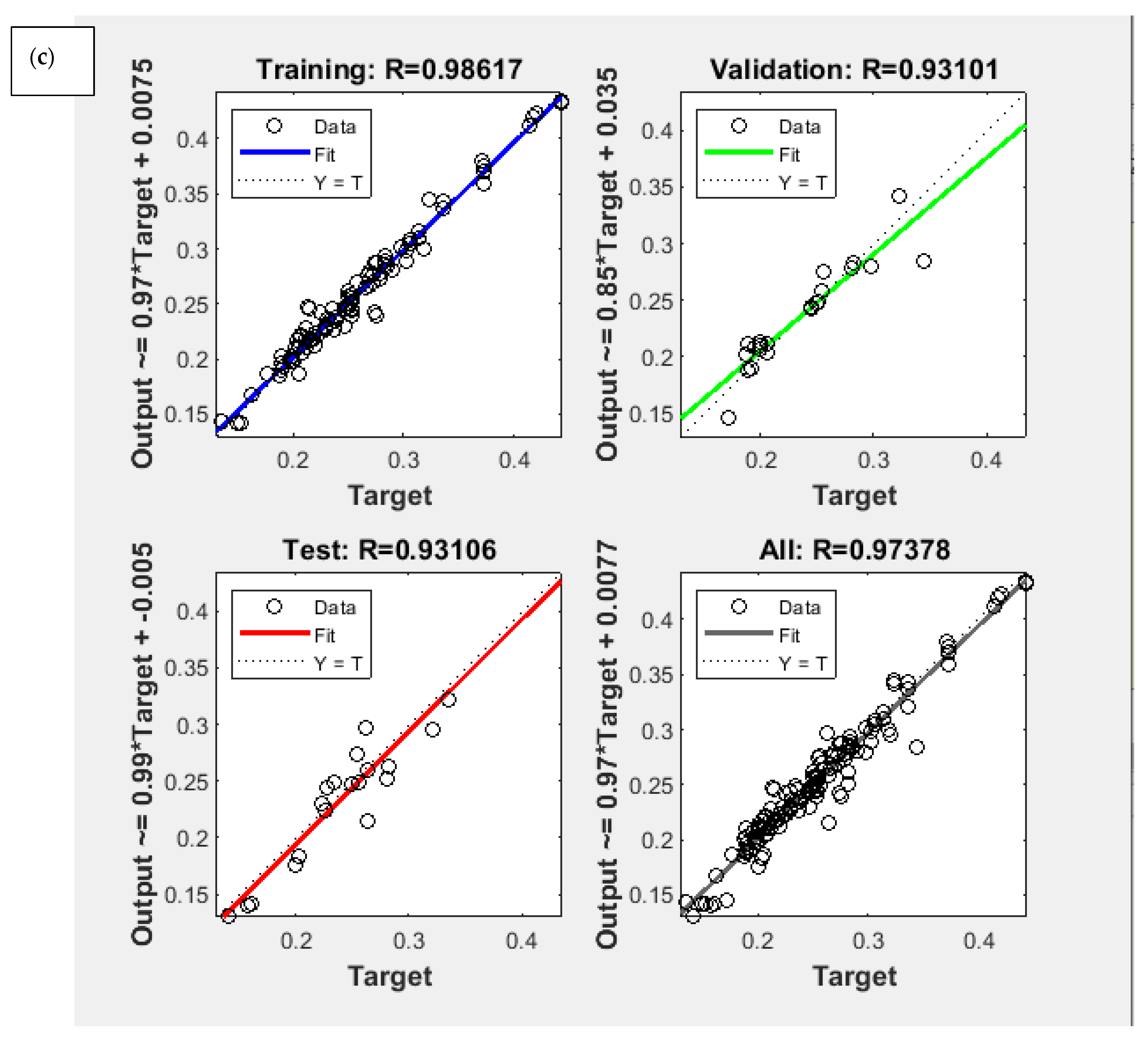


| Back Propagation Algorithm | Number of Neurones in 1st Layer | Number of Neurones in 2nd Layer | Transfer Function in 1st Hidden Layer | Transfer Function in 2nd Hidden Layer | Train Error (%) | Test Error (%) | |
|---|---|---|---|---|---|---|---|
| A | TrainLM | 24 | 29 | Tan-sig | Log-sig | 4.326 | 7.760 |
| B | TrainBR | 20 | 10 | Tan-sig | Log-sig | 4.412 | 7.160 |
| C | TrainCGF | 20 | 9 | Tan-sig | Log-sig | 4.332 | 7.566 |
| Back Propagation Algorithm | Number of Neurones in 1st Layer | Number of Neurones in 2nd Layer | Transfer Function in 1st Hidden Layer | Transfer Function in 2nd Hidden Layer | Train Error (%) | Test Error (%) | |
|---|---|---|---|---|---|---|---|
| A | TrainCGF | 13 | 20 | Tan-sig | Log-sig | 2.518 | 3.782 |
| Parameter | Value |
|---|---|
| population size | 40 chromosomes |
| mutation rate | 0.1 |
| crossover rate | 0.85 over 40 generations |
| Execution time for each network | 10 times |
| Laser Power (W) | Scanning Speed (mm/s) | Laser Beam Radius (mm) | Displacement (mm) (NSGA) | Residual Stress (NSGA) | Displacement (mm) (FE Simulation) | Residual Stress (FE Simulation) |
|---|---|---|---|---|---|---|
| 684.93 | 10.46 | 0.59 | 1.56 | 450.57 | 1.62 | 489 |
| 713.12 | 10.73 | 0.57 | 1.46 | 457.17 | 1.51 | 491 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasempour-Mouziraji, M.; Afonso, D.; Alves de Sousa, R. On the Prediction and Optimisation of Processing Parameters in Directed Energy Deposition of SS316L via Finite Element Simulation and Machine Learning. Materials 2025, 18, 1039. https://doi.org/10.3390/ma18051039
Ghasempour-Mouziraji M, Afonso D, Alves de Sousa R. On the Prediction and Optimisation of Processing Parameters in Directed Energy Deposition of SS316L via Finite Element Simulation and Machine Learning. Materials. 2025; 18(5):1039. https://doi.org/10.3390/ma18051039
Chicago/Turabian StyleGhasempour-Mouziraji, Mehran, Daniel Afonso, and Ricardo Alves de Sousa. 2025. "On the Prediction and Optimisation of Processing Parameters in Directed Energy Deposition of SS316L via Finite Element Simulation and Machine Learning" Materials 18, no. 5: 1039. https://doi.org/10.3390/ma18051039
APA StyleGhasempour-Mouziraji, M., Afonso, D., & Alves de Sousa, R. (2025). On the Prediction and Optimisation of Processing Parameters in Directed Energy Deposition of SS316L via Finite Element Simulation and Machine Learning. Materials, 18(5), 1039. https://doi.org/10.3390/ma18051039








