Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts
Abstract
1. Introduction
2. Theoretical Background
2.1. Strain Energy Density Function
2.2. Hyperelastic Model
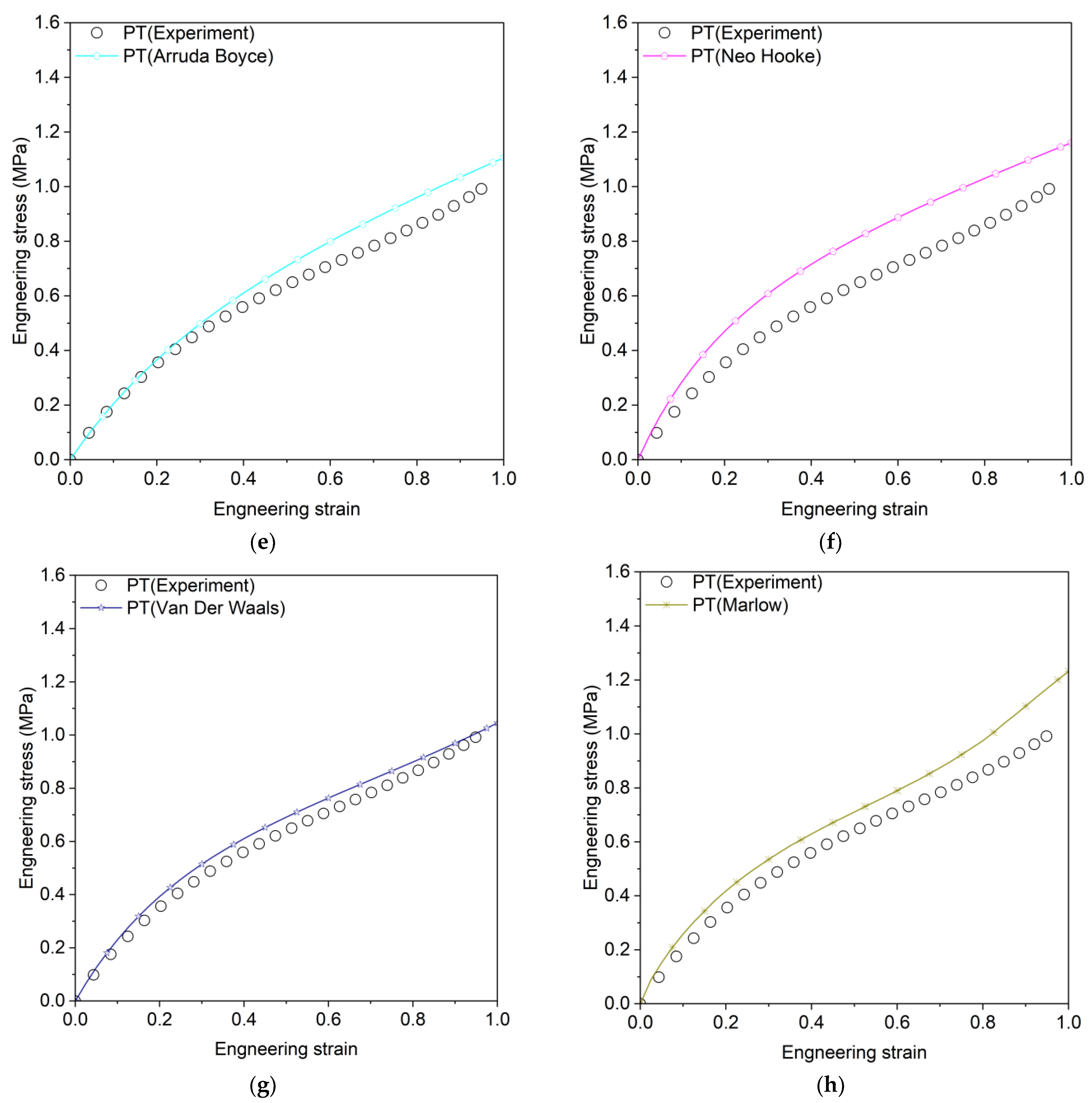
2.2.1. Arruda–Boyce Model
2.2.2. Marlow Model
2.2.3. Mooney–Rivlin Model
2.2.4. Neo-Hookean Model
2.2.5. Ogden Model
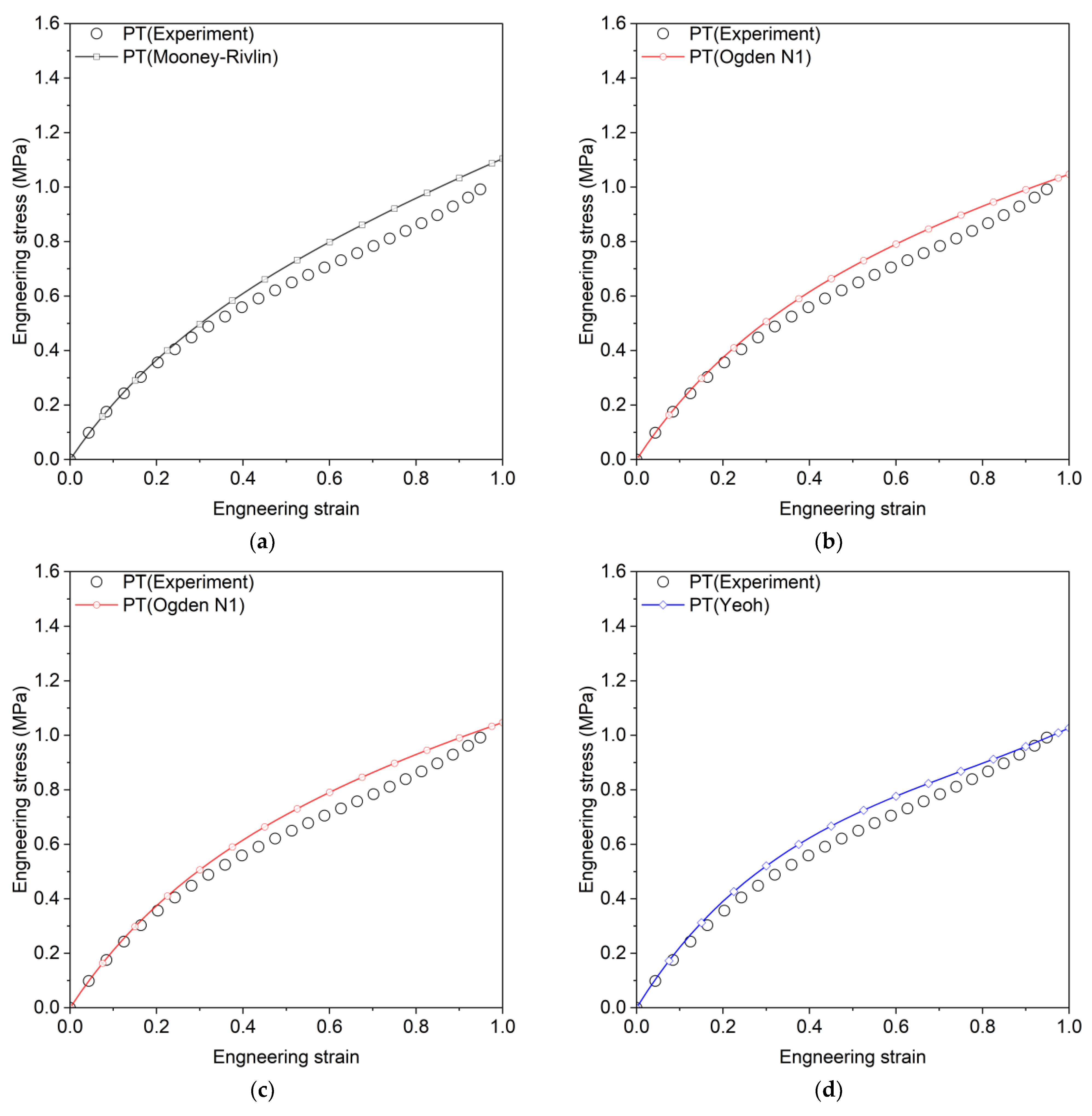
2.2.6. Yeoh Model
2.2.7. Van Der Waals Model
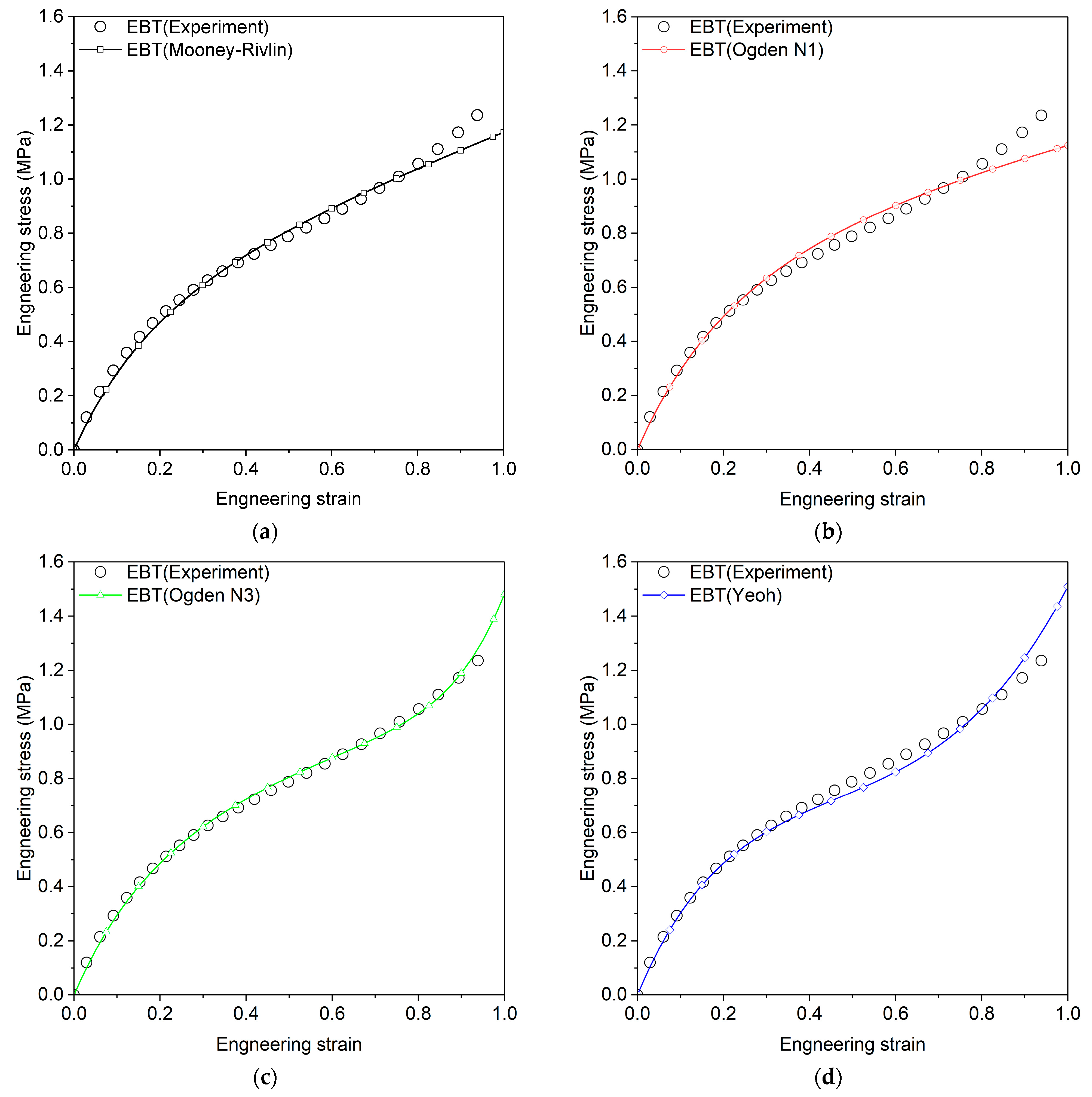
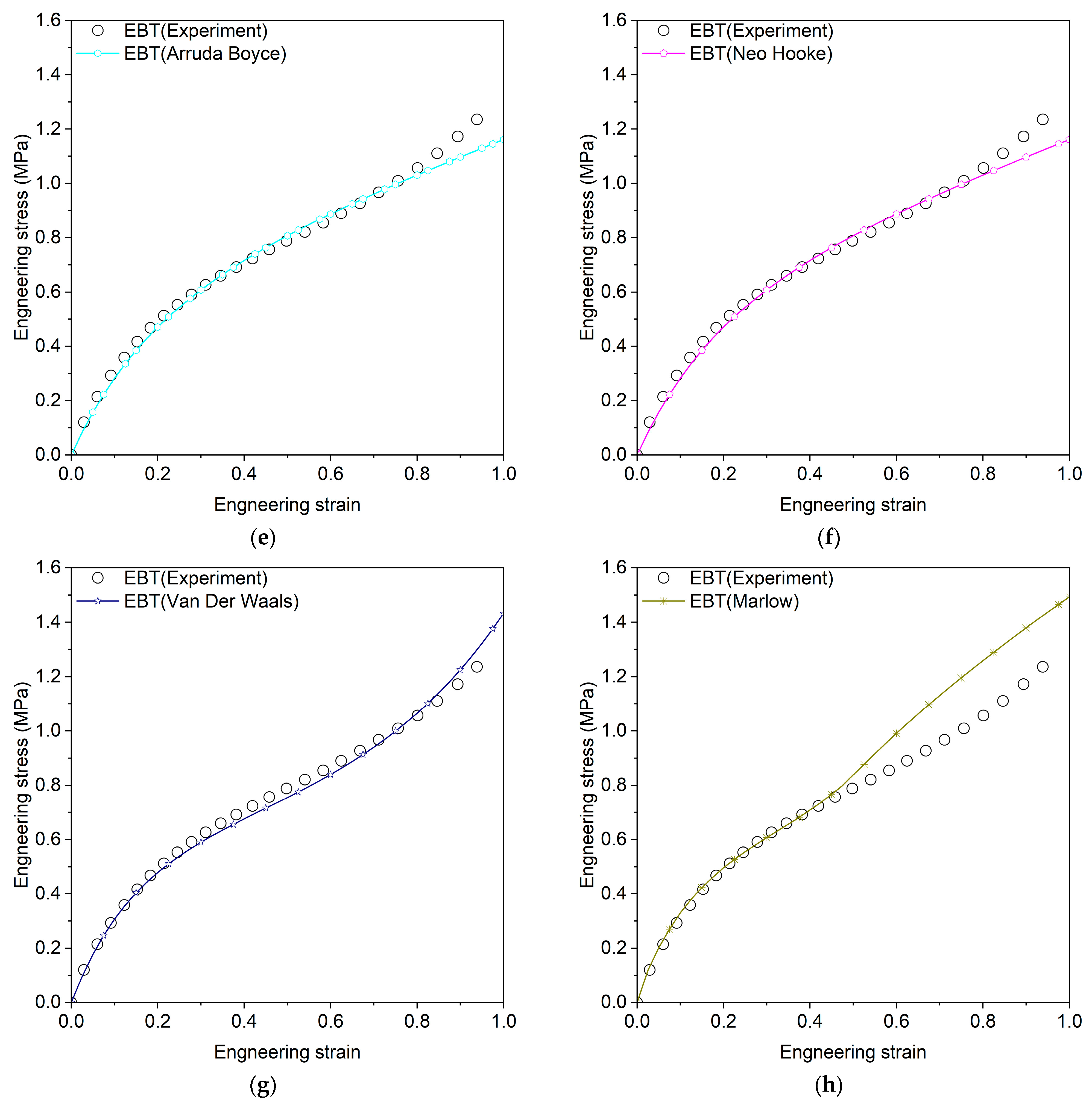
3. Hyperelastic Model Parameters Identification
3.1. Previous Experiments for Material Constant Calibration
3.2. Review of Hyperelastic Models
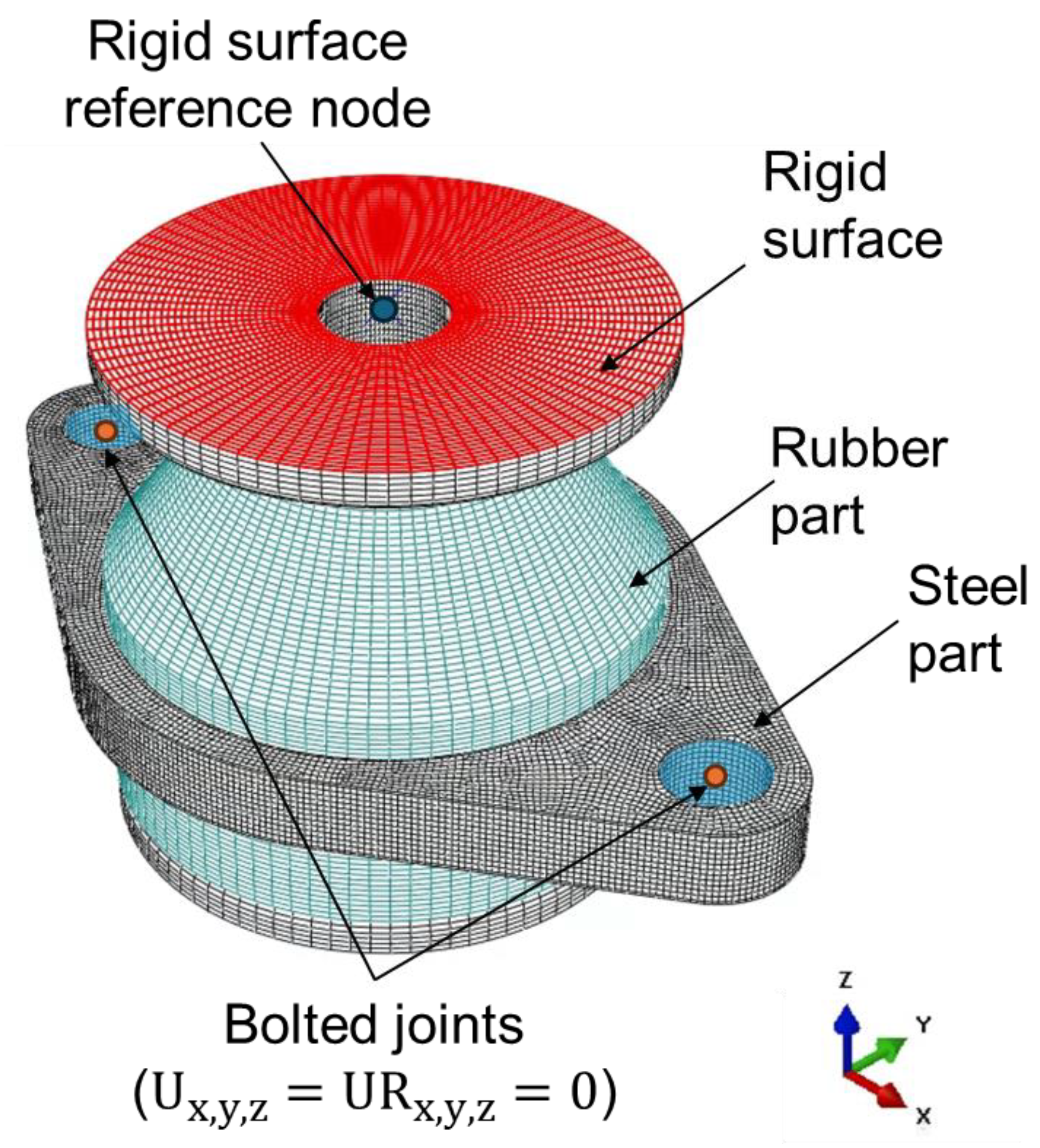
4. Finite Element Implementation of Resilient Mount
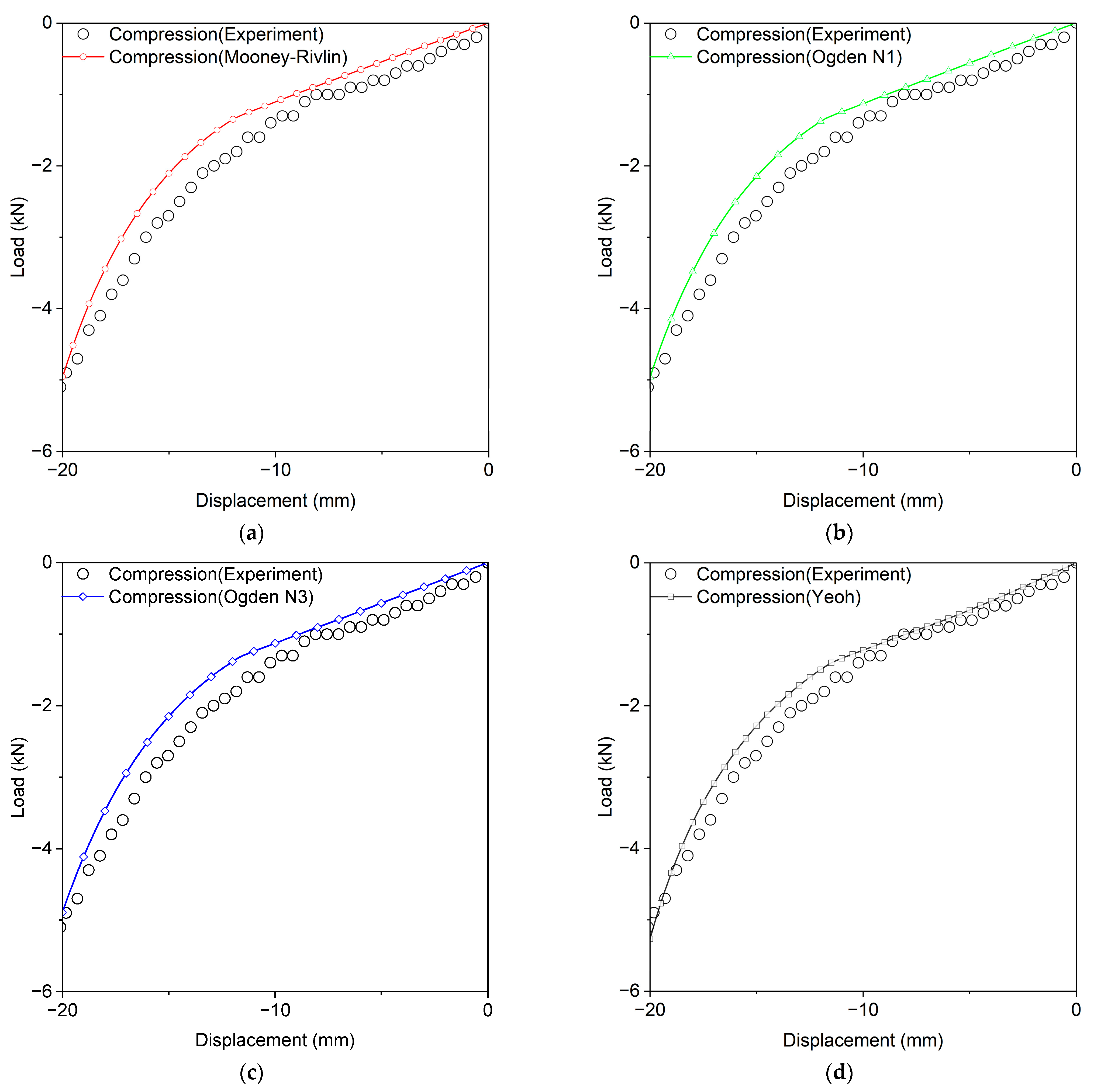
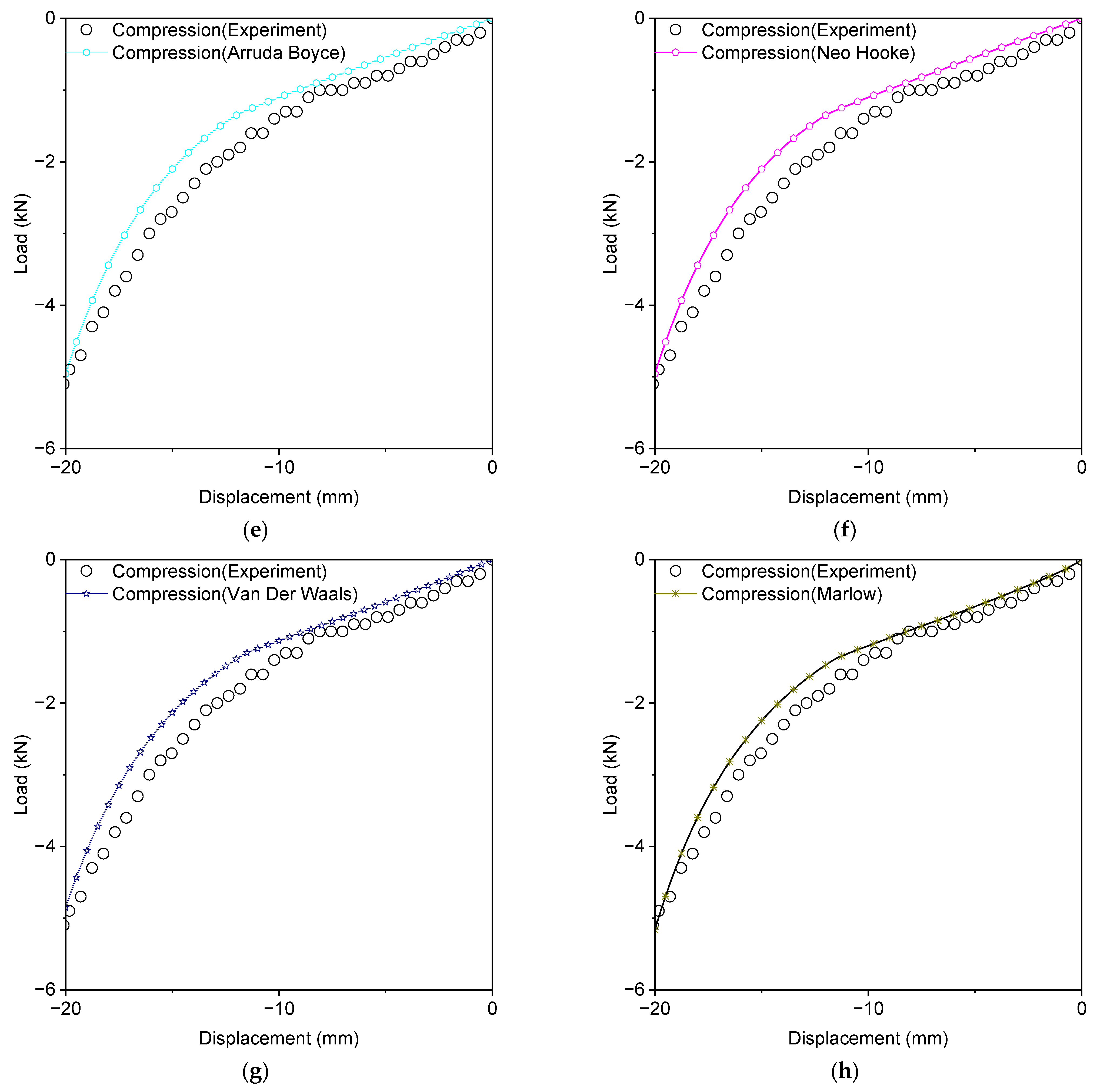
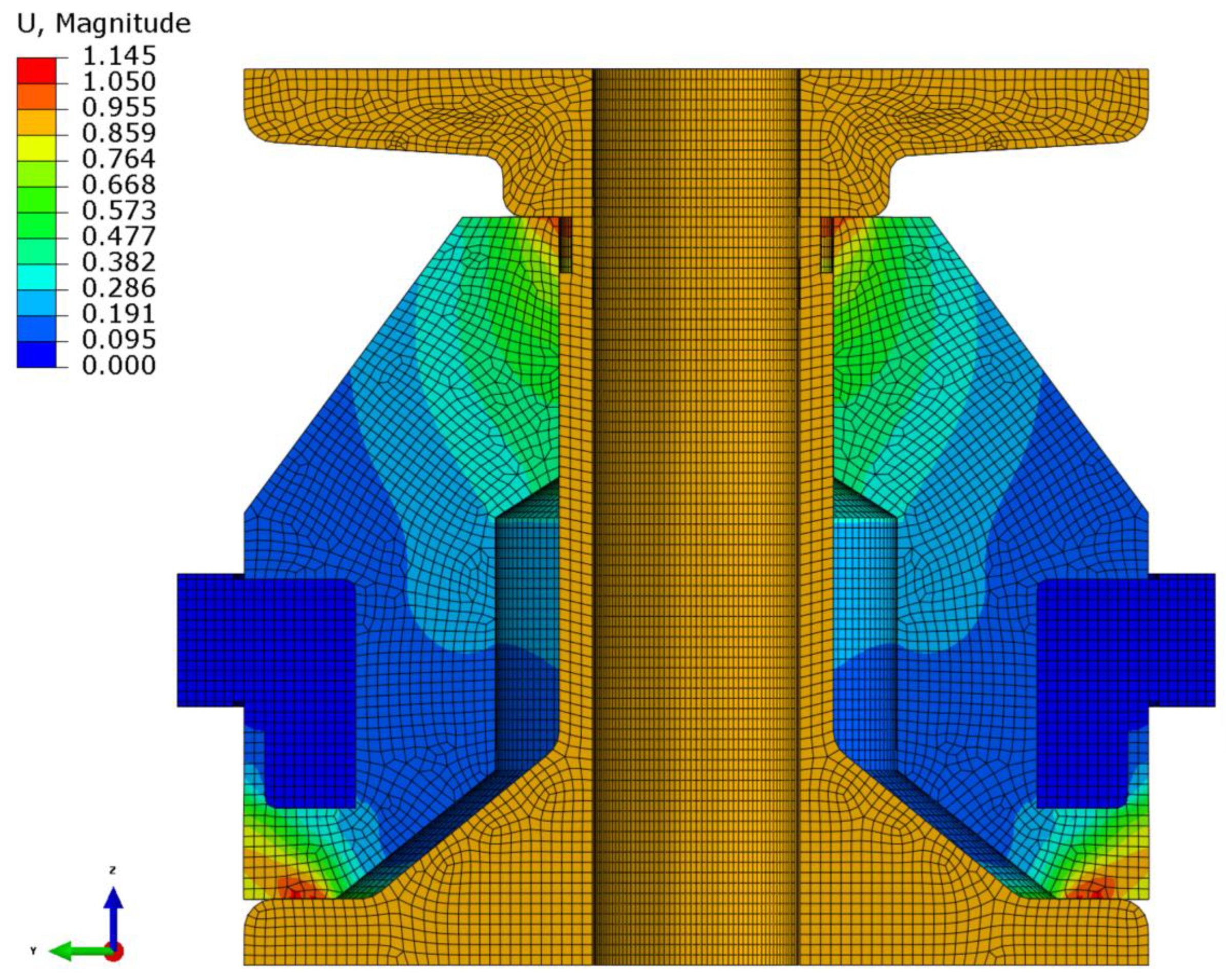
4.1. Static Analysis
4.2. Dynamic Analysis
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amin, A.F.; Wiraguna, S.I.; Bhuiyan, A.R.; Okui, Y. Hyperelasticity Model for Finite Element Analysis of Natural and High Damping Rubbers in Compression and Shear. J. Eng. Mech. 2006, 132, 54–64. [Google Scholar] [CrossRef]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y. Classic strain energy functions and constitutive tests of rubber-like materials. Rubber Chem. Technol. 2015, 88, 604–627. [Google Scholar] [CrossRef]
- Gorash, Y.; Comlekci, T.; Hamilton, R. CAE-Based application for identification and verification of hyperelastic parameters. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 231, 611–626. [Google Scholar] [CrossRef]
- Nörenberg, N.; Mahnken, R. Parameter identification for rubber materials with artificial spatially distributed data. Comput. Mech. 2015, 56, 353–370. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Li, A. Parameter Identification Methods for Hyperelastic and Hyper-Viscoelastic Models. Appl. Sci. 2016, 6, 386. [Google Scholar] [CrossRef]
- Kari, L. Dynamic transfer stiffness measurements of vibration isolators in the audible frequency range. Noise Control. Eng. J. 2001, 49, 88. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, J.S.; Kim, K.J.; Ahn, T.; Choi, B.I.; Lee, H.J.; Woo, C.S.; Kim, K.S. Prediction of dynamic stiffness on rubber components considering preloads. Mater. Und Werkst. 2013, 44, 372–379. [Google Scholar] [CrossRef]
- Moro, L.; Biot, M. Laboratory tests pave the way for the knowledge of dynamic response of resilient mountings on board ships. In Proceedings of the The International Symposium on Practical Design of Ships and Other Floating Structures (PRADS), CECO, Changwon City, Republic of Korea, 20–25 October 2013. [Google Scholar]
- Carrella, A. Nonlinear identifications using transmissibility: Dynamic characterisation of Anti Vibration Mounts (AVMs) with standard approach and nonlinear analysis. Int. J. Mech. Sci. 2012, 63, 74–85. [Google Scholar] [CrossRef]
- Külcü, İ.D. A hyperelastic constitutive model for rubber-like materials. Arch. Appl. Mech. 2020, 90, 615–622. [Google Scholar] [CrossRef]
- Plagge, J.; Ricker, A.; Kröger, N.H.; Wriggers, P.; Klüppel, M. Efficient modeling of filled rubber assuming stress-induced microscopic restructurization. Int. J. Eng. Sci. 2020, 151, 103291. [Google Scholar] [CrossRef]
- Miroshnychenko, D.; Green, W.A. Heuristic search for a predictive strain-energy function in nonlinear elasticity. Int. J. Solids Struct. 2009, 46, 271–286. [Google Scholar] [CrossRef][Green Version]
- Nicholson, D.W.; Nelson, N.W.; Lin, B.; Farinella, A. Finite Element Analysis of Hyperelastic Components. Appl. Mech. Rev. 1998, 51, 303–320. [Google Scholar] [CrossRef]
- Seibert, D.J.; Schöcke, N. Direct Comparison of Some Recent Rubber Elasticity Models. Rubber Chem. Technol. 2000, 73, 366–384. [Google Scholar] [CrossRef]
- Horgan, C.O.; Smayda, M.G. The importance of the second strain invariant in the constitutive modeling of elastomers and soft biomaterials. Mech. Mater. 2012, 51, 43–52. [Google Scholar] [CrossRef]
- Luo, R.K.; Wang, W.; Xu, Q.; Li, X. An energy dissipation approach on complete loading-unloading and dynamic impact predictions with experimental verification for rubber anti-vibration component. Polym. Test. 2017, 63, 314–322. [Google Scholar] [CrossRef]
- Fragasso, J.; Moro, L.; Lye, L.M.; Quinton, B.W.T. Characterization of resilient mounts for marine diesel engines: Prediction of static response via nonlinear analysis and response surface methodology. Ocean. Eng. 2019, 171, 14–24. [Google Scholar] [CrossRef]
- Íñiguez-Macedo, S.; Lostado-Lorza, R.; Escribano-García, R.; Martínez-Calvo, M.Á. Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization. Materials 2019, 12, 1019. [Google Scholar] [CrossRef]
- Fragasso, J.; Moro, L. Structure-borne noise of marine diesel engines: Dynamic characterization of resilient mounts. Ocean. Eng. 2022, 261, 112116. [Google Scholar] [CrossRef]
- Gong, D.; Duan, Y.; Wang, K.; Zhou, J. Modelling rubber dynamic stiffness for numerical predictions of the effects of temperature and speed on the vibration of a railway vehicle car body. J. Sound. Vib. 2019, 449, 121–139. [Google Scholar] [CrossRef]
- Emminger, C.; Çakmak, U.D.; Preuer, R.; Graz, I.; Major, Z. Hyperelastic material parameter determination and numerical study of TPU and PDMS dampers. Materials 2021, 14, 7639. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Guan, X.; Lu, P.; Guo, R. Simulation Research on Dynamic Characteristics of Hydraulic Mount. Chin. J. Mech. Eng. 2021, 34, 49. [Google Scholar] [CrossRef]
- Danko, J.; Nemec, T.; Milesich, T.; Magdolen, Ľ. Dynamic Stiffness Determination of the Rubber Bushing Fem Modelwith Viscoelastic Material Behaviour. Stroj. Časopis J. Mech. Eng. 2022, 72, 121–128. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A comparative study of 85 hyperelastic constitutive models for both unfilled rubber and highly filled rubber nanocomposite material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Sun, J.; Liu, X.-A.; Ou Yang, Y.-H.; Shangguan, W.-B. Parameters Identification of Mooney-Rivlin Model for Rubber Mount Based on Surrogate Model; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Mollaee, S.; Budgett, D.M.; Taberner, A.J.; Nielsen, P.M.F. Hyperelastic constitutive model parameters identification using optical-based techniques and hybrid optimisation. Int. J. Mech. Mater. Des. 2024, 20, 233–249. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Marlow, R.S. A general first-invariant hyperelastic constitutive model. Const. Models Rubber 2003, 157–160. Available online: https://www.tib.eu/en/search/id/BLCP%3ACN049725784/A-general-first-invariant-hyperelastic-constitutive/ (accessed on 16 December 2024).
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Saunders, D.W. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. London. A. Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of Elastic Properties of Carbon-Black-Filled Rubber Vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- van der Waals, J.D. On the Continuity of the Gaseous and Liquid States; Rowlinson, J.S., Ed.; Courier Corporation: North Chelmsford, MA, USA, 1988; p. 297. [Google Scholar]
- Park, S.-J.; Park, B.; Lee, J.-Y.; Shin, Y.-H.; Jeong, C.-L.; Kim, S.-J.; Kim, K. Study on Dynamic Characteristics of Resilient Mount Under Preload. Materials 2024, 17, 5096. [Google Scholar] [CrossRef]
- MIL-M-17508F; Military Specification: Mounts, Resilient: Types 6E100, 6E150, 7E450, 6E900, 6E2000, 5E3500, 6E100BB, 6E150BB, 7E450BB, and 6e900BB. Department of Navy: Monterey, CA, USA, 1990.

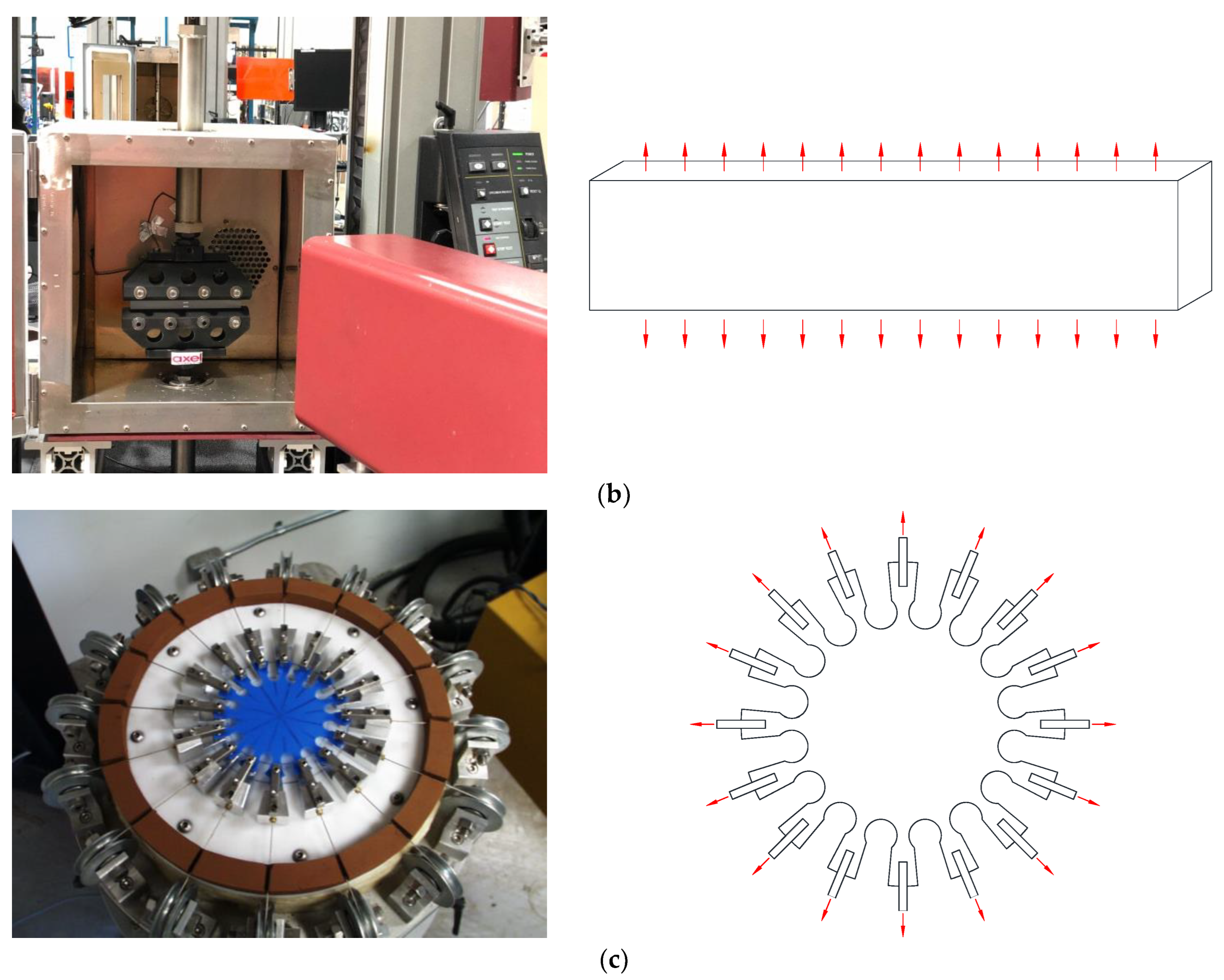


| Model | Strain Energy Density Function | Parameters |
|---|---|---|
| Arruda–Boyce | ||
| Marlow | - | |
| Mooney–Rivlin | ||
| Neo-Hookean | ||
| Ogden | ||
| Van Der Waals | ||
| Yoeh |
| Model | ) | |||
|---|---|---|---|---|
| UT | EBT | PT | ||
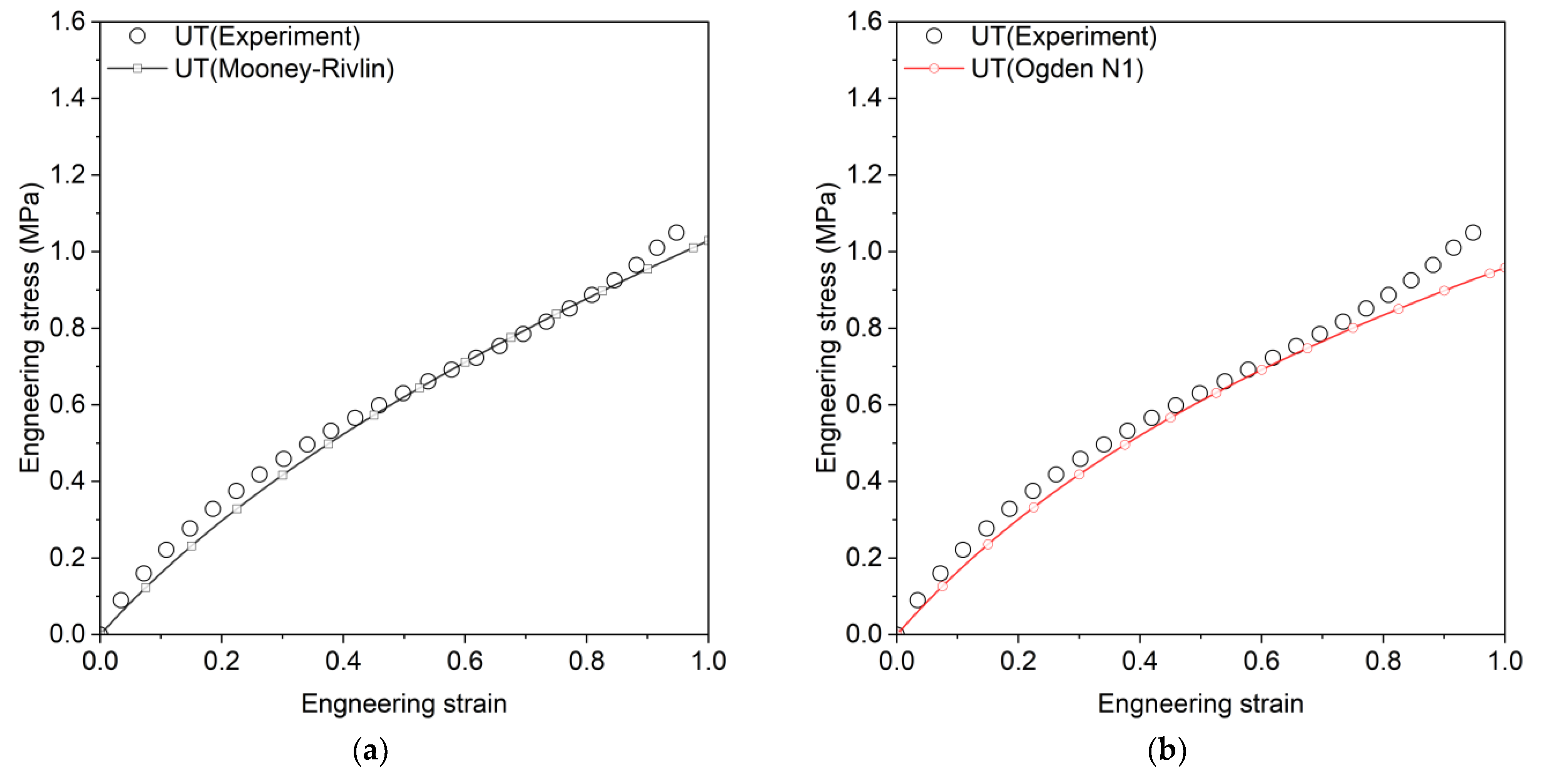
| Arruda–Boyce | , | 0.9879 | 0.9882 | 0.9309 |
| Marlow | - | 1.0 | 0.8525 | 0.8795 |
| 0.9874 | 0.9899 | 0.9322 | ||
| Neo-Hookean | 0.9879 | 0.9882 | 0.6803 | |
| Odden N1 | 0.973 | 0.9803 | 0.9539 | |
| Ogden N3 | 0.9643 | 0.9978 | 0.5970 | |
| Van Der Waals | 0.9769 | 0.9926 | 0.9738 | |
| Yoeh | 0.9773 | 0.9879 | 0.9663 | |
| Label | Strain Energy (J) | Error (%) |
|---|---|---|
| Experiment | 34.446 | - |
| Arruda–Boyce | 29.354 | 14.78256 |
| Marlow | 31.685 | 8.015444 |
| Mooney–Rivlin | 29.344 | 14.81159 |
| Neo-Hookean | 29.354 | 14.78256 |
| Odden N1 | 29.843 | 13.36294 |
| Ogden N3 | 29.847 | 13.35133 |
| Van Der Waals | 29.806 | 13.47036 |
| Yoeh | 32.061 | 6.923881 |
| Label | Order (Hz) | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Arruda–Boyce | 108.98 | 271.14 | 288.79 | 338.04 |
| Marlow | 108.94 | 271.03 | 288.66 | 337.91 |
| Mooney–Rivlin | 108.98 | 271.14 | 288.79 | 338.04 |
| Neo-Hookean | 108.98 | 271.14 | 288.79 | 338.04 |
| Odden N1 | 111.54 | 277.81 | 295.89 | 346.24 |
| Ogden N3 | 111.67 | 277.84 | 295.93 | 346.40 |
| Van Der Waals | 118.44 | 294.68 | 313.89 | 367.42 |
| Yoeh | 113.61 | 282.67 | 301.08 | 352.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-J. Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts. Materials 2025, 18, 311. https://doi.org/10.3390/ma18020311
Park S-J. Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts. Materials. 2025; 18(2):311. https://doi.org/10.3390/ma18020311
Chicago/Turabian StylePark, Sung-Ju. 2025. "Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts" Materials 18, no. 2: 311. https://doi.org/10.3390/ma18020311
APA StylePark, S.-J. (2025). Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts. Materials, 18(2), 311. https://doi.org/10.3390/ma18020311






