Cross-Scale Modeling of CFRP Stacking Sequence in Filament-Wound Composite Pressure Vessels: In-Plane and Inter-Layer Homogenization Analysis
Highlights
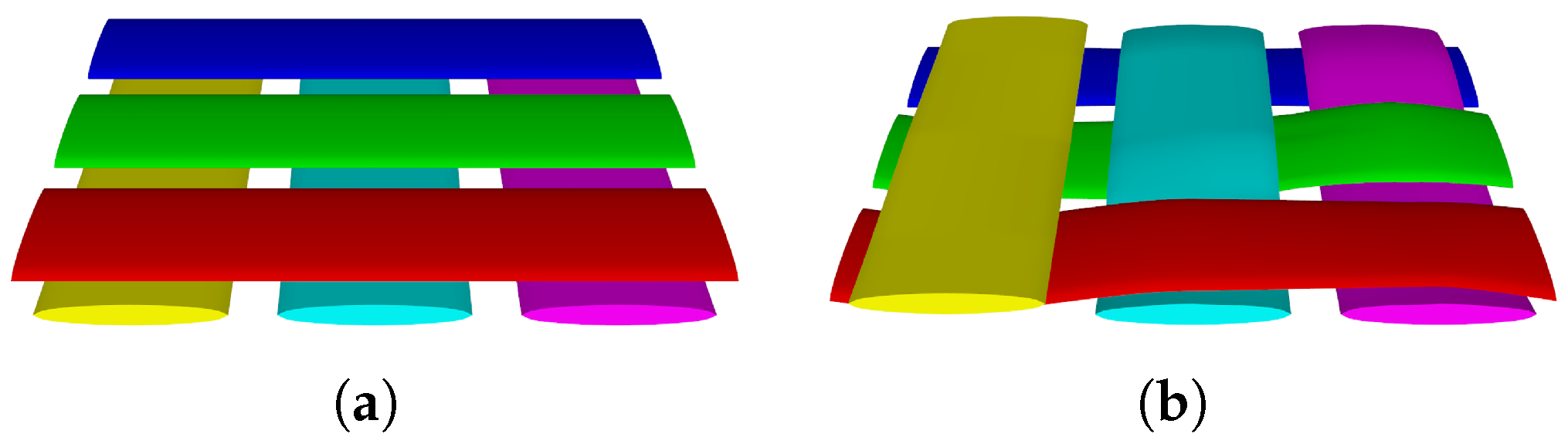
- The laminate in-plane structure can represent typical RVEs of winding patterns.
- The inter-layer homogenization can model the structural response.
- Particle homogenization with innermost plys for composite layers can predict the burst pressure.
- The less intense alternate hoop and helical winding mode has higher burst pressure.
Abstract
1. Introduction
2. Analytical Homogenization
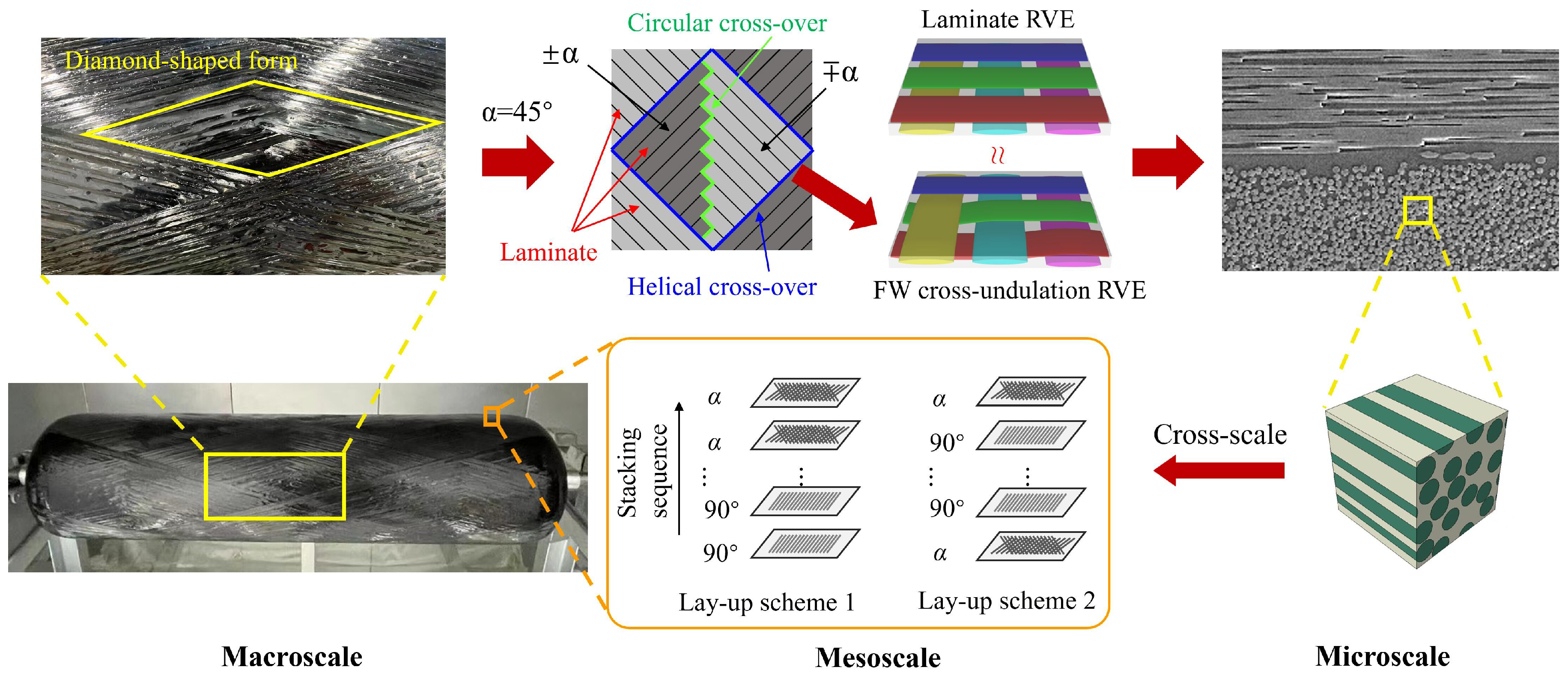
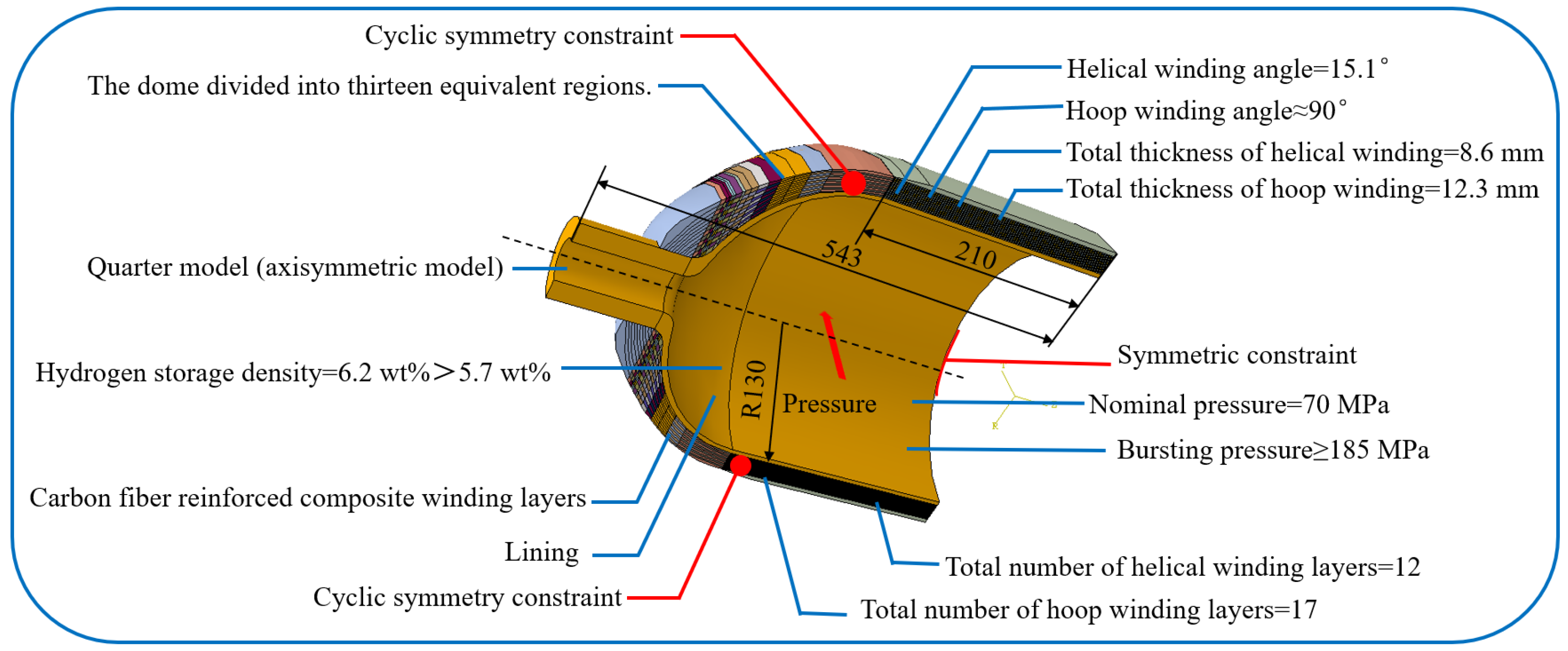
3. Geometric Design of Composite Pressure Vessel
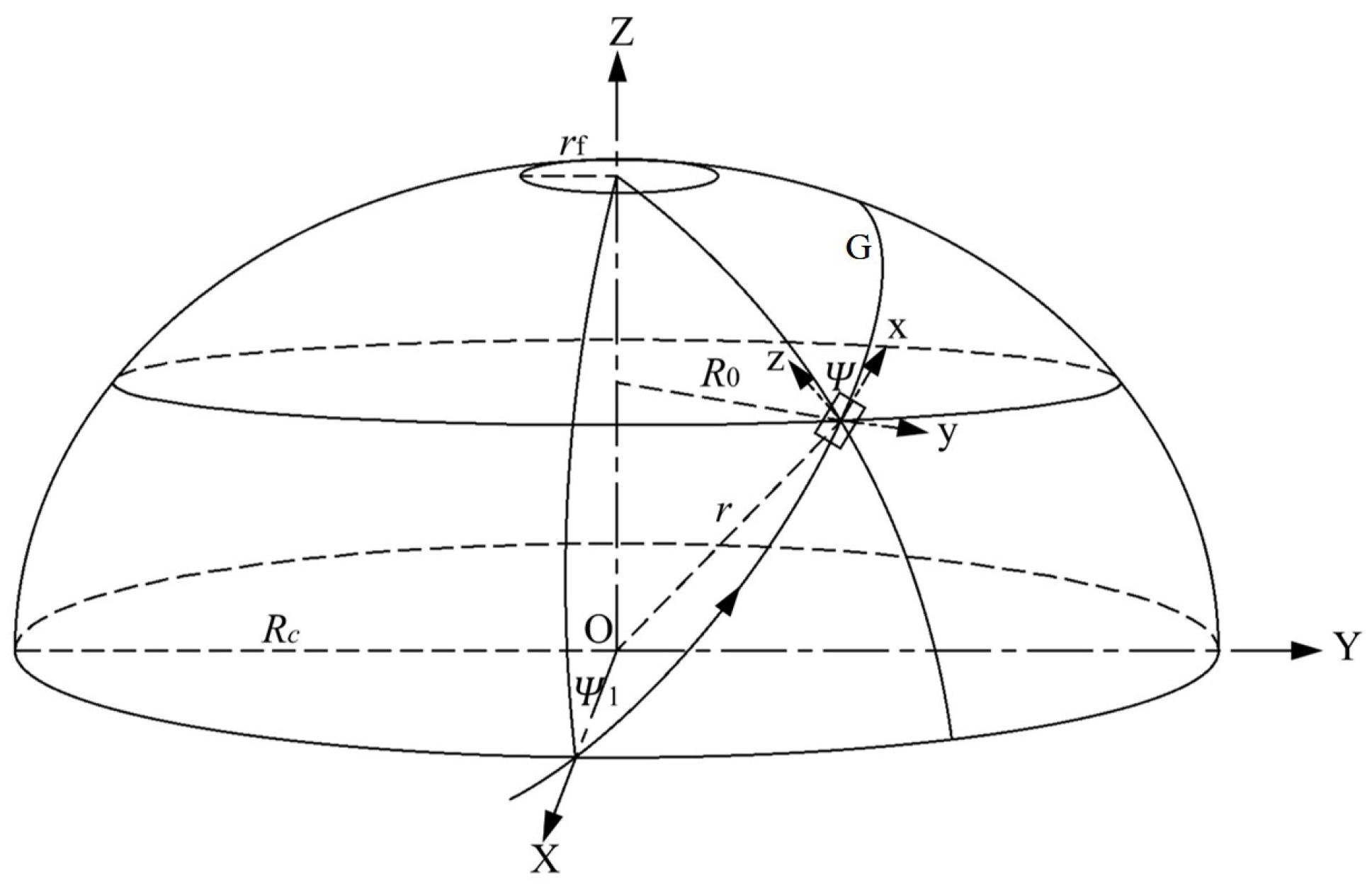
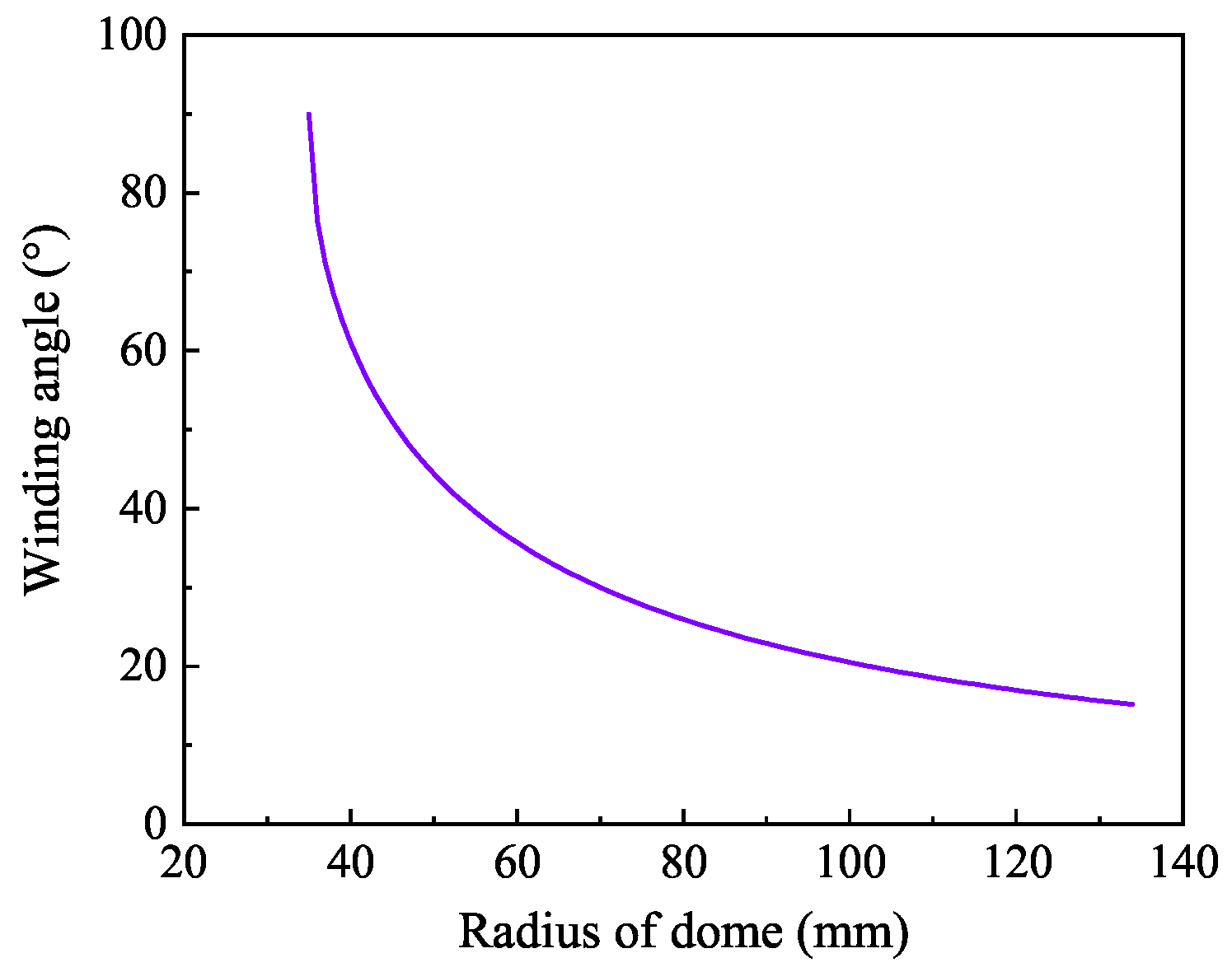
3.1. Winding Angle and Thickness
3.2. Type IV Pressure Vessel Design
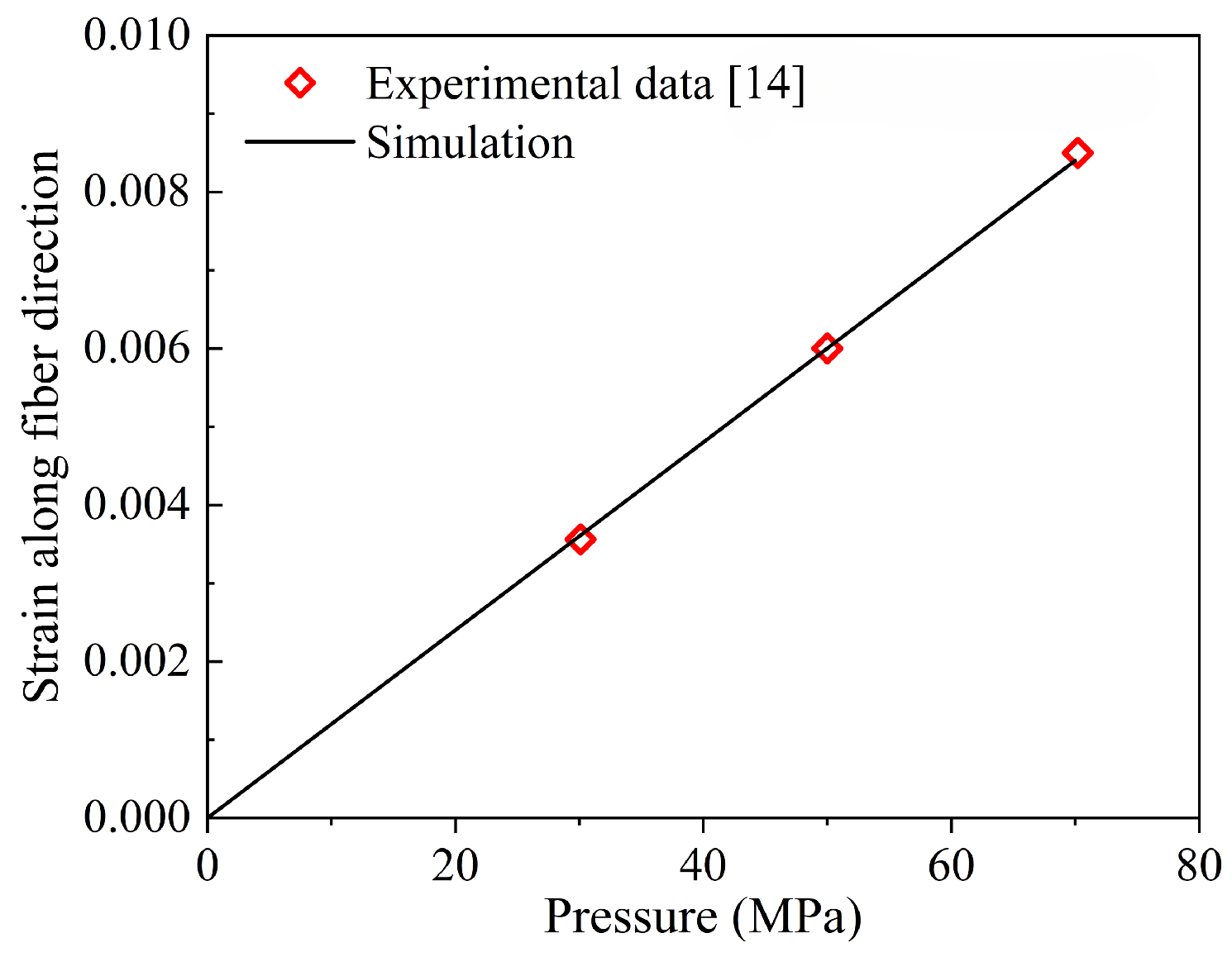
3.3. Validation of Pressure Vessel Design
3.4. Lay-Up Sequences
4. Cross-Scale Modeling of Pressure Vessel Composite Layer
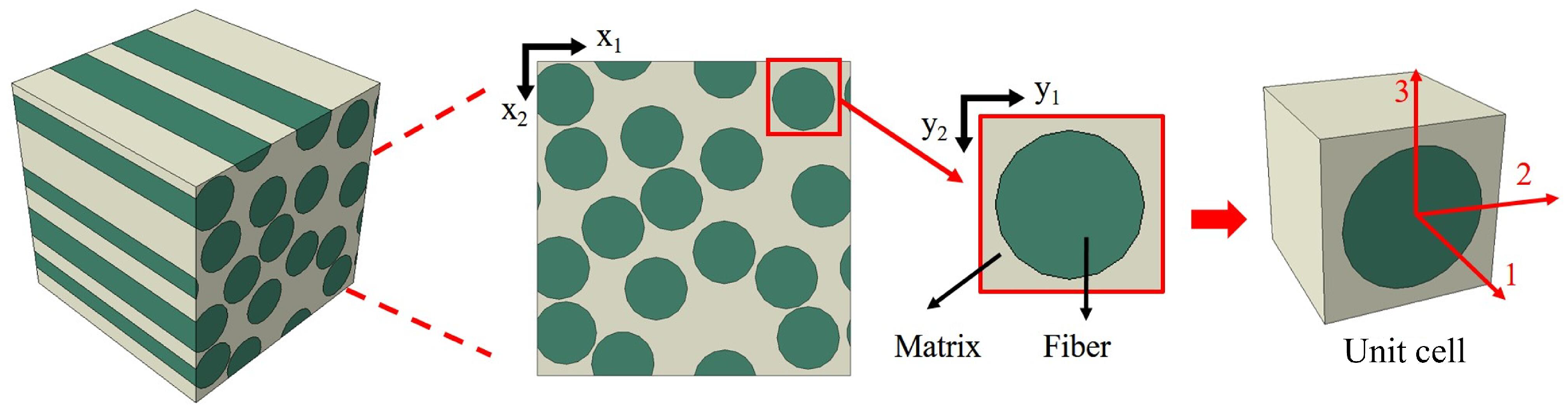
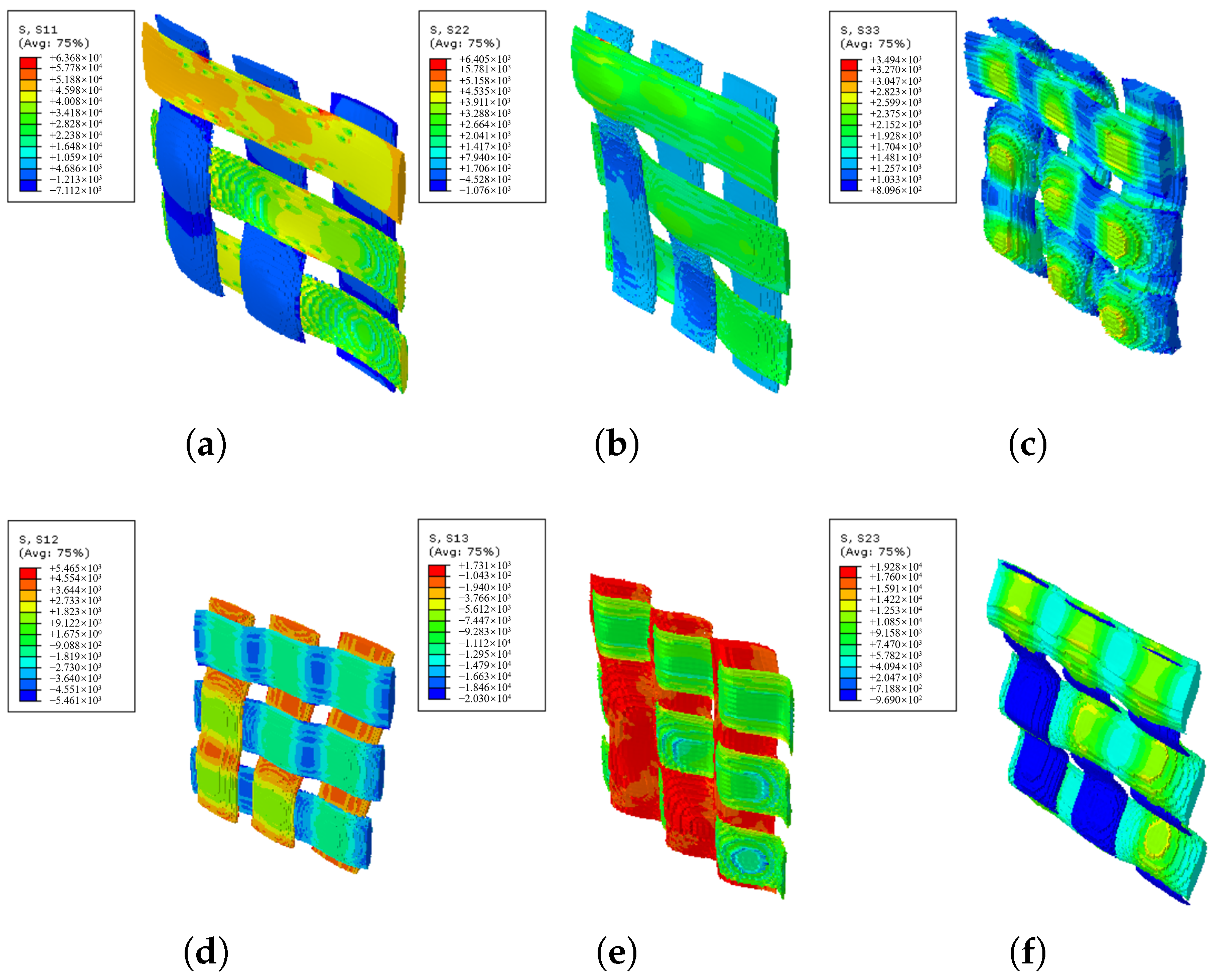
4.1. In-Plane RVE Homogenization
4.2. Inter-Layer Homogenization
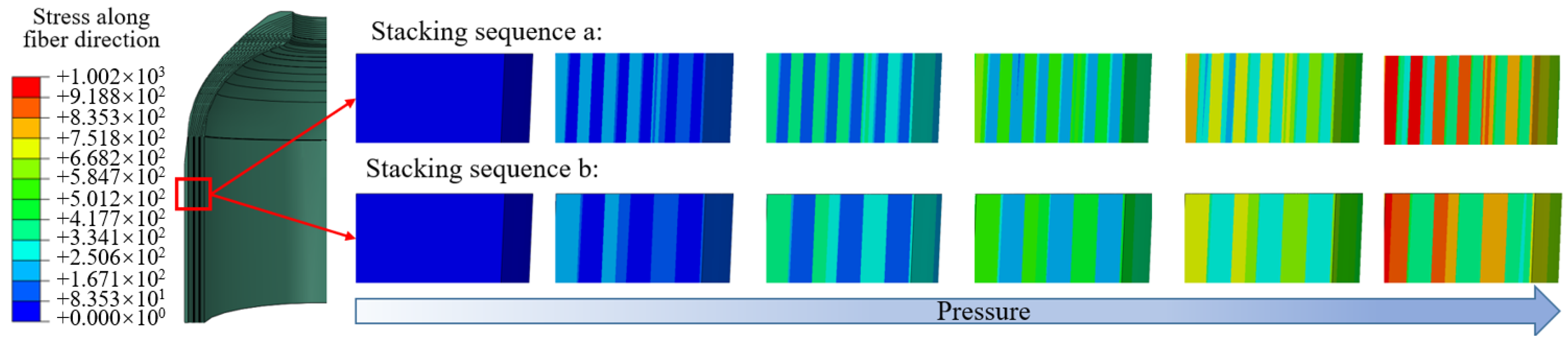
5. Cross-Scale Analysis of Lay-Up Sequence
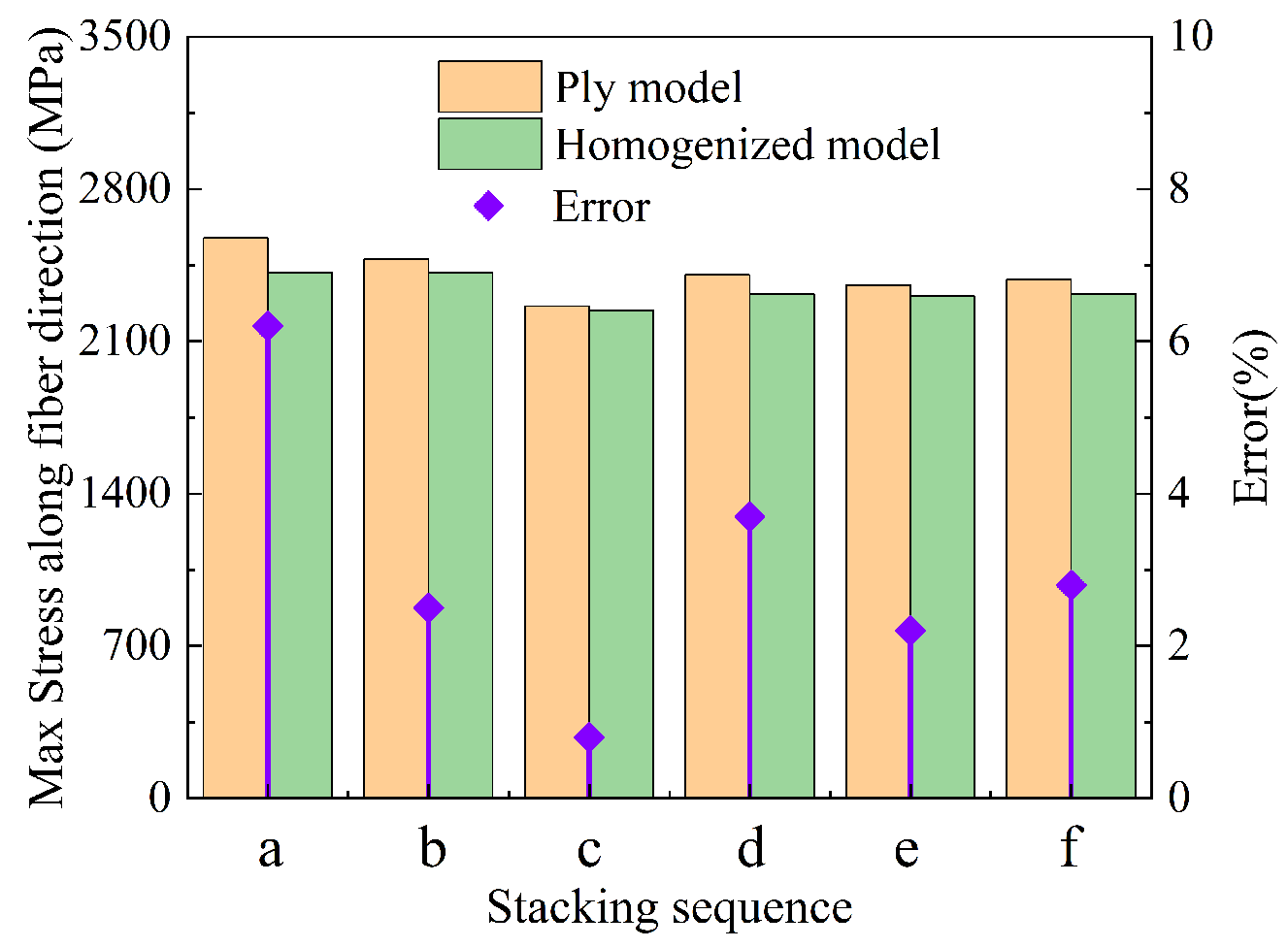
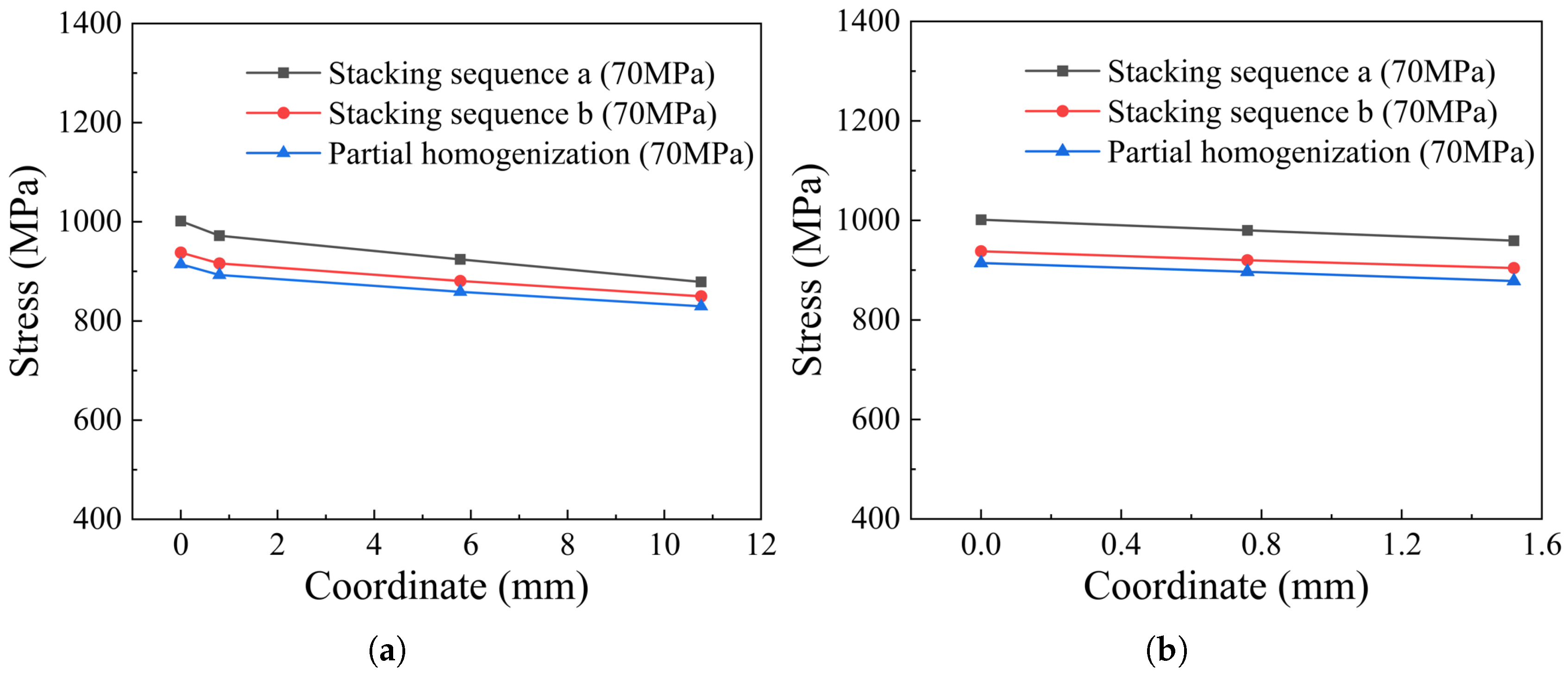
5.1. Comparison of Mechanical Responses
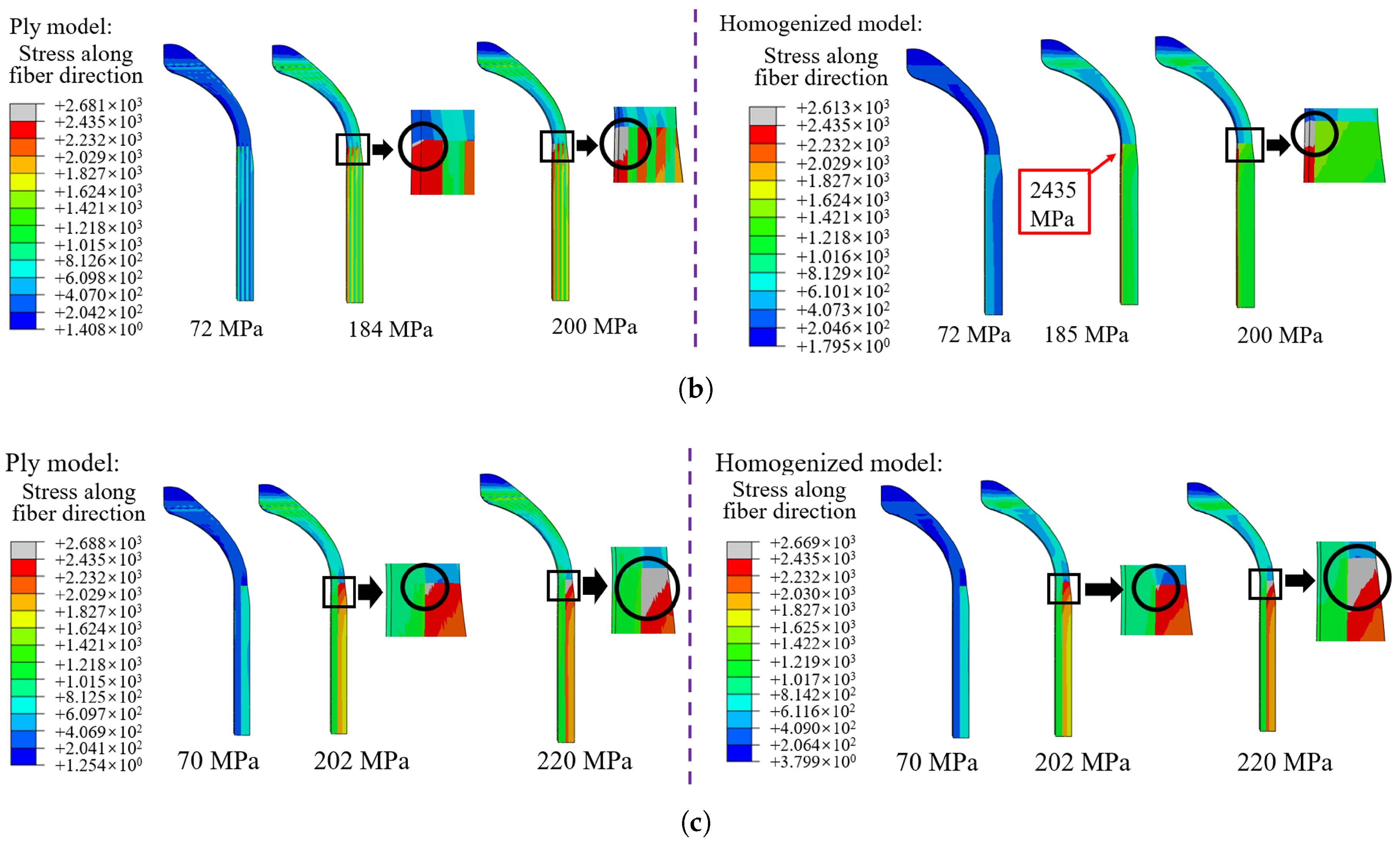
5.2. Comparison of Burst Pressure
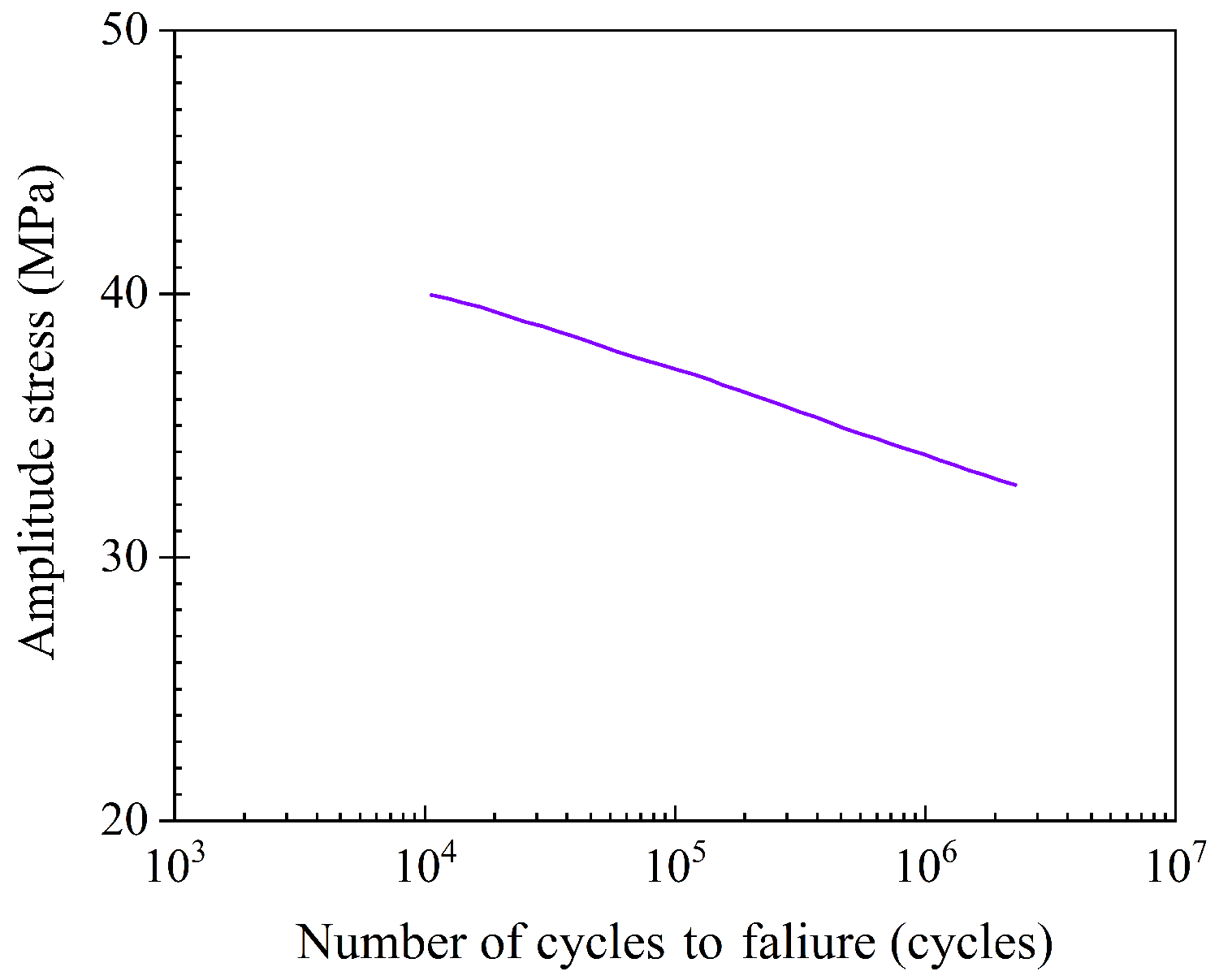
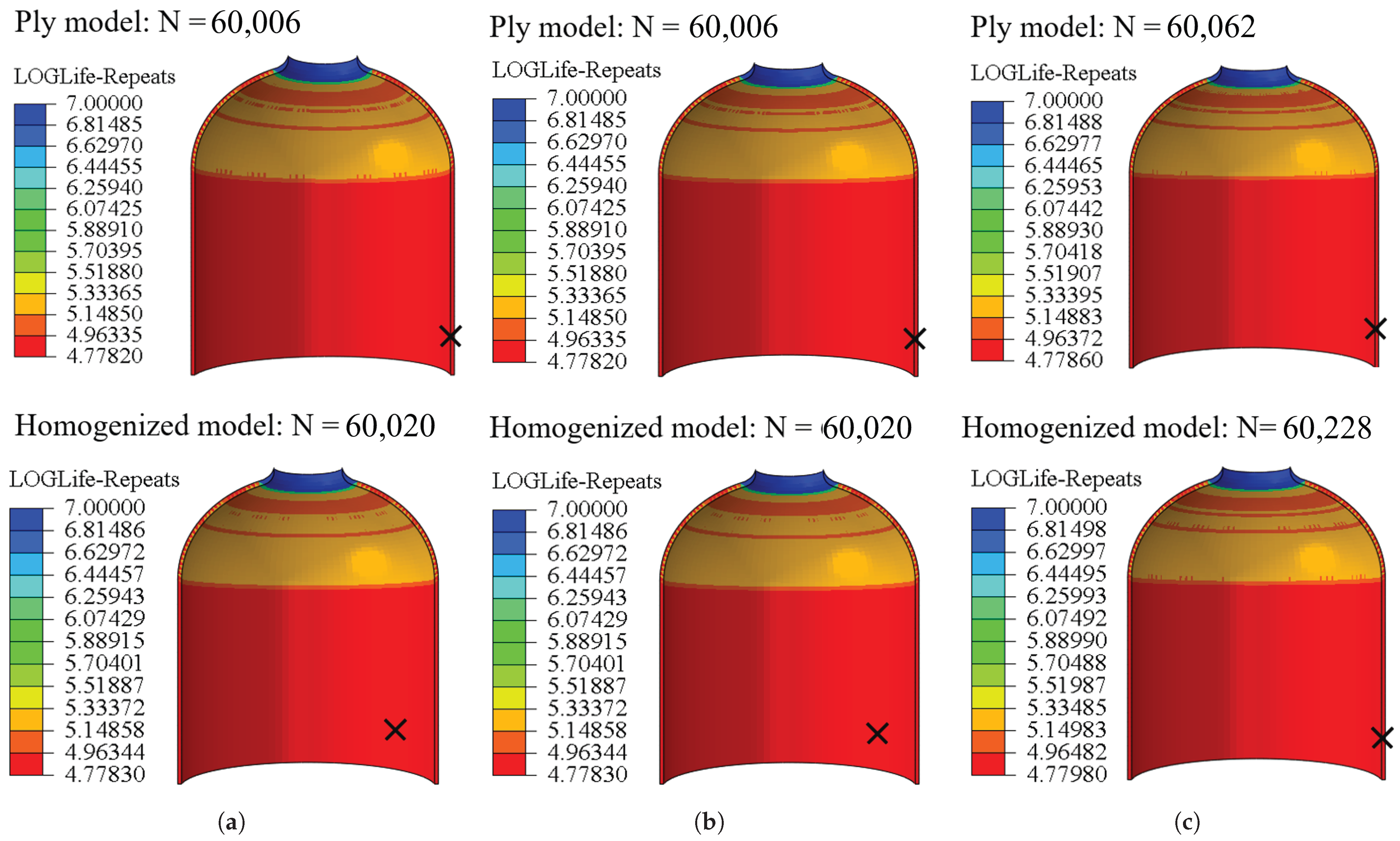
5.3. Comparison of Liner Fatigue Life
6. Conclusions
- (1)
- In the frame of the homogenization approach, the laminate can represent the in-plane FW cross-undulation RVE structure. Therefore, the effective elastic modulus of the CFRP layer can be modeled as the modulus of a laminate layer in composite pressure vessel simulations.
- (2)
- Inter-layer homogenization can model the structural response, including the radial and axial displacements, consistent with the validated ply model. Keeping the two innermost layers as mesoscale plies, partial homogenization for the alternate CFRP layers can predict the burst pressure with tensile strength of the Hashin failure criterion with a deviation of less than 7.56%. The model with fewer alternating hoop and helical winding layers has higher burst pressure, which needs further experimental validation.
- (3)
- By coupling ABAQUS® with FE-SAFE and incorporating an S-N curve for polyamide PA66, fatigue life analysis of the Type IV hydrogen composite tank liner is conducted. The results indicate that the fatigue cycles of the liner exhibit only 0.28% variation across different stacking sequences, demonstrating that homogenization has a negligible impact on lifecycle predictions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, S.; Zhou, Y.; He, S.; Wu, H. Development of Computational Methods of Design by Analysis for Pressure Vessel Components; Atomic Energy Press: Beijing, China, 2005. [Google Scholar]
- Peters, D.; Maslowski, A.P. Overview of Revisions to the ASME Boiler and Pressure Vessel Code Section VIII Division 3 for the 2015 Edition and Near Future. In Proceedings of the Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56987, p. V005T05A012. [Google Scholar]
- Khobragade, R.; Hiwase, V. Design, and analysis of pressure vessel with hemispherical and flat circular end. Int. J. Eng. Sci. Comput. 2017, 7, 12458–12469. [Google Scholar]
- Krużelecki, J.; Proszowski, R. Shape optimization of thin-walled pressure vessel end closures. Struct. Multidiscip. Optim. 2012, 46, 739–754. [Google Scholar] [CrossRef]
- Zheng, J.; Shu, X.; Wu, Y.; Xu, H.; Lu, Q.; Liao, B.; Zhang, B. Investigation on the plastic deformation during the stamping of ellipsoidal heads for pressure vessels. Thin-Walled Struct. 2018, 127, 135–144. [Google Scholar] [CrossRef]
- Liao, B.; Jia, L. Finite element analysis of dynamic responses of composite pressure vessels under low velocity impact by using a three-dimensional laminated media model. Thin-Walled Struct. 2018, 129, 488–501. [Google Scholar] [CrossRef]
- Cohen, D.; Mantell, S.C.; Zhao, L. The effect of fiber volume fraction on filament wound composite pressure vessel strength. Compos. Part B Eng. 2001, 32, 413–429. [Google Scholar] [CrossRef]
- Sulaiman, S.; Borazjani, S.; Tang, S. Finite element analysis of filament-wound composite pressure vessel under internal pressure. IOP Conf. Ser. Mater. Sci. Eng. 2013, 50, 012061. [Google Scholar] [CrossRef]
- Błachut, A.; Wollmann, T.; Panek, M.; Vater, M.; Kaleta, J.; Detyna, J.; Hoschützky, S.; Gude, M. Influence of fiber tension during filament winding on the mechanical properties of composite vessels. Compos. Struct. 2023, 304, 116337. [Google Scholar] [CrossRef]
- Toudehdehghan, A.; Hong, T.W. A critical review and analysis of pressure vessel structures. IOP Conf. Ser. Mater. Sci. Eng. 2019, 469, 012009. [Google Scholar] [CrossRef]
- McLaughlan, P.B.; Forth, S.C.; Grimes-Ledesma, L.R. Composite Overwrapped Pressure Vessels, a Primer; Technical Report; National Aeronautics and Space Administration: Houston, TX, USA, 2011. [Google Scholar]
- Barral, K.; Barthélémy, H. Hydrogen high pressure tanks storages: Overview and new trends due to H2 Energy specifications and constraints. In Proceedings of the WHEC, Lyon, France, 13–16 June 2006; Volume 16, pp. 13–16. [Google Scholar]
- Heidari-Rarani, M.; Ahmadi-Jebeli, M. Finite element modeling of failure in IV type composite pressure vessel using WCM plug-in in ABAQUS software. Modares Mech. Eng. 2018, 18, 191–200. [Google Scholar]
- Ramirez, J.P.B.; Halm, D.; Grandidier, J.C.; Villalonga, S.; Nony, F. 700 bar type IV high pressure hydrogen storage vessel burst–Simulation and experimental validation. Int. J. Hydrogen Energy 2015, 40, 13183–13192. [Google Scholar] [CrossRef]
- Cohen, D. Influence of filament winding parameters on composite vessel quality and strength. Compos. Part A Appl. Sci. Manuf. 1997, 28, 1035–1047. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, M.; Zu, L.; Jia, X.; Shen, A.; Yang, Q.; Xu, K. Investigation on failure behaviors of 70 MPa Type IV carbon fiber overwound hydrogen storage vessels. Compos. Struct. 2021, 259, 113387. [Google Scholar] [CrossRef]
- Farhood, N.H.; Karuppanan, S.; Ya, H.; Baharom, M.A. Burst pressure investigation of filament wound type IV composite pressure vessel. AIP Conf. Proc. 2017, 1901, 030017. [Google Scholar] [CrossRef]
- Mian, H.H.; Wang, G.; Dar, U.A.; Zhang, W. Optimization of composite material system and lay-up to achieve minimum weight pressure vessel. Appl. Compos. Mater. 2013, 20, 873–889. [Google Scholar] [CrossRef]
- Bertin, M.; Villalonga, S.; Vernède, M.; Magnier, C.; Tissier, P.; Nony, F. Mechanical behaviour of 700 bar type IV high pressure vessel: Comparison between simulations and experiments through Osirhys IV project. In Proceedings of the 15th European Conference on Composite Materials (ECCM-15), Venice, Italy, 24–28 June 2012; p. 8. [Google Scholar]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; American Mathematical Society: Providence, RI, USA, 2011; Volume 374. [Google Scholar]
- Bakhvalov, N.S.; Panasenko, G. Homogenisation: Averaging Processes in Periodic Media: Mathematical Problems in the Mechanics of Composite Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 36. [Google Scholar]
- Cai, Y.; Sun, H. Numerical prediction of viscoelastic behaviors of three-dimensionally braided resin matrix composites. J. Mater. Sci. Eng. 2012, 30, 271–275. [Google Scholar]
- Yin, D.M.; Li, B.M.; Xiao, H.C. Prediction of three-dimensional elastic behavior of filament-wound composites based on the bridging model. Def. Technol. 2021, 17, 609–616. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Domaszewski, M. Microstructure modelling and prediction of effective elastic properties of 3D multiphase and multilayer braided composite. Mater. Sci. Technol. 2011, 27, 1213–1221. [Google Scholar] [CrossRef]
- Zhang, C.; Binienda, W.K.; Goldberg, R.K.; Kohlman, L.W. Meso-scale failure modeling of single layer triaxial braided composite using finite element method. Compos. Part A Appl. Sci. Manuf. 2014, 58, 36–46. [Google Scholar] [CrossRef]
- May, M.; Nossek, M.; Petrinic, N.; Hiermaier, S.; Thoma, K. Adaptive multi-scale modeling of high velocity impact on composite panels. Compos. Part A Appl. Sci. Manuf. 2014, 58, 56–64. [Google Scholar] [CrossRef]
- Tang, H.; Zhou, G.; Sun, Q.; Avinesh, O.; Meng, Z.; Engler-Pinto, C.; Su, X. Experimental and computational analysis of bending fatigue failure in chopped carbon fiber chip reinforced composites. Compos. Struct. 2021, 275, 114402. [Google Scholar] [CrossRef]
- Czapliński, T.; Maciejewski, L.; Zietek, G. Modeling of high pressure composite vessels. In Proceedings of the 10th International Conference on Composite Science and Technology, Lisbon, Portugal, 2–4 September 2015. [Google Scholar]
- Zhang, N.; Gao, S.; Song, M.; Chen, Y.; Zhao, X.; Liang, J.; Feng, J. A Multiscale Study of CFRP Based on Asymptotic Homogenization with Application to Mechanical Analysis of Composite Pressure Vessels. Polymers 2022, 14, 2817. [Google Scholar] [CrossRef]
- Almeida, J.H.S., Jr.; Ribeiro, M.L.; Tita, V.; Amico, S.C. Stacking sequence optimization in composite tubes under internal pressure based on genetic algorithm accounting for progressive damage. Compos. Struct. 2017, 178, 20–26. [Google Scholar] [CrossRef]
- Nebe, M.; Asijee, T.; Braun, C.; Van Campen, J.; Walther, F. Experimental and analytical analysis on the stacking sequence of composite pressure vessels. Compos. Struct. 2020, 247, 112429. [Google Scholar] [CrossRef]
- Li, C.; Qin, Z.; Li, Y.; Chen, Z.; Liu, J.; Liang, J.; Feng, J. Investigation on mechanical behaviors under fatigue load of stacking sequences considering autofrettage process for highly reliable hydrogen storage vessel. J. Energy Storage 2024, 82, 110538. [Google Scholar] [CrossRef]
- Qi, Z.; Liu, Y.; Chen, W. An approach to predict the mechanical properties of CFRP based on cross-scale simulation. Compos. Struct. 2019, 210, 339–347. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]
- Lin, S.; Yang, L.; Xu, H.; Jia, X.; Yang, X.; Zu, L. Progressive damage analysis for multiscale modelling of composite pressure vessels based on Puck failure criterion. Compos. Struct. 2021, 255, 113046. [Google Scholar] [CrossRef]
- Rafiee, R.; Salehi, A. A novel recursive multi-scale modeling for predicting the burst pressure of filament wound composite pressure vessels. Appl. Phys. A 2022, 128, 388. [Google Scholar] [CrossRef]
- Takemoto, S.; Yoshikawa, N. Strength evaluation of CFRP structure of high pressure hydrogen tank based on mesoscale analysis. Mater. Today Commun. 2022, 32, 103966. [Google Scholar] [CrossRef]
- Rouf, K.; Worswick, M.J.; Montesano, J. Experimentally verified dual-scale modelling framework for predicting the strain rate-dependent nonlinear anisotropic deformation response of unidirectional non-crimp fabric composites. Compos. Struct. 2023, 303, 116384. [Google Scholar] [CrossRef]
- Zhao, X.; Liang, J.; Liu, J.; Feng, J.; Qin, Z.; Gao, H.; Guo, Z.; Jia, Z. A novel multi-filament winding technique for type III composite pressure vessel: From CFRP cross-undulation concept to structural performance validation. Int. J. Hydrogen Energy 2023, 48, 17237–17250. [Google Scholar] [CrossRef]
- Yuan, Z.; Fish, J. Toward realization of computational homogenization in practice. Int. J. Numer. Methods Eng. 2008, 73, 361–380. [Google Scholar]
- Abbena, E.; Salamon, S.; Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Menezes, E.A.W.; Lisbôa, T.V.; Almeida, J.H.S., Jr.; Spickenheuer, A.; Amico, S.C.; Marczak, R.J. On the winding pattern influence for filament wound cylinders under axial compression, torsion, and internal pressure loads. Thin-Walled Struct. 2023, 191, 111041. [Google Scholar] [CrossRef]
- Morozov, E.V. The effect of filament-winding mosaic patterns on the strengthof thin-walled composite shells. Compos. Struct. 2006, 76, 123–129. [Google Scholar] [CrossRef]
- Lisbôa, T.V.; Almeida, J.H.S., Jr.; Spickenheuer, A.; Stommel, M.; Amico, S.C.; Marczak, R.J. FEM updating for damage modeling of composite cylinders under radial compression considering the winding pattern. Thin-Walled Struct. 2022, 173, 108954. [Google Scholar] [CrossRef]
- Liang, J.G.; Li, C.Y.; Liu, J.L.; Feng, J.; Chen, Z.C.; Li, Y.H.; Wu, T.; Zhang, X.X. Prediction and optimization of failures in high-pressure hydrogen storagevessels: A review. Renew. Sustain. Energy Rev. 2026, 226, 116236. [Google Scholar]
- Rousseau, J.; Perreux, D.; Verdiere, N. The influence of winding patterns on the damage behaviour of filament-wound pipes. Compos. Sci. Technol. 1999, 59, 1439–1449. [Google Scholar] [CrossRef]
- Zu, L.; Xu, H.; Chen, S.J.; He, J.X.; Zhang, Q.; Ren, P.; Zhang, G.M.; Wang, L.Q.; Wu, Q.G.; Fu, J.H. Multi-objective optimization of different dome reinforcement methods for composite cases. Chin. J. Aeronaut. 2023, 36, 299–314. [Google Scholar] [CrossRef]
- Zheng, C.X.; Wang, L.; Li, R.; Wei, Z.X.; Zhou, W.W. Fatigue test of carbon epoxy composite high pressure hydrogen storage vessel under hydrogen environment. J. Zhejiang Univ. Sci. A 2013, 14, 393–400. [Google Scholar] [CrossRef]
- Nouri, M.; Ashenai Ghasemi, F.; Sherbaf, G.R.; Kashyzadeh, K.R. Fatigue Analysis of a Type-IV CNG Composite Cylinder with Variable Wall-Thickness and Polyethylene Liner. Mech. Compos. Mater. 2023, 59, 927–944. [Google Scholar]
- Klemenc, J.; Wagner, A.; Fajdiga, M. Modeling the S-N Curves of Polyamide PA66 Using a Serial Hybrid Neural Network. J. Eng. Mater. Technol. 2011, 133, 031005. [Google Scholar] [CrossRef]
- Kim, H.J.; Cho, J.-R. Numerical Analysis of Fatigue Life of Wind Turbine BladesReinforced with Graphene Platelets. Appl. Sci. 2025, 15, 1866. [Google Scholar]











| Material | Density | E (MPa) | |
|---|---|---|---|
| T700SC-12K | 1.8 | 230,000 | 0.3 |
| 914 epoxy | 1.14 | 4000 | 0.39 |
| 115,943 | 16,077 | 16,077 | 0.34 | 0.34 | 0.39 | 4201 | 4201 | 3124 |
| 185 | 35 | 134 | 6.4 | 12.3 | 8.6 | 41.4 | 47.8 | 15.1° | 0.76 |
| 25,569 | 25,569 | 8257 | 0.10 | 0.52 | 0.52 | 2089 | 1901 | 1901 | |
| 24,478 | 24,470 | 8153 | 0.11 | 0.53 | 0.53 | 2085 | 1916 | 1916 |
| No. | Angle | Graphic | ||||||
|---|---|---|---|---|---|---|---|---|
| 1# | 90° | 16.1 | 16.1 | 116 | 3.12 | 4.20 | 4.20 | 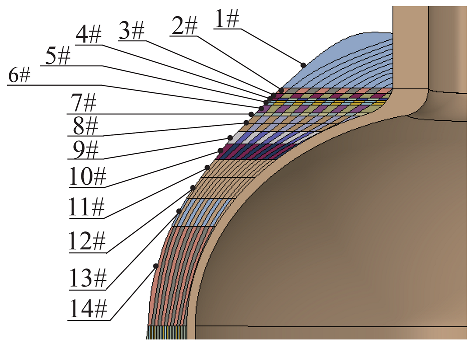 |
| 2# | 76.5° | 15.3 | 16.2 | 99.4 | 3.17 | 9.70 | 4.12 | |
| 3# | 71.1° | 14.5 | 16.3 | 83.0 | 3.21 | 14.2 | 4.05 | |
| 4# | 67.1° | 13.9 | 16.5 | 68.4 | 3.25 | 17.9 | 3.99 | |
| 5# | 63.8° | 13.4 | 16.6 | 56.0 | 3.29 | 20.9 | 3.94 | |
| 6# | 60° | 12.8 | 16.9 | 42.7 | 3.34 | 24.1 | 3.87 | |
| 7# | 51.1° | 12.7 | 17.5 | 21.5 | 3.48 | 29.6 | 3.70 | |
| 8# | 44.4° | 15.5 | 17.8 | 14.7 | 3.56 | 30.8 | 3.57 | 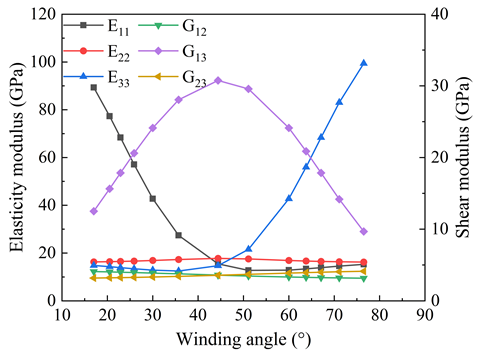 |
| 9# | 35.7° | 27.4 | 17.3 | 12.5 | 3.76 | 28.1 | 3.42 | |
| 10# | 30° | 42.7 | 16.9 | 12.8 | 3.87 | 24.1 | 3.34 | |
| 11# | 25.9° | 57.1 | 16.6 | 13.4 | 3.94 | 20.6 | 3.29 | |
| 12# | 22.9° | 68.4 | 16.5 | 13.9 | 3.09 | 17.9 | 3.25 | |
| 13# | 20.5° | 77.3 | 16.4 | 14.3 | 4.03 | 15.6 | 3.23 | |
| 14# | 17° | 89.3 | 16.3 | 14.8 | 4.08 | 12.5 | 3.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Shi, J.; Zhao, X.; Li, H.; Shen, H.; Liang, J.; Feng, J. Cross-Scale Modeling of CFRP Stacking Sequence in Filament-Wound Composite Pressure Vessels: In-Plane and Inter-Layer Homogenization Analysis. Materials 2025, 18, 4612. https://doi.org/10.3390/ma18194612
Wang Z, Shi J, Zhao X, Li H, Shen H, Liang J, Feng J. Cross-Scale Modeling of CFRP Stacking Sequence in Filament-Wound Composite Pressure Vessels: In-Plane and Inter-Layer Homogenization Analysis. Materials. 2025; 18(19):4612. https://doi.org/10.3390/ma18194612
Chicago/Turabian StyleWang, Ziqi, Ji Shi, Xiaodong Zhao, Hui Li, Huiming Shen, Jianguo Liang, and Jun Feng. 2025. "Cross-Scale Modeling of CFRP Stacking Sequence in Filament-Wound Composite Pressure Vessels: In-Plane and Inter-Layer Homogenization Analysis" Materials 18, no. 19: 4612. https://doi.org/10.3390/ma18194612
APA StyleWang, Z., Shi, J., Zhao, X., Li, H., Shen, H., Liang, J., & Feng, J. (2025). Cross-Scale Modeling of CFRP Stacking Sequence in Filament-Wound Composite Pressure Vessels: In-Plane and Inter-Layer Homogenization Analysis. Materials, 18(19), 4612. https://doi.org/10.3390/ma18194612







