Curve-Based Infill Pattern Optimization for 3D Printed Polymeric Scaffolds for Trabecular Bone Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
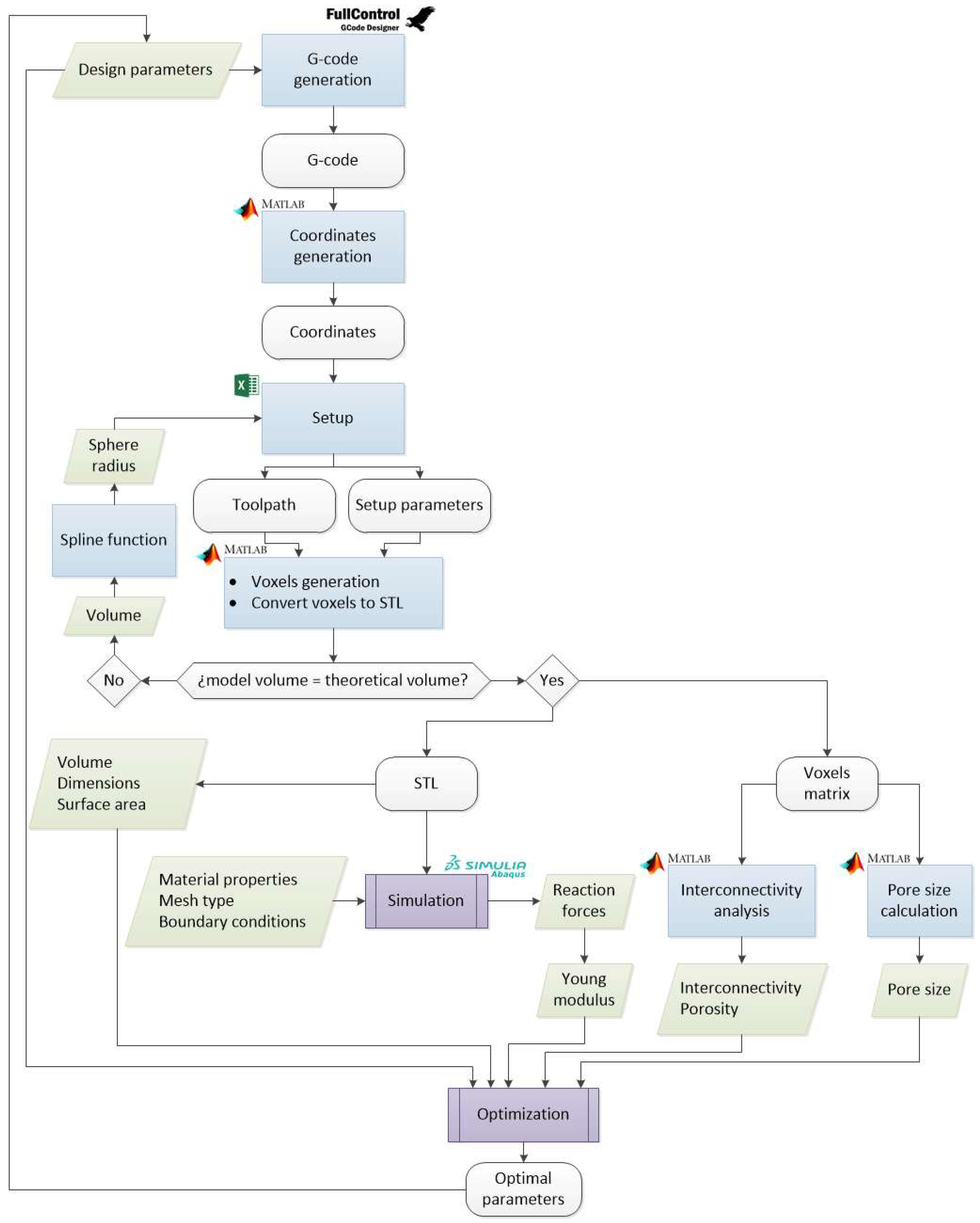
2.2. Modeling and Optimization Method
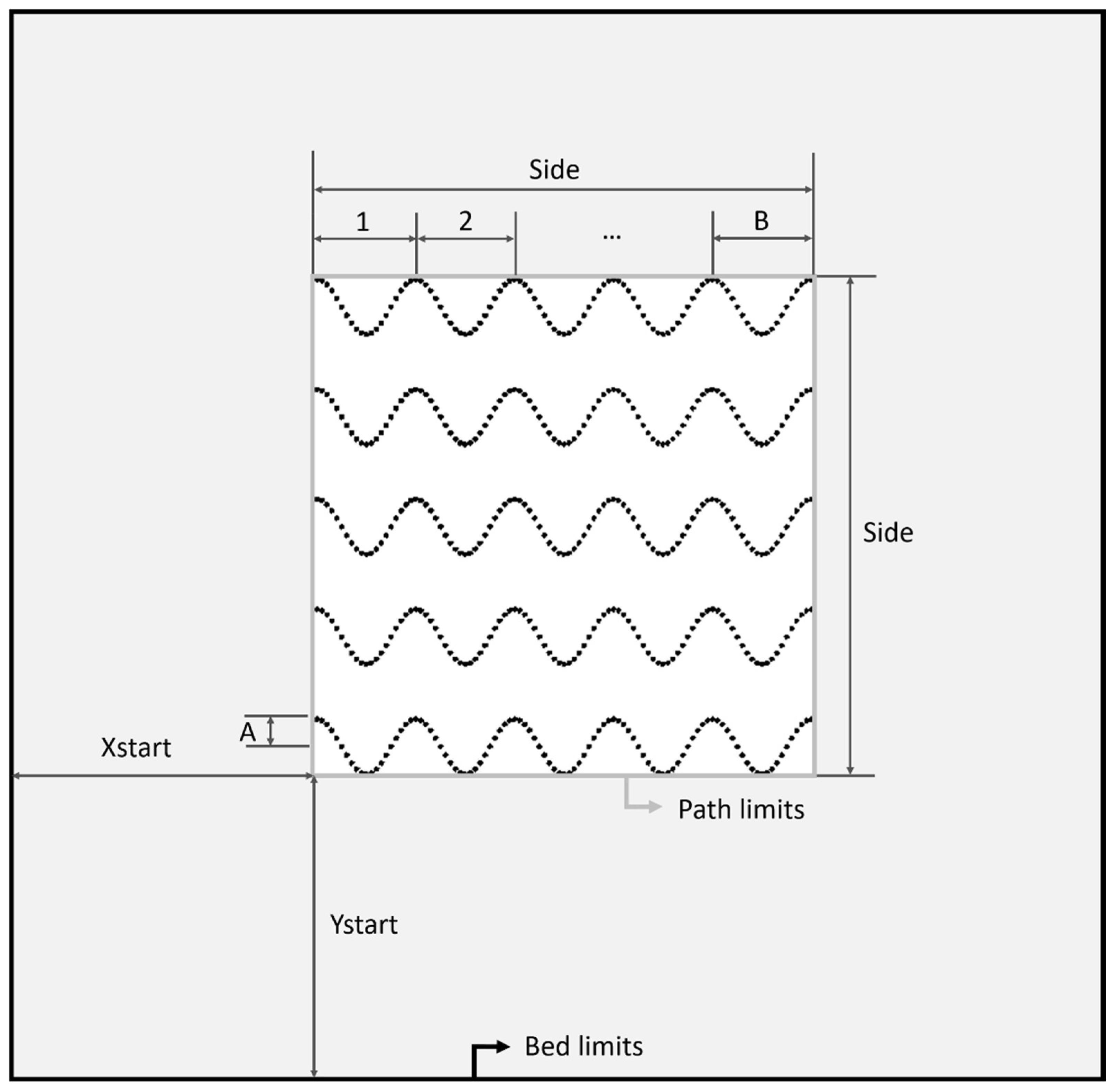
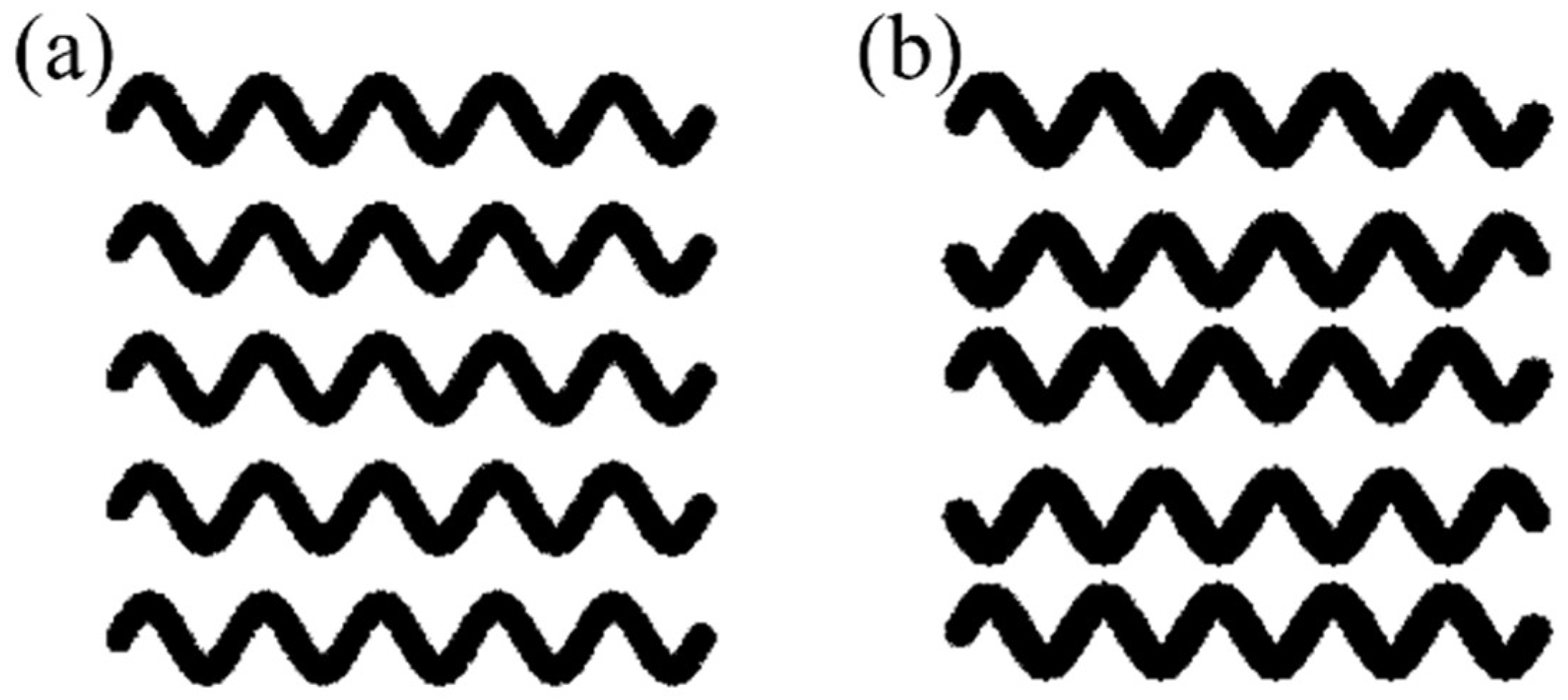
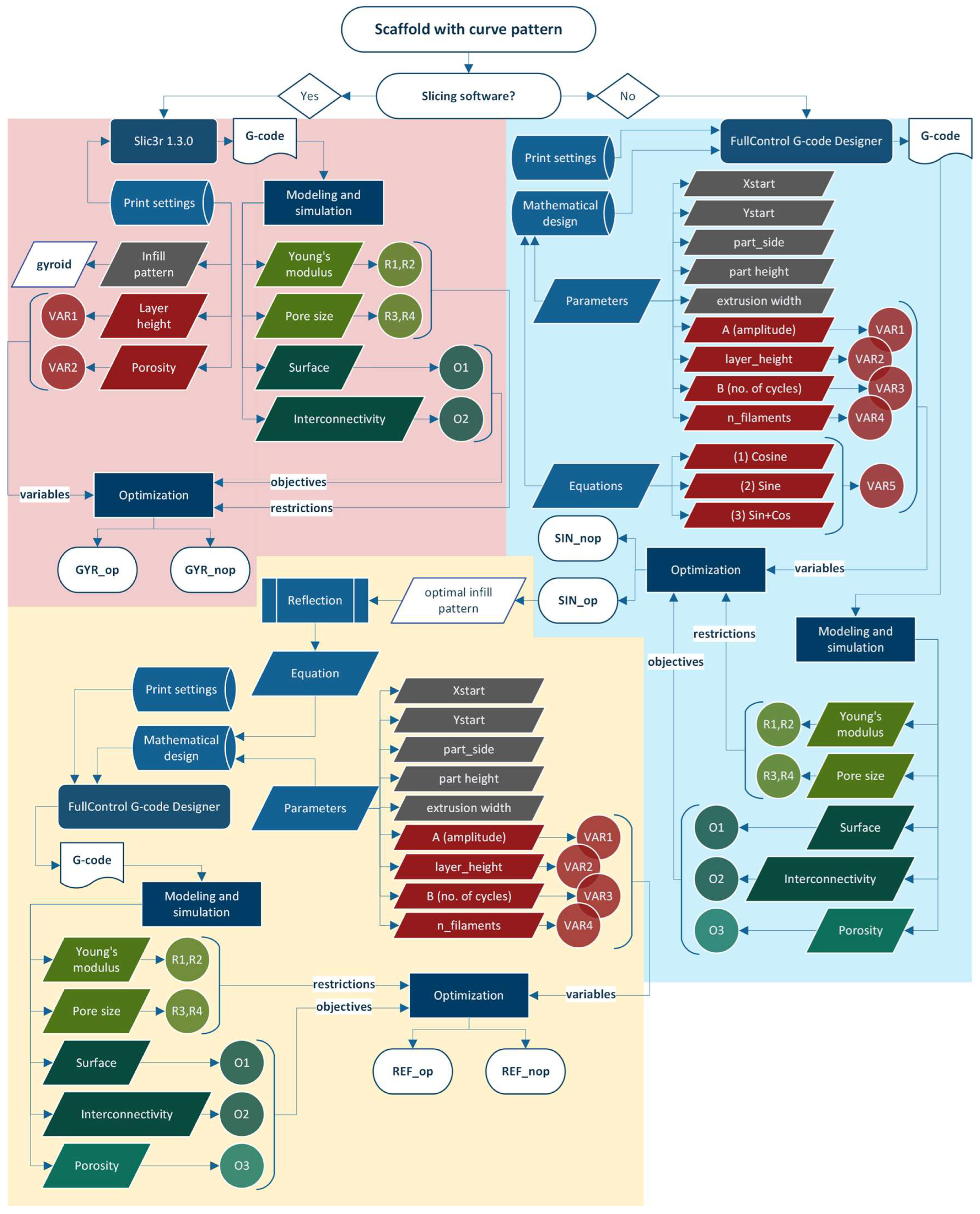
2.2.1. Scaffold Design
2.2.2. Modeling
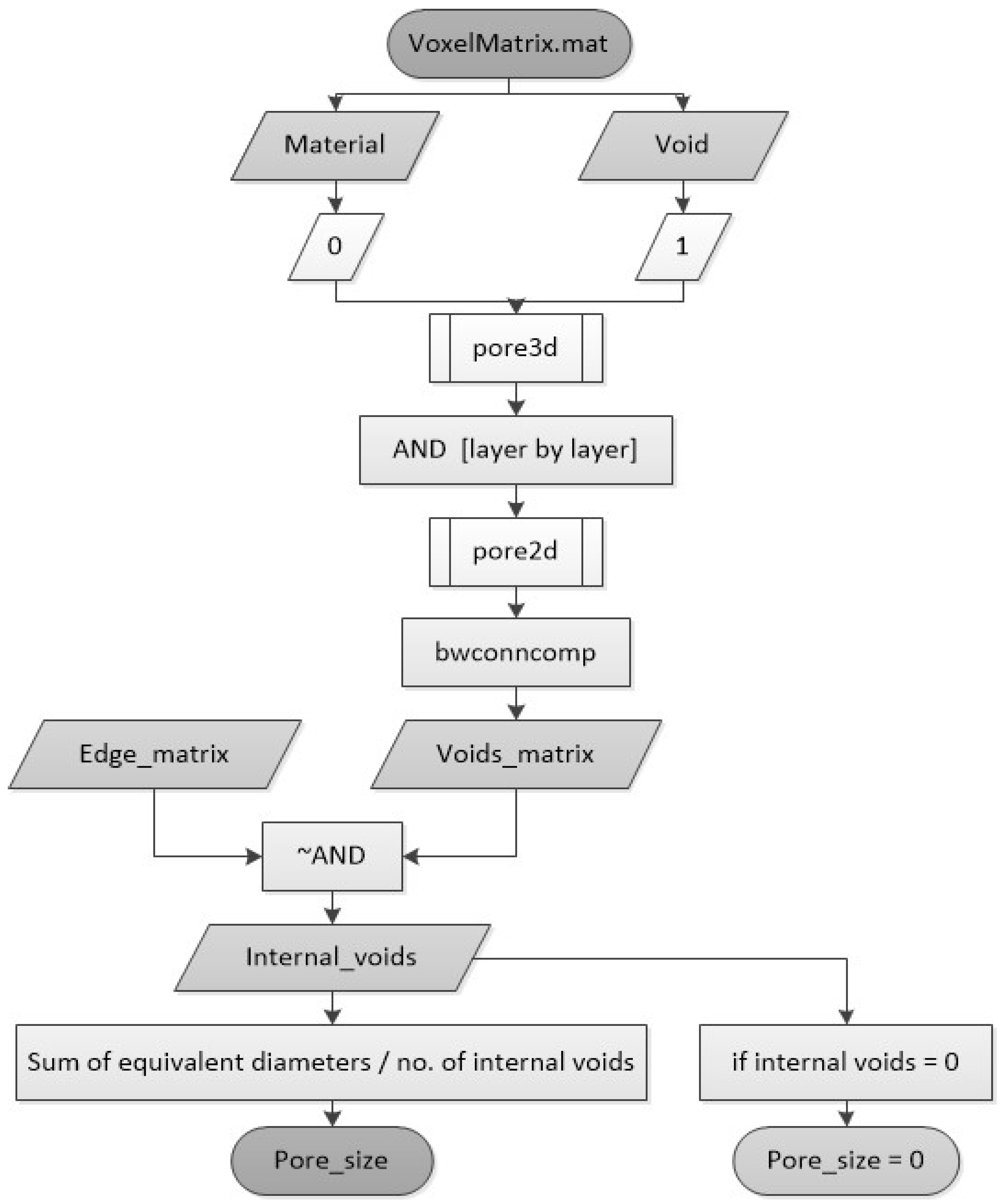
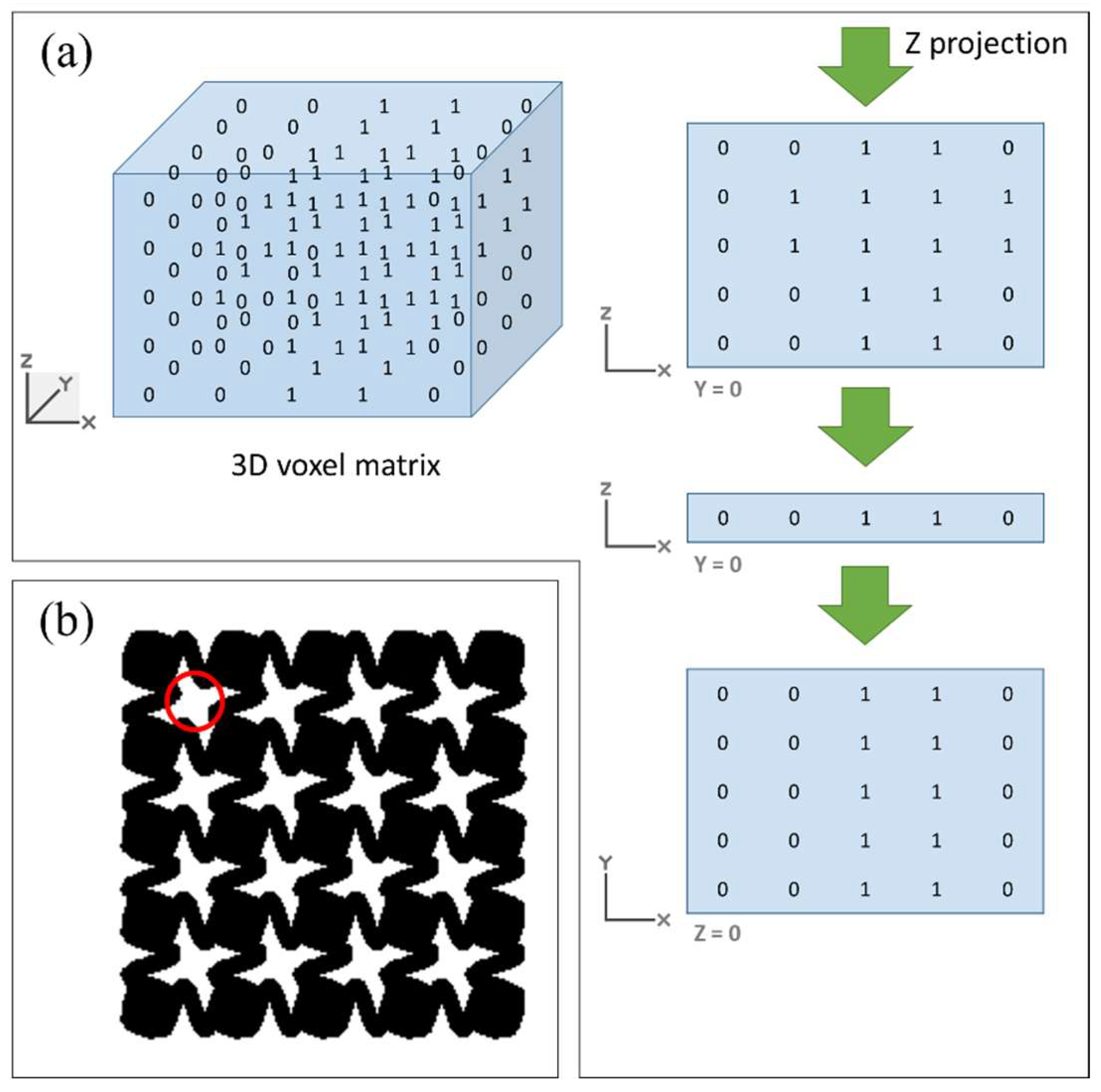
2.2.3. Interconnectivity and Porosity
2.2.4. Pore Size
2.2.5. Surface
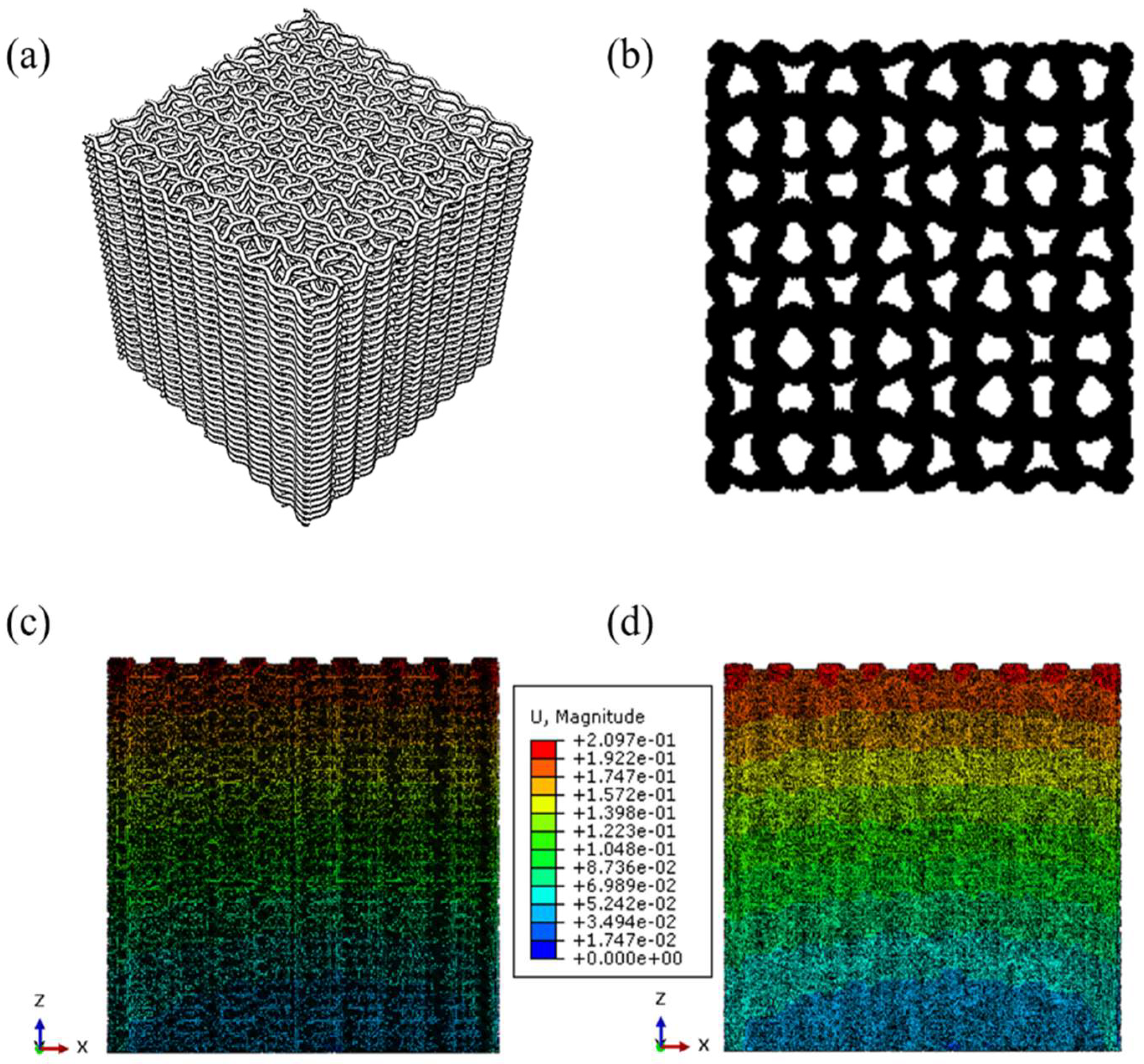
2.2.6. Finite Element Analysis
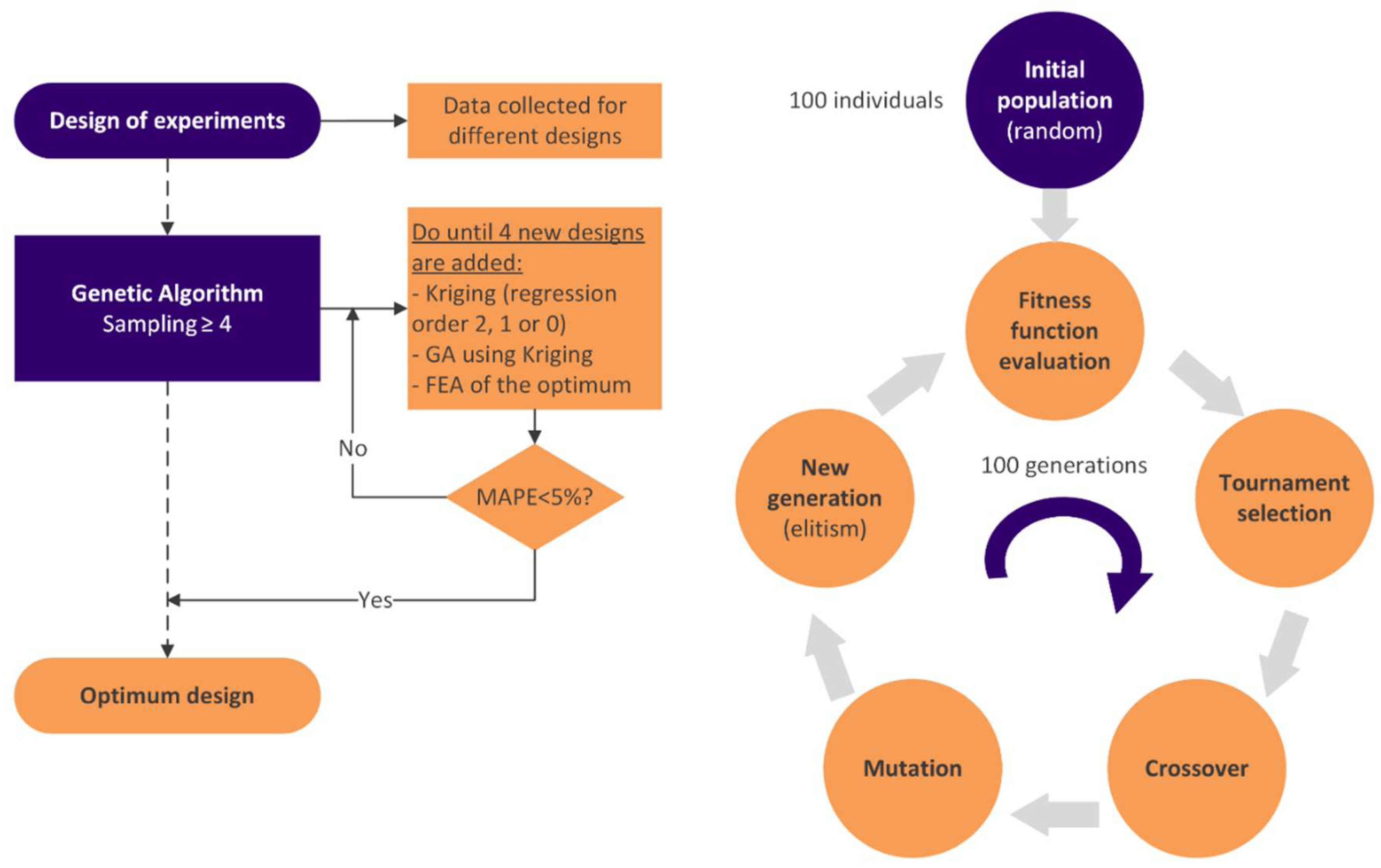
2.2.7. Optimization
2.3. Biological Test
2.3.1. Cell Culture and Seeding
2.3.2. Cell Metabolic Activity Evaluation
2.4. Statistical Analysis
3. Results and Discussion
3.1. Preliminary Optimization
3.2. Modeling and Simulation Results
3.3. Optimization Process
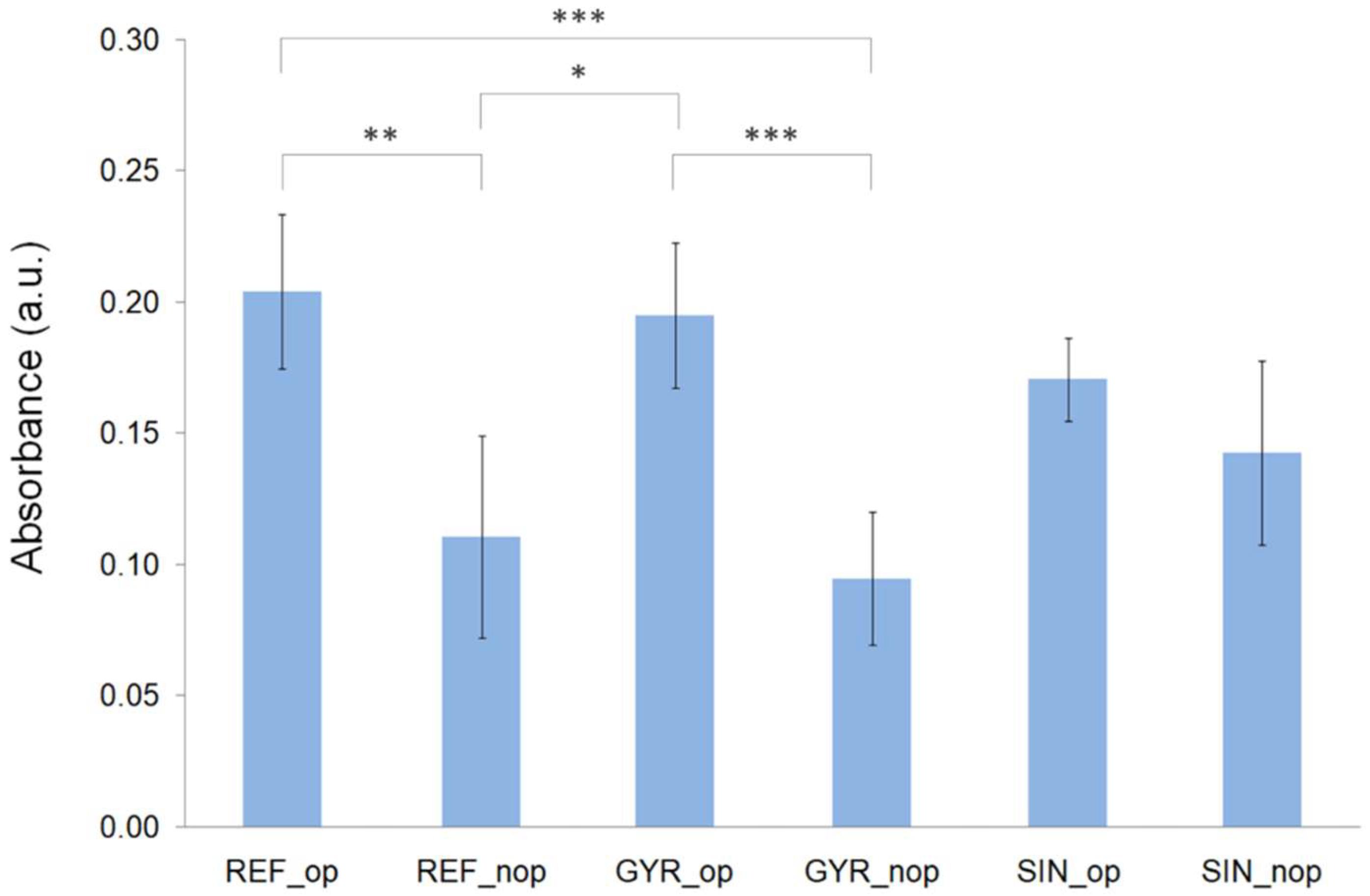
3.4. Biological Test Results
3.5. New Criteria Application
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naghieh, S.; Karamooz Ravari, M.R.; Badrossamay, M.; Foroozmehr, E.; Kadkhodaei, M.; Karamooz Ravari, M.R.; Badrossamay, M.; Foroozmehr, E.; Kadkhodaei, M. Numerical Investigation of the Mechanical Properties of the Additive Manufactured Bone Scaffolds Fabricated by FDM: The Effect of Layer Penetration and Post-Heating. J. Mech. Behav. Biomed. Mater. 2016, 59, 241–250. [Google Scholar] [CrossRef]
- Velasco, M.A.; Narváez-Tovar, C.A.; Garzón-Alvarado, D.A. Design, Materials, and Mechanobiology of Biodegradable Scaffolds for Bone Tissue Engineering. Biomed. Res. Int. 2015, 2015, 729076. [Google Scholar] [CrossRef]
- Qu, H. Additive Manufacturing for Bone Tissue Engineering Scaffolds. Mater. Today Commun. 2020, 24, 101024. [Google Scholar] [CrossRef]
- Singh, D.; Babbar, A.; Jain, V.; Gupta, D.; Saxena, S.; Dwibedi, V. Synthesis, Characterization, and Bioactivity Investigation of Biomimetic Biodegradable PLA Scaffold Fabricated by Fused Filament Fabrication Process. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 121. [Google Scholar] [CrossRef]
- Temple, J.P.; Hutton, D.L.; Hung, B.P.; Huri, P.Y.; Cook, C.A.; Kondragunta, R.; Jia, X.; Grayson, W.L. Engineering Anatomically Shaped Vascularized Bone Grafts with HASCs and 3D-Printed PCL Scaffolds. J. Biomed. Mater. Res.—Part A 2014, 102, 4317–4325. [Google Scholar] [CrossRef]
- Roopavath, U.K.; Malferrari, S.; Van Haver, A.; Verstreken, F.; Rath, S.N.; Kalaskar, D.M. Optimization of Extrusion Based Ceramic 3D Printing Process for Complex Bony Designs. Mater. Des. 2019, 162, 263–270. [Google Scholar] [CrossRef]
- Yánez, A.; Herrera, A.; Martel, O.; Monopoli, D.; Afonso, H. Compressive Behaviour of Gyroid Lattice Structures for Human Cancellous Bone Implant Applications. Mater. Sci. Eng. C 2016, 68, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.J. Porous Scaffold Design for Tissue Engineering. Nat. Mater. 2005, 4, 518–524. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A. Bone Tissue Regeneration: The Role of Scaffold Geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef]
- Guyot, Y.; Papantoniou, I.; Luyten, F.P.; Geris, L. Coupling Curvature-Dependent and Shear Stress-Stimulated Neotissue Growth in Dynamic Bioreactor Cultures: A 3D Computational Model of a Complete Scaffold. Biomech. Model. Mechanobiol. 2016, 15, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Egan, P.F.; Shea, K.A.; Ferguson, S.J. Simulated Tissue Growth for 3D Printed Scaffolds. Biomech. Model. Mechanobiol. 2018, 17, 1481–1495. [Google Scholar] [CrossRef]
- Zein, I.; Hutmacher, D.W.; Tan, K.C.; Teoh, S.H. Fused Deposition Modeling of Novel Scaffold Architectures for Tissue Engineering Applications. Biomaterials 2002, 23, 1169–1185. [Google Scholar] [CrossRef]
- Hollister, S.J.; Maddox, R.D.; Taboas, J.M. Optimal Design and Fabrication of Scaffolds to Mimic Tissue Properties. Biomaterials 2002, 23, 4095–4103. [Google Scholar] [CrossRef] [PubMed]
- Iordache, F. Bioprinted Scaffolds. In Materials for Biomedical Engineering; Elsevier Inc.: Amsterdam, The Netherlands, 2019; pp. 35–60. ISBN 9780128169018. [Google Scholar]
- Collins, M.N.; Ren, G.; Young, K.; Pina, S.; Reis, R.L.; Oliveira, J.M. Scaffold Fabrication Technologies and Structure/Function Properties in Bone Tissue Engineering. Adv. Funct. Mater. 2021, 31, 2010609. [Google Scholar] [CrossRef]
- Paris, M.; Götz, A.; Hettrich, I.; Bidan, C.M.; Dunlop, J.W.C.; Razi, H.; Zizak, I.; Hutmacher, D.W.; Fratzl, P.; Duda, G.N.; et al. Scaffold Curvature-Mediated Novel Biomineralization Process Originates a Continuous Soft Tissue-to-Bone Interface. Acta Biomater. 2017, 60, 64–80. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Jin, J.; Li, L.; He, S.-y.; Zhou, P.; Jiang, Q.; Wen, C. In Silico and in Vivo Studies of the Effect of Surface Curvature on the Osteoconduction of Porous Scaffolds. Biotechnol. Bioeng. 2022, 119, 591–604. [Google Scholar] [CrossRef]
- Loh, G.H.; Pei, E.; Harrison, D.; Monzón, M.D. An Overview of Functionally Graded Additive Manufacturing. Addit. Manuf. 2018, 23, 34–44. [Google Scholar] [CrossRef]
- McCaw, J.C.S.; Cuan-Urquizo, E. Curved-Layered Additive Manufacturing of Non-Planar, Parametric Lattice Structures. Mater. Des. 2018, 160, 949–963. [Google Scholar] [CrossRef]
- Jung, J.W.; Lee, J.S.; Cho, D.W. Computer-Aided Multiple-Head 3D Printing System for Printing of Heterogeneous Organ/Tissue Constructs. Sci. Rep. 2016, 6, 21685. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.-W.W.; Lee, S.J.; Ko, I.K.; Kengla, C.; Yoo, J.J.; Atala, A. A 3D Bioprinting System to Produce Human-Scale Tissue Constructs with Structural Integrity. Nat. Biotechnol. 2016, 34, 312–319. [Google Scholar] [CrossRef] [PubMed]
- Gleadall, A. FullControl GCode Designer: Open-Source Software for Unconstrained Design in Additive Manufacturing. Addit. Manuf. 2021, 46, 102109. [Google Scholar] [CrossRef]
- Gleadall, A.; Ashcroft, I.; Segal, J. VOLCO: A Predictive Model for 3D Printed Microarchitecture. Addit. Manuf. 2018, 21, 605–618. [Google Scholar] [CrossRef]
- Vega, G.; Paz, R.; Gleadall, A.; Monzón, M.; Alemán-Domínguez, M.E. Comparison of CAD and Voxel-Based Modelling Methodologies for the Mechanical Simulation of Extrusion-Based 3D Printed Scaffolds. Materials 2021, 14, 5670. [Google Scholar] [CrossRef]
- Monzón, M.; Paz, R.; Wang, L.; Donate, R. The Effect of the Manufacturing Process on the Properties of Freeze- Dried Cellulose Reinforced Alginate-Based Scaffolds. In Proceedings of the 2nd International Conference on Biomaterials, Bio-Design and Manufacturing (BDCM 2019), Tianjin, China, 5–6 September 2019. [Google Scholar]
- Sun, H.; Al-Marzouqi, H.; Vega, S. EPCI: A New Tool for Predicting Absolute Permeability from Computed Tomography Images. Geophysics 2019, 84, F97–F102. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Zhang, L.; Zhou, Q.; Luo, L. Automated Quantitative Assessment of Three-Dimensional Bioprinted Hydrogel Scaffolds Using Optical Coherence Tomography. Biomed. Opt. Express 2016, 7, 894. [Google Scholar] [CrossRef]
- Moore, M.J.; Jabbari, E.; Ritman, E.L.; Lu, L.; Currier, B.L.; Windebank, A.J.; Yaszemski, M.J. Quantitative Analysis of Interconnectivity of Porous Biodegradable Scaffolds with Micro-Computed Tomography. J. Biomed. Mater. Res.—Part A 2004, 71, 258–267. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE—A Matlab Kriging Toolbox; Version 2.0; IMM: Lyngby, Denmark, 2002. [Google Scholar]
- Bordón, P.; Paz, R.; Monzón, M.D. Evaluation of the Performance of Atomic Diffusion Additive Manufacturing Electrodes in Electrical Discharge Machining. Materials 2022, 15, 5953. [Google Scholar] [CrossRef]
- Paz, R.; Pei, E.; Monzón, M.; Ortega, F.; Suárez, L. Lightweight Parametric Design Optimization for 4D Printed Parts. Integr. Comput. Aided. Eng. 2017, 24, 225–240. [Google Scholar] [CrossRef]




| Material Properties of PLA—Smartfil | |
|---|---|
| Diameter | 1.75 mm |
| Density | 1.24 g/cm3 |
| Tensile Strength | 114 MPa |
| Elongation at Break | 100% |
| Tensile Modulus | 3861 MPa |
| Elmendorf Tear | 13 g/mL |
| Print Temperature | 220 ± 20 °C |
| Hot Pad | 0–60 °C |
| Heat Deflection Temperature | 65 °C |
| Vicat Softening Temperature | 85 °C |
| Group | Variables | Values | Restrictions | Objectives | |||
|---|---|---|---|---|---|---|---|
| Sinusoidal | VAR1 | Amplitude (mm) | 0.1, 0.5 | R1,R2 | Young’s modulus | O1 | Surface area |
| VAR2 | layer_height (mm) | 0.15, 0.3 | O2 | Interconnectivity | |||
| VAR3 | B (cycles) | 5, 9 | R3,R4 | Pore size | O3 | Porosity * | |
| VAR4 | n_filaments | 5, 9 | |||||
| VAR5 | Infill pattern | 1 (cos), 2 (sin), 3 (cos + sin) | |||||
| Reflected sinusoidal | VAR1 | Amplitude (mm) | 0.1, 0.5 | R1,R2 | Young’s modulus | O1 | Surface area |
| VAR2 | layer_height (mm) | 0.15, 0.3 | O2 | Interconnectivity | |||
| VAR3 | B (cycles) | 5, 9 | R3,R4 | Pore size | O3 | Porosity * | |
| VAR4 | n_filaments | 5, 9 | |||||
| Gyroid | VAR1 | layer_height (mm) | 0.15, 0.3 | R1,R2 | Young’s modulus | O1 | Surface area |
| VAR2 | Porosity (%) | 50, 70 | R3,R4 | Pore size | O2 | Interconnectivity | |
| SAMPLE | VAR1 (mm) | VAR2 (mm) | VAR3 | VAR4 | VAR5 | R1, R2 (MPa) | R3, R4 (µm) | O1 (mm2) | O2 (%) | O3 (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.3 | 5 | 5 | 1 | 104.37 | 352.90 | 3227.82 | 70.58 | 70.59 |
| 2 | 0.5 | 0.3 | 5 | 5 | 2 | 262.71 | 635.61 | 3369 | 70.59 | 70.59 |
| 3 | 0.5 | 0.3 | 5 | 5 | 3 | 50.06 | 549.62 | 3262.06 | 70.59 | 70.59 |
| 4 | 0.5 | 0.15 | 5 | 5 | 1 | 63.63 | 351.72 | 4289.07 | 69.69 | 69.70 |
| 5 | 0.5 | 0.15 | 5 | 5 | 2 | 226.87 | 627.40 | 4550.87 | 69.69 | 69.70 |
| 6 | 0.5 | 0.15 | 5 | 5 | 3 | 11.59 | 143.11 | 4342.28 | 69.69 | 69.70 |
| 7 | 0.5 | 0.3 | 5 | 9 | 1 | 919.59 | 133.02 | 5098.52 | 47.04 | 47.06 |
| 8 | 0.5 | 0.3 | 5 | 9 | 2 | 1241.58 | 231.03 | 5118.21 | 47.05 | 47.06 |
| 9 | 0.5 | 0.3 | 5 | 9 | 3 | 648.44 | 0.00 | 5382.06 | 47.05 | 47.06 |
| 10 | 0.5 | 0.15 | 5 | 9 | 1 | 649.85 | 156.46 | 6073.25 | 45.44 | 45.47 |
| 11 | 0.5 | 0.15 | 5 | 9 | 2 | 1182.57 | 245.09 | 6023.88 | 45.44 | 45.47 |
| 12 | 0.5 | 0.15 | 5 | 9 | 3 | 30.33 | 59.18 | 6697.14 | 45.40 | 45.46 |
| 13 | 0.5 | 0.3 | 9 | 5 | 1 | 516.05 | 242.82 | 4012.04 | 56.83 | 56.85 |
| 14 | 0.5 | 0.3 | 9 | 5 | 2 | 760.54 | 1241.40 | 4070.59 | 56.60 | 56.62 |
| 15 | 0.5 | 0.3 | 9 | 5 | 3 | 1076.63 | 793.13 | 3703.97 | 56.84 | 56.85 |
| 16 | 0.5 | 0.15 | 9 | 5 | 1 | 361.19 | 307.99 | 5235.3 | 55.46 | 55.47 |
| 17 | 0.5 | 0.15 | 9 | 5 | 2 | 652.57 | 255.49 | 5415.32 | 55.70 | 55.71 |
| 18 | 0.5 | 0.15 | 9 | 5 | 3 | 270.14 | 912.24 | 4562.62 | 55.69 | 55.71 |
| 19 | 0.5 | 0.3 | 9 | 9 | 1 | 564.31 * | 56.42 | 4609.76 | 22.16 | 22.33 |
| 20 | 0.5 | 0.3 | 9 | 9 | 2 | 644.57 * | 0.00 | 4914.08 | 21.58 | 21.91 |
| 21 | 0.5 | 0.3 | 9 | 9 | 3 | 610.35 * | 0.00 | 4546.22 | 21.36 | 22.33 |
| 22 | 0.5 | 0.15 | 9 | 9 | 1 | 496.53 * | 83.50 | 5321.86 | 19.75 | 19.85 |
| 23 | 0.5 | 0.15 | 9 | 9 | 2 | 619.24 * | 58.61 | 6048.98 | 20.07 | 20.28 |
| 24 | 0.5 | 0.15 | 9 | 9 | 3 | 409.47 * | 0.00 | 5032.75 | 20.08 | 20.28 |
| 25 | 0.1 | 0.3 | 5 | 9 | 1 | 446.87 | 606.92 | 3528.91 | 64.42 | 64.42 |
| 26 | 0.1 | 0.3 | 5 | 9 | 2 | 544.52 | 731.10 | 3527.88 | 64.42 | 64.42 |
| 27 | 0.1 | 0.3 | 5 | 9 | 3 | 551.10 | 594.93 | 3142.19 | 64.42 | 64.42 |
| 28 | 0.1 | 0.15 | 5 | 9 | 1 | 330.80 | 732.59 | 4540.49 | 63.44 | 63.44 |
| 29 | 0.1 | 0.15 | 5 | 9 | 2 | 517.13 | 827.24 | 4521.83 | 63.44 | 63.44 |
| 30 | 0.1 | 0.15 | 5 | 9 | 3 | 410.48 | 659.61 | 3735.44 | 63.44 | 63.44 |
| 31 | 0.1 | 0.3 | 9 | 9 | 1 | 535.30 | 610.42 | 3829.16 | 62.38 | 62.39 |
| 32 | 0.1 | 0.3 | 9 | 9 | 2 | 605.39 | 637.16 | 3841.97 | 62.38 | 62.39 |
| 33 | 0.1 | 0.3 | 9 | 9 | 3 | 606.23 | 564.31 | 3401.87 | 62.39 | 62.39 |
| 34 | 0.1 | 0.15 | 9 | 9 | 1 | 430.24 | 705.68 | 4865.84 | 61.33 | 61.33 |
| 35 | 0.1 | 0.15 | 9 | 9 | 2 | 573.01 | 748.56 | 4886.62 | 61.33 | 61.33 |
| 36 | 0.1 | 0.15 | 9 | 9 | 3 | 496.30 | 631.74 | 3999.08 | 61.33 | 61.33 |
| 37 | 0.1 | 0.3 | 5 | 5 | 1 | 114.34 | 1887.70 | 2121.09 | 80.24 | 80.24 |
| 38 | 0.1 | 0.3 | 5 | 5 | 2 | 165.76 | 2015.30 | 2118.5 | 80.23 | 80.24 |
| 39 | 0.1 | 0.3 | 5 | 5 | 3 | 148.50 | 1842.70 | 1829.11 | 81.16 | 81.17 |
| 40 | 0.1 | 0.15 | 5 | 5 | 1 | 88.24 | 1991.70 | 2855.25 | 79.69 | 79.69 |
| 41 | 0.1 | 0.15 | 5 | 5 | 2 | 155.94 | 2101.40 | 2847.43 | 79.69 | 79.69 |
| 42 | 0.1 | 0.15 | 5 | 5 | 3 | 112.98 | 1815.60 | 2268.07 | 81.07 | 81.07 |
| 43 | 0.1 | 0.3 | 9 | 5 | 1 | 147.83 | 1587.90 | 2315.75 | 79.10 | 79.10 |
| 44 | 0.1 | 0.3 | 9 | 5 | 2 | 182.56 | 1776.70 | 2318.08 | 79.10 | 79.10 |
| 45 | 0.1 | 0.3 | 9 | 5 | 3 | 176.06 | 1559.40 | 1987.34 | 80.11 | 80.12 |
| 46 | 0.1 | 0.15 | 9 | 5 | 1 | 119.39 | 1860.20 | 3110.26 | 78.52 | 78.52 |
| 47 | 0.1 | 0.15 | 9 | 5 | 2 | 172.49 | 1755.30 | 3119.82 | 78.52 | 78.52 |
| 48 | 0.1 | 0.15 | 9 | 5 | 3 | 141.86 | 1706.30 | 2453.67 | 80.01 | 80.01 |
| SAMPLE | VAR1 (mm) | VAR2 (mm) | VAR3 | VAR4 | R1, R2 (MPa) | R3, R4 (µm) | O1 (mm2) | O2 (%) | O3 (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.15 | 5 | 5 | 384.75 | 1095.5 | 3063.87 | 75.61 | 75.61 |
| 2 | 0.1 | 0.3 | 5 | 5 | 99.84 | 1015.8 | 2313.63 | 75.87 | 75.87 |
| 3 | 0.1 | 0.15 | 5 | 9 | 1071.58 | 1015.8 | 4524.43 | 75.62 | 75.62 |
| 4 | 0.1 | 0.3 | 5 | 9 | 667.33 | 559.39 | 3631.86 | 56.56 | 56.56 |
| 5 | 0.1 | 0.15 | 9 | 5 | 405.02 | 925.04 | 3342.48 | 73.93 | 73.93 |
| 6 | 0.1 | 0.3 | 9 | 5 | 107.72 | 890.29 | 2515.22 | 74.49 | 74.49 |
| 7 | 0.1 | 0.15 | 9 | 9 | 1175.36 | 584.00 | 4822.78 | 53.08 | 53.08 |
| 8 | 0.1 | 0.3 | 9 | 9 | 745.06 | 465.47 | 3913.4 | 54.08 | 54.09 |
| 9 | 0.5 | 0.3 | 5 | 5 | 380.68 | 981.94 | 3368.68 | 64.12 | 64.13 |
| 10 | 0.5 | 0.15 | 5 | 9 | 2250.45 | 244.24 | 4029.16 | 35.18 | 35.25 |
| 11 | 0.5 | 0.3 | 5 | 9 | 1352.73 | 227.11 | 3920.02 | 36.08 | 36.10 |
| 12 | 0.5 | 0.15 | 9 | 5 | 1464.82 | 422.17 | 4607.59 | 46.78 | 46.87 |
| 13 | 0.5 | 0.3 | 9 | 5 | 968.80 | 269.26 | 3765.03 | 47.39 | 47.40 |
| 14 | 0.5 | 0.15 | 9 | 9 | 3413.70 | 0 | 861.47 | 12.65 | 12.67 |
| 15 | 0.5 | 0.3 | 9 | 9 | 3365.57 | 0 | 960.14 | 10.56 | 10.57 |
| 16 | 0.1 | 0.15 | 5 | 5 | 384.75 | 1095.5 | 3063.87 | 75.61 | 75.61 |
| SAMPLE | VAR1 (mm) | VAR2 (%) | R1, R2 (MPa) | R3, R4 (µm) | O1 (mm2) | O2 (%) |
|---|---|---|---|---|---|---|
| 1 | 0.3 | 50 | 567.45 | 500.83 | 2703.41 | 63.77 |
| 2 | 0.3 | 70 | 239.37 | 408.31 | 1702.67 | 77.45 |
| 3 | 0.15 | 50 | 1234.88 | 732.89 | 2090.98 | 42.11 |
| 4 | 0.15 | 70 | 534.22 | 545.91 | 1460.05 | 62.82 |
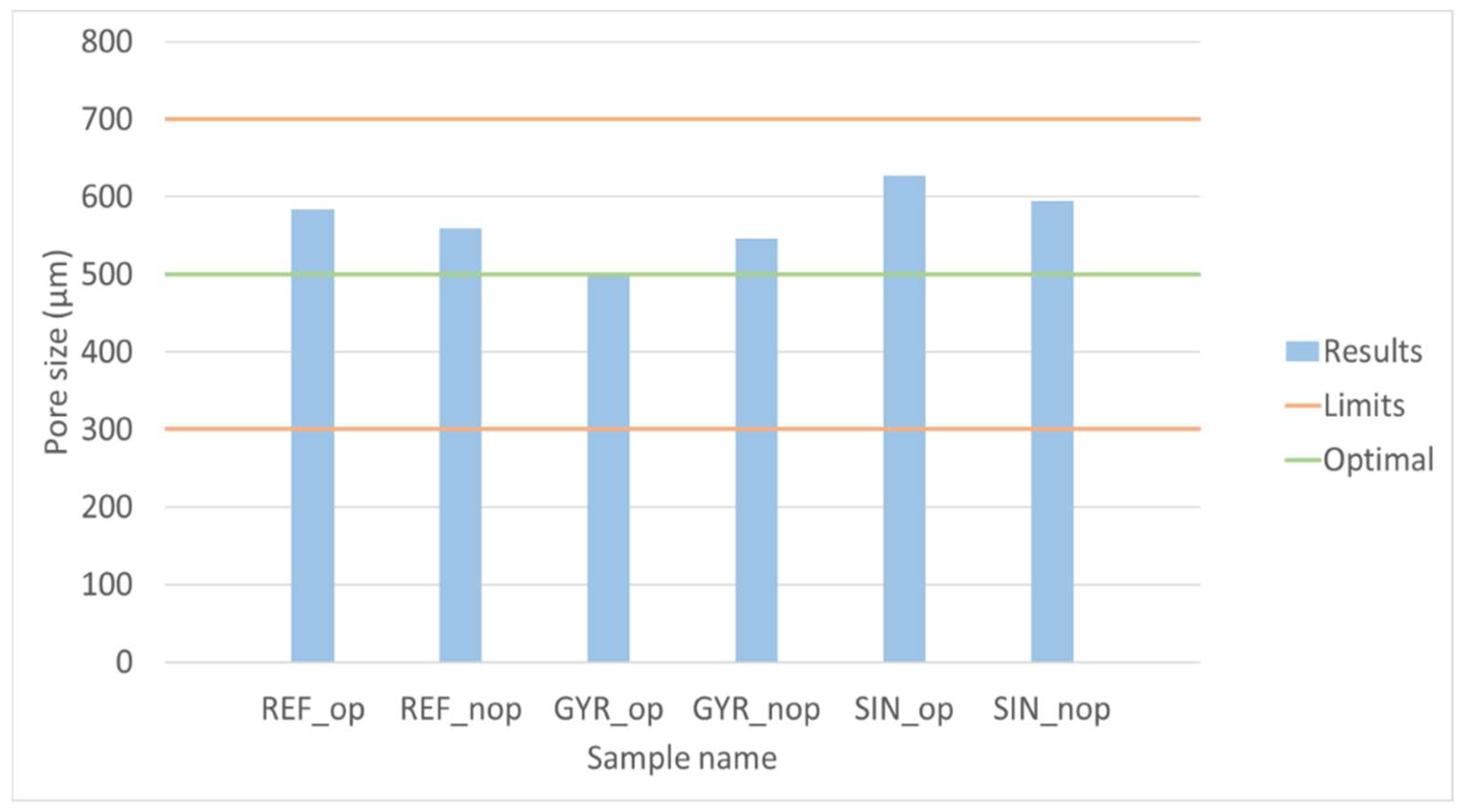
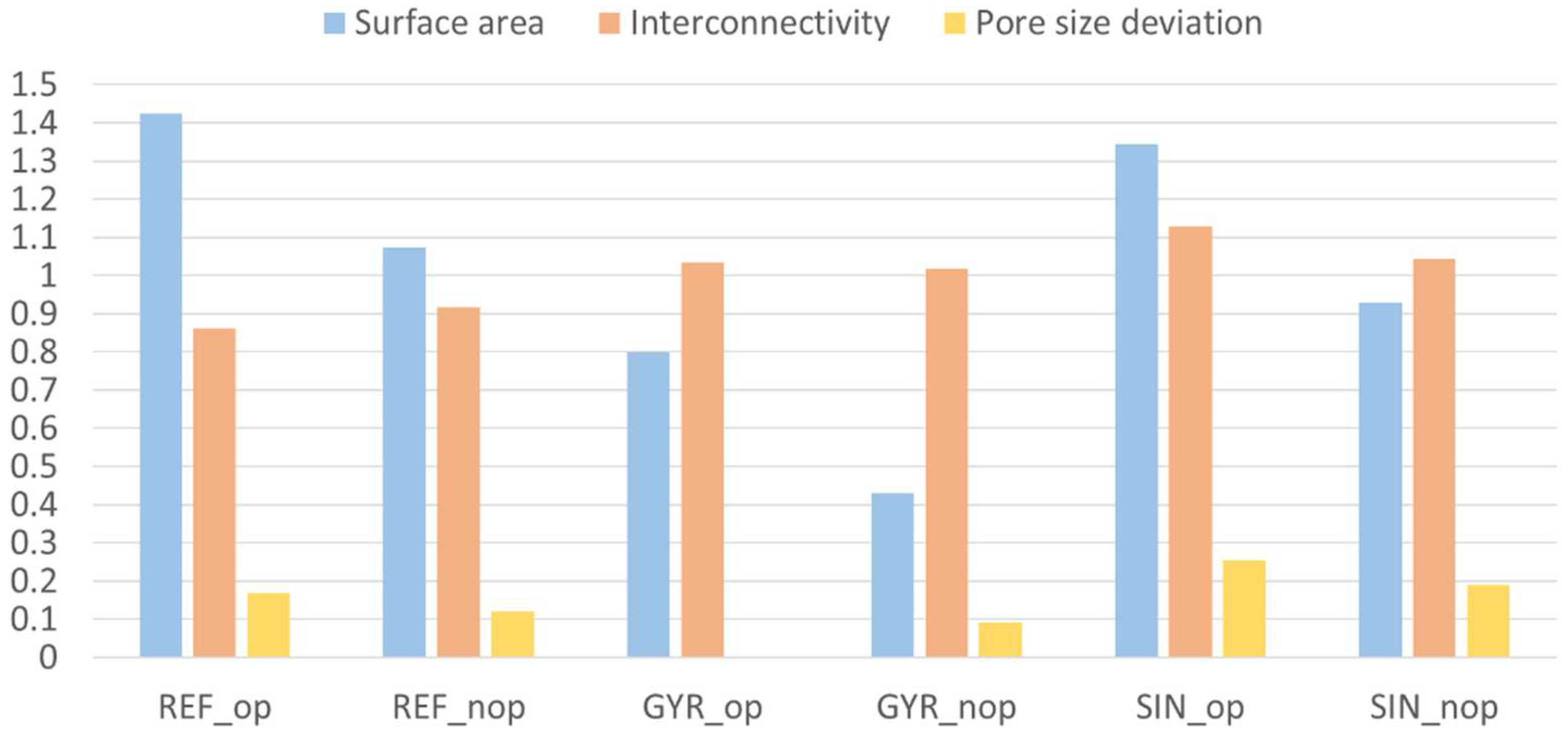
| Configuration | Sample | Young’s Modulus (MPa) | Pore Size (µm) | Surface Area (mm2) | Interconnectivity (%) | Porosity (%) | Fitness Function | Name |
|---|---|---|---|---|---|---|---|---|
| Reflected | 7 | 1175.36 | 584.00 | 4822.78 | 53.08 | 53.08 | 1.23 | REF_op |
| Reflected | 4 | 667.33 | 559.39 | 3631.86 | 56.56 | 56.56 | 1.08 | REF_nop |
| Gyroid | 1 | 567.45 | 500.83 | 2703.41 | 63.77 | 50.00 | 1.20 | GYR_op |
| Gyroid | 4 | 534.22 | 545.91 | 1460.05 | 62.82 | 70.00 | 0.88 | GYR_nop |
| Sinusoidal | 5 | 226.87 | 627.40 | 4550.87 | 69.69 | 69.70 | 1.15 | SIN_op |
| Sinusoidal | 27 | 551.10 | 594.93 | 3142.19 | 64.42 | 64.42 | 0.93 | SIN_nop |
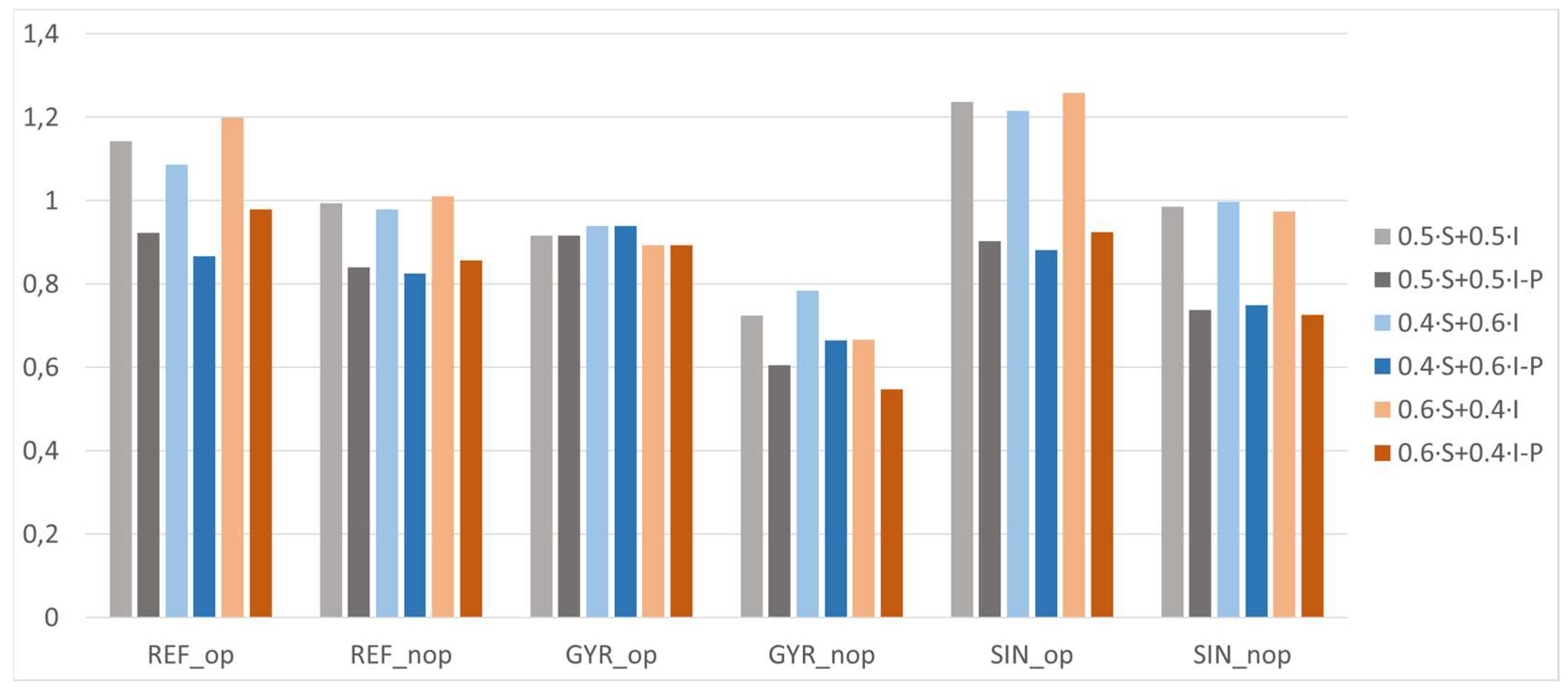
| Comparison Criteria | 0.5·S + 0.5·I | 0.5·S + 0.5·I-P | 0.4·S + 0.6·I | 0.4·S + 0.6·I-P | 0.6·S + 0.4·I | 0.6·S + 0.4·I-P | |
|---|---|---|---|---|---|---|---|
| Ranking | 1 | SIN_op | REF_op | SIN_op | GYR_op | SIN_op | REF_op |
| 2 | REF_op | GYR_op | REF_op | SIN_op | REF_op | SIN_op | |
| 3 | REF_nop | SIN_op | SIN_nop | REF_op | REF_nop | GYR_op | |
| 4 | SIN_nop | REF_nop | REF_nop | REF_nop | SIN_nop | REF_nop | |
| 5 | GYR_op | SIN_nop | GYR_op | SIN_nop | GYR_op | SIN_nop | |
| 6 | GYR_nop | GYR_nop | GYR_nop | GYR_nop | GYR_nop | GYR_nop | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vega, G.; Paz, R.; Monzón, M.; Donate, R.; Gleadall, A. Curve-Based Infill Pattern Optimization for 3D Printed Polymeric Scaffolds for Trabecular Bone Applications. Materials 2025, 18, 4055. https://doi.org/10.3390/ma18174055
Vega G, Paz R, Monzón M, Donate R, Gleadall A. Curve-Based Infill Pattern Optimization for 3D Printed Polymeric Scaffolds for Trabecular Bone Applications. Materials. 2025; 18(17):4055. https://doi.org/10.3390/ma18174055
Chicago/Turabian StyleVega, Gisela, Rubén Paz, Mario Monzón, Ricardo Donate, and Andrew Gleadall. 2025. "Curve-Based Infill Pattern Optimization for 3D Printed Polymeric Scaffolds for Trabecular Bone Applications" Materials 18, no. 17: 4055. https://doi.org/10.3390/ma18174055
APA StyleVega, G., Paz, R., Monzón, M., Donate, R., & Gleadall, A. (2025). Curve-Based Infill Pattern Optimization for 3D Printed Polymeric Scaffolds for Trabecular Bone Applications. Materials, 18(17), 4055. https://doi.org/10.3390/ma18174055








