Negative Mass in the Systems Driven by Entropic Forces
Abstract
1. Introduction
2. Materials and Methods
3. Results
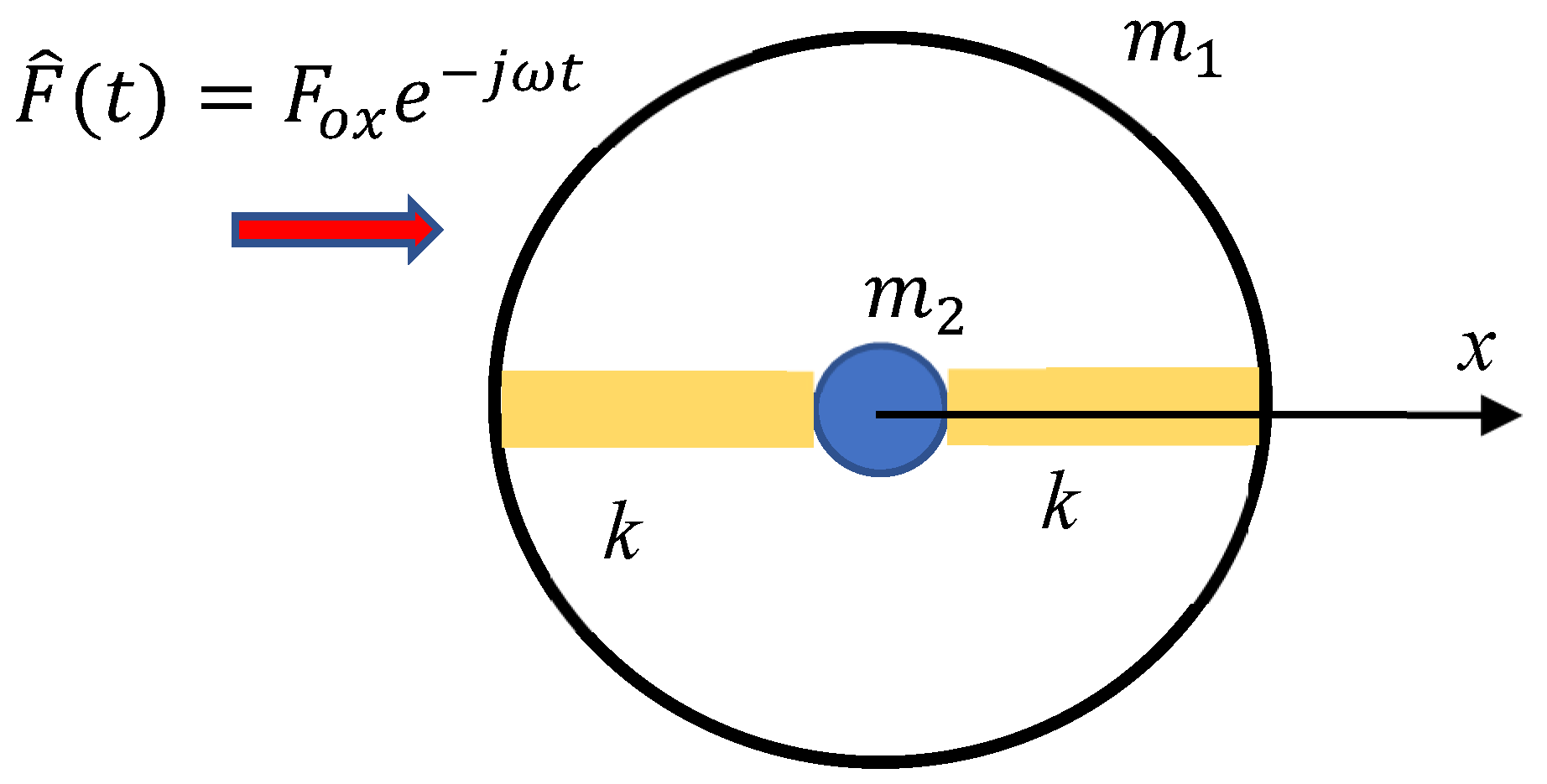
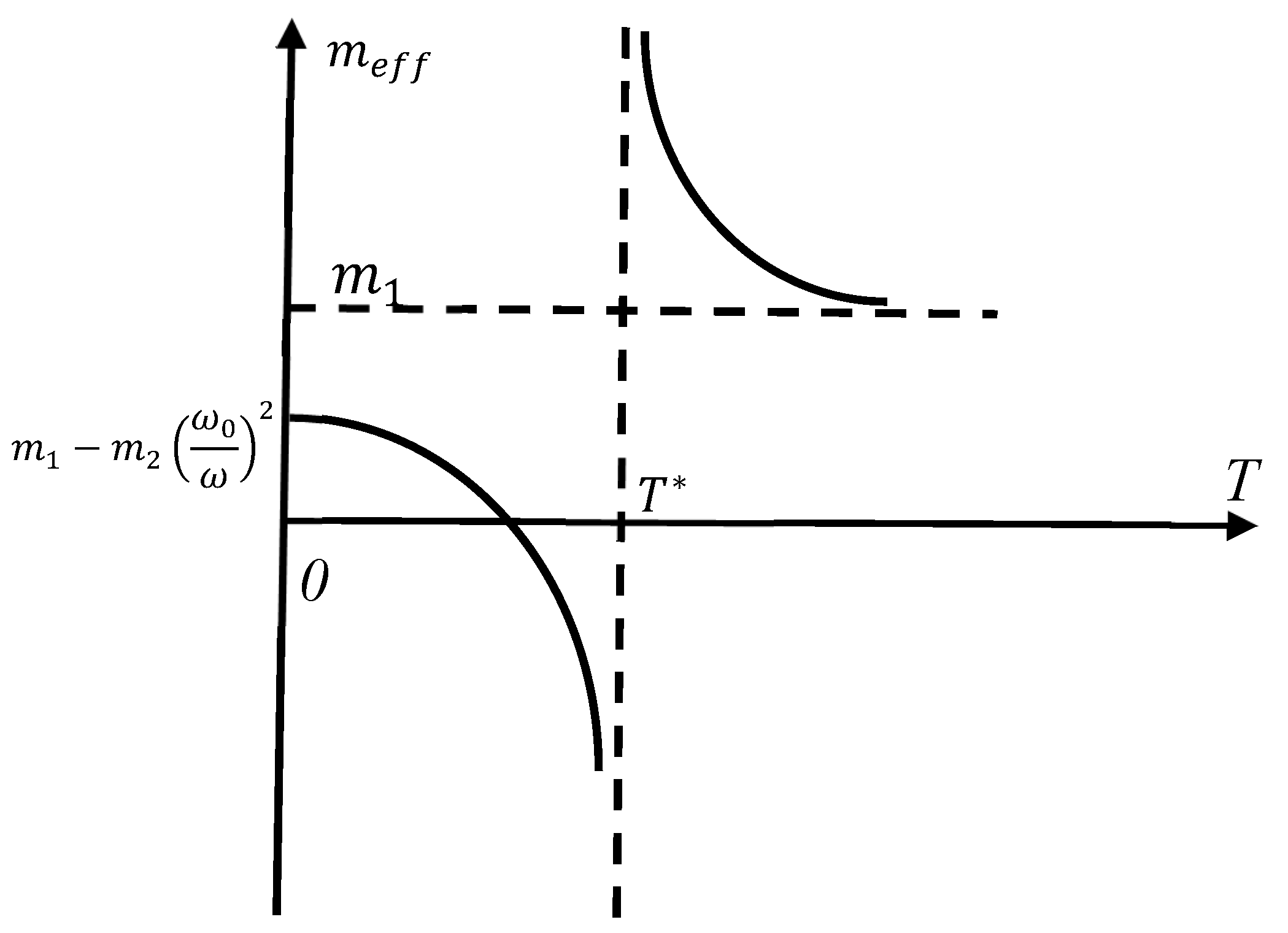
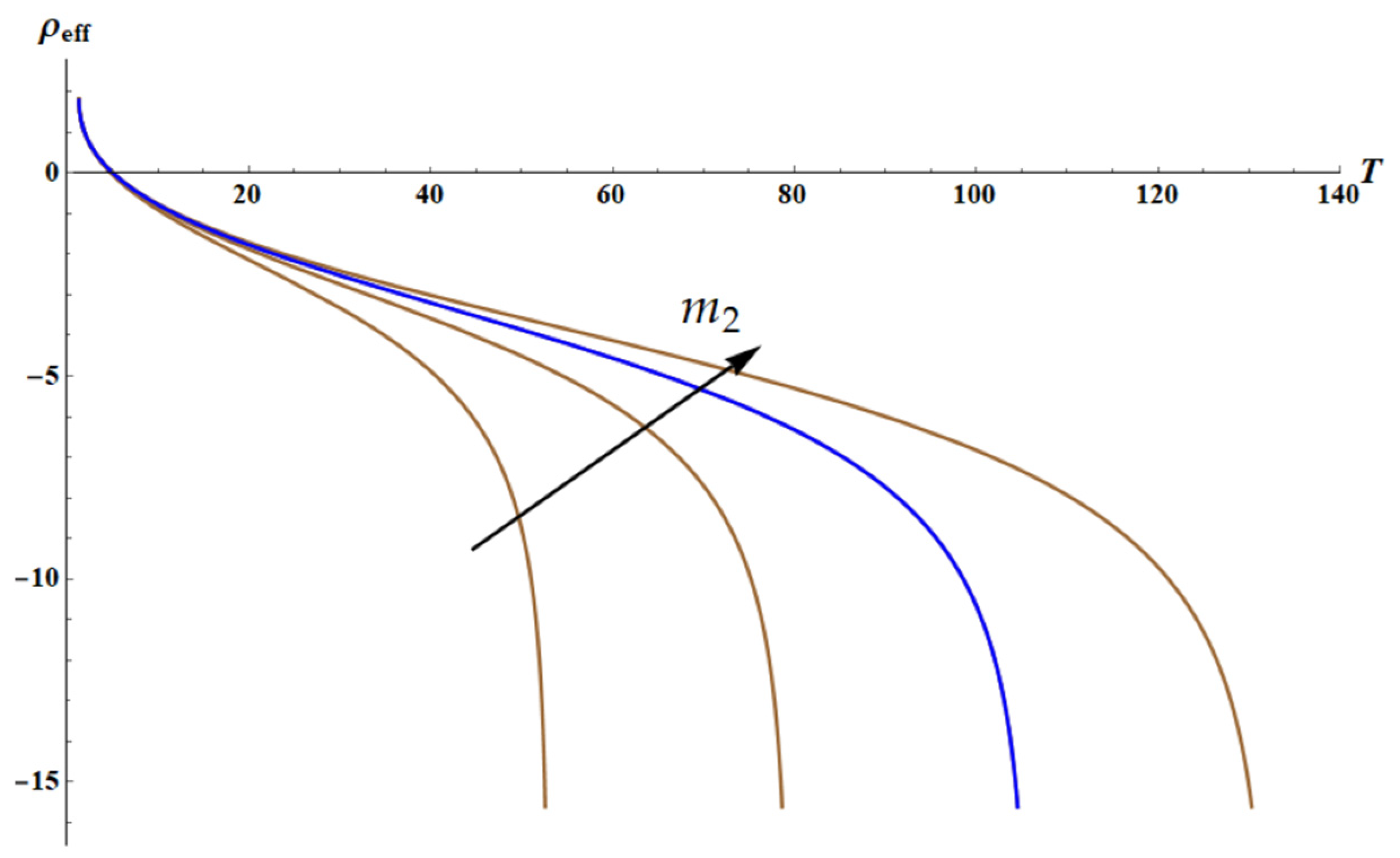
3.1. Negative Mass in the Core–Shell System Driven by Entropic Elastic Force
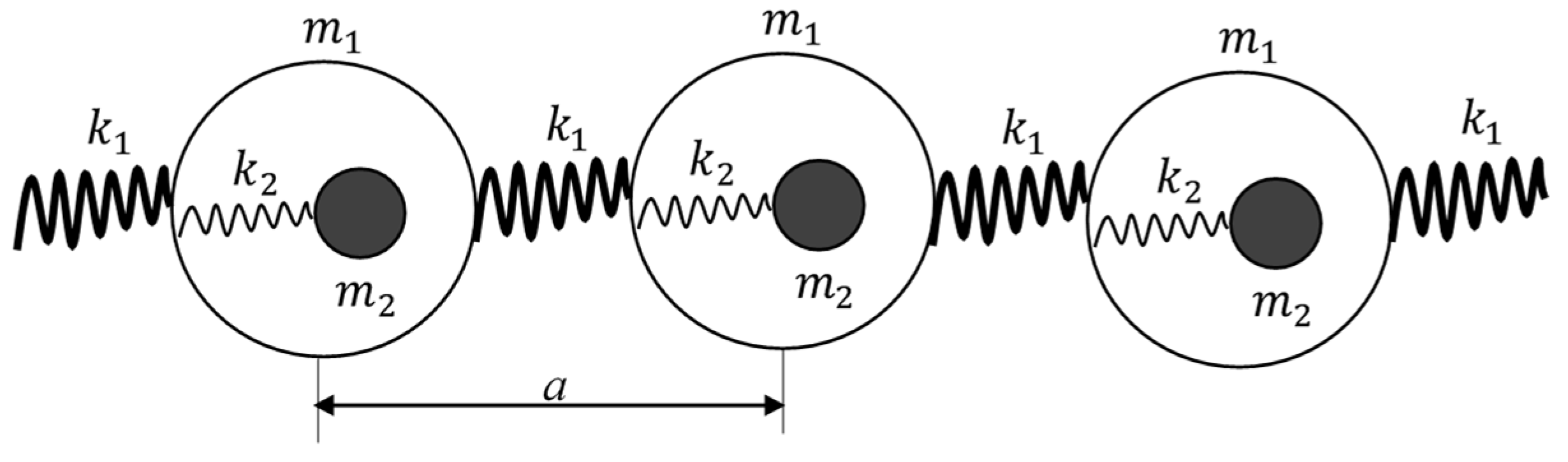
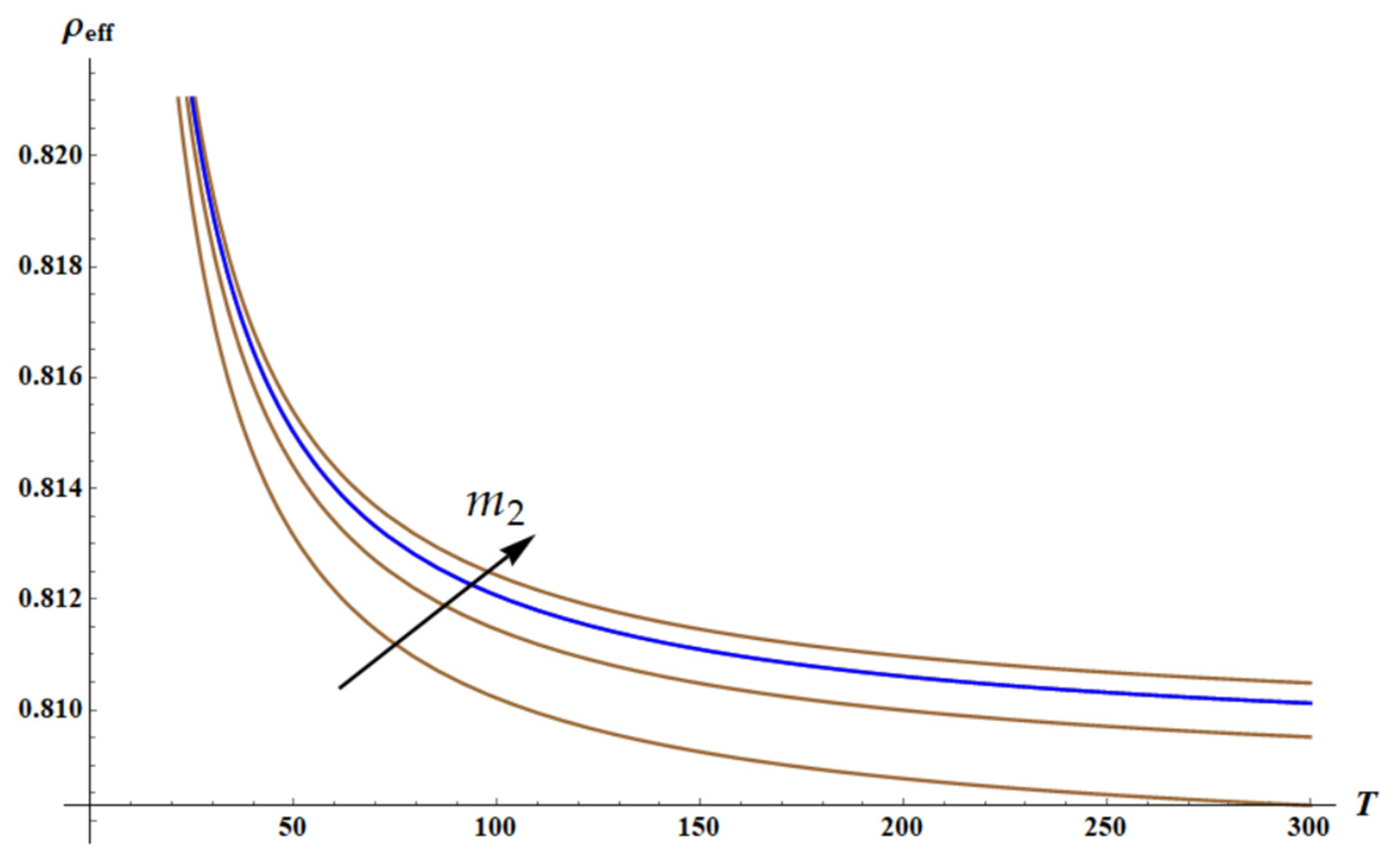
3.2. Negative Density of the Chain of Core–Shell Systems Driven by Elastic Forces
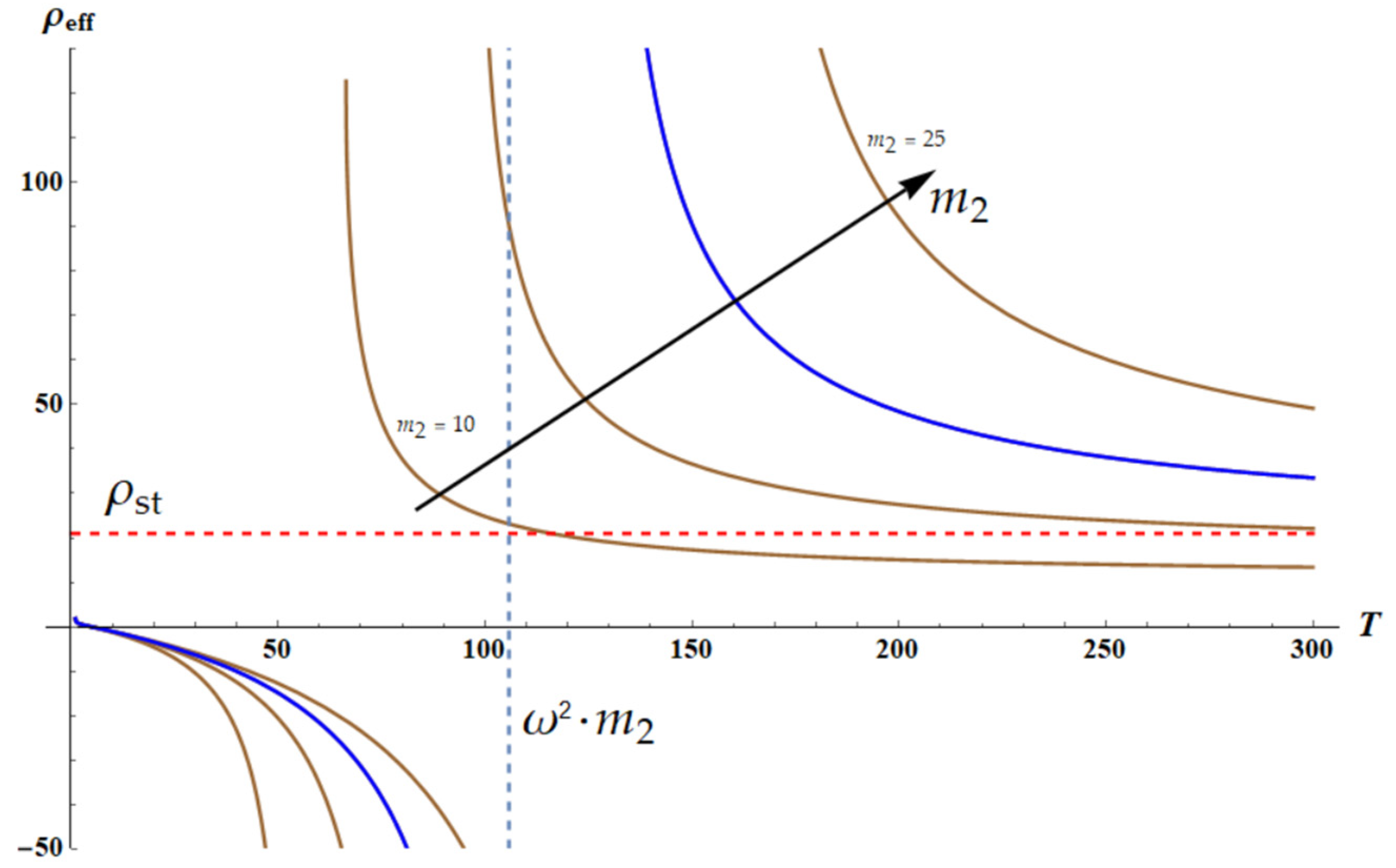
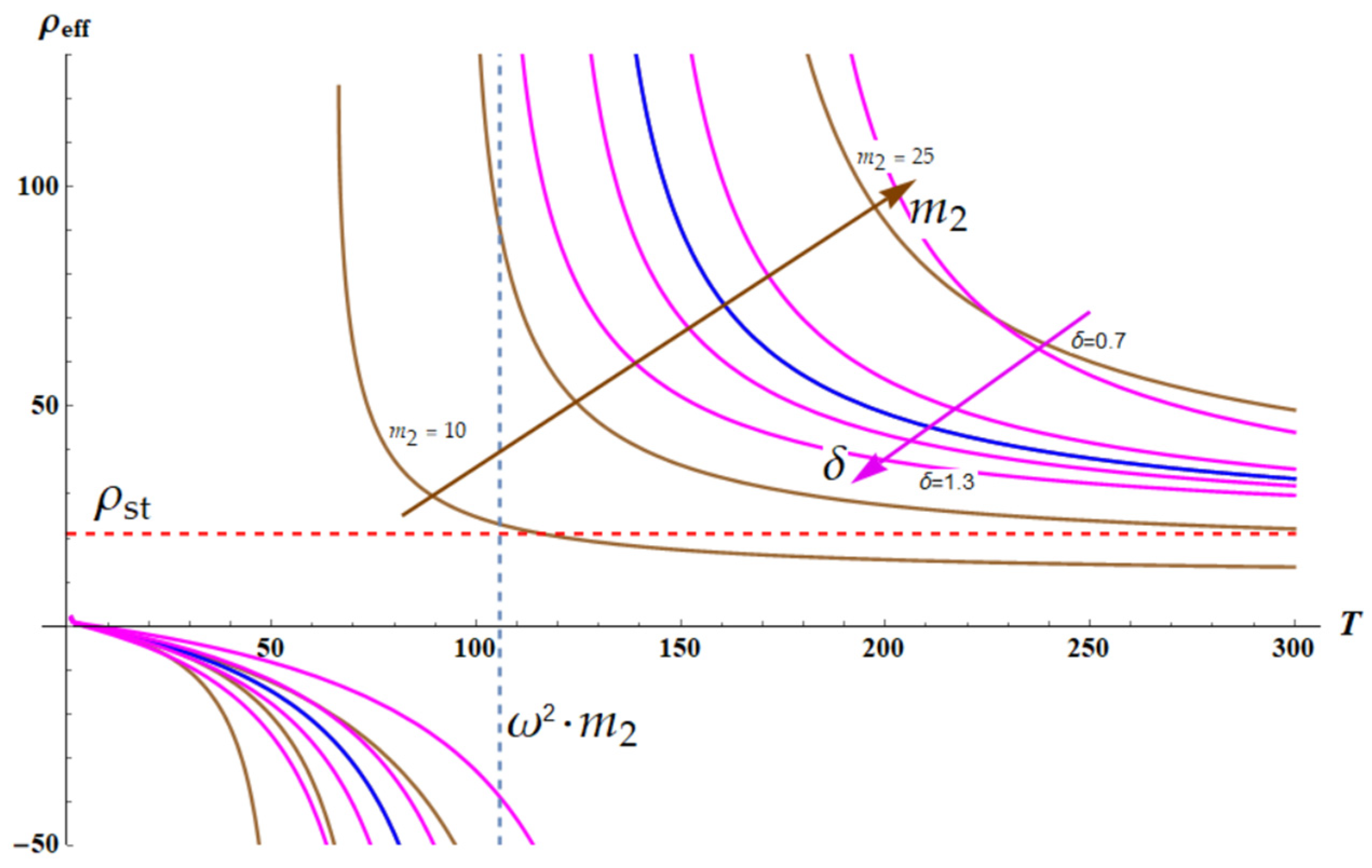
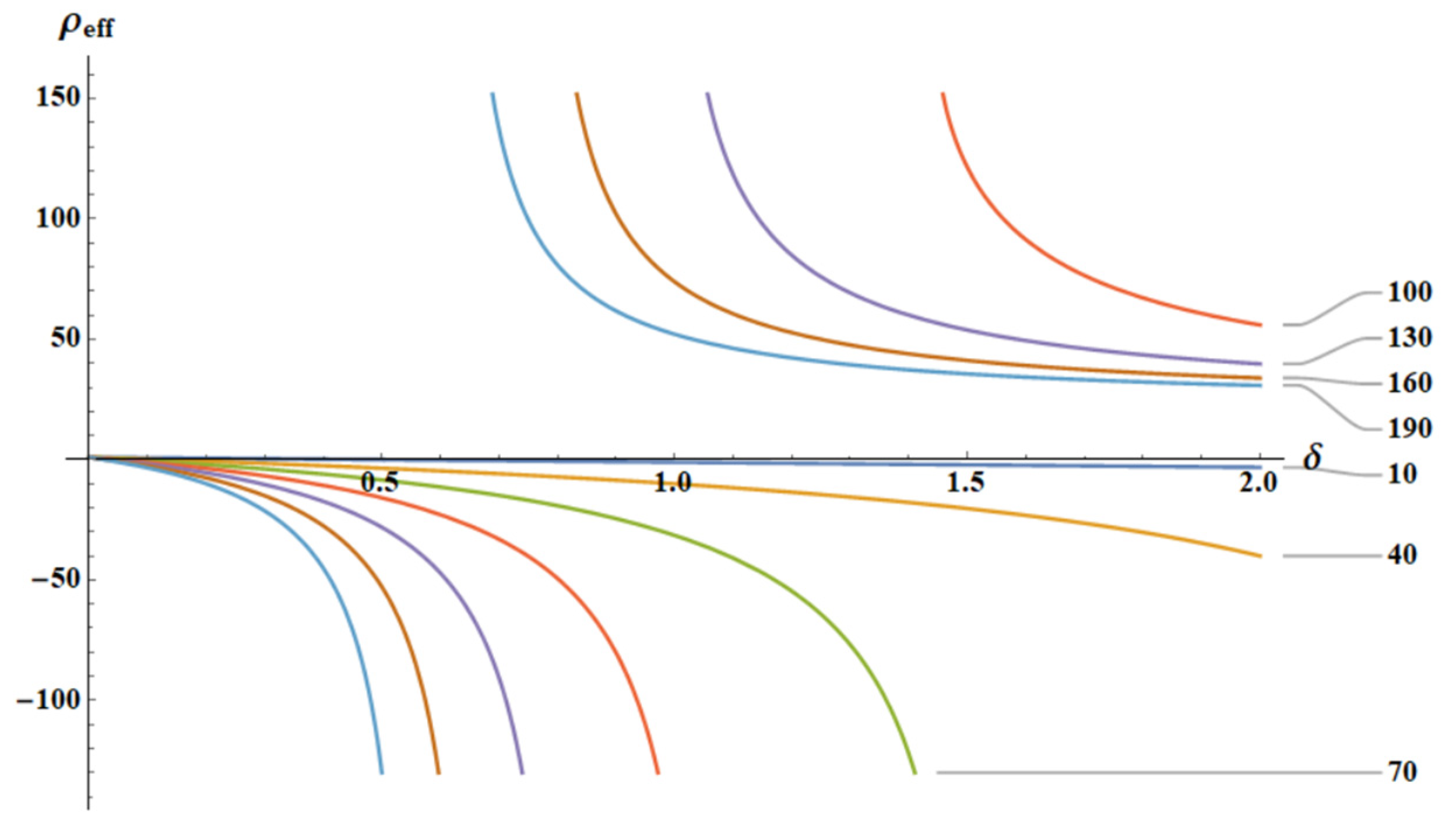
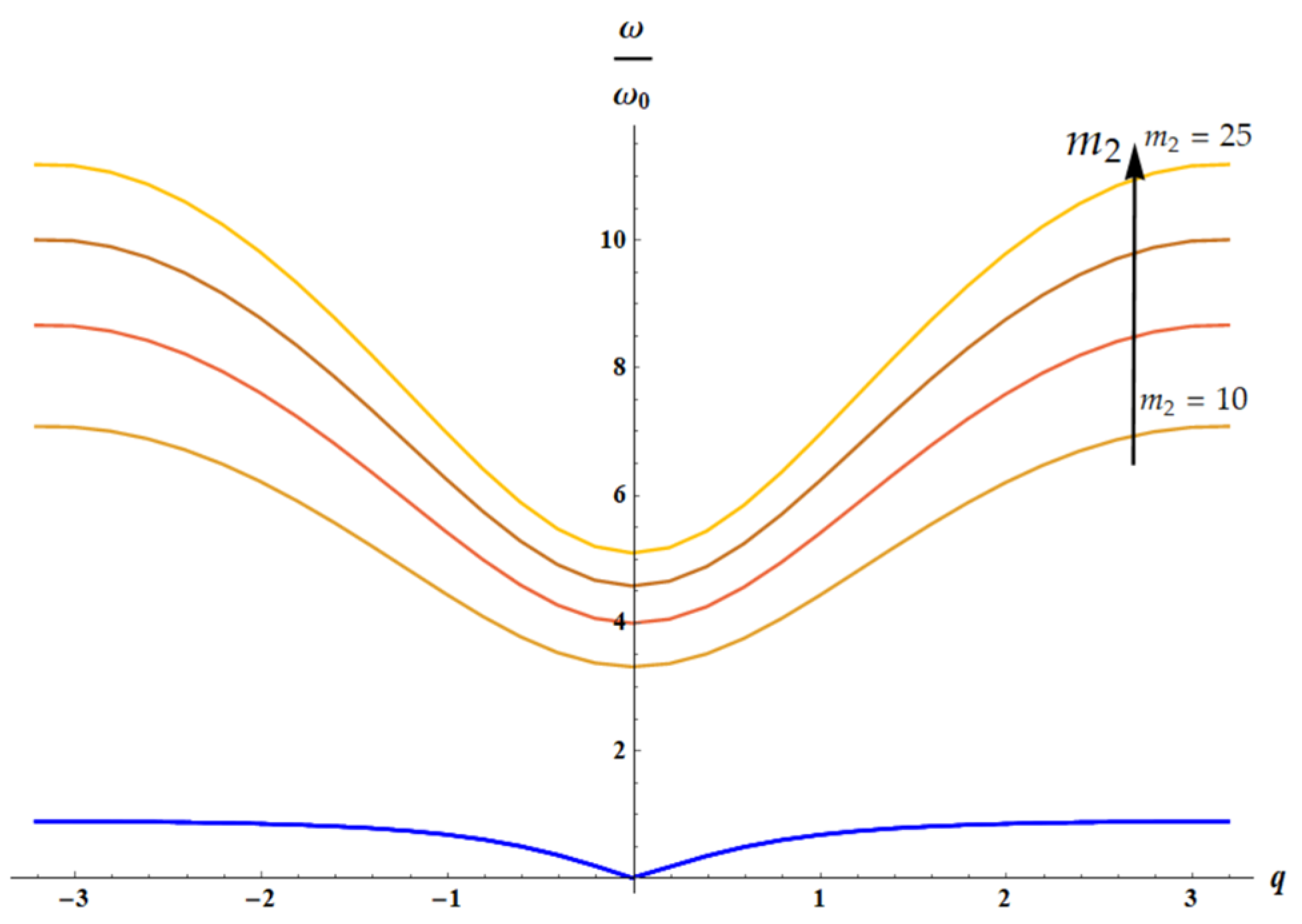
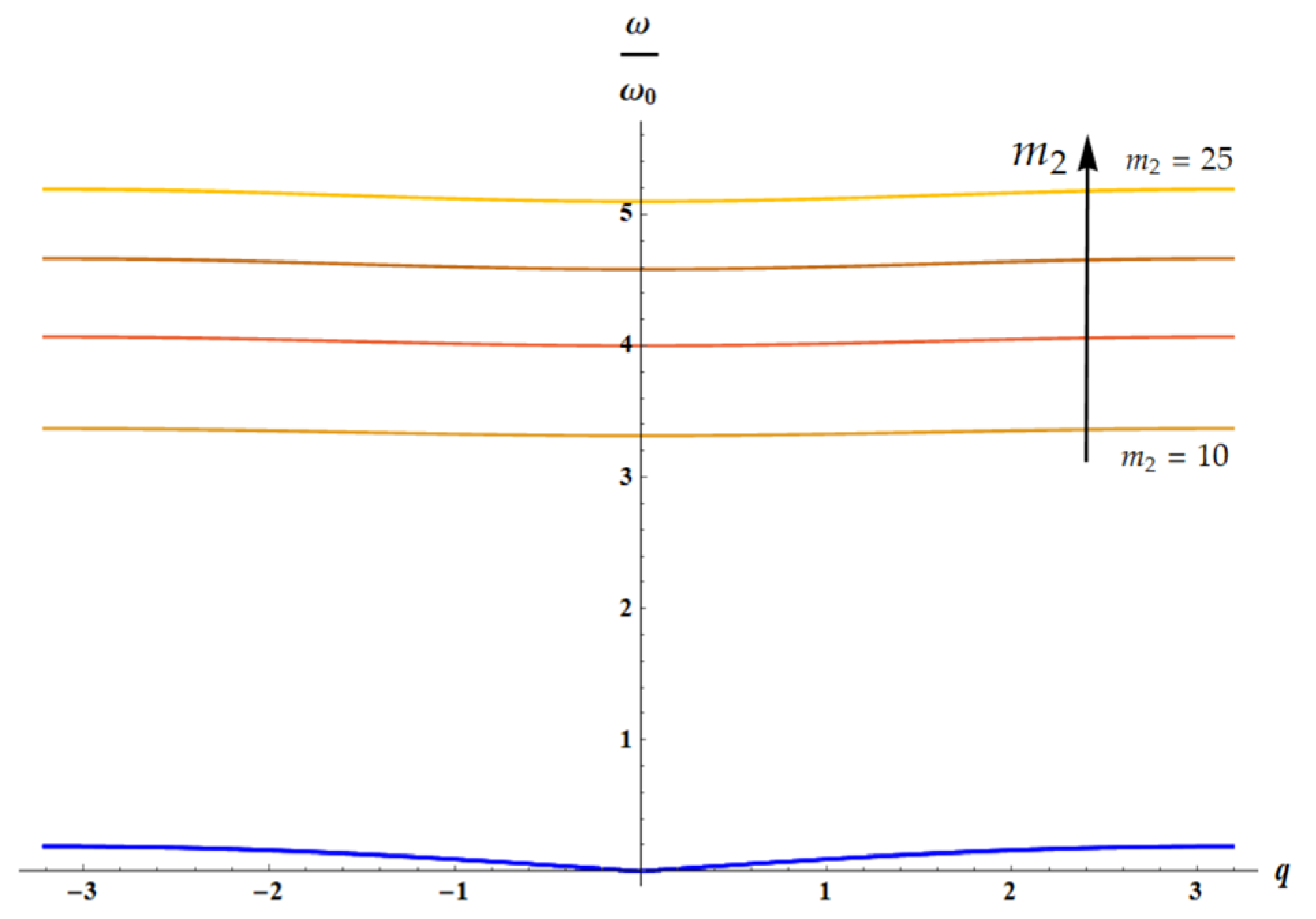
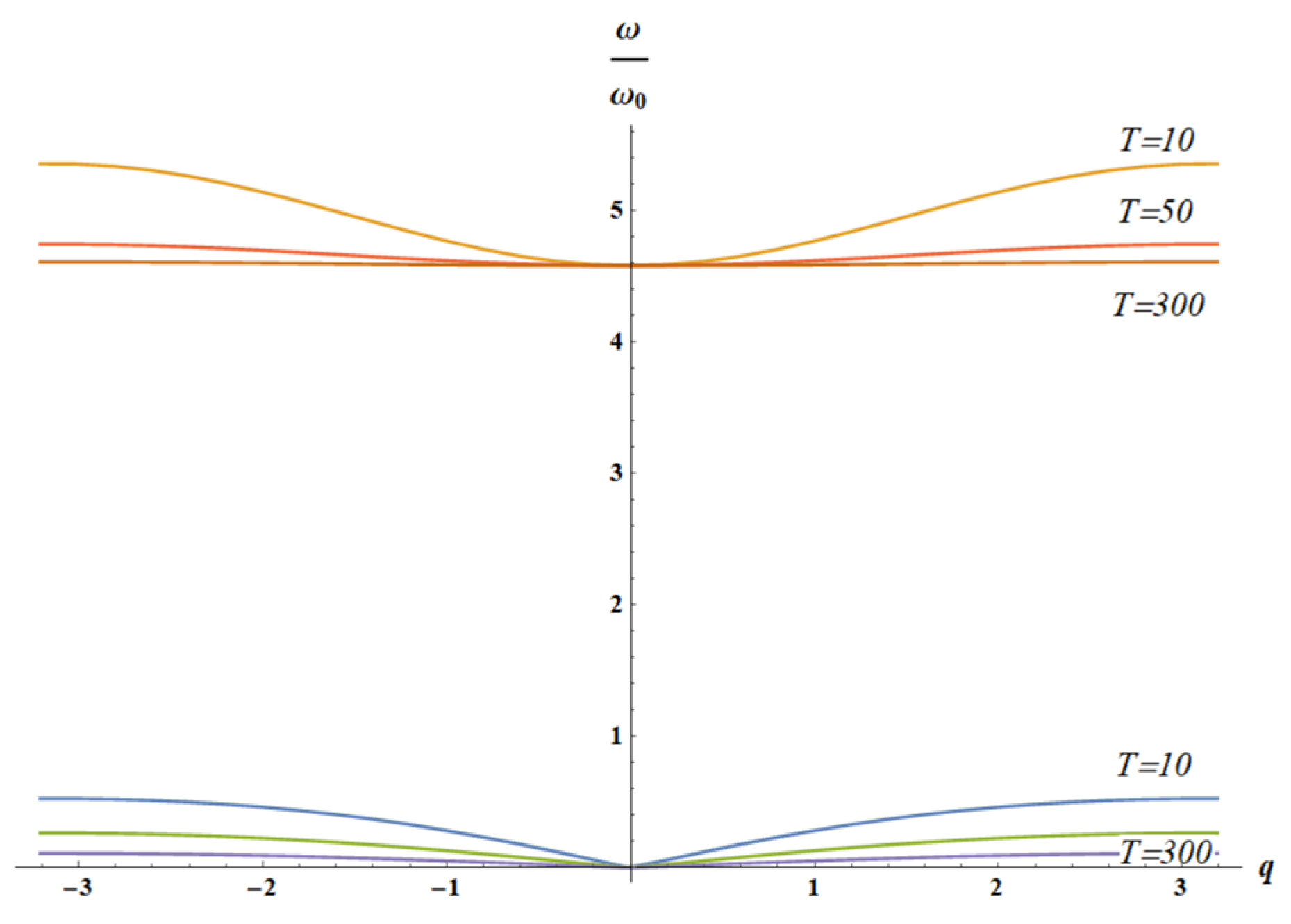
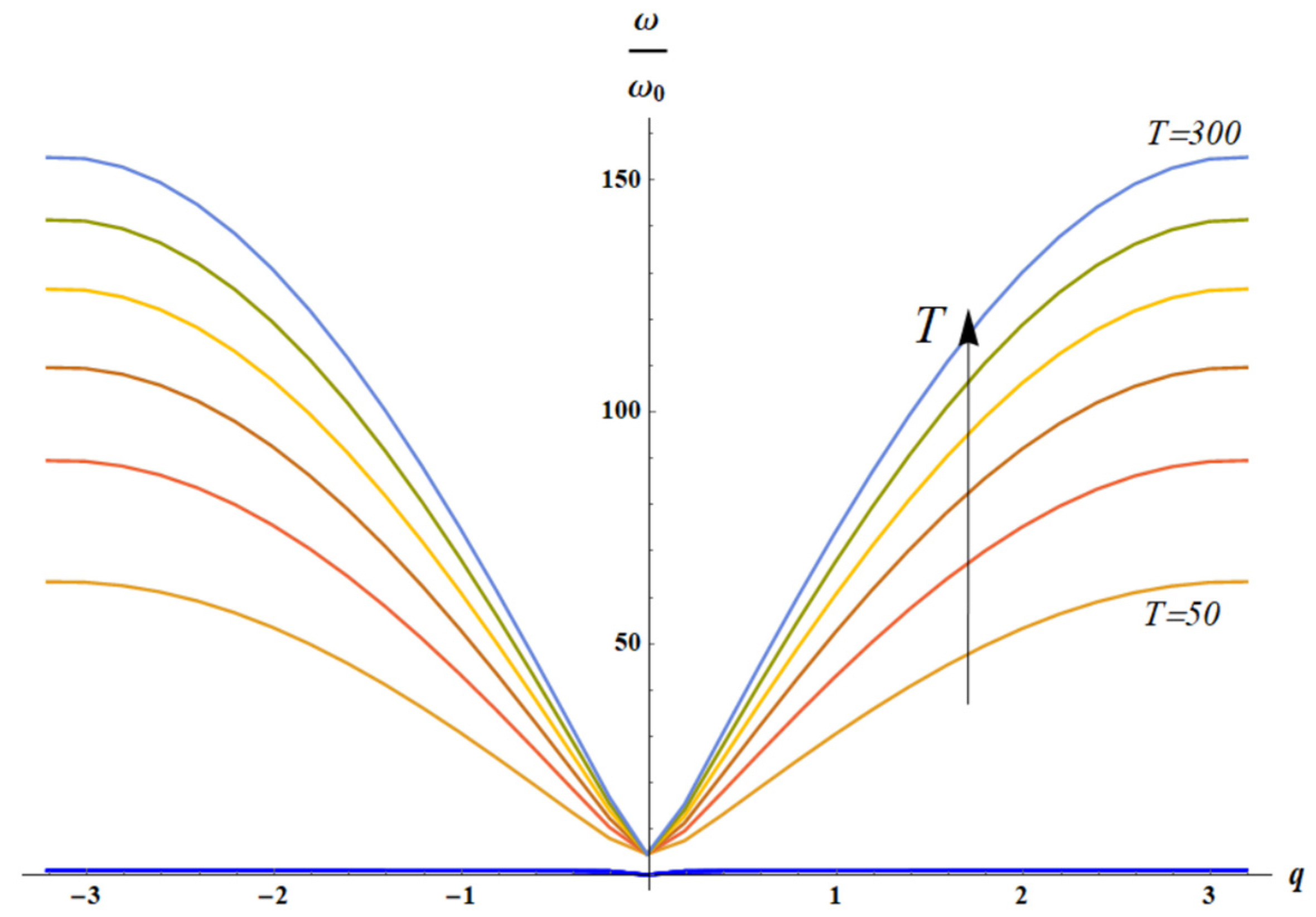
3.3. Dispersion Equations: Influence of the Temperature
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, P.L.; Tabachnik, J. Entropic Forces—Making the Connection between Mechanics and Thermodynamics in an Exactly Soluble Model. Eur. J. Phys. 2013, 34, 729–736. [Google Scholar] [CrossRef]
- Wissner-Gross, A.D.; Freer, C.E. Causal Entropic Forces. Phys. Rev. Lett. 2013, 110, 168702. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.M. Statistical Mechanics of Entropic Forces: Disassembling a Toy. Eur. J. Phys. 2010, 31, 1353–1367. [Google Scholar] [CrossRef]
- Gedde, U.W. Polymer Physics; Springer: Dordrecht, The Netherlands, 2001; ISBN 978-0-412-62640-1. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics, 1st ed.; Oxford University Press: Oxford, UK, 2003; ISBN 019852059X. [Google Scholar]
- Graessley, W.W. Polymeric Liquids and Networks; Garland Science: New York, NY, USA, 2003; ISBN 9780203506127. [Google Scholar]
- Kartsovnik, V.I.; Volchenkov, D. Elastic Entropic Forces in Polymer Deformation. Entropy 2022, 24, 1260. [Google Scholar] [CrossRef]
- Tskhovrebova, L.; Trinick, J.; Sleep, J.A.; Simmons, R.M. Elasticity and Unfolding of Single Molecules of the Giant Muscle Protein Titin. Nature 1997, 387, 308–312. [Google Scholar] [CrossRef]
- Braun, M.; Lansky, Z.; Hilitski, F.; Dogic, Z.; Diez, S. Entropic Forces Drive Contraction of Cytoskeletal Networks. BioEssays 2016, 38, 474–481. [Google Scholar] [CrossRef]
- Verlinde, E. On the Origin of Gravity and the Laws of Newton. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Wang, T. Coulomb Force as an Entropic Force. Phys. Rev. D 2010, 81, 104045. [Google Scholar] [CrossRef]
- Bormashenko, E. Magnetic Entropic Forces Emerging in the System of Elementary Magnets Exposed to the Magnetic Field. Entropy 2022, 24, 299. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Paul, J. Thermoelastic characterization of carbon nanotube reinforced PDMS elastomer. J. Polym. Eng. 2021, 41, 87–94. [Google Scholar] [CrossRef]
- Park, H.; Park, S.; Park, J.M.; Sung, B.J. Entropic contribution to the nonlinear mechanical properties of thermoplastic elastomers. Macromolecules 2025, 58, 1993–2004. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Buehler, M.J.; Wong, S.Y. Entropic elasticity controls nanomechanics of single tropocollagen molecules. Biophys. J. 2007, 93, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Ito, K. Novel entropic elasticity of polymeric materials: Why is slide-ring gel so soft? Polym. J. 2012, 44, 38–41. [Google Scholar] [CrossRef]
- Wendt, D.; Bozin, E.; Neuefeind, J.; Page, K.; Ku, W.; Wang, L.; Fultz, B.; Tkachenko, A.V.; Zaliznyak, I.A. Entropic elasticity and negative thermal expansion in a simple cubic crystal. Sci. Adv. 2019, 5, eaay2748. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Chan, C.T.; Li, J.; Fung, K.H. On Extending the Concept of Double Negativity to Acoustic Waves. J. Zhejiang Univ.-Sci. A 2006, 7, 24–28. [Google Scholar] [CrossRef]
- Milton, G.W.; Willis, J.R. On Modifications of Newton’s Second Law and Linear Continuum Elastodynamics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 855–880. [Google Scholar] [CrossRef]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An Elastic Metamaterial with Simultaneously Negative Mass Density and Bulk Modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled Membranes with Doubly Negative Mass Density and Bulk Modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef] [PubMed]
- Lončar, J.; Igrec, B.; Babić, D. Negative-Inertia Converters: Devices Manifesting Negative Mass and Negative Moment of Inertia. Symmetry 2022, 14, 529. [Google Scholar] [CrossRef]
- Ramachandran, R.; Nosonovsky, M. Vibro-Levitation and Inverted Pendulum: Parametric Resonance in Vibrating Droplets and Soft Materials. Soft Matter 2014, 10, 4633–4639. [Google Scholar] [CrossRef]
- Hasan, M.S.; Nosonovsky, M. Method of Separation of Vibrational Motions for Applications Involving Wetting, Superhydrophobicity, and Microparticle Extraction. Phys. Rev. Fluids 2020, 5, 054201. [Google Scholar] [CrossRef]
- Bormashenko, E. Bioinspired Materials and Metamaterials; CRC Press: Boca Raton, FL, USA, 2025; ISBN 9781003178477. [Google Scholar]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the Negative Effective Mass Density in Acoustic Metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Bormashenko, E.; Legchenkova, I. Negative Effective Mass in Plasmonic Systems. Materials 2020, 13, 1890. [Google Scholar] [CrossRef]
- Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials 2020, 13, 3512. [Google Scholar] [CrossRef]
- Kshetrimayum, R.S. A Brief Intro to Metamaterials. IEEE Potentials 2005, 23, 44–46. [Google Scholar] [CrossRef]
- Karami, B.; Ghayesh, M.H. Dynamics of Graphene Origami-Enabled Auxetic Metamaterial Beams via Various Shear Deformation Theories. Int. J. Eng. Sci. 2024, 203, 104123. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Luo, K.; Tian, Q.; Hu, H. Dynamic Modeling and Simulation of Hard-Magnetic Soft Beams Interacting with Environment via High-Order Finite Elements of ANCF. Int. J. Eng. Sci. 2024, 202, 104102. [Google Scholar] [CrossRef]
- Sang, S.; Mhannawee, A.; Wang, Z. A Design of Active Elastic Metamaterials with Negative Mass Density and Tunable Bulk Modulus. Acta Mech. 2019, 230, 1003–1008. [Google Scholar] [CrossRef]
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D Acoustic Metamaterial with Negative Index. Nat. Mater. 2015, 14, 384–388. [Google Scholar] [CrossRef]
- Feynman, R. The Feynman Lectures on Physics; Addison Wesley Publishinng Co.: Reading, MA, USA, 1964. [Google Scholar]
- Ogata, K. System Dynamics, 4th ed.; Pearson: London, UK, 2003. [Google Scholar]
- Manevitch, L.I.; Gendelman, O.V. Tractable Models of Solid Mechanics: Foundations of Engineering Mechanics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-15371-6. [Google Scholar]
- Sandberg, R.; Svendsen, W.; Mølhave, K.; Boisen, A. Temperature and Pressure Dependence of Resonance in Multi-Layer Microcantilevers. J. Micromech. Microeng. 2005, 15, 1454–1458. [Google Scholar] [CrossRef]
- Fantini, C.; Jorio, A.; Souza, M.; Strano, M.S.; Dresselhaus, M.S.; Pimenta, M.A. Optical Transition Energies for Carbon Nanotubes from Resonant Raman Spectroscopy: Environment and Temperature Effects. Phys. Rev. Lett. 2004, 93, 147406. [Google Scholar] [CrossRef]
- Livneh, T. Resonant Raman Scattering in UO2 Revisited. Phys. Rev. B 2022, 105, 045115. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Ekimov, E.A.; Prokof’ev, V.Y. Temperature Dependence of the Fano Resonance in Nanodiamonds Synthesized at High Static Pressures. JETP Lett. 2022, 115, 651–656. [Google Scholar] [CrossRef]
- Yao, S.; Zhou, X.; Hu, G. Experimental Study on Negative Effective Mass in a 1D Mass–Spring System. New J. Phys. 2008, 10, 043020. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Mechanics: Volume 1 (Course of Theoretical Physics S); Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Rico-Pasto, M.; Ritort, F. Temperature-dependent elastic properties of DNA. Biophys. Rep. 2022, 2, 100067. [Google Scholar] [CrossRef] [PubMed]
- Fok, L.; Zhang, X. Negative Acoustic Index Metamaterial. Phys. Rev. B 2011, 83, 214304. [Google Scholar] [CrossRef]
- Cavassilas, N.; Autran, J.-L.; Aniel, F.; Fishman, G. Energy and temperature dependence of electron effective masses in silicon. J. Appl. Phys. 2002, 92, 1431–1433. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, Y.; Sheng, P.; Zhang, Z.-Q. Hybrid elastic solids. Nat. Mater. 2011, 10, 620–624. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Zhou, X.; Hu, G. Investigation of the negative-mass behaviors occurring below a cut-off frequency. New J. Phys. 2010, 12, 103025. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E.; Gilevich, A.; Shoval, S. Negative Mass in the Systems Driven by Entropic Forces. Materials 2025, 18, 3958. https://doi.org/10.3390/ma18173958
Bormashenko E, Gilevich A, Shoval S. Negative Mass in the Systems Driven by Entropic Forces. Materials. 2025; 18(17):3958. https://doi.org/10.3390/ma18173958
Chicago/Turabian StyleBormashenko, Edward, Artem Gilevich, and Shraga Shoval. 2025. "Negative Mass in the Systems Driven by Entropic Forces" Materials 18, no. 17: 3958. https://doi.org/10.3390/ma18173958
APA StyleBormashenko, E., Gilevich, A., & Shoval, S. (2025). Negative Mass in the Systems Driven by Entropic Forces. Materials, 18(17), 3958. https://doi.org/10.3390/ma18173958







