Numerical Simulation of Arc Welding in Large Flange Shafts Based on a Novel Combined Heat Source Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Experimental Procedure
2.2. Welding Test
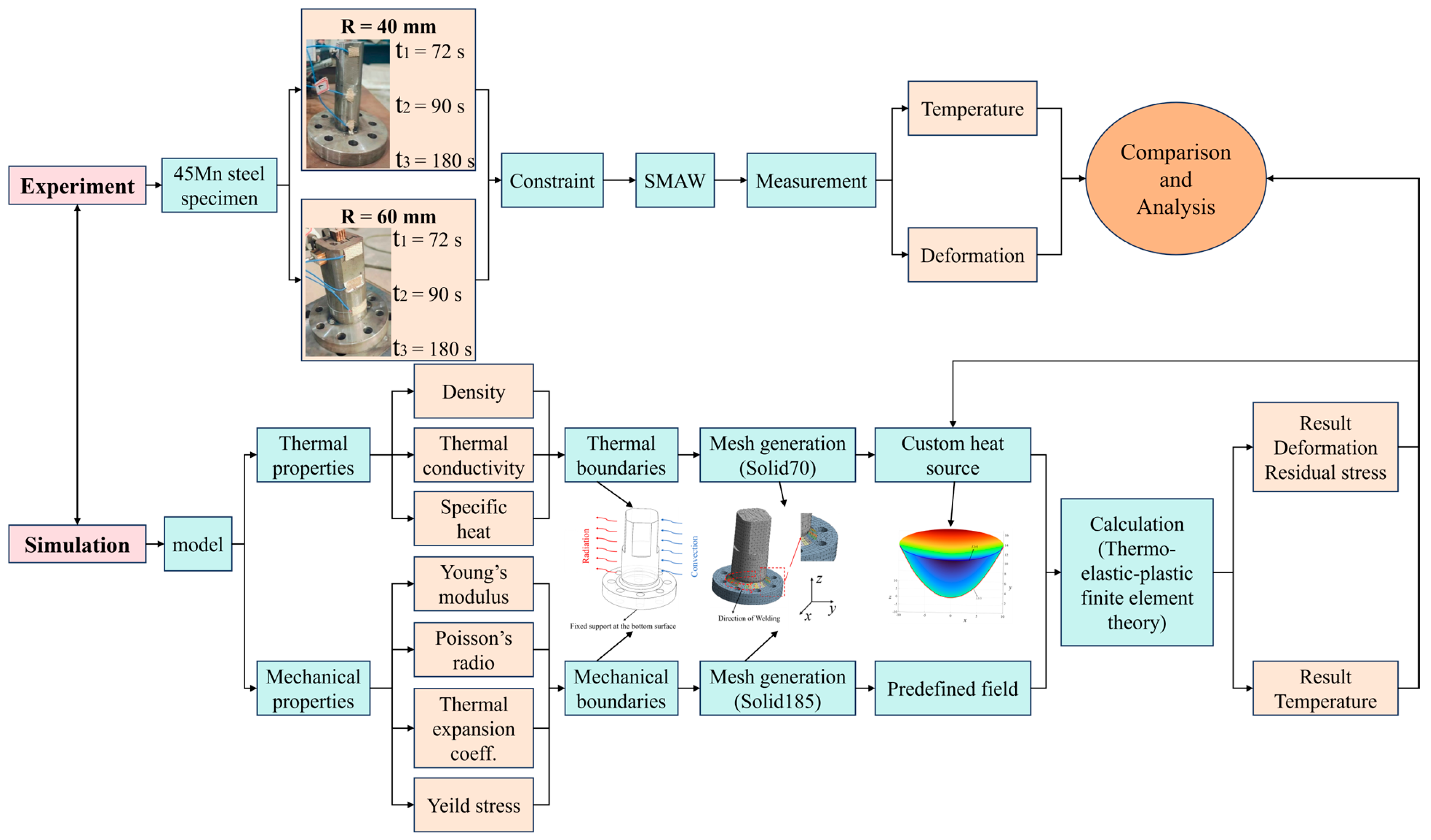
3. Simulation Methodology
3.1. Computational Framework
3.2. Welding Simulation Model
3.2.1. Heat Source Model
3.2.2. Thermal Conductivity Calculation
3.2.3. Thermal Radiation Calculation
3.2.4. Mesh Model and Boundary Conditions
3.3. Finite Element Analysis of Welding Strain Field
3.4. Material Proporties
4. Results and Discussion
4.1. Validation of the Welding Heat Source Model
4.2. Finite Element Analysis of Welding
4.2.1. Analysis of the Welding Temperature Field
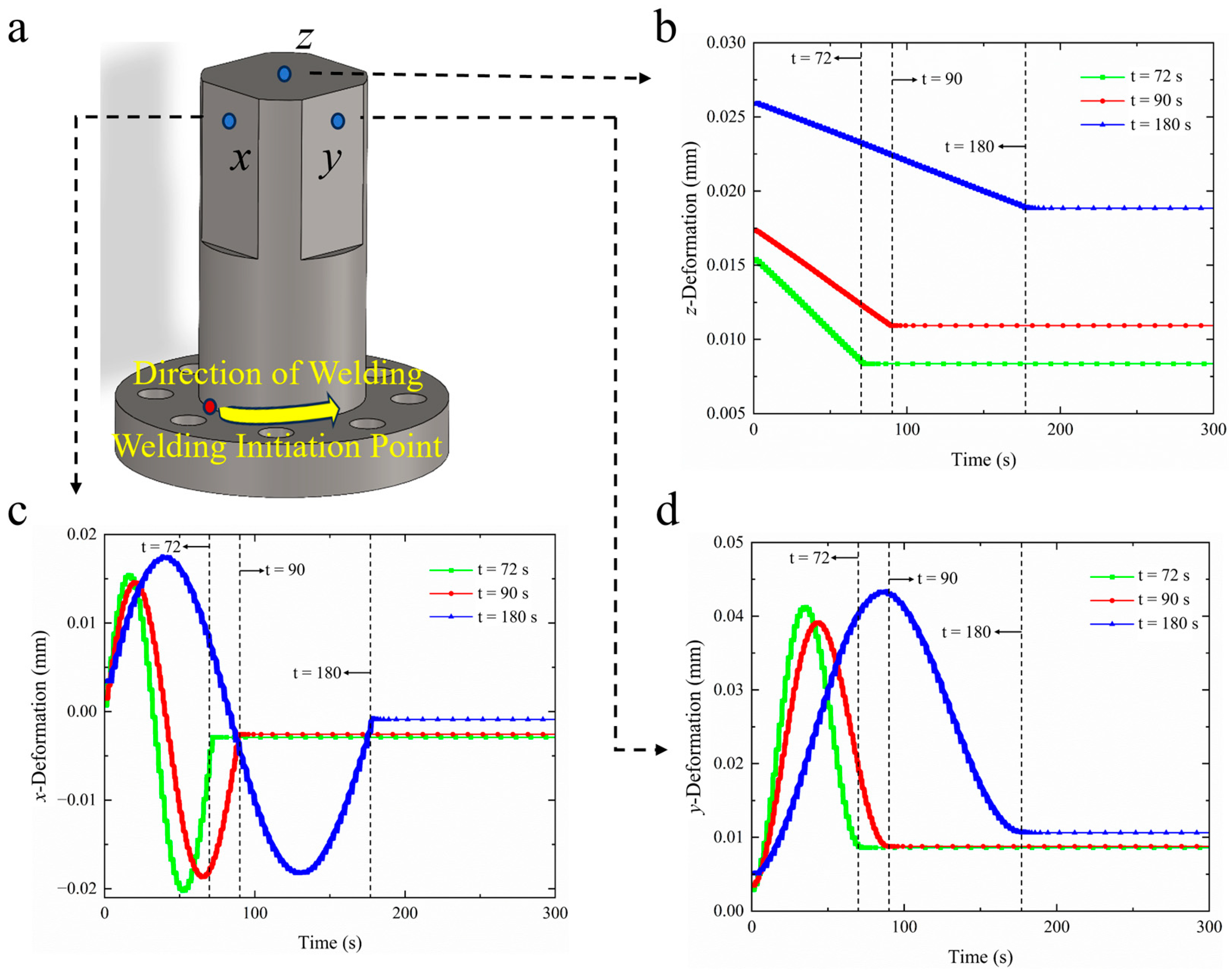
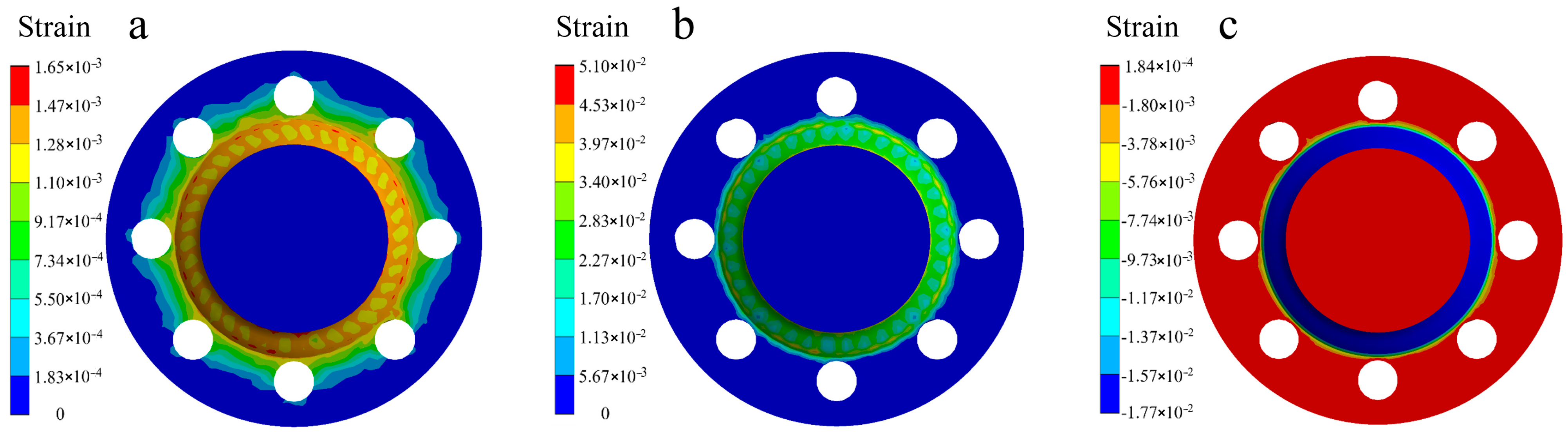
4.2.2. Deformation Field Analysis
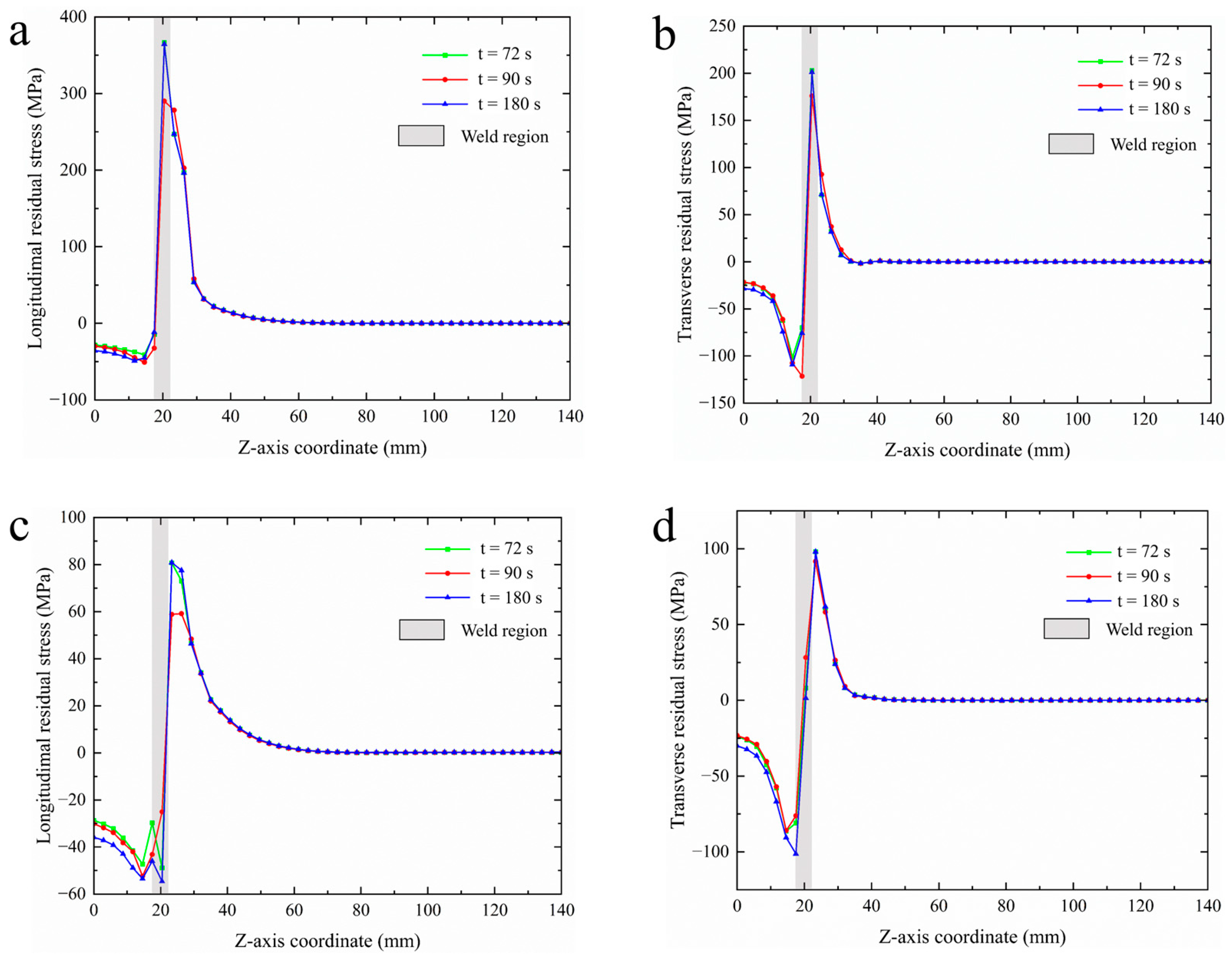
4.2.3. Analysis of Welding Residual Stress Field
4.2.4. Influence of Welding Time on Residual Stress
5. Conclusions
- (1)
- A combined heat source model was developed based on the geometric characteristics of the weld pool. By extracting the actual weld fusion line profile and fitting a rotational heat source distribution, the model achieved a highly accurate simulation of the complex “crescent-shaped” weld pool. Compared to the traditional double-ellipsoidal model (33.3% error) and the homogeneous volumetric model (11.1% error), the proposed model reduced the weld pool depth error to only 2.2% without requiring complex parameter calibration. This presents a more efficient and reliable approach to heat source modeling for arc welding simulations.
- (2)
- The evolution of temperature and deformation fields during the welding process was systematically investigated. The simulation revealed pronounced temperature gradients along the component thickness, with higher peak temperatures and faster heating rates occurring at regions closer to the weld seam. Deformation analysis demonstrated that, while the welding duration significantly influences the magnitude of deformation, it does not alter the overall deformation pattern. Among the evaluated conditions, a welding time of 90 s appears to be more suitable for large-diameter flange shafts, effectively reducing residual deformation. Furthermore, increasing the shaft diameter was shown to enhance the structural stiffness, thereby mitigating welding-induced distortion. Those findings offer valuable references for evaluating the risk of welding deformation and cracking, and support the development of preventive strategies to ensure structural integrity during fabrication.
- (3)
- The simulation results of residual stress revealed that longitudinal residual stresses are generally higher than transverse residual stresses. Along the welding direction, stresses were primarily concentrated within the weld zone and adjacent heat-affected regions. The distribution trend remained consistent across different welding durations, characterized by an initial rise following arc ignition, a stabilized peak during steady-state welding, and a decline after arc termination. Notably, when the welding time was set to 90 s, the residual stress gradient perpendicular to the welding direction was reduced by 19%, indicating that a properly extended welding duration can effectively alleviate stress concentration and help minimize the risk of structural warping and distortion.
- (4)
- Based on simulation results, a welding time of 90 s may be a preferable choice for arc welding of 45Mn steel flange shafts of this dimension.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Heat flux density | |
| Welding thermal efficiency | |
| Welding voltage | |
| Welding current | |
| Heat source effective volume | |
| Welding heat input | |
| Filler wire density | |
| Filler wire radius | |
| Wire feed speed | |
| Filler wire fusion enthalpy | |
| Temperature-dependent density | |
| Temperature-dependent specific heat | |
| Temperature-dependent thermal conductivity | |
| Energy distribution fraction in the front half of the ellipsoidal heat source | |
| Length of the back half of the ellipsoidal heat source | |
| Depth of the ellipsoidal heat source | |
| The normal stresses acting along three directions that are orthogonal to each other, respectively | |
| Plastic strain increment | |
| Partial derivative of the scalar function with respect to the vector function | |
| Welding time | |
| Heat source energy density | |
| Heat transfer coefficient | |
| Emissivity | |
| Stefan–Boltzmann constant | |
| Initial environmental temperature | |
| Total strain | |
| Elastic strain | |
| Plastic strain | |
| Thermal strain | |
| Creep strain | |
| Phase transformation strain | |
| Energy distribution fraction in the rear half of the ellipsoidal heat source | |
| Length of the front half of the ellipsoidal heat source | |
| Width of the ellipsoidal heat source | |
| Equivalent stress | |
| Uniaxial tensile yield limit | |
| Plastic multiplier |
References
- Guo, Q.; Yang, Z.; Xu, J.; Jiang, Y.; Wang, W.; Liu, Z.; Zhao, W.; Sun, Y. Progress, challenges and trends on vision sensing technologies in automatic/intelligent robotic welding: State-of-the-art review. Robot. Comput. -Integr. Manuf. 2024, 89, 102767. [Google Scholar] [CrossRef]
- Abdeltawab, N.M.; Elshazly, M.; Shash, A.Y.; Sherbiny, M.E. Studying the effect of processing parameters on the microstructure, strength, hardness, and corrosion characteristics of friction stir dissimilar welded AA5083 and AA7075 aluminum alloys reinforced with Al-SiC matrix. Heliyon 2025, 11, e41362. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Yamashita, T.; Ushioda, K.; Tsutsumi, S.; Morisada, Y.; Fujii, H. Linear friction welding of T-Joints in low carbon steel: Effect of welding parameters on joint quality. J. Adv. Join. Process. 2024, 10, 100267. [Google Scholar] [CrossRef]
- Shengfang, Z.; Jiaheng, M.; Ziguang, W.; Ziyuan, L.; Zhihua, S.; Fujian, M. Research on welding deformation of hollow thin-walled complex structural parts based on plane bending theory of constant section beam. J. Manuf. Process. 2023, 95, 330–341. [Google Scholar] [CrossRef]
- Anawa, E.M.; Olabi, A.-G. Control of welding residual stress for dissimilar laser welded materials. J. Mater. Process. Technol. 2008, 204, 22–33. [Google Scholar] [CrossRef]
- Tabatabaeian, A.; Ghasemi, A.R.; Shokrieh, M.M.; Marzbanrad, B.; Baraheni, M.; Fotouhi, M. Residual stress in engineering materials: A review. Adv. Eng. Mater. 2022, 24, 2100786. [Google Scholar] [CrossRef]
- Niku-Lari, A. Residual Stresses: Technology—Applications—Effects; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Lopez-Jauregi, A.; Esnaola, J.; Ulacia, I.; Urrutibeascoa, I.; Madariaga, A. Fatigue analysis of multipass welded joints considering residual stresses. Int. J. Fatigue 2015, 79, 75–85. [Google Scholar] [CrossRef]
- Sonsino, C. Effect of residual stresses on the fatigue behaviour of welded joints depending on loading conditions and weld geometry. Int. J. Fatigue 2009, 31, 88–101. [Google Scholar] [CrossRef]
- Dai, W.; Zhang, C.; Yue, H.; Li, Q.; Guo, C.; Zhang, J.; Zhao, G.; Yang, X. A review on the fatigue performance of micro-arc oxidation coated Al alloys with micro-defects and residual stress. J. Mater. Res. Technol. 2023, 25, 4554–4581. [Google Scholar] [CrossRef]
- Ghasri-Khouzani, M.; Peng, H.; Rogge, R.; Attardo, R.; Ostiguy, P.; Neidig, J.; Billo, R.; Hoelzle, D.; Shankar, M. Experimental measurement of residual stress and distortion in additively manufactured stainless steel components with various dimensions. Mater. Sci. Eng. A 2017, 707, 689–700. [Google Scholar] [CrossRef]
- Masoudi, S.; Amirian, G.; Saeedi, E.; Ahmadi, M. The effect of quench-induced residual stresses on the distortion of machined thin-walled parts. J. Mater. Eng. Perform. 2015, 24, 3933–3941. [Google Scholar] [CrossRef]
- Alipooramirabad, H.; Ghomashchi, R.; Paradowska, A.; Reid, M. Residual stress-microstructure-mechanical property interrelationships in multipass HSLA steel welds. J. Mater. Process. Technol. 2016, 231, 456–467. [Google Scholar] [CrossRef]
- Rae, W.; Lomas, Z.; Jackson, M.; Rahimi, S. Measurements of residual stress and microstructural evolution in electron beam welded Ti-6Al-4V using multiple techniques. Mater. Charact. 2017, 132, 10–19. [Google Scholar] [CrossRef]
- Rossini, N.; Dassisti, M.; Benyounis, K.; Olabi, A.-G. Methods of measuring residual stresses in components. Mater. Des. 2012, 35, 572–588. [Google Scholar] [CrossRef]
- Yan, H.; Zeng, X.; Cui, Y.; Zou, D. Numerical and experimental study of residual stress in multi-pass laser welded 5A06 alloy ultra-thick plate. J. Mater. Res. Technol. 2024, 28, 4116–4130. [Google Scholar] [CrossRef]
- He, M.; Wang, Q.; He, Y.; Wang, J.; Ma, N.; Wang, Y. Effects of ultrasonic vibration on residual stress distribution and local mechanical properties of AA6061/Ti6Al4V dissimilar joints by resistance spot welding. J. Mater. Res. Technol. 2024, 33, 1322–1333. [Google Scholar] [CrossRef]
- Li, B.; Li, G.; Wang, J.; Chen, B.; Wang, Y.; Dai, Y.; Dong, G. Residual stress tests and predictive model of friction stir welded normal-strength aluminium alloy H-shaped sections. Eng. Struct. 2024, 319, 118789. [Google Scholar] [CrossRef]
- Malschaert, D.; Veljkovic, M.; Maljaars, J. Numerical simulations of residual stress formation and its effect on fatigue crack propagation in a fillet welded T-joint. Eng. Fract. Mech. 2024, 306, 110236. [Google Scholar] [CrossRef]
- Dehkordi, Y.G.; Anaraki, A.P.; Shahani, A.R. Study of the effective parameters on welding residual stress relaxation in aluminum cylindrical shells under cyclic pressure. Thin-Walled Struct. 2019, 143, 106235. [Google Scholar] [CrossRef]
- Jones, K.W.; Bush, R.W. Investigation of residual stress relaxation in cold expanded holes by the slitting method. Eng. Fract. Mech. 2017, 179, 213–224. [Google Scholar] [CrossRef]
- Alinaghian, M.; Alinaghian, I.; Honarpisheh, M. Residual stress measurement of single point incremental formed Al/Cu bimetal using incremental hole-drilling method. Int. J. Lightweight Mater. Manuf. 2019, 2, 131–139. [Google Scholar] [CrossRef]
- Magnier, A.; Scholtes, B.; Niendorf, T. On the reliability of residual stress measurements in polycarbonate samples by the hole drilling method. Polym. Test. 2018, 71, 329–334. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Wu, H.; Miao, K.; Wu, H.; Li, R.; Liu, C.; Fang, W.; Fan, G. Research progress of residual stress measurement methods. Heliyon 2024, 10, e28348. [Google Scholar] [CrossRef]
- Dell’Avvocato, G.; Rashkovets, M.; Mancini, E.; Contuzzi, N.; Casalino, G.; Palumbo, D.; Galietti, U. Innovative non-destructive thermographic evaluation of mechanical properties in dissimilar aluminium Probeless Friction Stir Spot Welded (P-FSSW) Joints. Eng. Fail. Anal. 2025, 177, 109675. [Google Scholar] [CrossRef]
- Mutafi, A.; Irwan, J.; Yidris, N.; Alshalif, A.F.; Saif, Y.; Abdulrahman, H.; Mutaafi, A.; Al-Ashmori, Y.Y.; Amran, M.; Maureira-Carsalade, N. Residual stresses in cold-formed steel sections: An overview of influences and measurement techniques. Forces Mech. 2025, 18, 100306. [Google Scholar] [CrossRef]
- Brar, G.S.; Singh, C.S. FEA of residual stress in cruciform welded joint of hollow sectional tubes. J. Constr. Steel Res. 2014, 102, 44–58. [Google Scholar] [CrossRef]
- Park, J.H.; Na, M.G. Estimation of residual stress in dissimilar metals welding using deep fuzzy neural networks with rule-dropout. Nucl. Eng. Technol. 2024, 56, 4149–4157. [Google Scholar] [CrossRef]
- Murugan, N.; Narayanan, R. Finite element simulation of residual stresses and their measurement by contour method. Mater. Des. 2009, 30, 2067–2071. [Google Scholar] [CrossRef]
- Gadallah, R.; Tsutsumi, S.; Hiraoka, K.; Murakawa, H. Prediction of residual stresses induced by low transformation temperature weld wires and its validation using the contour method. Mar. Struct. 2015, 44, 232–253. [Google Scholar] [CrossRef]
- Shi, L.; Price, A.H.; Hung, W.N. Use of contour method for welding residual stress assessment. Procedia Manuf. 2018, 26, 276–285. [Google Scholar] [CrossRef]
- Ke, W.; Bu, X.; Oliveira, J.; Xu, W.; Wang, Z.; Zeng, Z. Modeling and numerical study of keyhole-induced porosity formation in laser beam oscillating welding of 5A06 aluminum alloy. Opt. Laser Technol. 2021, 133, 106540. [Google Scholar] [CrossRef]
- Jia, J.; Luo, M.; Li, T.; Xiao, J. Application progress of heat source model for fusion welding. Weld. Join. 2023, 5, 58–64. [Google Scholar]
- Wu, C.; Zhang, T.; Feng, Y. Numerical analysis of the heat and fluid flow in a weld pool with a dynamic keyhole. Int. J. Heat Fluid Flow 2013, 40, 186–197. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Wu, B.; Gong, S. Numerical investigation on the variation of welding stresses after material removal from a thick titanium alloy plate joined by electron beam welding. Mater. Des. 2012, 34, 609–617. [Google Scholar] [CrossRef]
- Wang, R.; Song, Z.; Yang, J.; Li, X.; Weng, Y.; Ren, X.; Qin, Q.; Song, J.; Mo, Z. Temperature field simulation and experimental investigation for column-faced 45 steel via ultrafast electron beam scanning. Surf. Coat. Technol. 2025, 497, 131802. [Google Scholar] [CrossRef]
- Yang, J.; Dong, H.; Wu, G.; Xiong, F. Experimental and numerical simulation study on microstructure, residual stress and mechanical properties of Fe–Mn–C–Cr cryogenic high-manganese steel arc-welded joint. J. Mater. Res. Technol. 2025, 35, 1335–1347. [Google Scholar] [CrossRef]
- Nagira, T.; Kitano, H.; Kimura, T.; Yoshinaka, F.; Takamori, S.; Sawaguchi, T.; Yamashita, T.; Aoki, Y.; Fujii, H.; Takeuchi, A.; et al. In-situ observation of solidification behaviors of Fe-Mn-Cr-Ni-Si alloy during TIG melt-run welding using synchrotron radiation X-ray. Mater. Charact. 2024, 214, 114093. [Google Scholar] [CrossRef]
- GB/T 711-2017; Hot-Rolled Quality Carbon Structural Steel Plates, Sheets and Strips. China Standard Press: Beijing, China, 2017.
- AWS A5.1/A5.1M–2012; AWS Specification for Carbon Steel Covered Electrodes for Shielded Metal Arc Welding. American Welding Society: Doral, FL, USA, 2012.
- GB/T 228.1-2010; Metallic Materials-Tensile Testing—Part 1: Method of Test at Room Temperature. China Standard Press: Beijing, China, 2010.
- Wang, H.; Wang, A.; Wang, J.; Zhang, J.; Du, T.; Shen, J. Optimizing quaternary chemical additives and steel fiber dispersion in CSA cement based HPC for rapid repair engineering. Constr. Build. Mater. 2025, 489, 142265. [Google Scholar] [CrossRef]
- Lundbäck, A.; Runnemalm, H. Validation of three-dimensional finite element model for electron beam welding of Inconel 718. Sci. Technol. Weld. Join. 2005, 10, 717–724. [Google Scholar] [CrossRef]
- Ferro, P.; Zambon, A.; Bonollo, F. Investigation of electron-beam welding in wrought Inconel 706—experimental and numerical analysis. Mater. Sci. Eng. A 2004, 392, 94–105. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Hussein, K.; Huaxin, L.; Yenkai, W. A comparative study of the residual deformation of an automotive gear-case assembly due to deep-penetration high-energy welding. J. Mater. Process. Tech. 2007, 190, 109–116. [Google Scholar]
- Yaghi, A.H.; Hyde, T.H.; Becker, A.A.; Williams, J.A.; Sun, W. Residual stress simulation in welded sections of P91 pipes. J. Mater. Process. Tech. 2005, 167, 480–487. [Google Scholar] [CrossRef]
- Alhafadhi, M.; Shehab, M.A.; Alsigar, M.; Kumar, S.S.; Elfallah, S.S.S.; Sahm, A.A.A.; Helal, M.H.F. Numerical Simulation of Residual Stresses Induced by MIG Welding Considering Initial Conditions. Mater. Sci. Forum 2025, 1153, 33–41. [Google Scholar] [CrossRef]
- Hemmatzadeh, M.; Moshayedi, H.; Sattari-Far, I. Influence of heat input and radius to pipe thickness ratio on the residual stresses in circumferential arc welded pipes of API X46 steels. Int. J. Press. Vessel. Pip. 2017, 150, 62–71. [Google Scholar] [CrossRef]
- Perez, J.; Kaiser, I.; Badea, F. Improvement of beam type element models of welded tubular junctions for fatigue analysis using artificial neural networks. Heliyon 2024, 10, e40181. [Google Scholar] [CrossRef]
- Weiss, J.; Knezevic, M. Effects of element type on accuracy of microstructural mesh crystal plasticity finite element simulations and comparisons with elasto-viscoplastic fast Fourier transform predictions. Comput. Mater. Sci. 2024, 240, 113002. [Google Scholar] [CrossRef]
- Syla, N.; Dalipi, B.; Elezaj, N.; Aliaj, F.; Tolaj, Z.; Zeqiraj, A. Finite-element modeling of the N concentration profile in 31CrMoV9 steel after gas nitriding. Emerg. Mater. Res. 2020, 9, 375–377. [Google Scholar] [CrossRef]
- Anicode, S.; Madenci, E. Three-dimensional moisture diffusion simulation with time dependent saturated concentration in ANSYS through native thermal and spring elements. Microelectron. Reliab. 2021, 123, 114167. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J.; Martinásek, J. Inelastic finite element analysis of lateral buckling for beam structures. Procedia Eng. 2017, 172, 481–488. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, J.; Liu, X.; Tang, J.; Huang, B. Effect of the groove type when considering a thermometallurgical-mechanical model of the welding residual stress and deformation in an S355JR-316L dissimilar welded joint. J. Manuf. Process. 2019, 45, 290–303. [Google Scholar] [CrossRef]
- Chengxun, Z.; Zhijun, Q.; Hanliang, Z.; Zhiyang, W.; Ondrej, M.; Mihail, I.; Zengxi, P.; Jiangtao, X.; Huijun, L. On the Effect of Heat Input and Interpass Temperature on the Performance of Inconel 625 Alloy Deposited Using Wire Arc Additive Manufacturing–Cold Metal Transfer Process. Metals 2021, 12, 46. [Google Scholar] [CrossRef]
- He, Y.; Yang, Z.; Yang, D.; Duan, R.; Xu, J.; Wang, W.; Shi, M.; Xu, G.; Chen, S. Numerical simulation of local cooling on residual stress and deformation of welded joints of unequal thickness plates. J. Mater. Res. Technol. 2025, 36, 8410–8420. [Google Scholar] [CrossRef]
- Qiang, B.; Lei, D.; Yang, H.; Xu, D.; Huang, J.; Wang, L.; Li, Y. Experimental investigation of high-temperature mechanical and creep properties of high-strength steel Q500qE. J. Constr. Steel Res. 2025, 234, 109732. [Google Scholar] [CrossRef]
- Yu, W.; Feng, C.; Xin-quan, Y. Design of new biomedical titanium alloy based on d-electron alloy design theory and JMatPro software. Trans. Nonferrous Met. Soc. China 2013, 23, 3027–3032. [Google Scholar]
- Liu, S.; Long, M.; Zhang, S.; Zhao, Y.; Zhao, J.; Feng, Y.; Chen, D.; Ma, M. Study on the prediction of tensile strength and phase transition for ultra-high strength hot stamping steel. J. Mater. Res. Technol. 2020, 9, 14244–14253. [Google Scholar] [CrossRef]
- Alikhani, A.A.; Ghasemi, A.; Pirjamadi, A.; Peng, Z.; Pouranvari, M. Understanding microstructural evolution and metallurgical challenges in wire-arc directed energy deposition of 430 ferritic stainless steel. Mater. Charact. 2025, 219, 114645. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, K.-H. Comparative study on girth weld-induced residual stresses between austenitic and duplex stainless steel pipe welds. Appl. Therm. Eng. 2014, 63, 140–150. [Google Scholar] [CrossRef]
















| Material | C | Si | Mn | P | S | Ni | Cr | Cu | Mo | V | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 45Mn steel | 0.46 | 0.24 | 0.71 | 0.016 | 0.006 | - | 0.0131 | 0.0097 | - | - | Bal. |
| E5015 | 0.15 | 0.90 | 1.60 | 0.035 | 0.035 | 0.30 | 0.20 | - | 0.30 | 0.08 | Bal. |
| Process Parameters | Single-Pass Welding |
|---|---|
| Power (W) | 4080 |
| Current (A) | 170 |
| Voltage (V) | 24 |
| Shielding Gas | CO2 |
| Shielding Gas Flow Rate (L/min) | 15 |
| Welding Thermal Efficiency | 0.8 |
| Mesh Size (mm) | Measuring Point | Peak Temperature (°C) | Time of Peak Temperature (s) | |
|---|---|---|---|---|
| Refined Area | Non-Refined Area | |||
| 0.5 | 1 | G | 212 | 192 |
| H | 161 | 485 | ||
| I | 145 | 618 | ||
| 2 | 4 | G | 195 | 215 |
| H | 148 | 520 | ||
| I | 132 | 640 | ||
| 1 | 2 | G | 206 | 200 |
| H | 157 | 500 | ||
| I | 142 | 625 | ||
| 1 | 1 | G | 207 | 198 |
| H | 158 | 495 | ||
| I | 143 | 623 | ||
| 1 | 3 | G | 203 | 204 |
| H | 154 | 505 | ||
| I | 139 | 630 | ||
| 0.8 | 2 | G | 204 | 197 |
| H | 156 | 498 | ||
| I | 142 | 625 | ||
| 1.2 | 2 | G | 201 | 203 |
| H | 155 | 503 | ||
| I | 141 | 627 | ||
| Material | Temperature (°C) | Density (g/cm3) | Thermal Conductivity (W/(m∙°C)) | Specific Heat (J/(g∙°C)) | Young’s Modulus (GPa) | Poisson’s Radio | Thermal Expansion Coeff. (10−6/°C) | Yield Stress (MPa) |
|---|---|---|---|---|---|---|---|---|
| 45Mn steel | 25 | 8.04 | 17.06 | 0.452 | 199.47 | 0.293 | 11.70 | 355.18 |
| 100 | 8.00 | 17.98 | 0.475 | 192.90 | 0.297 | 24.53 | 300.03 | |
| 200 | 7.94 | 19.20 | 0.498 | 184.03 | 0.303 | 24.53 | 261.78 | |
| 400 | 7.83 | 21.62 | 0.534 | 165.90 | 0.315 | 24.53 | 226.48 | |
| 700 | 7.66 | 25.25 | 0.582 | 137.72 | 0.333 | 24.55 | 204.72 | |
| 1000 | 7.50 | 28.86 | 0.629 | 108.36 | 0.350 | 24.61 | 23.34 | |
| 1300 | 7.35 | 32.47 | 0.679 | 77.82 | 0.368 | 24.72 | 3.11 | |
| 1600 | 6.89 | 35.63 | 0.829 | 0 | 0.500 | 35.54 | 0 | |
| E5015 | 25 | 7.84 | 63.63 | 0.447 | 210.13 | 0.290 | 12.50 | 391.43 |
| 100 | 7.82 | 59.82 | 0.478 | 206.81 | 0.292 | 12.68 | 327.69 | |
| 200 | 7.79 | 54.64 | 0.517 | 200.99 | 0.296 | 13.05 | 281.71 | |
| 400 | 7.72 | 44.30 | 0.629 | 182.92 | 0.304 | 13.87 | 240.02 | |
| 700 | 7.61 | 33.69 | 0.945 | 142.93 | 0.316 | 15.09 | 105.80 | |
| 1000 | 7.55 | 28.90 | 0.625 | 105.71 | 0.352 | 13.12 | 22.69 | |
| 1300 | 7.39 | 32.47 | 0.674 | 74.762 | 0.370 | 15.99 | 5.73 | |
| 1600 | 6.93 | 34.96 | 0.825 | 0 | 0.500 | 27.79 | 0 |
| Measuring Point | Type | Peak Temperature (°C) |
|---|---|---|
| G | Combined heat source | 206 |
| Uniform volumetric heat source | 221 | |
| Double-ellipsoidal heat source | 216 | |
| Experimental | 210 | |
| H | Combined heat source | 157 |
| Uniform volumetric heat source | 145 | |
| Double-ellipsoidal heat source | 163 | |
| Experimental | 160 | |
| I | Combined heat source | 142 |
| Uniform volumetric heat source | 148 | |
| Double-ellipsoidal heat source | 128 | |
| Experimental | 145 |
| Sampling Line | Type (Welding Time) | Max Residual Stress (MPa) | Min Residual Stress (MPa) |
|---|---|---|---|
| L1 | 72 s | 293.57 | 240.52 |
| 90 s | 259.48 | 190.95 | |
| 180 s | 293.92 | 230.33 | |
| L2 | 72 s | 372.4 | 320.74 |
| 90 s | 325.34 | 279.85 | |
| 180 s | 381.46 | 316.25 |
| Sampling Line | Type (Welding Time) | Max Longitudinal Residual Stress (MPa) | Min Longitudinal Residual Stress (MPa) | Max Transverse Residual Stress (MPa) | Min Transverse Residual Stress (MPa) |
|---|---|---|---|---|---|
| L3 | 72 s | 880.2 | −58.5 | 833.4 | −98.3 |
| 90 s | 670.2 | −60.6 | 581.7 | −83.9 | |
| 180 s | 860.6 | −46.9 | 825.3 | −109.5 | |
| L4 | 72 s | 1.8 | −49.2 | −2.8 | −40.4 |
| 90 s | 1.9 | −51.4 | −4.1 | −41.2 | |
| 180 s | 1.3 | −57.8 | −5.1 | −45.8 |
| Sampling Line | Type (Welding Time) | Max Longitudinal Residual Stress (MPa) | Min Longitudinal Residual Stress (MPa) | Max Transverse Residual Stress (MPa) | Min Transverse Residual Stress (MPa) |
|---|---|---|---|---|---|
| L5 | 72 s | 366.6 | −41.0 | 202.9 | −101.7 |
| 90 s | 290.2 | −50.8 | 176.0 | −121.5 | |
| 180 s | 364.7 | −48.8 | 201.2 | −109.1 | |
| L6 | 72 s | 80.8 | −48.9 | 98.1 | −86.3 |
| 90 s | 59.2 | −52.4 | 91.7 | −85.9 | |
| 180 s | 80.9 | −54.6 | 98.0 | −101.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Yang, C.; Liu, W.; Liu, K.; Shi, F.; Tan, Z.; Cao, P.; Wang, D. Numerical Simulation of Arc Welding in Large Flange Shafts Based on a Novel Combined Heat Source Model. Materials 2025, 18, 3932. https://doi.org/10.3390/ma18173932
Xu Z, Yang C, Liu W, Liu K, Shi F, Tan Z, Cao P, Wang D. Numerical Simulation of Arc Welding in Large Flange Shafts Based on a Novel Combined Heat Source Model. Materials. 2025; 18(17):3932. https://doi.org/10.3390/ma18173932
Chicago/Turabian StyleXu, Zhiqiang, Chaolong Yang, Wenzheng Liu, Ketong Liu, Feiting Shi, Zhifei Tan, Peng Cao, and Di Wang. 2025. "Numerical Simulation of Arc Welding in Large Flange Shafts Based on a Novel Combined Heat Source Model" Materials 18, no. 17: 3932. https://doi.org/10.3390/ma18173932
APA StyleXu, Z., Yang, C., Liu, W., Liu, K., Shi, F., Tan, Z., Cao, P., & Wang, D. (2025). Numerical Simulation of Arc Welding in Large Flange Shafts Based on a Novel Combined Heat Source Model. Materials, 18(17), 3932. https://doi.org/10.3390/ma18173932







