Origin of Bilinear Low Cycle Fatigue in Ti-6Al-4V Alloy: A Crystal Plasticity Study
Abstract
1. Introduction
- Model Development and Validation: To develop and validate a high-fidelity CPFEM model that can accurately reproduce the cyclic mechanical response and LCF life of Ti-6Al-4V, including its bilinear characteristic.
- Quantitative Mechanistic Analysis: To systematically compare the evolution of micro-scale plastic strain fields under high and low strain amplitudes using this model, and to quantitatively characterize the evolution of deformation heterogeneity from a statistical perspective by introducing the coefficient of variation (CV) as a key metric.
- Exploration of Physical Origins: To investigate the relationship between the evolution of deformation heterogeneity and the macroscopic energy response through a multi-scale energy dissipation analysis, aiming to elucidate the underlying driving mechanism of the bilinear phenomenon from a physical standpoint.
2. Theoretical Framework and Computational Methods
2.1. Crystal Plasticity Constitutive Model
2.1.1. Isotropic Softening
2.1.2. Kinematic Hardening
2.2. Construction and Validation of the Representative Volume Element (RVE)
2.3. Model Parameter Calibration and Validation
2.3.1. Establishment of Elastic Constants
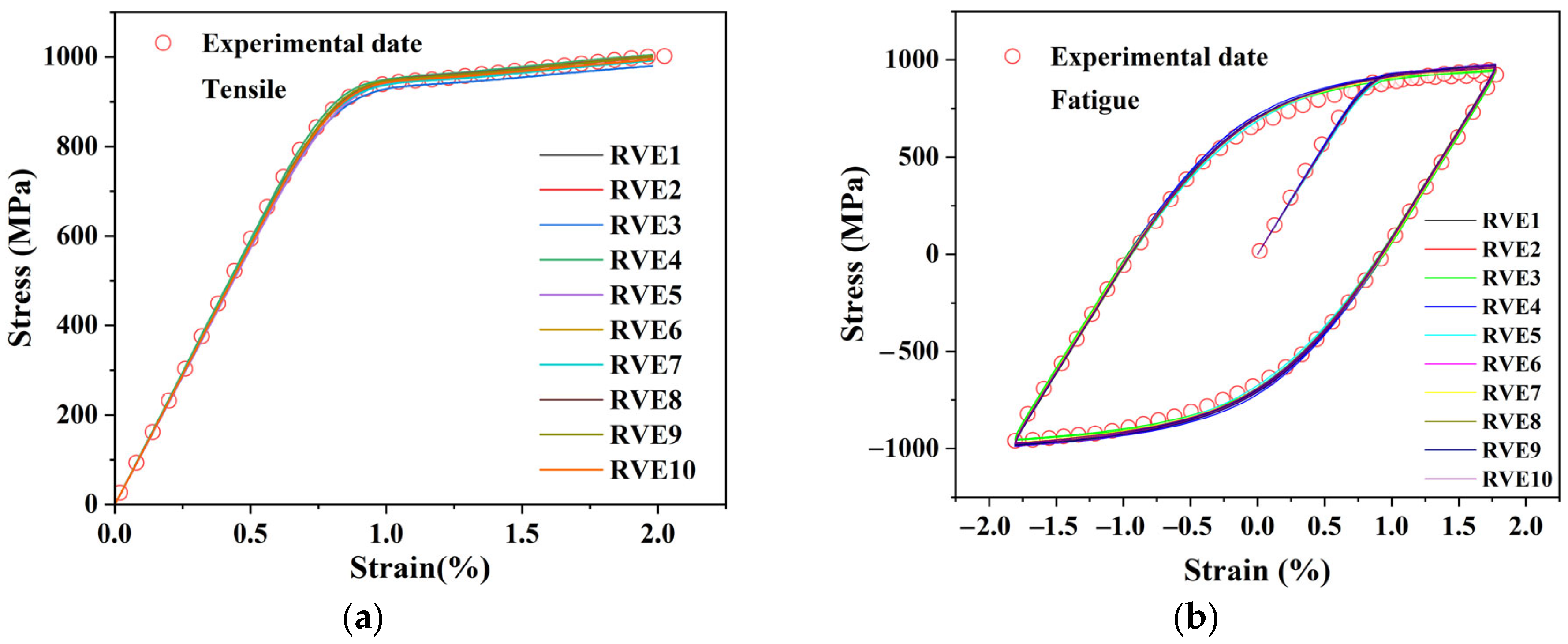
2.3.2. Calibration of Plastic Parameters and Model Validation
2.4. Framework for Fatigue Crack Initiation and Propagation
2.4.1. Criterion for Crack Initiation
2.4.2. Law for Damage Evolution and Propagation
2.4.3. Calibration of Damage Model Parameters
3. Results and Discussion
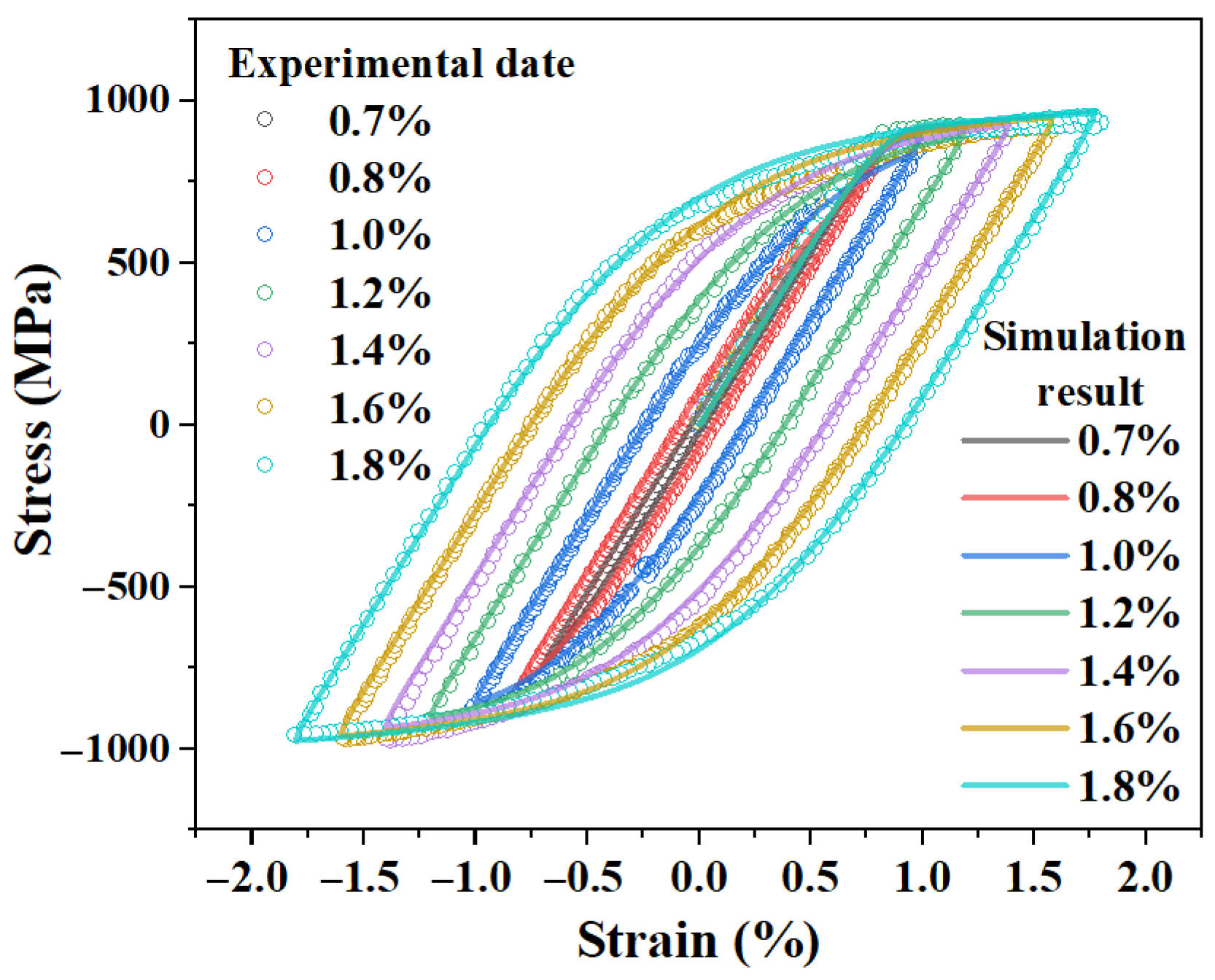
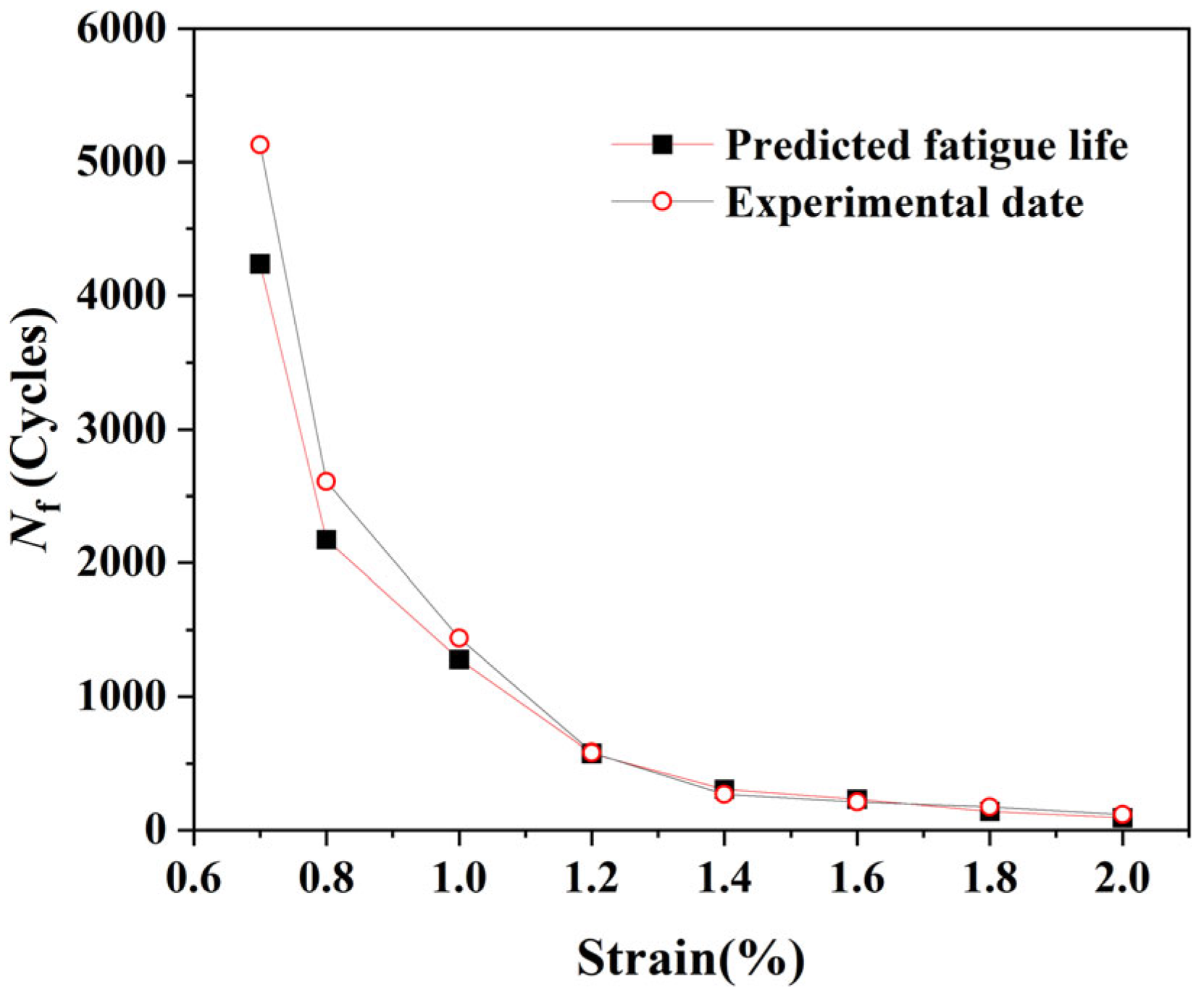
3.1. Model Validation: From Microscopic Damage Modes to Macroscopic Life Prediction
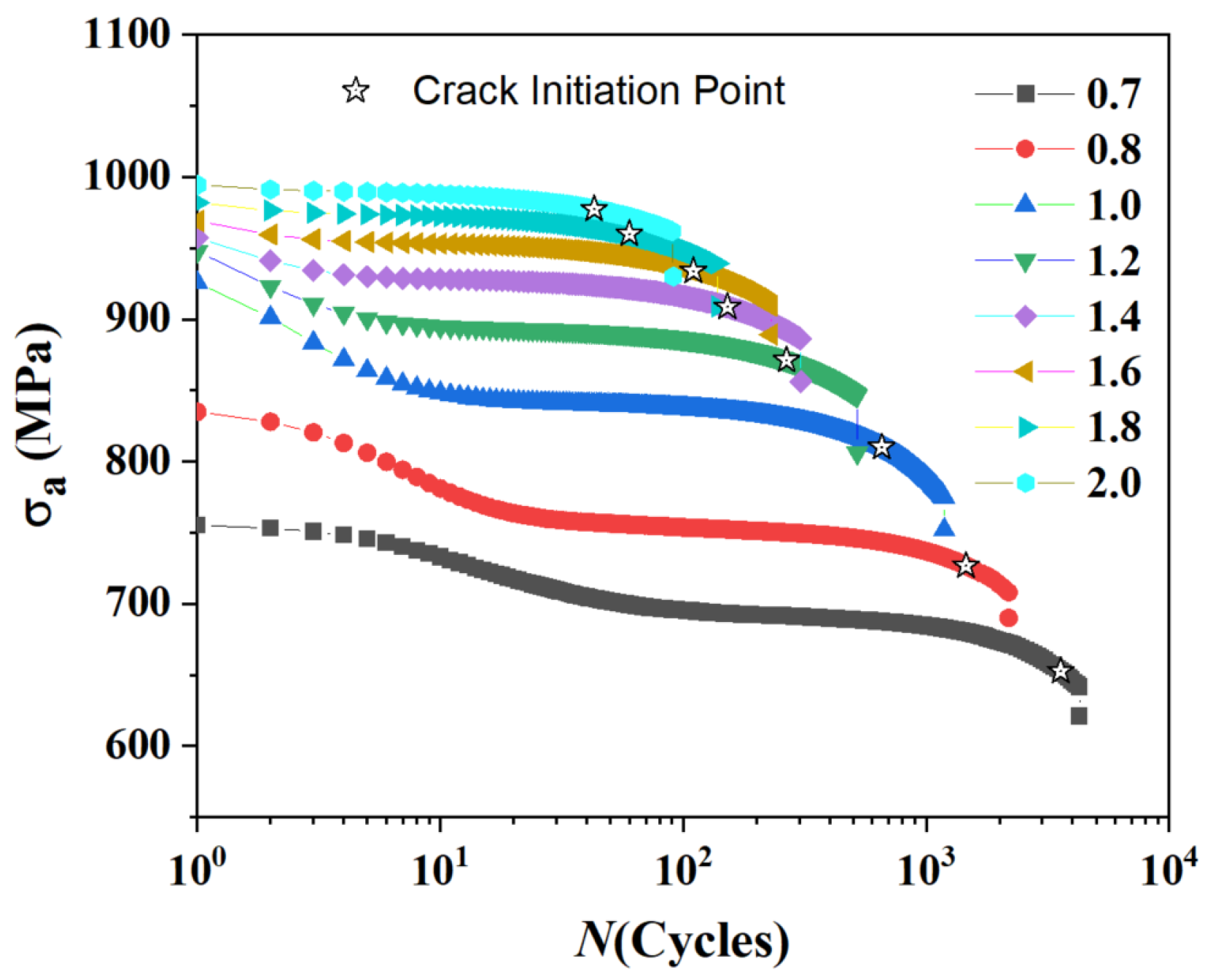
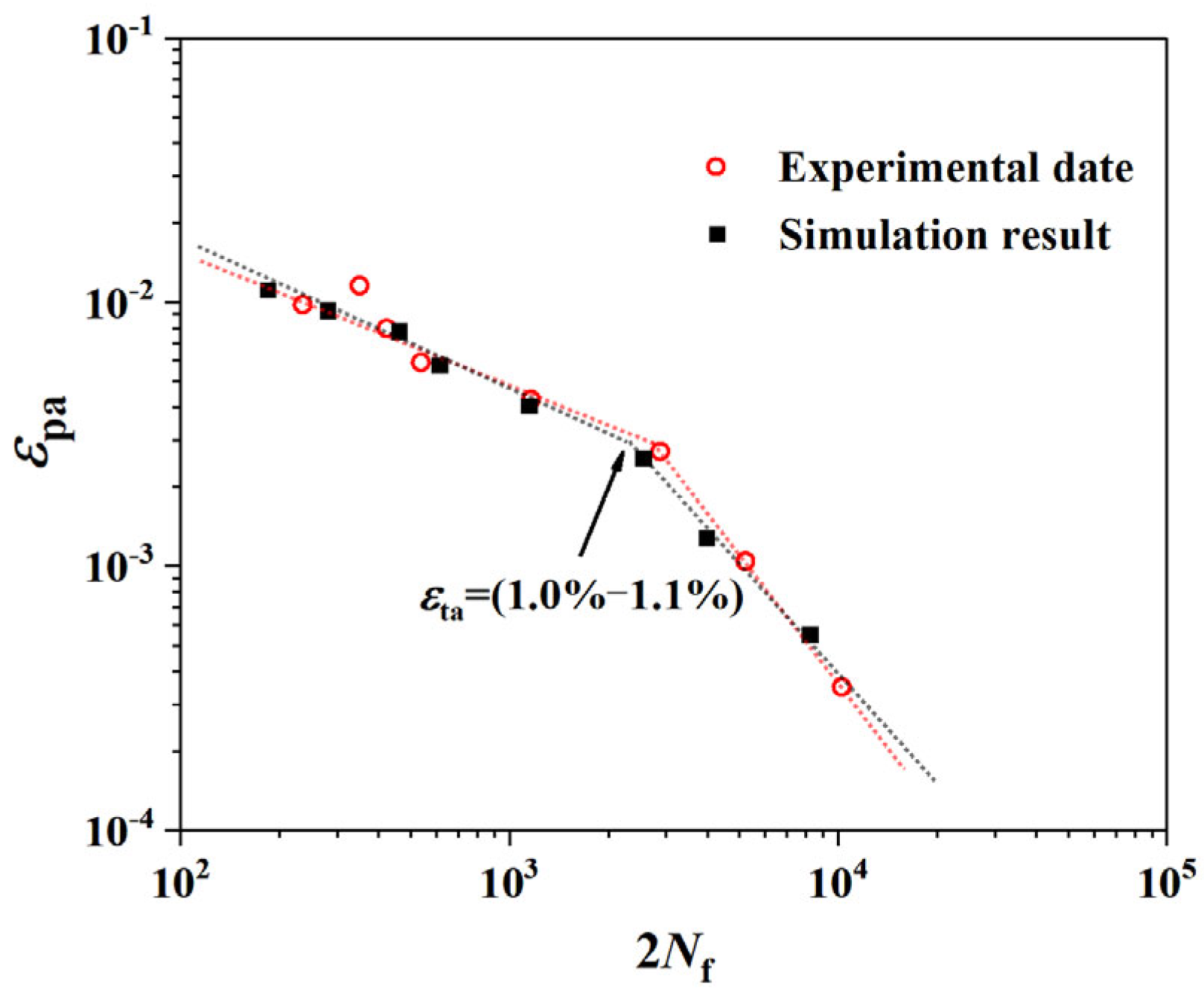
3.2. Bilinearity of the C-M Curve
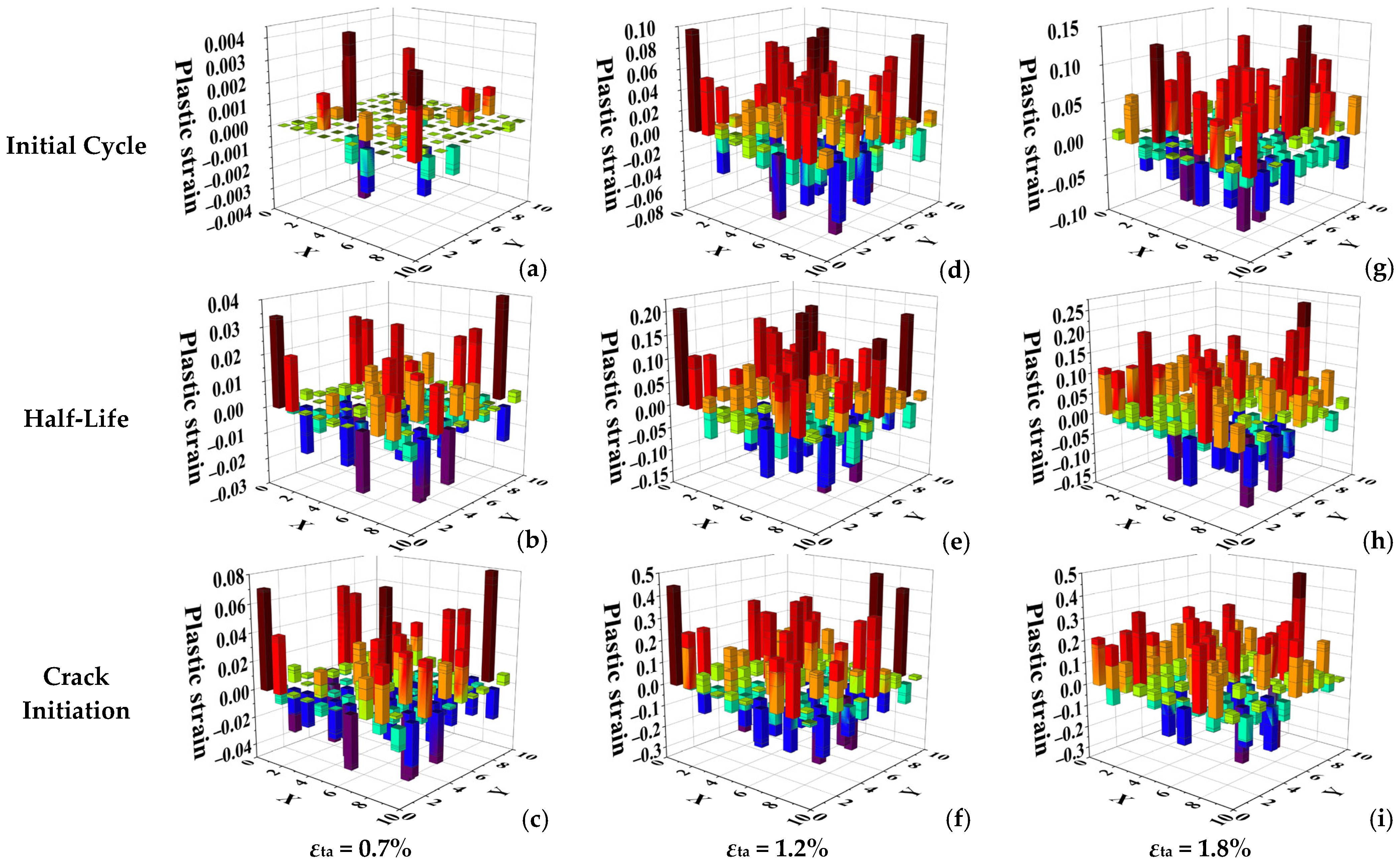
3.3. Qualitative Analysis of Microscopic Deformation Inhomogeneity
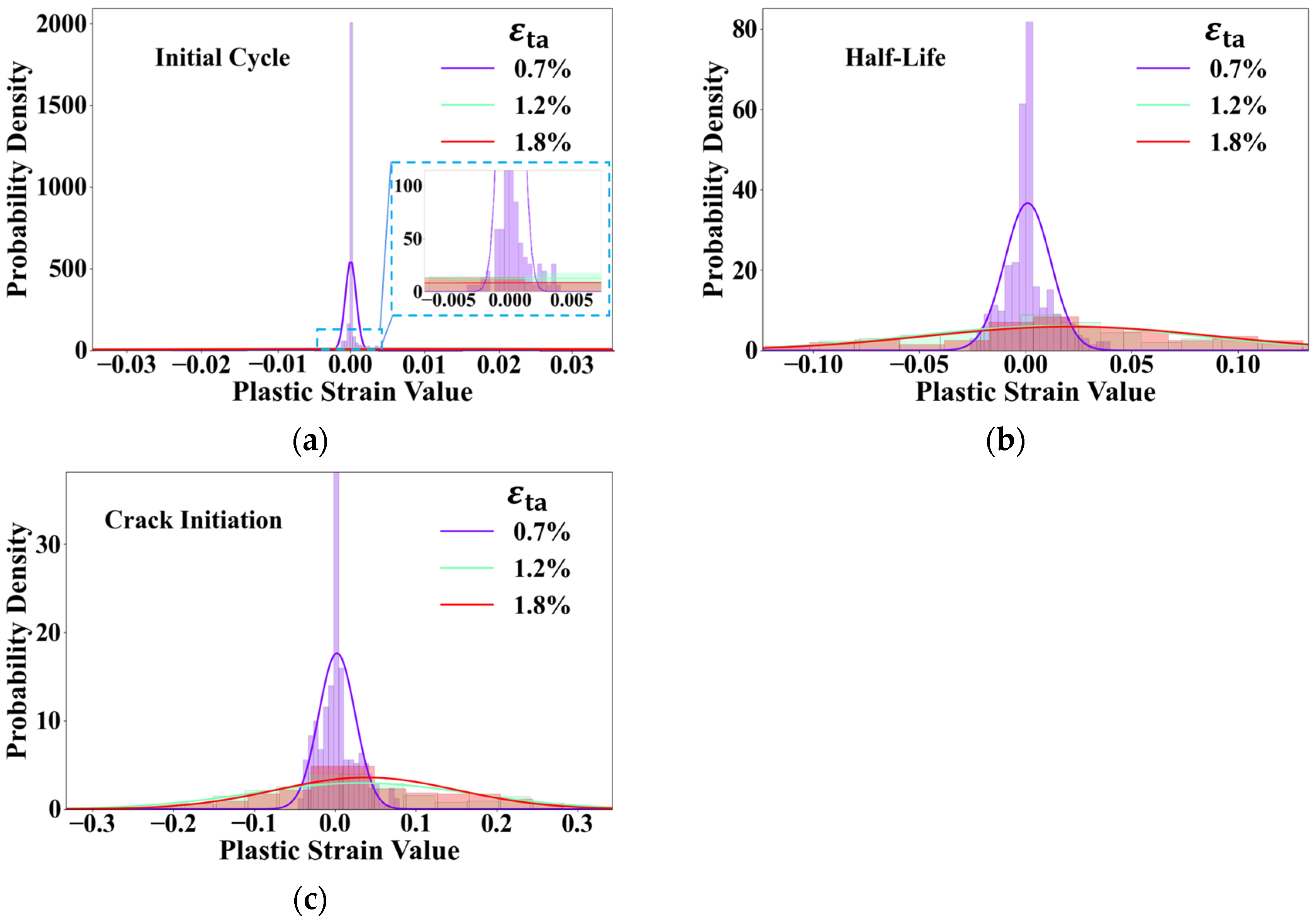
3.4. Quantification of Deformation Inhomogeneity
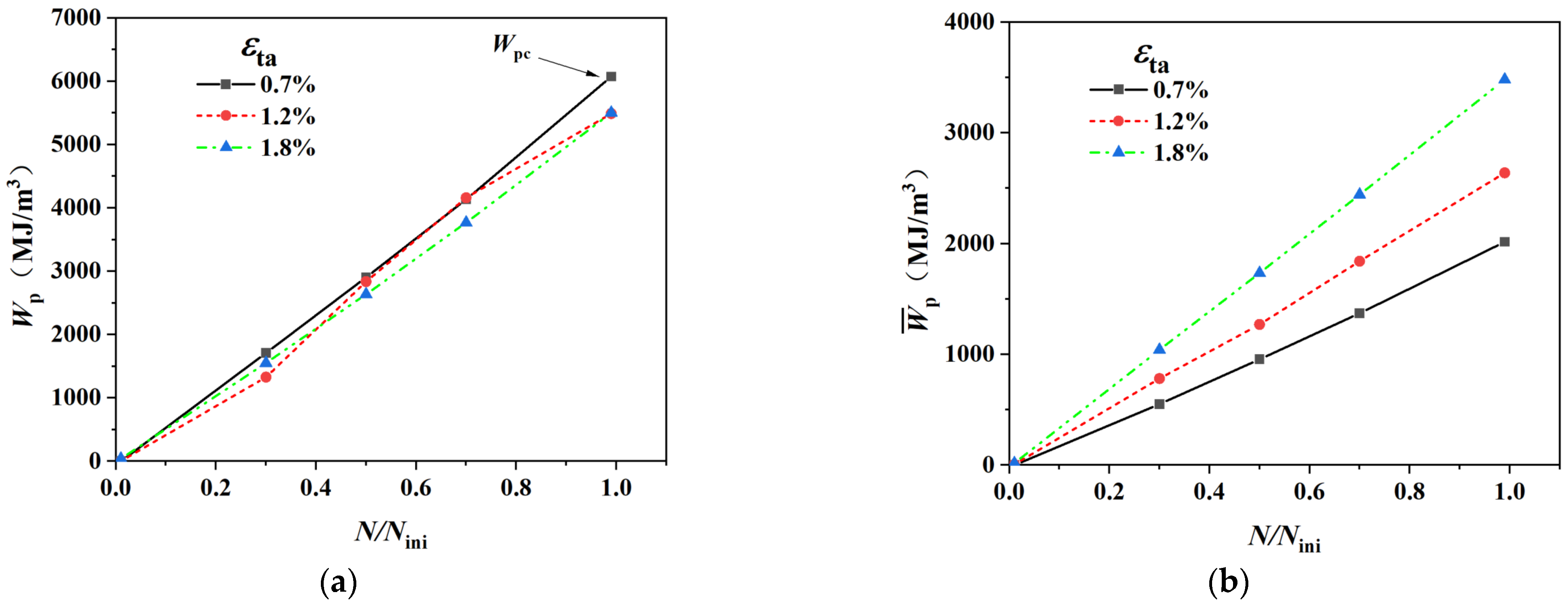
3.5. The Duality of Energy Dissipation: From Microscopic Conservation to Macroscopic Variability
4. Conclusions
- Successful Reproduction and Validation: The developed crystal plasticity model successfully reproduced key fatigue characteristics of the Ti-6Al-4V alloy, including its cyclic stress response, hysteresis loops, and the bilinear Coffin-Manson (C-M) curve. The predicted fatigue lives show excellent agreement with experimental data, thereby validating the accuracy and effectiveness of the proposed coupled analysis framework.
- Revealing the Unified Origin of Bilinearity: From Deformation Inhomogeneity to Failure Mode Transition: The origin of the bilinear behavior is a transition in the microscopic failure mode, which is directly driven by the evolution of plastic deformation inhomogeneity. At low strain amplitudes, the deformation remains highly localized (quantified by a high Coefficient of Variation, CV), concentrating damage accumulation within a few “hot-spot” grains. This confinement of damage naturally leads to the initiation and stable propagation of a single, dominant crack. Conversely, at high strain amplitudes, the deformation rapidly homogenizes (indicated by a low CV), creating multiple potential weak links across the microstructure. This distributed damage landscape results in a failure mode characterized by multi-site crack initiation and subsequent coalescence. Therefore, the evolution of deformation inhomogeneity is the direct cause of the shift in failure mode, which together constitute the unified physical origin of the macroscopic bilinear characteristic.
- Underlying Physical Consequence: From an energy dissipation perspective, a “duality of damage” was identified: while the microscopic energy dissipation threshold () required for crack initiation in a single “critical” grain is conserved, the macroscopic average energy dissipation () required for overall material failure is variable. This discrepancy is attributed to the different energy transfer efficiencies governed by the degree of deformation inhomogeneity (CV), which ultimately gives rise to the bilinear characteristic of the C-M curve.
- Limitations and Outlook: The proposed “microscopic energy conservation” hypothesis is an inference drawn from a specific material and model; its universality requires further validation. Furthermore, the single-phase α-Ti approximation, while justified by the low β-phase fraction in the alloy, is a simplification. The presence of the β-phase could introduce local stress/strain concentrations at α/β interfaces, potentially influencing crack initiation sites. Similarly, this study was conducted under idealized conditions, excluding environmental factors such as oxidation and temperature, which could alter slip system activity and surface energy, thereby affecting both deformation heterogeneity and damage evolution. Future work should be directed towards two main areas: (i) computationally, extending the proposed framework to a wider range of metallic materials to test the generality of this energy law; and (ii) experimentally, leveraging high-resolution in situ characterization techniques to directly measure energy dissipation in real three-dimensional grains, which would provide definitive experimental support for the theory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soni, R.; Verma, R. A Critical Review of Recent Advances in the Aerospace Materials. Mater. Today Proc. 2024, 113, 180–184. [Google Scholar] [CrossRef]
- C, R.; Shanmugam, R.; Ramoni, M.; Bk, G. A Review on Additive Manufacturing for Aerospace Application. Mater. Res. Express 2024, 11, 022001. [Google Scholar] [CrossRef]
- Shi, S.; Deng, Q. Microstructure Stability and Damage Mechanisms in an α/β Ti-6Al-4V-0.55Fe Alloy during Low Cycle Dwell-Fatigue at Room Temperature. Int. J. Fatigue 2022, 155, 106585. [Google Scholar] [CrossRef]
- Lavogiez, C.; Dureau, C. Crack Initiation Mechanisms in Ti-6Al-4V Subjected to Cold Dwell-Fatigue, Low-Cycle Fatigue and High-Cycle Fatigue Loadings. Acta Mater. 2023, 244, 118560. [Google Scholar] [CrossRef]
- Ren, Y.M.; Lin, X.; Yang, H.O.; Tan, H.; Chen, J.; Jian, Z.Y.; Li, J.Q.; Huang, W.D. Microstructural Features of Ti-6Al-4V Manufactured via High Power Laser Directed Energy Deposition under Low-Cycle Fatigue. J. Mater. Sci. Technol. 2021, 83, 18–33. [Google Scholar] [CrossRef]
- Cruzado, A.; Lucarini, S.; LLorca, J.; Segurado, J. Microstructure-Based Fatigue Life Model of Metallic Alloys with Bilinear Coffin-Manson Behavior. Int. J. Fatigue 2018, 107, 40–48. [Google Scholar] [CrossRef]
- Rai, R.K.; Paulose, N.; Sahu, J.K. The Effects of Microstructure and Temperature on the Deformation Heterogeneities and Fatigue Behaviour of a Ni-Based Superalloy. Philos. Mag. 2024, 104, 537–556. [Google Scholar] [CrossRef]
- Güler, B.; Şimşek, Ü.; Yalçinkaya, T.; Efe, M. Grain-Scale Investigations of Deformation Heterogeneities in Aluminum Alloys; AIP Publishing LLC: Palermo, Italy, 2018; p. 170005. [Google Scholar]
- Radhakrishnan, V.M. On Bilinearity of Manson-Coffin Low-Cycle-Fatigue Relationship; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Gao, P.F.; Lei, Z.N.; Li, Y.K.; Zhan, M. Low-Cycle Fatigue Behavior and Property of TA15 Titanium Alloy with Tri-Modal Microstructure. Mater. Sci. Eng. A 2018, 736, 1–11. [Google Scholar] [CrossRef]
- Nie, B.; Song, Y.; Huang, X.; Qi, H.; Zhao, Z.; Chen, D. Low Cycle Fatigue Behavior of TC21 Titanium Alloy with Bi-Lamellar Basketweave Microstructure. Crystals 2022, 12, 796. [Google Scholar] [CrossRef]
- Saitova, L.; Hoppel, H.; Goken, M.; Semenova, I.; Valiev, R. Cyclic Deformation Behavior and Fatigue Lives of Ultrafine-Grained Ti-6AL-4V ELI Alloy for Medical Use. Int. J. Fatigue 2009, 31, 322–331. [Google Scholar] [CrossRef]
- Sun, Y.; Alexandrov, I.V. Optimized Low-Cycle Fatigue Behavior and Fracture Characteristics of Ti–6Al–4V Alloy by Fe Microalloying. J. Mater. Res. Technol. 2021, 15, 5277–5287. [Google Scholar] [CrossRef]
- Gao, Z.; Jia, Z.; Ji, J.; Liu, D.; Guo, T.; Ding, Y. Texture Evolution and Dislocation Behavior in a Nickel-Based Superalloy during Hot Compression. Adv. Eng. Mater. 2020, 22, 1900892. [Google Scholar] [CrossRef]
- Poh, L.H.; Peerlings, R.H.J.; Geers, M.G.D.; Swaddiwudhipong, S. Homogenization towards a Grain-Size Dependent Plasticity Theory for Single Slip. J. Mech. Phys. Solids 2013, 61, 913–927. [Google Scholar] [CrossRef]
- Bridier, F.; McDowell, D.L.; Villechaise, P.; Mendez, J. Crystal Plasticity Modeling of Slip Activity in Ti–6Al–4V under High Cycle Fatigue Loading. Int. J. Plast. 2009, 25, 1066–1082. [Google Scholar] [CrossRef]
- Somlo, K.; Poulios, K. Anisotropic Tensile Behaviour of Additively Manufactured Ti-6Al-4V Simulated with Crystal Plasticity. Mech. Mater. 2021, 162, 104034. [Google Scholar] [CrossRef]
- Arcidiacono, M.F.; Violatos, I.; Rahimi, S. Predicting Fatigue Crack Initiation in Milled Aerospace Grade Ti-6Al-4V Parts Using CPFEM; Cawte, E.R., Cockings, H.L., Stekovic, S., Yates, J.R., Eds.; Engineering Integrity Society: Newark, UK, 2024; pp. 115–126. ISBN 978-0-9544368-7-2. [Google Scholar]
- Gontarz, J.; Podgórski, J. Comparison of Various Criteria Determining the Direction of Crack Propagation Using the UDMGINI User Procedure Implemented in Abaqus. Materials 2021, 14, 3382. [Google Scholar] [CrossRef]
- Yang, J.; Guo, H. Constraints-Related Microscopic Fatigue Crack Propagation Behaviour of Polycrystalline Alloys. Heliyon 2024, 10, e25071. [Google Scholar] [CrossRef]
- Xie, B.; Yu, T.; Li, R.; Luo, Z.; Baxevanakis, K.P.; Zhang, P. Experimentally Validated Macro-Mesoscopic Simulation Study on the Fatigue Short Crack Initiation and Propagation in Polycrystalline Structure Utilizing CP-XFEM. Eng. Fract. Mech. 2025, 319, 110995. [Google Scholar] [CrossRef]
- Gu, T.; Stopka, K.S. Prediction of Maximum Fatigue Indicator Parameters for Duplex Ti–6Al–4V Using Extreme Value Theory. Acta Mater. 2020, 188, 504–516. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material Rate Dependence and Localized Deformation in Crystalline Solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Bate, P.; Hutchinson, B. The Effect of Elastic Interactions between Displacive Transformations on Textures in Steels. Acta Mater. 2000, 48, 3183–3192. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Z.; Xue, K. Cyclic Deformation Response and Micromechanisms of Ti Alloy Ti–5Al–5V–5Mo–3Cr–0.5Fe. Mater. Sci. Eng. A 2011, 528, 8723–8732. [Google Scholar] [CrossRef]
- Xu, H.; Ye, D.; Mei, L. A Study of the Back Stress and the Friction Stress Behaviors of Ti-6Al-4V Alloy during Low Cycle Fatigue at Room Temperature. Mater. Sci. Eng. A 2017, 700, 530–539. [Google Scholar] [CrossRef]
- Kumar, R.; Sanyal, S. Deformation and Damage Mechanisms during Clockwise Diamond and Counter Clockwise Diamond Thermomechanical Fatigue in Timetal 834 Alloy. Int. J. Fatigue 2024, 179, 108039. [Google Scholar] [CrossRef]
- Marano, A.; Gélébart, L.; Forest, S. Intragranular Localization Induced by Softening Crystal Plasticity: Analysis of Slip and Kink Bands Localization Modes from High Resolution FFT-Simulations Results. Acta Mater. 2019, 175, 262–275. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, H.; Zhuang, X.; Wu, H.; Zhao, Z. Comparative Study of Various Hardening Models for the Prediction of Plastic Responses under Strain Path Change Conditions. Int. J. Mater. Form. 2022, 15, 38. [Google Scholar] [CrossRef]
- Reyne, B.; Barlat, F. A New Concept for Continuum Distortional Plasticity. Int. J. Plast. 2022, 155, 103303. [Google Scholar] [CrossRef]
- Jiang, Y.; Kurath, P. Characteristics of the Armstrong-Frederick Type Plasticity Models. Int. J. Plast. 1996, 12, 387–415. [Google Scholar] [CrossRef]
- Liu, Y.; Dunne, F.P.E. The Mechanistic Link between Macrozones and Dwell Fatigue in Titanium Alloys. Int. J. Fatigue 2021, 142, 105971. [Google Scholar] [CrossRef]
- Yin, L.; Umezawa, O. Crystal Plasticity Analysis of Temperature-Sensitive Dwell Fatigue in Ti-6Al-4V Titanium Alloy for an Aero-Engine Fan Disc. Int. J. Fatigue 2022, 156, 106688. [Google Scholar] [CrossRef]
- Yang, P.Q.; Zhang, X.P.; Yao, Z.Q.; Shivpuri, R. Investigation on the Crystal Plasticity of α Phase Ti-6Al-4V Based on Nano-Indentation Simulation and Experiment. Mater. Charact. 2023, 203, 113074. [Google Scholar] [CrossRef]
- Zhang, M.; Bridier, F.; Villechaise, P.; Mendez, J.; McDowell, D.L. Simulation of Slip Band Evolution in Duplex Ti–6Al–4V. Acta Mater. 2010, 58, 1087–1096. [Google Scholar] [CrossRef]
- Tan, C.; Sun, Q.; Zhang, G.; Zhao, Y. High-Cycle Fatigue of a Titanium Alloy: The Role of Microstructure in Slip Irreversibility and Crack Initiation. J. Mater. Sci. 2020, 55, 12476–12487. [Google Scholar] [CrossRef]
- Abdolvand, H. Development of Microstructure-Sensitive Damage Models for Zirconium Polycrystals. Int. J. Plast. 2022, 149, 103156. [Google Scholar] [CrossRef]
- Lee, J.; Sharpe, W. Short Fatigue Crack Behavior in Notched 2024-T3 Aluminum Specimens; NASA: Washington, DC, USA, 1986; p. 180314. [Google Scholar]
- Lu, D.; Zhang, K.; Hu, G.; Lan, Y.; Chang, Y. Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation. Materials 2020, 13, 3069. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, S. Quantitatively Assessing the Contributions of Temperature-Dependent Deformation-Induced Martensitic Transformation to Uniform Elongation and Work Hardening of TRIP-Assisted Duplex Stainless Steel via Crystal Plasticity. Mater. Sci. Eng. A 2023, 887, 145758. [Google Scholar] [CrossRef]




| Elastic Constants/GPa | |||||||
|---|---|---|---|---|---|---|---|
| Phase 1 | C11 | C12 | C13 | C23 | C33 | C44 | C66 |
| α | 139 | 79 | 69 | 68 | 167 | 41 | 29 |
MPa | H MPa | s−1 | m | MPa | /MPa | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Basal α | Prismatic α | Pyramidal α | 1st/2nd Pyramidal c + α | |||||||
| 115 | 0.004 | −10 | 0.02 | 15 | 48,000 | 400 | 380 | 330 | 460 | 600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Yang, D.; Li, W.; Guo, Z.; Liu, Y. Origin of Bilinear Low Cycle Fatigue in Ti-6Al-4V Alloy: A Crystal Plasticity Study. Materials 2025, 18, 3931. https://doi.org/10.3390/ma18173931
Xu H, Yang D, Li W, Guo Z, Liu Y. Origin of Bilinear Low Cycle Fatigue in Ti-6Al-4V Alloy: A Crystal Plasticity Study. Materials. 2025; 18(17):3931. https://doi.org/10.3390/ma18173931
Chicago/Turabian StyleXu, Haifeng, Dianxi Yang, Wei Li, Zhengxiao Guo, and Yinghonglin Liu. 2025. "Origin of Bilinear Low Cycle Fatigue in Ti-6Al-4V Alloy: A Crystal Plasticity Study" Materials 18, no. 17: 3931. https://doi.org/10.3390/ma18173931
APA StyleXu, H., Yang, D., Li, W., Guo, Z., & Liu, Y. (2025). Origin of Bilinear Low Cycle Fatigue in Ti-6Al-4V Alloy: A Crystal Plasticity Study. Materials, 18(17), 3931. https://doi.org/10.3390/ma18173931






