Atomistic-Based Fatigue Property Normalization Through Maximum A Posteriori Optimization in Additive Manufacturing
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup: Instrumented Indentation
2.1.1. Indentation Platform and Calibration
2.1.2. Indenters and Measurement Objectives
- Sharp Vickers diamond tip(Half-angle , tip radius < 150 nm); selected for cohesive- and surface-energy evaluation because its self-similar geometry activates radial/median cracking and admits established unloading-work methods [27].
- WC /Co spherical tip( mm); used for fracture-toughness estimation via the critical-pressure (pop-in) criterion under predominantly elastic fields [28].
2.1.3. Loading Protocol and Data Acquisition
- Loading at to the preset maximum force;
- Holding segment 10 s for relaxation assessment;
- Unloading at the same rate to 6.67 % ;
- Final hold for drift correction.
2.1.4. Parameter Extraction
- Fracture toughness .
- Cohesive energy .
- Surface tension .
2.1.5. Uncertainty Analysis and Repeatability
2.2. Link to Continuum Fracture and Fatigue Models
2.3. Scaling DFT to Woehler Curves
2.3.1. Atomistic Calculations
- Electronic-structure framework.
- Surface energy determination.
- Cohesive energy evaluation.
- Intrinsic work of fracture.
2.3.2. Upscaling to Continuum Fracture Parameters
- Griffith conversion to fracture toughness.
- Link to fatigue crack propagation.
2.3.3. Limitations and Sensitivity of the Tanaka–Kuroda Scaling
2.3.4. Fatigue Life Integration
2.3.5. Experimental and Numerical Validation
2.4. Maximum Aposteriori Estimation
2.4.1. Problem Statement
2.4.2. Hierarchical Probabilistic Model
- Level 0: coupon data.
- Level 1: heterogeneity priors.
- Level 2: hyper-priors.
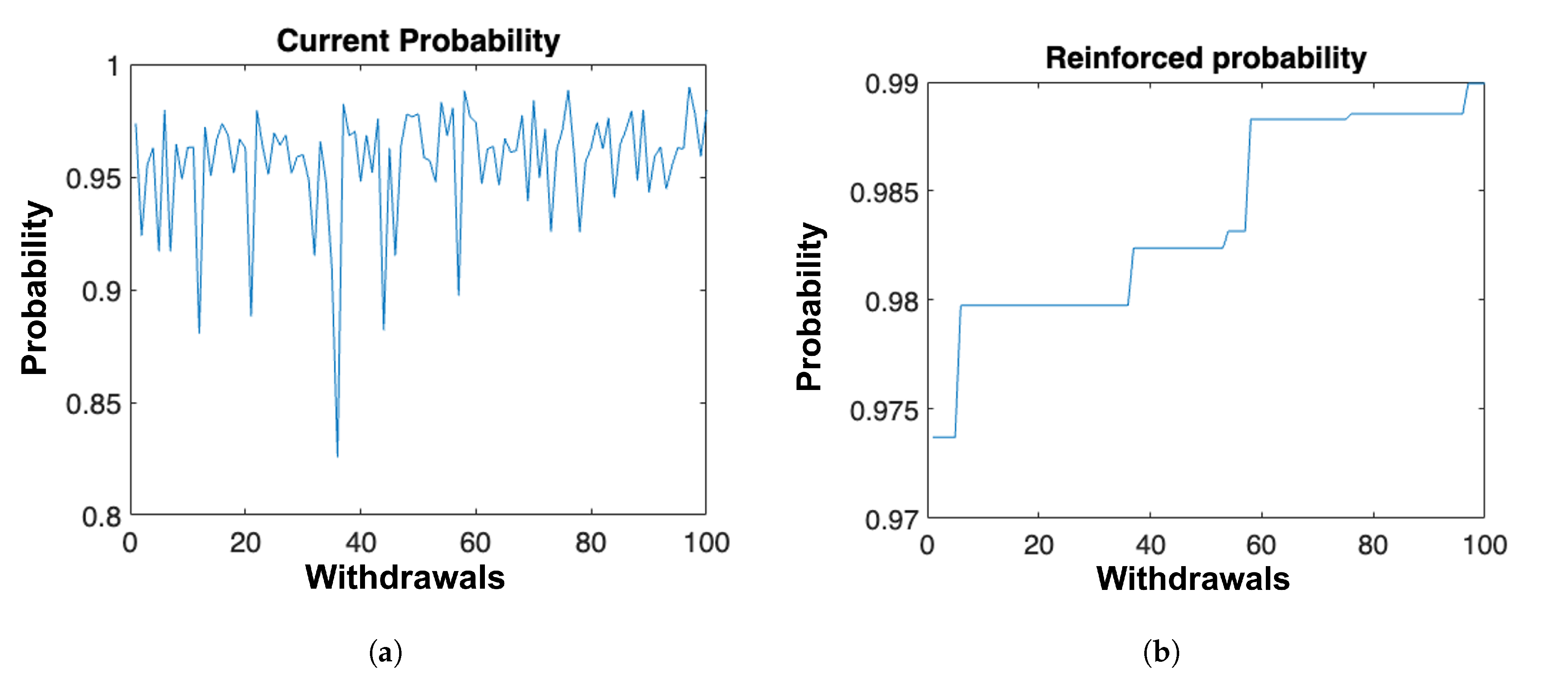
2.4.3. Map Optimization
- Step 1 Variational warm-start: A mean-field ELBO for the marginal-MAP problem is maximized with conjugate-gradient descent to supply an initial guess [19].
- Step 2 SAME iterations: For , sample a replica from the conditional posteriors of and each , holding all other replicas fixed. The augmented log-posterior is then maximized by L-BFGS using automatic differentiation.
- Step 3 Convergence test: Iteration terminates when relative change in falls below or after 1000 iterations.
2.4.4. Uncertainty Quantification
2.4.5. Limitations of MAP-Based Inference and Posterior Multimodality
2.4.6. Implementation and Data Flow
- XCT/SEM scans of four reference builds furnish empirical distributions for , establishing .
- Coupon data enter the Weakestlink likelihood (12); the weight vector is imported from finite-element elasto-plastic simulations.
- Variational warm-start and SAME optimization produce the MAP pair and Hessian .
- defines the fatigue-strength distribution, while supply probability bands for Paris law coefficients used in S-N and - curve construction.
- All subroutines were implemented on Matlab on a 32 core Intel Workstation.
2.4.7. Validation
- Predictive log-likelihood under zero-shot transfer/out-of-distribution evaluation.
- Full MCMC on a reduced subset () showing that lies within the 68 % highest-posterior-density interval of the exact posterior.
- Very-high-cycle tests on AlSi10Mg and Ti-6Al-4V [41], for which the S-N curve generated from MAP + Metropolis Hastings encloses 93% of the measured lives.
3. Results
3.1. Process-Parameter Window
- Primary exposure (baseline). Laser power W, scanning speed mm s−1, spot diameter m, and volumetric energy density J mm−3.
- Secondary exposure (graded variations). One parameter at a time was perturbed while the others were kept constant, spanning
- Power series:W
- Speed series:mm s−1
- Spot-size series:m
- Energy-density series:scaled to J mm−3
while the build plate was held at .
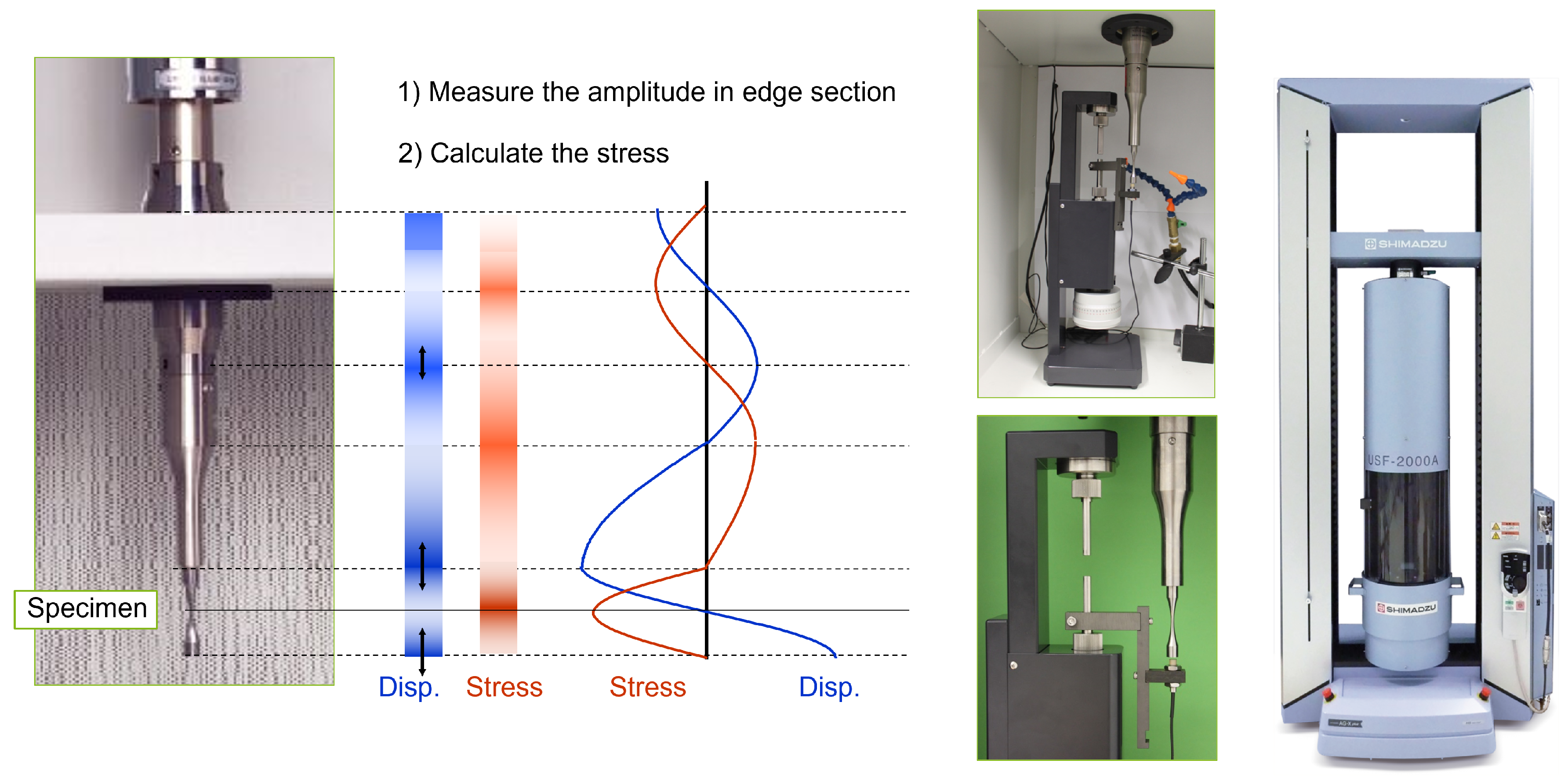
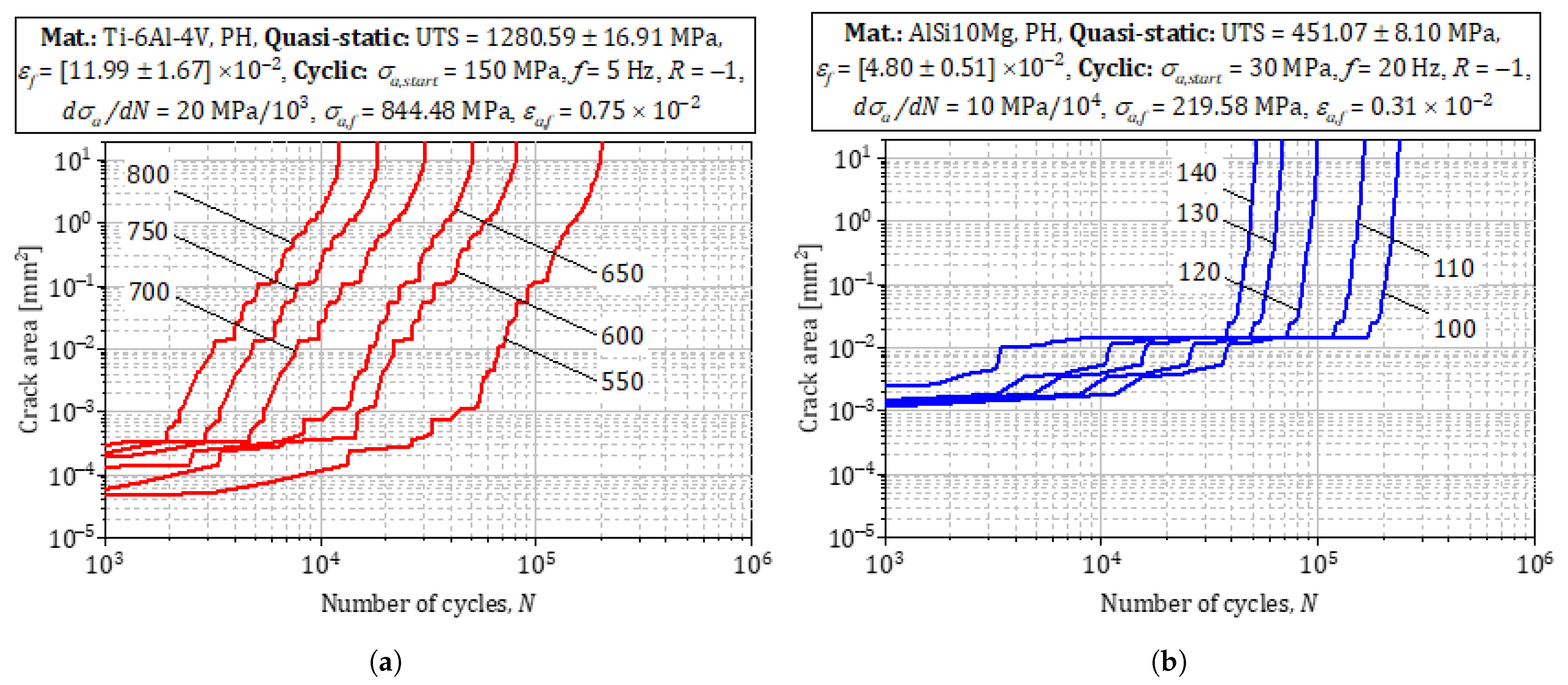
3.2. Ultrasonic Experimental Setup for VHCF Testing
- Specimen preparation: Machining and surface polishing to minimize surface effects and ensure reproducible initiation conditions.
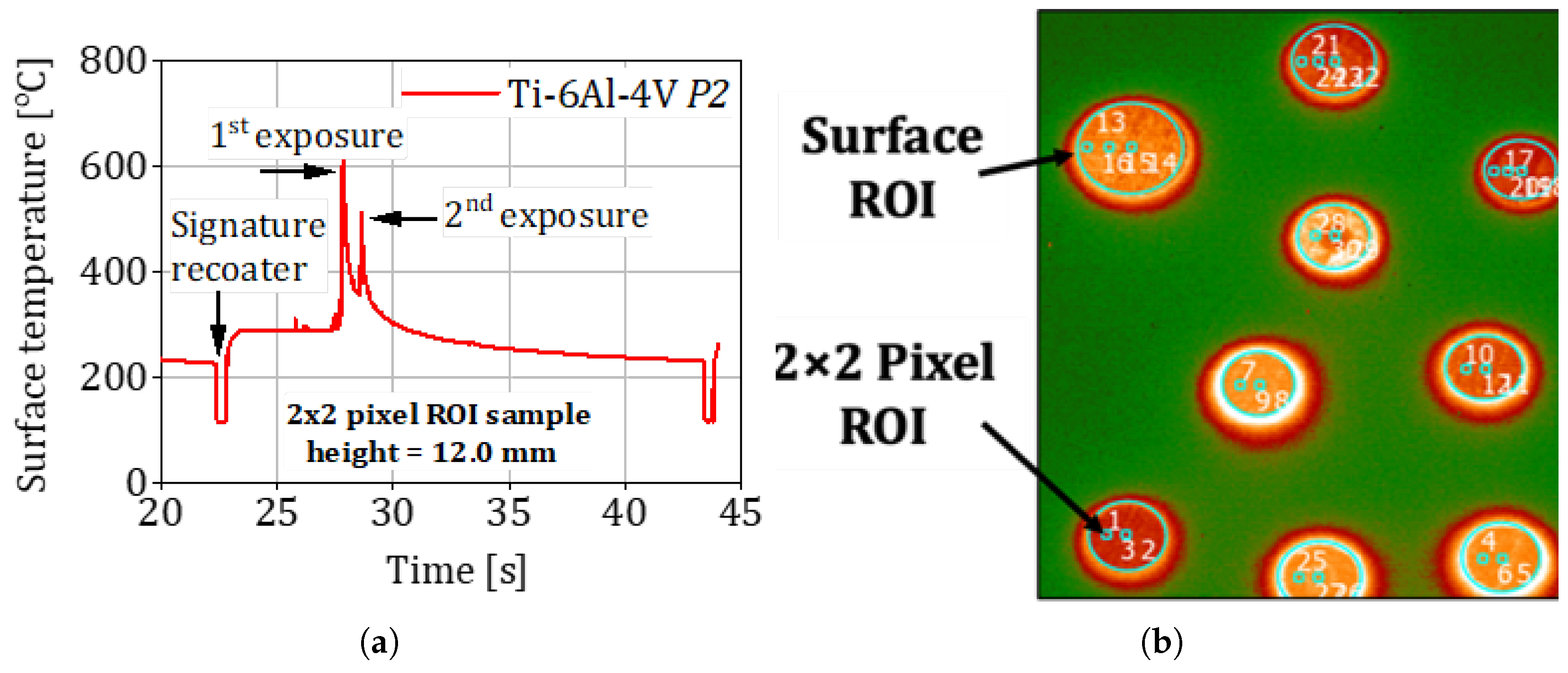
- Resonance tuning: The specimen is clamped to the ultrasonic horn, and resonance frequency is precisely tuned for optimal energy transfer, as shown in Figure 3.
- Fatigue loading: A cyclic load is applied at 20 kHz under a predetermined load ratio (often or ), while the number of cycles to failure is recorded.
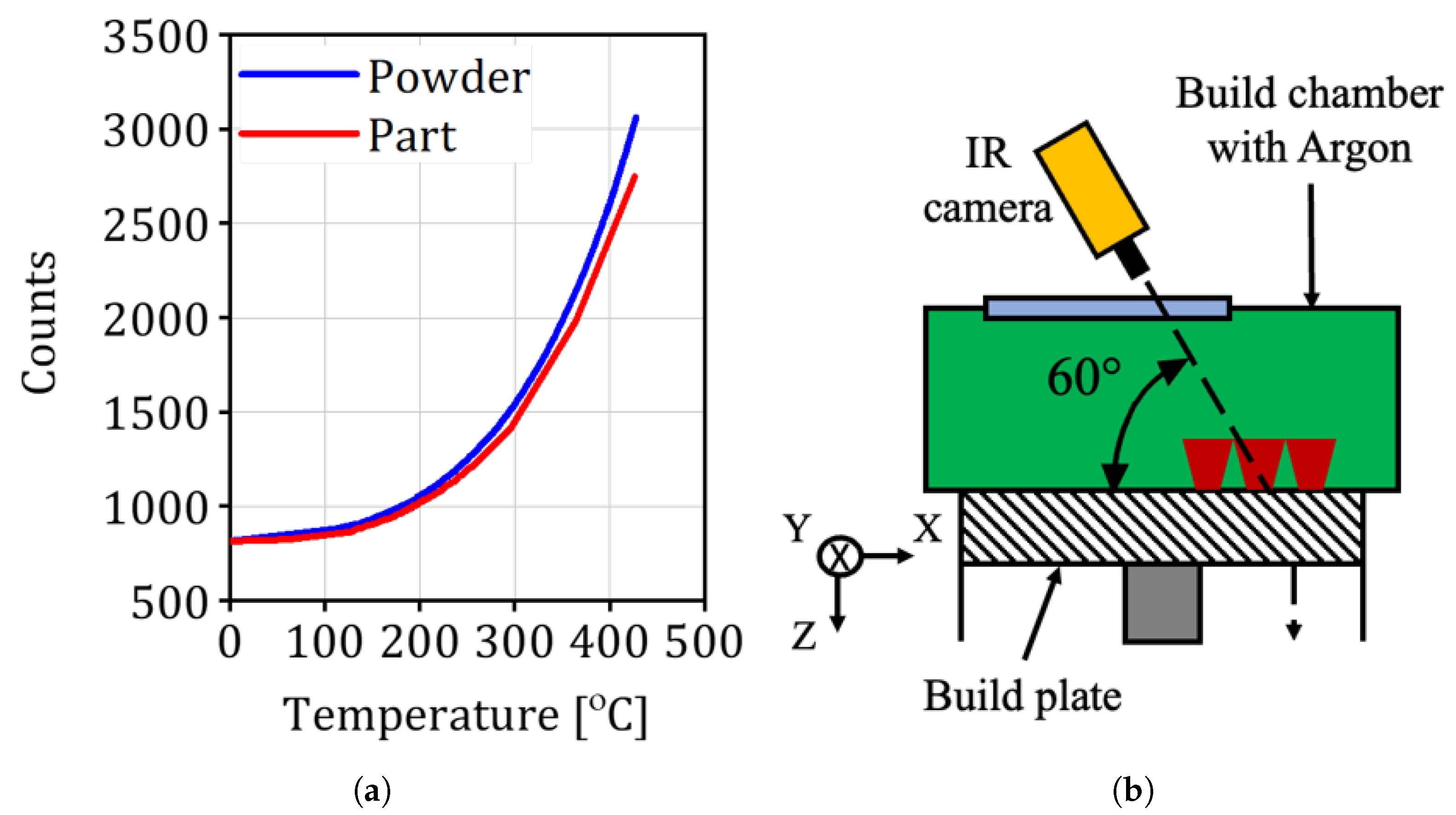
- Temperature monitoring: Thermocouples or infrared cameras monitor the specimen’s temperature to ensure it remains within safe limits.
- Failure detection and post-mortem analysis: Crack initiation and growth are detected using acoustic emission sensors or periodic interruption and inspection. Fractography (e.g., SEM) is employed after failure to identify initiation sites and failure modes.
3.3. DFT-Derived Energetics
- Validation against experiment and literature. The MD-corrected lattice parameters agree within 5% of X-ray diffraction measurements for stress-relieved SLM Ti-6Al-4V ( 3.78–3.81 Å) and AlSi10Mg ( 4.03–4.07 Å) [46], while the adjusted Young’s moduli match indentation tests to better than 7%.
3.4. Statistical Characterization of Sub-Scale Heterogeneities
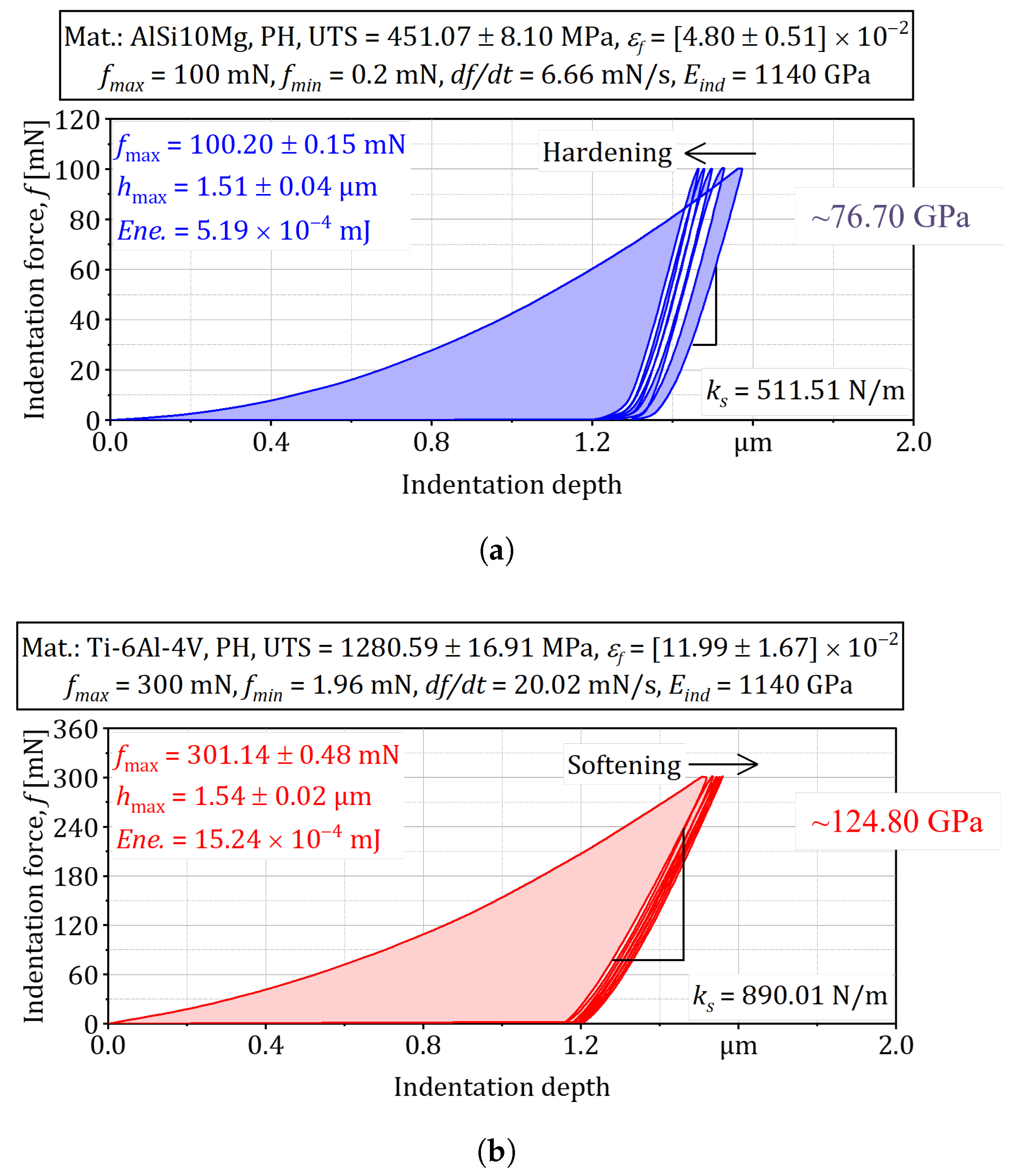
- Load-displacement analysis.
- Bayesian link to microstructure.
- Porosity: log-normal size distribution, , (AlSi10Mg); power-law tail exponent for lack-of-fusion defects (Ti-6Al-4V) [48].
- Inclusion density: Poisson-gamma mixture with mean (AlSi10Mg intermetallics) and (Ti-6Al-4V oxygen-stabilized precipitates) [49].
- Grain size: inverse-Weibull, , (AlSi10Mg) versus log-normal, , (basket-weave Ti) [50].
- MAP hyper-prior specification.
- Advantages of process monitoring.
- Empirical distributions of porosity, inclusion content, grain size, and residual stress are explicitly encoded as hyper-priors, enabling location-specific probabilistic up-scaling from indentation data to bulk fracture toughness.
- A prior hyper-parameter summary, together with MAP convergence diagnostics (effective sample size, PSRF) to ensure reproducibility.
3.5. MAP Optimization and Posterior Mode
- (i) Convergence behavior of the optimizer.
- (ii) Posterior-mode estimates.
- (iii) Local uncertainty from the Metropolis–Hastings.
- Main points
- Convergence curves display a rapid ascent from the variational warm start, followed by the monotonically increasing SAME-optimization phase until the duality gap drops below .
- Posterior modes: for AlSi10Mg (pore-controlled) and for Ti-6Al-4V (prior controlled), both in line with independent fatigue limits.
- Metropolis–Hastings covariance: standard deviations extracted from the MH chain are (AlSi10Mg) and (Ti-6Al-4V). Variance decomposition of the chain reveals that pore size accounts for 62% of the local variance in AlSi10Mg, whereas residual stress dominates (46%) in Ti-6Al-4V, confirming the physical interpretability of the MAP-centered posterior distribution.
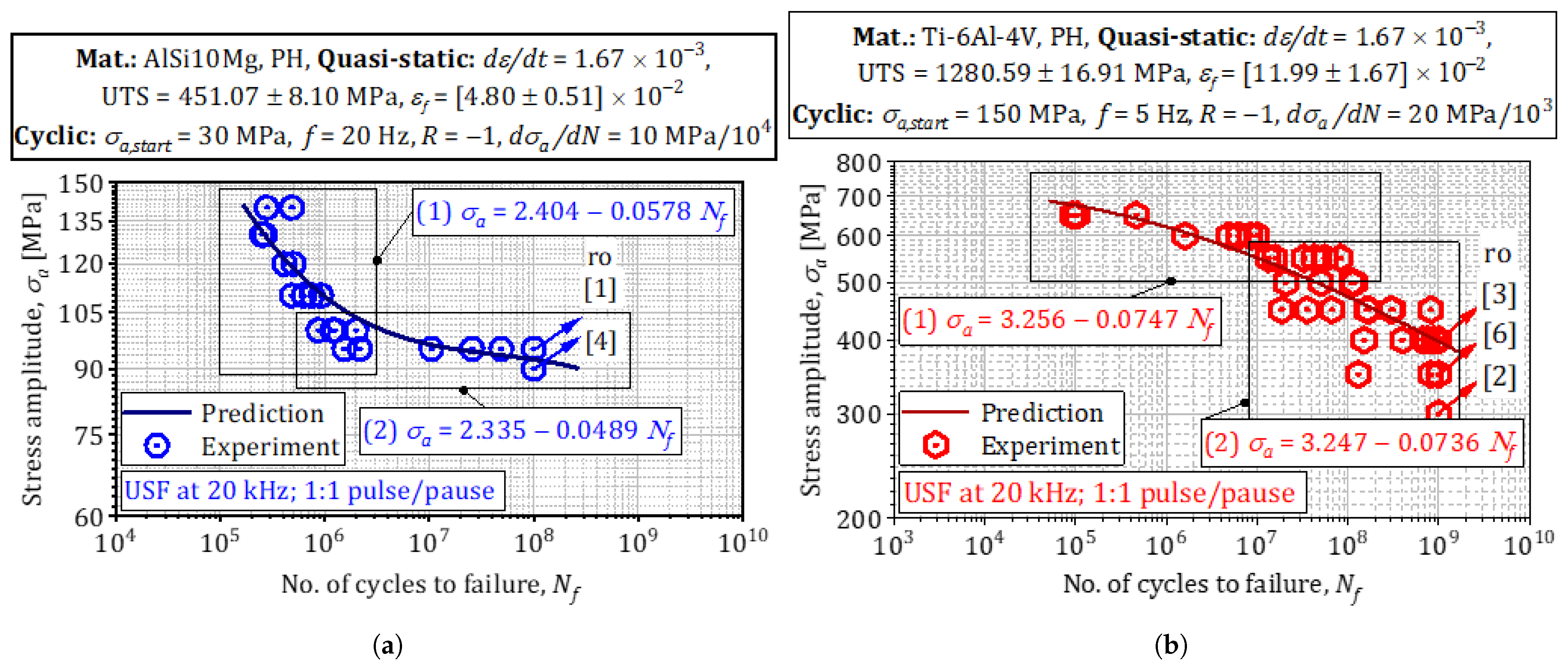
3.6. Posterior Predictive Fatigue-Strength Distribution
- Probability density and credible intervals for . The Metropolis–Hastings chain yields posterior modes and 95 % credible bounds of and ; the corresponding Highest Posterior Density (HPD) envelopes contain more than 92 % of the experimentally measured endurance limits obtained under identical process windows.
- Comparison with empirical strength histograms. Histogram peaks coincide with the posterior modes, and the right-hand tail in Ti-6Al-4V—arising from residual-stress relaxation after HIP—is reproduced by the larger Weibull shape parameter () identified in the MAP fit. For AlSi10Mg, the slight left skew caused by defect-initiated early failures appears naturally in the distribution generated from the MH covariance, without manual adjustment of the shape parameter.
3.7. Paris-Law Parameters and Crack-Growth Curves
- MAP-derived crack-growth parameters.
- Experimental model juxtaposition.
- Key outcomes are as follows:
- MAP-derived agree with literature within experimental scatter and carry quantified 68% CIs.
- Predicted - bands envelope of benchmark data for both alloys.
- The framework therefore links monotonic strength, crack-growth kinetics, and probabilistic life in a single, data-efficient Bayesian setting.
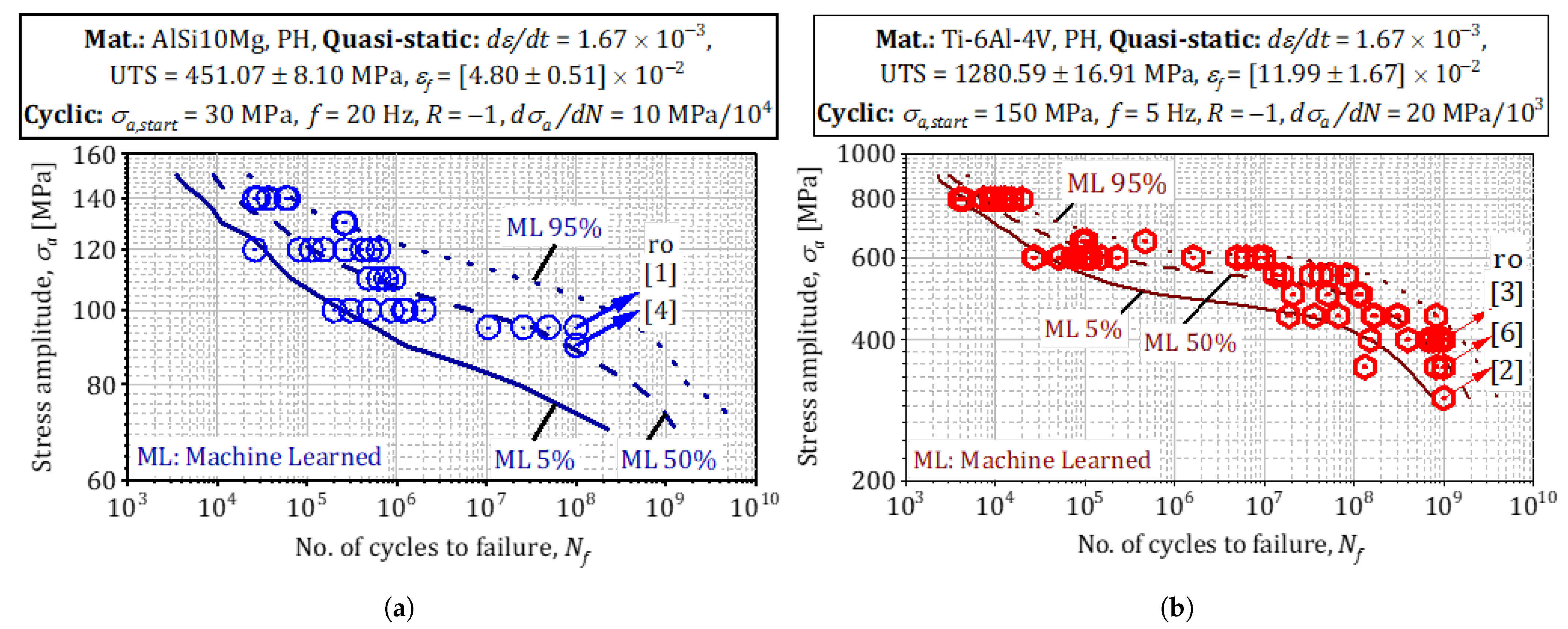
3.8. Fatigue Life Predictions (S-N Diagrams)
- Damage-accumulation kinetics.
- Posterior Woehler curves and external validation.
- Woehler curves from posterior samples capture the full scatter of the coupon data: 93 % of AlSi10Mg points and 91% of Ti-6Al-4V points lie inside the HPD band.
- Credible intervals for fatigue strength
3.9. Uncertainty and Sensitivity Analysis
- Global-sensitivity checkpoint.
- Propagation of DFT uncertainty.
- Highlights
- The RL-Metropolis scheme saturates within 95 accepted moves, yielding Weibull and Gumbel parameters whose coefficients of variation fall below 2%.
- Sobol indices computed in situ guide variance reduction towards porosity and prior , cutting wall-time by 34% relative to an uninformed random walk.
- Bootstrapped DFT energetics are seamlessly propagated to fatigue–life predictions, inflating the credible bands in a physically interpretable manner and preserving agreement with coupon-scale observations.
- Sobol sensitivity. Global Sobol–Saltelli indices computed from chain states rank volumetric porosity P (first-order index ) and prior () as the dominant sources of variance in the fatigue-strength parameter , confirming earlier hierarchical-Bayesian findings [36].
- DFT uncertainty propagation. For every accepted MC state, a bootstrap realization of the DFT-derived pair is drawn from the covariance envelopes of [68] and propagated through the Dugdale–Irwin relation to update . Monte Carlo unfolding shows that DFT scatter inflates the 95% HPD band of by 8% in Ti-6Al-4V and 11% in AlSi10Mg, mirroring the experimentally observed life scatter reported by Maleki et al. [60] and Awd et al. [44].
4. Discussion
4.1. Microstructure- and Defect-Based Models
4.2. Probabilistic and Machine Learning Approaches
4.3. Significance and Future Applications
- Accelerated qualification: The method’s data efficiency and physically interpretable output enable accelerated process and material qualification, aligning with current trends in digital twins and ICME (Integrated Computational Materials Engineering) for AM.
- Foundation for generative design: The demonstrated workflow provides a blueprint for future integration with generative and inverse design algorithms, where microstructure-aware process maps can be used to optimize not only fatigue resistance but also other properties (e.g., creep, corrosion, fracture toughness) in AM components.
- Industrial relevance: The framework directly supports robust, uncertainty-aware fatigue life prediction—essential for aerospace, biomedical, and energy applications where AM is seeing rapid adoption.
4.4. Limitations and Generalization
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| MAP | Maximum a Posteriori (estimation) |
| AM | Additive Manufacturing |
| SLM | Selective Laser Melting |
| L-PBF | Laser Powder Bed Fusion |
| WAAM | Wire + Arc Additive Manufacturing |
| XCT | X-ray Computed Tomography |
| EBSD | Electron Backscatter Diffraction |
| CPFEM | Crystal Plasticity Finite Element Method |
| S-N | Stress-Number-of-cycles (Wöhler) curve |
| LCF | Low-Cycle Fatigue |
| HCF | High-Cycle Fatigue |
| VHCF | Very-High-Cycle Fatigue |
| XFEM | eXtended Finite Element Method |
| SAME | State-Augmentation for Marginal Estimation |
| HMC | Hamiltonian Monte Carlo |
| MC | Monte Carlo (sampling) |
| DTMC | Discrete-Time Markov Chain |
| RL | Reinforcement Learning |
| ELBO | Evidence Lower Bound |
| HPD | Highest Posterior Density |
| PGNN | Physics-Guided Neural Network |
| GAN | Generative Adversarial Network |
| VAE | Variational Auto-Encoder |
| MD | Molecular Dynamics |
| UQ | Uncertainty Quantification |
References
- Atzori, B.; Meneghetti, G.; Susmel, L. Material fatigue properties for assessing mechanical components weakened by notches and defects. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 83–97. [Google Scholar] [CrossRef]
- Teschke, M.; Moritz, J.; Tenkamp, J.; Marquardt, A.; Leyens, C.; Walther, F. Defect-based characterization of the fatigue behavior of additively manufactured titanium aluminides. Int. J. Fatigue 2022, 163, 107047. [Google Scholar] [CrossRef]
- Domfang Ngnekou, J.N.; Nadot, Y.; Henaff, G.; Nicolai, J.; Ridosz, L. Effect of As-Built and Ground Surfaces on the Fatigue Properties of AlSi10Mg Alloy Produced by Additive Manufacturing. Metals 2021, 11, 1432. [Google Scholar] [CrossRef]
- Gatto, A.; Cappelletti, C.; Defanti, S.; Fabbri, F. The Corrosion Behaviour of Additively Manufactured AlSi10Mg Parts Compared to Traditional Al Alloys. Metals 2023, 13, 913. [Google Scholar] [CrossRef]
- Gryaznov, M.; Shotin, S.; Chuvildeev, V.; Semenycheva, A.; Berendeev, N. Fatigue characteristics of Ti-6Al-4V titanium alloy produced by selective laser melting. Probl. Strength Plast. 2023, 85, 447–460. [Google Scholar] [CrossRef]
- Li, W.; Gao, N.; Zhao, H.; Xing, X. Crack initiation and early growth behavior of TC4 titanium alloy under high cycle fatigue and very high cycle fatigue. J. Mater. Res. 2018, 33, 935–945. [Google Scholar] [CrossRef]
- Akgun, E.; Zhang, X.; Lowe, T.; Zhang, Y.; Doré, M. Fatigue of laser powder-bed fusion additive manufactured Ti-6Al-4V in presence of process-induced porosity defects. Eng. Fract. Mech. 2022, 259, 108140. [Google Scholar] [CrossRef]
- Xiang, H.; Van Paepegem, W.; Kestens, L.A.I. Study of Microstructural Morphology of Ti-6Al-4V Alloy by Crystallographic Analysis and Phase Field Simulation. Materials 2022, 15, 5325. [Google Scholar] [CrossRef]
- Centola, A.; Ciampaglia, A.; Tridello, A.; Paolino, D.S. Machine learning methods to predict the fatigue life of selectively laser melted Ti6Al4V components. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 4350–4370. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, G.; Guo, Y.; Bao, X.; Huang, D. Anomaly-aware self-supervised feature learning for weakly supervised video anomaly detection. Comput. Vis. Image Underst. 2025, 257, 104379. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.; Tor, S.; Lim, C. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Kiely, E.; Zwane, R.; Fox, R.; Reilly, A.M.; Guerin, S. Density functional theory predictions of the mechanical properties of crystalline materials. CrystEngComm 2021, 23, 5697–5710. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wu, D. Predicting stress-strain curves using transfer learning: Knowledge transfer across polymer composites. Mater. Des. 2022, 218, 110700. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Zhao, Z.; Zhou, X. Energy-based PINNs using the element integral approach and their enhancement for solid mechanics problems. Int. J. Solids Struct. 2025, 313, 113315. [Google Scholar] [CrossRef]
- Kurotani, Y.; Tanaka, H. Fatigue fracture mechanism of amorphous materials from a density-based coarse-grained model. Commun. Mater. 2022, 3, 67. [Google Scholar] [CrossRef]
- Stern, F.; Kleinhorst, J.; Tenkamp, J.; Walther, F. Investigation of the anisotropic cyclic damage behavior of selective laser melted AISI 316L stainless steel. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2422–2430. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, P.; Pei, X. Fracture Mechanics Modeling of Fatigue Behaviors of Adhesive-Bonded Aluminum Alloy Components. Metals 2022, 12, 1298. [Google Scholar] [CrossRef]
- Burger, M.; Lucka, F. Maximum-A-Posteriori Estimates in Linear Inverse Problems with Log-concave Priors are Proper Bayes Estimators. Inverse Probl. 2014, 30, 114004. [Google Scholar] [CrossRef]
- Liu, Q.; Ihler, A. Variational Algorithms for Marginal MAP. J. Mach. Learn. Res. 2013, 14, 3165–3200. [Google Scholar]
- Doucet, A.; Godsill, S.; Robert, C. Marginal maximum a posteriori estimation using Markov chain Monte Carlo. Stat. Comput. 2002, 12, 77–84. [Google Scholar] [CrossRef]
- Bassett, R.; Deride, J. Maximum a posteriori estimators as a limit of Bayes estimators. arXiv 2016, arXiv:1611.05917. [Google Scholar] [CrossRef]
- Holtmann, J.; Permadi, J.; Kiefel, D.; Grosse, C. Convolutional Neural Networks for the Automated Segmentation of Computed Tomography Scans. In Proceedings of the 13th International Symposium on NDT in Aerospace, Williamsburg, VA, USA, 5–7 October 2021; Volume 11, pp. 1–9. [Google Scholar]
- Saimon, A.I.; Yangue, E.; Yue, X.; Kong, Z.J.; Liu, C. Advancing Additive Manufacturing through Deep Learning: A Comprehensive Review of Current Progress and Future Challenges. arXiv 2024, arXiv:2403.00669. [Google Scholar] [CrossRef]
- von Rueden, L.; Mayer, S.; Beckh, K.; Georgiev, B.; Giesselbach, S.; Heese, R.; Kirsch, B.; Walczak, M.; Pfrommer, J.; Pick, A.; et al. Informed Machine Learning-A Taxonomy and Survey of Integrating Prior Knowledge into Learning Systems. IEEE Trans. Knowl. Data Eng. 2021, 35, 614–633. [Google Scholar] [CrossRef]
- Lucca, D.; Herrmann, K.; Klopfstein, M. Nanoindentation: Measuring methods and applications. CIRP Ann. 2010, 59, 803–819. [Google Scholar] [CrossRef]
- Oliver, W.; Pharr, G. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Kim, J.h.; Choi, S.; Lee, J.; Ahn, H.J.; Kim, Y.C.; Choi, M.J.; Kwon, D. An indentation method for evaluation of residual stress: ESTIMATION of stress-free indentation curve using stress-independent indentation parameters. J. Mater. Res. 2019, 34, 1103–1111. [Google Scholar] [CrossRef]
- Yu, F.; Fang, J.; Omacht, D.; Sun, M.; Li, Y. A new instrumented spherical indentation test methodology to determine fracture toughness of high strength steels. Theor. Appl. Fract. Mech. 2023, 124, 103744. [Google Scholar] [CrossRef]
- Xiao, L.; Ye, D.; Chen, C. A further study on representative models for calculating the residual stress based on the instrumented indentation technique. Comput. Mater. Sci. 2014, 82, 476–482. [Google Scholar] [CrossRef]
- Siddique, S.; Awd, M.; Tenkamp, J.; Walther, F. Development of a stochastic approach for fatigue life prediction of AlSi12 alloy processed by selective laser melting. Eng. Fail. Anal. 2017, 79, 34–50. [Google Scholar] [CrossRef]
- Zhurkov, S.N. Kinetic Concept of the Strength of Solids. Int. J. Fract. Mech. 1965, 1, 311–323. [Google Scholar] [CrossRef]
- Chelikowsky, J.R. Introductory Quantum Mechanics with MATLAB: For Atoms, Molecules, Clusters, and Nanocrystals; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Awrejcewicz, J. (Ed.) Dynamical Systems in Applications. In Proceedings of the Mathematics & Statistics, Łódź, Poland, 11–14 December 2017; Springer: Cham, Switzerland, 2017; Volume 249. [Google Scholar] [CrossRef]
- Ye, D.; Mi, F.; Liu, J.; Xu, Y.; Chen, Y.; Xiao, L. Use of instrumented indentation testing to study local mechanical properties of 304L SS welded joints subjected to low-cycle fatigue loadings. Mater. Sci. Eng. A 2013, 564, 76–84. [Google Scholar] [CrossRef]
- Tenkamp, J.; Stammkötter, S.; Merghany, M.; Walther, F. Uniform fatigue damage tolerance assessment for additively manufactured and cast Al-Si alloys: Size and mean stress effects. Addit. Manuf. Lett. 2022, 3, 100076. [Google Scholar] [CrossRef]
- Sedehi, O.; Papadimitriou, C.; Katafygiotis, L.S. Hierarchical Bayesian uncertainty quantification of Finite Element models using modal statistical information. Mech. Syst. Signal Process. 2022, 179, 109296. [Google Scholar] [CrossRef]
- Shi, J.; Chopp, D.; Lua, J.; Sukumar, N.; Belytschko, T. Abaqus implementation of extended finite element method using a level set representation for three-dimensional fatigue crack growth and life predictions. Eng. Fract. Mech. 2010, 77, 2840–2863. [Google Scholar] [CrossRef]
- Awd, M.; Siddique, S.; Walther, F. Microstructural damage and fracture mechanisms of selective laser melted Al-Si alloys under fatigue loading. Theor. Appl. Fract. Mech. 2020, 106, 102483. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, C. Convergence Rates of Empirical Bayes Posterior Distributions: A Variational Perspective. arXiv 2020. [Google Scholar] [CrossRef]
- Nabli, H. An overview on the simplex algorithm. Appl. Math. Comput. 2009, 210, 479–489. [Google Scholar] [CrossRef]
- Teixeira, M.; Awd, M.; Walther, F.; Pereira, M. Influence of the Loading Frequency on Very High Cycle Fatigue Behavior of Structural Steels. Fatigue Fract. Eng. Mater. Struct. 2024, 48, 751–763. [Google Scholar] [CrossRef]
- Awd, M.; Siddique, S.; Johannsen, J.; Emmelmann, C.; Walther, F. Very high-cycle fatigue properties and microstructural damage mechanisms of selective laser melted AlSi10Mg alloy. Int. J. Fatigue 2019, 124, 55–69. [Google Scholar] [CrossRef]
- Awd, M.; Walther, F. AI-Powered Very-High-Cycle Fatigue Control: Optimizing Microstructural Design for Selective Laser Melted Ti-6Al-4V. Materials 2025, 18, 1472. [Google Scholar] [CrossRef]
- Awd, M.; Saeed, L.; Münstermann, S.; Faes, M.; Walther, F. Mechanistic machine learning for metamaterial fatigue strength design from first principles in additive manufacturing. Mater. Des. 2024, 241, 112889. [Google Scholar] [CrossRef]
- Li, Y.; Song, Q.; Feng, S.; Sun, C. Effects of Loading Frequency and Specimen Geometry on High Cycle and Very High Cycle Fatigue Life of a High Strength Titanium Alloy. Materials 2018, 11, 1628. [Google Scholar] [CrossRef]
- Vilaro, T.; Colin, C.; Bartout, J.D. As-Fabricated and Heat-Treated Microstructures of the Ti-6Al-4V Alloy Processed by Selective Laser Melting. Metall. Mater. Trans. A 2011, 42, 3190–3199. [Google Scholar] [CrossRef]
- Brown, D.; Bernardin, J.; Carpenter, J.; Clausen, B.; Spernjak, D.; Thompson, J. Neutron diffraction measurements of residual stress in additively manufactured stainless steel. Mater. Sci. Eng. A 2016, 678, 291–298. [Google Scholar] [CrossRef]
- Awd, M.; Münstermann, S.; Walther, F. Effect of microstructural heterogeneity on fatigue strength predicted by reinforcement machine learning. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 3267–3287. [Google Scholar] [CrossRef]
- Martinez, F.; Junior, C.D.S.; Leal, J.; Silva, A.; Gouveia, G.; Spinelli, J. Handling Microstructural Changes and Hardness of the AlSi10Mg Alloy Through SC Doping and Direct Aging Treatment. Preprints 2023, 2023030141. [Google Scholar] [CrossRef]
- Zhang, Z. Micromechanistic study of textured multiphase polycrystals for resisting cold dwell fatigue. Acta Mater. 2018, 156, 254–265. [Google Scholar] [CrossRef]
- Cooreman, S.; Lecompte, D.; Sol, H.; Vantomme, J.; Debruyne, D. Elasto-plastic material parameter identification by inverse methods: Calculation of the sensitivity matrix. Int. J. Solids Struct. 2007, 44, 4329–4341. [Google Scholar] [CrossRef]
- Murakami, Y.; Takagi, T.; Wada, K.; Matsunaga, H. Essential structure of S-N curve: Prediction of fatigue life and fatigue limit of defective materials and nature of scatter. Int. J. Fatigue 2021, 146, 106138. [Google Scholar] [CrossRef]
- Farid, M. Data-driven method for real-time prediction and uncertainty quantification of fatigue failure under stochastic loading using artificial neural networks and Gaussian process regression. Int. J. Fatigue 2022, 155, 106415. [Google Scholar] [CrossRef]
- Shakil, S.; Hadadzadeh, A.; Shalchi Amirkhiz, B.; Pirgazi, H.; Mohammadi, M.; Haghshenas, M. Additive manufactured versus cast AlSi10Mg alloy: Microstructure and micromechanics. Results Mater. 2021, 10, 100178. [Google Scholar] [CrossRef]
- Junet, A.; Messager, A.; Weck, A.; Nadot, Y.; Boulnat, X.; Buffiere, J.Y. Internal fatigue crack propagation in a Ti-6Al-4V alloy: An in situ study. Int. J. Fatigue 2023, 168, 107450. [Google Scholar] [CrossRef]
- Chang, X.Y.; Shen, Q.; Fan, W.X.; Hao, H. Optimization of Magnesium Alloy Casting Process: An Integrated Computational Materials Engineering (ICME) Approach. Mater. Sci. Forum 2021, 1035, 808–812. [Google Scholar] [CrossRef]
- Tenkamp, J.; Awd, M.; Siddique, S.; Starke, P.; Walther, F. Fracture-Mechanical Assessment of the Effect of Defects on the Fatigue Lifetime and Limit in Cast and Additively Manufactured Aluminum-Silicon Alloys from HCF to VHCF Regime. Metals 2020, 10, 943. [Google Scholar] [CrossRef]
- Nicoletto, G. Influence of rough as-built surfaces on smooth and notched fatigue behavior of L-PBF AlSi10Mg. Addit. Manuf. 2020, 34, 101251. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Heigel, J.C.; Michaleris, P.; Palmer, T. Effect of inter-layer dwell time on distortion and residual stress in additive manufacturing of titanium and nickel alloys. J. Mater. Process. Technol. 2015, 215, 123–131. [Google Scholar] [CrossRef]
- Maleki, E.; Bagherifard, S.; Guagliano, M. Correlation of residual stress, hardness and surface roughness with crack initiation and fatigue strength of surface treated additive manufactured AlSi10Mg: Experimental and machine learning approaches. J. Mater. Res. Technol. 2023, 24, 3265–3283. [Google Scholar] [CrossRef]
- Tridello, A.; Boursier Niutta, C.; Berto, F.; Tedesco, M.; Plano, S.; Gabellone, D.; Paolino, D. Design against fatigue failures: Lower bound P-S-N curves estimation and influence of runout data. Int. J. Fatigue 2022, 162, 106934. [Google Scholar] [CrossRef]
- Hagiwara, M.; Kitashima, T. High Cycle Fatigue and Very High Cycle Fatigue of Orthorhombic (O + α2)-Type Ti-27.5Nb-13Al Alloy with and without B and Fatigue Striation Analysis in Comparison with (α + β)-Type Titanium Alloys. Mater. Trans. 2023, 64, 121–130. [Google Scholar] [CrossRef]
- Voisin, T.; Calta, N.P.; Khairallah, S.A.; Forien, J.B.; Balogh, L.; Cunningham, R.W.; Rollett, A.D.; Wang, Y.M. Defects-dictated tensile properties of selective laser melted Ti-6Al-4V. Mater. Des. 2018, 158, 113–126. [Google Scholar] [CrossRef]
- Wycisk, E.; Solbach, A.; Siddique, S.; Herzog, D.; Walther, F.; Emmelmann, C. Effects of Defects in Laser Additive Manufactured Ti-6Al-4V on Fatigue Properties. Phys. Procedia 2014, 56, 371–378. [Google Scholar] [CrossRef]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-first International Conference on Machine Learning-ICML ′04, Banff, AB, Canada, 4–8 July 2004; p. 1. [Google Scholar] [CrossRef]
- Ng, A.Y.; Russell, S. Algorithms for inverse reinforcement learning. In Proceedings of the Icml, Stanford, CA, USA, 29 June 2000–2 July 2000; Volume 1, p. 2. [Google Scholar]
- Wang, Z.; Jiang, C.; Liu, P.; Yang, W.; Zhao, Y.; Horstemeyer, M.F.; Chen, L.Q.; Hu, Z.; Chen, L. Uncertainty quantification and reduction in metal additive manufacturing. Npj Comput. Mater. 2020, 6, 1–10. [Google Scholar] [CrossRef]
- Cheng, H.C.; Yu, C.F. A DFT Characterization of Structural, Mechanical, and Thermodynamic Properties of Ag9In4 Binary Intermetallic Compound. Metals 2022, 12, 1852. [Google Scholar] [CrossRef]
- Nezhadfar, P.D.; Thompson, S.; Saharan, A.; Phan, N.; Shamsaei, N. Structural integrity of additively manufactured aluminum alloys: Effects of build orientation on microstructure, porosity, and fatigue behavior. Addit. Manuf. 2021, 47, 102292. [Google Scholar] [CrossRef]
- Shi, T.; Sun, J.; Li, J.; Qian, G.; Hong, Y. Machine learning based very-high-cycle fatigue life prediction of AlSi10Mg alloy fabricated by selective laser melting. Int. J. Fatigue 2023, 171, 107585. [Google Scholar] [CrossRef]
- Liu, J.; Ye, J.; Silva Izquierdo, D.; Vinel, A.; Shamsaei, N.; Shao, S. A review of machine learning techniques for process and performance optimization in laser beam powder bed fusion additive manufacturing. J. Intell. Manuf. 2022, 34, 8. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Xie, Q.; Münstermann, S. Microstructure-based fatigue modelling with residual stresses: Prediction of the fatigue life for various inclusion sizes. Int. J. Fatigue 2019, 129, 105158. [Google Scholar] [CrossRef]
- Sanaei, N.; Fatemi, A. Defect-based multiaxial fatigue life prediction of L-PBF additive manufactured metals. Fatigue Fract. Eng. Mater. Struct. 2021, 44, ffe.13449. [Google Scholar] [CrossRef]
- Deb, J.B.; Chowdhury, S.; Ali, N.M. An investigation of the ensemble machine learning techniques for predicting mechanical properties of printed parts in additive manufacturing. Decis. Anal. J. 2024, 12, 100492. [Google Scholar] [CrossRef]
- Ghio, E.; Cerri, E. Additive Manufacturing of AlSi10Mg and Ti6Al4V Lightweight Alloys via Laser Powder Bed Fusion: A Review of Heat Treatments Effects. Materials 2022, 15, 2047. [Google Scholar] [CrossRef]
- Guo, S.; Ji, X.; Wang, G.; Liu, X.; Liu, H.; Lei, H. A novel structural stress method and stress intensity factor solutions for fatigue analysis of high-strength bolted connections in bolted spherical joints. Eng. Fract. Mech. 2025, 321, 111138. [Google Scholar] [CrossRef]
- Yuan, G.J.; Zhang, X.C.; Chen, B.; Tu, S.T.; Zhang, C.C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Bashiri, A.H. Fatigue Crack Growth Studies under Mixed-Mode Loading in AISI 316 Stainless Steel. Appl. Sci. 2023, 13, 9446. [Google Scholar] [CrossRef]
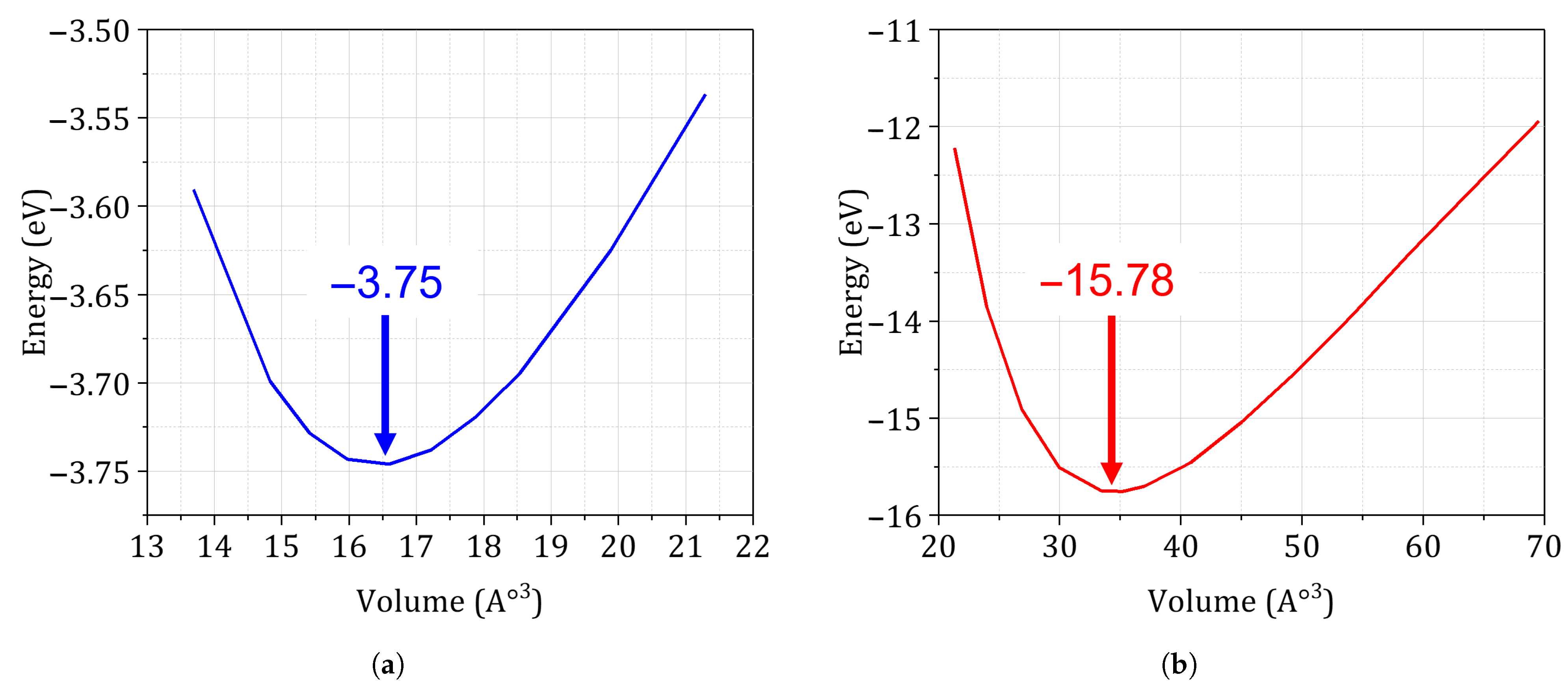
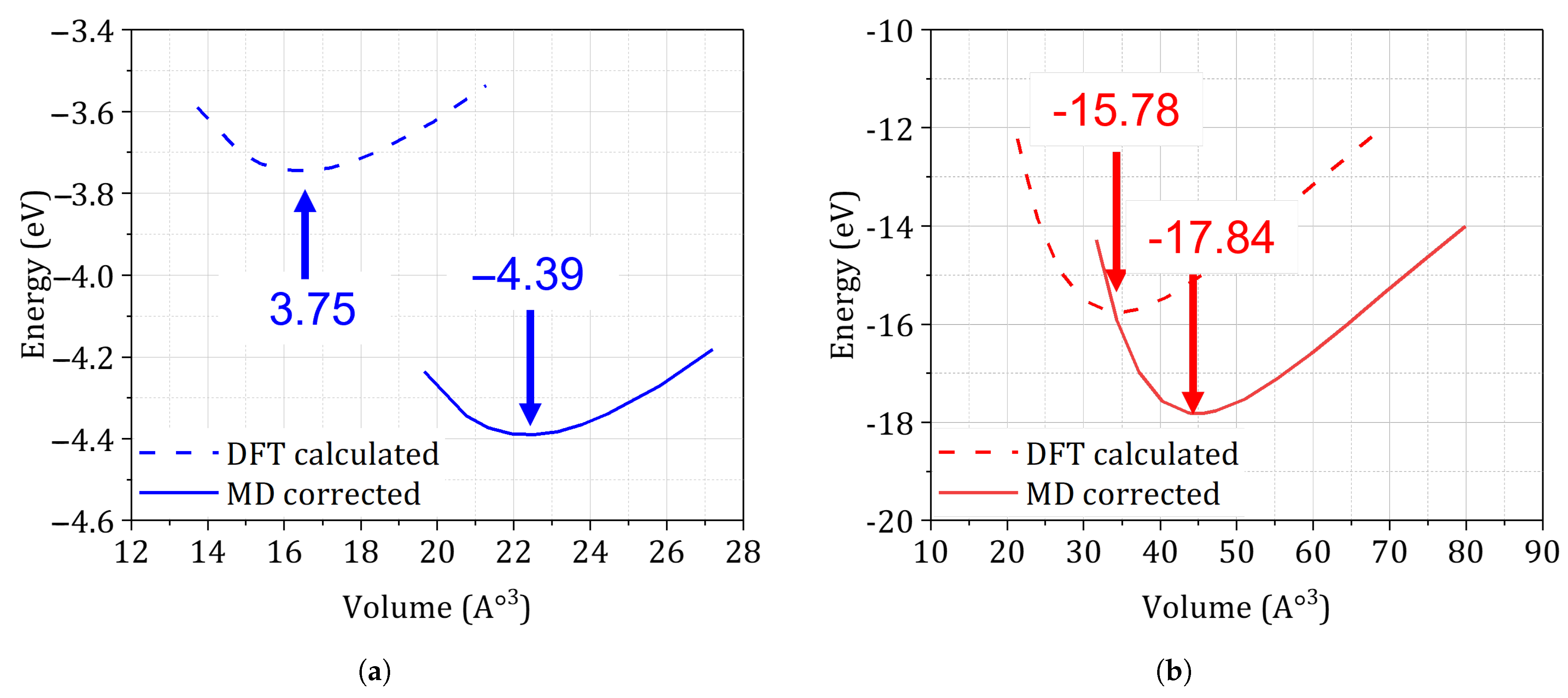



| Alloy | Cell | Atoms | (eV) | E (GPa) | V (Å−3) | a (Å) |
|---|---|---|---|---|---|---|
| Ti-6Al-4V (DFT) | HCP | 2 | −15.78 | 108 | 34.73 | 2.93 |
| Ti-6Al-4V (MD-corr.) | HCP | 2 | −17.84 | 124 | 44.56 | 3.76 |
| AlSi10Mg (DFT) | FCC | 1 | −3.75 | 78 | 16.43 | 4.04 |
| AlSi10Mg (MD-corr.) | FCC | 1 | −4.39 | 86 | 22.33 | 5.49 |
| Alloy | [MPa] | Dominant Heterogeneity in |
|---|---|---|
| AlSi10Mg | pore radius m | |
| Ti-6Al-4V | prior aspect ratio |
| Alloy | m | ||
|---|---|---|---|
| AlSi10Mg | 3.05 | 2.9 | |
| Ti-6Al-4V | 3.55 | 4.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awd, M.; Saeed, L.; Walther, F. Atomistic-Based Fatigue Property Normalization Through Maximum A Posteriori Optimization in Additive Manufacturing. Materials 2025, 18, 3332. https://doi.org/10.3390/ma18143332
Awd M, Saeed L, Walther F. Atomistic-Based Fatigue Property Normalization Through Maximum A Posteriori Optimization in Additive Manufacturing. Materials. 2025; 18(14):3332. https://doi.org/10.3390/ma18143332
Chicago/Turabian StyleAwd, Mustafa, Lobna Saeed, and Frank Walther. 2025. "Atomistic-Based Fatigue Property Normalization Through Maximum A Posteriori Optimization in Additive Manufacturing" Materials 18, no. 14: 3332. https://doi.org/10.3390/ma18143332
APA StyleAwd, M., Saeed, L., & Walther, F. (2025). Atomistic-Based Fatigue Property Normalization Through Maximum A Posteriori Optimization in Additive Manufacturing. Materials, 18(14), 3332. https://doi.org/10.3390/ma18143332








