A Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint
Abstract
1. Introduction
2. Stiffness Adjustment Scheme and Structure
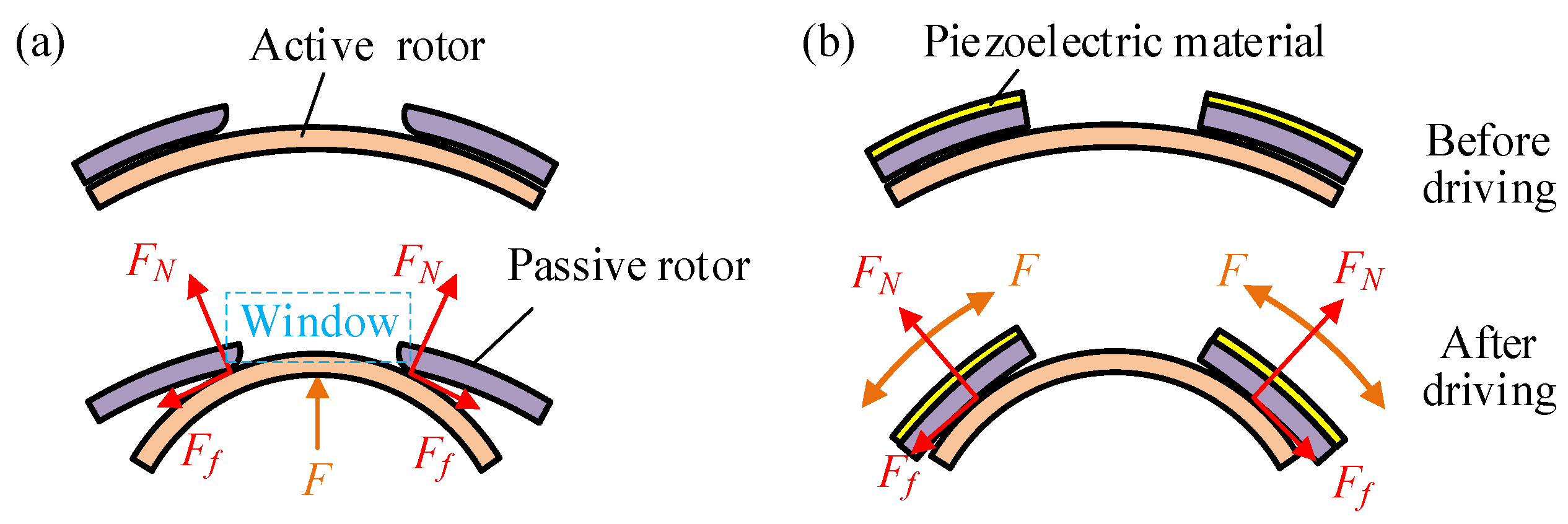
2.1. Stiffness Adjustment Scheme
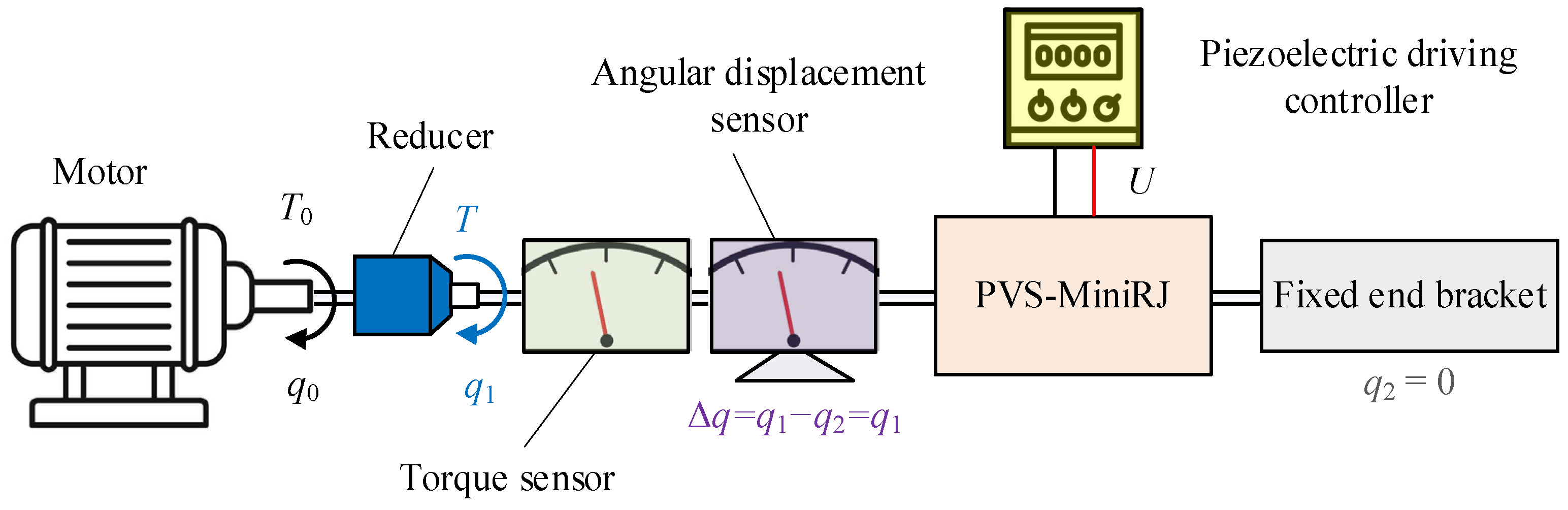
2.2. Driving and Transmission Path
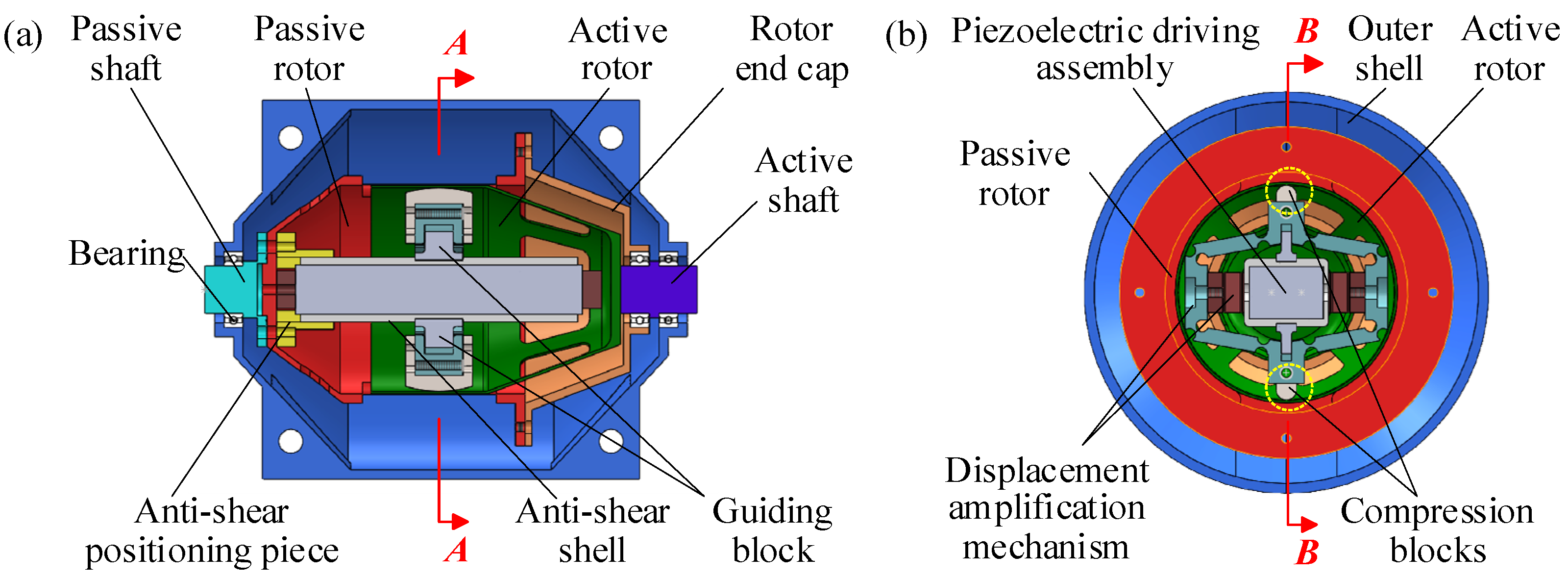
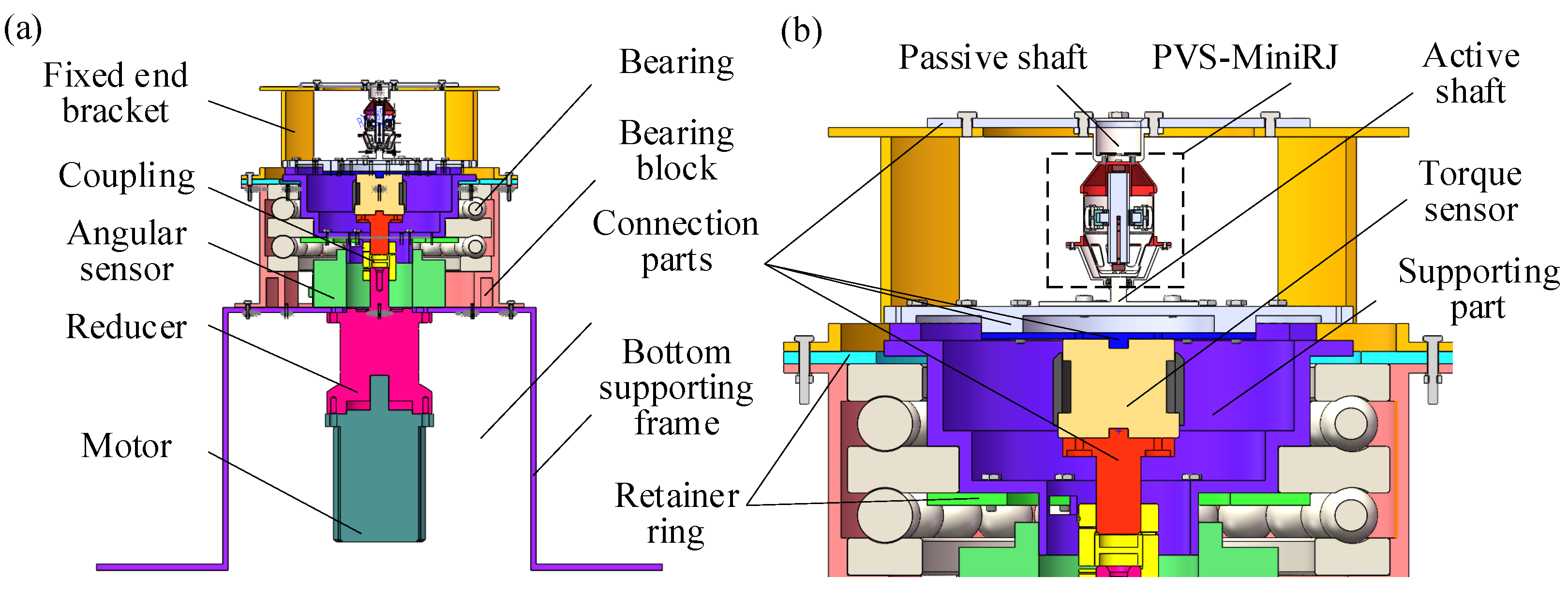
2.3. Structure-and-Assembly Relationship
2.3.1. Piezoelectric Driving Assembly
2.3.2. Displacement Amplification Assembly
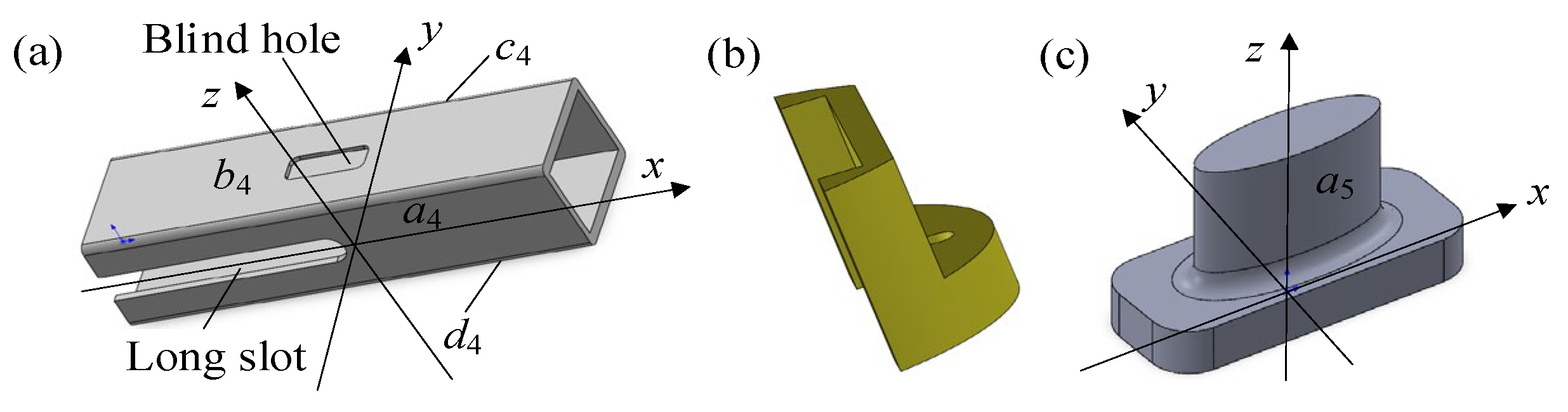
2.3.3. Compliant Transmission Assembly
2.3.4. Guiding and Anti-Shear Assembly
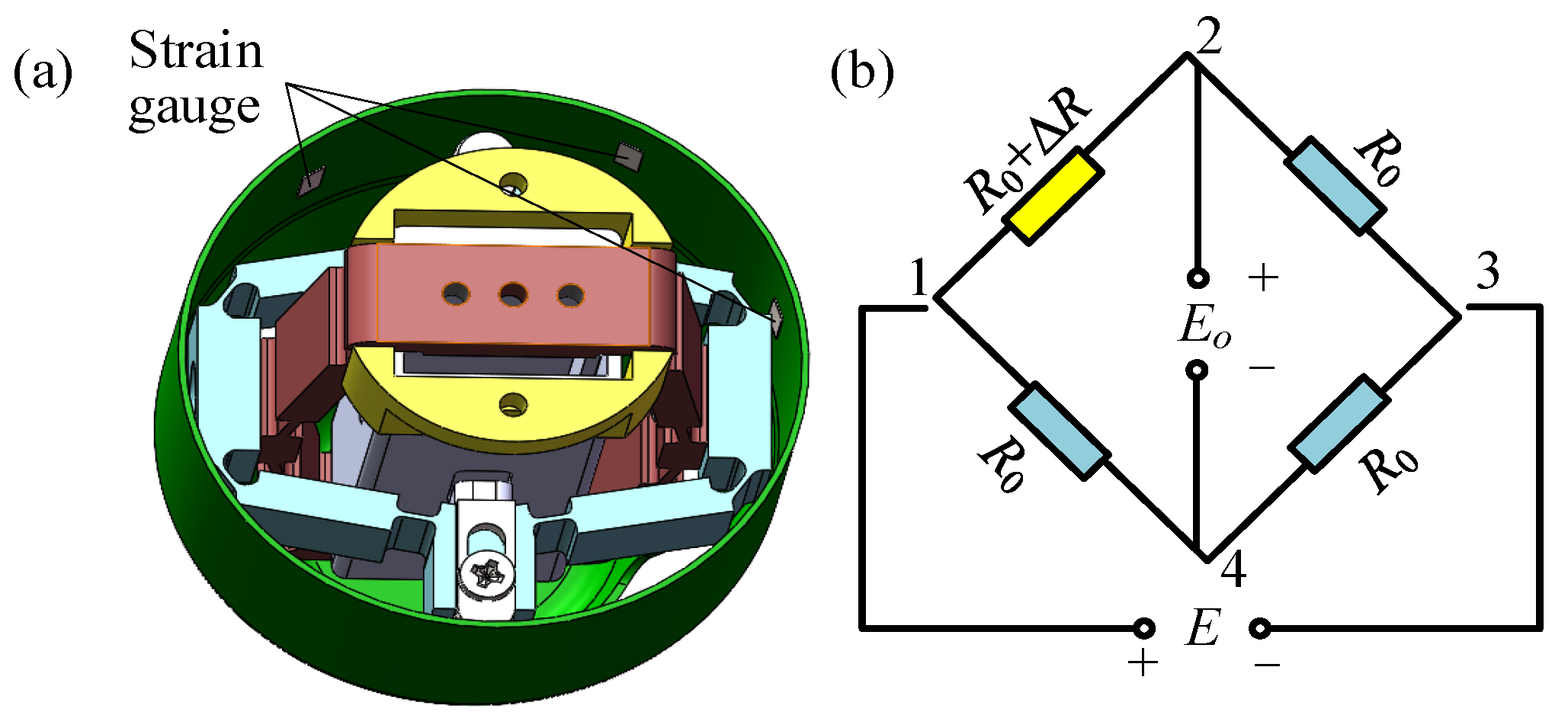
2.3.5. State Monitoring Assembly
3. Mechanical Modeling and Simulation Analysis
3.1. Mechanics Modeling of Adjustment Stiffness Process
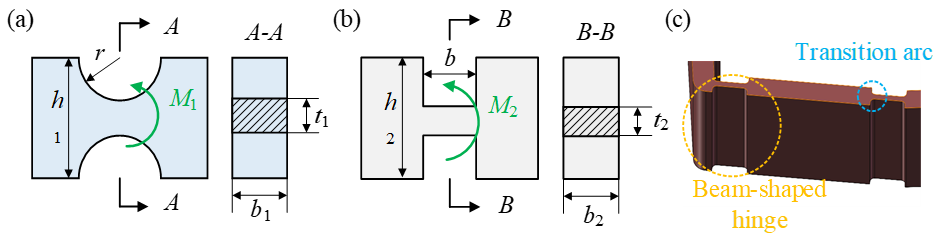
3.2. Force Analysis of Flexible Hinge
3.3. Simulation Analysis
3.3.1. Influence of Fout on Stiffness Adjustment
3.3.2. Influence of xout on Stiffness Adjustment
3.3.3. Influence of T on Stiffness Adjustment
3.4. The Purpose of Modeling and Simulation
4. Test Device and Experiments
4.1. Test Platform and Device
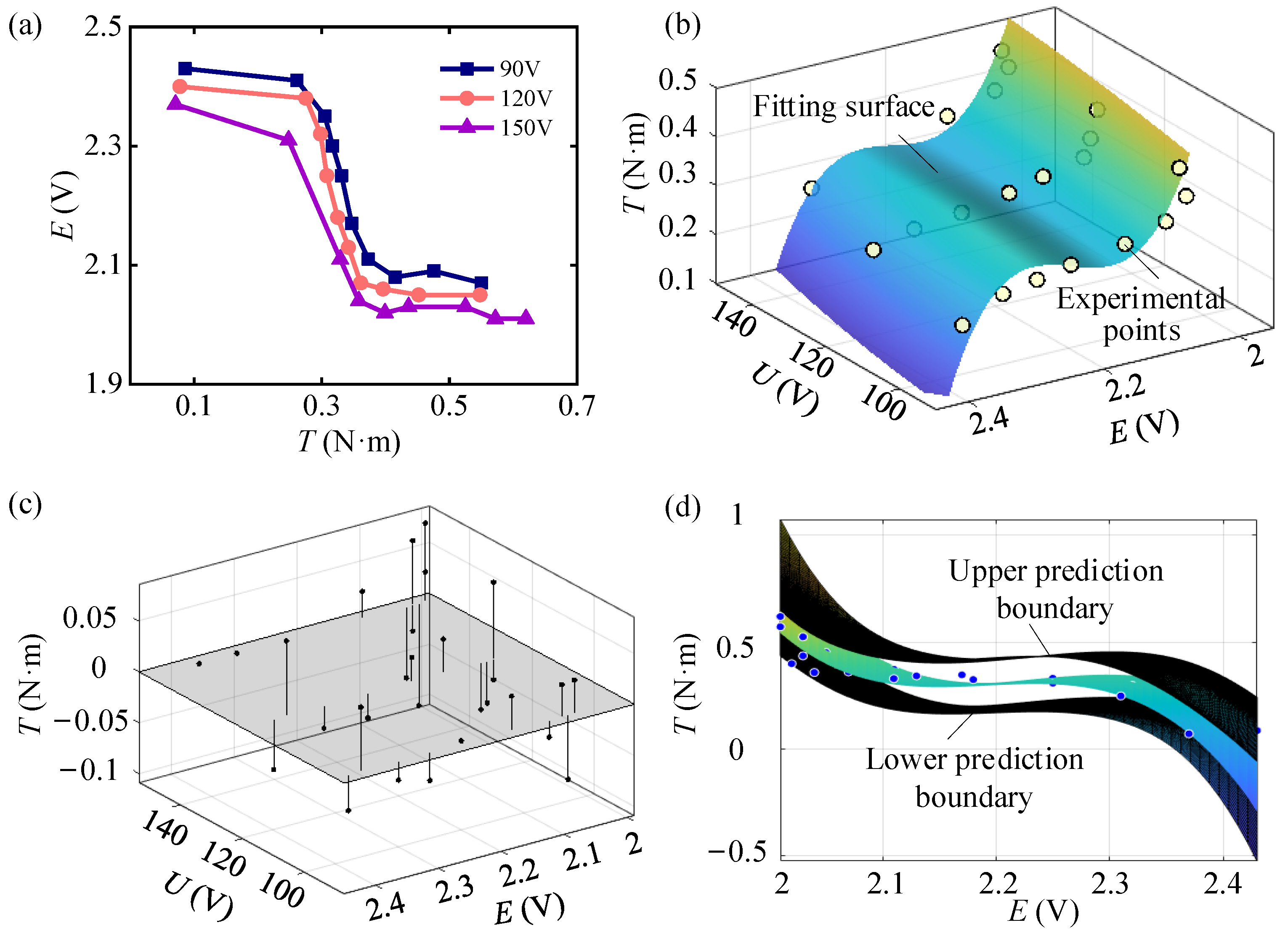
4.2. Stiffness Characteristic Test
- (1)
- Test 1
- (2)
- Test 2
4.3. Mechanical Monitoring Test
4.4. Error Analysis
5. Conclusions
- (1)
- Novel stiffness adjustment principle. This paper proposes a new method for joint stiffness control, exploiting piezoelectric stack expansion/contraction to dynamically regulate compressive and frictional forces between active and passive rotors. This enables direct actuation, rapid response, and a compact design. A beam-type flexure hinge displacement amplifier compensates for limited piezoelectric stroke. Integrated guiding/anti-shear components ensure reliability, while embedded strain gauges provide miniaturized sensing, achieving seamless actuation–sensing integration within the joint.
- (2)
- Stiffness-oriented mechanical modeling and simulation. This paper develops a detailed mechanical model linking the piezoelectric stack voltage, which is the control input, to active rotor deformation, which is the monitored variable. Comparative analysis reveals that the beam-type flexure hinge offers smoother deformation and superior force distribution versus circular hinges. Finite element simulations validate the stiffness adjustment concept and elucidate the influence of the piezoelectric force Fout, displacement xout, and external torque T on stiffness modulation.
- (3)
- Experimental validation and mechanical monitoring. These demonstrate significant variable stiffness capability through static load testing: the joint stiffness K ranges from 0.105 to 0.1822 N·m/° and 0.3778 to 0.4972 N·m/° for different configurations at U = 90 V to 150 V. The sensor calibration establishes relationships between the torque T, strain voltage E, and piezoelectric voltage U, enabling real-time mechanical state monitoring and closed-loop controllable stiffness adjustment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PVS-MiniRJ | Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint |
References
- Yang, B.; He, Y.; Han, J.; Liu, G. Modeling and control of rotor-flying multi-joint manipulator. IFAC-Pap. 2014, 47, 11024–11029. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Xie, M. Implementation of a single motor driven manipulator with multiple joints. Ind. Robot. 2011, 38, 48–57. [Google Scholar] [CrossRef]
- Li, W.; Chen, P.; Bai, D.; Zhu, X.; Togo, S.; Yokoi, H.; Jiang, Y. Modularization of 2-and 3-DoF coupled tendon-driven joints. IEEE Trans. Robot. 2020, 37, 905–917. [Google Scholar] [CrossRef]
- Liu, G.; Chen, W.; Wang, W.; Chen, Y. Design and analysis of a novel space deployable mechanism of ring and frustum type. Int. J. Adv. Manuf. Technol. 2018, 94, 3251–3264. [Google Scholar] [CrossRef]
- Pagani, A.; Augello, R.; Carrera, E. Numerical simulation of deployable ultra-thin composite shell structures for space ap-plications and comparison with experiments. Mech. Adv. Mater. Struct. 2022, 30, 1591–1603. [Google Scholar] [CrossRef]
- Liu, T.; Hao, G. Design of deployable structures by using bistable compliant mechanismsm. Micromachine 2022, 13, 651. [Google Scholar] [CrossRef]
- Xu, H.; Han, J.; Yun, H.; Chen, X. Calculation of the Hinge Moments of a Folding Wing Aircraft during the Flight-Folding Process. Int. J. Aerosp. Eng. 2019, 2019, 9362629. [Google Scholar] [CrossRef]
- Li, X.; Zhu, H.; Lin, W.; Chen, W.; Low, K.H. Structure-controlled variable stiffness robotic joint based on multiple rotary flexure hinges. IEEE Trans. Ind. Electron. 2020, 68, 12452–12461. [Google Scholar] [CrossRef]
- Baek, J.M.; Lee, S.H.; Moon, H.; Choi, H.R.; Koo, J.C. Three-degree-of-freedom switchable variable stiffness mechanism for minimization of repulsive force in robot assembly tasks. Int. J. Adv. Manuf. Technol. 2024, 134, 591–604. [Google Scholar] [CrossRef]
- Baek, J.M.; Han, M.G.; Koo, J.C. Linear multi-degree of freedom variable stiffness actuator for robotic assembly tasks. Microsyst. Technol. 2023, 29, 1643–1649. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, Q.; Chen, B.; Xu, D.; Shao, Z. Design and Evaluation of a Novel Torque-Controllable Variable Stiffness Actuator With Reconfigurability. IEEE/ASME Trans. Mechatron. 2021, 27, 292–303. [Google Scholar] [CrossRef]
- Kargar, S.M.; Parmiggiani, A.; Baggetta, M.; Ottonello, E.; Hao, G.; Berselli, G. Optimization of a tetrahedron compliant spherical joint via computer-aided engineering tools. Int. J. Adv. Manuf. Technol. 2024, 132, 1151–1162. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Chen, W.; Li, X.; Ma, J.; Teo, C.S.; Teo, T.J.; Lin, W. Weight Imprinting Classification-Based Force Grasping With a Variable-Stiffness Robotic Gripper. IEEE Trans. Autom. Sci. Eng. 2022, 19, 969–981. [Google Scholar] [CrossRef]
- Yang, S.; Chen, P.; Wang, D.; Yu, Y.; Liu, Y. Design and Analysis of a 2-DOF Actuator with Variable Stiffness Based on Leaf Springs. J. Bionic. Eng. 2022, 19, 1392–1404. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Y.; Xue, Y.; Jiang, J.; Zhang, Q.; Yue, H. A variable stiffness actuator based on leaf springs: Design, model and analysis. Actuators 2022, 11, 282. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Y.; Zhang, R.; Yue, H. RJVS: A novel, compact and integrated rotating joint with variable stiffness. Mech. Syst. Signal Process. 2023, 193, 110273. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.; Caldwell, D. Energy efficient actuators with adjustable stiffness: A review on AwAS, AwAS-II and CompACT VSA changing stiffness based on lever mechanism. Ind. Robot. 2015, 42, 242–251. [Google Scholar] [CrossRef]
- Petit, F.; Friedl, W.; Höppner, H.; Grebenstein, M. Analysis and synthesis of the bidirectional antagonistic variable stiffness mechanism. IEEE/ASME Trans. Mech. 2014, 20, 684–695. [Google Scholar] [CrossRef]
- Yu, H.S.; Song, J.B. Small-sized variable stiffness actuator module based on adjustable moment arm. Trans. Korean Soc. Mech. Eng. A 2013, 37, 1195–1200. [Google Scholar] [CrossRef][Green Version]
- Yu, J.; Zhao, Y.; Chen, G.; Gu, Y.; Wang, C.; Huang, S. Realizing Controllable Physical Interaction Based on an Electromagnetic Variable Stiffness Joint. J. Mech. Robot. 2019, 11, 054501. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, L.; Guo, H.; Li, H.; Sun, F.; Fang, L. Design and control of variable stiffness joint based on magnetic flux ad-justment mechanism. Ind. Robot. 2014, 51, 899–907. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, J.; Wang, H.; Chen, G.; Lai, X. Design of an electromagnetic prismatic joint with variable stiffness. Ind. Robot. 2017, 44, 222–230. [Google Scholar] [CrossRef]
- Pang, G.; Yang, G.; Heng, W.; Ye, Z.; Huang, X.; Yang, H.Y.; Pang, Z. CoboSkin: Soft robot skin with variable stiffness for safer human-robot collaboration. IEEE Trans. Ind. Electron. 2020, 68, 3303–3314. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, P.; Dong, D.; Zheng, J.; Chen, X.; Bai, L. Modeling and experimental evaluation of a pneumatic variable stiffness actuator. IEEE/ASME Trans. Mech. 2021, 27, 2462–2473. [Google Scholar] [CrossRef]
- Miskovic, L.; Dezman, M.; Petric, T. Pneumatic Quasi-Passive Variable Stiffness Mechanism for Energy Storage Applications. IEEE Robot. Autom. Lett. 2022, 7, 1705–1712. [Google Scholar] [CrossRef]
- Liao, T.; Kalairaj, M.S.; Cai, C.J.; Tse, Z.T.H.; Ren, H. Fully-Printable Soft Actuator with Variable Stiffness by Phase Transition and Hydraulic Regulations. Actuators 2021, 10, 269. [Google Scholar] [CrossRef]
- Ju, I.; Yun, D. Hydraulic variable stiffness mechanism for swimming locomotion optimization of soft robotic fish. Ocean Eng. 2023, 286, 115551. [Google Scholar] [CrossRef]
- Heepe, L.; Gorb, S.N. Biologically inspired mushroom-shaped adhesive microstructures. Annu. Rev. Mater. Res. 2014, 44, 173–203. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Yang, Y.; Li, Y. Soft robotic grippers based on particle transmission. IEEE/ASME Trans. Mech. 2019, 24, 969–978. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Yang, Y.; Wei, Y. Passive particle jamming and its stiffening of soft robotic grippers. IEEE Trans. Robot. 2017, 33, 446–455. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Zhou, H.; Zhao, C.; Barimah, B.; Li, B.; Xiang, C.; Li, L.; Gou, X.; Luo, M. Inflatable Particle-Jammed Robotic Gripper Based on Integration of Positive Pressure and Partial Filling. Soft Robot. 2022, 9, 309–323. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Zhang, J.; Li, Y.; Hong, J.; Wang, M.Y. Electrostatic layer jamming variable stiffness for soft robotics. IEEE/ASME Trans. Mech. 2019, 24, 424–433. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, F.; Guo, J.; Liu, L.; Liu, Y.; Leng, J. On variable stiffness of flexible parallel electroadhesive structures. Smart Mater. Struct. 2023, 32, 055004. [Google Scholar] [CrossRef]
- Farid, M.I.; Wu, W.; Guiwei, L.; Yu, Z. Research on imminent enlargements of smart materials and structures towards novel 4D printing (4DP: SMs-SSs). Int. J. Adv. Manuf. Technol. 2023, 126, 2803–2823. [Google Scholar] [CrossRef]
- Sreekumar, M.; Nagarajan, T.; Singaperumal, M. Kinetostatic Analysis of a Spatial Compliant Mechanism Actuated by Three Shape Memory Alloy Wires in Differential Form. Mech. Adv. Mater. Struct. 2010, 17, 225–236. [Google Scholar] [CrossRef]
- Sreesha, R.B.; Ladakhan, S.H.; Mudakavi, D.; Adinarayanappa, S.M. An experimental investigation on performance of NiTi-based shape memory alloy 4D printed actuators for bending application. Int. J. Adv. Manuf. Technol. 2022, 122, 4421–4436. [Google Scholar] [CrossRef]
- Cheng, Q.; Guo, N.; Fu, Y.; Zhang, D.; Zhang, S.; Zhang, X.; Chen, H.; Wang, L.; He, J. Study on preparation and stiffness of NiTi shape memory alloy/2A12 aluminum alloy laminated structure. Int. J. Adv. Manuf. Technol. 2022, 122, 4179–4189. [Google Scholar] [CrossRef]
- Munteanu, L.; Munteanu, A.; Sedlacik, M. Electrorheological fluids: A living review. Prog. Mater. Sci. 2025, 151, 101421. [Google Scholar] [CrossRef]
- Kitano, S.; Komatsuzaki, T.; Suzuki, I.; Nogawa, M.; Naito, H.; Tanaka, S. Development of a Rigidity Tunable Flexible Joint Using Magneto-Rheological Compounds—Toward a Multijoint Manipulator for Laparoscopic Surgery. Front. Robot. AI 2020, 7, 59. [Google Scholar] [CrossRef]
- Chattaraj, N.; Ananthasuresh, G.K.; Ganguli, R. Design of a distributed compliant mechanism using spring-lever model and topology optimization for piezoelectrically actuated flapping wings. Mech. Adv. Mater. Struct. 2019, 28, 118–126. [Google Scholar] [CrossRef]
- Zappino, E.; Carrera, E. Advanced modeling of embedded piezo-electric transducers for the health-monitoring of layered structures. Int. J. Smart. Nano Mater. 2020, 11, 325–342. [Google Scholar] [CrossRef]
- Prabhu, P.; Rao, M. Investigations on piezo actuator-based non-resonant type workpiece vibratory system for vibration-assisted micro-milling. Int. J. Adv. Manuf. Technol. 2024, 134, 3397–3416. [Google Scholar] [CrossRef]
- Ling, M.; Wu, S.; Luo, Z.; Chen, L.; Huang, T. An electromechanical dynamic stiffness matrix of piezoelectric stacks for sys-tematic design of micro/nano motion actuators. Smart Mater. Struct. 2023, 32, 115012. [Google Scholar] [CrossRef]
- Ma, H.W.; Yao, S.M.; Wang, L.Q.; Zhong, Z. Analysis of the displacement amplification ratio of bridge-type flexure hinge. Sens. Actuators A Phys. 2006, 132, 730–736. [Google Scholar] [CrossRef]
- Van Le, H.; Le, H.G.; Dao, T.-P. Kinetostatic and dynamic analysis for a new 2-DOF compliant mechanism for potential ap-plication in vibration-assisted polishing. Int. J. Adv. Manuf. Technol. 2024, 135, 2413–2436. [Google Scholar] [CrossRef]
- Xu, W.; King, T. Flexure hinges for piezoactuator displacement amplifiers: Flexibility, accuracy, and stress considerations. Precis. Eng. 1996, 19, 4–10. [Google Scholar] [CrossRef]
- Fan, W.; Zheng, Y.; Ma, J. A new type of low-stress flexible hinge displacement amplifying mechanism. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 443. [Google Scholar] [CrossRef]
- Bazaei, A.; Ettefagh, M.H.; Chen, Z. Displacement amplification and differential actuation in piezo driven nanopositioners. Mech. Syst. Signal Process 2021, 151, 107356. [Google Scholar] [CrossRef]














| Length | Width | Thickness | Maximum Displacement | Stiffness | Maximum Output Force | Resonance Frequency |
|---|---|---|---|---|---|---|
| 5 mm | 5 mm | 30 mm | 32 μm | 31.25 N/μm | 1000 N | 34 kHz |
| No. | Hinge Type | Parameters | Magnitude of Resistance Force to Deformation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fe = 5 N | Fe = 10 N | Fe = 20 N | ||||||||
| R or b | t1 or t2 | h1 or h2 | σVmax | λ1 | σVmax | λ1 | σVmax | λ1 | ||
| 1 | Circular | 0.35 mm | 0.4 mm | 1.5 mm | 115 MPa | 2.6 | 112 MPa | 2.3 | 99 MPa | 1.7 |
| 2 | Beam | 2.5 mm | 0.4 mm | 1.5 mm | 43 MPa | 2.8 | 49 MPa | 2.4 | 88 MPa | 1.5 |
| Measurement Number | 1 | 2 | 3 | Average |
|---|---|---|---|---|
| Length (mm) | 40.68 | 40.68 | 40.70 | 40.69 |
| Maximum diameter (mm) | 32.96 | 32.97 | 32.97 | 32.97 |
| Weight (g) | 43.42 | 43.43 | 43.44 | 43.43 |
| U (V) | Test 1 | Test 2 | ||||
|---|---|---|---|---|---|---|
| Δq (°) | T (N·m) | K (N·m/°) | Δq (°) | T (N·m) | K (N·m/°) | |
| 30 | 1.8 | 0.189 | 0.1050 | 0.36 | 0.136 | 0.3778 |
| 60 | 1.8 | 0.245 | 0.1361 | 0.36 | 0.142 | 0.3944 |
| 90 | 1.8 | 0.261 | 0.1450 | 0.36 | 0.152 | 0.4222 |
| 120 | 1.8 | 0.264 | 0.1467 | 0.36 | 0.176 | 0.4889 |
| 150 | 1.8 | 0.328 | 0.1822 | 0.36 | 0.179 | 0.4972 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yang, Y.; Ma, X.; Chen, C.; Qin, T.; Yue, H.; Ma, S. A Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint. Materials 2025, 18, 3289. https://doi.org/10.3390/ma18143289
Lu Y, Yang Y, Ma X, Chen C, Qin T, Yue H, Ma S. A Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint. Materials. 2025; 18(14):3289. https://doi.org/10.3390/ma18143289
Chicago/Turabian StyleLu, Yifan, Yifei Yang, Xiangyu Ma, Ce Chen, Tong Qin, Honghao Yue, and Siqi Ma. 2025. "A Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint" Materials 18, no. 14: 3289. https://doi.org/10.3390/ma18143289
APA StyleLu, Y., Yang, Y., Ma, X., Chen, C., Qin, T., Yue, H., & Ma, S. (2025). A Piezoelectric-Actuated Variable Stiffness Miniature Rotary Joint. Materials, 18(14), 3289. https://doi.org/10.3390/ma18143289







