Experimental Study on Mechanical Properties of European Oak and Norway Spruce Clear Wood
Abstract
1. Introduction
2. Literature Review
| Ref. | Species | [kg/m3] | Geometry W × T × L [mm3] | Moisture Content [%] | N. per Dir. [L, R, T] | Output |
|---|---|---|---|---|---|---|
| Poulsen et al. | Picea abies | 410 | Prisms | 12 | (NS, -, -) | Typical -d curves, |
| (1997) [18] | (Norway spruce) | (14 × 14 × 50) | failure mode | |||
| Reiterer et al. | Picea abies | 400–430 | Prisms | 12–13 | (10, 10, -) | Typical - curves, |
| (2001) [20] | (Norway spruce) | (10 × 10 × 20) | failure mode | |||
| Gindl and Teischinger | Picea abies | 400 | Prisms | 12 | (47, -, -) | Strength vs. density |
| (2002) [7] | (Norway spruce) | (12 × 12 × 6) | ||||
| Franke | Picea abies | 415 | Cubes | 9.9 | (5, 3, 3) | - curves, |
| (2008) [10] | (Norway spruce) | (40 × 40 × 40) | Strength, E-modulus | |||
| Zhong et al. (2014) [26] | Picea abies (Norway spruce) | 413 | Cuboids (20 × 20 × 30) | 12.7 | (3, 5, 4) | - curves, failure mode |
| Zauner and Niemz | Picea abies | 352–475 | Dog-bone | EMC | (8-12, -, -) | - curves, strength |
| (2014) [17] | (Norway spruce) | (different sizes) | ||||
| Aicher et al. | Picea abies | 440 | Prisms | 13.9 | (42, -, -) | Strength vs. MC, |
| (2016) [23] | (Norway spruce) | (20 × 20 × 120) | typical - curves | |||
| Prisms | (42, -, -) | |||||
| (30 × 30 × 60) | ||||||
| Bieniasz et al. | Picea abies | 422 | Prisms | 12 | (NS, -, -) | Strength, E-modulus |
| (2017) [8] | (Norway spruce) | (20 × 20 × 30) | ||||
| Akter and Bader | Picea abies | 499 | Dog-bone | 12 | (-, 2, 2) | - curves |
| (2020) [24] | (Norway spruce) | (50 × 60 × 20) | ||||
| 492 | Quadratic | (-, 2, 2) | ||||
| (50 × 50 × 20) | ||||||
| Šmídová et al. (2022) [11] | Picea abies (Norway spruce) | 463 | Prisms (45 × 70 × 90) | 8 | (5, -, -) | L-d curves, failure mode |
| Jakob and G.-Altmutter | Picea abies | 470 | Prisms | 10 | (-, 5, 5) | - curves |
| (2023) [25] | (Norway spruce) | (15 × 15 × 6) | ||||
| Li et al. | Picea abies | - | Prisms | 12 | (20, -, -) | L-d curves, strength |
| (2024) [16] | (Norway spruce) | (40 × 65 × DS) | failure mode |
| Ref. | Species | [kg/m3] | Geometry W × T × L [mm3] | Moisture Content [%] | N. per Dir. [L, R, T] | Output |
|---|---|---|---|---|---|---|
| Poulsen | Picea abies | - | Dog-bone | EMC | (-, -, 12) | - curves |
| (1998) [19] | (Norway spruce) | (20 × 20 × 20) | ||||
| Yoshihara and Ohta (2000) [9] | Picea sichtensis (Sitka spruce) | - | Dog-bone (2 × 10 × 140) | EMC | (5, 5, -) | Strength vs. off-axis angle |
| Dill-Langer et al. | Picea abies | 500 | Dog-bone | 12 | (-, 4, 5) | Typical - curves, |
| (2002) [32] | (Norway spruce) | (5 × 10 × 60) | failure mode | |||
| Miyauchi and Murata | Picea sp. | 552 | Dog-bone | 10.4 | (-, 22, -) | Strength, failure mode, |
| (2007) [12] | (Spruce) | (10 × 20 × 150) | typical - curves | |||
| Keunecke et al. | Picea abies | 470 | Dog-bone | EMC | (15, 15, 15) | E-modulus, |
| (2008) [14] | (Norway spruce) | (14 × 14 × 95) | Poisson’s ratio | |||
| Franke | Picea abies | 484 | Dog-bone | 12.4 | (40, -, -) | - curves, |
| (2008) [10] | (Norway spruce) | (2 × 20 × 475) | E-modulus | |||
| Kumpenza et al. | Picea abies | 465 | Dog-bone | 12 | (20, 24, 23) | E-modulus, |
| (2018) [15] | (Norway spruce) | (20 × 6 × 120) | Poisson’s ratio | |||
| Šmídová et al. (2022) [11] | Picea abies (Norway spruce) | 463 | Prisms (4 × 25 × 250) | 8 | (10, -, -) | L-d curves, failure mode |
3. Materials and Methods
4. Results and Discussion
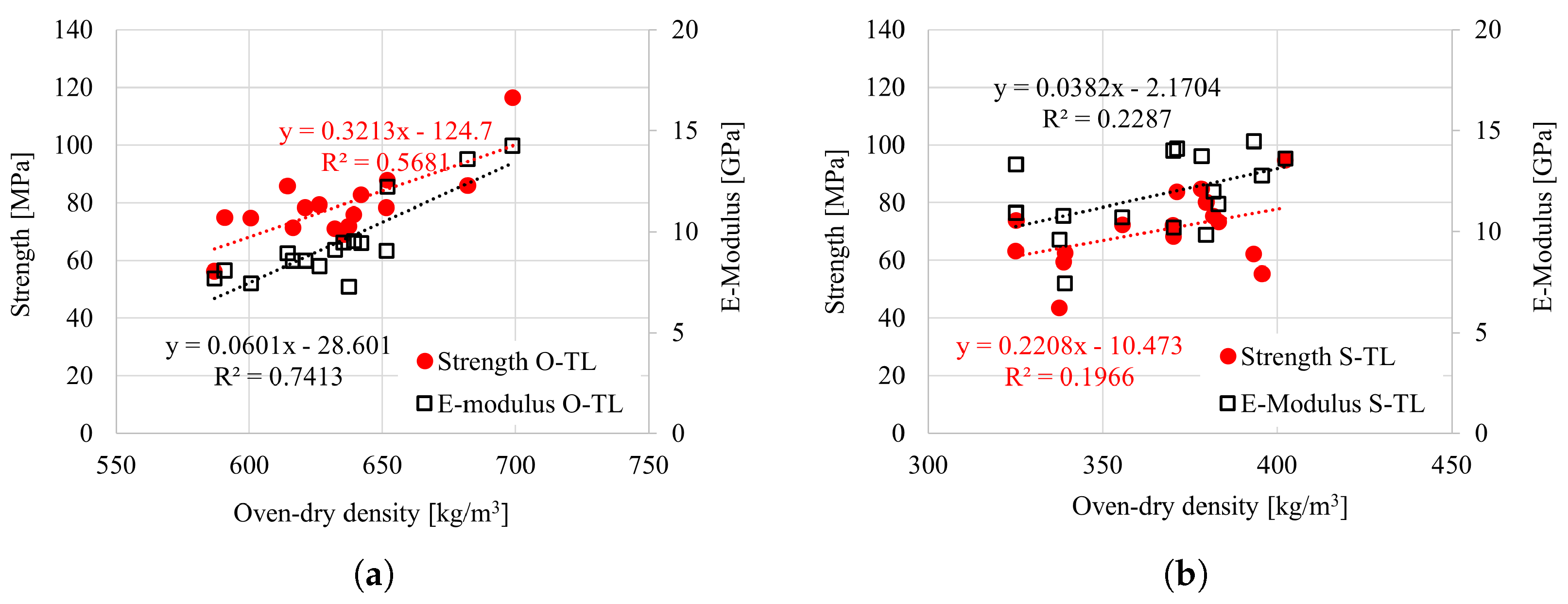
4.1. Uniaxial Tensile Test in the Longitudinal Direction
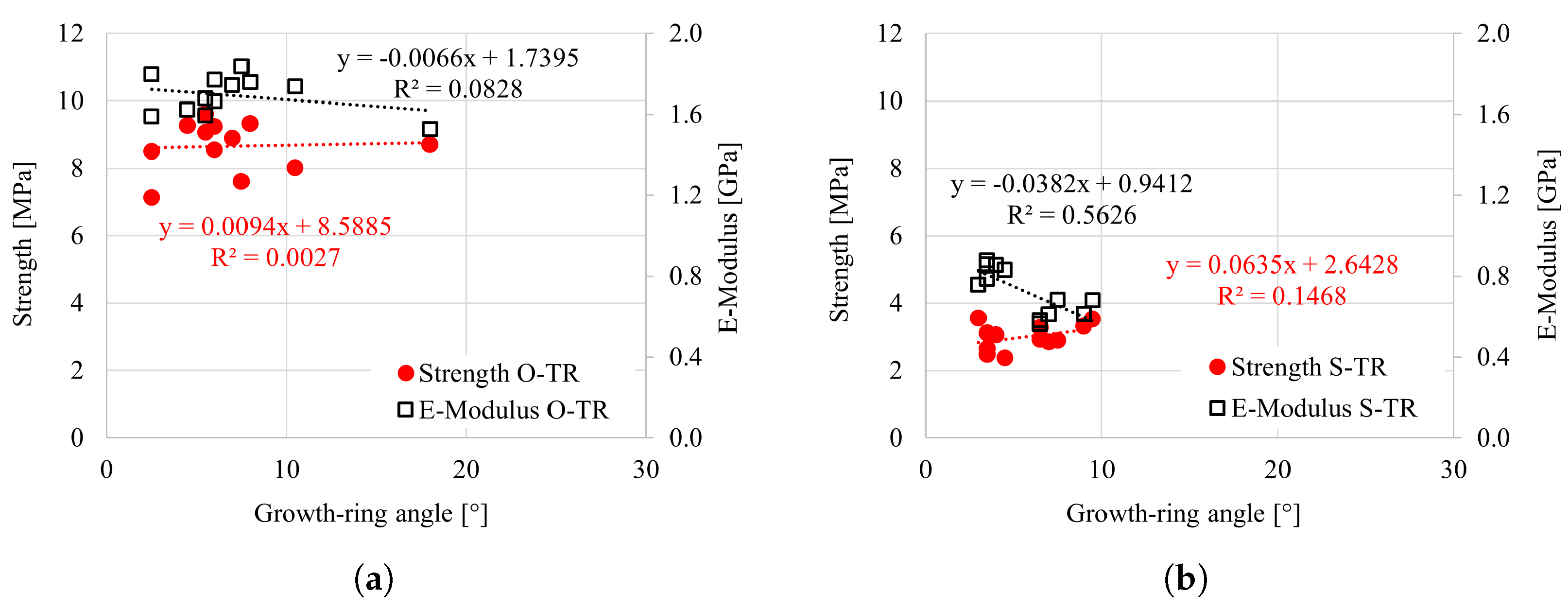
4.2. Uniaxial Tensile Test in the Radial Direction
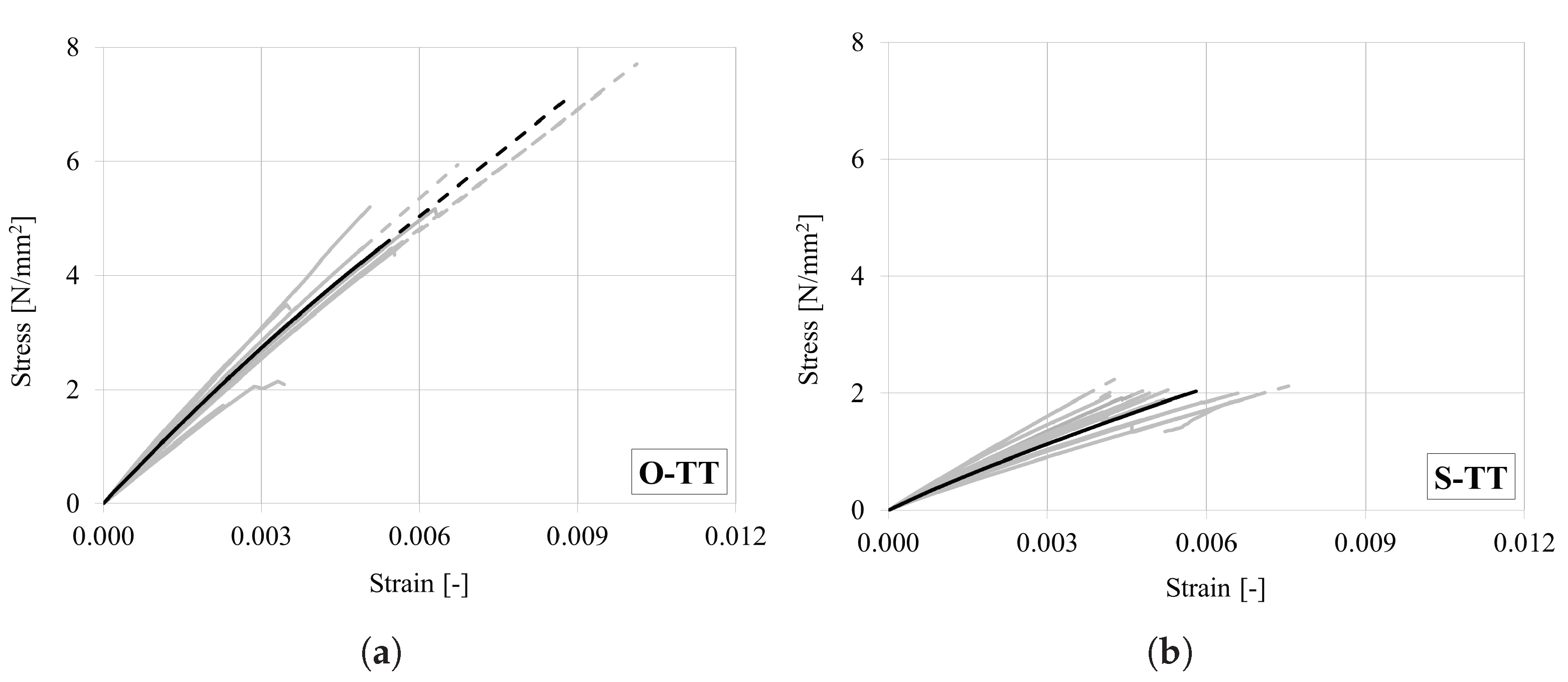
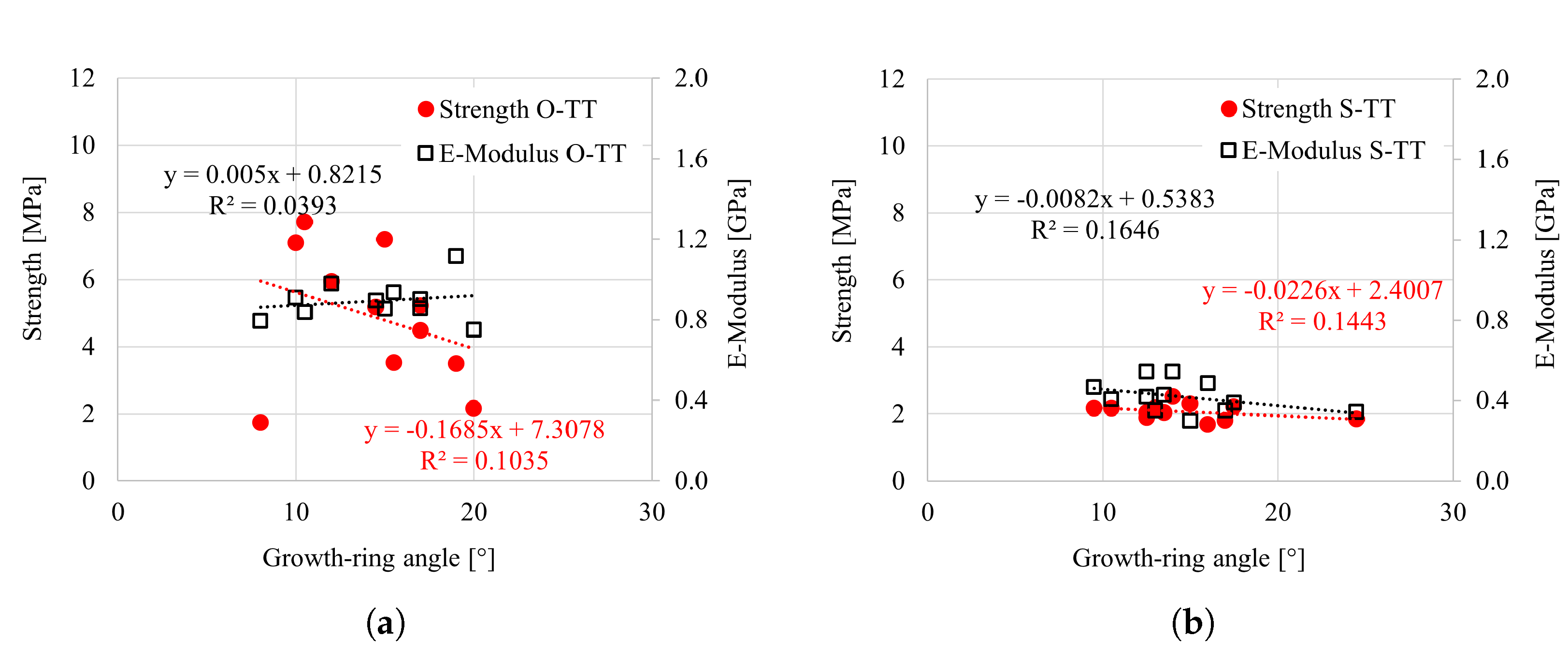
4.3. Uniaxial Tensile Test in the Tangential Direction
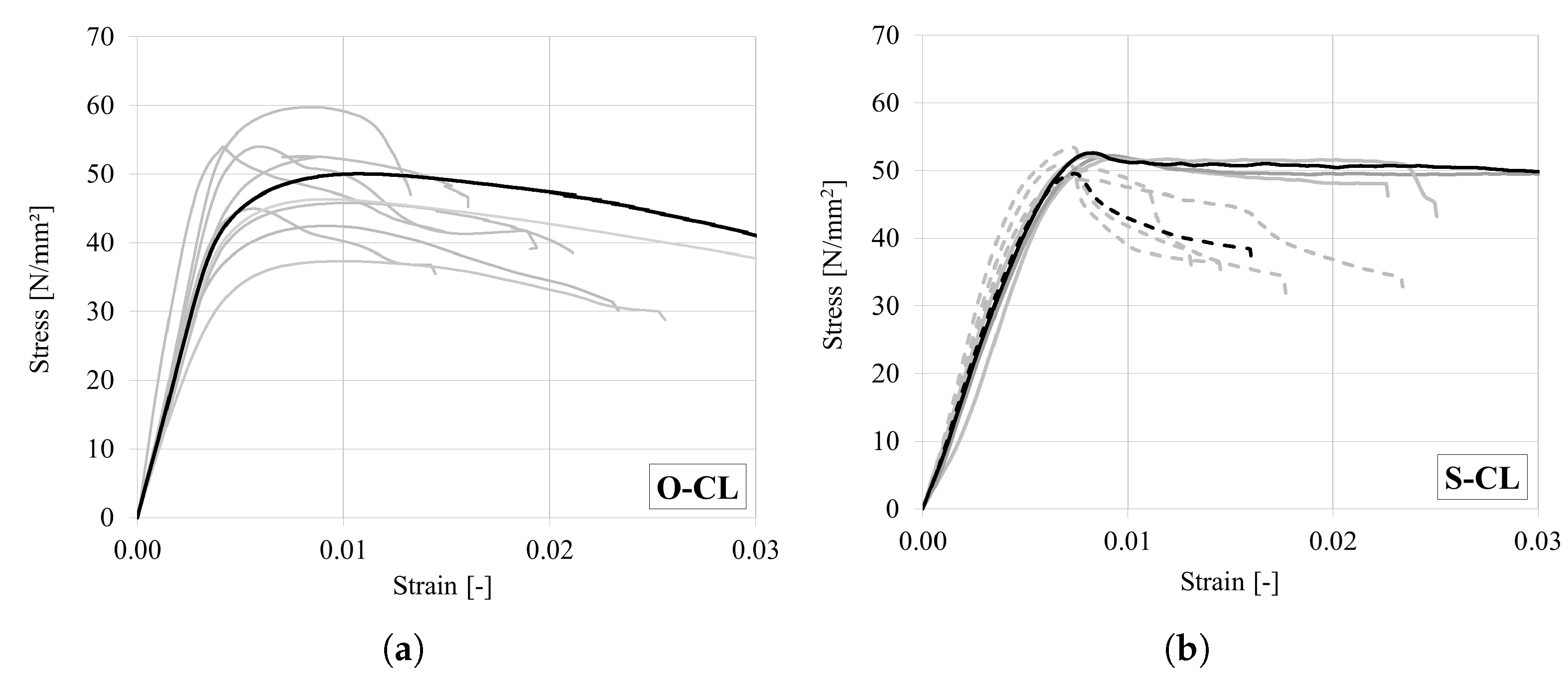
4.4. Uniaxial Compressive Test in the Longitudinal Direction
4.5. Uniaxial Compressive Test in the Radial Direction
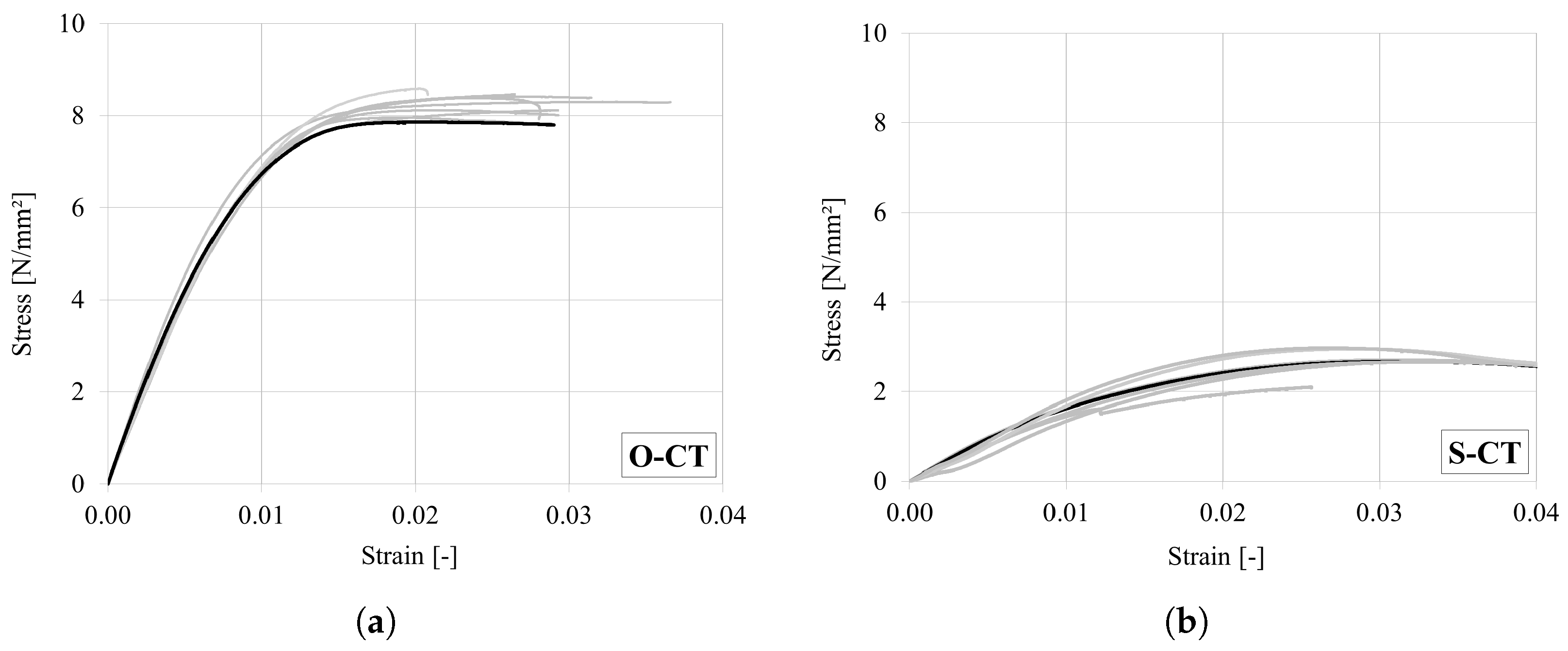
4.6. Uniaxial Compressive Test in the Tangential Direction
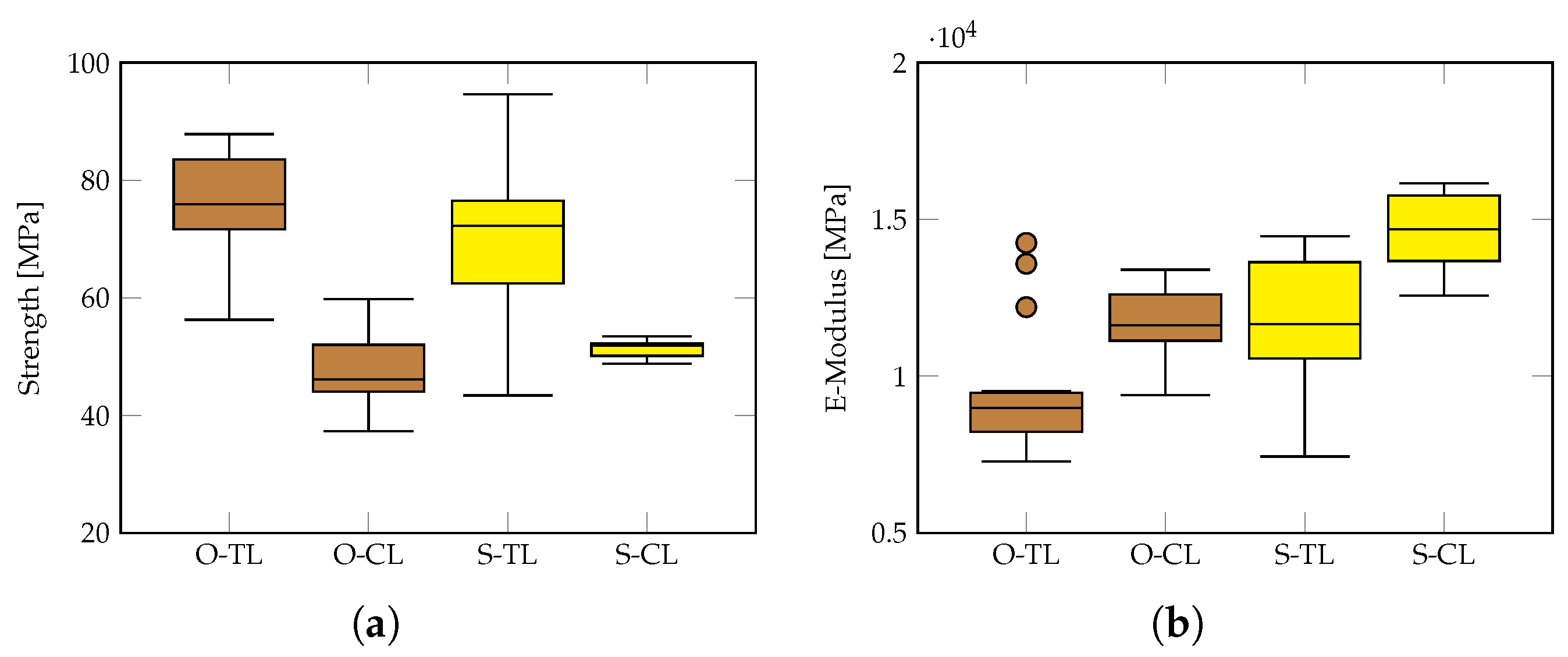
4.7. Influence of Relevant Parameters on the Strength and Elasticity Modulus
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niemz, P.; Teischinger, A.; Sandberg, D. Springer Handbook of Wood Science and Technology; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Kollmann, F.F.P.; Côté, W.A. Principles of Wood Science and Technology, Part I-Solid Wood; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar] [CrossRef]
- Bodig, J.; Jayne, B. Mechanics of Wood and Wood Composites; Krieger Publishing Company: Malabar, FL, USA, 1993. [Google Scholar]
- Repola, J.; Saranpää, P.; Tarvainen, V. Kuusi- ja mäntysahatavaran värinmuutokset kuivauksessa; Metsäntutkimuslaitoksen tiedonantoja, Metsäntutkimuslaitos: Vantaa, Finland, 2001. [Google Scholar]
- Sonderegger, W.; Mandallaz, D.; Niemz, P. An investigation of the influence of selected factors on the properties of spruce wood. Wood Sci. Technol. 2008, 42, 281–298. [Google Scholar] [CrossRef]
- Fajdiga, G.; Rajh, D.; Nečemer, B.; Glodež, S.; Šraml, M. Experimental and Numerical Determination of the Mechanical Properties of Spruce Wood. Forests 2019, 10, 1140. [Google Scholar] [CrossRef]
- Gindl, W.; Teischinger, A. Axial compression strength of Norway spruce related to structural variability and lignin content. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1623–1628. [Google Scholar] [CrossRef]
- Bieniasz, A.; Lachowicz, H.; Buraczyk, W.; Moskalik, T. Technical quality of wood of 35 years old Norway spruce (Picea abies L. H. Karst) growing on experimental plot in the Rogów Forest Experimental Station. Sylwan 2017, 161, 851–860. [Google Scholar] [CrossRef]
- Yoshihara, H.; Ohta, M. Estimation of the shear strength of wood by uniaxial-tension tests of off-axis specimens. J. Wood Sci. 2000, 46, 159–163. [Google Scholar] [CrossRef]
- Franke, S. Zur Beschreibung des Tragverhaltens von Holz unter Verwendung eines Photogrammetrischen Messsytems. Ph.D. Thesis, Fakultät Bauingenieurwesen, Bauhaus-Universität Weimar, Weimar, Germany, 2008. [Google Scholar]
- Šmídová, E.; Kabele, P.; Šejnoha, M. Material parameters of European spruce for tensile–shear fracture modeling. Eng. Struct. 2022, 270, 114534. [Google Scholar] [CrossRef]
- Miyauchi, K.; Murata, K. Strain-softening behavior of wood under tension perpendicular to the grain. J. Wood Sci. 2007, 53, 463–469. [Google Scholar] [CrossRef]
- Widehammar, S. Stress-strain relationships for spruce wood: Influence of strain rate, moisture content and loading direction. Exp. Mech. 2004, 44, 44–48. [Google Scholar] [CrossRef]
- Keunecke, D.; Hering, S.; Niemz, P. Three-dimensional elastic behaviour of common yew and Norway spruce. Wood Sci. Technol. 2008, 42, 633–647. [Google Scholar] [CrossRef]
- Kumpenza, C.; Matz, P.; Halbauer, P.; Grabner, M.; Steiner, G.; Feist, F.; Müller, U. Measuring Poisson’s ratio: Mechanical characterization of spruce wood by means of non-contact optical gauging techniques. Wood Sci. Technol. 2018, 52, 1451–1471. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J.; Xu, G.; Li, W. Compression test and size effect study of defective wood. Wood Mater. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Zauner, M.; Niemz, P. Uniaxial compression of rotationally symmetric Norway spruce samples: Surface deformation and size effect. Wood Sci. Technol. 2014, 48, 1019–1032. [Google Scholar] [CrossRef]
- Poulsen, J.; Moran, P.; Shih, C.; Byskov, E. Kink band initiation and band broadening in clear wood under compressive loading. Mech. Mater. 1997, 25, 67–77. [Google Scholar] [CrossRef]
- Poulsen, J.S. Compression in Clear Wood. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 1998. [Google Scholar]
- Reiterer, A.; Stanzl-Tschegg, S.E. Compressive behaviour of softwood under uniaxial loading at different orientations to the grain. Mech. Mater. 2001, 33, 705–715. [Google Scholar] [CrossRef]
- Tabarsa, T.; Chui, Y.H. Characterizing microscopic behavior of wood under transverse compression. Part II. Effect of species and loading directions. Wood Fiber Sci. 2001, 33, 223–232. [Google Scholar]
- Gindl, W. Comparing Mechanical Properties of Normal and Compression Wood in Norway Spruce: The Role of Lignin in Compression Parallel to the Grain. Holzforschung 2002, 56, 395–401. [Google Scholar] [CrossRef]
- Aicher, S.; Stapf, G. Compressive strength parallel to the fiber of spruce with high moisture content. Eur. J. Wood Wood Prod. 2016, 74, 527–542. [Google Scholar] [CrossRef]
- Akter, S.T.; Bader, T.K. Experimental assessment of failure criteria for the interaction of normal stress perpendicular to the grain with rolling shear stress in Norway spruce clear wood. Eur. J. Wood Wood Prod. 2020, 78, 1105–1123. [Google Scholar] [CrossRef]
- Jakob, M.; Gindl-Altmutter, W. The effect of partial delignification on the stress–strain relationship in transverse compression. J. Mater. Sci. 2023, 58, 1071–1085. [Google Scholar] [CrossRef]
- Zhong, W.z.; Rusinek, A.; Jankowiak, T.; Huang, X.; Abed, F. Experimental and Numerical Investigation on Compression Orthotropic Properties of Spruce Wood in Axial and Transverse Loading Directions. Eng. Trans. 2014, 62, 381–401. [Google Scholar]
- Ljungdahl, J.; Berglund, L.A.; Burman, M. Transverse anisotropy of compressive failure in European oak—A digital speckle photography study. Holzforschung 2006, 60, 190–195. [Google Scholar] [CrossRef]
- Gustafsson, S. The strength properties of Swedish oak and beech. Drewno 2010, 53, 67–83. [Google Scholar]
- Wolkmer, T.; Lorenz, T.; Hass, P.; Niemz, O. Influence of heat pressure steaming (HPS) on the mechanical and physical properties of common oak wood. Eur. J. Wood Wood Prod. 2014, 72, 249–259. [Google Scholar] [CrossRef]
- Ozyhar, T.; Mohl, L.; Hering, S.; Hass, P.; Zeindler, L.; Ackermann, R.; Niemz, P. Orthotropic hygric and mechanical material properties of oak wood. Wood Mater. Sci. Eng. 2016, 11, 36–45. [Google Scholar] [CrossRef]
- Ümit, B.; As, N.; Dündar, T.; Korkmaz, O. Micro-Mechanical Properties of Oak Wood and Comparison with Standard-Sized Samples. Maderas. Cienc. Tecnol. 2017, 19, 481–494. [Google Scholar] [CrossRef]
- Dill-Langer, G.; Lütze, S.; Aicher, S. Microfracture in wood monitored by confocal laser scanning microscopy. Wood Sci. Technol. 2002, 36, 487–499. [Google Scholar] [CrossRef]
- DIN 52377; Prüfung von Sperrholz—Bestimmung des Zug-Elastizitätsmodulus und der Zugfestigkeit. Deutsches Institute für Normung e.V.: Berlin, Germany, 1978.
- DIN EN 408; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. Deutsches Institut für Normung e.V.: Berlin, Germany, 2012.
- DIN EN 13183-1; Feuchtegehalt eines Stückes Schnittholz Teil 1: Bestimmung durch Darrverfahren. Deutsches Institute für Normung e.V.: Berlin, Germany, 2002.
- DIN 52188; Prüfung von Holz—Bestimmung der Zugfestigkeit parallel zur Faser. Deutsches Institute für Normung e.V.: Berlin, Germany, 1979.
- ISO 13061-17; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens. Part 17: Determination of Ultimate Stress in Compression Parallel to Grain. ISO: Geneva, Switzerland, 2017.
- DIN 52185; Testing of Wood; Compression Test Parallel to Grain. Deutsches Institute für Normung e.V.: Berlin, Germany, 1976.
- Ozyhar, T.; Hering, S.; Niemz, P. Moisture-dependent elastic and strength anisotropy of European beech wood in tension. J. Mater. Sci. 2012, 47, 6141–6150. [Google Scholar] [CrossRef]
- DIN 68364; Kennwerte von Holzarten—Festigkeit, Elastizität, Resistenz. Deutsches Institute für Normung e.V.: Berlin, Germany, 2003.
- Al-musawi, H.; Matz, P.; Jakob, M.; Halbauer, P.; Krenke, T.; Müller, U. Stress–strain behaviour of wood in compression: Experimental and analytical investigations. Results Eng. 2024, 24, 103616. [Google Scholar] [CrossRef]
- Gambarelli, S.; Ožbolt, J. 3D hygro-mechanical meso-scale model for wood. Constr. Build. Mater. 2021, 311, 125283. [Google Scholar] [CrossRef]
- Fararoni Platas, R.N.; Gambarelli, S.; Bosnjak, J. Experimental and numerical investigation of a scaled timber composite (softwood and hardwood) column-to-slab connection. Constr. Build. Mater. 2025, 472, 140719. [Google Scholar] [CrossRef]
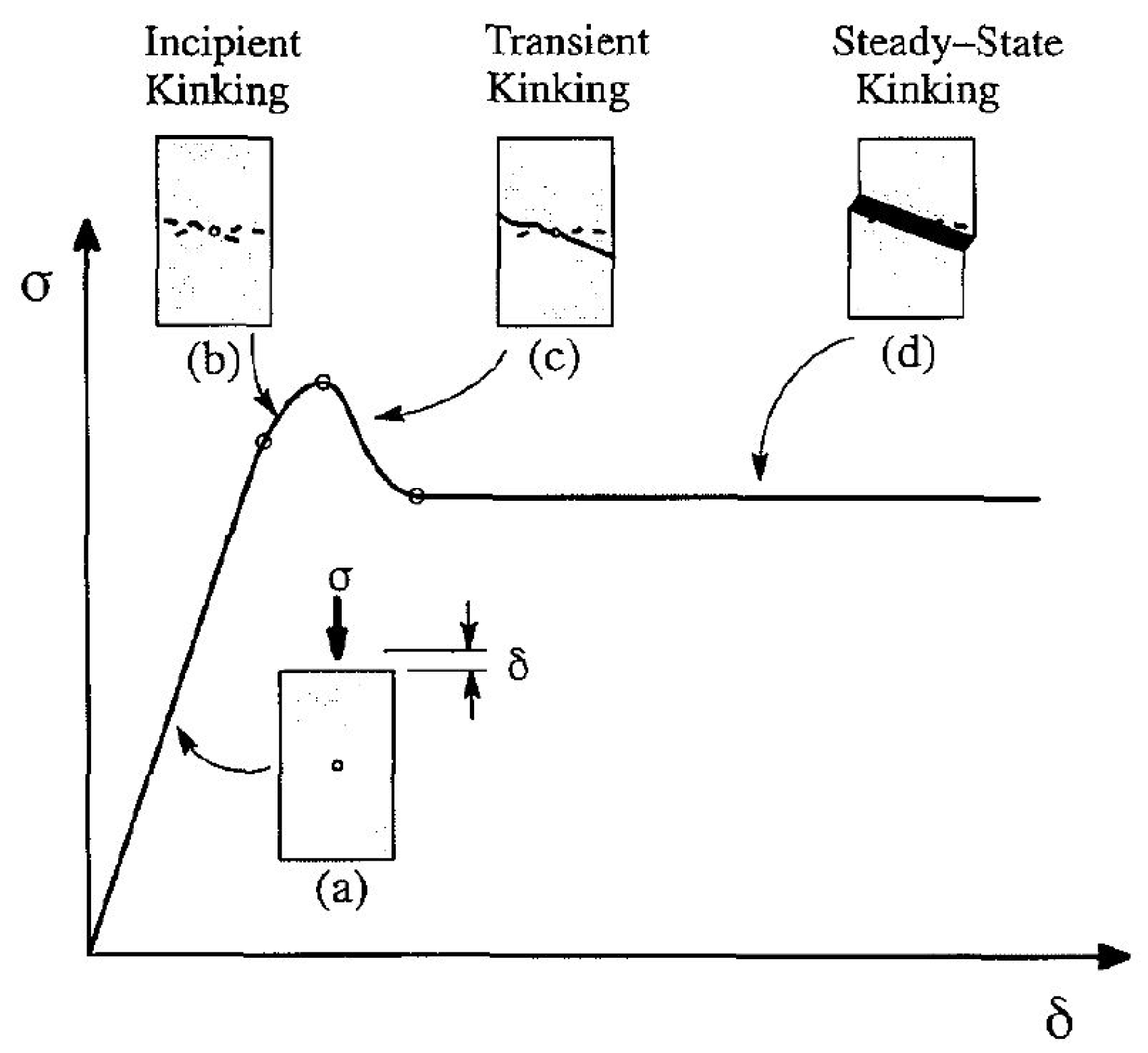



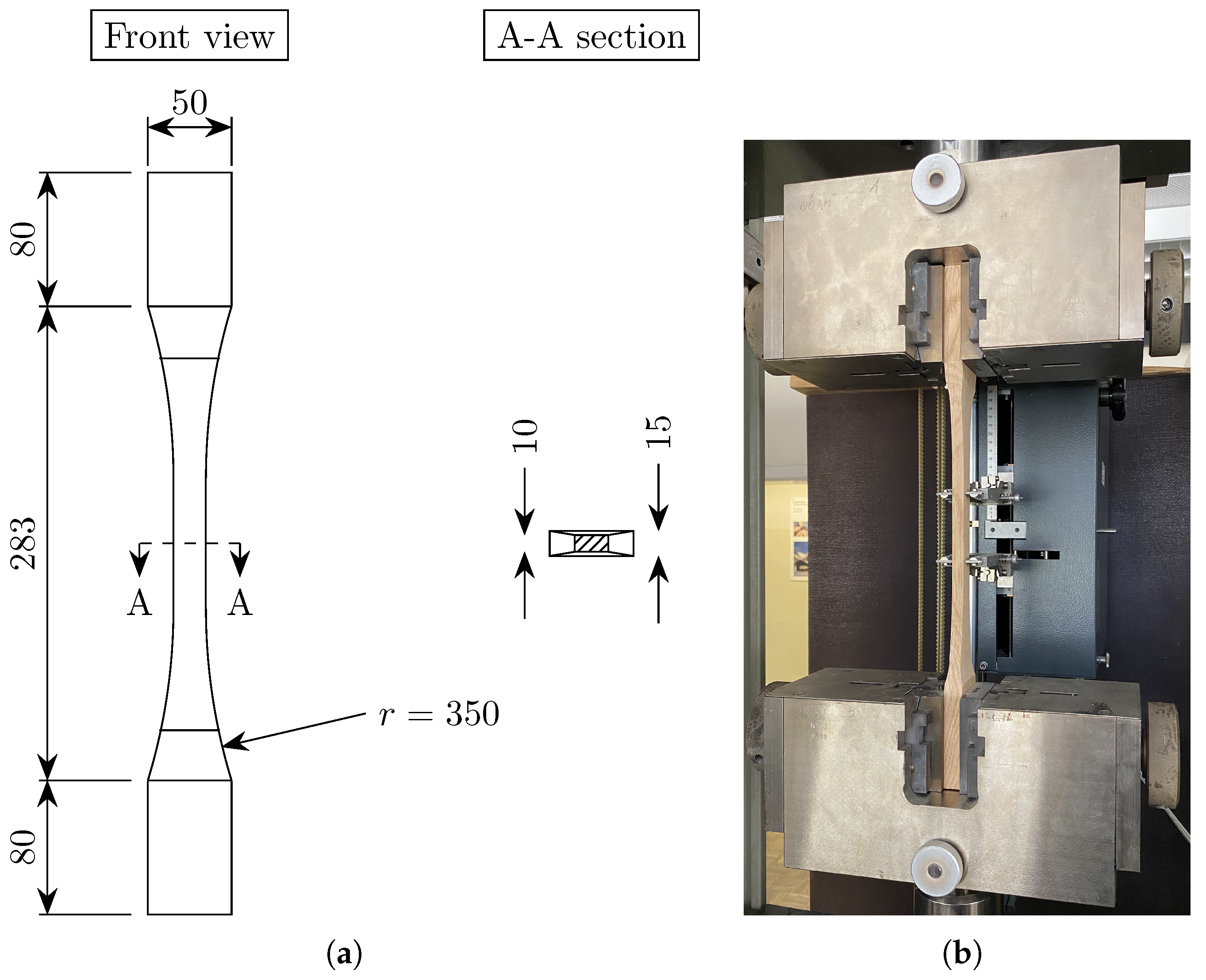
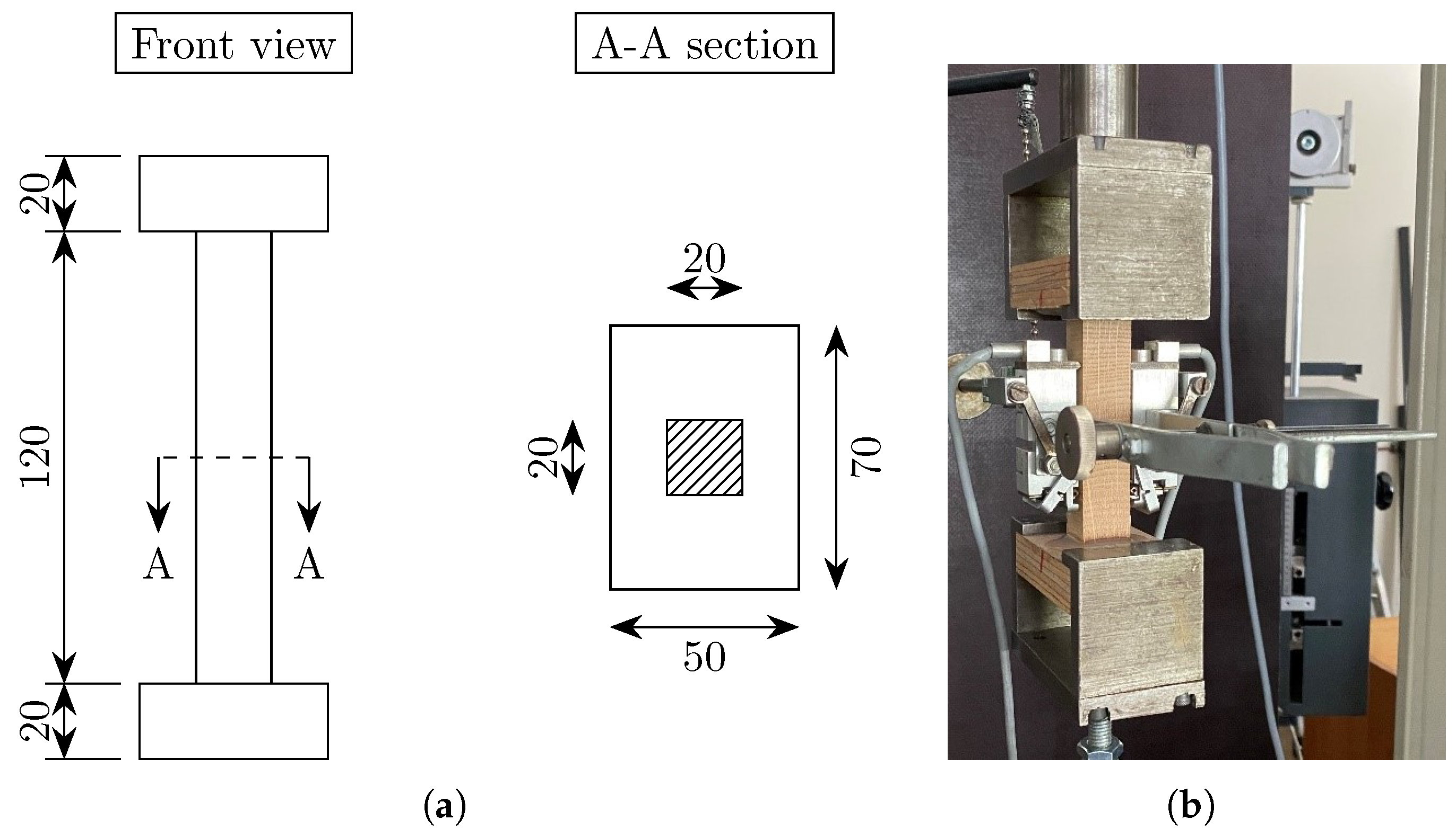










| Ref. | Species | [kg/m3] | Geometry W × T × L [mm3] | Moisture Content [%] | Load | N. per Dir. [L, R, T] | Output |
|---|---|---|---|---|---|---|---|
| Ljungdahl et al. | Quercus robur | 777 | Prisms | 11.6 | UC | (5, 5, 5) | - curves, |
| (2006) [27] | (European oak) | (50–55% RH) | (10 × 10 × 25) | (50–55% RH) | failure mode | ||
| Gustafsson | Quercus robur | 719 | Prisms | 5.26 | UC | (10, -, -) | - curves |
| (2010) [28] | (European oak) | (15 × 15 × 45) | |||||
| - | Dog-bone | 5.5 | UT | (5, -, -) | - curves | ||
| (NS) | |||||||
| Volkmer et al. | Quercus robur | 620–670 | Prisms | 11.0 | UC | (10, 10, 10) | Strength, E-modulus, |
| (2014) [29] | (European oak) | (20 × 20 × 30) (L) | Poisson’s ratio | ||||
| (15 × 15 × 45) (R,T) | |||||||
| Dog-bone | 10.8 | UT | (10, 10, 10) | Strength, E-modulus, | |||
| (20 × 6 × 470) (L) | Poisson’s ratio | ||||||
| (14 × 14 × 95) (R,T) | |||||||
| Ozyhar et al. | Quercus robur | 612 | Prisms | 13.1 | UC | (13, 13, 13) | Strength, E-modulus, |
| (2016) [30] | (European oak) | (15 × 15 × 45) | Poisson’s ratio | ||||
| Büyüksarı et al. | Quercus petraea | - | Prisms | 12 | UC | (398, -, -) | Compressive strength |
| (2017) [31] | (Sessile oak) | (20 × 20 × 30) | |||||
| Dog-bone | UT | (309, -, -) | Tensile strength | ||||
| (15 × 50 × 400) |
| Test | Load | Abbreviation | Geometry | Number of Specimens | ||
|---|---|---|---|---|---|---|
| Direction | Spruce | Oak | [mm3] | Spruce | Oak | |
| Tension | L | S-TL | O-TL | dog-bone | 16 | 16 |
| () | ||||||
| R | S-TR | O-TR | Square prism | 12 | 12 | |
| () | ||||||
| T | S-TT | O-TT | Square prism | 12 | 11 | |
| () | ||||||
| Compression | L | S-CL | O-CL | Square prism | 9 | 10 |
| () | ||||||
| R | S-CR | O-CR | Square prism | 12 | 9 | |
| () | ||||||
| T | S-CT | O-CT | Square prism | 7 | 10 | |
| () | ||||||
| Abbreviation | (CoV) | GRW (CoV) | GRA (CoV) | MC |
|---|---|---|---|---|
| [kg/m3] ([%]) | [mm] ([%]) | [°] ([%]) | [%] | |
| S-TL | 408.3 (6.4) | 2.0 (22.1) | 39.4 (58.1) | 11.7 |
| S-TR | 422.7 (2.7) | 1.9 (20.8) | 5.7 (38.7) | 12.9 |
| S-TT | 437.3 (3.6) | 2.5 (14.4) | 14.6 (25.7) | 12.3 |
| S-CL | 444.5 (5.9) | 2.7 (9.4) | - | 13.1 |
| S-CR | 434.4 (0.9) | 2.6 (4.4) | 0.45 (1.3) | 13.1 |
| S-CT | 446.0 (0.9) | 2.5 (3.9) | 18.8 (11.8) | 13.4 |
| Abbreviation | (CoV) | GRW (CoV) | GRA (CoV) | MC |
|---|---|---|---|---|
| [kg/m3] ([%]) | [mm] ([%]) | [°] ([%]) | [%] | |
| O-TL | 707.5 (4.5) | 1.8 (13.3) | 67.4 (9.3) | 11.8 |
| O-TR | 698.5 (2.2) | 2.3 (7.3) | 7.0 (56.8) | 13.2 |
| O-TT | 690.1 (3.2) | 2.1 (5.1) | 14.5 (25.4) | 14.1 |
| O-CL | 727.9 (4.2) | 2.2 (6.6) | - | 13.6 |
| O-CR | 709.7 (2.6) | 2.0 (5.7) | 11.8 (25.4) | 13.6 |
| O-CT | 689.0 (3.3) | 2.1 (7.8) | 19.5 (17.2) | 13.6 |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
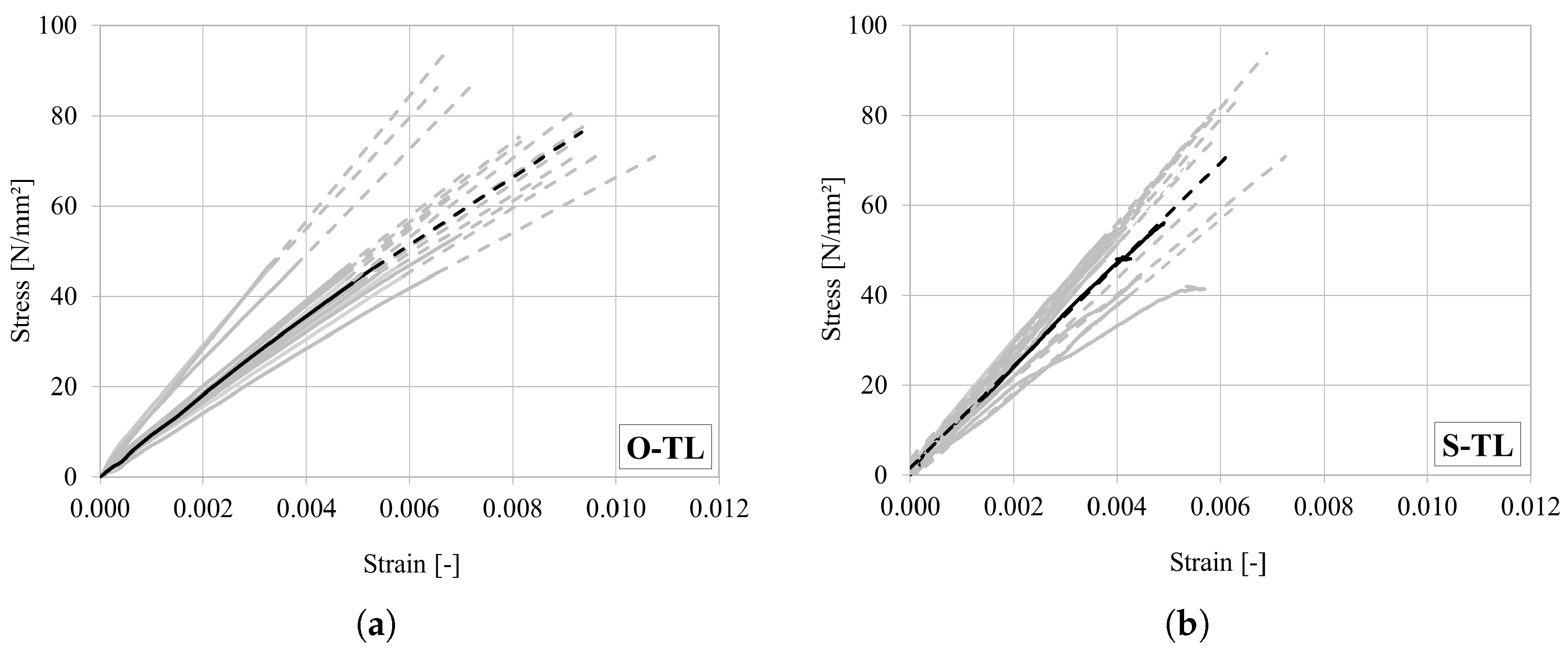
| O-TL | 10 | Brittle tension | 78.6 (15.7) | 9456.7 (21.3) |
| 4 | Splinter | |||
| 1 | Shear | |||
| 1 | Shear and tension | |||
| S-TL | 4 | Brittle tension | 70.3 (17.4) | 11,794.4 (16.6) |
| 11 | Splinter | |||
| - | Shear | |||
| 1 | Shear and tension |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
| O-TR | 12 | Brittle tension | 8.7 (8.3) | 1693.2 (5.4) |
| S-TR | 12 | Brittle tension | 3.0 (12.1) | 724.6 (15.4) |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
| O-TT | 11 | Brittle tension | 4.9 (39.5) | 893.4 (10.4) |
| S-TT | 12 | Brittle tension | 2.1 (10.8) | 418.5 (18.2) |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
| O-CL | 6 | Shearing | 49.7 (10.8) | 11,679.0 (9.0) |
| - | End rolling | |||
| S-CL | 5 | Shearing | 51.5 (2.7) | 14,422.0 (8.3) |
| 3 | End rolling |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
| O-CR | 9 | Cell buckling | 11.1 (7.0) | 1482.0 (8.8) |
| S-CR | 12 | Cell buckling | 3.2 (3.0) | 939.3 (16.2) |
| Test | N. Spec. | Failure Type | Strength (CoV) | Stiffness (CoV) |
|---|---|---|---|---|
| [MPa] ([%]) | [MPa] ([%]) | |||
| O-CT | 7 | Cell buckling | 8.2 (2.6) | 857.0 (5.7) |
| 3 | Shearing | |||
| S-CT | 7 | Cell buckling | 2.7 (9.9) | 370.8 (11.0) |
| - | Shearing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambarelli, S.; Bošnjak, J.; Fararoni Platas, R.N.; Jin, K. Experimental Study on Mechanical Properties of European Oak and Norway Spruce Clear Wood. Materials 2025, 18, 3257. https://doi.org/10.3390/ma18143257
Gambarelli S, Bošnjak J, Fararoni Platas RN, Jin K. Experimental Study on Mechanical Properties of European Oak and Norway Spruce Clear Wood. Materials. 2025; 18(14):3257. https://doi.org/10.3390/ma18143257
Chicago/Turabian StyleGambarelli, Serena, Josipa Bošnjak, Rey Noé Fararoni Platas, and Kexin Jin. 2025. "Experimental Study on Mechanical Properties of European Oak and Norway Spruce Clear Wood" Materials 18, no. 14: 3257. https://doi.org/10.3390/ma18143257
APA StyleGambarelli, S., Bošnjak, J., Fararoni Platas, R. N., & Jin, K. (2025). Experimental Study on Mechanical Properties of European Oak and Norway Spruce Clear Wood. Materials, 18(14), 3257. https://doi.org/10.3390/ma18143257






