A Sintering–Resting Strategy of Microwave Heating for Lithium Hydride Ceramic Based on Numerical Analysis of Thermal Effects
Abstract
1. Introduction
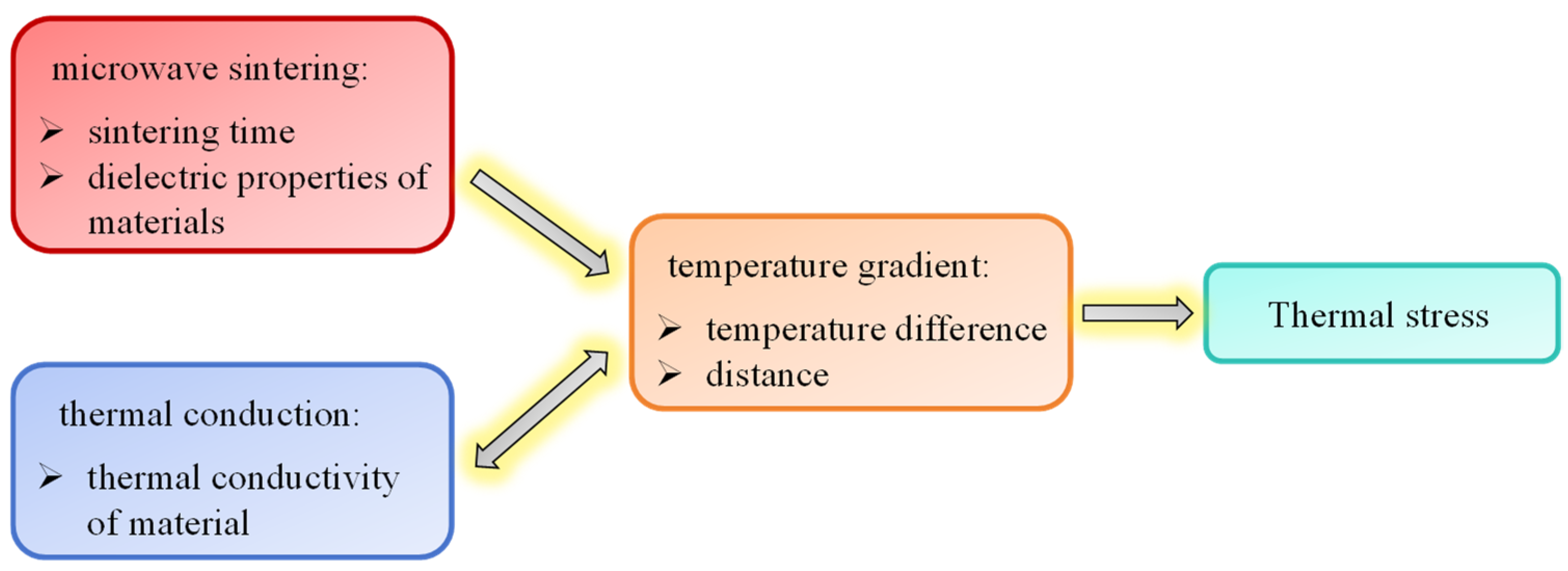
2. The Basic Equations of Electromagnetic–Thermal-Force Coupling in Microwave Sintering
2.1. The Basic Equations for Microwave Electromagnetic Field
2.2. The Basic Equation of Microwave Heating and Thermal Transfer
2.3. The Basic Equations for Thermal Stresses
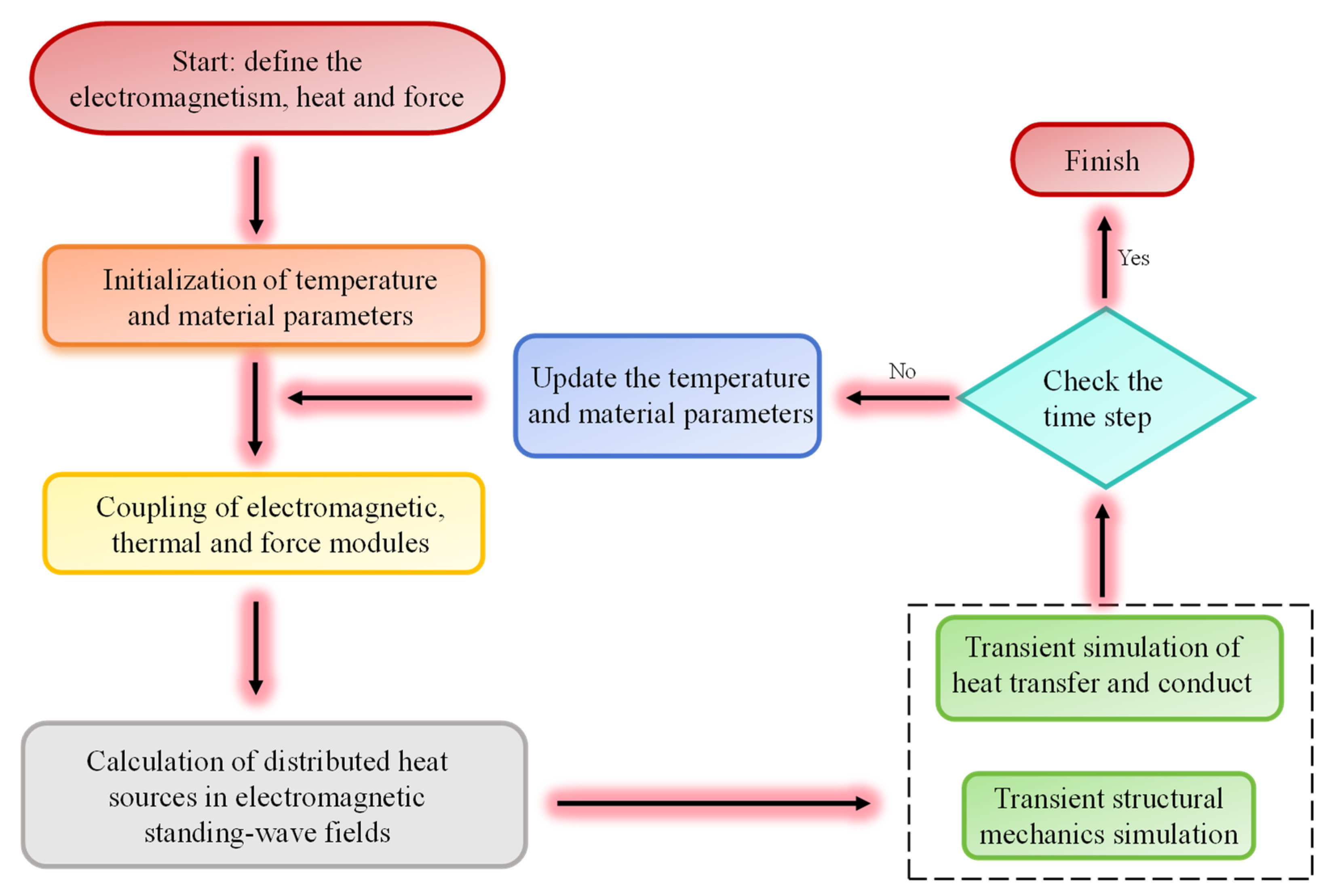
3. Numerical Modeling and the Simulation Method
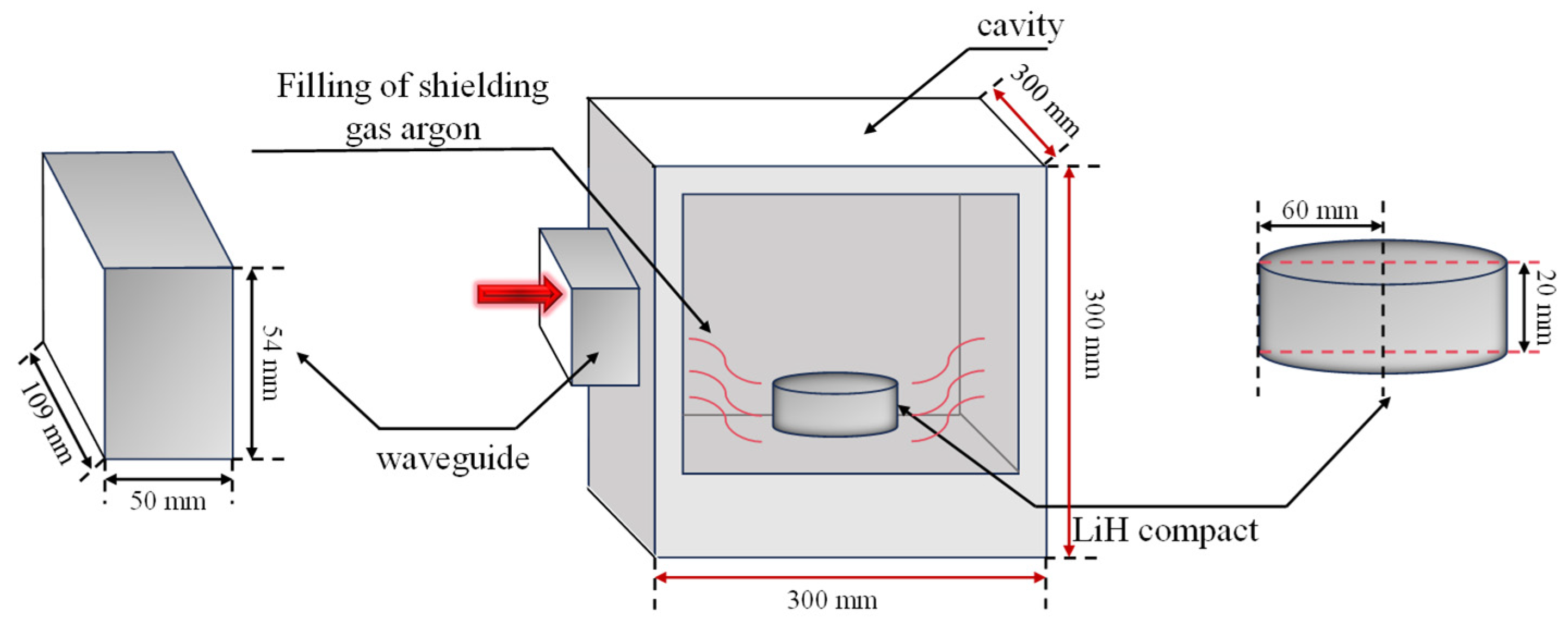
3.1. The Setup of the Microwave Oven Model
3.2. Material Properties Varied with Temperature
3.3. The Implicit Method in Modeling a Rotary Sample in Microwave Heating
4. Results and Discussion
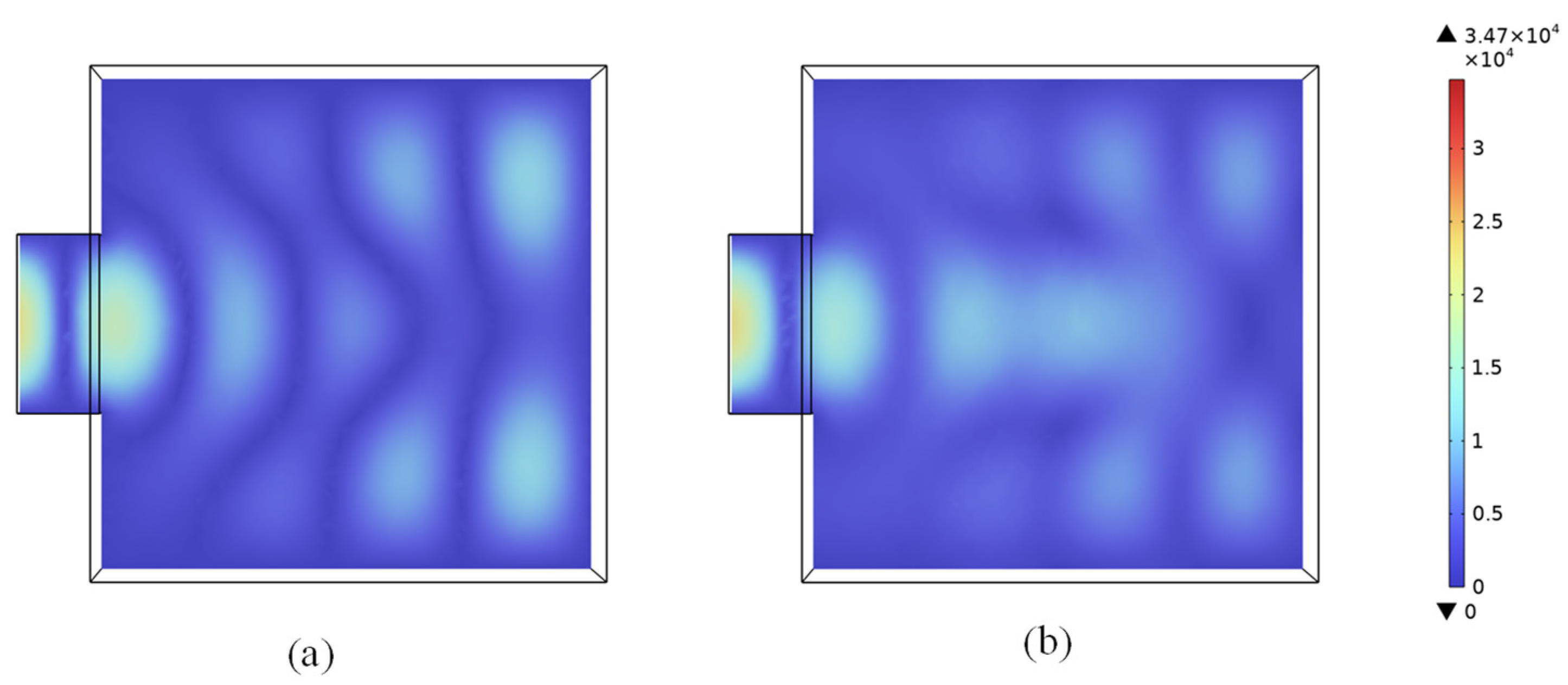
4.1. The Electromagnetic Field in the Microwave Cavity
4.2. Microwave Heating Effect of LiH Ceramics
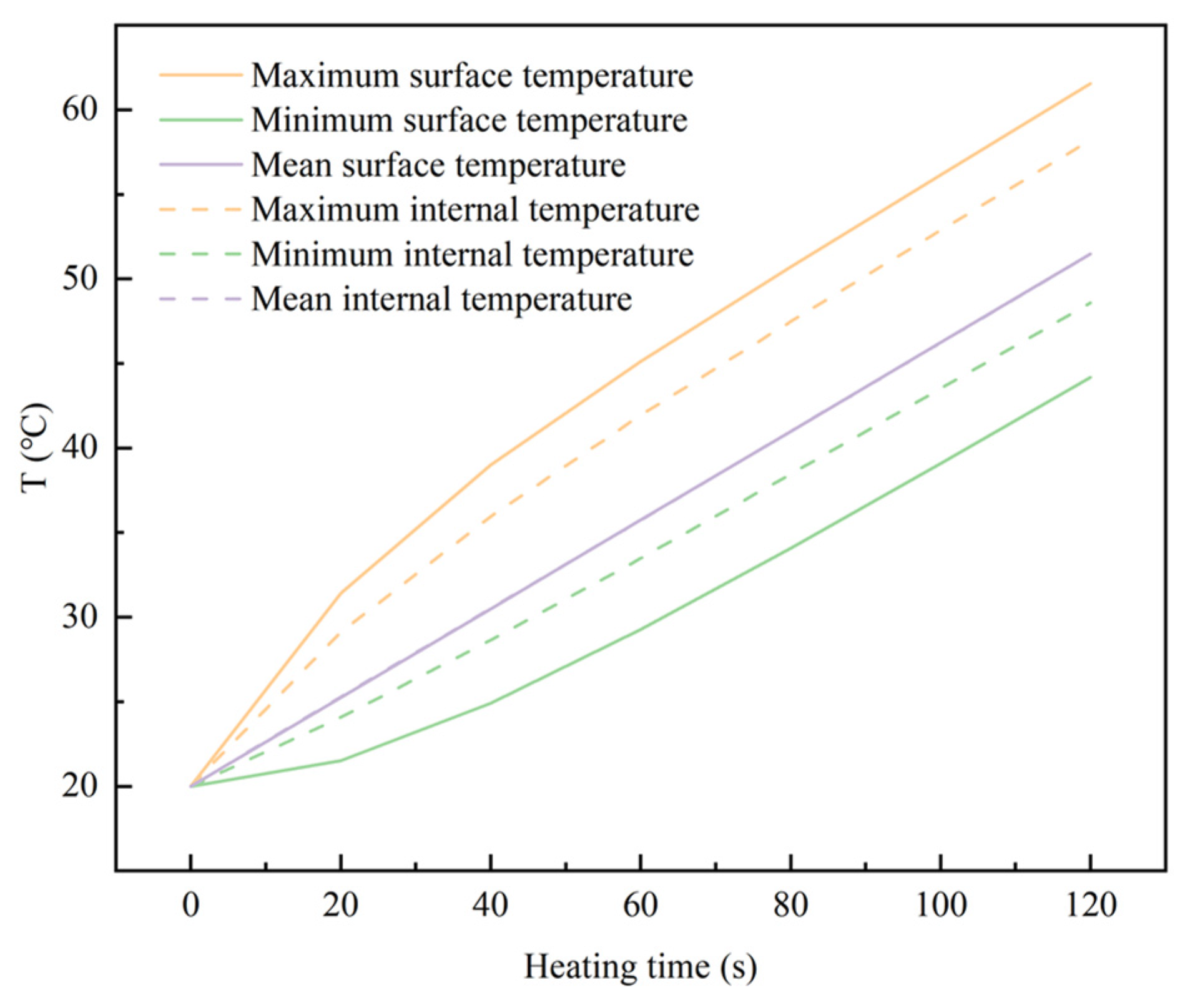
4.2.1. The Temperature Distribution of the LiH Compact
4.2.2. The Effect of Dielectric Property on Heating
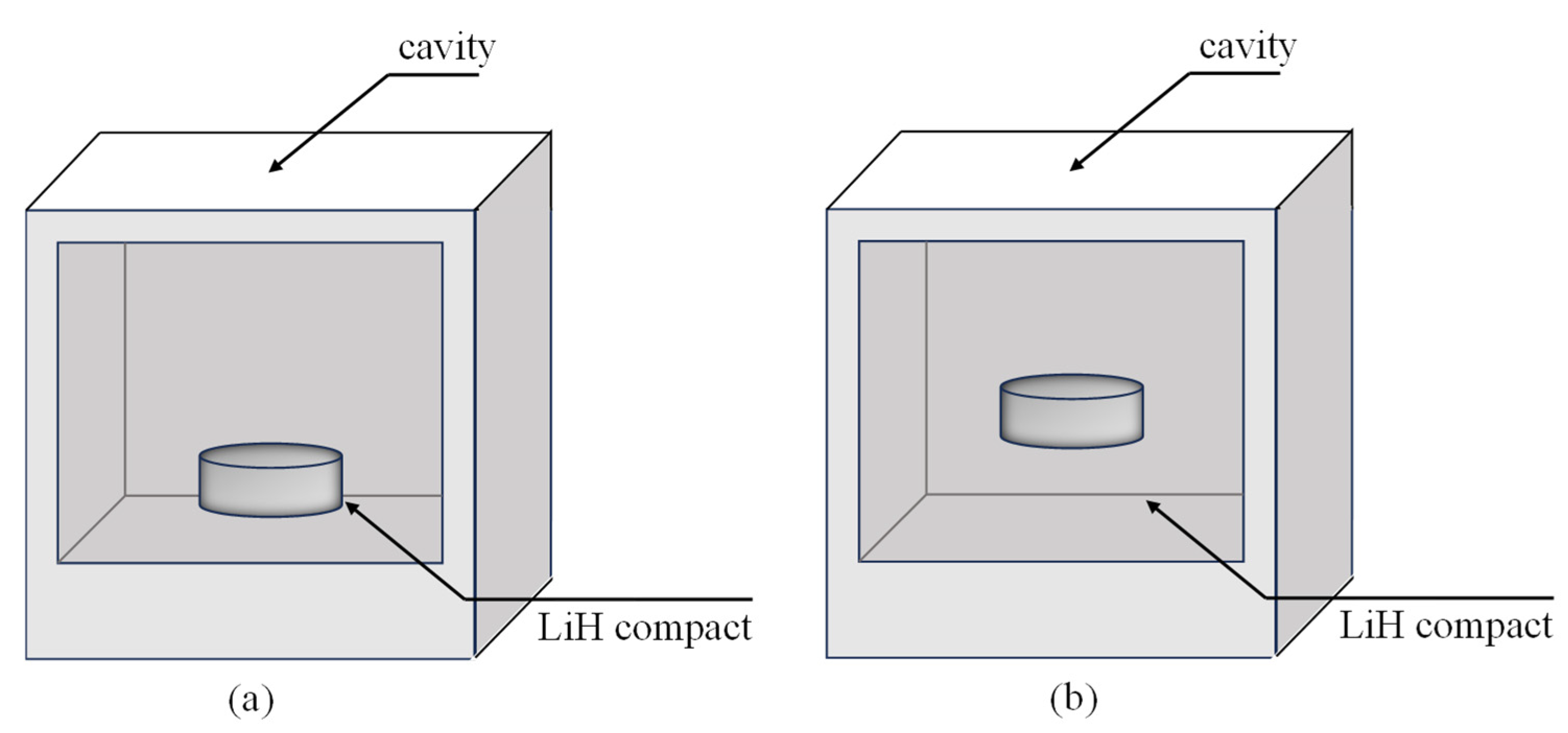
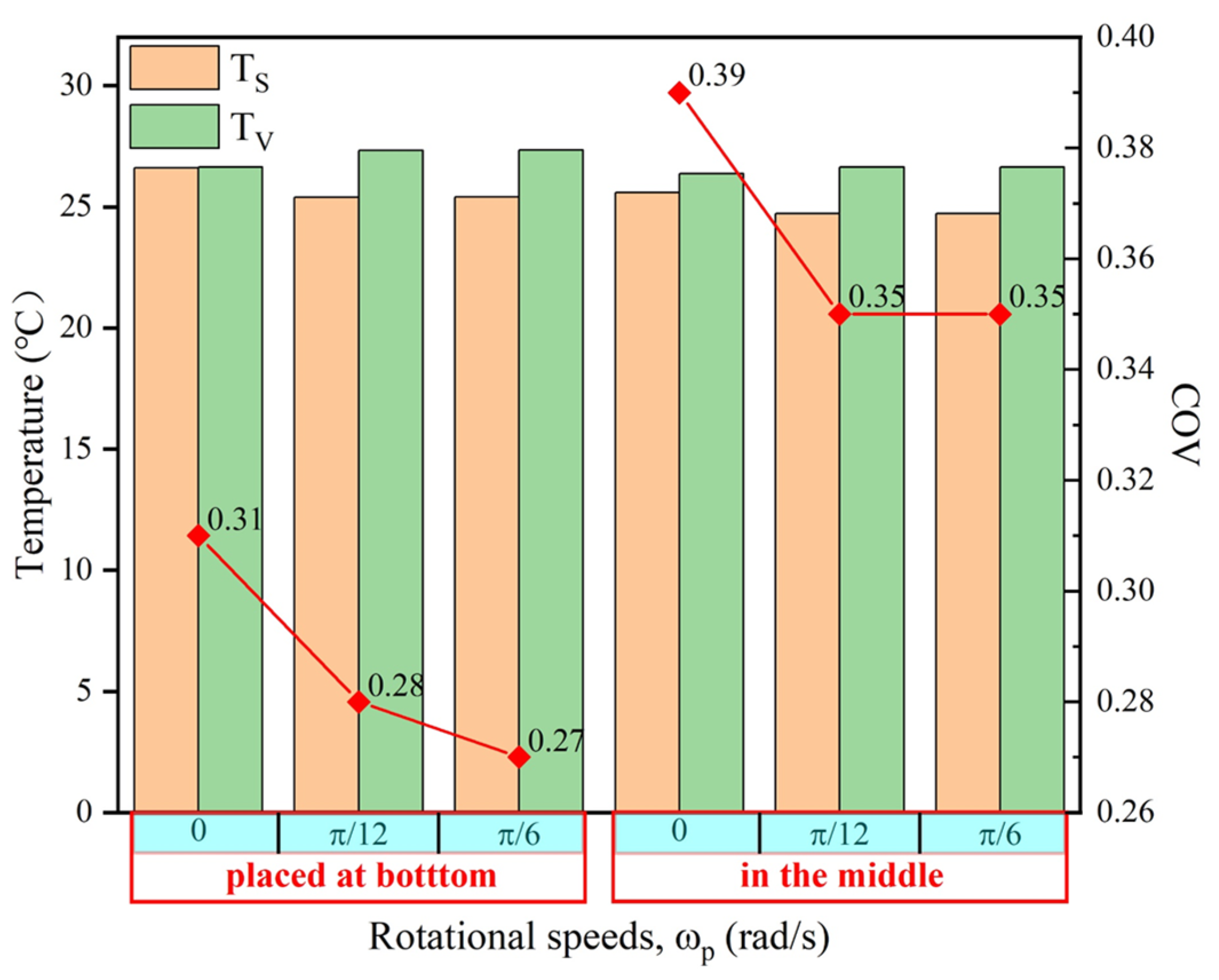
4.2.3. Microwave Heating at Different Positions and Rotary Heating
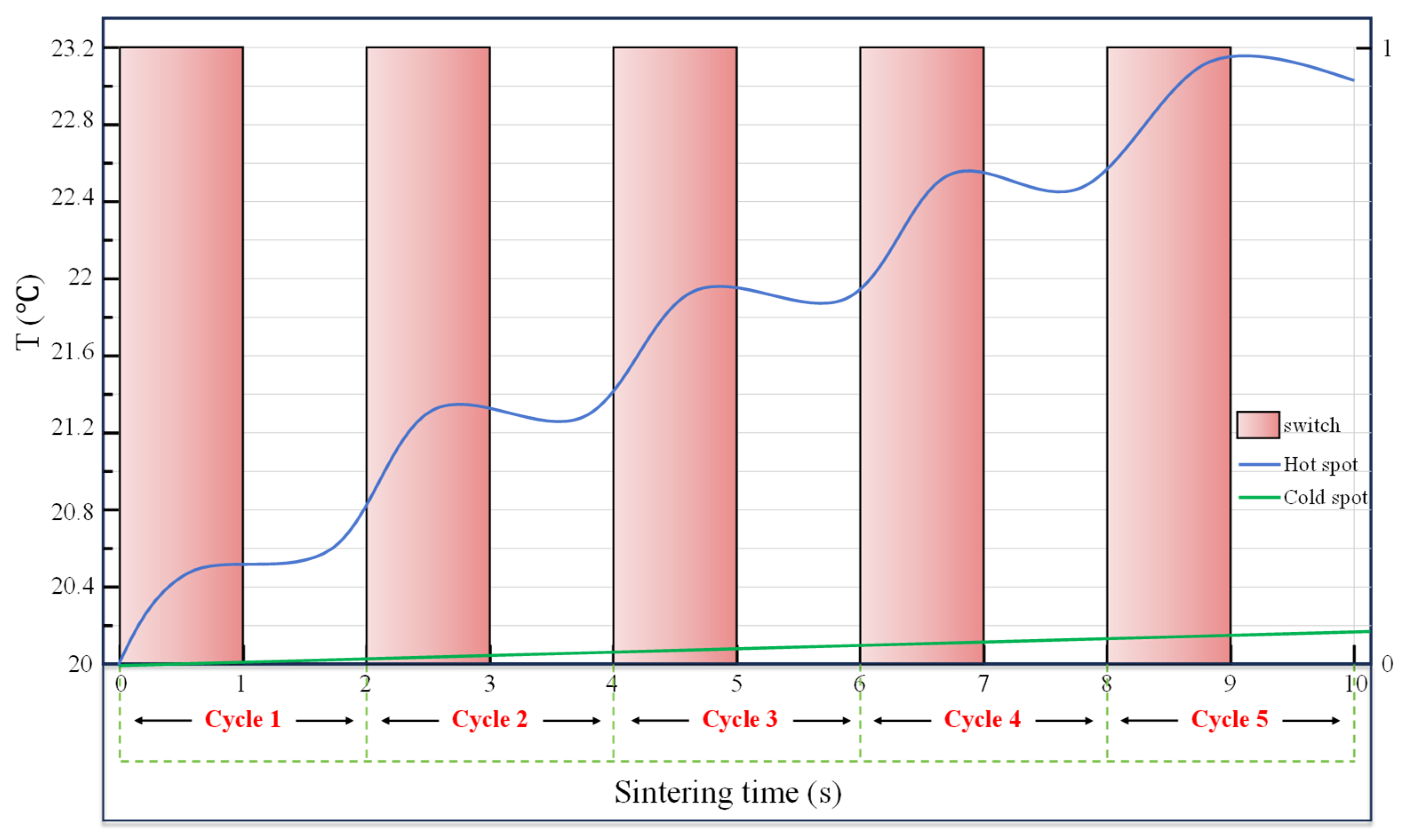
4.3. A Sintering–Resting Strategy of Microwave Heating Based on PFAD
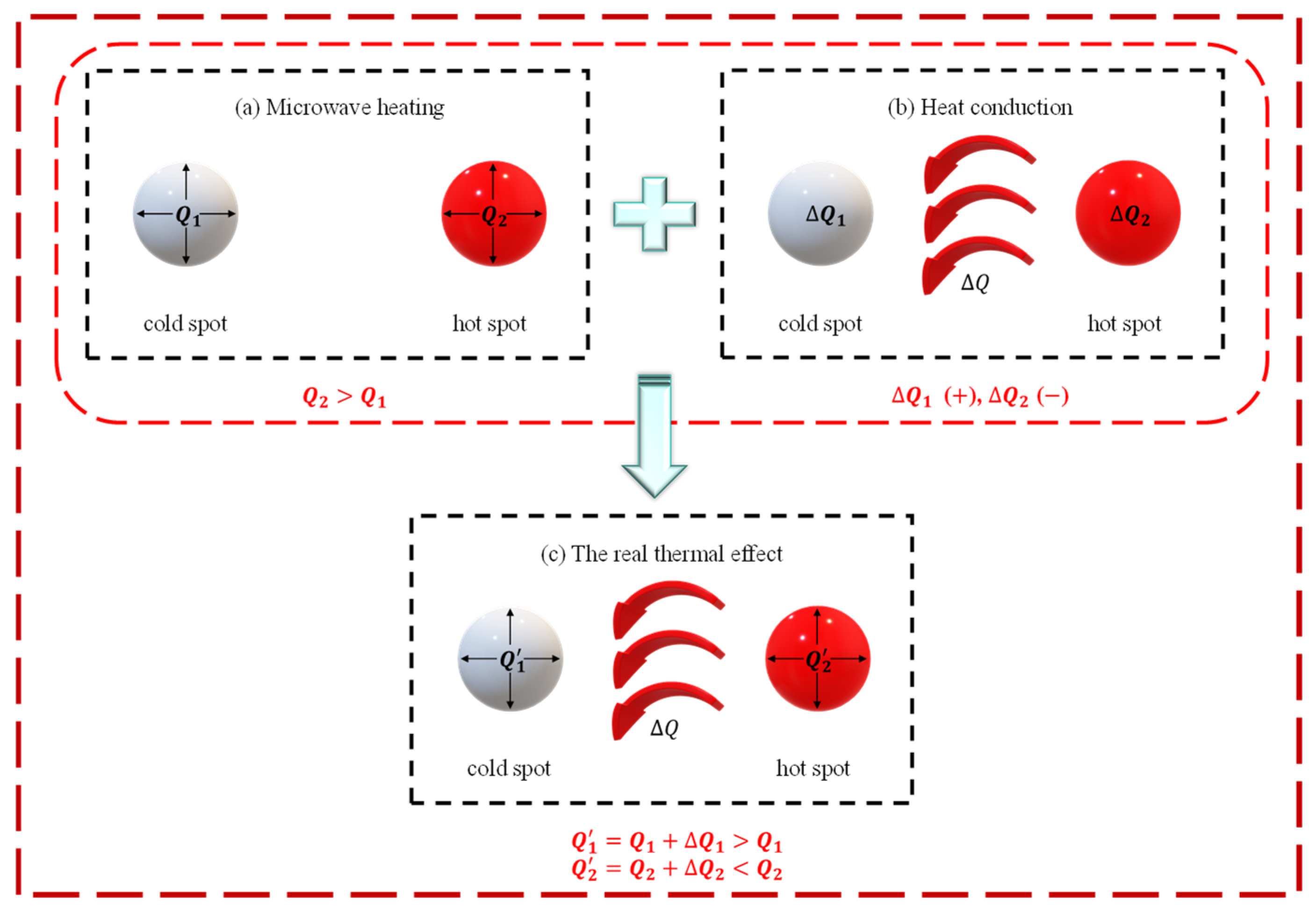
4.3.1. Competition Between Microwave Heating and Thermal Conductivity in Temperature
4.3.2. Unit Cycle of Sintering–Resting Heating Method
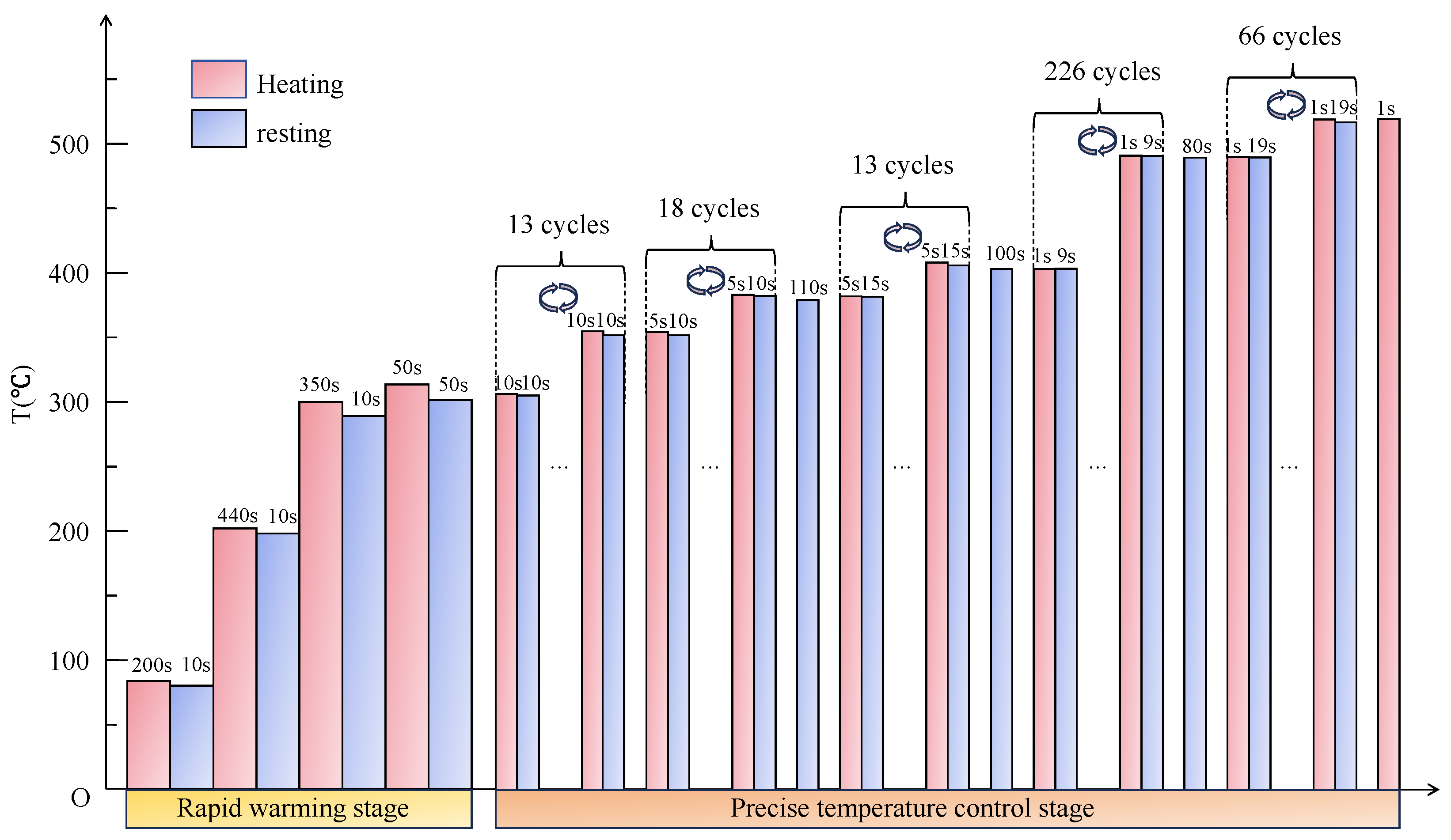
4.3.3. Parameter Design of the Sintering–Resting Heating Mode for Sintering LiH Based on PFAD
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, H.Y.; Chen, F.G.; Han, Y.; Yang, M.M.; Li, G.D.; Liang, R.C. Research Status of Metal Hydrides for Neutron Shielding. Mater. Rep. 2019, 33, 484–487. [Google Scholar]
- Wang, W.; Li, Q.; Yang, X.; Le, G. A Review of Irradiation Stability of Lithium Hydride Neutron Shielding Material. Mater. Sci. Technol. 2016, 32, 434–437. [Google Scholar]
- Craft, A.E.; King, J.C. Radiation Shielding Options for a Nuclear Reactor Power System Landed on the Lunar Surface. Nucl. Technol. 2010, 172, 255–272. [Google Scholar] [CrossRef]
- Poeth, D. The Evaluation of Lithium Hydride for Use in a Space Nuclear Reactor Shield, Including a Historical Perspective; Knolls Atomic Power Lab.: Niskayuna, NY, USA, 2005; Report MDO-723-0048. [Google Scholar]
- Welch, F.H. Properties of Lithium Hydride. III. Summary of Ge-Anpd Data; General Electric Co. Aircraft Nuclear Propulsion Dept.: Cincinnati, OH, USA, 1961. [Google Scholar]
- Xiang, M.; Zhang, Y.; Hong, M.; Liu, Z.; Leng, J.; Zhang, Y.; Zhang, J.; Wang, W. Fabrication and Characterization of LiH Ceramic Pebbles by Wet Process. J. Nucl. Mater. 2014, 452, 343–347. [Google Scholar] [CrossRef]
- Zalkin, A. The Thermal Expansion of LiH; Lawrence Livermore National Lab.: Livermore, CA, USA, 1953; Report UCRL-4239. [Google Scholar]
- Kingery, W.D. Factors Affecting Thermal Stress Resistance of Ceramic Materials. J. Am. Ceram. Soc. 1955, 38, 3–15. [Google Scholar] [CrossRef]
- Park, S.J.; Hong, B.H.; Baik, S.C.; Oh, K.H. Finite Element Analysis of Hot Rolled Coil Cooling. ISIJ Int. 1998, 38, 1262–1269. [Google Scholar] [CrossRef]
- Smith, R.L.; Miser, J.W. Compilation of the Properties of Lithium Hydride; NASA: Greenbelt, MD, USA, 1963.
- Zhang, W.; Peng, L.; Xie, Y.; Zhou, D.; Shi, Y.; Wan, Y. Dynamic Fatigue Behavior of Lithium Hydride at Elevated Temperatures. Ceram. Int. 2022, 48, 10827–10833. [Google Scholar] [CrossRef]
- Shi, Y.; Peng, L.; Zhang, W.; Li, Q.; Li, Q.; Ye, L. In Situ Evolution of Pores in Lithium Hydride at Elevated Temperatures Characterized by X-ray Computed Tomography. Crystals 2021, 11, 1093. [Google Scholar] [CrossRef]
- Okress, E.C.; Brown, W.C.; Moreno, T.; Goubau, G.; Heenan, N.I.; George, R.H. Microwave Power Engineering. IEEE Spectr. 1964, 1, 76. [Google Scholar] [CrossRef]
- Yadoji, P.; Peelamedu, R.; Agrawal, D.; Roy, R. Microwave Sintering of Ni–Zn Ferrites: Comparison with Conventional Sintering. Mater. Sci. Eng. B 2003, 98, 269–278. [Google Scholar] [CrossRef]
- Xu, G.; Li, J.; Wang, C.; Du, X.; Lu, D.; Xie, B.; Wang, X.; Lu, C.; Liu, H.; Dong, S.; et al. The Formation/Decomposition Equilibrium of LiH and Its Contribution on Anode Failure in Practical Lithium Metal Batteries. Angew. Chem. Int. Ed. 2021, 60, 7770–7776. [Google Scholar] [CrossRef]
- Singhal, C.; Murtaza, Q. Parvej Microwave Sintering of Advanced Composites Materials: A Review. Mater. Today Proc. 2018, 5, 24287–24298. [Google Scholar] [CrossRef]
- Rybakov, K.I.; Olevsky, E.A.; Krikun, E.V. Microwave Sintering: Fundamentals and Modeling. J. Am. Ceram. Soc. 2013, 96, 1003–1020. [Google Scholar] [CrossRef]
- El Khaled, D.; Novas, N.; Gazquez, J.A.; Manzano-Agugliaro, F. Microwave Dielectric Heating: Applications on Metals Processing. Renew. Sustain. Energy Rev. 2018, 82, 2880–2892. [Google Scholar]
- Lu, Y.J.; Gao, J.Y.; Ye, X.L.; Guo, S.; Shuai, M.; Yang, L.; Hou, M.; Gao, L.; Chen, K.; Huang, B. The High Temperature Dielectric Properties and Temperature Rise Behavior of Lithium Hydride in Microwave Field. Ceram. Int. 2025, 51, 9939–9946. [Google Scholar] [CrossRef]
- Lu, Y.J.; Gao, J.Y.; Ye, X.L.; Yang, L.; Gao, L.; Hou, M.; Chen, K.; Guo, S. Microwave Sintering Reactor Design for Lithium Hydride Ceramics: From Dielectric Properties to Electromagnetic Thermal Behavior. Int. J. Hydrogen Energy 2025, 98, 1185–1194. [Google Scholar] [CrossRef]
- Gao, Y.P.; Chen, H.Y.; Shuai, M.B.; Zeng, X.; Zhao, S. Density Functional Study on the Mechanics, Thermodynamics, and H Diffusion Mechanism of LiH. Int. J. Hydrogen Energy 2024, 54, 740–750. [Google Scholar] [CrossRef]
- Yu, E.; Pan, Y. Influence of Noble Metals on the Electronic and Optical Properties of LiH Hydride: First-Principles Calculations. Int. J. Hydrogen Energy 2021, 46, 35342–35350. [Google Scholar] [CrossRef]
- Shi, Y.F.; Zhang, W.Z.; Peng, L.; Chen, S.; Xie, Y.; Zhu, C.; Wan, Y. Effect of Temperature on Damage Mechanism and Fracture Behavior of LiH Ceramic under 3-Point Bending at Different Loading Rates. Ceram. Int. 2024, 50, 33506–33517. [Google Scholar] [CrossRef]
- Evans, P.W.F.; Bustillos, C.G.; Charalambous, H.; Wilson-Heid, A.E.; Shittu, J.; Swift, A.J.; Root, J.; Du Frane, W.L. Pressureless Sintering of Lithium Hydride. J. Eur. Ceram. Soc. 2025, 45, 117152. [Google Scholar] [CrossRef]
- Yan, H.Z.; Chen, H.Y.; Shuai, M.B.; Zeng, X.; Huang, B. Thermal Stresses of Large-Dimension Lithium Hydride Ceramics during the Sintering Process and Strength Analysis Based on Process-Based Failure Assessment Diagram. Ceram. Int. 2024, 50, 3930–3939. [Google Scholar] [CrossRef]
- Panerai, F.; Chazot, O. Characterization of Gas/Surface Interactions for Ceramic Matrix Composites in High Enthalpy, Low Pressure Air Flow. Mater. Chem. Phys. 2012, 134, 597–607. [Google Scholar] [CrossRef]
- Scatteia, L.; Alfano, D.; Monteverde, F.; Sans, J.-L.; Balat-Pichelin, M. Effect of the Machining Method on the Catalycity and Emissivity of ZrB2 and ZrB2-HfB2-Based Ceramics. J. Am. Ceram. Soc. 2008, 91, 1461–1468. [Google Scholar] [CrossRef]
- Pitchai, K.; Chen, J.; Birla, S.; Gonzalez, R.; Jones, D.; Subbiah, J. A Microwave Heat Transfer Model for a Rotating Multi-Component Meal in a Domestic Oven: Development and Validation. J. Food Eng. 2014, 128, 60–71. [Google Scholar] [CrossRef]
- Qiu, Z.L.; Kezhao; Wang, X.S.; He, L.F. Studying on the High-Temperature Tensile Property of 7LiH. Rare Met. Mater. Eng. 2006, 35, 1560–1563. [Google Scholar]
- Lu, Y.; Shuai, M.; Gao, J.; Ye, X.; Guo, S.; Yang, L.; Huang, B.; Zhang, J.; Hou, M.; Gao, L.; et al. Numerical Simulation and Experimental Analysis for Microwave Sintering Process of Lithium Hydride (LiH). Materials 2024, 17, 5342. [Google Scholar] [CrossRef]
- Ye, J.H.; Zhu, H.C.; Liao, Y.H.; Liao, Y.-H.; Zhou, Y.-P.; Huang, K.-M. Implicit Function and Level Set Methods for Computa-tion of Moving Elements During Microwave Heating. IEEE Trans. Microw. Theory Tech. 2017, 65, 4773–4784. [Google Scholar] [CrossRef]
- Ye, J.; Xia, Y.; Yi, Q.; Zhu, H.; Yang, Y.; Huang, K.; Shi, K. Multiphysics Modeling of Microwave Heating of Solid Samples in Rotary Lifting Motion in a Rectangular Multi-Mode Cavity. Innov. Food Sci. Emerg. Technol. 2021, 73, 102767. [Google Scholar] [CrossRef]




| Temperature (°C) | Specific Heat (J/kg/°C) | Density (kg/m3) | Thermal Conductivity (W/m/°C) | Expansion Coefficient (10−6/°C) | Young’s Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 20 | 3716.25 | 770 | 6.904 | 26.8 | 47.3 | 0.08 | 15.96 |
| 100 | 6.527 | 35.5 | 44.7 | 0.10 | 14.98 | ||
| 150 | / | 39.4 | / | / | / | ||
| 200 | 5.732 | 41.3 | 42.3 | 0.11 | 18.82 | ||
| 250 | / | 42.4 | / | 0.11 | / | ||
| 300 | 5.146 | 43.4 | 40.2 | 0.11 | 19.96 | ||
| 350 | / | 44.2 | / | / | 16.97 | ||
| 400 | 4.686 | 46.0 | 38.0 | 0.12 | 12.93 | ||
| 450 | / | 47.9 | / | / | 6.95 | ||
| 500 | 4.310 | 49.5 | 36.4 | 0.12 | 3.98 | ||
| 600 | 4.100 | / | 35.5 | 0.11 | 0.77 |
| Dielectric Loss Factor | Distance (mm) | Cold Point Temperature (°C) | Hot Point Temperature (°C) | (°C/mm) | COV |
|---|---|---|---|---|---|
| 0.01 | 37.498 | 20.445 | 26.055 | 0.149 | 0.35 |
| 0.02 | 20.58 | 27.892 | 0.195 | 0.37 | |
| 0.03 | 20.713 | 29.7 | 0.240 | 0.41 | |
| 0.04 | 20.845 | 31.478 | 0.284 | 0.43 |
| Group | Case | Heating Time (s) | Thermal Conductivity | Temperature at Cold Spots (°C) | Temperature at Hot Spots (°C) | Nominal Temperature Gradient (°C/mm) |
|---|---|---|---|---|---|---|
| (a) | 1 | 10 | 0 | 20.001 | 27.367 | 0.196 |
| 2 | 20 | 0 | 20.002 | 34.735 | 0.393 | |
| (b) | 3 | 10 | K(T) | 20.449 | 26.39 | 0.158 |
| 4 | 20 | K(T) | 21.558 | 31.356 | 0.261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chen, H.; Shuai, M.; Zeng, X.; Huang, B. A Sintering–Resting Strategy of Microwave Heating for Lithium Hydride Ceramic Based on Numerical Analysis of Thermal Effects. Materials 2025, 18, 2832. https://doi.org/10.3390/ma18122832
Zhang W, Chen H, Shuai M, Zeng X, Huang B. A Sintering–Resting Strategy of Microwave Heating for Lithium Hydride Ceramic Based on Numerical Analysis of Thermal Effects. Materials. 2025; 18(12):2832. https://doi.org/10.3390/ma18122832
Chicago/Turabian StyleZhang, Wenyan, Huayan Chen, Maobing Shuai, Xiangguo Zeng, and Bin Huang. 2025. "A Sintering–Resting Strategy of Microwave Heating for Lithium Hydride Ceramic Based on Numerical Analysis of Thermal Effects" Materials 18, no. 12: 2832. https://doi.org/10.3390/ma18122832
APA StyleZhang, W., Chen, H., Shuai, M., Zeng, X., & Huang, B. (2025). A Sintering–Resting Strategy of Microwave Heating for Lithium Hydride Ceramic Based on Numerical Analysis of Thermal Effects. Materials, 18(12), 2832. https://doi.org/10.3390/ma18122832






