Active Fault Dislocation-Induced Mechanical Response of Polyurethane-Solidified Track in Tunnels
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Parameter Determination
2.2. Rock Mass–Tunnel–Track Finite Element Model
2.3. Vehicle–Track Dynamics Model
2.4. Model Parameters
2.5. Calculation Scheme
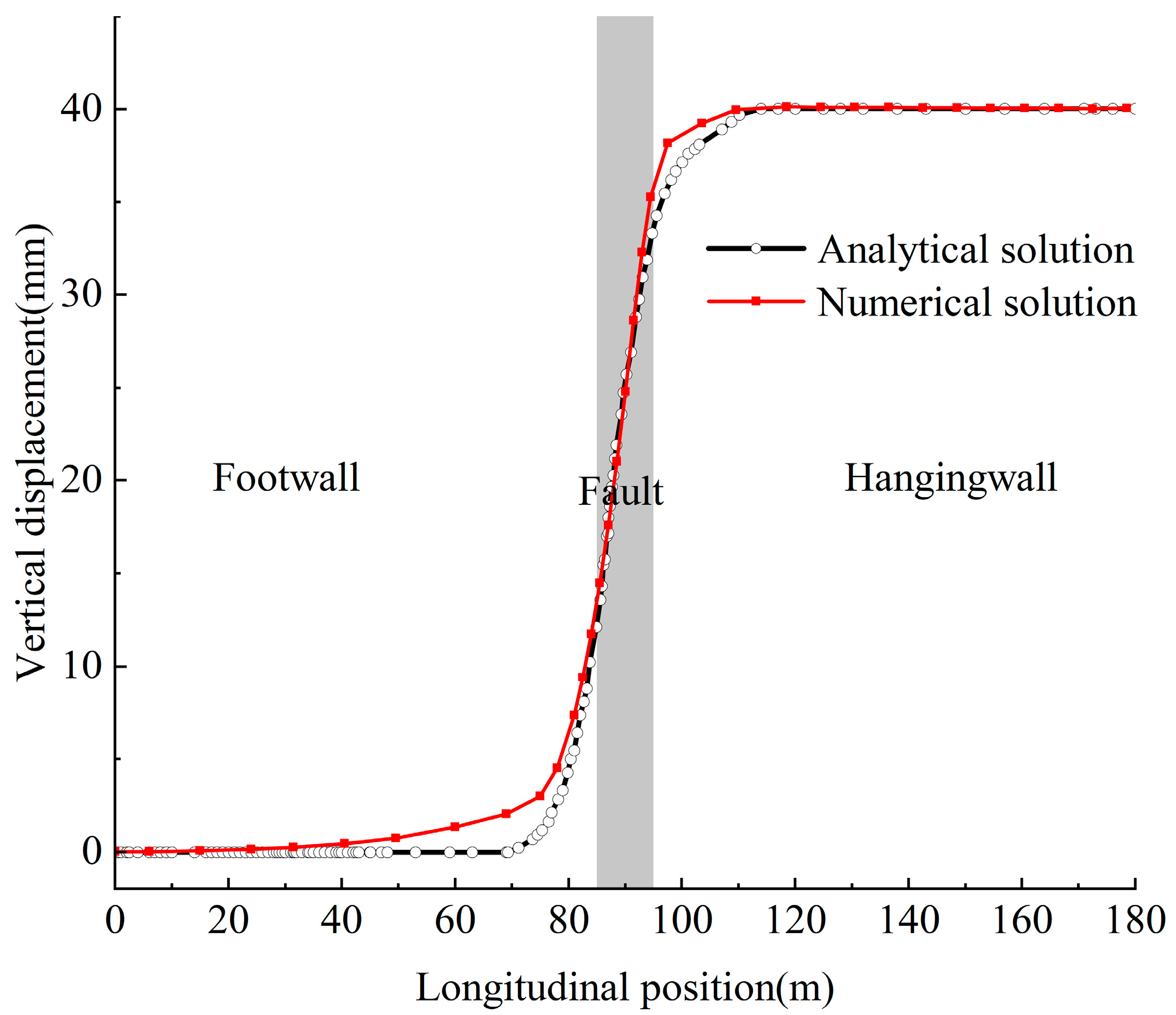
2.6. Model Validation
3. Results and Discussion
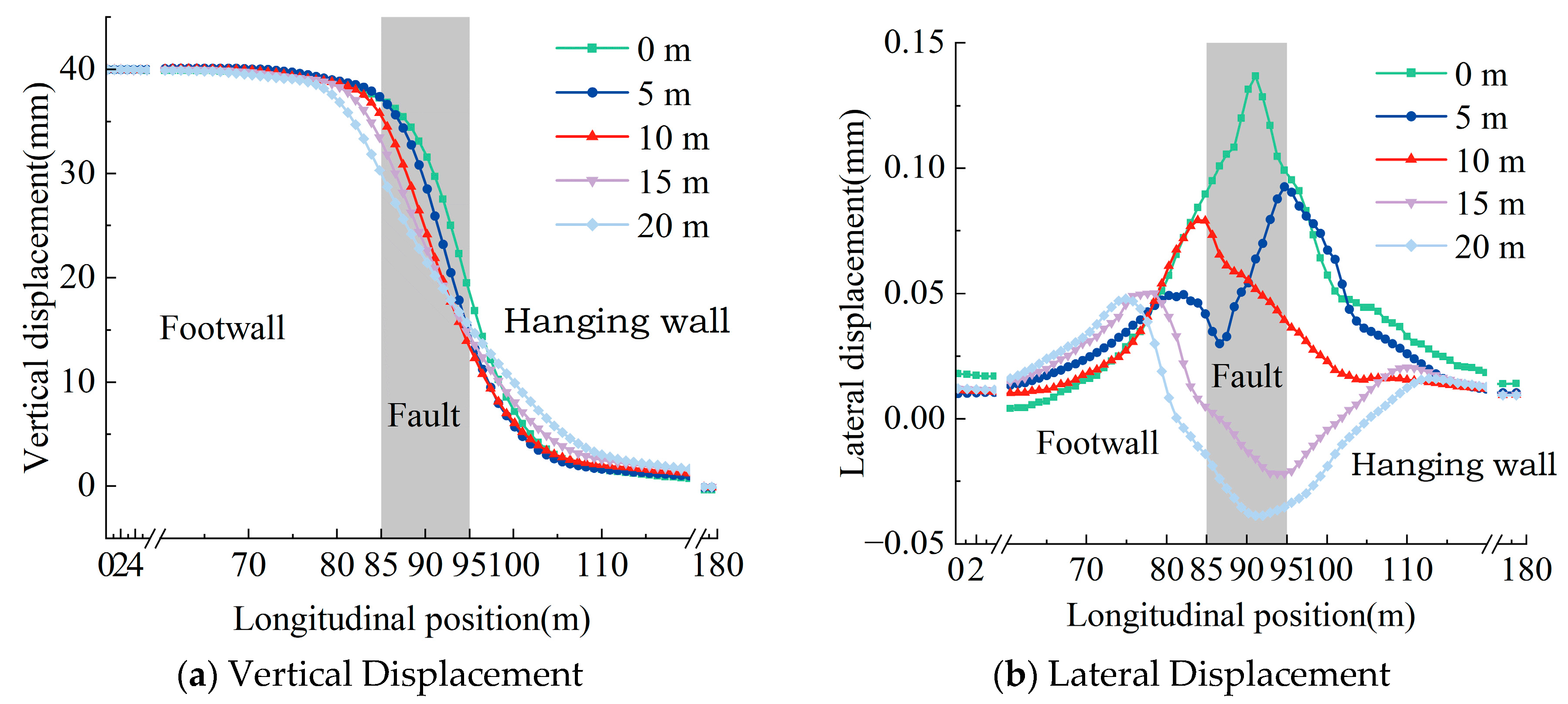
3.1. Analysis of Track Structure Response Under Normal Fault Dislocation
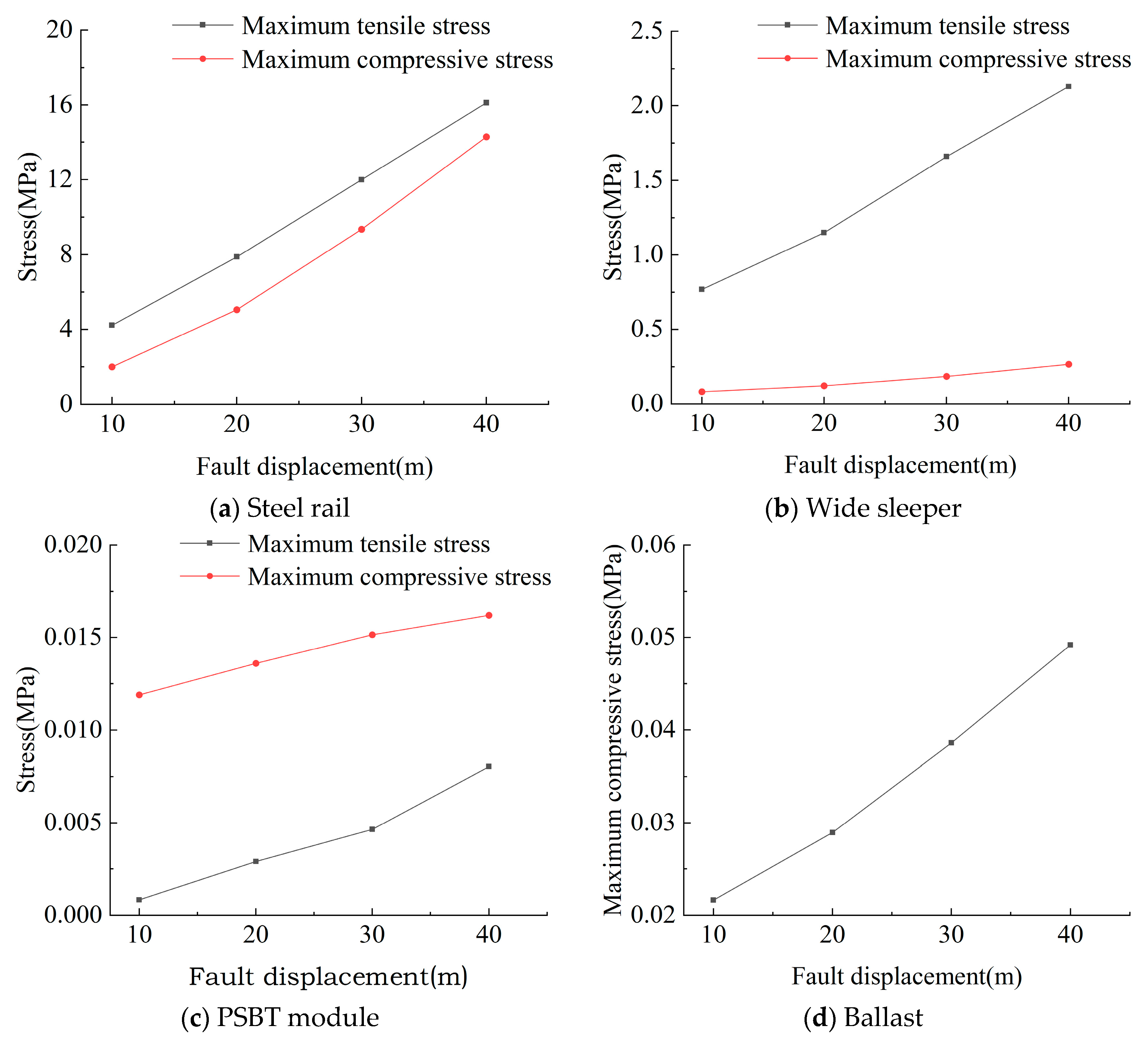
3.1.1. Impact of Fault Displacement
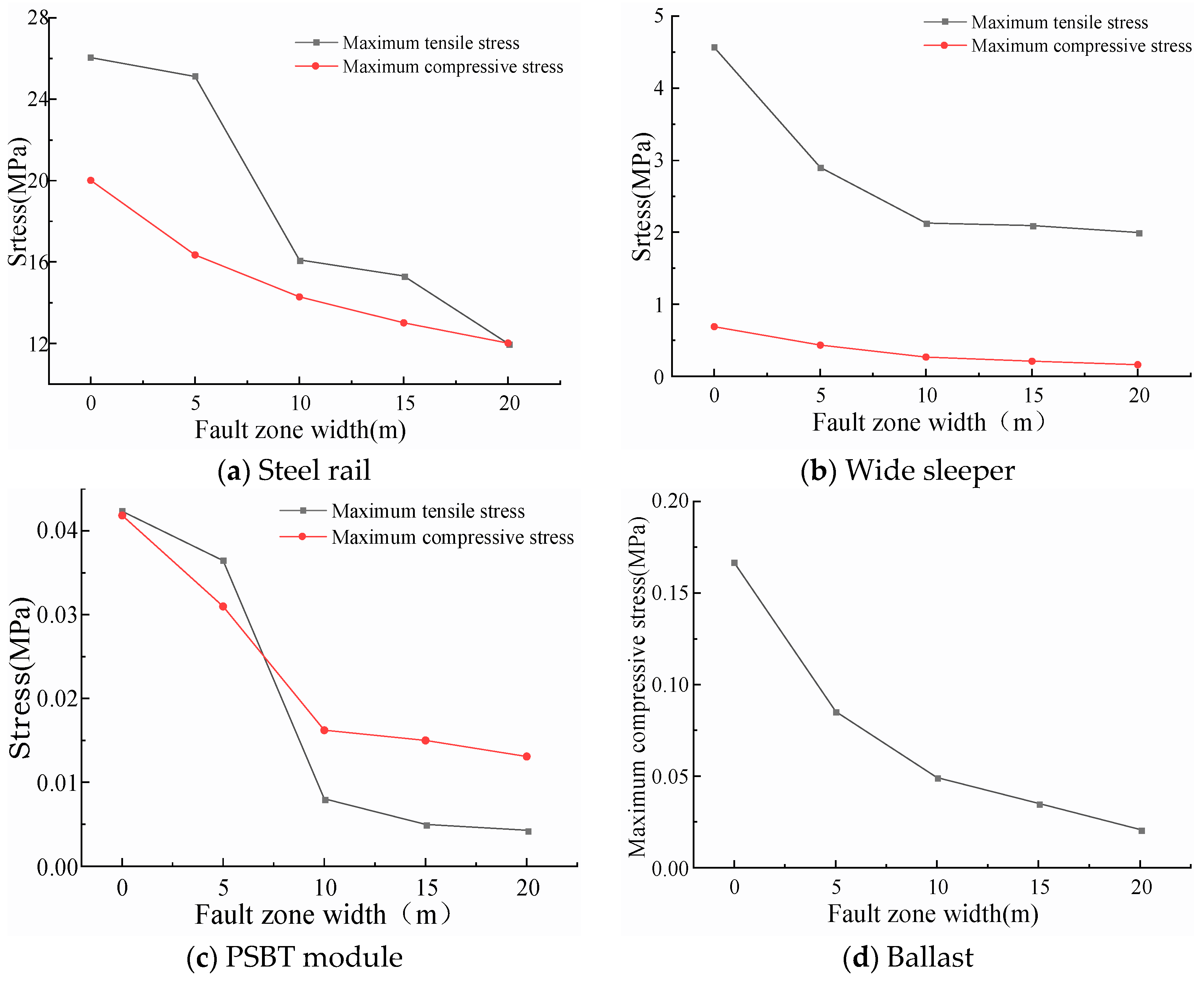
3.1.2. Impact of Fault Zone Width
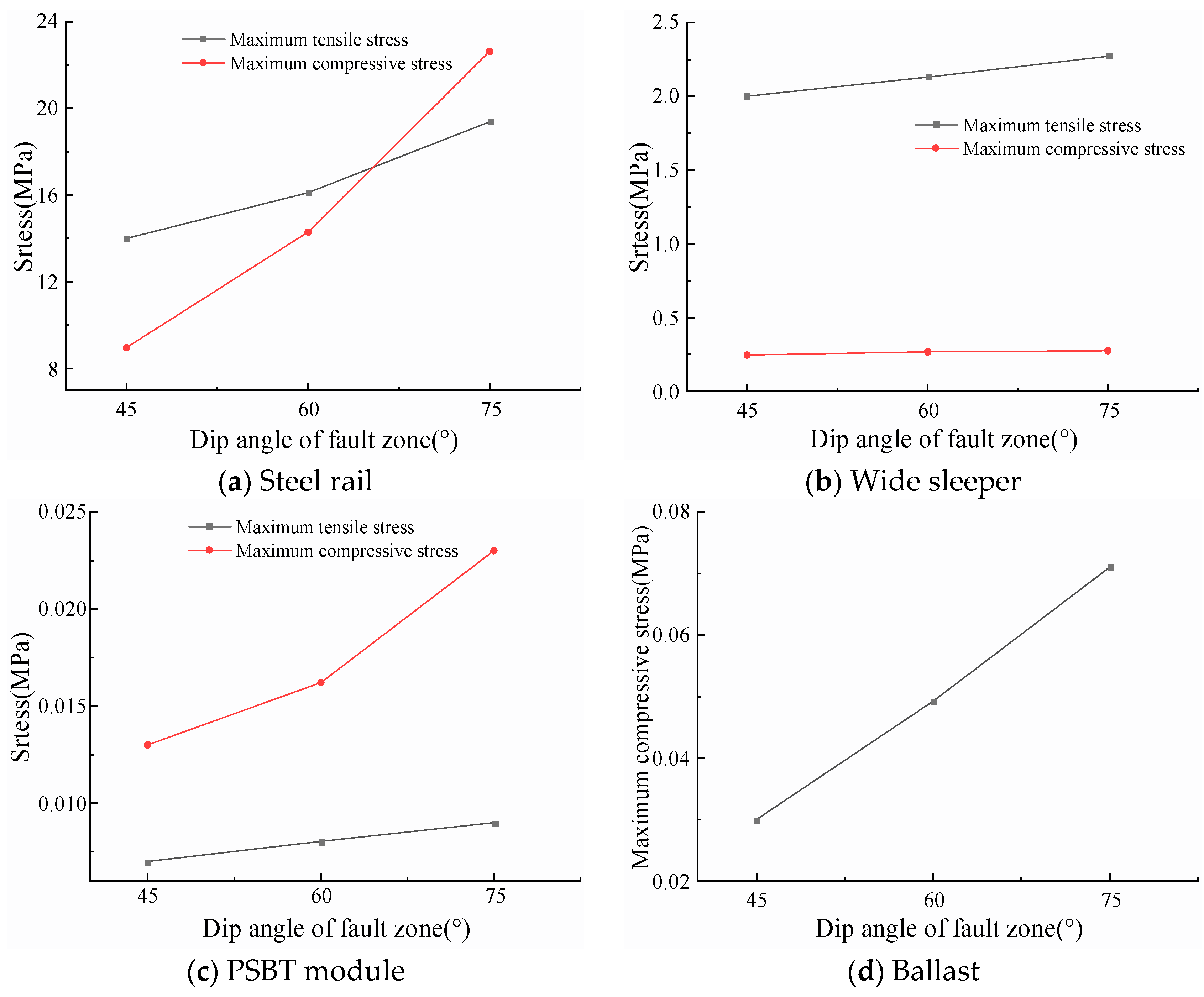
3.1.3. Impact of Fault Zone Dip Angle

3.2. Impact of Normal Fault Dislocation on Train Dynamic Response
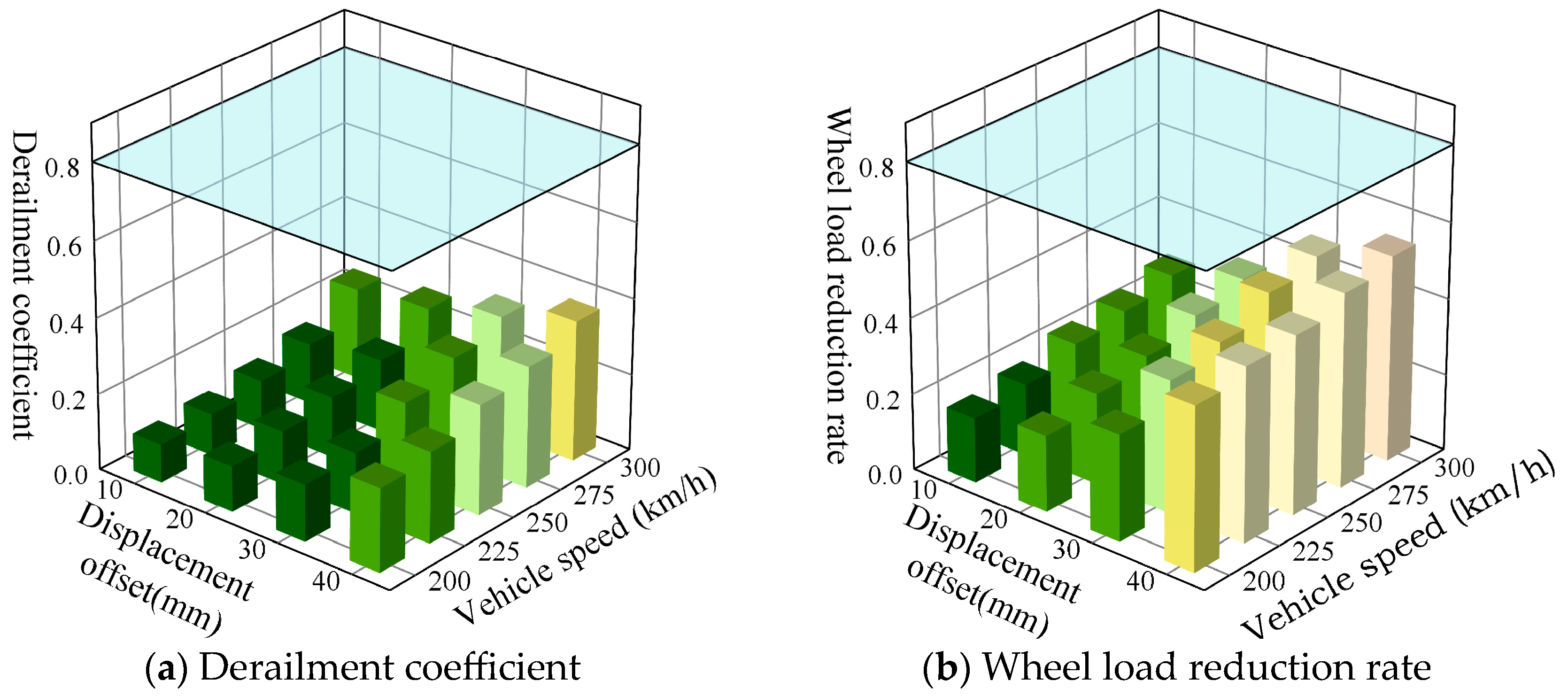
3.2.1. Impact of Fault Displacement
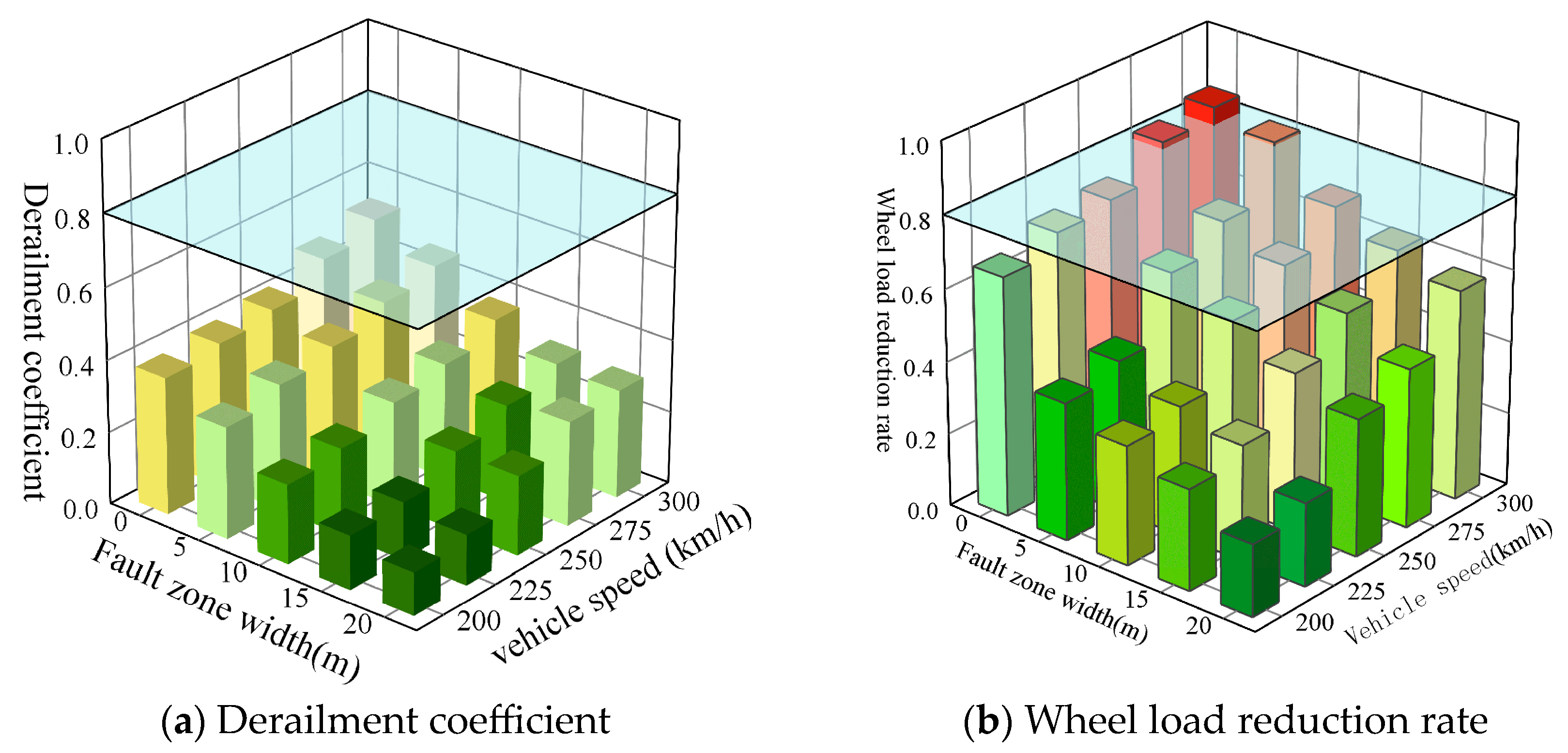
3.2.2. Impact of Fault Zone Width
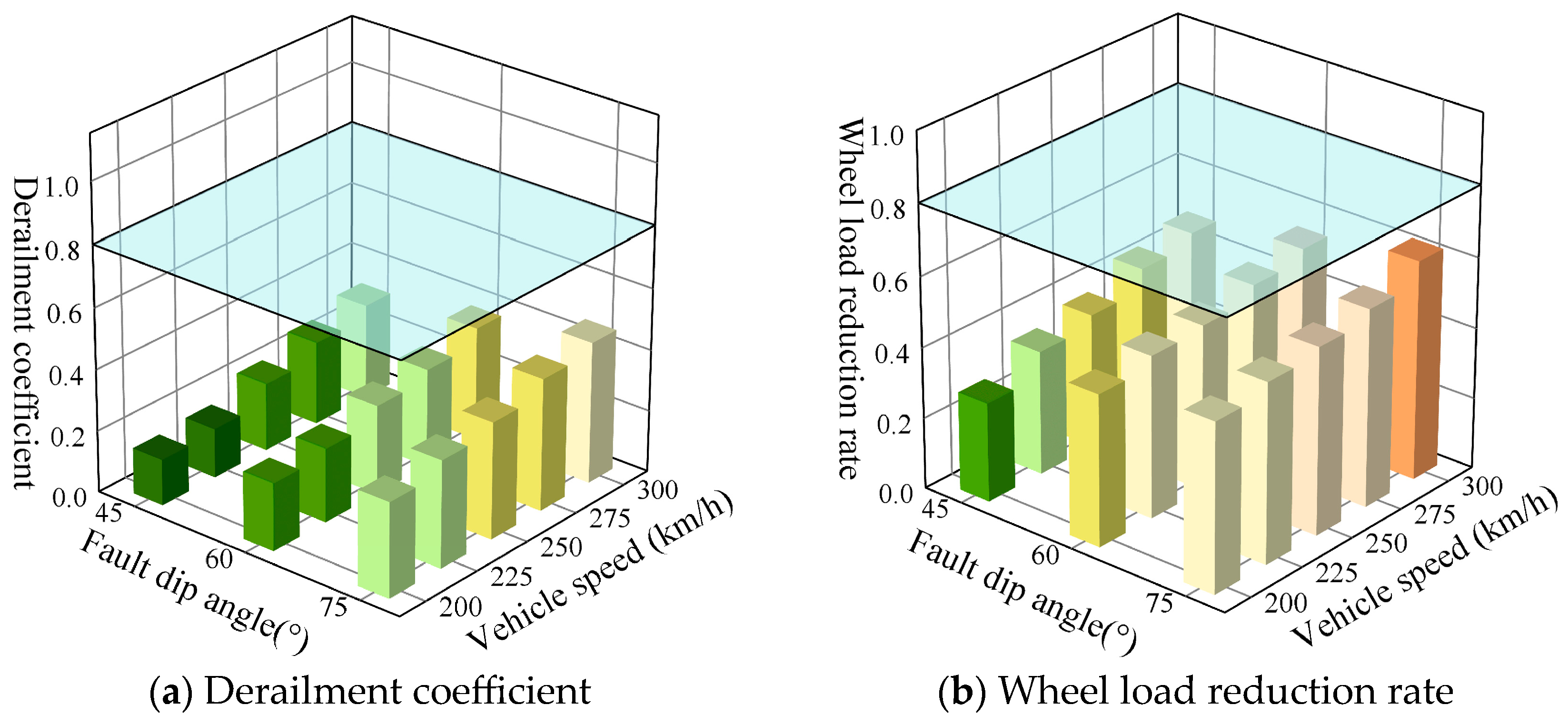
3.2.3. Impact of Fault Zone Dip Angle
4. Conclusions
- Under normal fault dislocation, the track structure undergoes substantial vertical deformation, with the rail’s vertical deformation closely approximating the applied displacement value. The deformation range in the rail extends beyond the fault zone’s width. The impact of fault displacement on the deformation and stress state of the track structure primarily concentrates within the active fault zone and its immediate vicinity, with the scope and magnitude of this impact varying based on the structural characteristics of the fault zone and the differing components of the track structure.
- In the context of normal fault displacement, an increase in the displacement and dip angle of the active fault zone, coupled with a decrease in its width, results in heightened stress levels on each track component.
- Focused on the PSTB, variations in material properties lead to differing stress experiences among track components. Notably, the wide sleeper, which experiences the second-highest stress levels after the rail in the track structure, poses a potential risk of cracking and represents a structural weakness.
- An increase in the displacement of the active fault zone, a decrease in its width, an increase in its dip angle, and an increase in train speed all contribute to an elevation in the derailment coefficient and wheel load reduction rate, potentially surpassing safety thresholds to a certain extent. To guarantee train operation safety, under normal fault displacement conditions and for prefabricated wide sleeper polyurethane solidified track beds with only an active fault plane, a displacement of 40 mm, and a fault zone dip angle of 60°, it is advisable to restrict the train speed to 250 km/h.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiao, R.L. An approach to subgrade design methods for high speed railway passing through fault zone. Railw. Stand. Des. 2015, 59, 13–17. [Google Scholar]
- Cai, X.H.; Yu, P.; Zhou, L.H.; Li, Y.M.; Liu, C. Research on dynamic response of metro track structure in active fault zone areas. Railw. Stand. Des. 2017, 61, 14–19. [Google Scholar]
- Gao, Z.Z. Selection of track structure for high-speed railway crossing active fault zone. Chin. Railw. 2022, 3, 75–80. [Google Scholar]
- Ling, X.; Xiao, H.; Liu, G.P.; Zhang, M. Discrete element modeling of polyurethane-stabilized ballast under monotonic and cyclic triaxial loading. Constr. Build. Mater. 2020, 255, 119370. [Google Scholar] [CrossRef]
- Bai, H.J. The impact of the tanlu fault zone on the Xuzhou–lianyungang high-speed railway and Engineering response Measures. Railw. Stand. Des. 2021, 65, 46–51. [Google Scholar]
- Woodward, P.K.; EL, K.A.; Laghrouche, O.; Medero, G.; Banimahd, M. Application of polyurethane geocomposites to help maintain track geometry for high-speed ballasted railway tracks. J. Zhejiang Univ.-Sci. A 2012, 13, 836–849. [Google Scholar] [CrossRef]
- Jing, G.Q.; Qie, L.C.; Markine, V.; Jia, W. Polyurethane reinforced ballasted track: Review, innovation and challenge. Constr. Build. Mater. 2019, 208, 734–748. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, Q.; Zhang, G.; Zhang, M.; Mei, X. Response and mechanism of a tunnel subjected to combined fault rupture deformation and subsequent seismic excitation. Transp. Geotech. 2022, 34, 100749. [Google Scholar]
- Zhou, G.X.; Sheng, Q.; Cui, Z.; Wang, T.; Ma, Y. Investigating the Deformation and Failure Mechanism of a Submarine Tunnel with Flexible Joints Subjected to Strike-Slip Faults. J. Mar. Sci. Eng. 2021, 9, 1412. [Google Scholar] [CrossRef]
- Tian, S.; Wu, K.F.; Yu, L.; Li, X.; Gong, J.F.; Wang, X.D. Key technology of anti-seismic for railway tunnels crossing active fault zone. Tunn. Constr. 2022, 42, 1351–1364. [Google Scholar]
- Zhong, Z.L.; Wang, Z.; Zhao, M.; Du, X. Structural damage assessment of mountain tunnels in fault fracture zone subjected to multiple strike-slip fault movement. Tunn. Undergr. Space Technol. 2020, 104, 103527. [Google Scholar] [CrossRef]
- Wang, J.; Sheng, J.; Zhao, M.D.; Wang, X. Numerical simulation analysis of the influence of Karakax fault dislocation on near-fault tunnel. Earthq. Eng. Eng. Dyn. 2022, 42, 235–242. [Google Scholar]
- Xiong, Z.W.; Liu, J.X.; Wang, P.; Liu, G.; Xiao, J.; Yu, S. Field dynamic performance testing and analysis of polyurethane track and ballasted track in a high-speed railway. J. Civ. Struct. Health Monit. 2021, 11, 867–877. [Google Scholar] [CrossRef]
- Shao, S.; Ji, D.Y. Coupled Discrete-finite Element Method for Settlement Analysis of Transition Zone between Ballasted and Ballastless Track with Polyurethane Reinforcement Based on Computer Aided Technology. J. Phys. Conf. Ser. 2020, 1574, 012007. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Q.B.; Wang, H.; Qie, L.C.; Lou, L.W.; Yu, W.Y.; Yi, Q. Dynamic Characteristics of Track Structure with Wide Sleeper Slab Solidified Ballast Bed in Urban Rail Transit. Chin. Railw. Sci. 2021, 42, 19–26. [Google Scholar]
- He, Q.; Sun, H.K.; Li, C.Z.; Ma, Y.S.; Wang, P.; Wang, K. Analysis of Track Irregularity Data of Polyurethane Curing Ballast Bed for High Speed Railway. Railw. Eng. 2022, 62, 21–26. [Google Scholar]
- Xiao, J.L.; Jing, P.; Yu, S.X.; Wang, P. Analysis on the track quality evolution law of polyurethane-reinforced ballasted track in high-speed railway. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 993–1005. [Google Scholar] [CrossRef]
- Cai, X.P.; Zhong, Y.L.; Hao, X.C.; Zhang, Y.; Cui, R. Dynamic behavior of a polyurethane foam solidified ballasted track in a heavy haul railway tunnel. Adv. Struct. Eng. 2019, 22, 751–764. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Chen, W.; Luo, S.; Wang, W.; Yuan, Q.; Sheng, X. Experimental investigation and soft bond modelling analysis on mechanical behaviours of foamed polyurethane solidified ballast. Constr. Build. Mater. 2024, 440, 137434. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, W.Y.; Qie, L.C.; Sheng, Z.; Li, Y. Grading analysis of resilient polyurethane solidified ballasted bed using the discrete element method. Constr. Build. Mater. 2024, 457, 139464. [Google Scholar] [CrossRef]
- Song, Y.; Du, Y.L.; Zhang, X.M.; Sun, B. Evaluating the Effect of Wheel Polygons on Dynamic Track Performance in High-Speed Railway Systems Using Co-Simulation Analysis. Appl. Sci. 2019, 9, 4165. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W.M. A three-dimensional dynamic model for train-track interactions. Appl. Math. Model. 2019, 76, 443–465. [Google Scholar] [CrossRef]
- Chen, W.; Wu, P.; Xu, L.; Wang, J.; Wang, W.; Lou, P. Response of prefabricated-polyurethane reinforced ballasted track to dislocation in tunnels through active fault zone. Int. J. Rail Transp. 2024, 12, 1064–1084. [Google Scholar] [CrossRef]
- Ma, Y.L.; Sheng, Q.; Zhang, G.M.; Cui, Z. A 3D Discrete-Continuum Coupling Approach for Investigating the Deformation and Failure Mechanism of Tunnels across an Active Fault: A Case Study of Xianglushan Tunnel. Appl. Sci. 2019, 9, 2318. [Google Scholar] [CrossRef]
- Yan, G.M.; Zhao, B.M.; Wang, Z.J.; Gao, B. Simplified analytical solution for responses of fault-crossing tunnels with flexible joints under fault movement. Structure 2022, 45, 984–998. [Google Scholar] [CrossRef]
- Li, L.; Xian, L.P.; Yao, C.F.; Guo, D.; Liu, C. Numerical Modeling of Seismic Responses and Seismic Measures of Tunnel Crossing a Fault Zone: A Case Study. Adv. Mater. Sci. Eng. 2020, 2020, 5640561. [Google Scholar] [CrossRef]
- Jiao, N.; Sun, S.; Liu, J.Y.; Guo, Q.; Ding, J.; Wan, X. Analysis of existing railway deformation caused by double shield tunnel construction in soil–rock composite stratum. Energy Rep. 2023, 9, 159–165. [Google Scholar] [CrossRef]
- Costa, P.A. Ballast mats for the reduction of railway traffic vibrations. Numerical study. Soil. Dyn. Earthq. Eng. 2012, 42, 137–150. [Google Scholar] [CrossRef]
- Wang, H.Y.; Markine, V.L. Methodology for the comprehensive analysis of railway transition zones. Comput. Geotech. 2018, 99, 64–79. [Google Scholar] [CrossRef]
- Lee, J.; Oh, K.; Park, Y.; Choi, J. Study on the Applicability of Dynamic Factor Standards by Comparison of Spring Constant Based Dynamic Factor of Ballasted and Concrete Track Structures. Appl. Sci. 2020, 10, 8361. [Google Scholar] [CrossRef]
- Qie, L.C.; Wang, H.; Xu, Y.; Xu, Y.X.; Xu, L.S. Research on Deformation Control Measure in Construction of Polyurethane Solidified Ballast Bed for Datong-Xi’an High Speed Railway. Chin. Railw. Sci. 2018, 39, 1–7. [Google Scholar]
- Tian, S.; Ling, X.Z.; Li, T.; Chan, A.; Georgescu, I.-R. Evaluating the Service Performance of Heavy Axle Load Ballasted Railway by Using Numerical Simulation Method. Appl. Sci. 2022, 12, 2539. [Google Scholar] [CrossRef]
- Liu, G.Z.; Qiao, Y.F.; He, M.C.; Fan, Y. An analytical solution of longitudinal response of tunnels under dislocation of active fault. Rock Soil Mech. 2020, 41, 923–932. [Google Scholar]
- GB/T 5599-2019; Standardization Administration of the People’s Republic of China: Specification for Dynamic Performance Evaluation and Test Appraisal of Rolling Stock. China Railway Publishing House: Beijing, China, 2019.
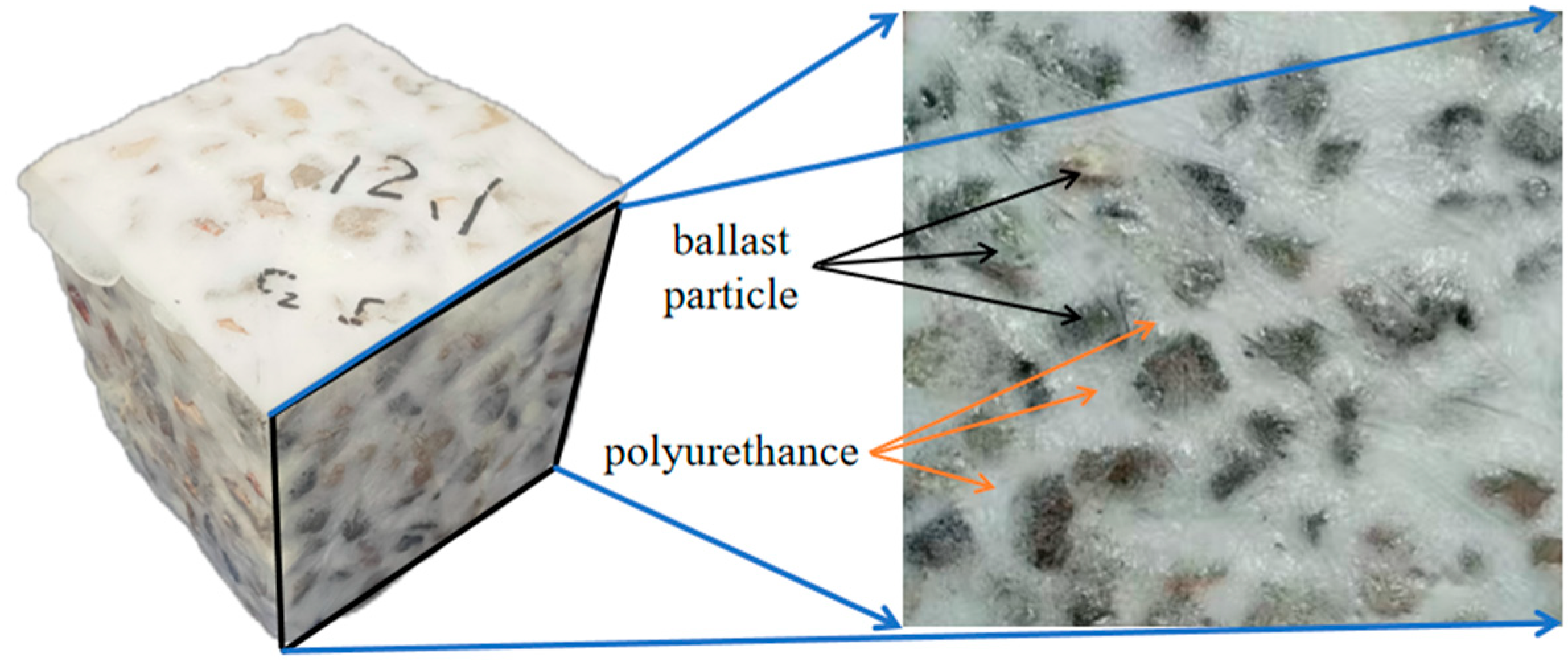
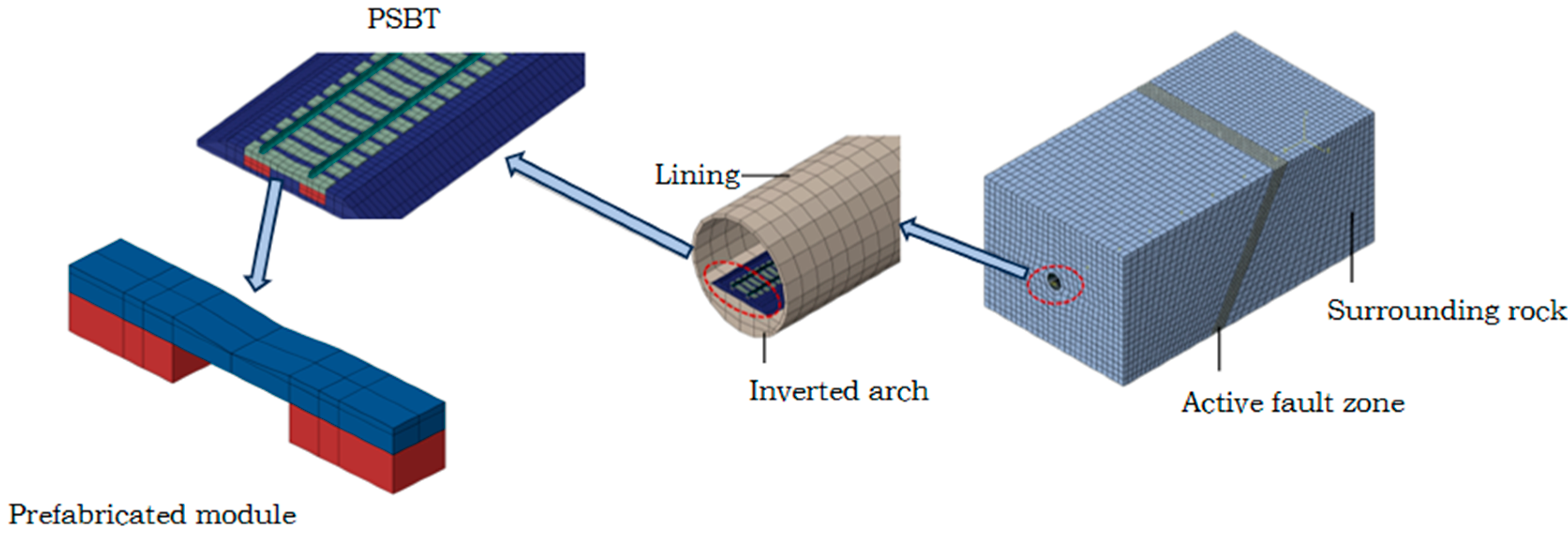
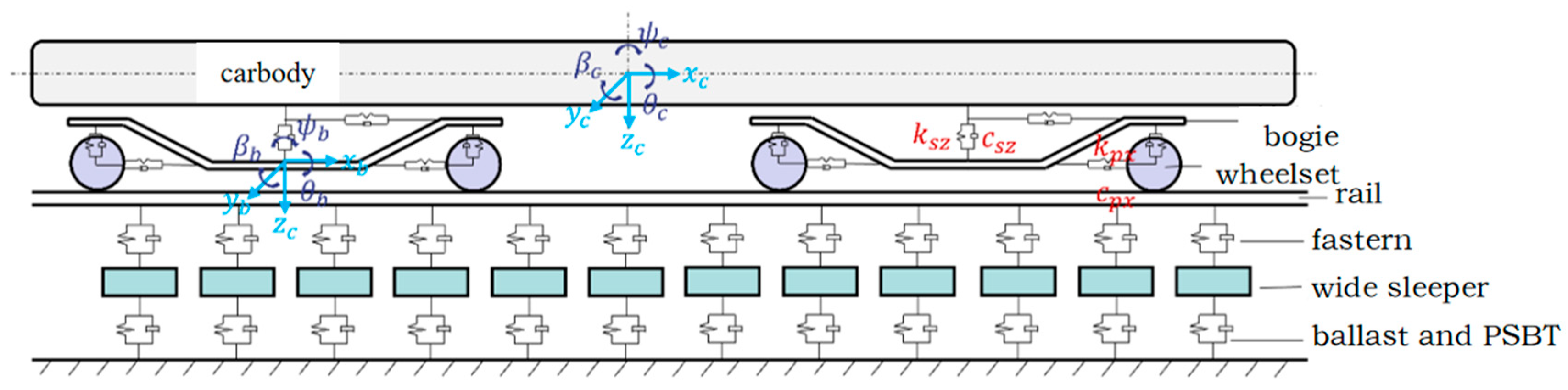
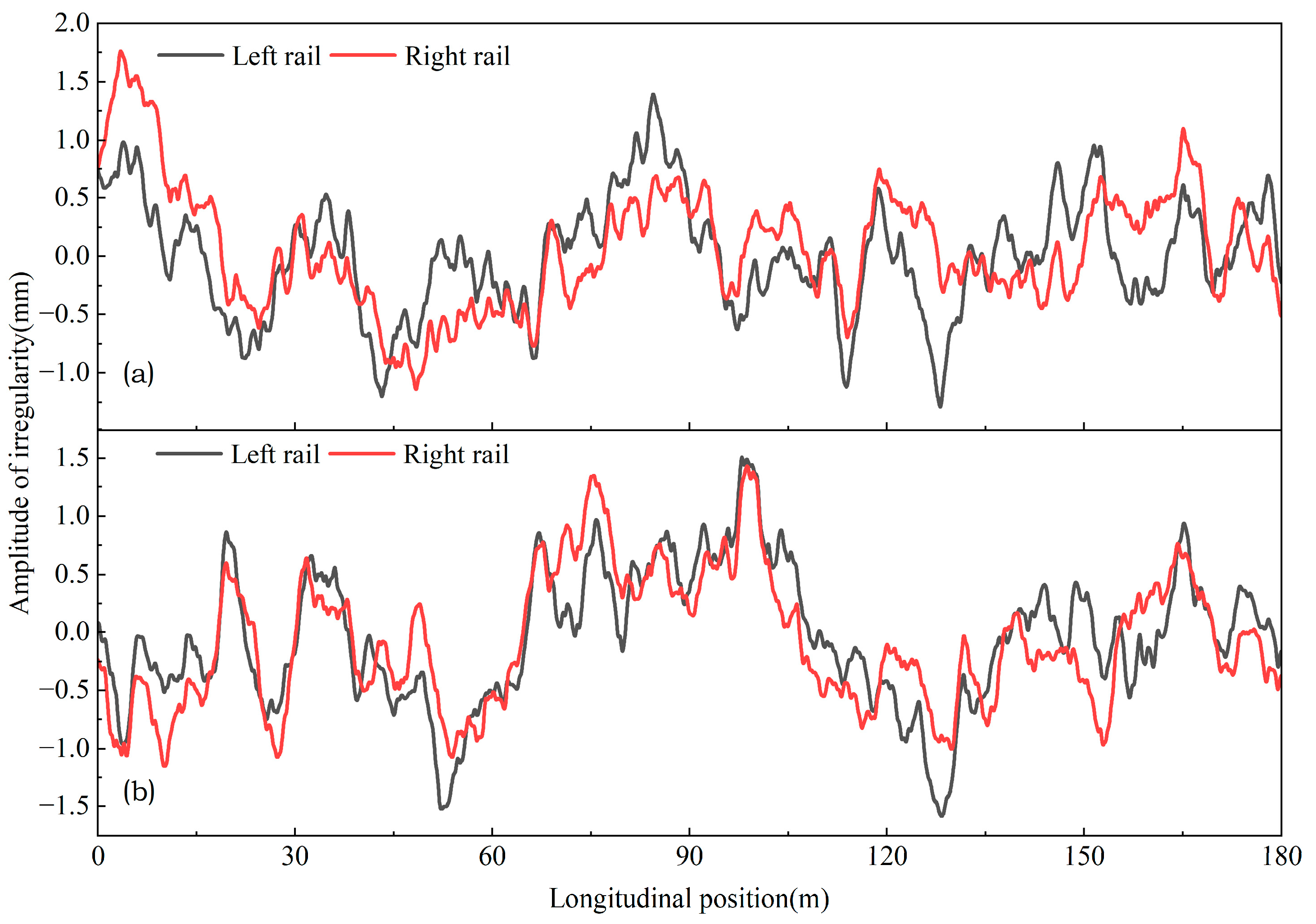

| Component | Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|
| Surrounding rock | 3800 | 0.31 | 2200 |
| Fault zone | 500 | 0.45 | 1900 |
| Lining | 32,500 | 0.2 | 2400 |
| Component | Parameters | Unit | Value |
|---|---|---|---|
| Steel rail | Density | kg/m3 | 7850 |
| Elastic modulus | MPa | 2.6 × 105 | |
| Poisson’s ratio | / | 0.167 | |
| Wide sleeper | Density | kg/m3 | 2500 |
| Elastic modulus | MPa | 3.65 × 104 | |
| Poisson’s ratio | / | 0.2 | |
| Polyurethane solidified track bed | Density | kg/m3 | 1900 |
| Elastic modulus | MPa | 60 | |
| Poisson’s ratio | / | 0.17 | |
| α damping coefficient | / | 3 | |
| β damping coefficient | / | 2.5 × 10−5 | |
| Ballast | Density | kg/m3 | 1800 |
| Elastic modulus | MPa | 130 | |
| Poisson’s ratio | / | 0.27 | |
| α damping coefficient | / | 3 | |
| β damping coefficient | / | 2.5 × 10−5 | |
| Fastener system | Vertical stiffness | MN/m | 120 |
| Lateral stiffness | MN/m | 40 | |
| Longitudinal stiffness | MN/m | 20 | |
| Vertical damping | N·s/m | 2 × 104 | |
| Lateral damping | N·s/m | 2 × 104 | |
| Longitudinal damping | N·s/m | 2 × 104 | |
| Vertical stiffness | MN/m | 120 |
| Work Condition | Displacement Due to Fault Movement (mm) | Width of Fault Zone (m) | Dip Angle of Fault Zone (°) |
|---|---|---|---|
| 1–4 | 10/20/30/40 | 10 | 60 |
| 5–9 | 40 | 0/5/10/15/20 | 60 |
| 10–12 | 40 | 10 | 45/60/75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wu, D.; Yu, M.; Wu, P.; Zhang, Y.; Luo, S.; Xu, L. Active Fault Dislocation-Induced Mechanical Response of Polyurethane-Solidified Track in Tunnels. Materials 2025, 18, 2492. https://doi.org/10.3390/ma18112492
Chen W, Wu D, Yu M, Wu P, Zhang Y, Luo S, Xu L. Active Fault Dislocation-Induced Mechanical Response of Polyurethane-Solidified Track in Tunnels. Materials. 2025; 18(11):2492. https://doi.org/10.3390/ma18112492
Chicago/Turabian StyleChen, Wei, Dan Wu, Minzhe Yu, Pei Wu, Yushuo Zhang, Shang Luo, and Lei Xu. 2025. "Active Fault Dislocation-Induced Mechanical Response of Polyurethane-Solidified Track in Tunnels" Materials 18, no. 11: 2492. https://doi.org/10.3390/ma18112492
APA StyleChen, W., Wu, D., Yu, M., Wu, P., Zhang, Y., Luo, S., & Xu, L. (2025). Active Fault Dislocation-Induced Mechanical Response of Polyurethane-Solidified Track in Tunnels. Materials, 18(11), 2492. https://doi.org/10.3390/ma18112492






