A Dynamic Tensile Method Using a Modified M-Typed Specimen Loaded by Split Hopkinson Pressure Bar
Abstract
1. Introduction
2. Experimental Methodology
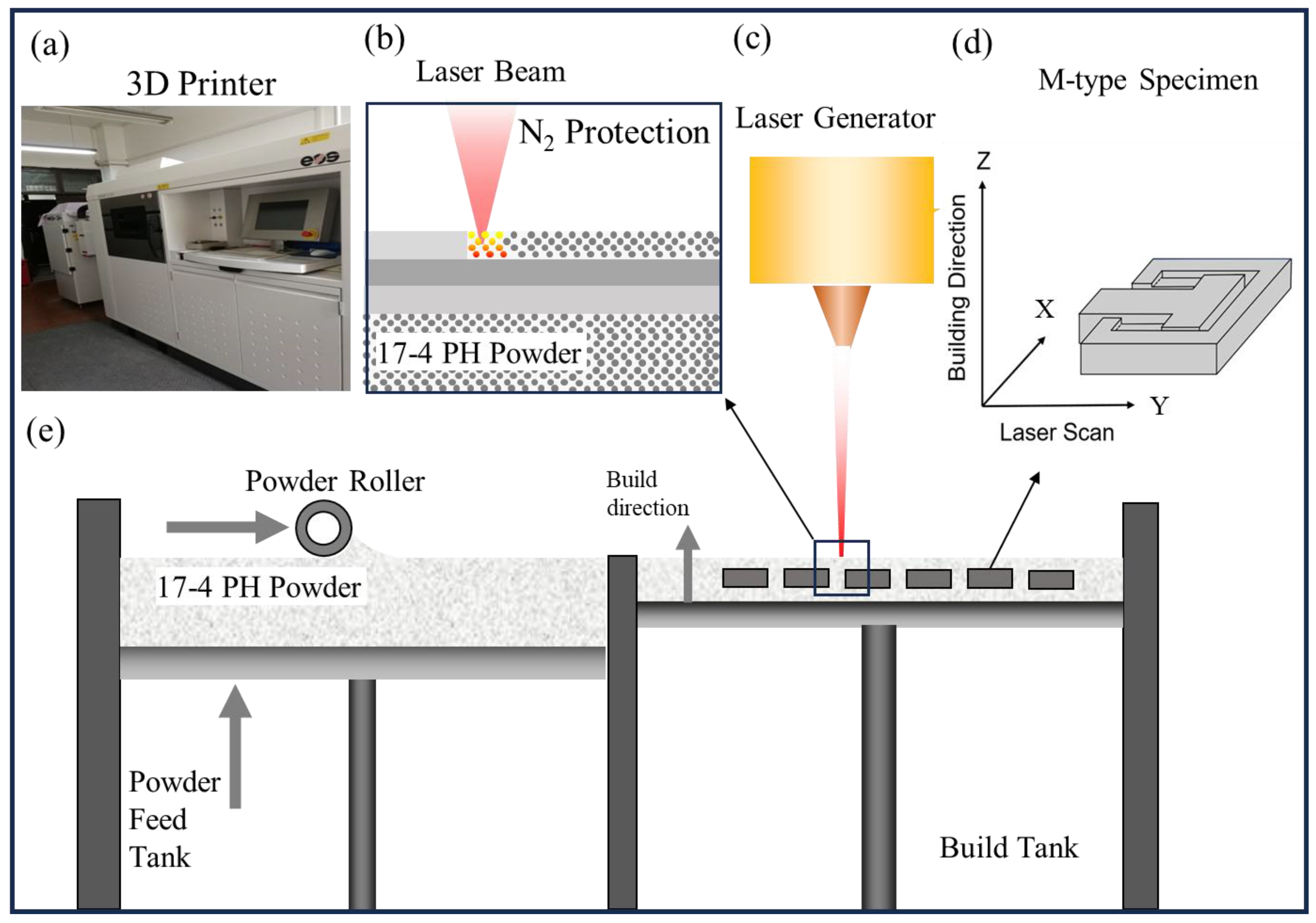
2.1. 3D-Printed Material
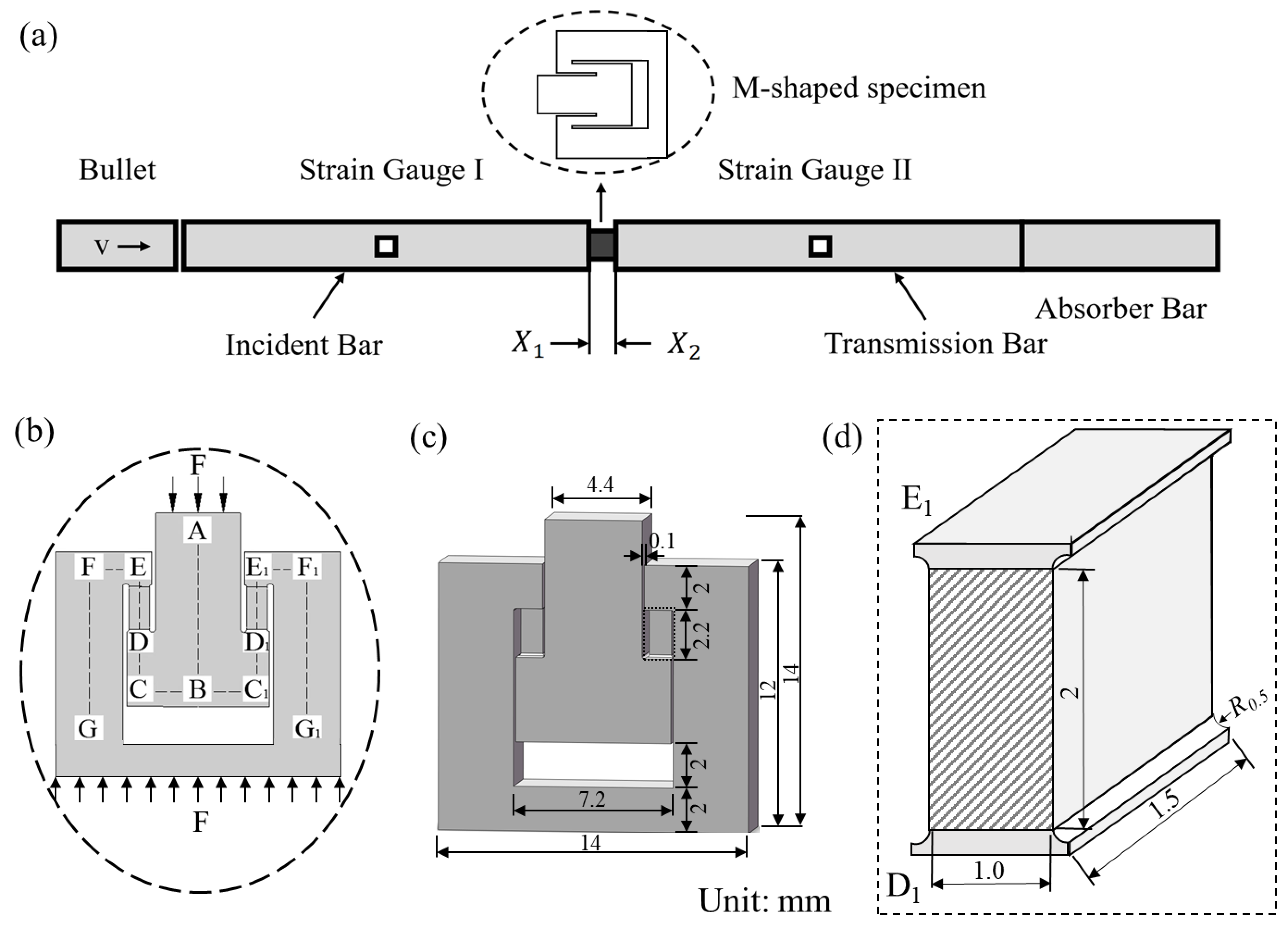
2.2. M-Type Tensile Method
2.2.1. Basic Framework
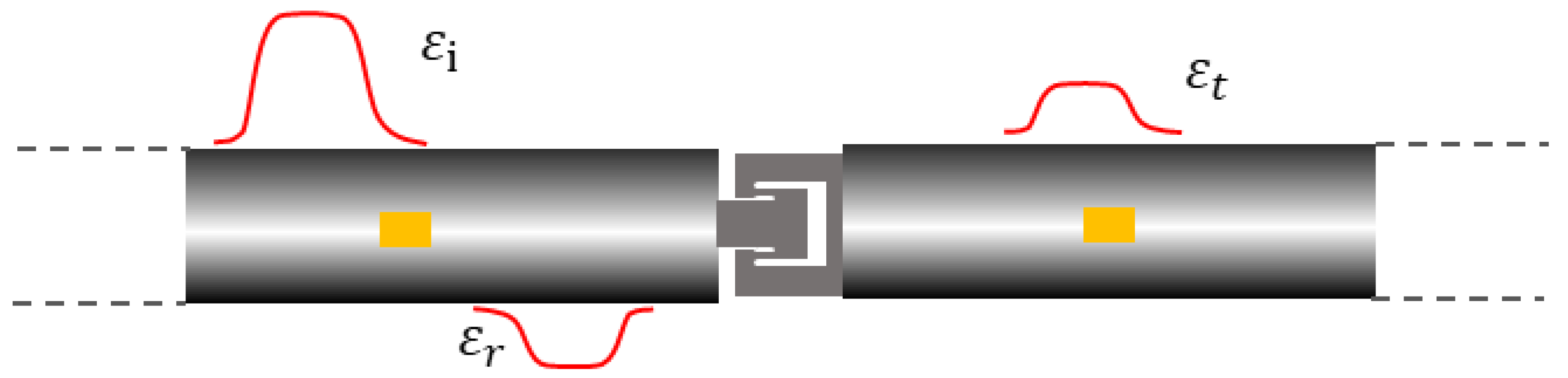
2.2.2. SHPB
2.2.3. Stress and Strain
2.3. Experimental Program
3. Numerical Simulation
3.1. FE Model
3.2. Specimen Shape
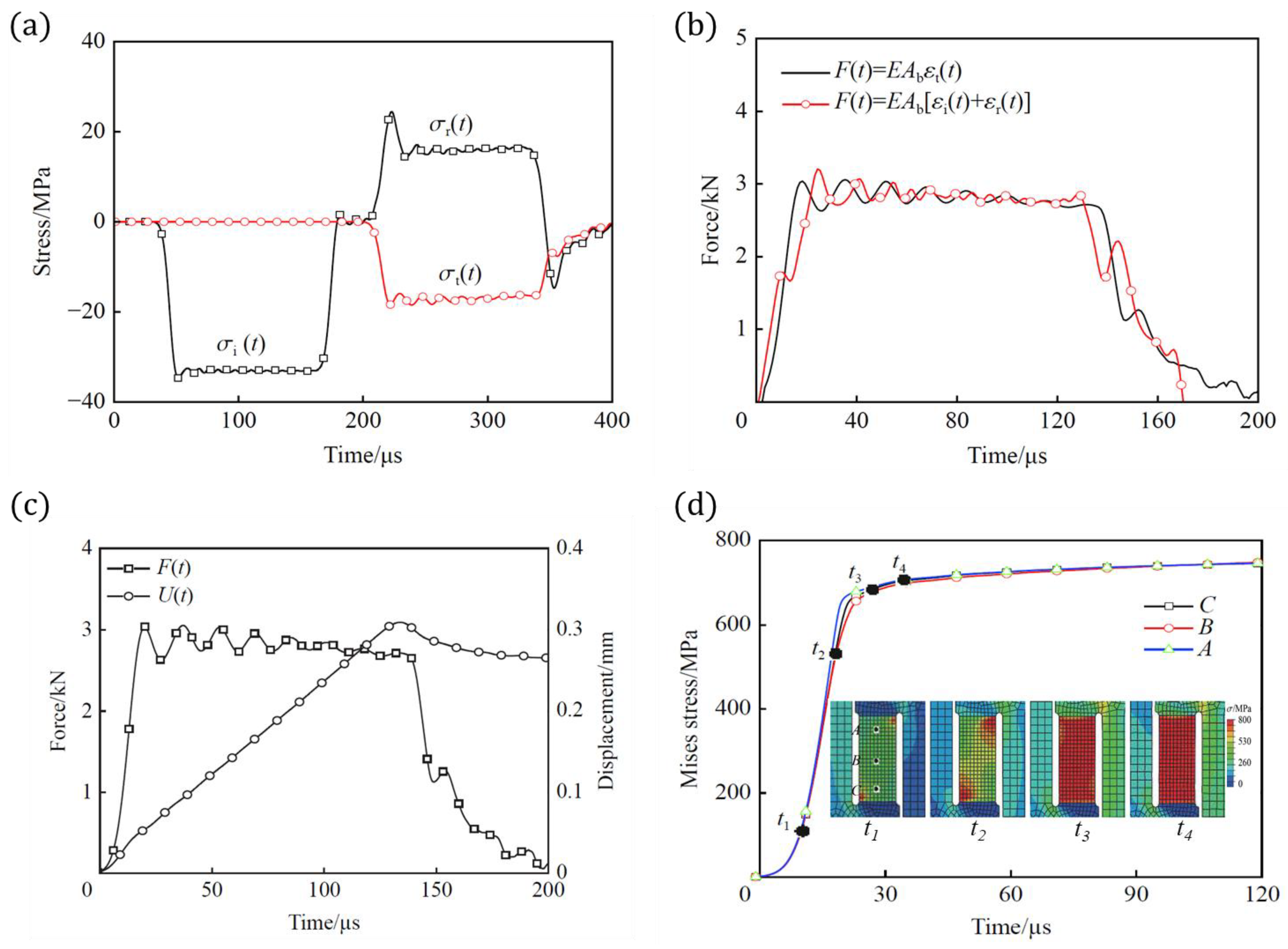
3.3. Verification of Stress Balance and Uniform
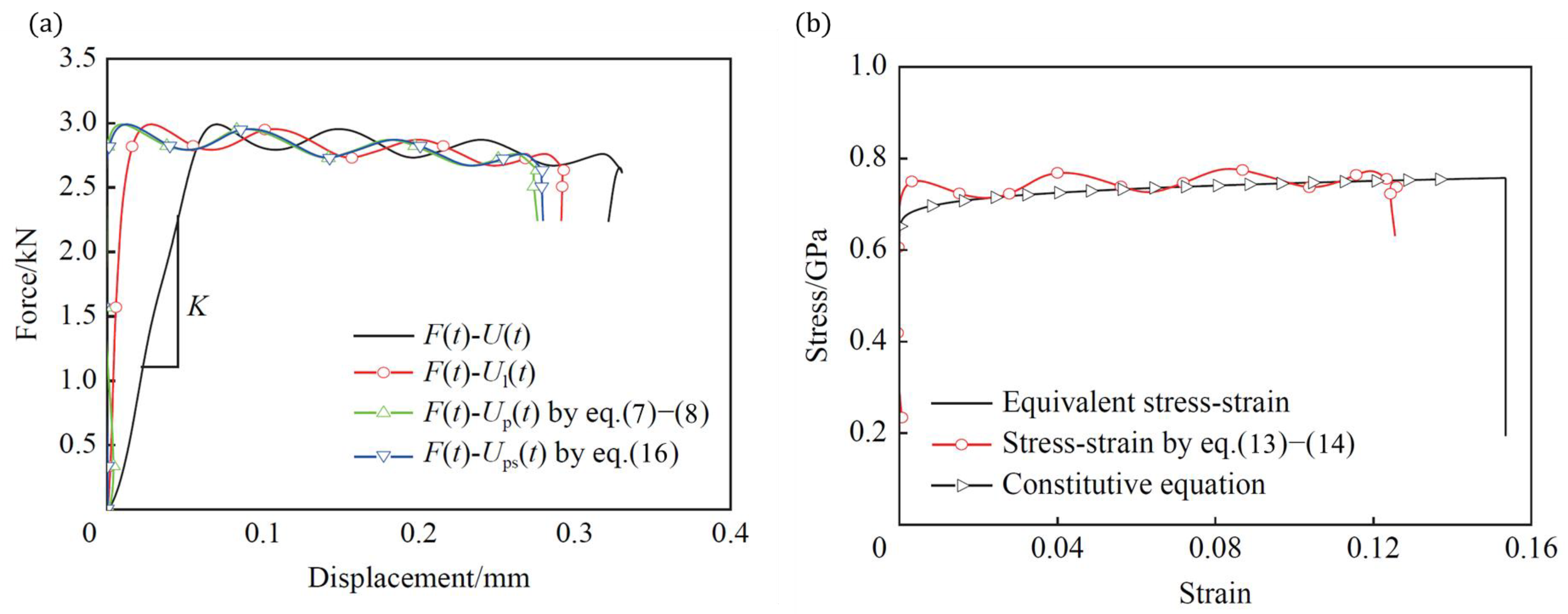
3.4. Numerical Correction of Stress–Strain Curve
4. Experimental Results
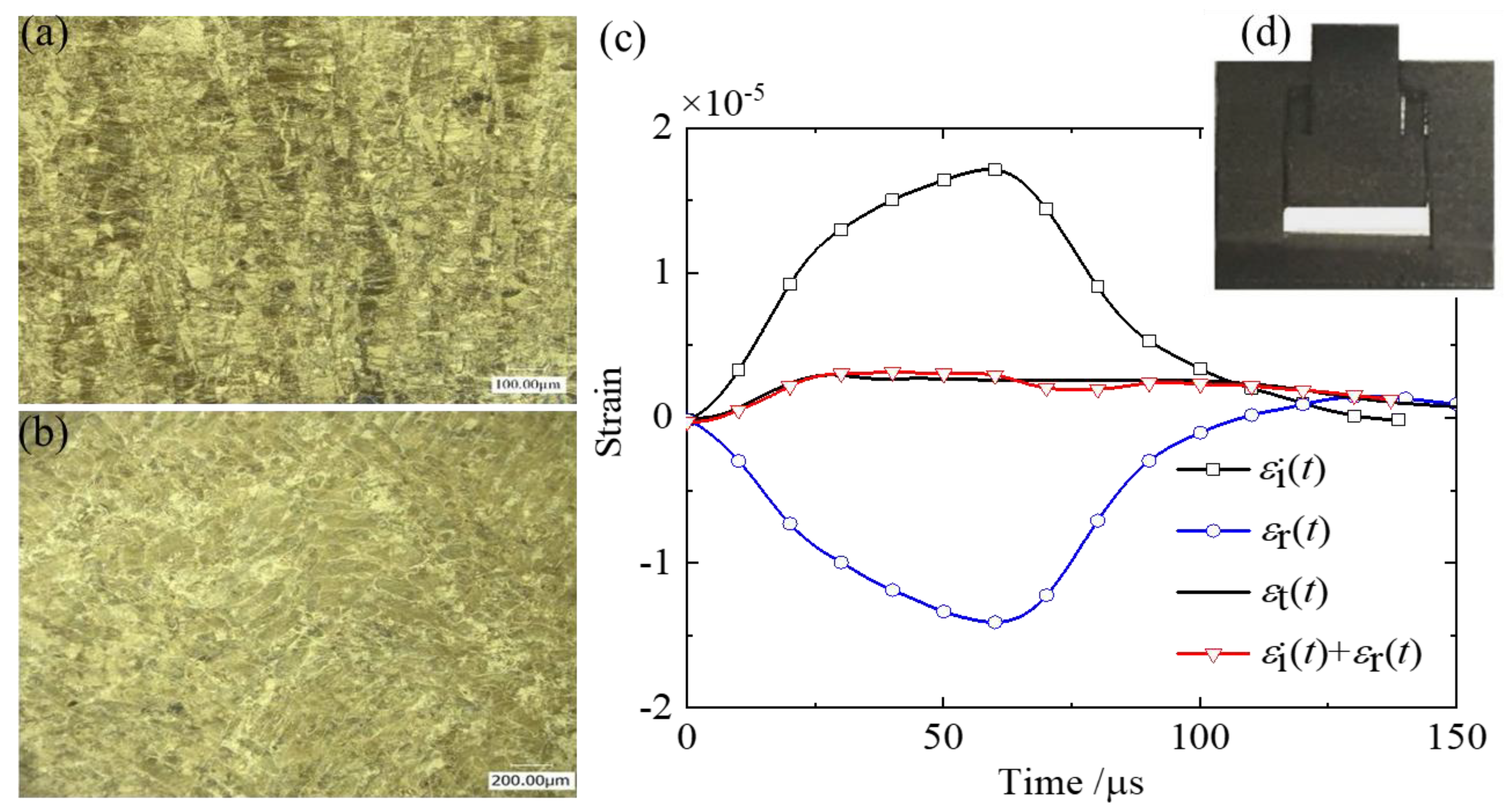
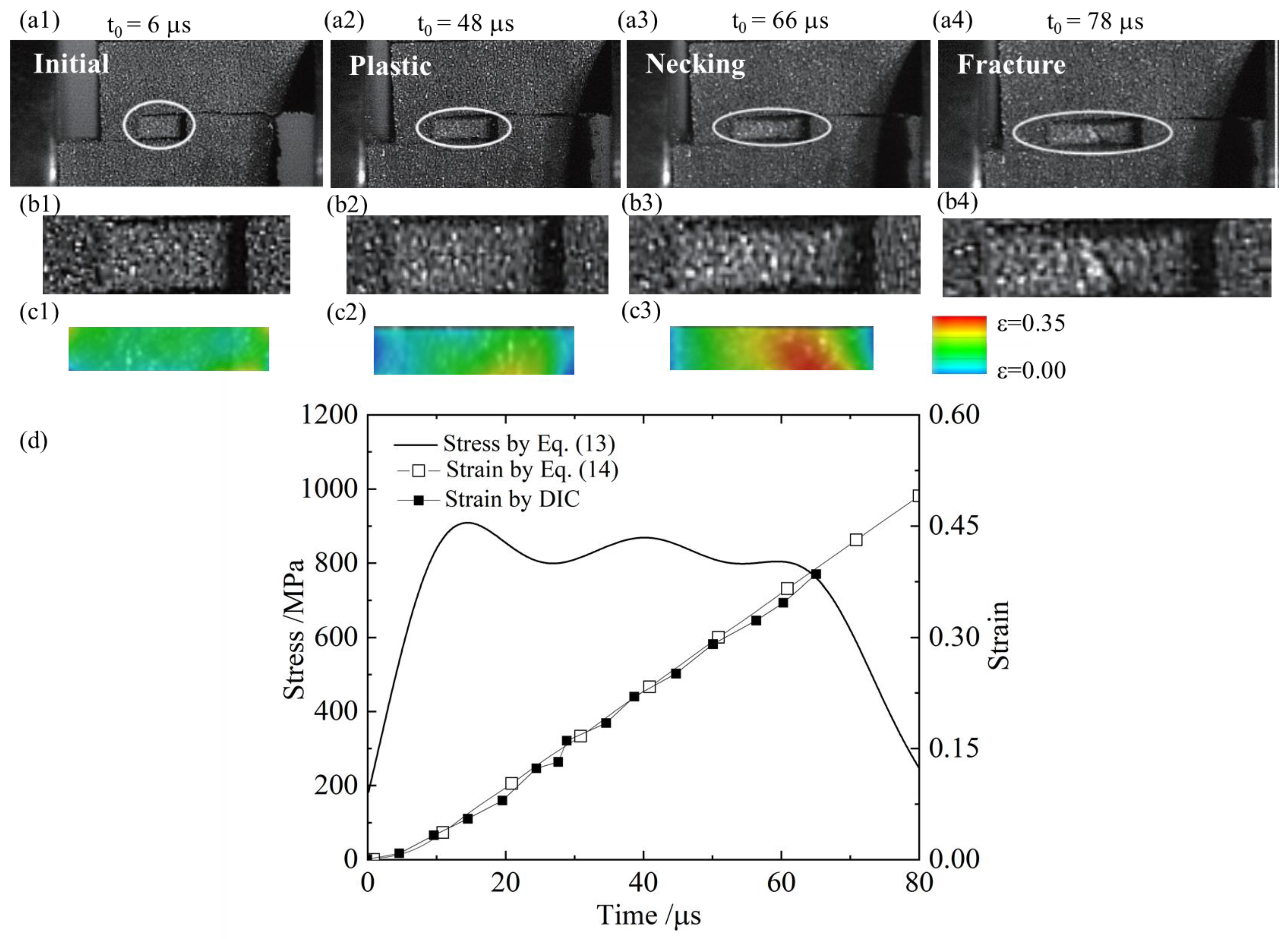
4.1. Dynamic Test
4.2. Evolution of Tensile Stress and Strain
4.3. Strain Rate
5. Further Research Perspectives
6. Conclusions
- The Hopkinson pressure bar allowed dynamic loading of closed M-type specimens while meeting the one-dimensional stress assumption. This approach eliminated connection challenges between specimens and bar ends, providing convenient loading and effective results.
- The FE method was conducted to obtain the stiffness of M-type specimen, which was used to improve the interpretation of physical test results. This approach allowed for accurate calculation of plastic strain in the gauge section.
- Compared with the conventional split Hopkinson tensile bar, in this study, the tensile method using the M-type specimen achieved both ultra-high strain rates (up to 6000 s−1) and large plastic deformations. Thus, this is a reliable method for assessing the dynamic tensile properties of stainless steel samples at high loading rates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nicholas, T. Tensile testing of materials at high rates of strain: An experimental technique is developed for testing materials at strain rates up to 103 s−1 in tension using a modification of the Split Hopkinson Bar or Kolsky Apparatus. Exp. Mech. 1981, 21, 177–185. [Google Scholar] [CrossRef]
- Fu, Y.; Yu, X.; Dong, X.; Zhou, F.; Ning, J.; Li, P.; Zheng, Y. Investigating the failure behaviors of RC beams without stirrups under impact loading. Int. J. Impact Eng. 2020, 137, 103432. [Google Scholar] [CrossRef]
- Liang, H.; Fang, X.; Yu, X.; Fu, Y.; Zhou, G. Investigating the Fracture Process and Tensile Mechanical Behaviours of Brittle Materials under Concentrated and Distributed Boundary Conditions. Appl. Sci. 2023, 13, 5273. [Google Scholar] [CrossRef]
- Yu, X.; Fu, Y.; Dong, X.; Zhou, F.; Ning, J. An Improved Lagrangian-Inverse Method for Evaluating the Dynamic Constitutive Parameters of Concrete. Materials 2020, 13, 1871. [Google Scholar] [CrossRef]
- Weckert, S.A.; Resnyansky, A.D. Experiments and modelling for characterisation and validation of a two-phase constitutive model for describing sands under explosive loading. Int. J. Impact Eng. 2022, 166, 104234. [Google Scholar] [CrossRef]
- Cisse, C.; Zaki, W.; Zineb, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Mott, P.H.; Twigg, J.N.; Roland, D.F.; Schrader, H.S.; Pathak, J.A.; Roland, C.M. High-speed tensile test instrument. Rev. Sci. Instrum. 2007, 78, 045105. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Pellegrino, A.; Heisserer, U.; Duke, P.W.; Curtis, P.T.; Morton, J.; Petrinic, N.; Tagarielli, V.L. A new technique for tensile testing of engineering materials and composites at high strain rates. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20190310. [Google Scholar] [CrossRef] [PubMed]
- Choi, I.; Lee, S.; Matlock, D.K.; Speer, J.G. Strain control during high speed tensile testing. J. Test. Eval. 2006, 34, 443–446. [Google Scholar] [CrossRef]
- Harding, J.W.E.O.C.; Wood, E.O.; Campbell, J.D. Tensile testing of materials at impact rates of strain. J. Mech. Eng. Sci. 1960, 2, 88–96. [Google Scholar] [CrossRef]
- Bhujangrao, T.; Froustey, C.; Iriondo, E.; Veiga, F.; Darnis, P.; Mata, F.G. Review of Intermediate Strain Rate Testing Devices. Metals 2020, 10, 894. [Google Scholar] [CrossRef]
- Hsu, T.; Zhang, L.; Gomez, T. A servo-control system for the universal panel tester. J. Test. Eval. 1995, 23, 424–430. [Google Scholar] [CrossRef]
- Hudson, J.A.; Crouch, S.L.; Fairhurst, C. Soft, stiff and servo-controlled testing machines: A review with reference to rock failure. Eng. Geol. 1972, 6, 155–189. [Google Scholar] [CrossRef]
- Xiao, X. Dynamic tensile testing of plastic materials. Polym. Test. 2007, 27, 164–178. [Google Scholar] [CrossRef]
- Bastias, P.C.; Kulkarni, S.M.; Kim, K.Y.; Gargas, J. Noncontacting strain measurements during tensile tests. Exp. Mech. 1996, 36, 78–83. [Google Scholar] [CrossRef]
- Roland, C.M.; Twigg, J.N.; Vu, Y.; Mott, P.H. High Strain Rate Mechanical Behavior of Polyurea. Polymer 2007, 48, 574–578. [Google Scholar] [CrossRef]
- Wu, H.; Ma, G.; Xia, Y. Experimental study of tensile properties of PMMA at intermediate strain rate. Mater. Lett. 2004, 58, 3681–3685. [Google Scholar] [CrossRef]
- Wang, W.; Ma, Y.; Yang, M.; Jiang, P.; Yuan, F.; Wu, X. Strain Rate Effect on Tensile Behavior for a High Specific Strength Steel: From Quasi-Static to Intermediate Strain Rates. Metals 2018, 8, 11. [Google Scholar] [CrossRef]
- Zhao, H. Material behaviour characterisation using SHPB techniques, tests and simulations. Comput. Struct. 2003, 81, 1301–1310. [Google Scholar] [CrossRef]
- Meng, H.; Li, Q.M. Correlation between the accuracy of a SHPB test and the stress uniformity based on numerical experiments. Int. J. Impact Eng. 2003, 28, 537–555. [Google Scholar] [CrossRef]
- Ni, P.; Tang, L.; Xu, P.; Wang, X.; Yang, B.; Liu, Y.; Liu, Z.; Jiang, Z.; Zhou, L. Correction method and verification of radial inertia and friction effects under a unified deformation framework in SHPB experiments on soft materials. Int. J. Impact Eng. 2025, 195, 105129. [Google Scholar] [CrossRef]
- Sasso, M.; Mancini, E.; Chiappini, G.; Utzeri, M.; Amodio, D. A 90-meter Split Hopkinson Tension–Torsion Bar: Design, Construction and First Tests. J. Dyn. Behav. Mater. 2024, 1–20. [Google Scholar] [CrossRef]
- Chen, W.W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Xu, Y.; Lopez, M.A.; Zhou, J.; Farbaniec, L.; Patsias, S.; Macdougall, D.; Reed, J.; Petrinic, N.; Eakins, D.; Siviour, C.; et al. Experimental analysis of the multiaxial failure stress locus of commercially pure titanium at low and high rates of strain. Int. J. Impact Eng. 2022, 170, 104341. [Google Scholar] [CrossRef]
- Mochalova, V.; Utkin, A.; Savinykh, A.; Garkushin, G. Pulse compression and tension of Kevlar/epoxy composite under shock wave action. Comp. Struct. 2021, 273, 114309. [Google Scholar] [CrossRef]
- Qi, L.; Li, H.; Jin, K.; Feng, Y.; Guo, Y.; Li, Y. Biaxial tensile behavior of Ti-6Al-4V under proportional loadings at high strain rates. Int. J. Impact Eng. 2023, 182, 104781. [Google Scholar] [CrossRef]
- Moreira, B.S.; Nunes, P.D.P.; da Silva, C.M.; Tenreiro, A.F.G.; Lopes, A.M.; Carbas, R.J.C.; Marques, E.A.S.; Parente, M.P.L.; da Silva, L.F.M. Numerical Design of a Thread-Optimized Gripping System for Lap Joint Testing in a Split Hopkinson Apparatus. Sensors 2023, 23, 2273. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.L. Foundation of Stress Waves; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Mohr, D.; Gary, G. M-shaped specimen for the high-strain rate tensile testing using a Split Hopkinson Pressure Bar apparatus. Exp. Mech. 2007, 47, 681–692. [Google Scholar] [CrossRef]
- Rafi, H.K.; Pal, D.; Patil, N.; Starr, T.L.; Stucker, B.E. Microstructure and Mechanical Behavior of 17-4 Precipitation Harden-able Steel Processed by Selective Laser Melting. J. Mater. Eng. Perform. 2014, 23, 4421–4428. [Google Scholar] [CrossRef]
- Luecke, W.E.; Slotwinski, J.A. Mechanical properties of austenitic stainless steel made by additive manufacturing. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 398–418. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.L.; Tang, H.P.; Ning, Y.P.; Liu, N.; Stjohn, D.H.; Qian, M. Microstructure and mechanical properties of long Ti-6Al-4V rods additively manufactured by selective electron beam melting out of a deep powder bed and the effect of subsequent hot isostatic pressing. Metall. Mater. Trans. A 2015, 46, 3824–3834. [Google Scholar] [CrossRef]
- Rodriguez, O.L.; Allison, P.G.; Whittington, W.R.; Francis, D.K.; Rivera, O.G.; Chou, K.; Gong, X.; Butler, T.M.; Burroughs, J.F. Dynamic tensile behavior of electron beams additive manufactured Ti6Al4V. Mater. Sci. Eng. A 2015, 641, 323–327. [Google Scholar] [CrossRef]
- Mcwilliams, B.; Pramanik, B.; Kudzal, A.; Taggart-Scarff, J. High strain rate compressive deformation behavior of an additively manufactured stainless steel. Addit. Manuf. 2018, 24, 432–439. [Google Scholar] [CrossRef]
- Shi, T.Y.; Liu, D.S.; Chen, W.; Xie, P.C.; Wang, X.F.; Wang, Y.G. Dynamic tensile behavior and spall fracture of GP1 stainless steel processed by selective laser melting. Explos. Shock Waves 2019, 39, 49–60. [Google Scholar] [CrossRef]
- Song, B.; Nishida, E.; Sanborn, B.; Maguire, M.; Adams, D.; Carroll, J.; Wise, J.; Reedlunn, B.; Bishop, J.; Palmer, T. Compressive and tensile stress–strain responses of additively manufactured (AM) 304L stainless steel at high strain rates. J. Dyn. Behav. Mater. 2017, 3, 412–425. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Shi, T.; Wang, Y. Tensile mechanical behavior and spall response of a selective laser melted 17-4 PH stainless steel. Metall. Mater. Trans. A 2021, 52, 2369–2388. [Google Scholar] [CrossRef]
- Ding, L.; Li, H.X.; Wang, Y.D.; Huang, Z.T. Heat Treatment on Microstructure and Tensile Strength of 316 Stainless Steel by Selective Laser Melting. Chin. J. Lasers 2015, 42, 179–185. [Google Scholar] [CrossRef]
- Lee, W.; Lin, C. Plastic deformation and fracture behaviour of Ti–6Al–4V alloy loaded with high strain rate under various temperatures. Mater. Sci. Eng. A 1998, 241, 48–59. [Google Scholar] [CrossRef]
- Cestino, E.; Frulla, G.; Piana, P.; Duella, R. Numerical/Experimental Validation of Thin-Walled Composite Box Beam Optimal Design. Aerospace 2020, 7, 111. [Google Scholar] [CrossRef]
- Gürdal, Z.; Tatting, B.F.; Wu, C.K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Pierron, F.; Vert, G.; Burguete, R.; Avril, S.; Rotinat, R.; Wisnom, M.R. Identification of the orthotropic elastic stiffnesses of composites with the virtual fields method: Sensitivity study and experimental validation. Strain 2007, 43, 250–259. [Google Scholar] [CrossRef]



| Parameters | Setting |
|---|---|
| Subset | 15 × 15 pixel2 |
| Step | 5 pixels |
| Magnification factor | 0.6 mm/pixel |
| Strain filter size | Gaussian (5) |
| Matching criterion | Normalized squared differences |
| Interpolation | Optimized 8-tap interpolation |
| Shape function | Affine |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Fan, J.; Yu, X.; Fu, Y.; Zhou, G.; Wang, X.; Dong, X. A Dynamic Tensile Method Using a Modified M-Typed Specimen Loaded by Split Hopkinson Pressure Bar. Materials 2025, 18, 149. https://doi.org/10.3390/ma18010149
Lin Y, Fan J, Yu X, Fu Y, Zhou G, Wang X, Dong X. A Dynamic Tensile Method Using a Modified M-Typed Specimen Loaded by Split Hopkinson Pressure Bar. Materials. 2025; 18(1):149. https://doi.org/10.3390/ma18010149
Chicago/Turabian StyleLin, Yuan, Jitang Fan, Xinlu Yu, Yingqian Fu, Gangyi Zhou, Xu Wang, and Xinlong Dong. 2025. "A Dynamic Tensile Method Using a Modified M-Typed Specimen Loaded by Split Hopkinson Pressure Bar" Materials 18, no. 1: 149. https://doi.org/10.3390/ma18010149
APA StyleLin, Y., Fan, J., Yu, X., Fu, Y., Zhou, G., Wang, X., & Dong, X. (2025). A Dynamic Tensile Method Using a Modified M-Typed Specimen Loaded by Split Hopkinson Pressure Bar. Materials, 18(1), 149. https://doi.org/10.3390/ma18010149





