Mathematical Models of Grinding Forces in the Hob Cutter Sharpening Process
Abstract
1. Introduction
2. The Conditions and Methodology of the Research
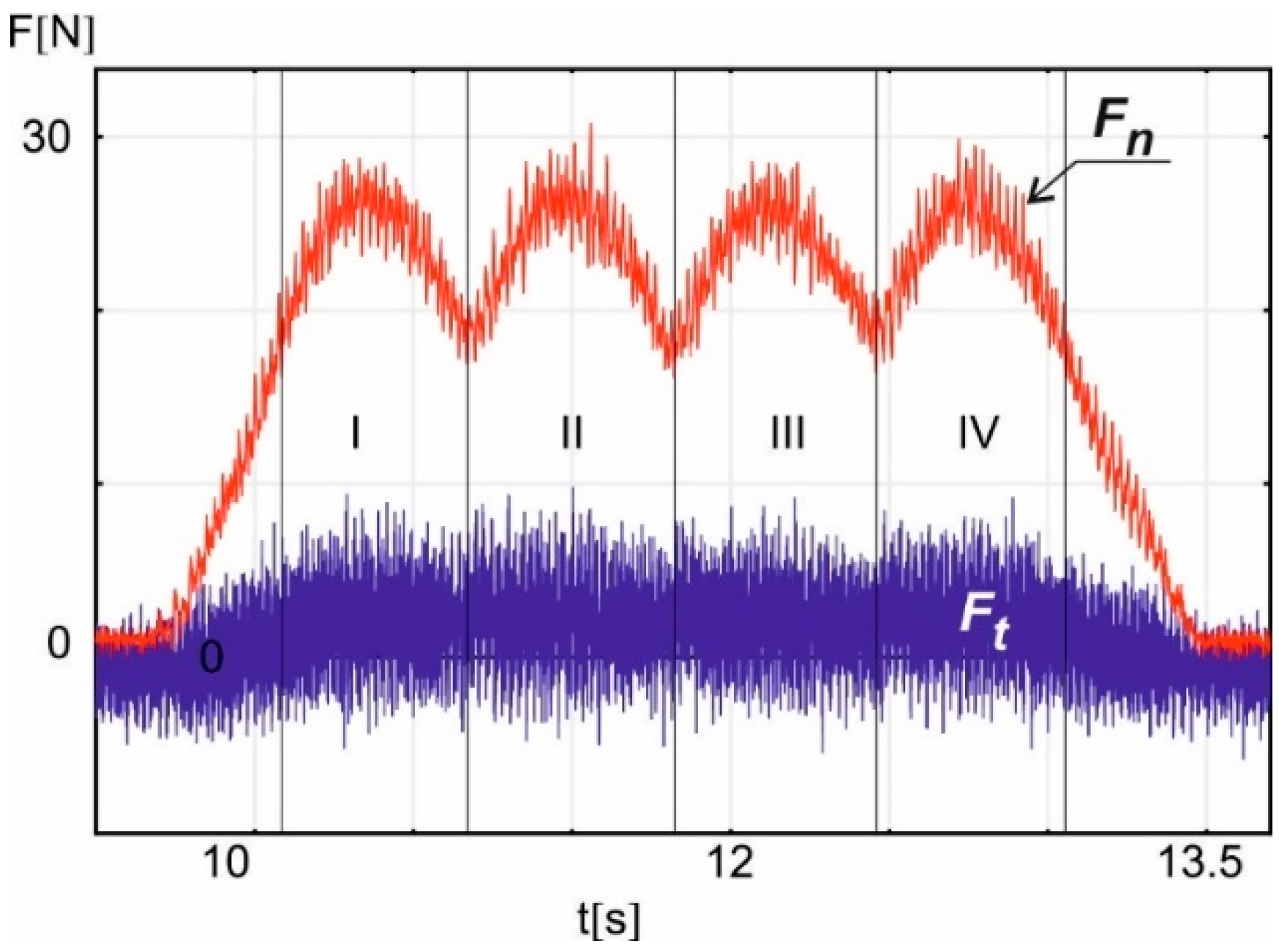
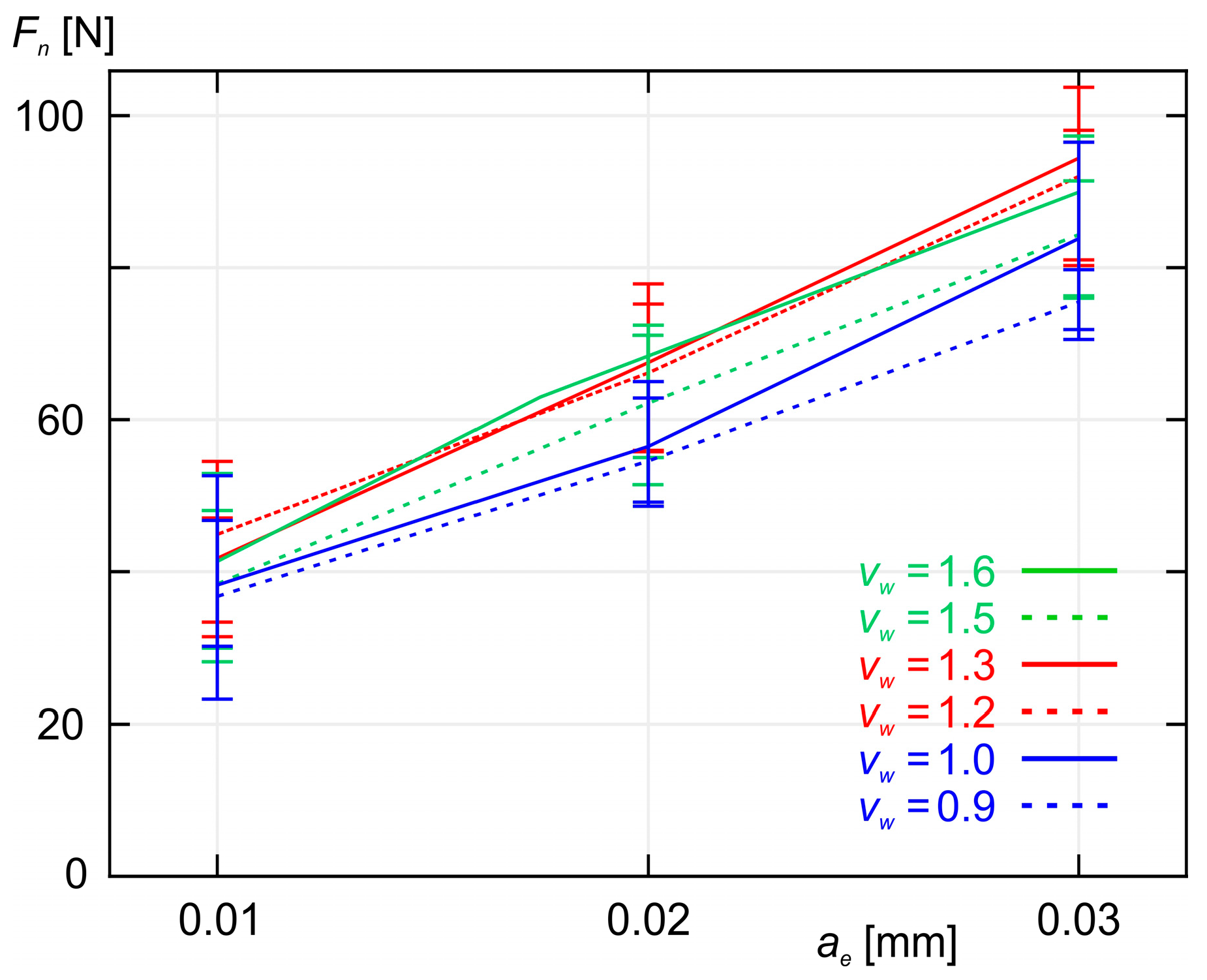
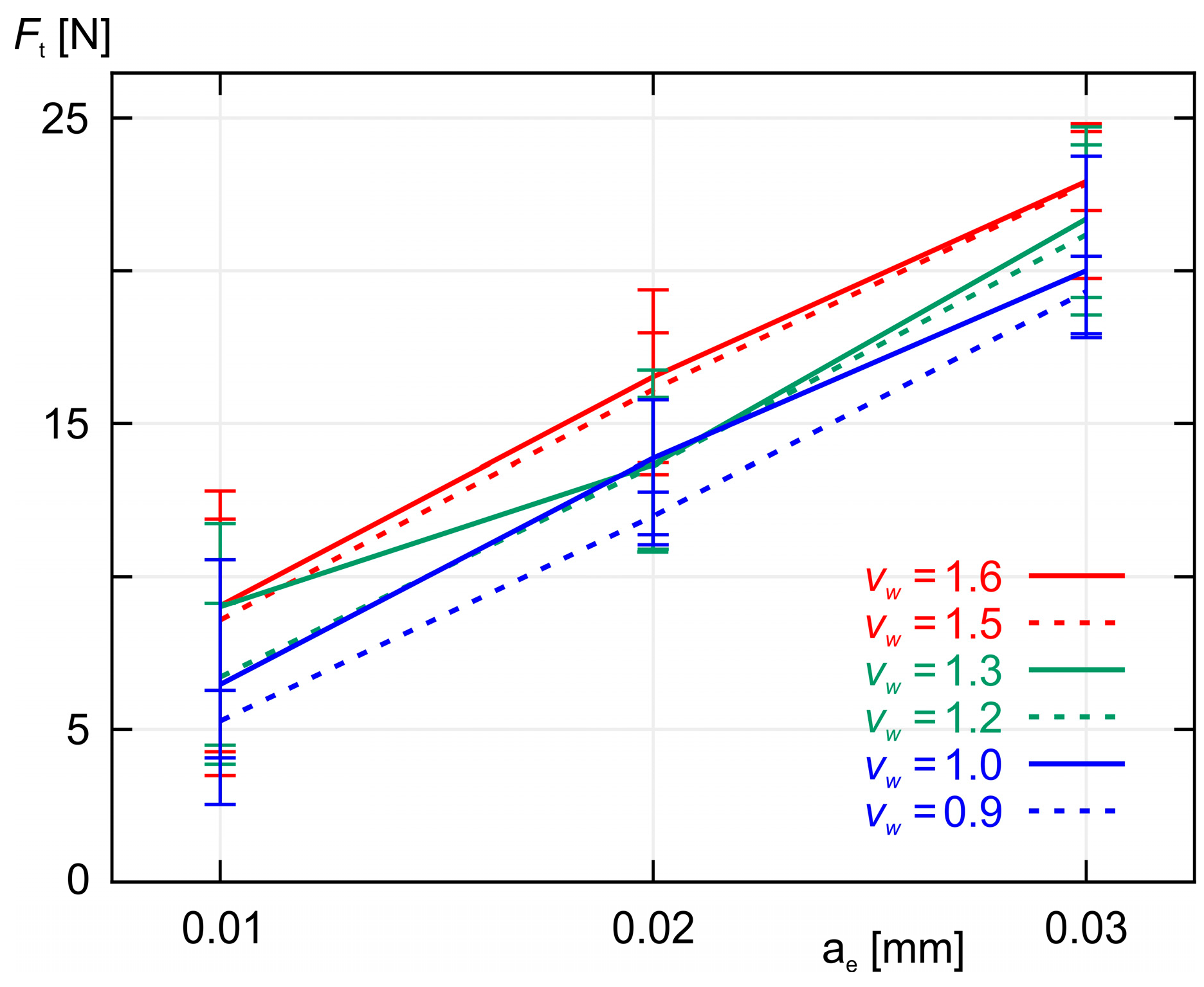
3. Experimental Results
4. Force Models of Grinding Process
4.1. The Polynominal Model Force
- K—grinding coefficient, N/mm;
- f—exponential coefficient;
- vw—workpiece speed, m/min;
- vs—grinding wheel peripheral speed, m/s;
- ae—grinding depth, mm;
- D—grinding wheel outer diameter, mm.
- vs = 30.1 m/s;
- D = 125 mm.
4.2. The Regression Analysis Procedure
- F0—constant of the equation;
- fv, fa—exponents of the equation.
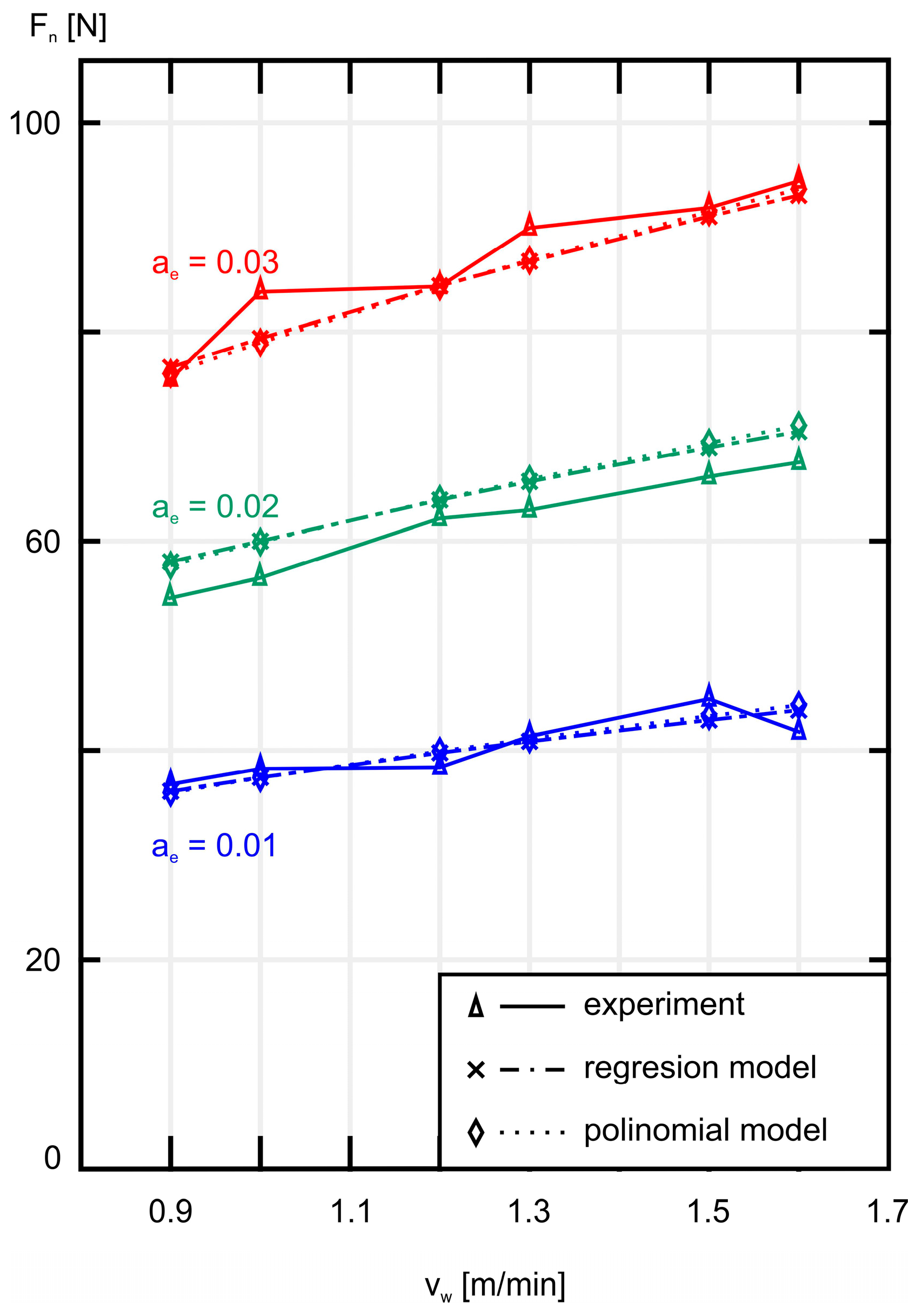
4.3. Comparison of Models and Experiment Results
5. Conclusions
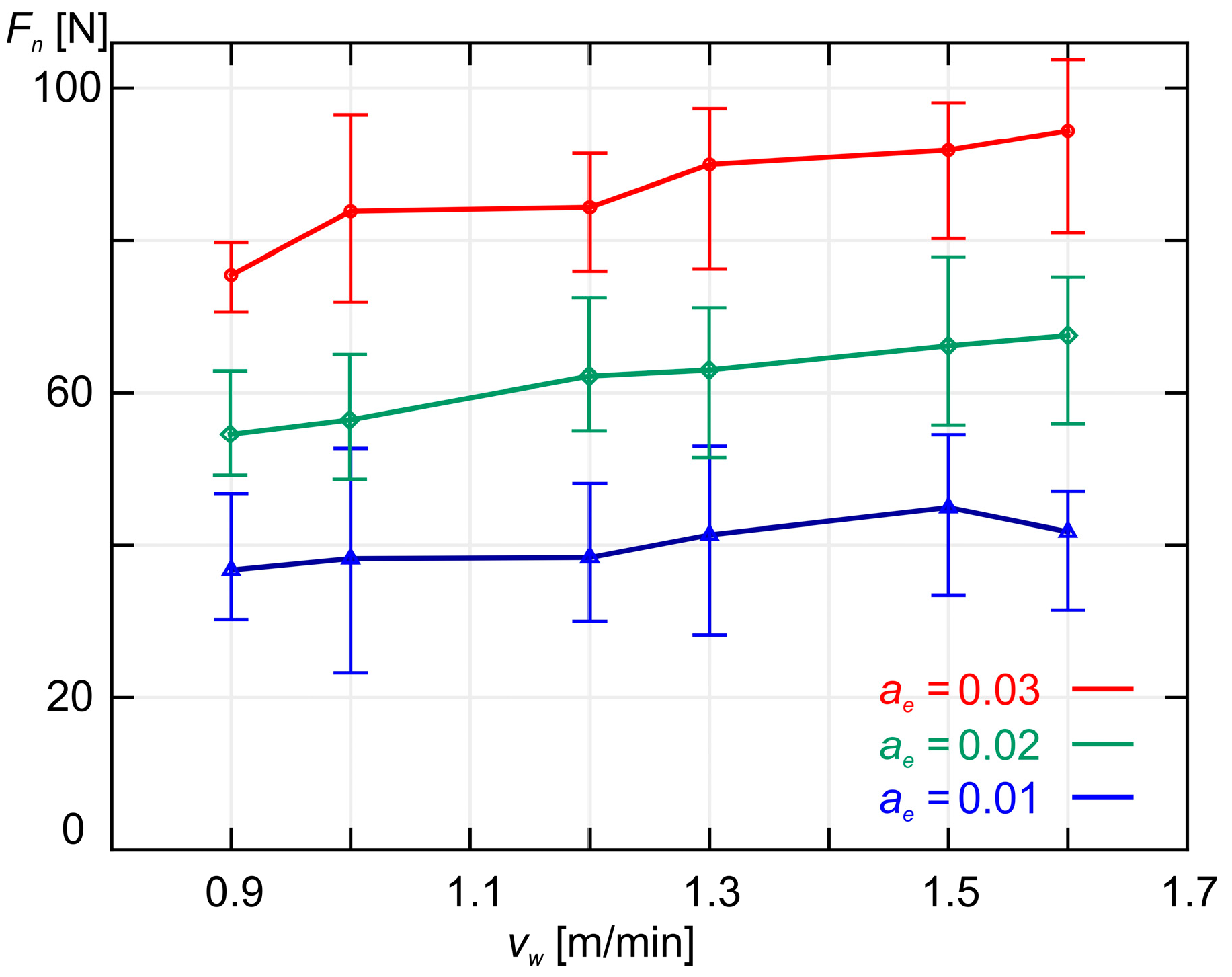
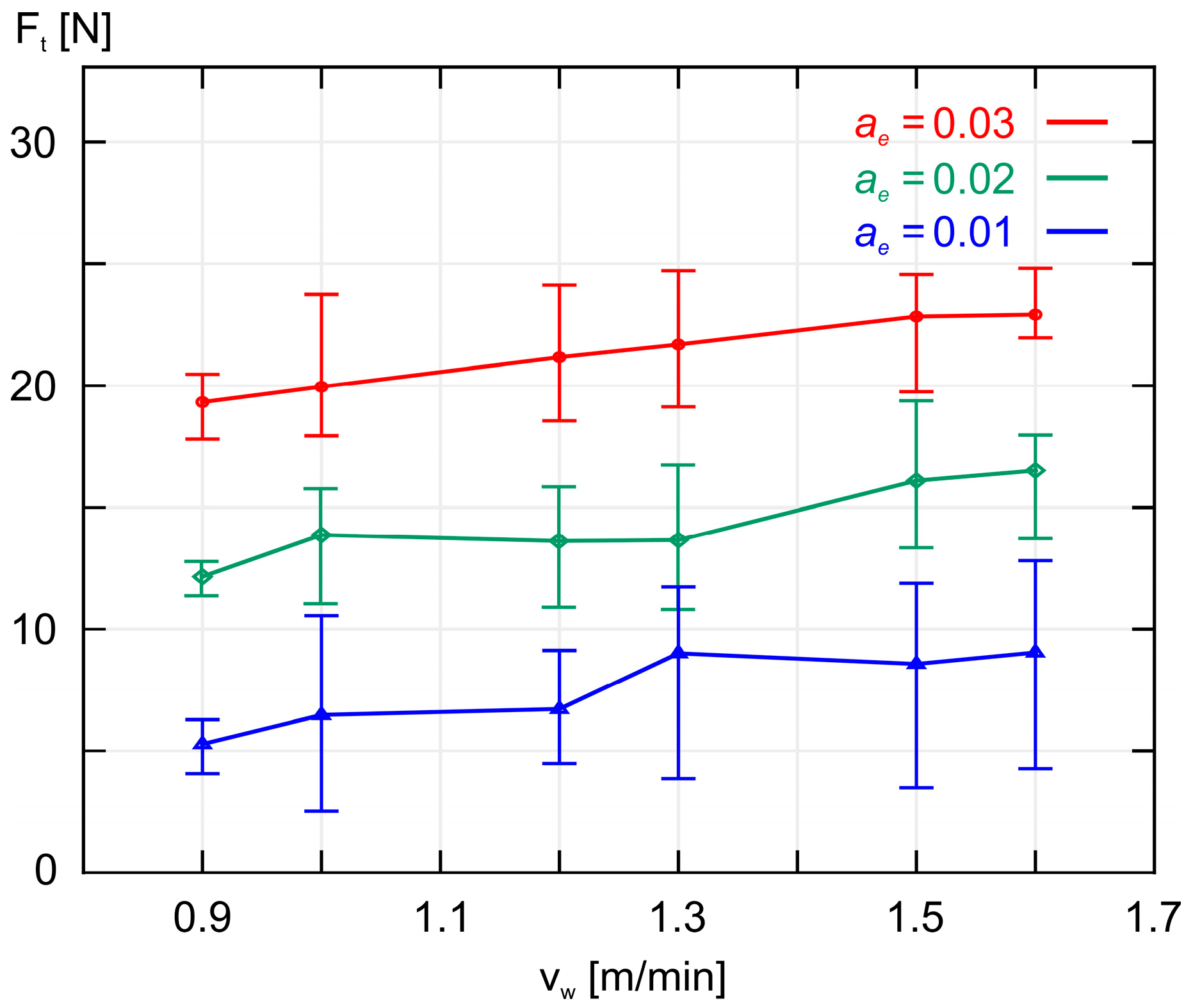
- Both the experimental results and the results obtained from the calculations based on the models indicate that as the grinding depth ae increases, the values of the grinding force components (Fn and Ft) also increase, which was expected. A similar relationship was found when the workpiece speed vw was increased.
- In the case of the normal component Fn, the overall percentage average errors for both models remain small, amounting to 3.241% for the regression model and 3.228% for the polynomial model. For the tangential component Ft, the overall percentage average error for both models is small, amounting to 1.409% for the regression model and 1.727% for the polynomial model.
- The values of both grinding force components calculated based on the mathematical models are consistent with the results obtained from the experiment. In the case of the Fn component, the calculated values in both cases deviate insignificantly from the experimental values, while for the Ft component, the results show a very small relative error despite the irregular course of the experimental results, which should be considered very satisfactory. Additionally, the high value of the multiple regression coefficient for both models demonstrates compliance with the experimental results.
- The developed models provide a good basis for analyzing the hob cutter sharpening process with variable grinding parameters, and can also be used in modelling the dynamic grinding process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korecki, M.; Wołowiec-Korecka, E. Glenn. Single-piece, high-volume, low-distortion case hardening of gears. Therm. Process. 2016, 9, 32–39. [Google Scholar]
- Stachurski, W.; Sawicki, J.; Wójcik, R.; Nadolny, K. Influence of application of hybrid MQL-CCA method of applying coolant during hob cutter sharpening on cutting blade surface condition. J. Clean. Prod. 2018, 171, 892–910. [Google Scholar] [CrossRef]
- Moderow, R. The right and wrong of modern hob sharpening. Gear Technol. 1992, 34–38. [Google Scholar]
- Kruszyński, B.; Wójcik, R. Residual stress in grinding. J. Mater. Process. Technol. 2001, 109, 254–257. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Grinding Technology: Theory and Applications of Machining with Abrasives, 2nd ed.; Industrial Press Inc.: New York, NY, USA, 2008. [Google Scholar]
- Stachurski, W.; Nadolny, K. Influence of the condition of the surface layer of a hob cutter sharpened using the MQL-CCA hybrid method of coolant provision on its operational wear. Int. J. Adv. Manuf. Technol. 2018, 98, 2185–2200. [Google Scholar] [CrossRef]
- Rowe, W.B. Principles of Modern Grinding Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Stachurski, W.; Dębkowski, R.; Rosik, R.; Święcik, R.; Pawłowski, W. Evaluation of the influence of the cooling method used during grinding on the operating properties of ceramic grinding wheels made with different abrasives. Adv. Sci. Technol. Res. J. 2023, 17, 1–18. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Cui, X.; Said, Z.; Sharma, S.; Liu, M.; Gao, T.; Zhou, Z.; Wang, X.; Li, C. Mechanical behavior and modeling of grinding force: A comparative analysis. J. Manuf. Process. 2023, 102, 921–954. [Google Scholar] [CrossRef]
- Li, B.; Li, X.; Hou, S.; Yang, S.; Li, Z.; Qian, J.; He, Z. Prediction and analysis of grinding force on grinding heads based on grain measurement statistics and single-grain grinding simulation. Int. J. Adv. Manuf. Technol. 2024, 132, 513–532. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.Y.; Zheng, Y.; Xing, W.; Wang, M. A grinding force prediction model with random distribution of abrasive grains: Considering material removal and undeformed chips. Int. J. Adv. Manuf. Technol. 2022, 120, 7219–7233. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, L. Analytical grinding force prediction with random abrasive grains of grinding wheels. Int. J. Mech. Sci. 2023, 250, 108310. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, J.; Wiercigroch, M. Non-linear analysis and quench control of chatter in a plunge grinding. Int. J. Non-Linear Mech. 2015, 70, 134–144. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, J.; Wiercigroch, M. Regenerative chatter in self-interrupted plunge grinding. Meccanica 2016, 51, 3185–3202. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, J.; Wiercigroch, M. Regenerative chatter in a plunge grinding process with workpiece imbalance. Int. J. Adv. Manuf. Technol. 2017, 89, 2845–2862. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, J.; Wiercigroch, M. Chatter in a transverse grinding process. J. Sound Vib. 2014, 333, 937–953. [Google Scholar] [CrossRef]
- Sun, C.; Deng, Y.; Lan, D.; Xiu, S. Modeling and predicting ground surface topography on grinding chatter. Procedia CIRP 2018, 71, 364–369. [Google Scholar] [CrossRef]
- Werner, G. Influence of work material on grinding forces. Ann. CIRP 1978, 27, 243–248. [Google Scholar]
- Meng, Q.; Guo, B.; Zhao, Q.; Li, H.N.; Jackson, M.J.; Linke, B.S.; Luo, X. Modelling of grinding mechanics: A review. Chin. J. Aeronaut. 2022, 36, 25–39. [Google Scholar] [CrossRef]
- Mishra, V.K.; Salonitis, K. Empirical estimation of grinding specific forces and energy based on a modified Werner grinding model. Procedia CIRP 2013, 8, 287–292. [Google Scholar] [CrossRef]
- Cieciura, M.; Zacharski, J. Probabilistic Methods in Practice; Vizja Press & IT: Warsaw, Poland, 2007. [Google Scholar]
- Kruszyński, B.; Midera, S.; Kaczmarek, J. Forces in generating gear grinding-theoretical and experimental approach. CIRP Ann.–Manuf. Technol. 1998, 47, 287–290. [Google Scholar] [CrossRef]
- Stachurski, W.; Midera, S.; Kruszyński, B. Mathematical model describing the course of the process of wear of a hob cutter for various methods of cutting fluid supply. Eksploat. Niezawodn. 2016, 18, 123–127. [Google Scholar] [CrossRef]
- Stachurski, W.; Sawicki, J.; Krupanek, K.; Midera, S. Mathematical model for determining the expenditure of cooling and lubricating fluid reaching directly the grinding zone. Arch. Mater. Sci. Eng. 2018, 94, 27–34. [Google Scholar] [CrossRef]
- Korzyński, M. Methodology of the Experiment-Planning, Implementation and Statistical Analysis of the Results of Technological Experiments; WNT: Warsaw, Poland, 2013. [Google Scholar]


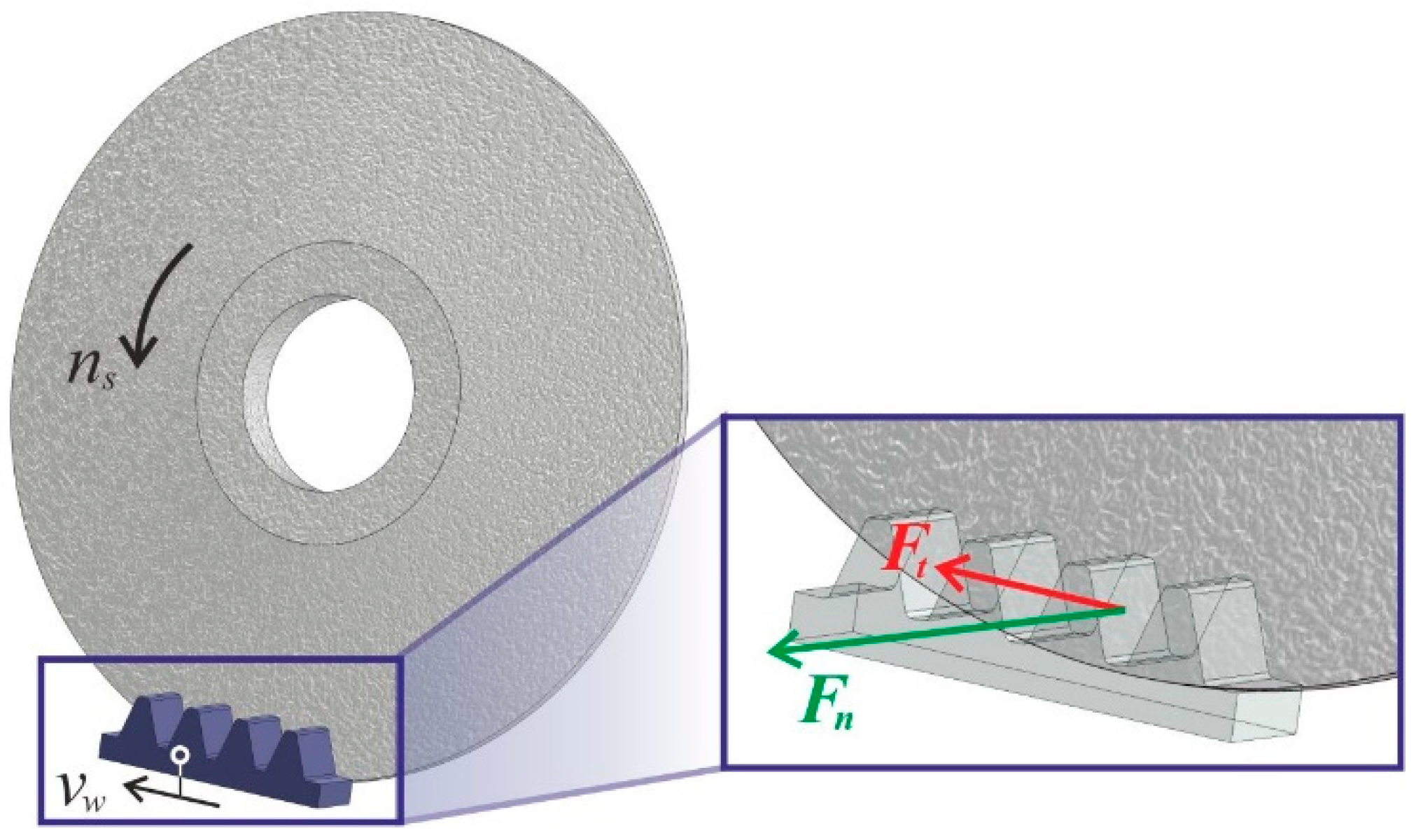

| Workpiece material | HS6-5-2, carburized and hardened with 62 ± 1 HRC |
| Grinding wheel | 38A60KVBE |
| Grinding wheel rotational speed | ns = 4600 rpm |
| Grinding wheel peripheral speed | vs = 30.1 m/s |
| Workpiece speed | vw1 = 0.9 m/min vw2 = 1.0 m/min vw3 = 1.2 m/min vw4 = 1.3 m/min vw5 = 1.5 m/min vw6 = 1.6 m/min |
| Machining allowance (working engagement, grinding depth) | ae1 = 0.01 mm ae2 = 0.02 mm ae3 = 0.03 mm |
| Number of passes: grinding/return | 1/1 |
| Grinding direction | Up grinding |
| Dresser | Single-point diamond dresser |
| Dresser weight | Qd = 1.0 kt (0.2 g) |
| Grinding wheel peripheral speed while dressing | vsd = 30.1 m/s |
| Dressing allowance | ad = 0.01 mm |
| Axial table feed speed while dressing | vfd = 40 mm/min |
| Number of dressing passes | id = 10 |
| Environments | WET—conventional flood method |
| Coolant | AGIP Aquamet 104 Plus in a 5% concentration |
| Coolant flow rate | Q = 3 L/min |
| Input Data | Regression Model | Polynomial Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vw [m/min] | ae [mm] | Normal Force Fn [N] (Experiment) | Normal Force Fn [N] (Regression Model) | Error |Δ| | Percentage Error · 100% | Average Error | Percentage Average Error | Normal Force Fn [N] (Polynomial Model) | Error |Δ| | Percentage Error · 100% | Average Error | Percentage Average Error |
| 0.9 | 0.01 | 37.799 | 36.086 | 1.713 | 4.533 | 1.597 | 3.820 | 35.968 | 1.831 | 4.844 | 1.620 | 3.896 |
| 1.0 | 39.294 | 37.394 | 1.900 | 4.835 | 37.367 | 1.927 | 4.903 | |||||
| 1.2 | 39.438 | 39.771 | 0.333 | 0.844 | 39.918 | 0.480 | 1.218 | |||||
| 1.3 | 42.405 | 40.862 | 1.543 | 3.640 | 41.092 | 1.313 | 3.095 | |||||
| 1.5 | 45.966 | 42.886 | 3.080 | 6.700 | 43.278 | 2.688 | 5.847 | |||||
| 1.6 | 42.817 | 43.832 | 1.015 | 2.371 | 44.302 | 1.485 | 3.468 | |||||
| 0.9 | 0.02 | 55.135 | 58.015 | 2.880 | 5.224 | 2.306 | 3.770 | 57.670 | 2.535 | 4.598 | 2.424 | 3.922 |
| 1.0 | 57.044 | 60.118 | 3.074 | 5.389 | 59.913 | 2.869 | 5.030 | |||||
| 1.2 | 62.764 | 63.940 | 1.176 | 1.873 | 64.003 | 1.239 | 1.975 | |||||
| 1.3 | 63.557 | 65.693 | 2.136 | 3.361 | 65.886 | 2.329 | 3.664 | |||||
| 1.5 | 66.745 | 68.949 | 2.204 | 3.302 | 69.391 | 2.646 | 3.964 | |||||
| 1.6 | 68.105 | 70.469 | 2.364 | 3.471 | 71.032 | 2.927 | 4.298 | |||||
| 0.9 | 0.03 | 75.480 | 76.588 | 1.108 | 1.469 | 1.841 | 2.132 | 76.013 | 0.533 | 0.706 | 1.611 | 1.868 |
| 1.0 | 83.828 | 79.365 | 4.463 | 5.324 | 78.969 | 4.859 | 5.796 | |||||
| 1.2 | 84.340 | 84.410 | 0.070 | 0.083 | 84.360 | 0.020 | 0.024 | |||||
| 1.3 | 89.932 | 86.725 | 3.207 | 3.566 | 86.842 | 3.090 | 3.436 | |||||
| 1.5 | 91.842 | 91.022 | 0.820 | 0.892 | 91.462 | 0.380 | 0.414 | |||||
| 1.6 | 94.408 | 93.030 | 1.378 | 1.460 | 93.625 | 0.783 | 0.830 | |||||
| Total average error: | 1.915 | 3.241 | Total average error: | 1.885 | 3.228 | |||||||
| Input Data | Regression Model | Polynomial Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vw [m/min] | ae [mm] | Tangential Force Ft [N] (Experiment) | Tangential Force Ft [N] (Regression Model) | Error |Δ| | Percentage Error · 100% | Average Error | Percentage Average Error | Tangential Force Ft [N] (Polynomial Model) | Error |Δ| | Percentage Error · 100% | Average Error | Percentage Average Error |
| 0.9 | 0.01 | 5.280 | 5.776 | 0.496 | 1.311 | 0.855 | 2.016 | 7.069 | 1.789 | 4.732 | 1.112 | 2.755 |
| 1.0 | 6.476 | 6.107 | 0.369 | 0.940 | 7.529 | 1.053 | 2.681 | |||||
| 1.2 | 6.719 | 6.725 | 0.006 | 0.015 | 8.399 | 1.680 | 4.260 | |||||
| 1.3 | 9.026 | 7.016 | 2.010 | 4.740 | 8.812 | 0.214 | 0.505 | |||||
| 1.5 | 8.587 | 7.568 | 1.019 | 2.218 | 9.601 | 1.014 | 2.207 | |||||
| 1.6 | 9.060 | 7.830 | 1.230 | 2.872 | 9.980 | 0.920 | 2.149 | |||||
| 0.9 | 0.02 | 12.501 | 11.975 | 0.526 | 0.954 | 0.724 | 1.185 | 12.305 | 0.196 | 0.356 | 0.628 | 1.025 |
| 1.0 | 14.272 | 12.662 | 1.610 | 2.823 | 13.107 | 1.165 | 2.042 | |||||
| 1.2 | 14.013 | 13.944 | 0.069 | 0.111 | 14.621 | 0.608 | 0.969 | |||||
| 1.3 | 14.053 | 14.547 | 0.494 | 0.777 | 15.340 | 1.287 | 2.025 | |||||
| 1.5 | 16.572 | 15.691 | 0.881 | 1.320 | 16.714 | 0.142 | 0.213 | |||||
| 1.6 | 17.001 | 16.236 | 0.765 | 1.124 | 17.373 | 0.372 | 0.547 | |||||
| 0.9 | 0.03 | 19.338 | 18.346 | 0.992 | 1.315 | 0.901 | 1.025 | 17.018 | 2.320 | 3.074 | 1.163 | 1.402 |
| 1.0 | 19.975 | 19.397 | 0.578 | 0.689 | 18.128 | 1.847 | 2.204 | |||||
| 1.2 | 21.197 | 21.361 | 0.164 | 0.195 | 20.221 | 0.976 | 1.157 | |||||
| 1.3 | 21.716 | 22.285 | 0.569 | 0.633 | 21.215 | 0.501 | 0.557 | |||||
| 1.5 | 22.865 | 24.038 | 1.173 | 1.277 | 23.116 | 0.251 | 0.273 | |||||
| 1.6 | 22.945 | 24.872 | 1.927 | 2.042 | 24.028 | 1.083 | 1.147 | |||||
| Total average error: | 0.827 | 1.409 | Total average error: | 0.968 | 1.727 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witkowski, B.; Stachurski, W.; Pawłowski, W.; Sikora, M.; Kępczak, N. Mathematical Models of Grinding Forces in the Hob Cutter Sharpening Process. Materials 2025, 18, 138. https://doi.org/10.3390/ma18010138
Witkowski B, Stachurski W, Pawłowski W, Sikora M, Kępczak N. Mathematical Models of Grinding Forces in the Hob Cutter Sharpening Process. Materials. 2025; 18(1):138. https://doi.org/10.3390/ma18010138
Chicago/Turabian StyleWitkowski, Błażej, Wojciech Stachurski, Witold Pawłowski, Małgorzata Sikora, and Norbert Kępczak. 2025. "Mathematical Models of Grinding Forces in the Hob Cutter Sharpening Process" Materials 18, no. 1: 138. https://doi.org/10.3390/ma18010138
APA StyleWitkowski, B., Stachurski, W., Pawłowski, W., Sikora, M., & Kępczak, N. (2025). Mathematical Models of Grinding Forces in the Hob Cutter Sharpening Process. Materials, 18(1), 138. https://doi.org/10.3390/ma18010138






