Numerical Study on Electromagnetic Hydraulic Forming Process to Overcome Limitations of Electromagnetic Forming Process
Abstract
1. Introduction
2. Numerical Modeling in LS-DYNA
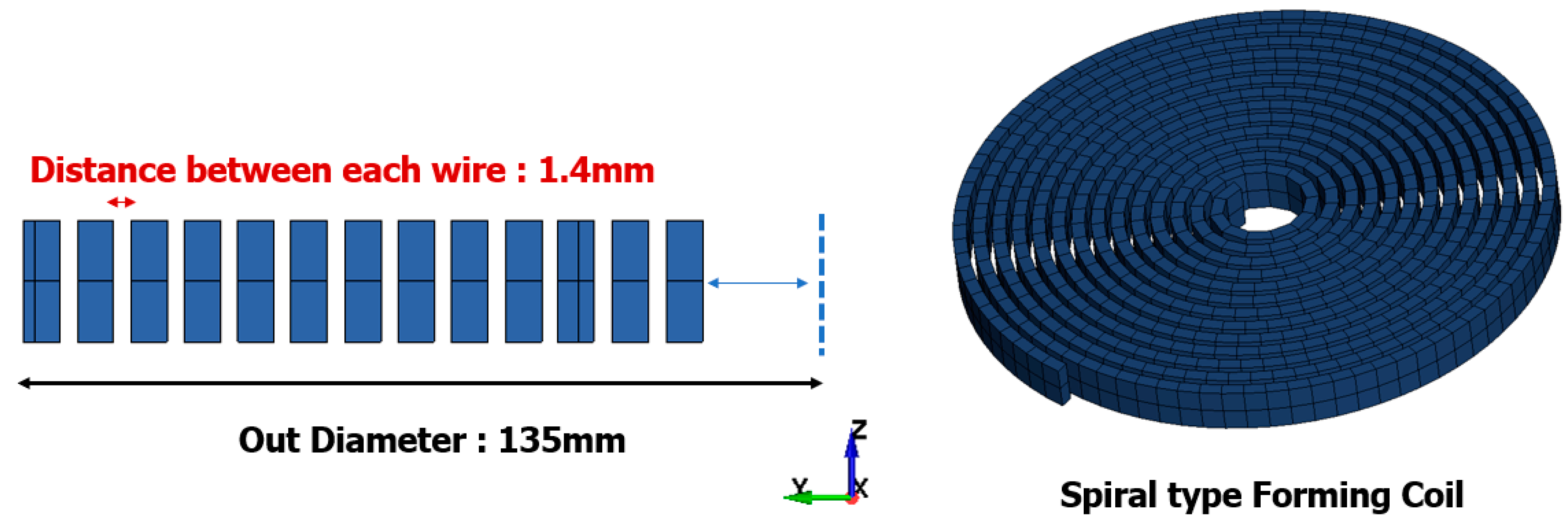
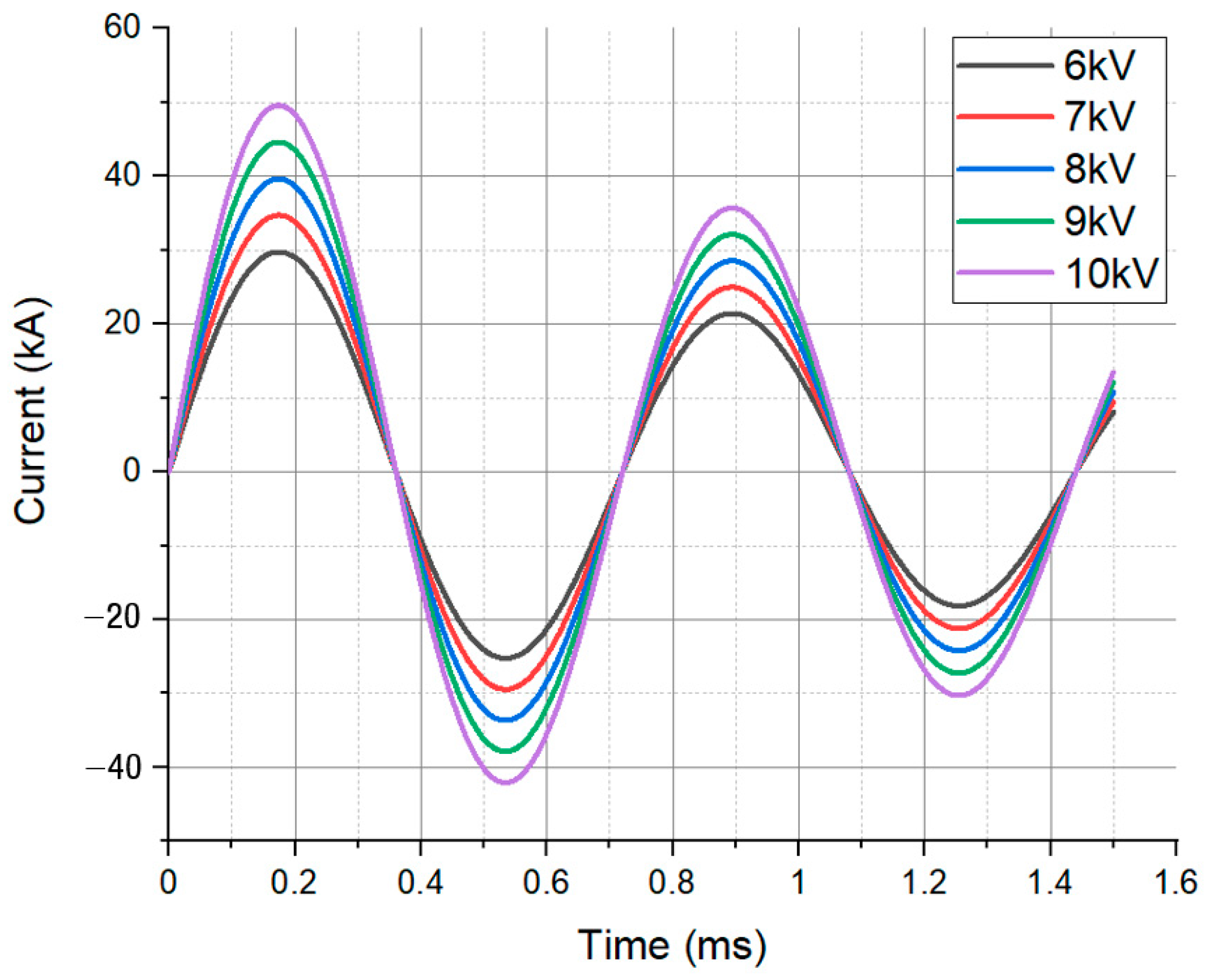
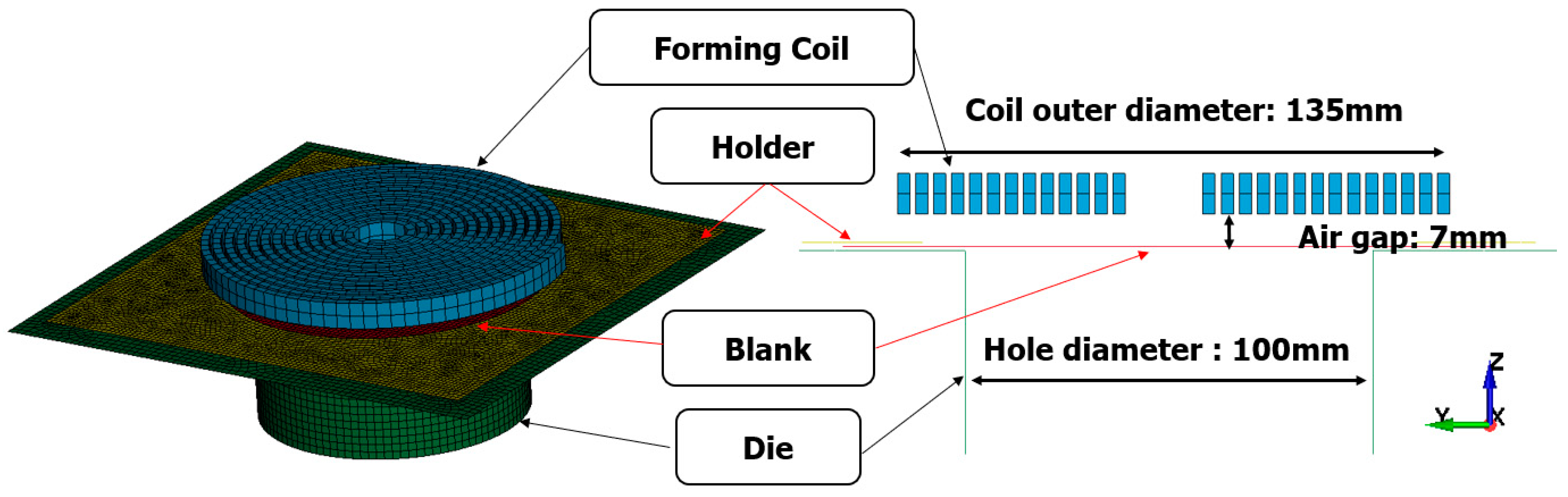
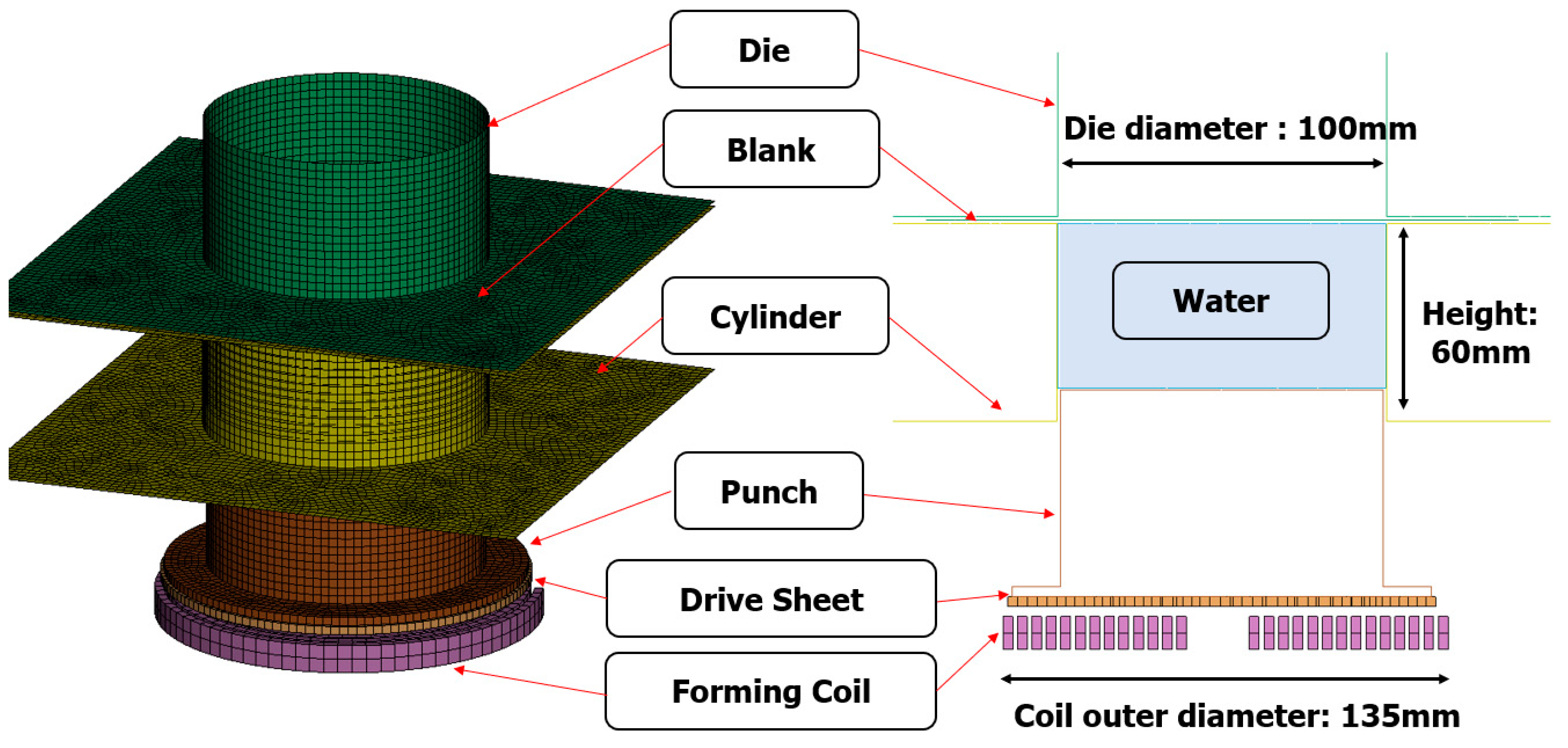
2.1. Electromagnetic Forming Modeling
2.2. Electromagnetic Hydraulic Forming Modeling
3. Comparison with EMF and EMHF in Finite Element Analysis (FEA)
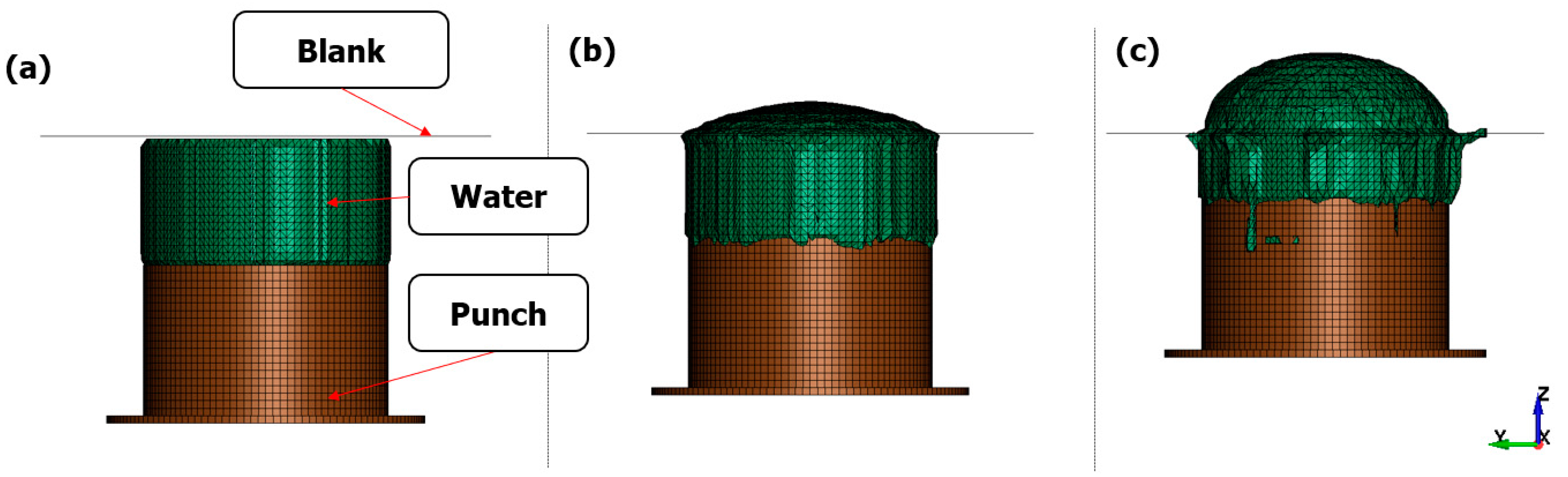
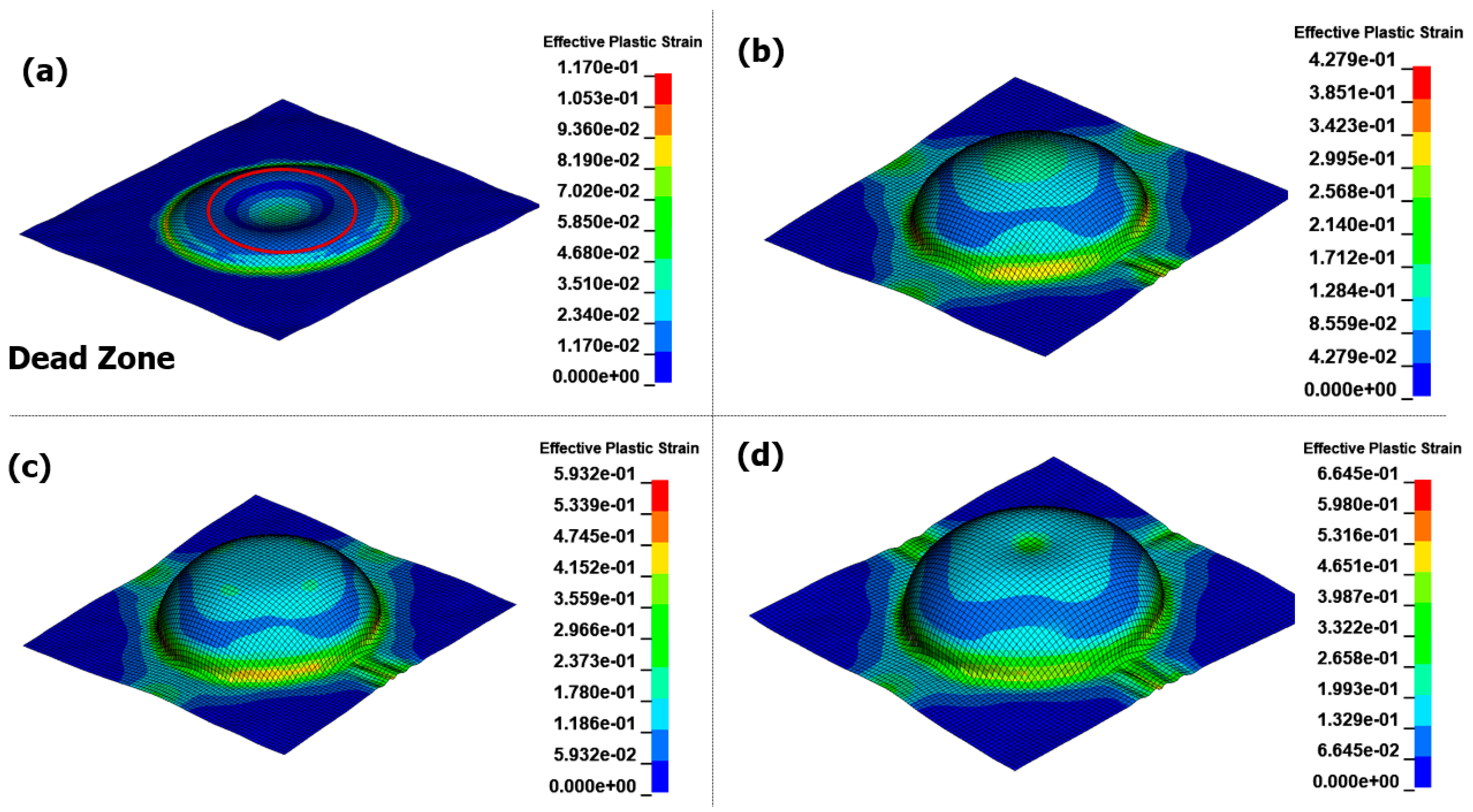
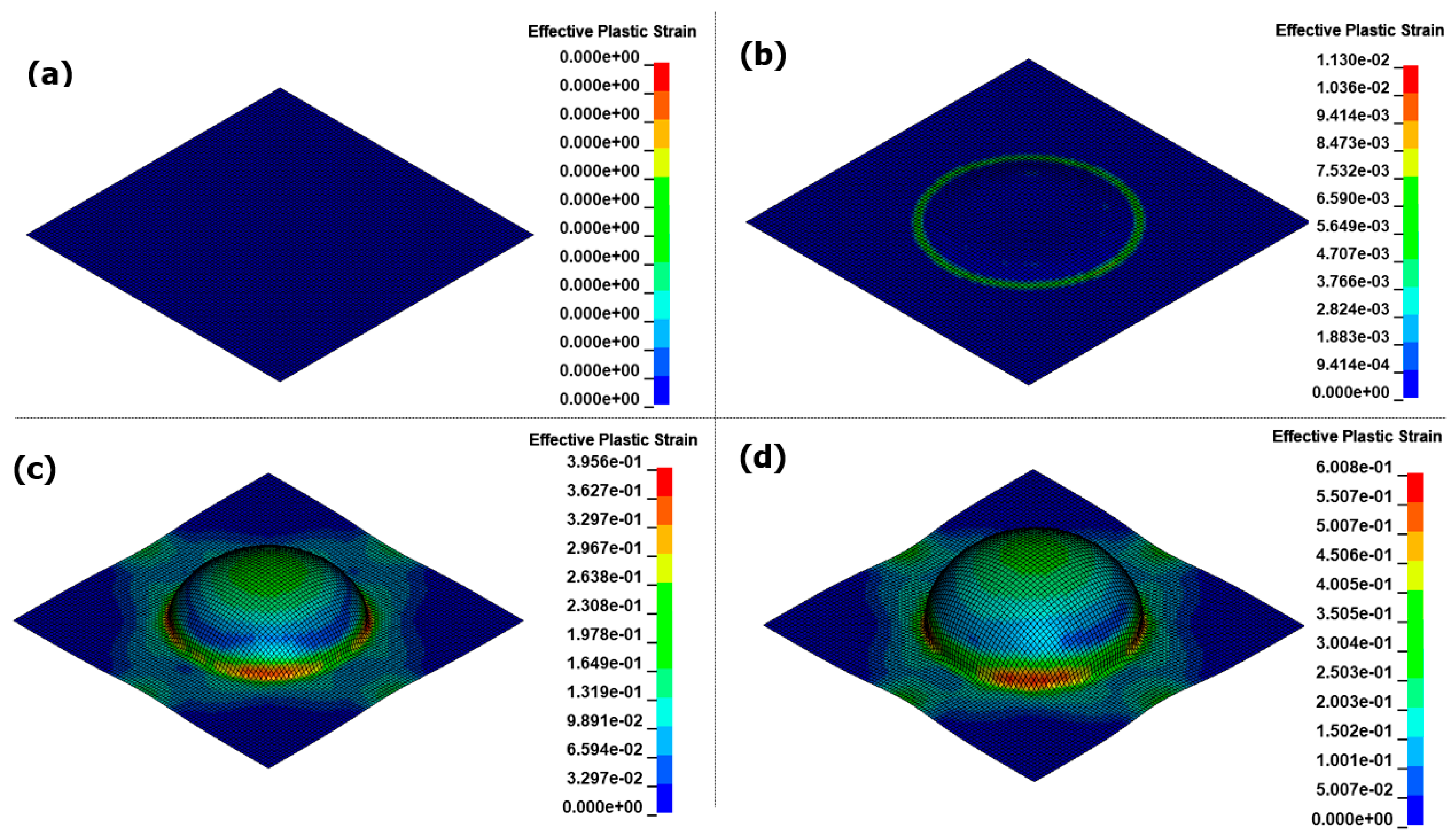
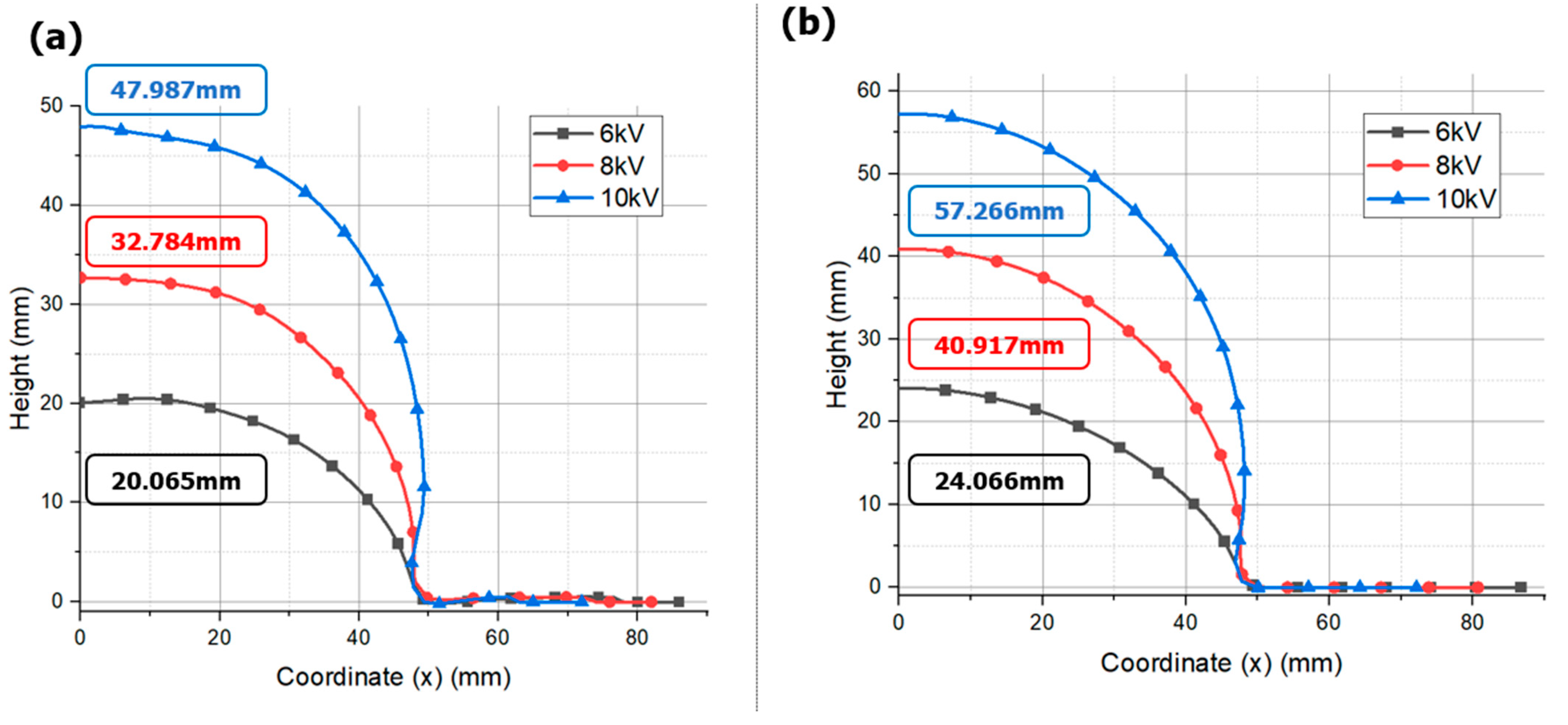
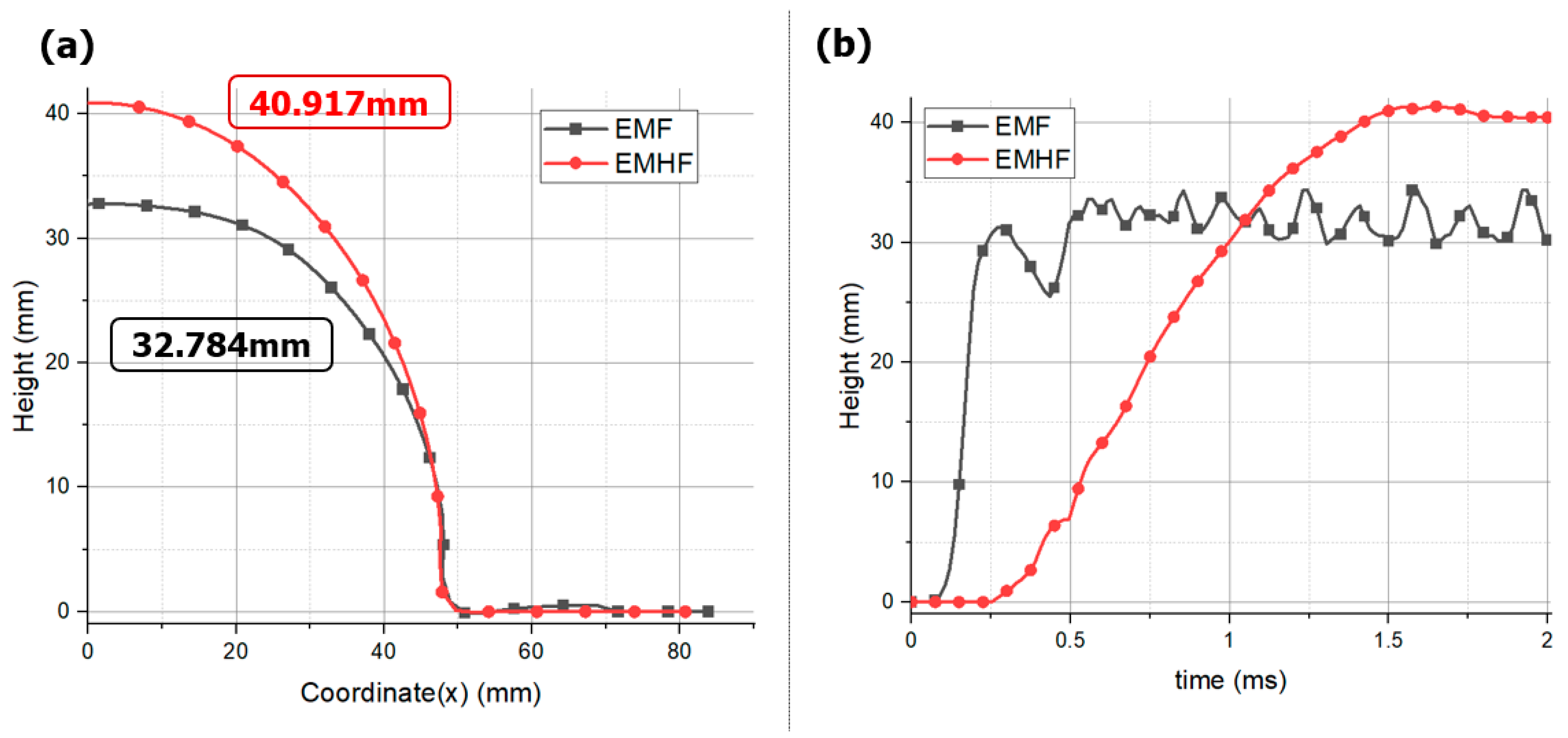
3.1. Free-Bulge Analysis
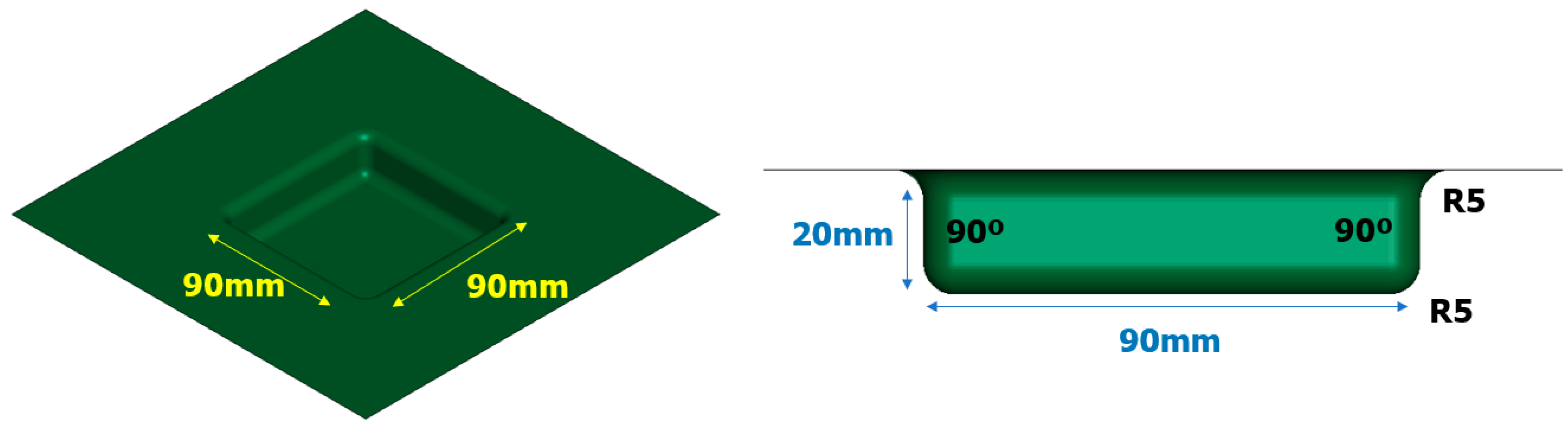
3.2. Rectangular Die Analysis
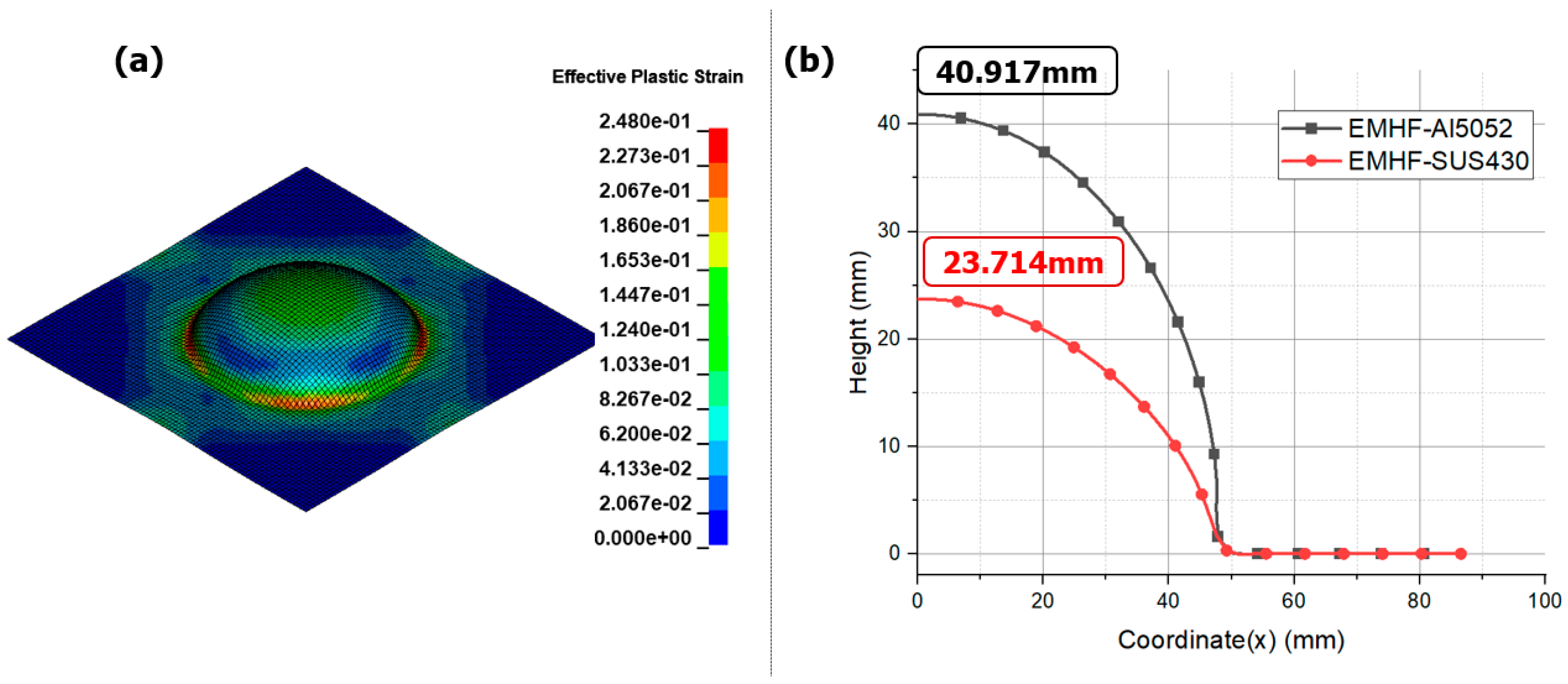
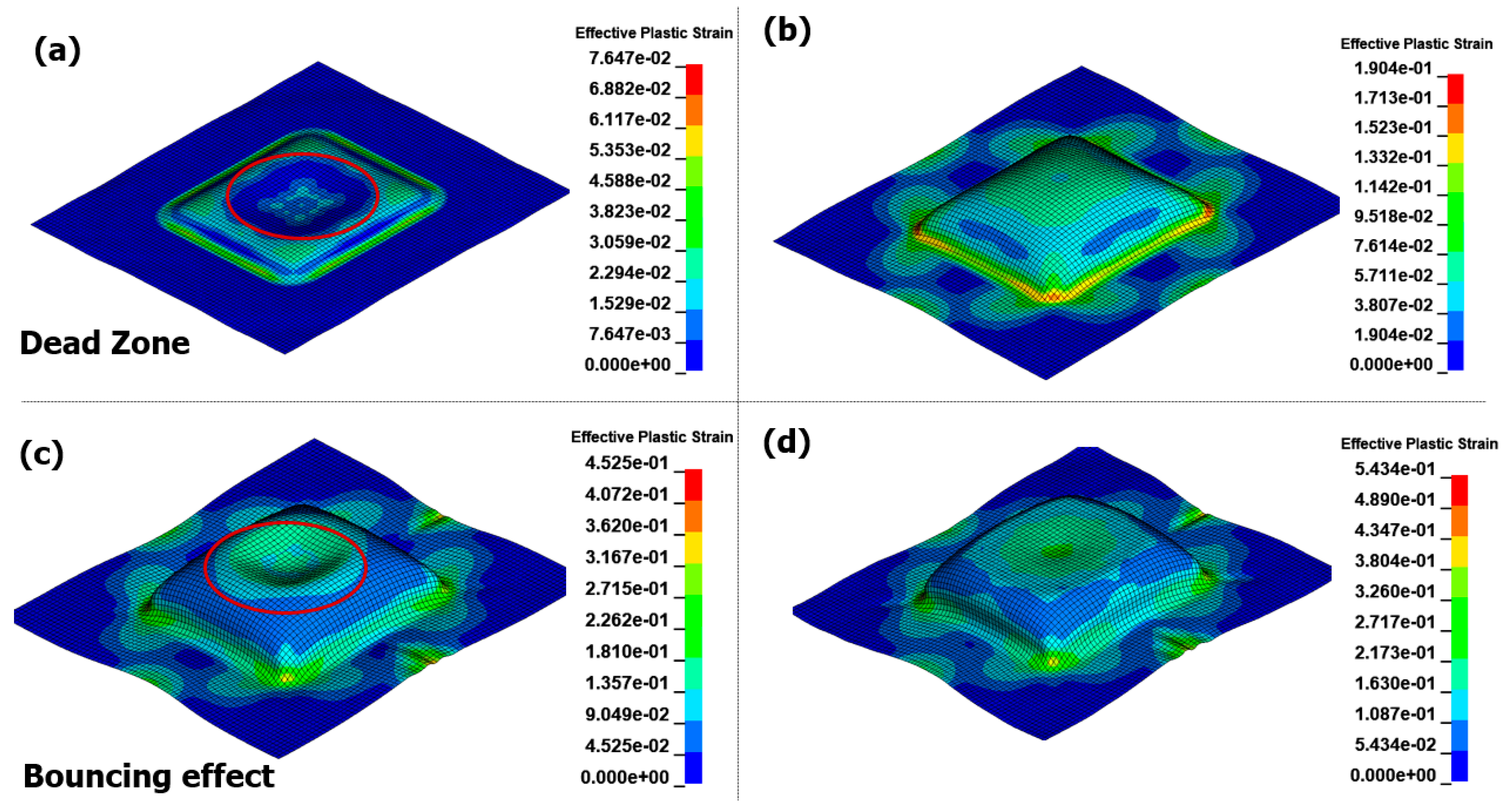
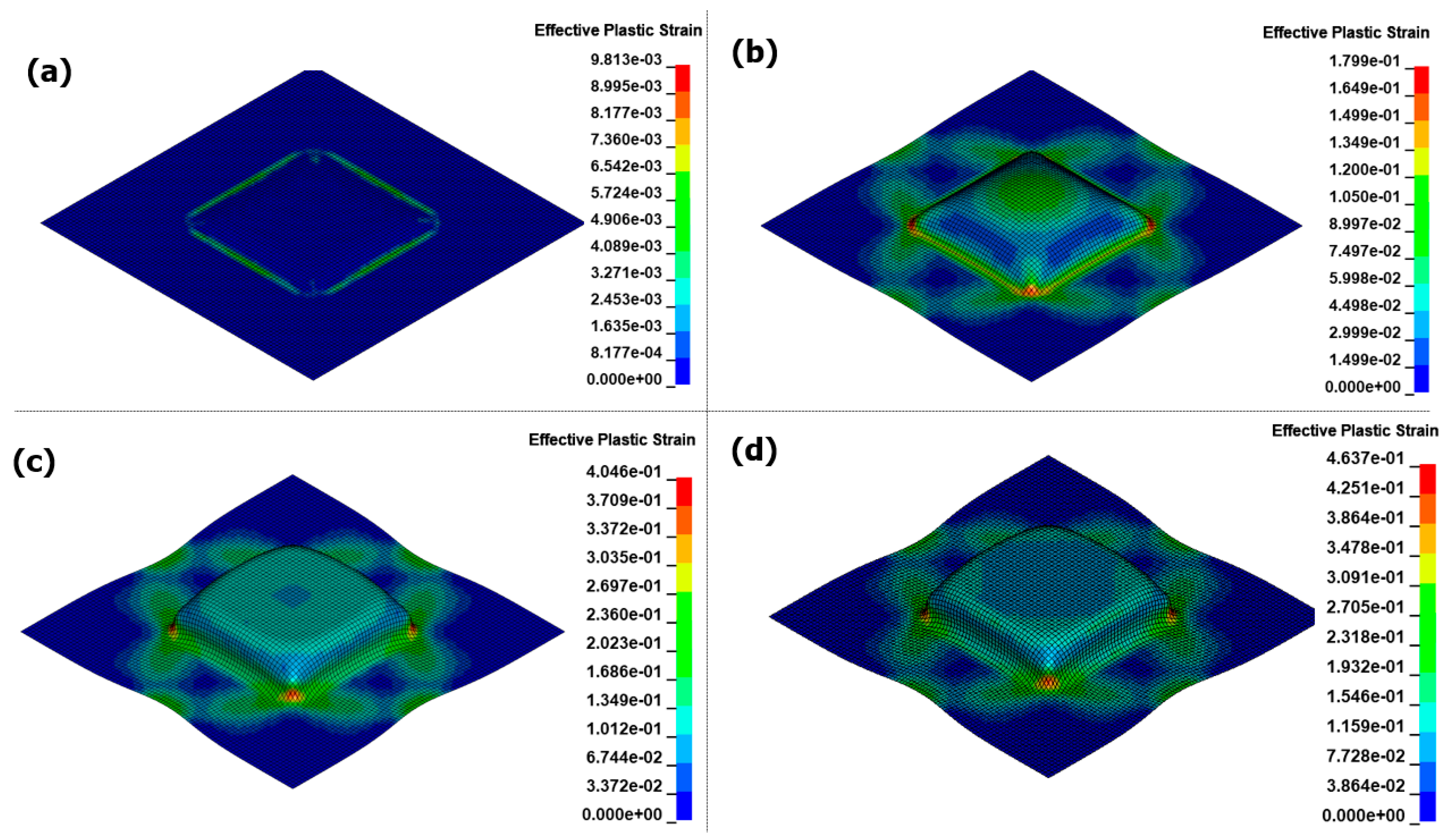
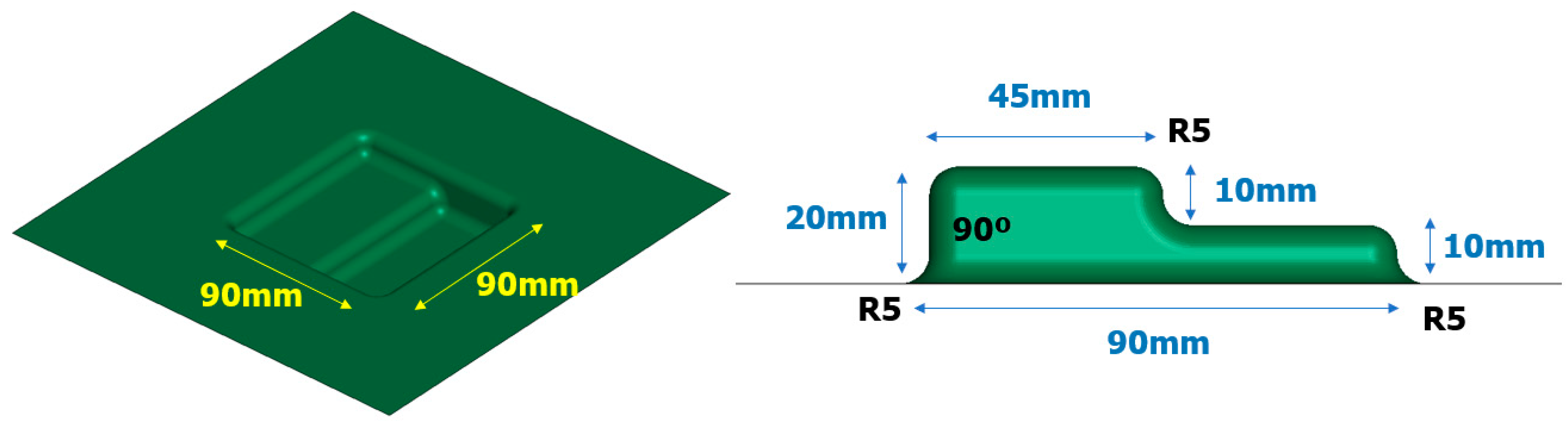
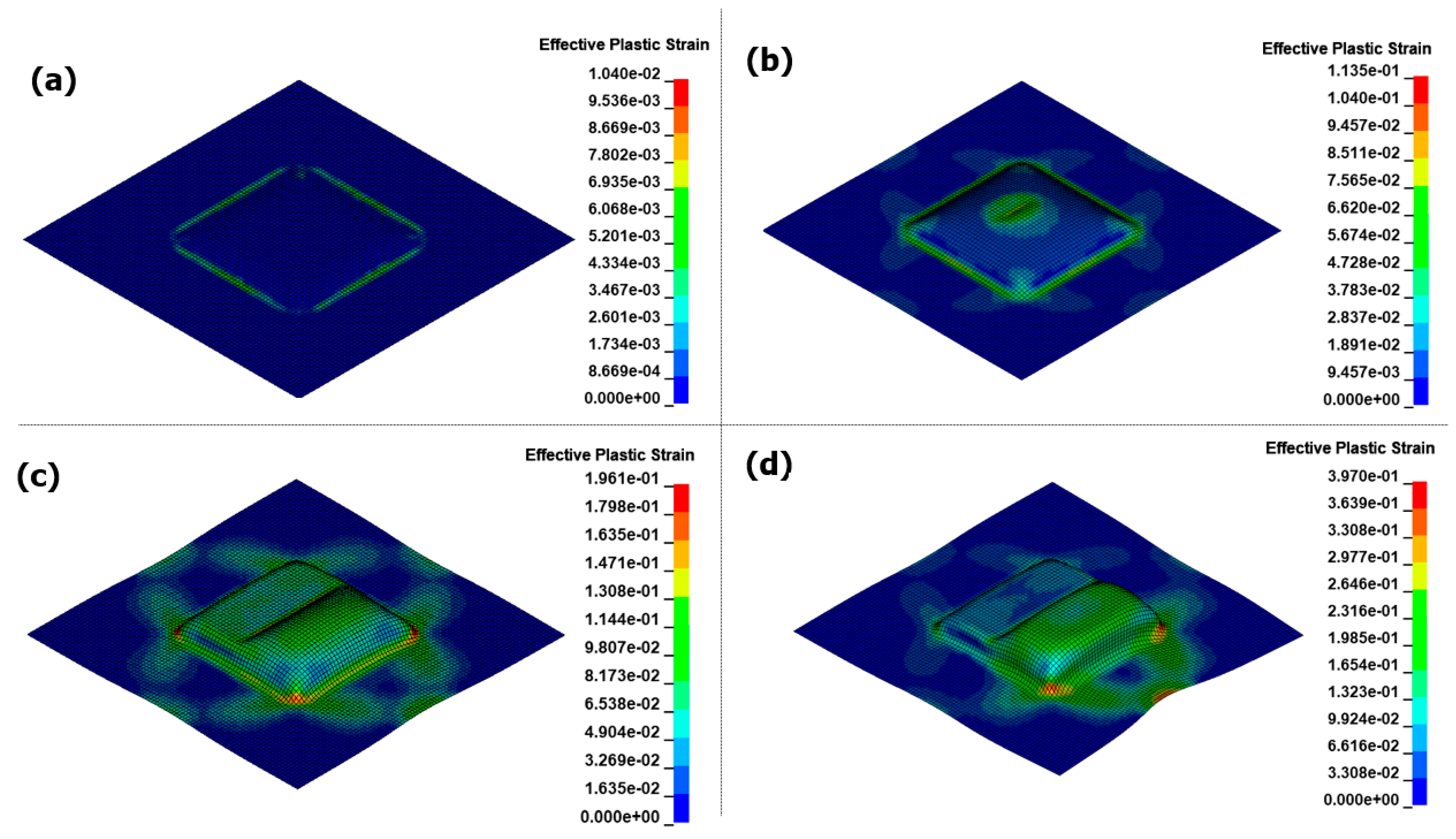
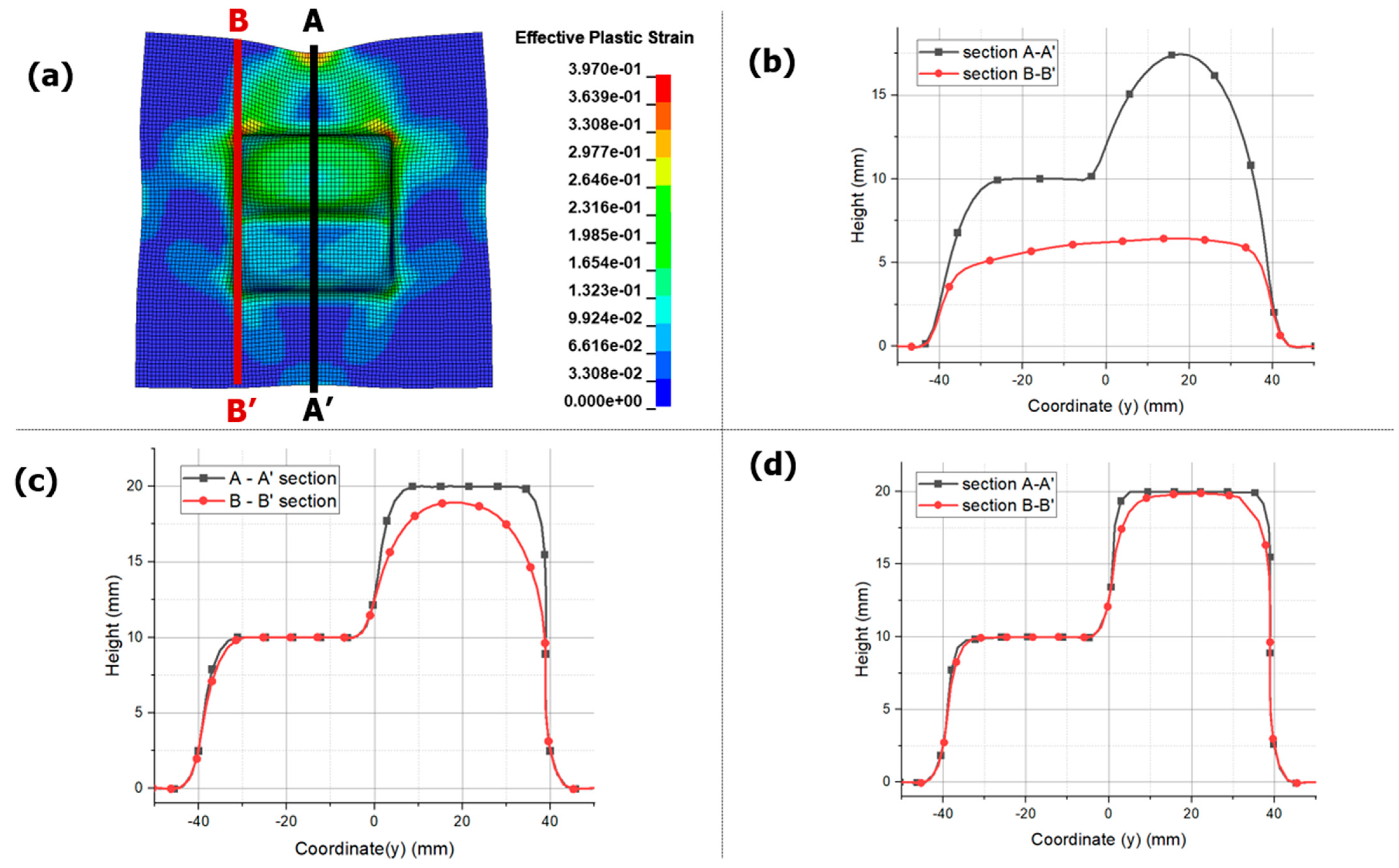
3.3. Asymmetry Die Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, S.B.; Huh, H.; Bok, H.H.; Moon, M.B. Forming limit diagram of auto-body steel sheets for high-speed sheet metal forming. J. Mater. Process. Technol. 2011, 211, 851–862. [Google Scholar] [CrossRef]
- Du, Z.; Yan, Z.; Cui, X.; Chen, B.; Yu, H.; Qiu, D.; Xia, W.; Deng, Z. Springback control and large skin manufacturing by high-speed vibration using electromagnetic forming. J. Mater. Process. Technol. 2022, 299, 117340. [Google Scholar] [CrossRef]
- Simoes, V.M.; Oliveira, M.C.; Laurent, H.; Menezes, L.F. The punch speed influence on warm forming and springback of two Al-Mg-Si alloys. J. Manuf. Process. 2019, 38, 266–278. [Google Scholar] [CrossRef]
- Mynors, D.J.; Zhang, B. Applications and capabilities of explosive forming. J. Mater. Process. Technol. 2002, 125–126, 1–25. [Google Scholar] [CrossRef]
- Mousavi, S.A.A.A.; Riahi, M.; Parast, A.H. Experimental and numerical analyses of explosive free forming. J. Mater. Process. Technol. 2007, 187–188, 512–516. [Google Scholar] [CrossRef]
- Kowsarinia, E.; Alizadeh, Y.; Pour, H.S. Theoretical and experimental study on the effects of explosive forming parameters on plastic wrinkling of annular plates. Int. J. Adv. Manuf. Technol. 2012, 67, 877–885. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Wan, M.; Yu, H.; Liu, L. Innovation applications of electromagnetic forming and its fundamental problems. Procedia Manuf. 2018, 15, 14–30. [Google Scholar] [CrossRef]
- Lai, Z.; Cao, Q.; Han, X.; Huang, Y.; Li, L. A comprehensive electromagnetic forming approach for large sheet metal forming. Procedia Eng. 2017, 207, 54–59. [Google Scholar] [CrossRef]
- Gayakwad, D.; Dargar, M.K.; Sharma, P.K.; Rana, R.S. A Review on Electromagnetic Forming Process. Procedia Mater. Sci. 2014, 6, 520–527. [Google Scholar] [CrossRef]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Rajak, A.K.; Kore, S.D. Applicaiton of electromagnetic forming in terminal crimping using differnet types of field shapers. J. Mech. Sci. Technol. 2018, 32, 4291–4297. [Google Scholar] [CrossRef]
- Li, Z.; Han, X.; Cao, Q.; Xiong, Q.; Li, L. Design, Fabrication, and Test of a High-Strength Uniform Pressure Actuator. IEEE Trans. Appl. Supercond. 2016, 26, 3700905. [Google Scholar] [CrossRef]
- Thibaudeau, E.; Kinsey, B.L. Analytical design and experimental validation of uniform pressure actuator for electromagnetic forming and welding. J. Mater. Process. Technol. 2015, 215, 251–263. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, Q.; Fu, J.; Li, Z.; Wan, Y.; Chen, Q.; Li, C.L.; Han, X. An inner-field uniform pressure actuator with high performance and its application to titanium bipolar plate forming. Int. J. Mach. Tools Manuf. 2020, 155, 103570. [Google Scholar] [CrossRef]
- Lueg-Althoff, J.; Beu, M.-A.; Güzel, A.; Rohr, T.; Hahn, M.; Tekkaya, A.E. Experimental and numerical investigations of joining by electromagnetic forming for aeronautical applications. AIP Conf. Proc. 2019, 2113, 050012. [Google Scholar]
- Xiong, Q.; Huang, H.; Xia, L.; Tang, H.; Qiu, L. A research based on advance dual-coil electromagnetic forming method on flanging of small-size tubes. Int. J. Adv. Manuf. Technol. 2019, 102, 4087–4094. [Google Scholar] [CrossRef]
- Xiong, Q.; Tang, H.; Deng, C.; Li, L.; Qiu, L. Electromagnetic Attraction-Based Bulge Forming in Small Tubes: Fundamentals and Simulations. IEEE Trans. Appl. Supercond. 2018, 28, 0600505. [Google Scholar] [CrossRef]
- Mamutov, A.V.; Golovashchenko, S.F.; Mamutov, V.S.; Bonnen, J.J.F. Modeling of electrohydraulic forming of sheet metal parts. J. Mater. Process. Technol. 2015, 219, 84–100. [Google Scholar] [CrossRef]
- Rohatgi, A.; Stephens, E.V.; Soulami, A.; Davies, R.W.; Smith, M.T. Experimental characterization of sheet metal deformation during electro-hydraulic forming. J. Mater. Process. Technol. 2011, 211, 1824–1833. [Google Scholar] [CrossRef]
- Melander, A.; Delic, A.; Björkblad, A.; Juntunen, P.; Samek, L.; Vadillo, L. Modelling of electro hydraulic free and die forming of sheet steels. Int. J. Mater. Form. 2013, 6, 223–231. [Google Scholar] [CrossRef]
- Nonlinear Dynamic Structure Analysis Program LS-DYNA. Available online: https://www.dynasupport.com (accessed on 23 February 2024).
- Shang, J.; L’Eplattenier, P.; Wilkerson, L.; Hatkevich, S. Numerical simulation and experimental study of electromagnetic forming. In Proceedings of the 11th International LS-DYNA® Users Conference, Dearborn, MI, USA, 6–8 June 2010. [Google Scholar]
- Liu, D.; Li, B.; Guo, Z.; Huang, Z. Finite element analysis on electromagnetic forming of DP780 high-strength steel sheets. Int. J. Adv. Manuf. Technol. 2021, 112, 1617–1629. [Google Scholar] [CrossRef]
- Zhang, S.; Kinsey, B. Importance of electrical and physical contact in electromagnetic forming simulations. Procedia Manuf. 2019, 34, 133–138. [Google Scholar] [CrossRef]
- Kumar, D.; Pawar, S.; Kore, S.D.; Nandy, A. Comparison of Coupled and Non-Coupled Finite Element Models for Joining of Cu-SS Tubes by Electromagnetic Forming. Procedia Manuf. 2020, 47, 673–677. [Google Scholar] [CrossRef]
- Oh, S.-H.; Kim, C.-N. A numerical study on the flow control and pumping characteristics of a radial flow thermo-pneumatic micropump with electromagnetic resistance. Int. J. Precis. Eng. Manuf. 2012, 13, 103–110. [Google Scholar] [CrossRef]
- Kamal, M.; Daehn, G.S. A Uniform Pressure Electromagnetic Actuator for Forming Flat Sheets. J. Manuf. Sci. Eng. 2007, 129, 369–379. [Google Scholar] [CrossRef]
- Li, F.; Mo, J.; Zhou, H. 3D Numerical simulation method of electromagnetic forming for low conductive metals with a driver. Int. J. Adv. Manuf. Technol. 2013, 64, 1575–1585. [Google Scholar] [CrossRef]
- Woo, M.-A.; Kim, H.-K.; Park, H.-G.; Kim, Y.-H.; Song, W.-J.; Kim, J. Numerical and experimental study on electrohydraulic forming process. Procedia Eng. 2017, 207, 311–316. [Google Scholar] [CrossRef]
- Mamutov, V.S.; Mamutov, A.V. Numerical simulation of electrohydraulic processes; EDP Sciences. MATEC Web Conf. 2018, 245, 09015. [Google Scholar] [CrossRef]
- Niaraki, R.J.; Fazli, A.; Soltanpour, M. Electromagnetically activated high-speed hydroforming process: A novel process to overcome the limitations of the electromagnetic forming process. CIRP J. Manuf. Sci. Technol. 2019, 27, 21–30. [Google Scholar] [CrossRef]
- Huang, L.; Ding, Z.; Zhou, Y.; Zeng, J.; Zou, J. Effect of the Radial Dimension of the Driver Sheet on the Electromagnetic Driven Forming. IEEE Access 2020, 8, 133503–133513. [Google Scholar] [CrossRef]
- Yan, Z.; Du, Z.; Cui, X.; Huang, C.; Meng, Y. Springback and deformation uniformity of high-strength aluminum alloy sheet using electromagnetic forming. Int. J. Adv. Manuf. Technol. 2021, 114, 1293–1308. [Google Scholar] [CrossRef]
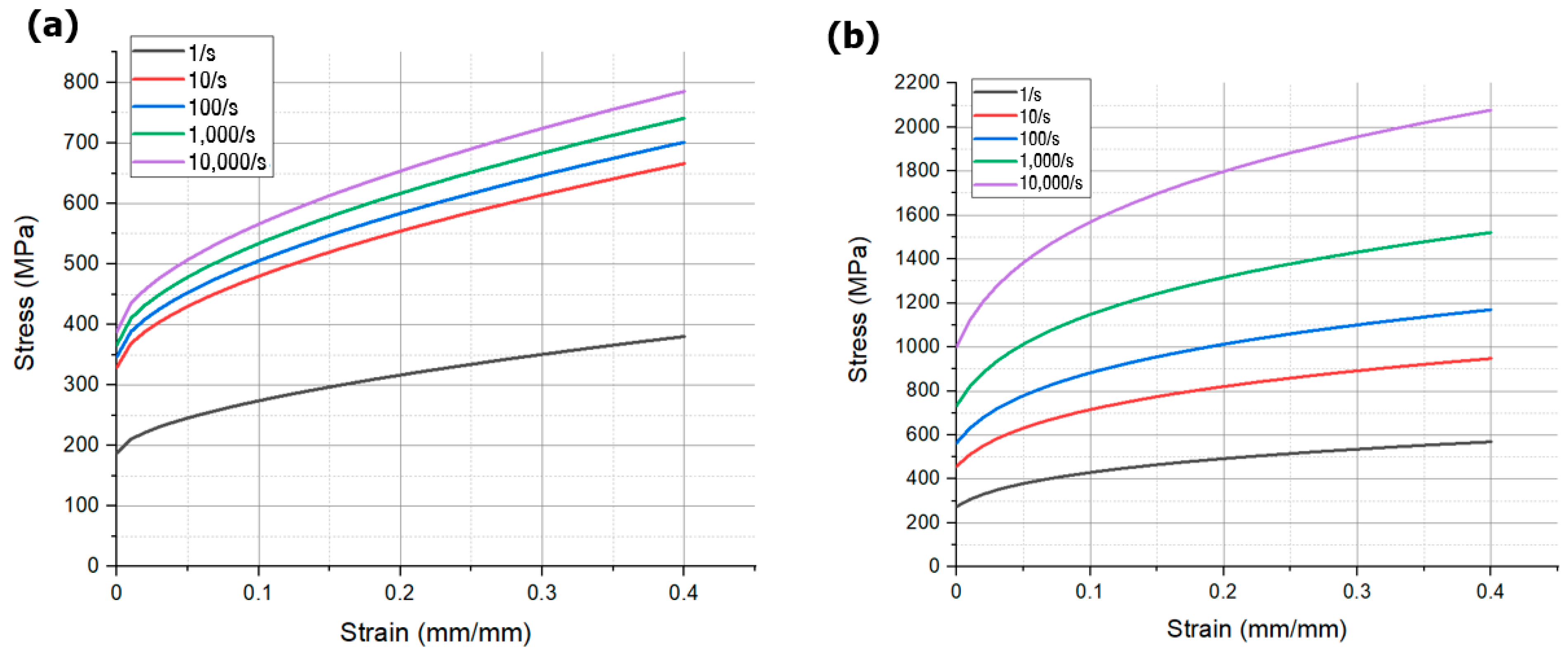


| A (MPa) | B (MPa) | n | |
|---|---|---|---|
| Al5052 | 188.03 | 327.07 | 0.58 |
| K (MPa) | n | ||
| SUS430 | 689.74 | 0.21 | |
| c | p | |
|---|---|---|
| Al5052 | 4232.7 | 22.5 |
| SUS430 | 76.26 | 5.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-B.; Kim, J. Numerical Study on Electromagnetic Hydraulic Forming Process to Overcome Limitations of Electromagnetic Forming Process. Materials 2024, 17, 1586. https://doi.org/10.3390/ma17071586
Kim Y-B, Kim J. Numerical Study on Electromagnetic Hydraulic Forming Process to Overcome Limitations of Electromagnetic Forming Process. Materials. 2024; 17(7):1586. https://doi.org/10.3390/ma17071586
Chicago/Turabian StyleKim, Yeon-Bok, and Jeong Kim. 2024. "Numerical Study on Electromagnetic Hydraulic Forming Process to Overcome Limitations of Electromagnetic Forming Process" Materials 17, no. 7: 1586. https://doi.org/10.3390/ma17071586
APA StyleKim, Y.-B., & Kim, J. (2024). Numerical Study on Electromagnetic Hydraulic Forming Process to Overcome Limitations of Electromagnetic Forming Process. Materials, 17(7), 1586. https://doi.org/10.3390/ma17071586






