Advances in Fatigue Performance of Metal Materials with Additive Manufacturing Based on Crystal Plasticity: A Comprehensive Review
Abstract
1. Introduction
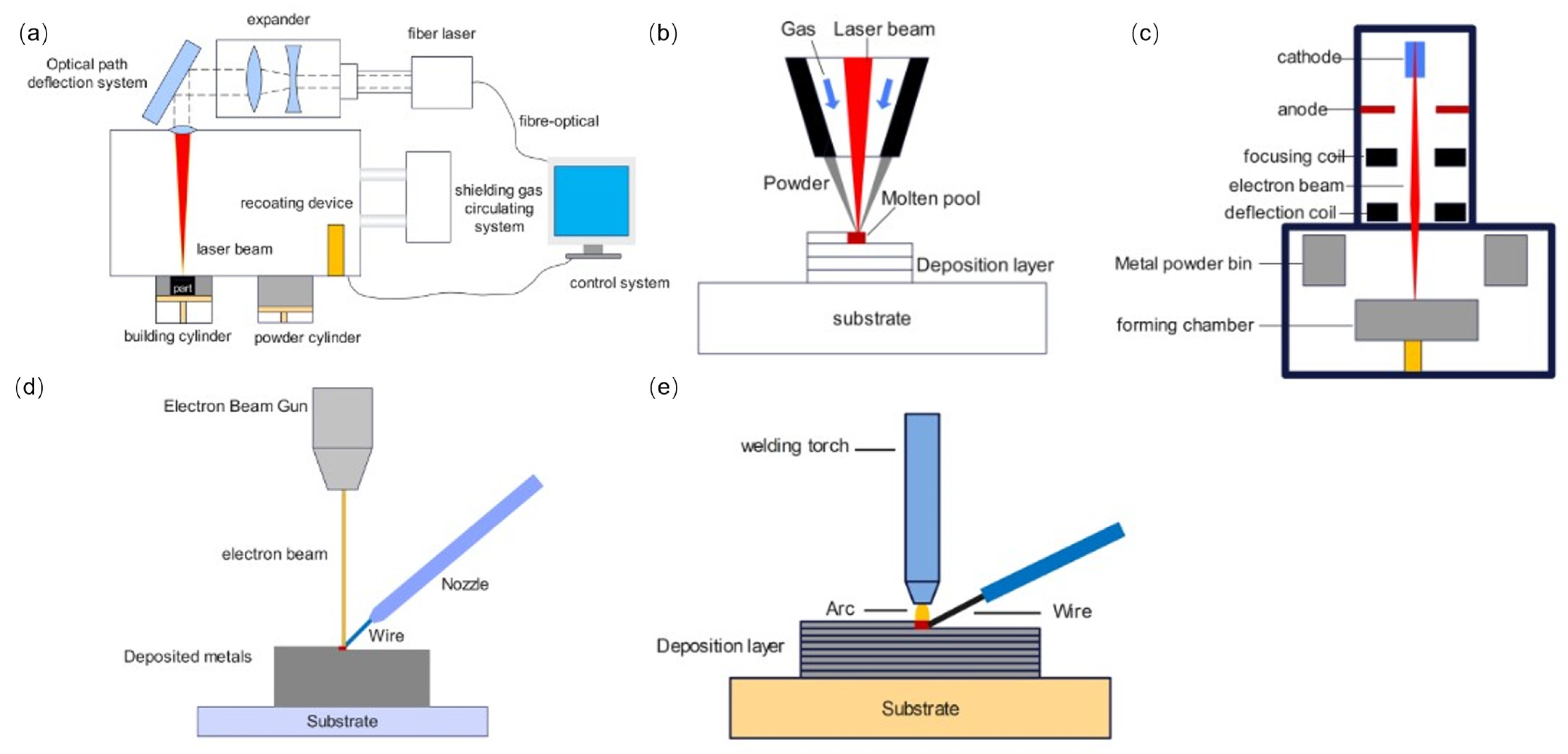
2. Metal Additive Manufacturing Formation Process
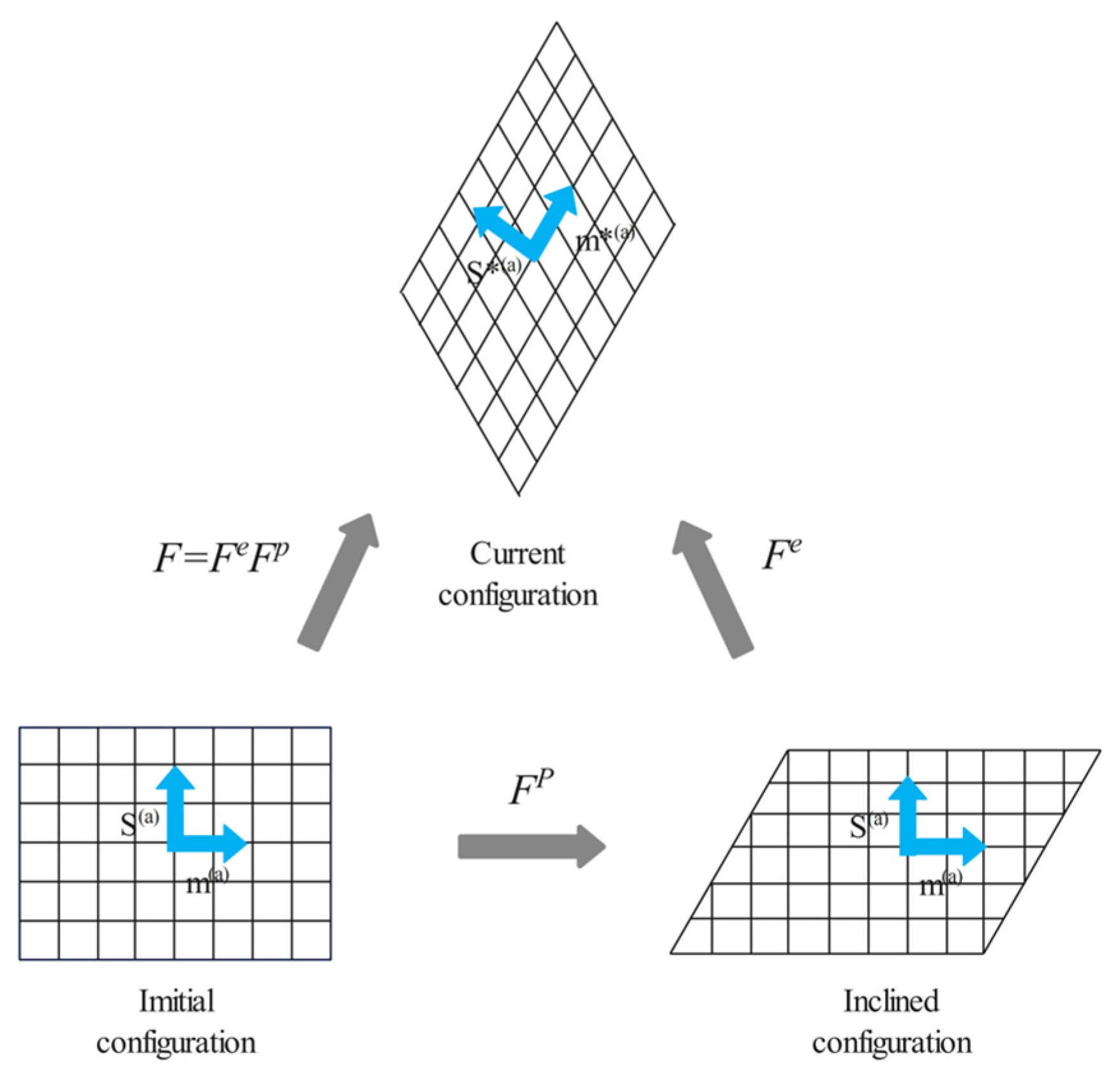
3. Review of the Development of Crystal Plasticity Theory
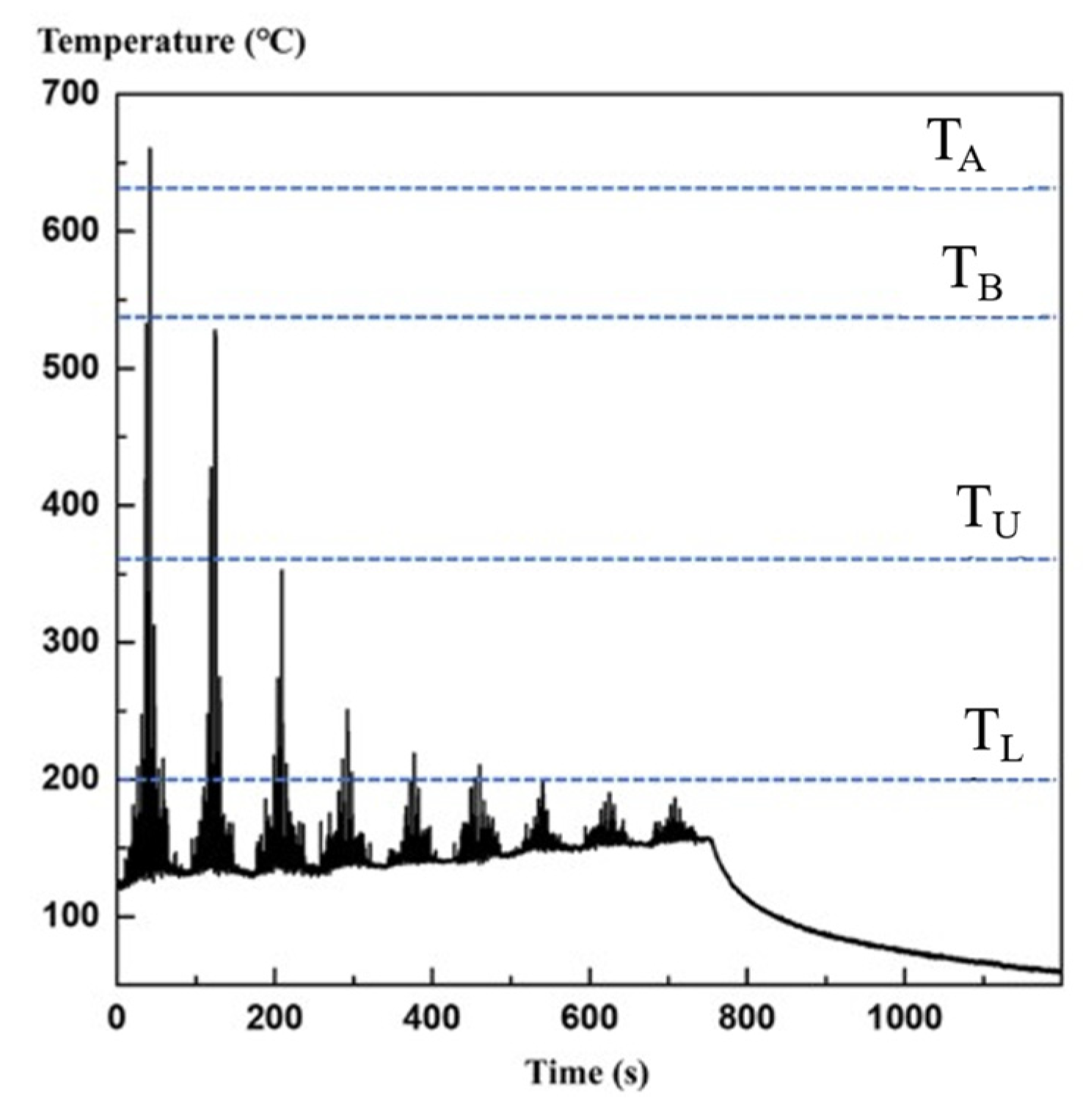
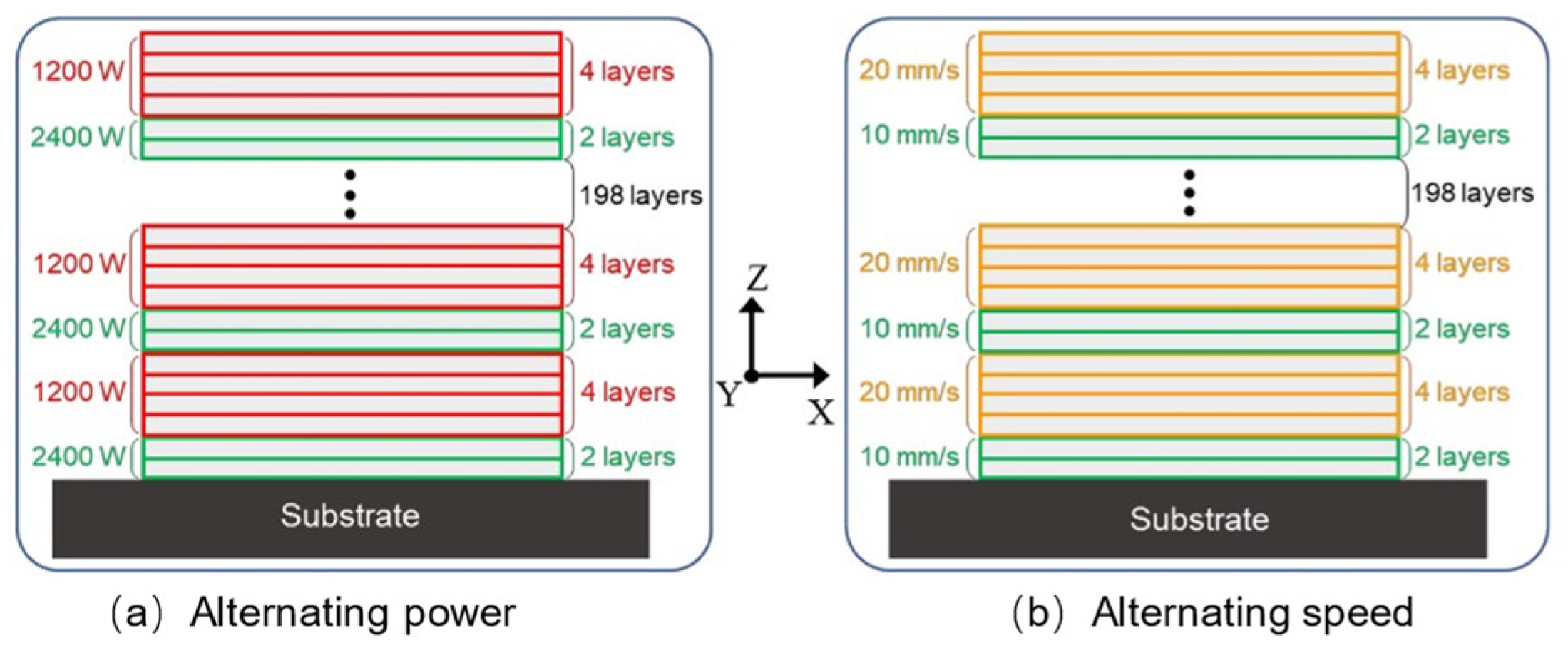
4. Additive Manufacturing Fatigue Simulation of Crystal Plasticity
5. Development Trends and Forecasts
- (1)
- At the theoretical level, we can incorporate physical fields such as metallurgy and thermodynamics to reflect the characteristics of additive manufacturing and establish a constitutive theory of multi-physical field coupling.
- (2)
- When applying the crystal plasticity finite element method, we can strengthen research on crystal plasticity simulation in the fatigue performance of metal additive manufacturing and explore the more essential relationship of “manufacturing process—material microstructure—fatigue performance”. In terms of the process control of additive manufacturing, exploring the optimization of microstructures, characterization of textures, defect-induced fatigue damage mechanism of metal additive manufacturing components, and other issues need more in-depth research.
- (3)
- We can develop efficient CPFEM numerical implementation algorithms.
- (4)
- We can develop modeling techniques that better reflect the microstructure of real materials to more accurately characterize the deformation mechanism of materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bandyopadhyay, A.; Zhang, Y.; Bose, S. Recent developments in metal additive manufacturing. Curr. Opin. Chem. Eng. 2020, 28, 96–104. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Design 2021, 209, 110008. [Google Scholar] [CrossRef]
- Dziubińska, A.; Surdacki, P.; Majerski, K. The analysis of deformability, structure and properties of AZ61 cast magnesium alloy in a new hammer forging process for aircraft mounts. Materials 2021, 14, 2593. [Google Scholar] [CrossRef] [PubMed]
- Fernández, D.S.; Wynne, B.P.; Crawforth, P.; Fox, K.; Jackson, M. The effect of forging texture and machining parameters on the fatigue performance of titanium alloy disc components. Int. J. Fatigue 2021, 142, 105949. [Google Scholar] [CrossRef]
- Fernández, D.S.; Wynne, B.P.; Crawforth, P.; Jackson, M. Titanium alloy microstructure fingerprint plots from in-process machining. Mater. Sci. Eng. 2021, 811, 141074. [Google Scholar] [CrossRef]
- Tan, C.; Li, R.; Su, J.; Du, D.; Du, Y.; Attard, B.; Chew, Y.; Zhang, H.; Lavernia, E.J.; Fautrelle, Y.; et al. Review on field assisted metal additive manufacturing. Int. J. Mach. Tools Manuf. 2023, 189, 104032. [Google Scholar] [CrossRef]
- Keicher, D. Beyond rapid prototyping to direct fabrication: Forming metallic hardware directly from a CAD solid model. Mater. Technol. 1998, 13, 5–7. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N. Additive manufacturing of fatigue resistant materials: Challenges and opportunities. Int. J. Fatigue 2017, 98, 14–31. [Google Scholar] [CrossRef]
- Gockel, J.; Sheridan, L.; Koerper, B.; Whip, B. The influence of additive manufacturing processing parameters on surface roughness and fatigue life. Int. J. Fatigue 2019, 124, 380–388. [Google Scholar] [CrossRef]
- Chern, A.H.; Nandwana, P.; Yuan, T.; Kirka, M.M.; Dehoff, R.R.; Liaw, P.K.; Duty, C.E. A review on the fatigue behavior of Ti-6Al-4V fabricated by electron beam melting additive manufacturing. Int. J. Fatigue 2019, 119, 173–184. [Google Scholar] [CrossRef]
- Lewandowski, J.; Seifi, M. Metal additive manufacturing: A review of mechanical properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Bieler, T.R.; Raabe, D. Crystal Plasticity Finite Element Methods: In Materials Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Cong, T.; Li, R.; Zheng, Z.; Ma, X.; Wu, S.; Zhang, R.; Berto, F.; Sun, J.; Qian, G. Experimental and computational investigation of weathering steel Q450NQR1 under high cycle fatigue loading via crystal plasticity finite element method. Int. J. Fatigue 2022, 159, 106772. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Wu, S.; Zhang, W.; Sun, J.; Qian, G. High-cycle and very-high-cycle fatigue lifetime prediction of additively manufactured AlSi10Mg via crystal plasticity finite element method. Int. J. Fatigue 2022, 155, 106577. [Google Scholar] [CrossRef]
- Li, J.; Yuan, H.; Chandrakar, A.; Moroni, L.; Habibovic, P. 3D porous Ti6Al4V-beta-tricalcium phosphate scaffolds directly fabricated by additive manufacturing. Acta Biomater. 2021, 126, 496–510. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Design 2019, 164, 107552. [Google Scholar] [CrossRef]
- Mishra, R.S.; Thapliyal, S. Design approaches for printability-performance synergy in Al alloys for laser-powder bed additive manufacturing. Mater. Design 2021, 204, 109640. [Google Scholar] [CrossRef]
- Kotadia, H.R.; Gibbons, G.; Das, A.; Howes, P.D. A review of Laser Powder Bed Fusion Additive Manufacturing of aluminium alloys: Microstructure and properties. Addit. Manuf. 2021, 46, 102155. [Google Scholar] [CrossRef]
- Mostafaei, A.; Ghiaasiaan, R.; Ho, I.-T.; Strayer, S.; Chang, K.-C.; Shamsaei, N.; Shao, S.; Paul, S.; Yeh, A.-C.; Tin, S.; et al. Additive Manufacturing of Nickel-based superalloys: A state-of-the-art review on process-structure-defect-property relationship. Prog. Mater. Sci. 2023, 101108. [Google Scholar] [CrossRef]
- Park, J.U.; Jun, S.Y.; Lee, B.H.; Jang, J.H.; Lee, B.S.; Lee, H.J.; Lee, J.H.; Hong, H.U. Alloy design of Ni-based superalloy with high γ′ volume fraction suitable for additive manufacturing and its deformation behavior. Addit. Manuf. 2022, 52, 102680. [Google Scholar] [CrossRef]
- Sarkar, R.; Chen, B.; Fitzpatrick, M.E.; Fabijanic, D.; Hilditch, T. Additive manufacturing-based repair of IN718 superalloy and high-cycle fatigue assessment of the joint. Addit. Manuf. 2022, 60, 103276. [Google Scholar]
- Sreeramagiri, P.; Bhagavatam, A.; Ramakrishnan, A.; Alrehaili, H.; Dinda, G.P. Design and development of a high-performance Ni-based superalloy WSU 150 for additive manufacturing. J. Mater. Sci. Technol. 2020, 47, 20–28. [Google Scholar] [CrossRef]
- Sadaf, M.; Bragaglia, M.; Nanni, F. A simple route for additive manufacturing of 316L stainless steel via Fused Filament Fabrication. J. Manuf. Proc. 2021, 67, 141–150. [Google Scholar] [CrossRef]
- Kürnsteiner, P.; Wilms, M.B.; Weisheit, A.; Gault, B.; Jägle, E.A.; Raabe, D. High-strength Damascus steel by additive manufacturing. Nature 2020, 582, 515–519. [Google Scholar] [CrossRef] [PubMed]
- Fedina, T.; Sundqvist, J.; Powell, J.; Kaplan, A.F. A comparative study of water and gas atomized low alloy steel powders for additive manufacturing. Addit. Manuf. 2020, 36, 101675. [Google Scholar] [CrossRef]
- Karunakaran, R.; Ortgies, S.; Tamayol, A.; Bobaru, F.; Sealy, M.P. Additive manufacturing of magnesium alloys. Bioact. Mater. 2020, 5, 44–54. [Google Scholar] [CrossRef]
- Zeng, Z.; Salehi, M.; Kopp, A.; Xu, S.; Esmaily, M.; Birbilis, N. Recent progress and perspectives in additive manufacturing of magnesium alloys. J. Magnes. Alloys 2022, 10, 1511–1541. [Google Scholar] [CrossRef]
- Srivastava, M.; Rathee, S.; Patel, V.; Kumar, A.; Koppad, P.G. A review of various materials for additive manufacturing: Recent trends and processing issues. J. Mater. Res. Technol. 2022, 21, 2612–2641. [Google Scholar] [CrossRef]
- Obeidi, M.A. Metal additive manufacturing by laser-powder bed fusion: Guidelines for process optimisation. Results Eng. 2022, 15, 100473. [Google Scholar] [CrossRef]
- Sing, S.L.; Yeong, W.Y. Laser powder bed fusion for metal additive manufacturing: Perspectives on recent developments. Virtual Phys. Prototyp. 2020, 15, 359–370. [Google Scholar] [CrossRef]
- Svetlizky, D.; Das, M.; Zheng, B.; Vyatskikh, A.L.; Bose, S.; Bandyopadhyay, A.; Schoenung, J.M.; Lavernia, E.J.; Eliaz, N. Directed energy deposition (DED) additive manufacturing: Physical characteristics, defects, challenges and applications. Mater. Today 2021, 49, 271–295. [Google Scholar] [CrossRef]
- Ahmadi, M.; Tabary, S.B.; Rahmatabadi, D.; Ebrahimi, M.; Abrinia, K.; Hashemi, R. Review of selective laser melting of magnesium alloys: Advantages, microstructure and mechanical characterizations, defects, challenges, and applications. J. Mater. Res. Technol. 2022, 19, 1537–1562. [Google Scholar] [CrossRef]
- Louvis, E.; Fox, P.; Sutcliffe, C. Selective laser melting of aluminium components. J. Mater. Process. Technol. 2011, 211, 275–284. [Google Scholar] [CrossRef]
- Sefene, E.M. State-of-the-art of selective laser melting process: A comprehensive review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Jia, H.; Sun, H.; Wang, H.; Wu, Y.; Wang, H. Scanning strategy in selective laser melting (SLM): A review. Int. J. Adv. Manuf. Technol. 2021, 113, 2413–2435. [Google Scholar] [CrossRef]
- Singla, A.K.; Banerjee, M.; Sharma, A.; Singh, J.; Bansal, A.; Gupta, M.K.; Khanna, N.; Shahi, A.; Goyal, D.K. Selective laser melting of Ti6Al4V alloy: Process parameters, defects and post-treatments. J. Manuf. Process. 2021, 64, 161–187. [Google Scholar] [CrossRef]
- Zhao, C.; Bai, Y.; Zhang, Y.; Wang, X.; Xue, J.M.; Wang, H. Influence of scanning strategy and building direction on microstructure and corrosion behaviour of selective laser melted 316 L stainless steel. Mater. Design 2021, 209, 109999. [Google Scholar] [CrossRef]
- Li, X.; Yi, D.; Wu, X.; Zhang, J.; Yang, X.; Zhao, Z.; Feng, Y.; Wang, J.; Bai, P.; Liu, B.; et al. Effect of construction angles on microstructure and mechanical properties of AlSi10Mg alloy fabricated by selective laser melting. J. Alloys Compd. 2021, 881, 160459. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, F.; Huang, C.; Lin, X.; Xia, C.; Wang, Z.; You, Q.; Liu, L. Achieving superior burn resistant and mechanical properties of Ti40 alloy by laser solid forming. J. Manuf. Proc. 2023, 102, 406–415. [Google Scholar] [CrossRef]
- Liang, S.; Yan, W. Study on the micro-structure and the nano-indentation responses of laser solid formed epitaxial Ni-based superalloy. J. Alloys Compd. 2022, 921, 166091. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, P.; Yang, L.; Le, G.; He, S.; He, X.; Liu, X.; Wang, W. Microstructure and mechanical properties of Be–Al alloy fabricated by laser solid forming. Mater. Sci. Eng. 2021, 799, 140335. [Google Scholar] [CrossRef]
- Li, Y.; Kan, W.; Zhang, Y.; Li, M.; Liang, X.; Yu, Y.; Lin, F. Microstructure, mechanical properties and strengthening mechanisms of IN738LC alloy produced by Electron Beam Selective Melting. Addit. Manuf. 2021, 47, 102371. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Yu, Y.; Li, H.; Kan, W.; Lin, F. Microstructures and mechanical properties evolution of IN939 alloy during electron beam selective melting process. J. Alloys Compd. 2021, 883, 160934. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Liu, B.; Guo, C.; Sun, J. Precipitation behavior in a Nb-5W-2Mo-1Zr niobium alloy fabricated by electron beam selective melting. Mater. Charact. 2021, 174, 111019. [Google Scholar] [CrossRef]
- Zhao, D.C.; Lin, F. Dual-detector electronic monitoring of electron beam selective melting. J. Mater. Process. Technol. 2021, 289, 116935. [Google Scholar] [CrossRef]
- Cui, R.; Wang, L.; Yao, L.; Li, B.; Su, Y.; Luo, L.; Chen, R.; Guo, J.; Fu, H. On the solidification behaviors of AlCu5MnCdVA alloy in electron beam freeform fabrication: Microstructural evolution, Cu segregation and cracking resistance. Addit. Manuf. 2022, 51, 102606. [Google Scholar] [CrossRef]
- Su, B.; Wang, B.; Luo, L.; Wang, L.; Li, B.; Liu, C.; Su, Y.; Xu, Y.; Huang, H.; Guo, J.; et al. Tuning microstructure and improving the corrosion resistance of Ti-6Al-3Nb-2Zr-1Mo alloy using the electron beam freeform fabrication. Chem. Eng. J. 2022, 444, 136524. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, L.; Wang, B.; Li, B.; Zhao, J.; Ding, B.; Cui, R.; Jiang, B.; Zhao, C.; Su, B.; et al. Multi-materials additive manufacturing of Ti64/Cu/316L by electron beam freeform fabrication. J. Mater. Res. Technol. 2023, 26, 8388–8405. [Google Scholar] [CrossRef]
- Osipovich, K.; Kalashnikov, K.; Chumaevskii, A.; Gurianov, D.; Kalashnikova, T.; Vorontsov, A.; Zykova, A.; Utyaganova, V.; Panfilov, A.; Nikolaeva, A.; et al. Wire-Feed Electron Beam Additive Manufacturing: A Review. Metals 2023, 13, 279. [Google Scholar] [CrossRef]
- Gong, X.; Anderson, T.; Chou, K. Review on powder-based electron beam additive manufacturing technology. In Proceedings of the ASME/ISCIE 2012 International Symposium on Flexible Automation, St. Louis, MO, USA, 18–20 June 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 507–515. [Google Scholar]
- Jafari, D.; Vaneker, T.H.; Gibson, I. Wire and arc additive manufacturing: Opportunities and challenges to control the quality and accuracy of manufactured parts. Mater. Design 2021, 202, 109471. [Google Scholar] [CrossRef]
- Lin, Z.; Song, K.; Yu, X. A review on wire and arc additive manufacturing of titanium alloy. J. Manuf. Proc. 2021, 70, 24–45. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. Ser. A 1934, 145, 362–387. [Google Scholar]
- Hill, R. Generalized constitutive relations for incremental deformation of metal crystals by multislip. J. Mech. Phys. Solids 1966, 14, 95–102. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Kalidindi, S.R. Incorporation of deformation twinning in crystal plasticity models. J. Mech. Phys. Solids 1998, 46, 267–290. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Schlögl, S.M.; Fischer, F.D. The role of slip and twinning in the deformation behaviour of polysynthetically twinned crystals of TiAl: A micromechanical model. Philos. Mag. A 1997, 75, 621–636. [Google Scholar] [CrossRef]
- Tomé, C.N.; Lebensohn, R.A.; Kocks, U.F. A model for texture development dominated by deformation twinning: Application to zirconium alloys. Acta Metall. Mater. 1991, 39, 2667–2680. [Google Scholar] [CrossRef]
- Doquet, V. Twinning and multiaxial cyclic plasticity of a low stacking-fault-energy fcc alloy. Acta Metall. Mater. 1993, 41, 2451–2459. [Google Scholar] [CrossRef]
- Van Houtte, P. Simulation of the rolling and shear texture of brass by the Taylor theory adapted for mechanical twinning. Acta Metall. 1978, 26, 591–604. [Google Scholar] [CrossRef]
- Asaro, R.J. Crystal plasticity. J. Appl. Mech. 1983, 50, 921–934. [Google Scholar] [CrossRef]
- Becker, R.; Panchanadeeswaran, S. Effects of grain interactions on deformation and local texture in polycrystals. Acta Metall. Mater. 1995, 43, 2701–2719. [Google Scholar] [CrossRef]
- Van Houtte, P.; Delannay, L.; Kalidindi, S.R. Comparison of two grain interaction models for polycrystal plasticity and deformation texture prediction. Int. J. Plast. 2002, 18, 359–377. [Google Scholar] [CrossRef]
- Van Houtte, P. A comprehensive mathematical formulation of an extended Taylor–Bishop–Hill model featuring relaxed constraints, the Renouard–Wintenberger theory and a strain rate sensitivity model. Textures Microstruct. 1988, 8, 313–350. [Google Scholar] [CrossRef]
- Honneff, H.; Mecking, H. Analysis of the deformation texture at different rolling conditions. In Proceedings of the Sixth International Conference on Textures of Materials, Tokyo, Japan, 28 September–3 October 1981; pp. 347–355. [Google Scholar]
- Habraken, A.M. Modelling the plastic anisotropy of metals. Arch. Comput. Methods Eng. 2004, 11, 3–96. [Google Scholar] [CrossRef]
- Lin, T.H. Analysis of elastic and plastic strains of a face-centred cubic crystal. J. Mech. Phys. Solids 1957, 5, 143–149. [Google Scholar] [CrossRef]
- Berveiller, M.; Zaoui, A. An extension of the self-consistent scheme to plastically-flowing polycrystals. J. Mech. Phys. Solids 1978, 26, 325–344. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. Lond. A Math. Phys. Sci. 1970, 319, 247–272. [Google Scholar]
- Iwakuma, T.; Nemat-Nasser, S. Finite elastic-plastic deformation of polycrystalline metals. Proc. R. Soc. Lond. A Math. Phys. Sci. 1984, 394, 87–119. [Google Scholar]
- Kröner, E. Zur plastischen verformung des vielkristalls. Acta Metall. 1961, 9, 155–161. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Tomé, C.N.; Huang, Y. A finite strain elastic–viscoplastic self-consistent model for polycrystalline materials. J. Mech. Phys. Solids 2010, 58, 594–612. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, Y.; Nagaumi, H.; Yang, X. Roles of dislocation slip and twinning in the creep performance of a wrought Mg-Zn-Mn alloy sheet. J. Alloys Compd. 2023, 967, 171631. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Logan, R.W.; Hosford, W.F. Upper-bound anisotropic yield locus calculations assuming <111>-pencil glide. Int. J. Mech. Sci. 1980, 22, 419–430. [Google Scholar]
- Yang, Q.; Marvel, C.J.; Shen, Y.; He, M.-R.; Du, J.; Hwang, C.; Gronske, E.D.; Xie, K.Y.; Mercurio, S.R.; An, Q.; et al. Activating dislocation mediated plasticity in boron carbide through Al-doping. Acta Mater. 2022, 241, 118412. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Y.; Wang, L.; Jia, H.; Zeng, X. The role of grain boundary plane in slip transfer during deformation of magnesium alloys. Acta Mater. 2022, 227, 117662. [Google Scholar] [CrossRef]
- Petersmann, M.; Antretter, T.; Cailletaud, G.; Sannikov, A.; Ehlenbröker, U.; Fischer, F. Unification of the non-linear geometric transformation theory of martensite and crystal plasticity-Application to dislocated lath martensite in steels. Int. J. Plast. 2019, 119, 140–155. [Google Scholar] [CrossRef]
- Jia, N.; Roters, F.; Eisenlohr, P.; Raabe, D.; Zhao, X. Simulation of shear banding in heterophase co-deformation: Example of plane strain compressed Cu–Ag and Cu–Nb metal matrix composites. Acta Mater. 2013, 61, 4591–4606. [Google Scholar] [CrossRef]
- Jia, N.; Roters, F.; Eisenlohr, P.; Kords, C.; Raabe, D. Non-crystallographic shear banding in crystal plasticity FEM simulations: Example of texture evolution in α-brass. Acta Mater. 2012, 60, 1099–1115. [Google Scholar] [CrossRef]
- Yuan, S.; Huang, M.; Zhu, Y.; Li, Z. A dislocation climb/glide coupled crystal plasticity constitutive model and its finite element implementation. Mech. Mater. 2018, 118, 44–61. [Google Scholar] [CrossRef]
- Yuan, S.; Zhu, Y.; Liang, S.; Huang, M.; Li, Z. Dislocation-density based size-dependent crystal plasticity framework accounting for climb of piled up dislocations at elevated temperature. Mech. Mater. 2019, 134, 85–97. [Google Scholar] [CrossRef]
- Venkataramani, G.; Kirane, K.; Ghosh, S. Microstructural parameters affecting creep induced load shedding in Ti-6242 by a size dependent crystal plasticity FE model. Int. J. Plast. 2008, 24, 428–454. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Kan, Q.; Xu, X. Physical mechanism based crystal plasticity model of NiTi shape memory alloys addressing the thermo-mechanical cyclic degeneration of shape memory effect. Mech. Mater. 2017, 112, 1–17. [Google Scholar] [CrossRef]
- Jeong, J.; Voyiadjis, G.Z. A physics-based crystal plasticity model for the prediction of the dislocation densities in micropillar compression. J. Mech. Phys. Solids 2022, 167, 105006. [Google Scholar] [CrossRef]
- Patra, A.; Chaudhary, S.; Pai, N.; Ramgopal, T.; Khandelwal, S.; Rao, A.; McDowell, D.L. ρ-CP: Open source dislocation density based crystal plasticity framework for simulating temperature-and strain rate-dependent deformation. Comput. Mater. Sci. 2023, 224, 112182. [Google Scholar] [CrossRef]
- Potirniche, G.P.; Horstemeyer, M.F.; Ling, X.W. An internal state variable damage model in crystal plasticity. Mech. Mater. 2007, 39, 941–952. [Google Scholar] [CrossRef]
- Li, H.W.; Yang, H.; Sun, Z.C. A robust integration algorithm for implementing rate dependent crystal plasticity into explicit finite element method. Int. J. Plast. 2008, 24, 267–288. [Google Scholar] [CrossRef]
- Rashid, M.M.; Nemat-Nasser, S. A constitutive algorithm for rate-dependent crystal plasticity. Comput. Methods Appl. Mech. Eng. 1992, 94, 201–228. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X.; Brochu, M.; Wang, X.; Harrison, N.M.; Leen, S.B.; Segurado, J. Understanding orientation-dependent plasticity in laser beam powder bed fusion stainless steel through crystal plasticity modelling. Mater. Sci. Eng. A 2022, 852, 143682. [Google Scholar] [CrossRef]
- Schilli, S.; Seifert, T.; Kreins, M.; Krupp, U. Bauschinger effect and latent hardening under cyclic micro-bending of Ni-base Alloy 718 single crystals: Part II. Single crystal plasticity modeling with latent kinematic hardening. Mater. Sci. Eng. A 2022, 830, 142030. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, X.; Li, J.; Chen, J.; Lin, X.; Wang, M.; Tan, H.; Huang, W. In-situ grain structure control in directed energy deposition of Ti6Al4V. Addit. Manuf. 2022, 55, 102865. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, F.; Wang, Y. Mechanical Anisotropy of Selective Laser Melted Ti-6Al-4V Using a Reduced-order Crystal Plasticity Finite Element Model. Chin. J. Mech. Eng. Addit. Manuf. Front. 2023, 2, 100062. [Google Scholar] [CrossRef]
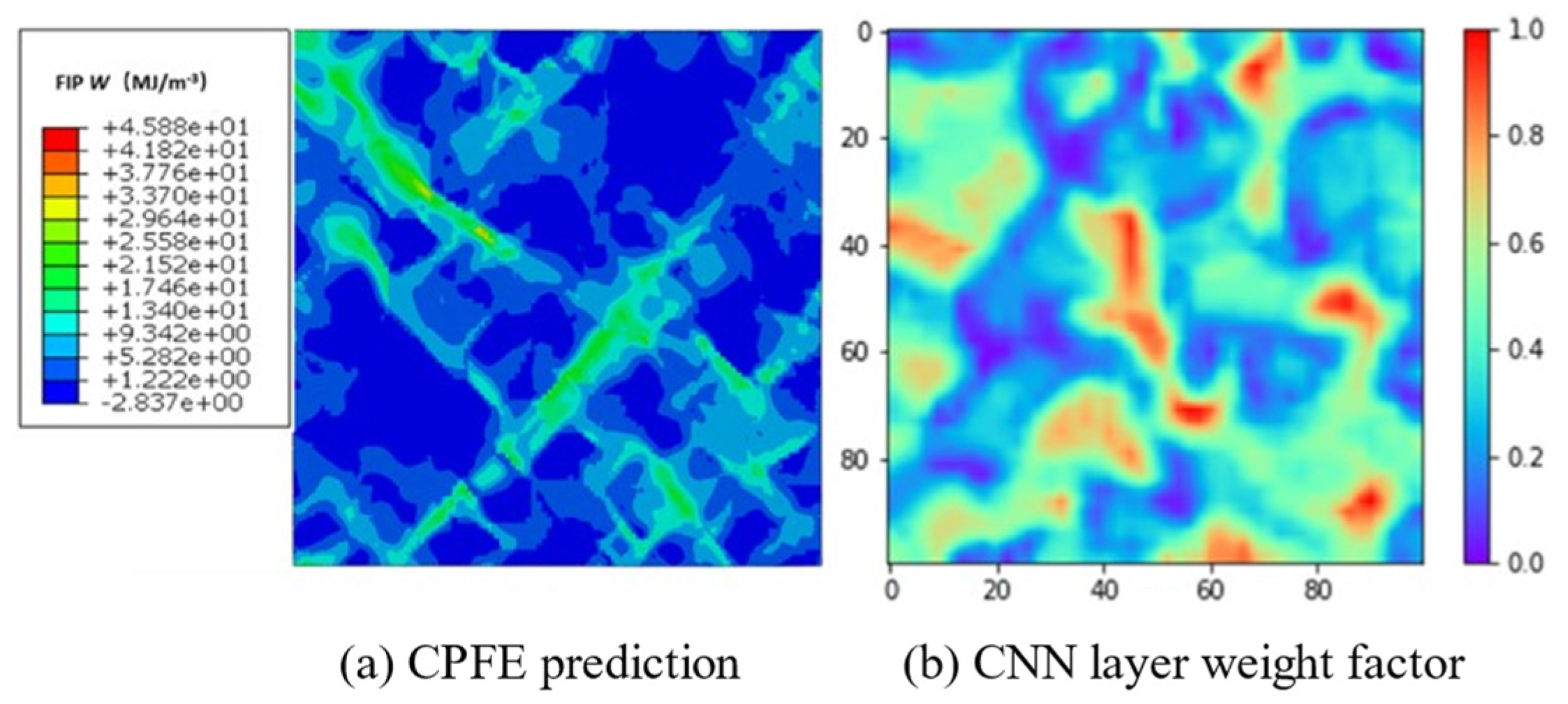
- Tu, Y.; Liu, Z.; Carneiro, L.; Ryan, C.M.; Parnell, A.C.; Leen, S.B.; Harrison, N.M. Towards an instant structure-property prediction quality control tool for additive manufactured steel using a crystal plasticity trained deep learning surrogate. Mater. Design 2022, 213, 110345. [Google Scholar] [CrossRef]
- Lakshmanan, A.; Yaghoobi, M.; Stopka, K.S.; Sundararaghavan, V. Crystal plasticity finite element modeling of grain size and morphology effects on yield strength and extreme value fatigue response. J. Mater. Res. Technol. 2022, 19, 3337–3354. [Google Scholar] [CrossRef]
- Cheng, J.; Fernandez-Zelaia, P.; Hu, X.; Kirka, M. Effect of microstructure on fatigue crack propagation in additive manufactured nickel-based superalloy Haynes 282, an experiment and crystal plasticity study. J. Mater. Sci. 2022, 57, 9741–9768. [Google Scholar] [CrossRef]
- Eghtesad, A.; Knezevic, M. A full-field crystal plasticity model including the effects of precipitates: Application to monotonic, load reversal, and low-cycle fatigue behavior of Inconel 718. Mater. Sci. Eng. A 2021, 803, 140478. [Google Scholar] [CrossRef]
- Yi, M.; Chang, K.; Liang, C.; Zhou, L.; Yang, Y.; Yi, X.; Xu, B. Computational study of evolution and fatigue dispersity of microstructures by additive manufacturing. Chin. J. Theor. Appl. Mech. 2021, 53, 3263–3273. (In Chinese) [Google Scholar]
- Zheng, D.; Li, Z.; Jiang, Y.; Li, R.; Wu, Y.; Tu, Y.; Cheng, X.; Fu, P.; Peng, L.; Tang, H. Effect of multiple thermal cycles on the microstructure evolution of GA151K alloy fabricated by laser-directed energy deposition. Addit. Manuf. 2022, 57, 102957. [Google Scholar] [CrossRef]
- Manonukul, A.; Dunne, F. High–and low–cycle fatigue crack initiation using polycrystal plasticity. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1881–1903. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Y.; Ma, X.; Qian, G.; Zhang, J.; Yang, Z.; Berto, F. Very-high-cycle fatigue behavior of AlSi10Mg manufactured by selected laser melting: Crystal plasticity modeling. Int. J. Fatigue 2021, 145, 106109. [Google Scholar] [CrossRef]
- Luo, Z.; Li, D.; Ojha, A.; Lai, W.-J.; Engler-Pinto, C.; Li, Z.; Peng, Y. Prediction of high cycle fatigue strength for additive manufactured metals by defects incorporated crystal plasticity modeling. Mater. Sci. Eng. A 2023, 870, 144832. [Google Scholar] [CrossRef]
- Cao, M.; Liu, Y.; Dunne, F.P.E. A crystal plasticity approach to understand fatigue response with respect to pores in additive manufactured aluminium alloys. Int. J. Fatigue 2022, 161, 106917. [Google Scholar] [CrossRef]
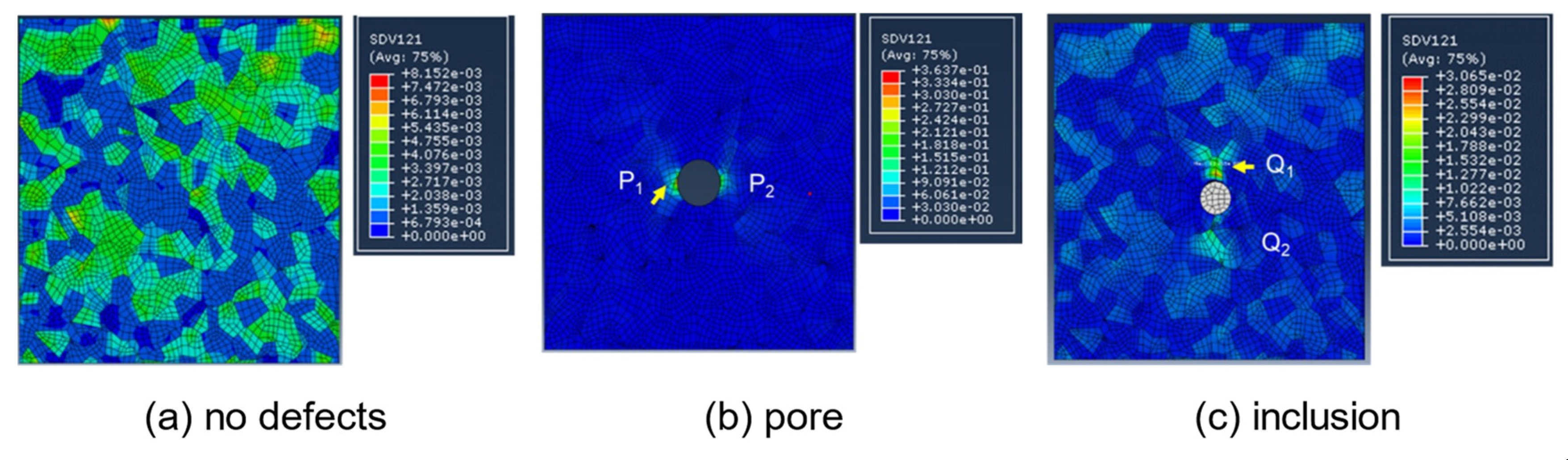
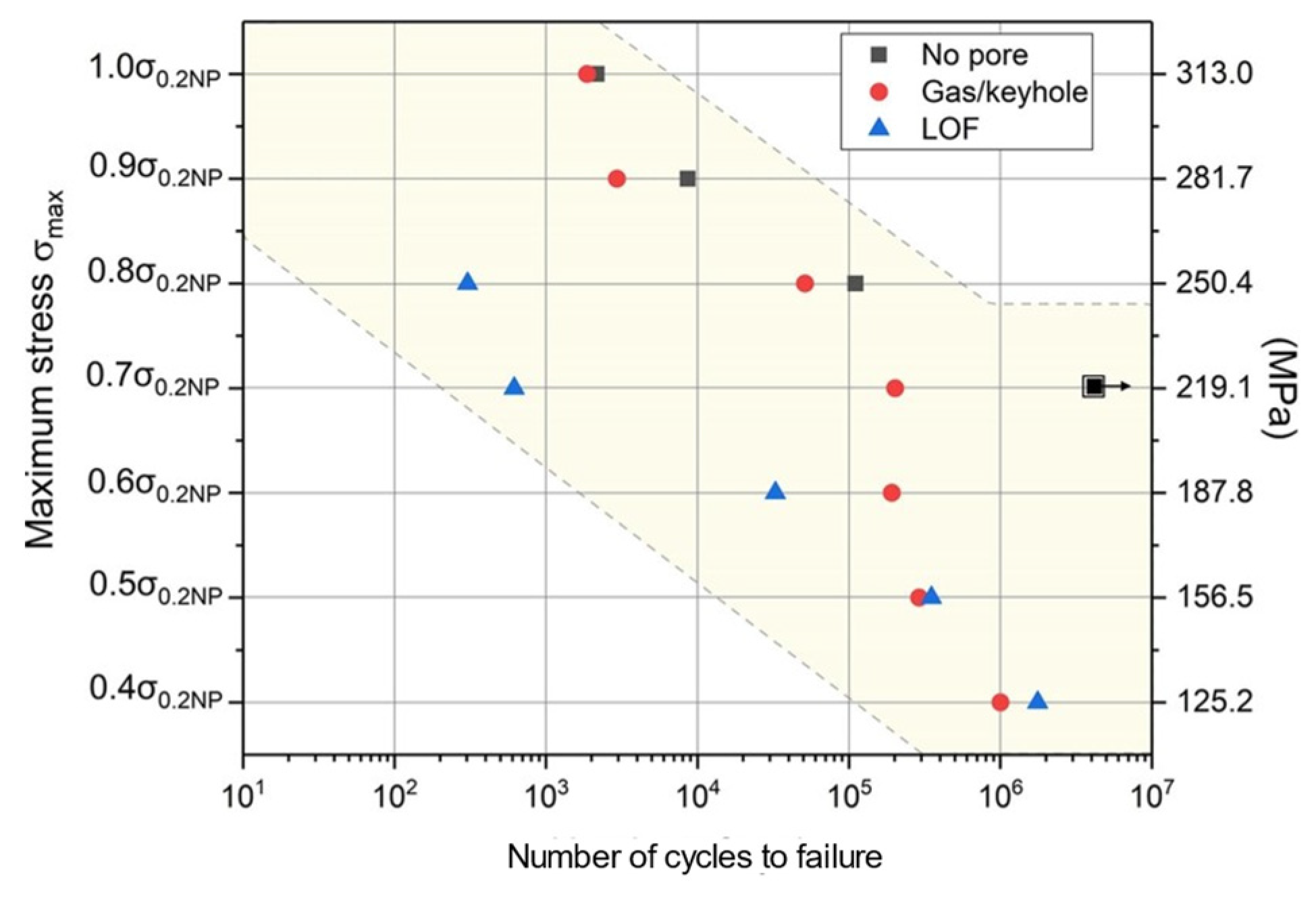
- Hu, Y.; Wu, S.; Withers, P.; Zhang, J.; Bao, H.; Fu, Y.; Kang, G. The effect of manufacturing defects on the fatigue life of selective laser melted Ti-6Al-4V structures. Mater. Design 2020, 192, 108708. [Google Scholar] [CrossRef]
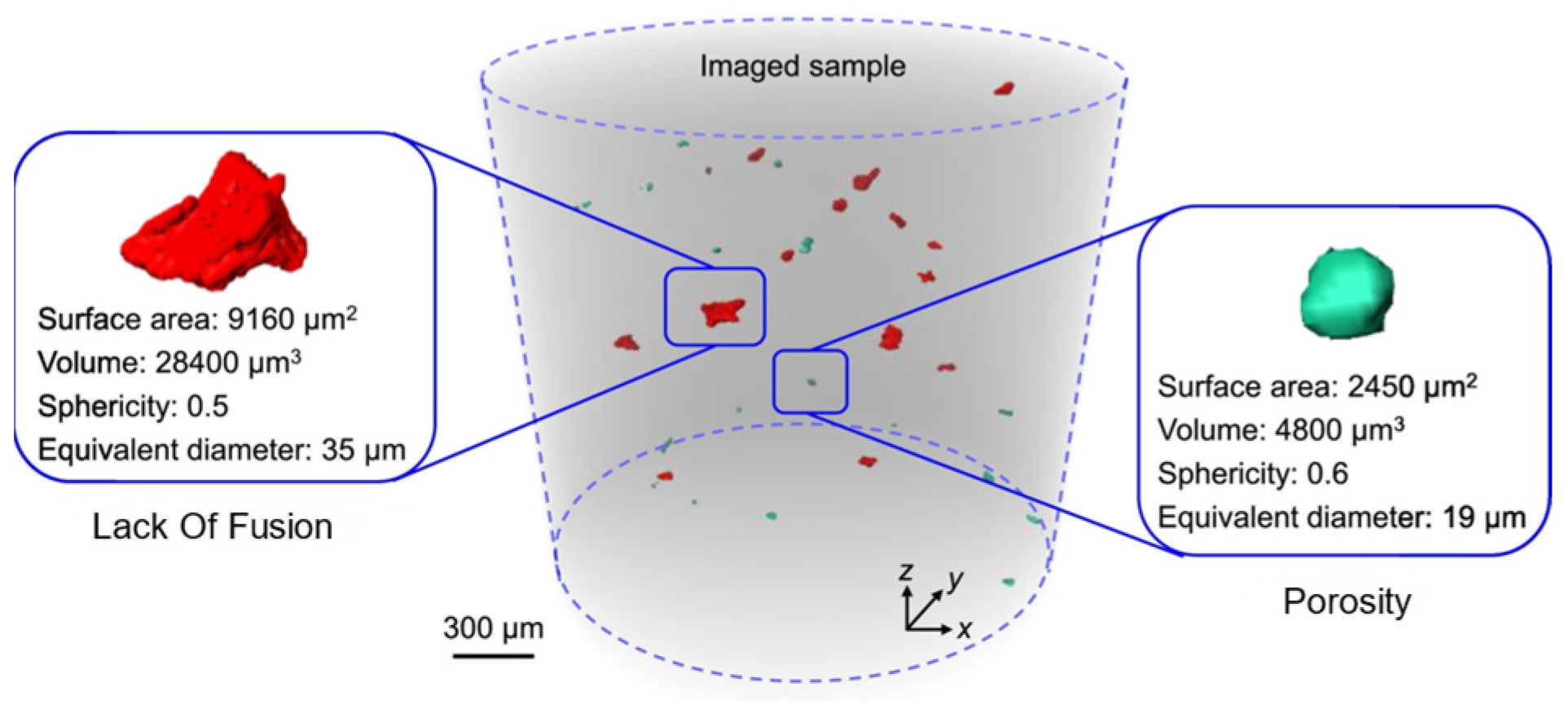
- Prithivirajan, V.; Sangid, M.D. The role of defects and critical pore size analysis in the fatigue response of additively manufactured IN718 via crystal plasticity. Mater. Design 2018, 150, 139–153. [Google Scholar] [CrossRef]
- Xu, Z.W.; Wang, Q.; Wang, X.S.; Tan, C.H.; Guo, M.H.; Gao, P.B. High cycle fatigue performance of AlSi10mg alloy produced by selective laser melting. Mech. Mater. 2020, 148, 103499. [Google Scholar] [CrossRef]
- Qin, Z.; Li, B.; Huang, X.; Zhang, H.; Chen, R.; Adeel, M.; Xue, H. The effect of laser shock peening on surface integrity and high and very high cycle fatigue properties of 2024-T351 aluminum alloy. Opt. Laser Technol. 2022, 149, 107897. [Google Scholar] [CrossRef]
- Li, B.; Qin, Z.; Zhang, H.; Xue, H. The effects of laser peening treatment on the very high cycle fatigue properties for AA2024-T351 alloy using a crystal plasticity framework. Eng. Fract. Mech. 2022, 275, 108840. [Google Scholar] [CrossRef]
- Kapoor, K.; Yoo, Y.S.J.; Book, T.A.; Kacher, J.P.; Sangid, M.D. Incorporating grain-level residual stresses and validating a crystal plasticity model of a two-phase Ti-6Al-4 V alloy produced via additive manufacturing. J. Mech. Phys. Solids 2018, 121, 447–462. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wang, A.; Wang, J.; Wang, Q.; Li, F.; Lu, K. Advances in Fatigue Performance of Metal Materials with Additive Manufacturing Based on Crystal Plasticity: A Comprehensive Review. Materials 2024, 17, 1019. https://doi.org/10.3390/ma17051019
Zhang W, Wang A, Wang J, Wang Q, Li F, Lu K. Advances in Fatigue Performance of Metal Materials with Additive Manufacturing Based on Crystal Plasticity: A Comprehensive Review. Materials. 2024; 17(5):1019. https://doi.org/10.3390/ma17051019
Chicago/Turabian StyleZhang, Wei, Anheng Wang, Jianbin Wang, Qiaoyu Wang, Fan Li, and Kuai Lu. 2024. "Advances in Fatigue Performance of Metal Materials with Additive Manufacturing Based on Crystal Plasticity: A Comprehensive Review" Materials 17, no. 5: 1019. https://doi.org/10.3390/ma17051019
APA StyleZhang, W., Wang, A., Wang, J., Wang, Q., Li, F., & Lu, K. (2024). Advances in Fatigue Performance of Metal Materials with Additive Manufacturing Based on Crystal Plasticity: A Comprehensive Review. Materials, 17(5), 1019. https://doi.org/10.3390/ma17051019





