3D Size-Dependent Dynamic Instability Analysis of FG Cylindrical Microshells Subjected to Combinations of Periodic Axial Compression and External Pressure Using a Hermitian C2 Finite Layer Method Based on the Consistent Couple Stress Theory
Abstract
1. Introduction
2. The Initial Stresses Induced at the Pre-Instability State
3. The CCST for Elastic Bodies
4. The System Equations at the Incremental Perturbation State
4.1. The CCST-Based Hermitian C2 FLM
4.1.1. Generalized Kinematics Models
4.1.2. Hamilton’s Principle
4.1.3. Layer Element Equations and Structural Equations
4.2. Bolotin’s Method
4.2.1. The Principal Instability Regions
4.2.2. The Secondary Instability Regions
4.3. Reduced Cases
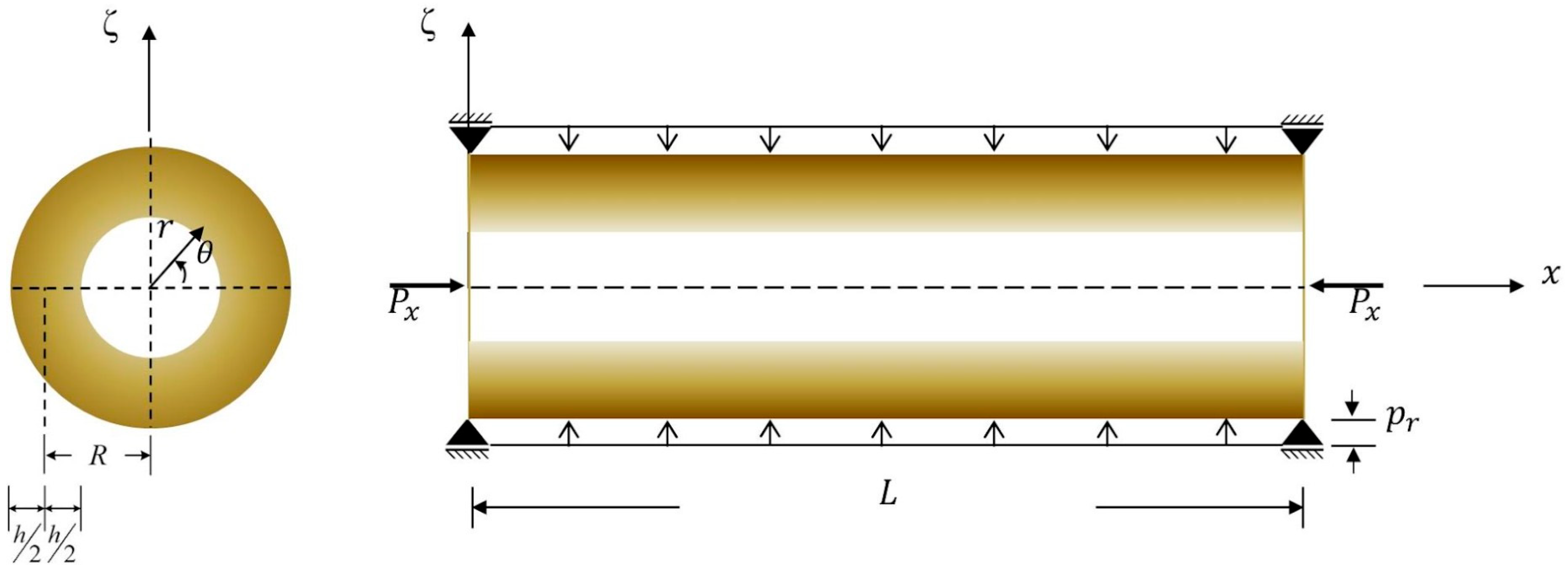
5. Numerical Examples
5.1. Static Buckling
5.2. Dynamic Instability
6. Concluding Remarks
- The CCST-based Hermite C2 FLM for analyzing FG cylindrical microshells can be reduced to those for analyzing FG cylindrical macroshells by setting a zero value to the material length-scale parameter. The static buckling and dynamic instability analyses of the reduced model showed that the CCST-based Hermite C2 FLM was validated by comparing the solutions it produced with the solutions obtained using the 3D elasticity theory and the 2D advanced shear deformation shell theories reported in the literature.
- The implementation of Bolotin’s method in the numerical examples showed that convergent solutions were obtained when two terms of the trigonometric functions were used. When arranging by descending order of bandwidth between the upper and lower bounds of excitation frequency, we obtain the following list of instability regions: the first principal instability region, the first secondary instability region, the second principal instability region, and the second secondary instability region.
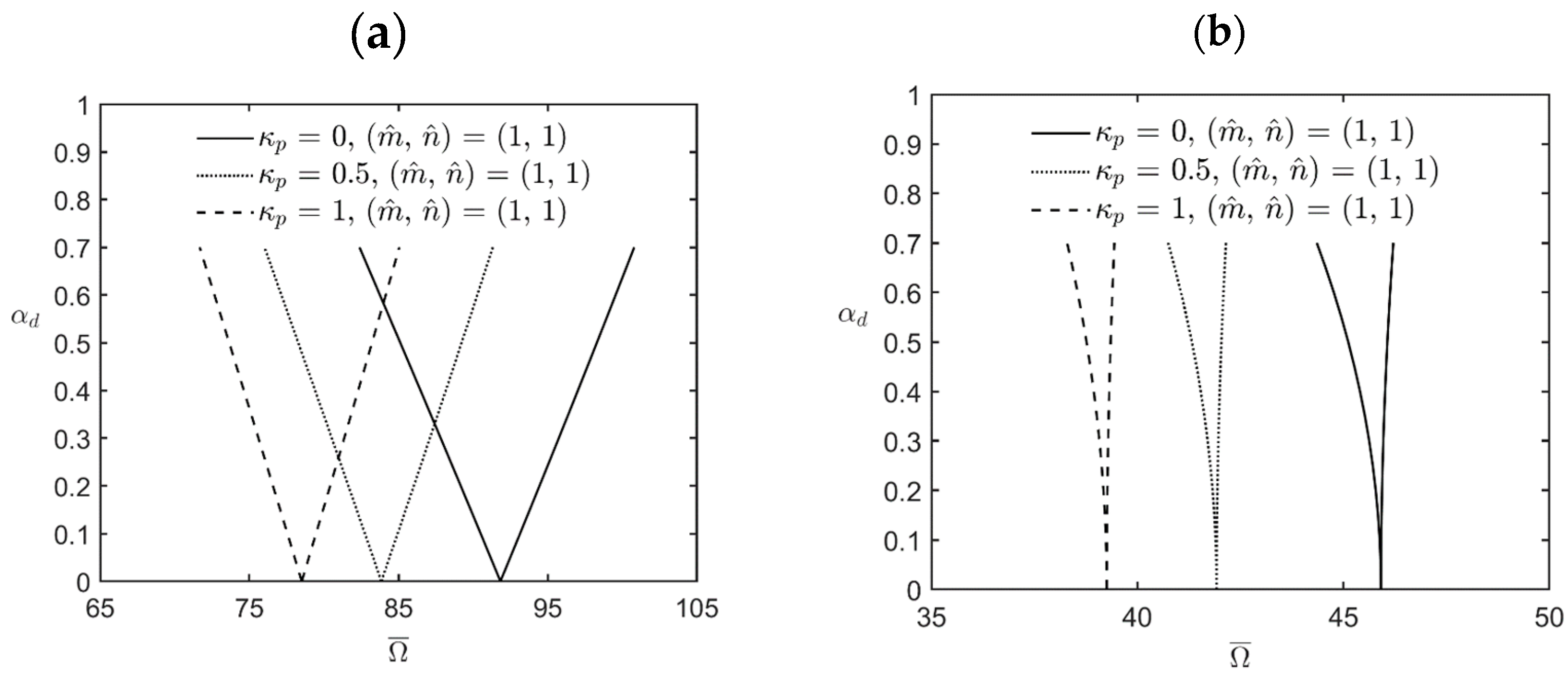
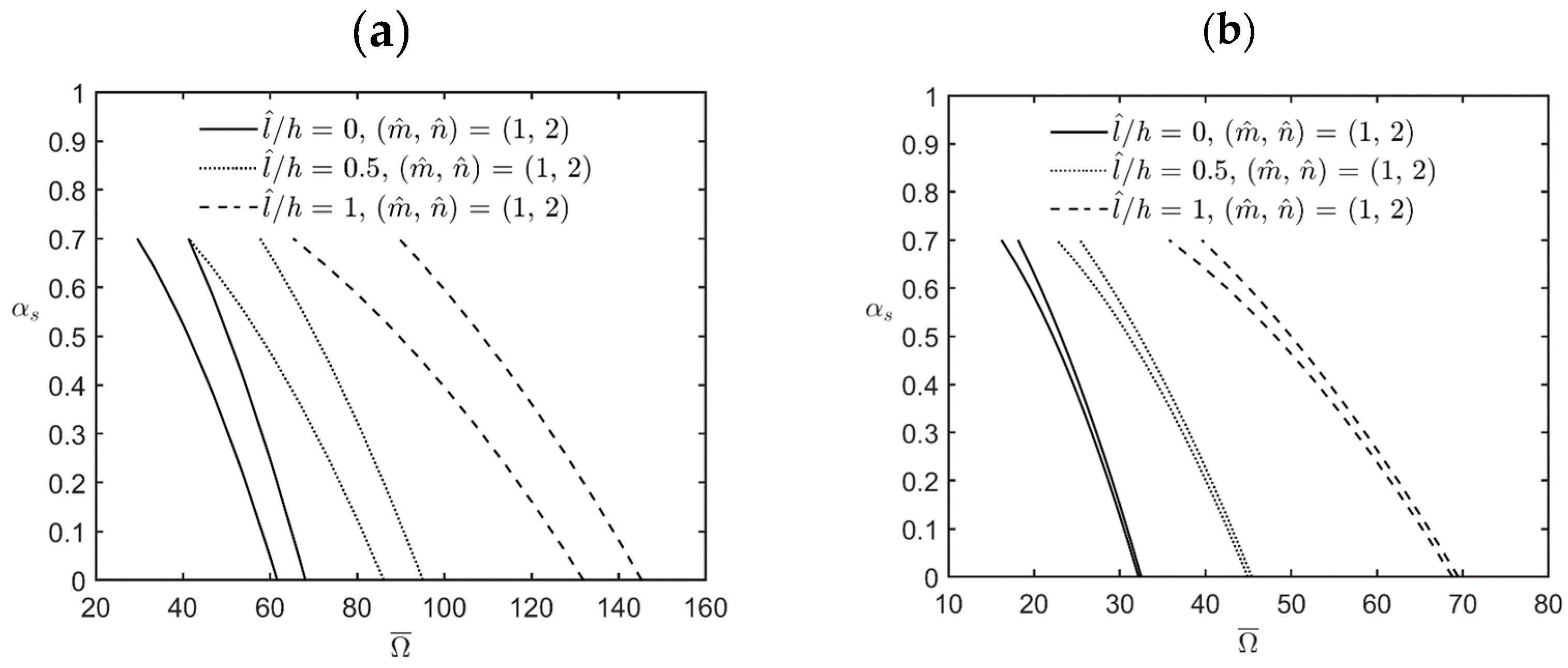
- The magnitude of the excitation frequency and its bandwidth between the upper and lower bounds of various instability regions increased when the value of the material length-scale parameter increased, which indicated that an increase in the value of the material length-scale parameter caused the microshell to stiffen, in turn increasing the magnitude of the excitation frequency and its bandwidth for the instability region.
- The magnitude of the excitation frequency and its bandwidth between the upper and lower bounds of various instability regions decreased when the value of the inhomogeneity index increased, which indicates that an increase in the value of caused the microshell to soften, in turn decreasing the magnitude of the excitation frequency and its bandwidth for the instability region.
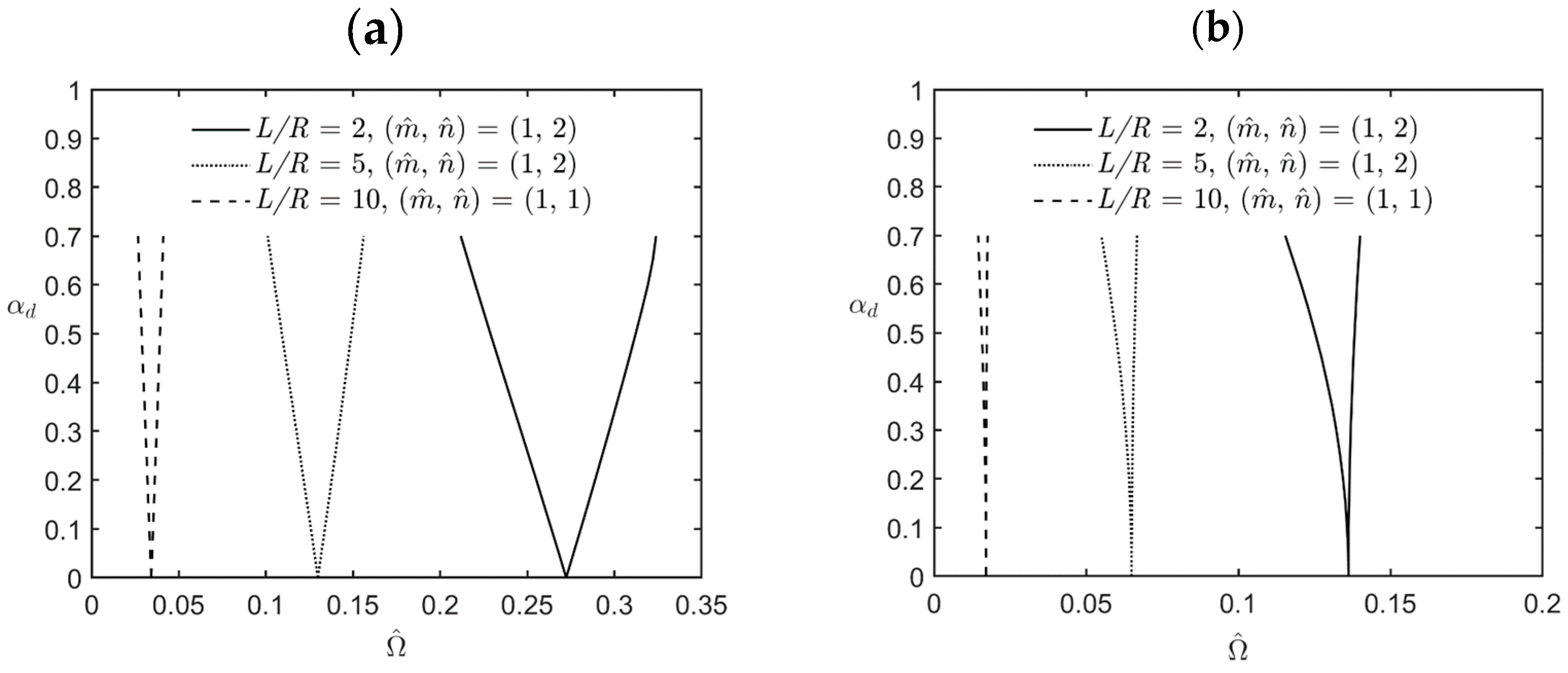
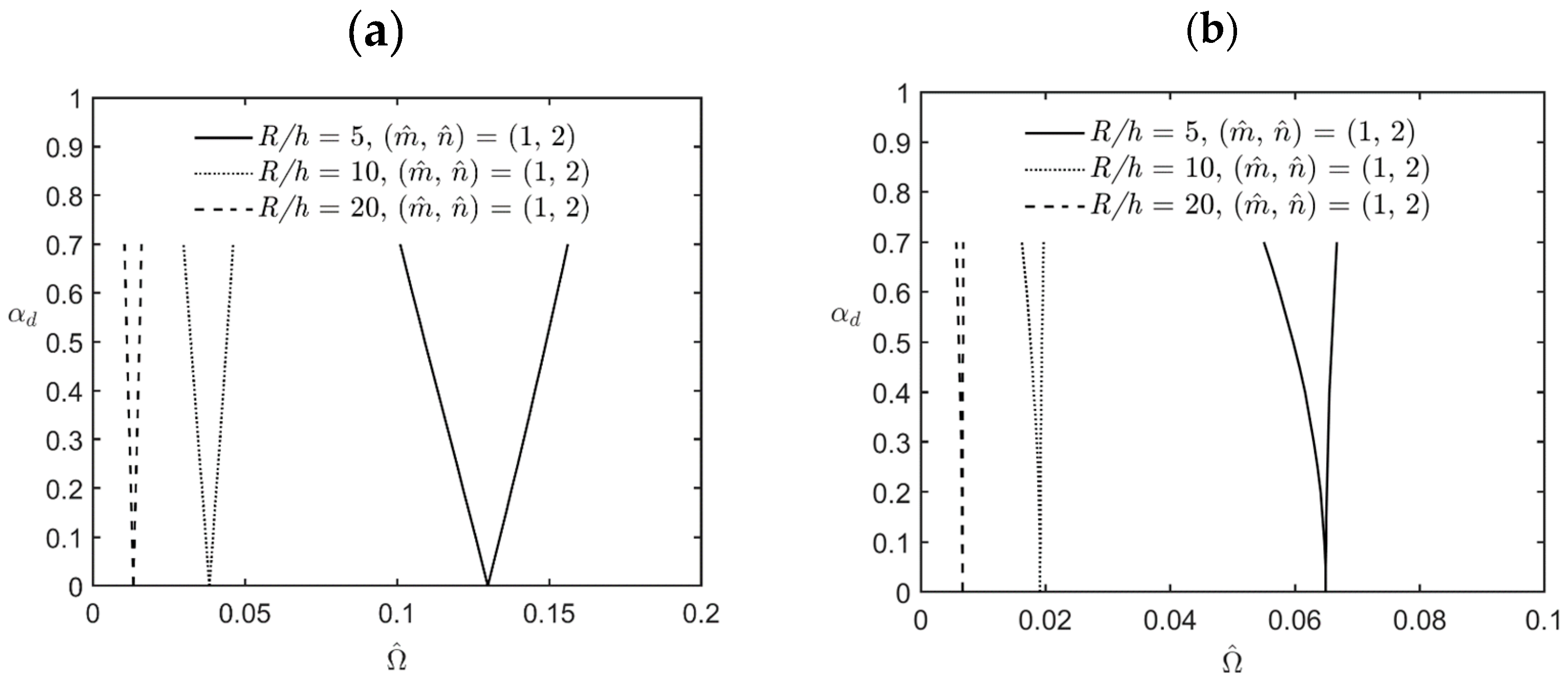
- The magnitude of the excitation frequency and its bandwidth between the upper and lower bounds of various instability regions decreased when the L/R ratio or the R/h ratio increased, which indicates that an increase in either the L/R ratio or the R/h ratio results in a decrease in the overall stiffness of the microshells, in turn decreasing the magnitude of the excitation frequency and its bandwidth for the instability region.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Detailed Expressions of Relevant Tensors in Equations (37)–(39)
Appendix B. The Detailed Expressions of Matrices
References
- Koizumi, M. FGM activities in Japan. Compos. Part B 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Proceeding and Applications; Kluwer Academic: Boston, MA, USA, 1999. [Google Scholar]
- Shen, H.S. Functionally Graded Materials, Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wu, C.P.; Li, K.W. Multi-objective optimization of functionally graded beams using a genetic algorithm with non-dominated sorting. J. Compos. Sci. 2021, 5, 92. [Google Scholar] [CrossRef]
- Ding, S.; Wu, C.P. Optimization of material composition to minimize the thermal stresses induced in FGM plates with temperature-dependent material properties. Int. J. Mech. Mater. Des. 2018, 14, 527–549. [Google Scholar] [CrossRef]
- Bharti, I.; Gupta, N.; Gupta, K.M. Novel applications of functionally graded nano, opto-electric and thermo-electric materials. Int. J. Mater. Mech. Manufact. 2013, 1, 221–224. [Google Scholar]
- Faudzi, A.A.M.; Sabzehmeidani, Y.; Suzumori, K. Application of micro-electro-mechanical systems (MEMS) as sensors: A review. J. Robot. Mechatr. 2020, 32, 281–288. [Google Scholar] [CrossRef]
- Hierold, C.; Jungen, A.; Srampfer, C.; Helbling, T. Nano electromechanical sensors based on carbon nanotubes. Sens. Actuators A Phys. 2007, 136, 51–61. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Wisnom, M.R. Size effects in the testing of fibre-composite materials. Compos. Sci. Technol. 1999, 59, 1937–1957. [Google Scholar] [CrossRef]
- McFarland, A.W.; Colton, J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 2005, 15, 1060–1067. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress-based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef]
- Koiter, W.T. Couple stresses in the theory of elasticity, I and II. Proc. Roy. Netherlands Acad. Arts Sci. 1964, 67, 17–44. [Google Scholar]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Argento, A.; Scott, R.A. Dynamic instability of layered anisotropic circular cylindrical shells, Part I: Theoretical development. J. Sound Vibr. 1993, 162, 311–322. [Google Scholar] [CrossRef]
- Argento, A.; Scott, R.A. Dynamic instability of layered anisotropic circular cylindrical shells, Part II: Numerical results. J. Sound Vibr. 1993, 162, 323–332. [Google Scholar] [CrossRef][Green Version]
- Xie, W.C. Dynamic Stability of Structures; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Bolotin, V.V. The Dynamic Stability of Elastic Systems; Holden-Day: San Francisco, CA, USA, 1964. [Google Scholar]
- Ganapathi, M.; Balamurugan, V. Dynamic instability analysis of a laminated composite circular cylindrical shell. Comput. Struct. 1998, 69, 181–189. [Google Scholar] [CrossRef]
- Ganapathi, M.; Patel, B.P. Parametric dynamic instability analysis of laminated composite conical shells. J. Reinf. Plast. Compos. 1999, 18, 1336–1346. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Pancar, E.B. The effect of heterogeneity on the parametric instability of axially excited orthotropic conical shells. Thin-Walled Struct. 2017, 115, 240–246. [Google Scholar] [CrossRef]
- Bert, C.W.; Birman, V. Parametric instability of thick, orthotropic, circular cylindrical shells. Acta Mech. 1988, 71, 61–76. [Google Scholar] [CrossRef]
- Ng, T.Y.; Hua, L.; Lam, K.Y.; Loy, C.T. Parametric instability of conical shells by the generalized differential quadrature method. Int. J. Numer. Methods Eng. 1999, 44, 819–837. [Google Scholar] [CrossRef]
- Wu, C.P.; Chiu, S.J. Thermally induced dynamic instability of laminated composite conical shells. Int. J. Solids Struct. 2002, 39, 3001–3021. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Influences of shear stresses on the dynamic instability of exponentially graded sandwich cylindrical shells. Compos. Part B 2015, 77, 349–362. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Parametric vibration of FGM conical shells under periodic lateral pressure within the shear deformation theory. Compos. Part B 2016, 89, 282–294. [Google Scholar] [CrossRef]
- Ganapathi, M.; Patel, B.P.; Sambandam, C.T.; Touratier, M. Dynamic instability analysis of circular conical shells. Compos. Struct. 1999, 46, 59–64. [Google Scholar] [CrossRef]
- Pradyumna, S.; Bandyopadhyay, J.N. Dynamic instability of functionally graded shells using higher-order theory. J. Eng. Mech. 2010, 136, 551–561. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R.; Darvizeh, A.; Sahmani, S. Axial buckling and dynamic stability of functionally graded microshells based on the modified couple stress theory. Int. J. Struct. Stab. Dyn. 2014, 15, 1450070. [Google Scholar] [CrossRef]
- Sahmani, S.; Ansari, R.; Gholami, R.; Darvizeh, A. Dynamic stability analysis of functionally graded higher-order shear deformable microshells based on the modified couple stress elasticity theory. Compos. Part B 2013, 51, 44–53. [Google Scholar] [CrossRef]
- Pham, Q.H.; Nguyen, P.C. Dynamic stability analysis of porous functionally graded microplates using a refined isogeometric approach. Compos. Struct. 2022, 284, 115086. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, C.H. Based on the consistent couple stress theory, a three-dimensional weak formulation for stress, deformation, and free vibration analyses of functionally graded microscale plates. Compos. Struct. 2022, 296, 115829. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. A Hermite-family C1 finite layer method for the three-dimensional free vibration analysis of exponentially graded piezoelectric microplates based on the consistent couple stress theory. Int. J. Struct. Stab. Dyn. 2023, 23, 2350044. [Google Scholar] [CrossRef]
- Soldatos, K.P.; Ye, J.Q. Three-dimensional static, dynamic, thermoelastic and buckling analysis of homogeneous and laminated composite cylinders. Compos. Struct. 1994, 29, 131–143. [Google Scholar] [CrossRef]
- Ye, J.Q.; Soldatos, K.P. Three-dimensional buckling analysis of laminated composite hollow cylinders and cylindrical panels. Int. J. Solids Struct. 1995, 32, 1949–1962. [Google Scholar] [CrossRef]
- Leissa, A.W. Buckling and postbuckling theory for laminated composite plates. In Buckling and Postbuckling of Composite Plates; Turvey, G.J., Marshall, I.H., Eds.; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Soldatos, K.P.; Hadjigeorgiou, V.P. Three-dimensional solution of the free vibration problem of homogeneous isotropic cylindrical shells and panels. J. Sound Vibr. 1990, 137, 369–384. [Google Scholar] [CrossRef]
- Wu, C.P.; Tsai, T.C. Exact solutions of functionally graded piezoelectric material sandwich cylinders by a modified Pagano method. Appl. Math. Modell. 2012, 36, 1910–1930. [Google Scholar] [CrossRef]
- Wu, C.P.; Jiang, R.Y. A state space differential reproducing kernel method for the buckling analysis of carbon nanotube-reinforced composite circular hollow cylinders. CMES—Comput. Model. Eng. Sci. 2014, 97, 239–279. [Google Scholar]
- Saada, A.S. Elasticity: Theory and Applications; Pergamon Press: New York, NY, USA, 1974. [Google Scholar]
- Vodenitcharova, T.; Ansourian, P. Buckling of circular cylindrical shells subject to uniform lateral pressure. Eng. Struct. 1996, 18, 604–614. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling analysis of pressure-loaded functionally graded cylindrical shells in thermal environments. Eng. Struct. 2003, 25, 487–497. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Vibration and stability of composite cylindrical shells containing an FG layer subjected to various loads. Struct. Eng. Mech. 2007, 27, 365–391. [Google Scholar] [CrossRef]
- Khazaeinejad, P.; Najafizadeh, M.M.; Jenabi, J. On the buckling of functionally graded cylindrical shells under combined external pressure and axial compression. J. Press. Vessel Technol. 2010, 132, 064501. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T.; Ansari, R. Size dependent buckling analysis of functionally graded piezoelectric cylindrical nanoshell. Compos. Struct. 2016, 152, 45–61. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Thermo-electro-mechanical buckling analysis of cylindrical nanoshell on the basis of modified couple stress theory. J. Mech. Sci. Technol. 2017, 31, 1773–1787. [Google Scholar] [CrossRef]
- Kim, S.E.; Kim, C.S. Buckling strength of the cylindrical shell and tank subjected to axially compressive loads. Thin-Walled Struct. 2002, 40, 329–353. [Google Scholar] [CrossRef]
- Ng, T.Y.; Lam, K.Y.; Reddy, J.N. Parametric resonance of a rotating cylindrical shell subjected to periodic axial loads. J. Sound Vibr. 1998, 214, 513–529. [Google Scholar] [CrossRef]

| (l/h) | Theories | L/R = 1 | L/R = 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R/h = 300 | R/h = 500 | R/h = 1000 | R/h = 3000 | R/h = 300 | R/h = 500 | R/h = 1000 | R/h = 3000 | ||
| 0 (0) | Two-node Hermitian C2 () | 1273.7314 | 349.4958 | 60.6715 | 3.8187 | 413.8408 | 115.0668 | 19.7346 | 1.2594 |
| Two-node Hermitian C2 () | 1273.7314 | 349.4958 | 60.6715 | 3.8188 | 413.8408 | 115.0668 | 19.7345 | 1.2592 | |
| Vodenitcharova and Ansourian [44] | 1269.6 | 348.43 | 60.488 | 3.8100 | 407.19 | NA | NA | 1.2510 | |
| Shen [45] | 1272.6 | 348.59 | 60.536 | 3.8144 | 402.60 | NA | NA | 1.2511 | |
| Sofiyev [46] | 1273.5 | 349.45 | 60.599 | 3.8153 | 412.62 | NA | NA | 1.2562 | |
| Khazaeinejad et al. [47] | 1273.1 | 349.39 | 60.595 | 3.8151 | 412.57 | NA | NA | 1.2564 | |
| Mehralian et al. [48] | 1273.2 | 349.40 | 60.597 | 3.8152 | 412.58 | NA | NA | 1.2561 | |
| (1, 11) | (1, 13) | (1, 15) | (1, 20) | (1, 7) | (1, 8) | (1, 9) | (1, 12) | ||
| 0.5 | Two-node Hermitian C2 () | 2219.8700 | 608.4825 | 104.7762 | 6.5912 | 700.4623 | 194.2209 | 33.9787 | 2.1644 |
| (0.25) | Two-node Hermitian C2 () | 2219.8700 | 608.4824 | 104.7761 | 6.5912 | 700.4624 | 194.2211 | 33.9785 | 2.1645 |
| (1, 10) | (1, 12) | (1, 14) | (1, 18) | (1, 6) | (1, 7) | (1, 8) | (1, 11) | ||
| 1.0 | Two-node Hermitian C2 () | 4578.1057 | 1247.0089 | 214.3564 | 13.3529 | 1467.7834 | 393.3222 | 69.1036 | 4.4041 |
| (0.5) | Two-node Hermitian C2 () | 4578.1057 | 1247.0088 | 214.3564 | 13.3530 | 1467.7834 | 393.3222 | 69.1036 | 4.4047 |
| (1, 9) | (1, 10) | (1, 12) | (1, 16) | (1, 5) | (1, 6) | (1, 7) | (1, 10) | ||
| 2R/h | Numerical Results (Kim and Kim [50]) | Analytical Results (Kim and Kim [50]) | MCST-Based LCST Results (Mehralian and Beni [49]) | CCST-Based FCLMs | ||
|---|---|---|---|---|---|---|
| Hermitian C2 | Relative Errors | |||||
| 800 | 0 | 1.5013 | 1.5141 | 1.5131 | 1.48742 | 1.73% |
| 1.0 | NA | NA | 3.4099 | 3.34969 | 1.80% | |
| 900 | 0 | 1.3586 | 1.3459 | 1.3450 | 1.33319 | 0.89% |
| 1.0 | NA | NA | 3.0464 | 3.01984 | 0.88% | |
| 1000 | 0 | 1.2111 | 1.2113 | 1.2105 | 1.19073 | 1.66% |
| 1.0 | NA | NA | 2.7497 | 2.71544 | 1.26% | |
| 1100 | 0 | 1.1021 | 1.1012 | 1.1005 | 1.08321 | 1.60% |
| 1.0 | NA | NA | 2.4842 | 2.44885 | 1.44% | |
| 1200 | 0 | 1.0170 | 1.0094 | 1.0087 | 1.00143 | 0.72% |
| 1.0 | NA | NA | 2.2783 | 2.24608 | 1.43% | |
| 1300 | 0 | 0.9365 | 0.9318 | 0.9311 | 0.92267 | 0.91% |
| 1.0 | NA | NA | 2.1164 | 2.08826 | 1.35% | |
| 1400 | 0 | 0.8654 | 0.8652 | 0.8646 | 0.85258 | 1.41% |
| 1.0 | NA | NA | 1.9674 | 1.95456 | 0.66% | |
| 1500 | 0 | 0.8075 | 0.8075 | 0.8069 | 0.79602 | 1.37% |
| 1.0 | NA | NA | 1.8309 | 1.81369 | 0.95% | |
| Theories | R/h = 10 | R/h = 100 | R/h = 500 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (0) | Two-node Hermitian C2 FCLM | 0 | 153.078 | 145.158 | 1.356 | 0.383 | 0.377 | 0.020 | 0.0065 | 0.0065 | 7.7299 × 10−4 |
| Khazaeinejad et al. [47] | 150.244 | 146.626 | NA | 0.370 | 0.366 | NA | 0.006 | 0.006 | NA | ||
| Two-node Hermitian C2 FCLM | 0.5 | 100.745 | 95.414 | 0.925 | 0.253 | 0.250 | 0.014 | 0.0044 | 0.0044 | 5.2023 × 10−4 | |
| Khazaeinejad et al. [47] | 97.934 | 95.575 | NA | 0.244 | 0.241 | NA | 0.004 | 0.004 | NA | ||
| Two-node Hermitian C2 FCLM | 1 | 78.106 | 73.924 | 0.730 | 0.197 | 0.194 | 0.011 | 0.0035 | 0.0034 | 4.0765 × 10−4 | |
| Khazaeinejad et al. [47] | 75.514 | 73.696 | NA | 0.189 | 0.187 | NA | 0.003 | 0.003 | NA | ||
| Two-node Hermitian C2 FCLM | 5 | 50.960 | 48.204 | 0.437 | 0.126 | 0.124 | 0.006 | 0.0021 | 0.0021 | 2.5206 × 10−4 | |
| Khazaeinejad et al. [47] | 49.357 | 48.169 | NA | 0.121 | 0.120 | NA | 0.002 | 0.002 | NA | ||
| (1, 2) | (1, 2) | (2, 2) | (1, 3) | (1, 3) | (1, 2) | (1, 4) | (1, 4) | (1, 4) | |||
| 0.5 (0.25) | Two-node Hermitian C2 FCLM | 0 | 305.332 | 289.533 | 1.483 | 0.719 | 0.708 | 0.023 | 0.0113 | 0.0112 | 0.0011 |
| Two-node Hermitian C2 FCLM | 0.5 | 210.961 | 199.796 | 1.101 | 0.498 | 0.491 | 0.016 | 0.0079 | 0.0078 | 7.7691 × 10−4 | |
| Two-node Hermitian C2 FCLM | 1 | 167.457 | 158.489 | 0.905 | 0.396 | 0.390 | 0.013 | 0.0063 | 0.0062 | 6.2731 × 10−4 | |
| (1, 2) | (1, 2) | (1, 1) | (1, 3) | (1, 3) | (1, 2) | (1, 4) | (1, 4) | (1, 3) | |||
| 1.0 (0.5) | Two-node Hermitian C2 FCLM | 0 | 757.117 | 717.920 | 1.486 | 1.728 | 1.647 | 0.031 | 0.0255 | 0.0253 | 0.0016 |
| Two-node Hermitian C2 FCLM | 0.5 | 537.975 | 509.495 | 1.103 | 1.232 | 1.190 | 0.022 | 0.0182 | 0.0181 | 0.0011 | |
| Two-node Hermitian C2 FCLM | 1 | 432.510 | 409.343 | 0.907 | 0.993 | 0.965 | 0.018 | 0.0147 | 0.0146 | 9.1795 × 10−4 | |
| (1, 2) | (1, 2) | (1, 1) | (1, 3) | (1, 2) | (1, 2) | (1, 4) | (1, 4) | (1, 3) | |||
| First Principal Instability Region | K-Term Approximations | |||||||
|---|---|---|---|---|---|---|---|---|
| K = 1 | K = 2 | K = 3 | ||||||
| Cosine Terms | Sine Terms | Cosine Terms | Sine Terms | Cosine Terms | Sine Terms | |||
| (1, 2) | 0 | Hermitian C2 FLM solutions | 0.64712 | 0.64712 | 0.64712 | 0.64712 | 0.64712 | 0.64712 |
| Ng et al.’s solutions [51] | 0.6485 | 0.6485 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.6519 | 0.6519 | NA | NA | NA | NA | ||
| 0.1 | Hermitian C2 FLM solutions | 0.64518 | 0.64907 | 0.64518 | 0.64907 | 0.64518 | 0.64907 | |
| Ng et al.’s solutions [51] | 0.6481 | 0.6488 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.6478 | 0.6560 | NA | NA | NA | NA | ||
| 0.3 | Hermitian C2 FLM solutions | 0.64126 | 0.65293 | 0.64127 | 0.65295 | 0.64127 | 0.65295 | |
| Ng et al.’s solutions [51] | 0.6475 | 0.6494 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.6396 | 0.6640 | NA | NA | NA | NA | ||
| 0.5 | Hermitian C2 FLM solutions | 0.63732 | 0.65678 | 0.63736 | 0.65681 | 0.63736 | 0.65681 | |
| Ng et al.’s solutions [51] | 0.6468 | 0.6500 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.6312 | 0.6720 | NA | NA | NA | NA | ||
| (1, 3) | 0 | Hermitian C2 FLM solutions | 0.37843 | 0.37843 | 0.37843 | 0.37843 | 0.37843 | 0.37843 |
| Ng et al.’s solutions [51] | 0.3778 | 0.3778 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.3719 | 0.3719 | NA | NA | NA | NA | ||
| 0.1 | Hermitian C2 FLM solutions | 0.37509 | 0.38174 | 0.37509 | 0.38175 | 0.37509 | 0.38175 | |
| Ng et al.’s solutions [51] | 0.3771 | 0.3784 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.3696 | 0.3742 | NA | NA | NA | NA | ||
| 0.3 | Hermitian C2 FLM solutions | 0.36831 | 0.38828 | 0.36838 | 0.38834 | 0.36838 | 0.38834 | |
| Ng et al.’s solutions [51] | 0.3757 | 0.3796 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.3649 | 0.3788 | NA | NA | NA | NA | ||
| 0.5 | Hermitian C2 FLM solutions | 0.36141 | 0.39471 | 0.36162 | 0.39487 | 0.36162 | 0.39487 | |
| Ng et al.’s solutions [51] | 0.3743 | 0.3807 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.3601 | 0.3834 | NA | NA | NA | NA | ||
| (1, 4) | 0 | Hermitian C2 FLM solutions | 0.24507 | 0.24507 | 0.24507 | 0.24507 | 0.24507 | 0.24507 |
| Ng et al.’s solutions [51] | 0.2473 | 0.2473 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.2471 | 0.2471 | NA | NA | NA | NA | ||
| 0.1 | Hermitian C2 FLM solutions | 0.23988 | 0.25015 | 0.23991 | 0.25018 | 0.23991 | 0.25018 | |
| Ng et al.’s solutions [51] | 0.2462 | 0.2481 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.2456 | 0.2487 | NA | NA | NA | NA | ||
| 0.3 | Hermitian C2 FLM solutions | 0.22914 | 0.26002 | 0.22944 | 0.26022 | 0.22944 | 0.26022 | |
| Ng et al.’s solutions [51] | 0.2441 | 0.2500 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.2425 | 0.2517 | NA | NA | NA | NA | ||
| 0.5 | Hermitian C2 FLM solutions | 0.21788 | 0.26953 | 0.21886 | 0.27002 | 0.21886 | 0.27002 | |
| Ng et al.’s solutions [51] | 0.2420 | 0.2518 | NA | NA | NA | NA | ||
| Sofiyev’s solutions [28] | 0.2393 | 0.2547 | NA | NA | NA | NA | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-P.; Wu, M.-L.; Hsu, H.-T. 3D Size-Dependent Dynamic Instability Analysis of FG Cylindrical Microshells Subjected to Combinations of Periodic Axial Compression and External Pressure Using a Hermitian C2 Finite Layer Method Based on the Consistent Couple Stress Theory. Materials 2024, 17, 810. https://doi.org/10.3390/ma17040810
Wu C-P, Wu M-L, Hsu H-T. 3D Size-Dependent Dynamic Instability Analysis of FG Cylindrical Microshells Subjected to Combinations of Periodic Axial Compression and External Pressure Using a Hermitian C2 Finite Layer Method Based on the Consistent Couple Stress Theory. Materials. 2024; 17(4):810. https://doi.org/10.3390/ma17040810
Chicago/Turabian StyleWu, Chih-Ping, Meng-Luen Wu, and Hao-Ting Hsu. 2024. "3D Size-Dependent Dynamic Instability Analysis of FG Cylindrical Microshells Subjected to Combinations of Periodic Axial Compression and External Pressure Using a Hermitian C2 Finite Layer Method Based on the Consistent Couple Stress Theory" Materials 17, no. 4: 810. https://doi.org/10.3390/ma17040810
APA StyleWu, C.-P., Wu, M.-L., & Hsu, H.-T. (2024). 3D Size-Dependent Dynamic Instability Analysis of FG Cylindrical Microshells Subjected to Combinations of Periodic Axial Compression and External Pressure Using a Hermitian C2 Finite Layer Method Based on the Consistent Couple Stress Theory. Materials, 17(4), 810. https://doi.org/10.3390/ma17040810







