1. Introduction
The global steel industry has entered a new stage [
1]. Medium- and heavy-plate steel, as important types of steel, have irreplaceable roles in national construction economics, national security, and other aspects [
2]. With the continuous changes in customers’ demands, larger weighted plate units are needed [
3]. When the conventional rolling process is used to produce large units of weighted products, the required length of a slab is larger than the equipment’s limit, so the current rolling mill capacity cannot meet the production requirements. In addition, in the production of plates with small spread ratios, the plate needs to be turned twice, as not doing so would reduce the production efficiency. These problems can be solved with the angular rolling process [
4]. During the angular rolling production process, the center line of the slab is rolled away from the initial rolling direction at a specific angle [
5,
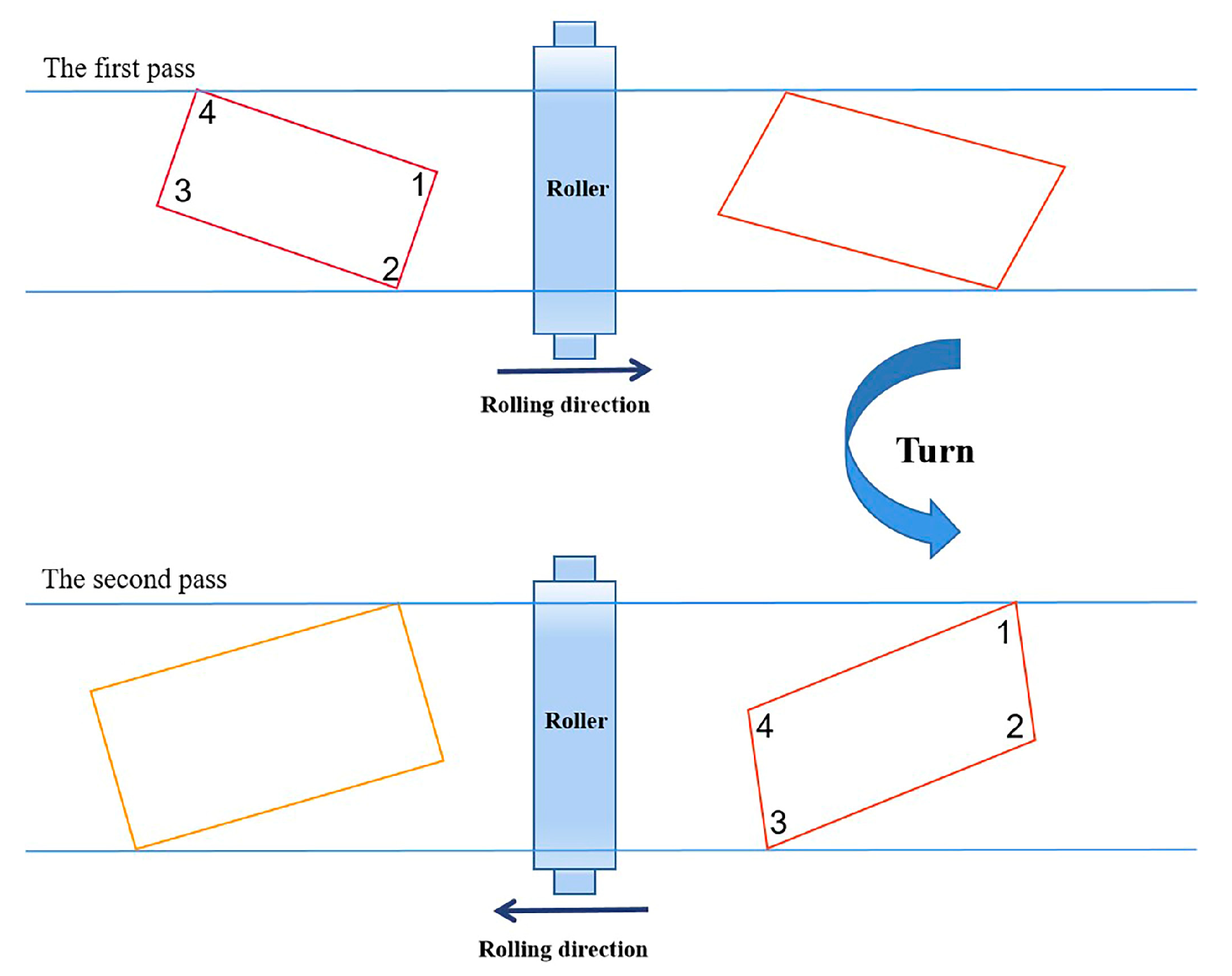
6]. Angular rolling is a rolling technique between broadening rolling and elongation rolling, as shown in
Figure 1. During the angular rolling process, the rolled piece is first rotated to a certain angle to initially locate the No. 1 corner within the roll gap. The plan view pattern of the rolled piece is rolled to become a parallelogram. Then, the rolled piece is turned in order to locate the No. 4 corner within the roll gap. The plan view pattern of the rolled piece is rolled from a parallelogram to a rectangle again [
7].
The angular rolling process was first studied by scientists in the former Soviet Union, where the width formula for angular rolling was proposed. In China, in the 1990s, Li proposed a new formula for angular rolling [
8]. Cao et al. developed a calculation model and an automatic control system for the angular rolling process [
9]. Cao et al. explored the method of rotation angle control and obtained empirical widening parameters [
10]. During the development and theoretical study of the angular rolling process, Zhou studied the effects of angular rolling process on plate mechanical properties and the improvement in mill rolling conditions [
4]. Hao et al. established a mathematical model based on the influence function method to calculate the thickness distribution and rolling force during angular rolling [
11].
As demonstrated in the current research on plate rolling processes, using finite element software for simulation and analysis can greatly reduce research costs. DEFORM finite element software is specifically designed for metal forming and is a heat treatment process simulation software, covering all processes from metal solidification to heat treatment, microstructure changes, and so on, with a powerful three-dimensional deformation analysis ability. DEFORM uses a high-precision hexahedral mesh and advanced algorithm, which not only ensures the accuracy of the simulation but also shortens the calculation time. Data similar to real-world situations can be obtained by establishing a reasonable finite element model. Finite element simulation studies have achieved good results regarding the evolution behavior of voids [
12], the prediction of the plan view pattern, the shape changing rule during plate rolling [
13,
14,
15,
16], and the width spreading of angular rolling [
17,
18]. DEFORM-3D, a finite element software which is suitable for rolling process studies, has also been applied to different aspects of strip and plate rolling process studies. Simultaneously, the experimental validation results demonstrated the reliability of numerical simulations using DEFORM [
19,
20,
21,
22,
23].
The main problem that occurs during the practical application of angular rolling technology is that the rectangular pattern is difficult to control. The rectangularity degree is closely related to the yield rate, which is an important factor affecting economic indicators. The method used to improve the rectangularity degree in conventional rolling mainly involves plan view pattern control technology [
24]. Jiao et al. developed a mathematical model for plan view pattern prediction and online control [
25,
26,
27], while Shigemori et al. proposed a parameter identification technique with a locally weighted regression model for the plan view pattern control of the plates [
28].
The plan view pattern control method used in conventional rolling technology is difficult to apply to the angular rolling process. Finding ways through which to improve the plan view pattern of the plate after angular rolling is a tough problem in current research. Hao proposed a method to predict the plan view pattern of the plate after angular rolling by segmenting the plate [
29]. Jiao et al. used the trigonometric function and the principle of constant volume to predict the plan view pattern changing during the two-pass angular rolling process and investigated the relationship between the two passes that still reverts to a rectangular pattern after a two-pass process, under ideal conditions [
30,
31].
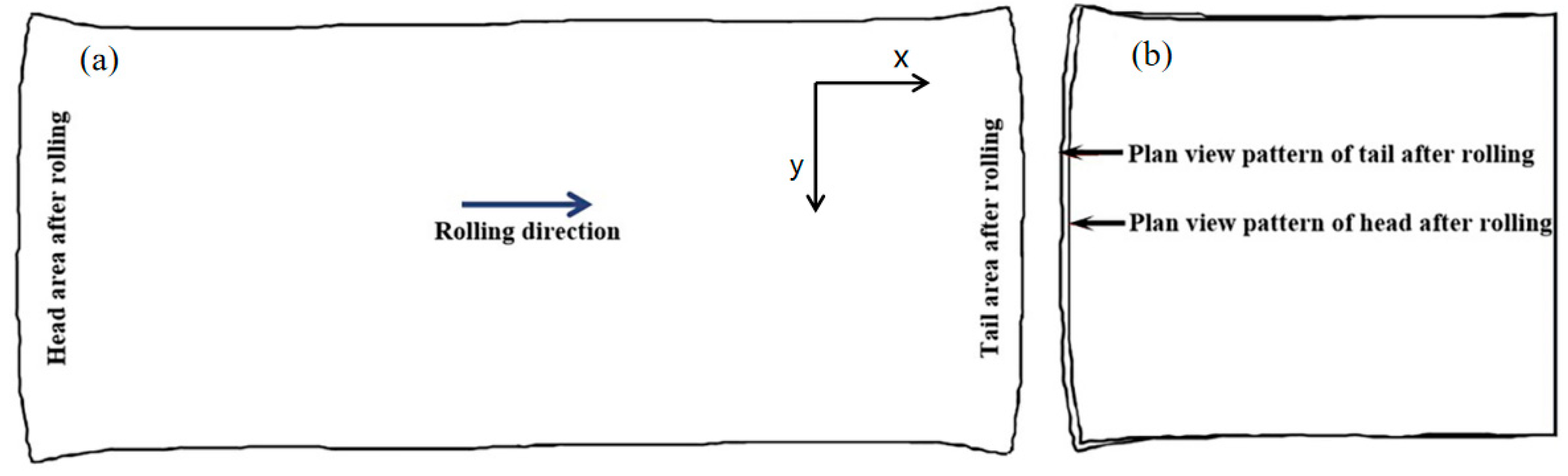
However, the two-pass angular rolling processes described above are based on ideal conditions, where the biting and throwing stages are considered symmetrical. The difference between the biting and throwing stages of the plate deformation is ignored. In the actual production process, it is difficult to ensure that the plane pattern of the rolled piece is completely symmetrical after it undergoes the two-pass angular rolling process.
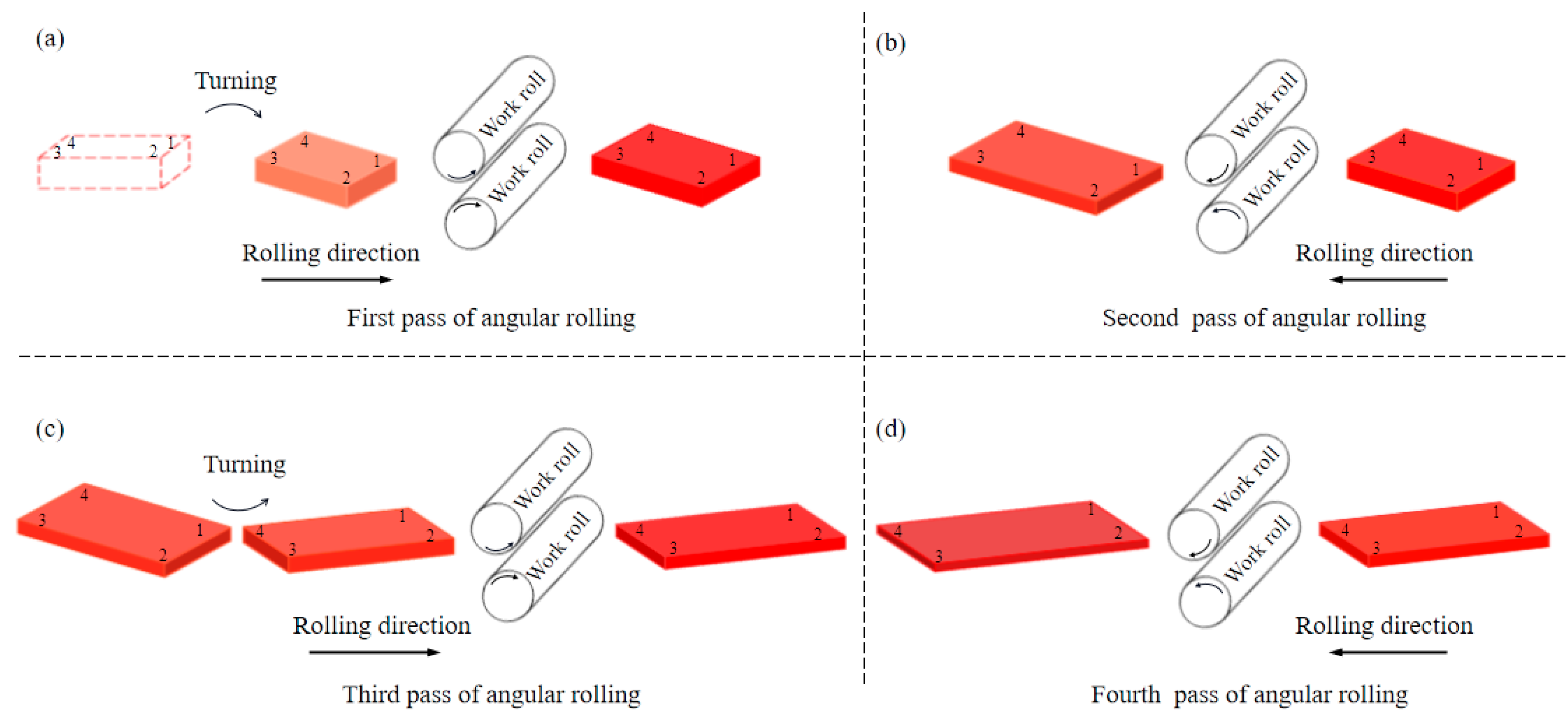
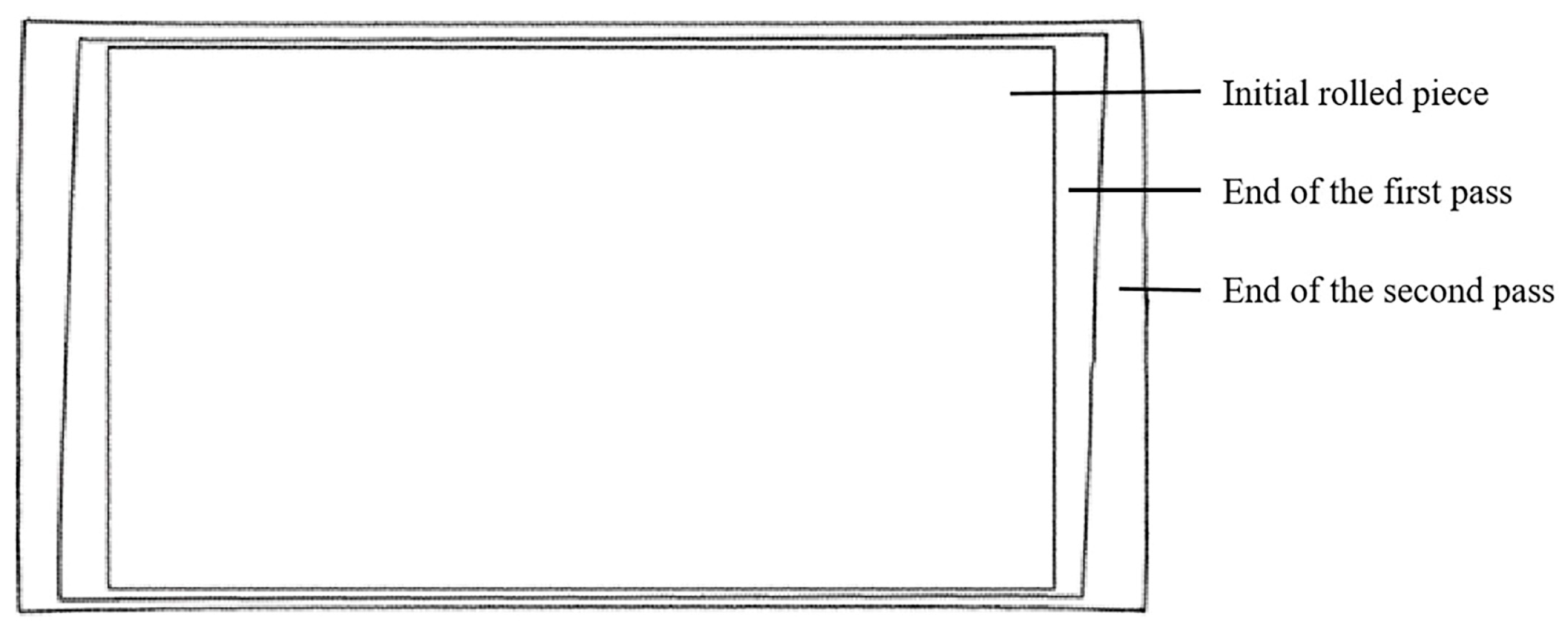
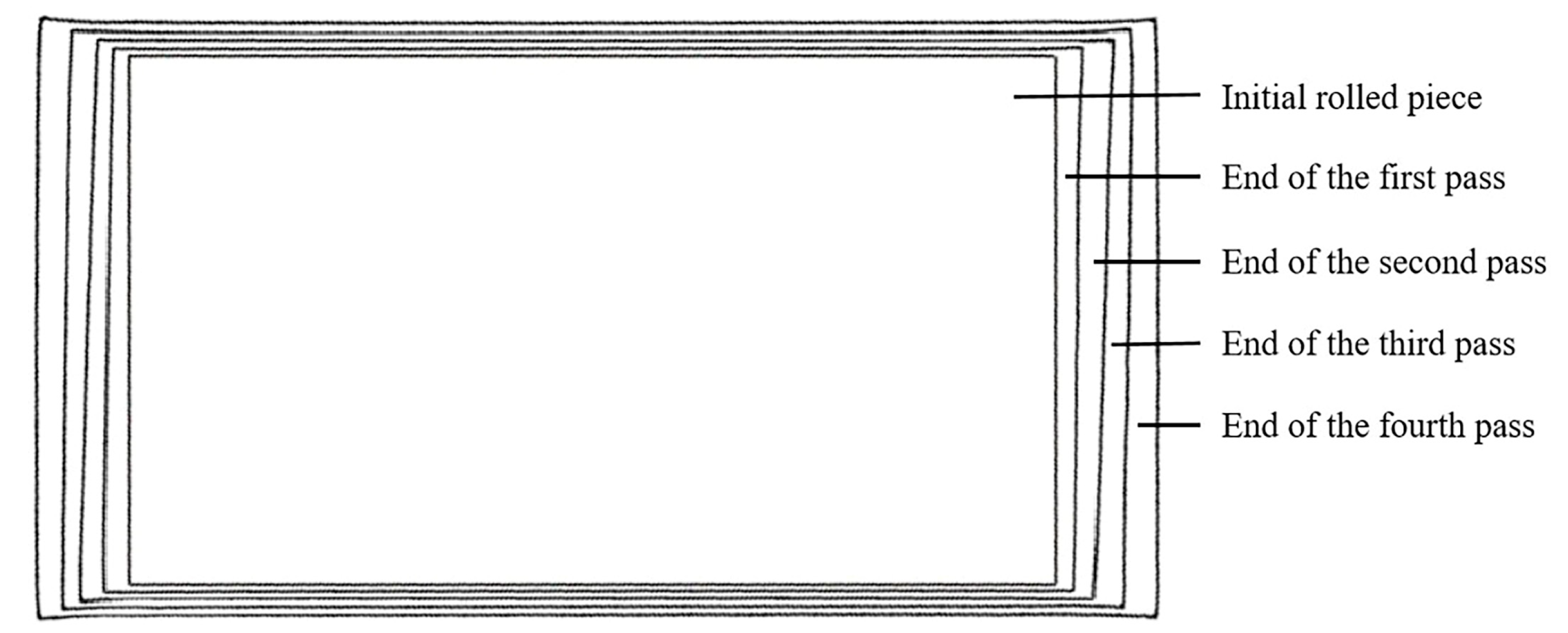
When the two-pass angular rolling process is adopted, because the first bite is into the two corners on the same side as the lengthwise direction, different metal flow degrees on both sides lead to uneven deformation, which affects the rectangularity effect of the plate. In this paper, based on the difference between the biting and throwing stages of plate deformation, the two-pass angular rolling process is transformed into a four-pass angular rolling process. The whole process is shown in
Figure 2. Corner 1 is first bitten into the roll gap, then a reverse rolling pass is carried out without turning the rolled piece. Corner 3 is rolled, and the rolled piece becomes a parallelogram. Then, the rolled piece is turned, and corner 2 is rolled. Finally, another reverse rolling pass is carried out, corner 4 is rolled, and the rolled piece becomes a rectangle again. In this process, each corner of the rolled piece was rolled through a biting phase and a throwing phase. With this process, the plan view pattern after angular rolling may be improved.
In this paper, the effect of the angular rolling process on the plan view pattern of the plate was studied. In the second part of this paper, conventional rolling and angular rolling processes were investigated using the finite element numerical simulation method. The formula for characteristic rectangular value was proposed, in order to characterize the rectangularity degree of the rolled plate. In the third part of this paper, the effects of the one-group two- and four-pass angular rolling processes on the plan view pattern of rolled pieces were analyzed. In the fourth part, the simulation results were further validated through rolling experiments.
5. Conclusions
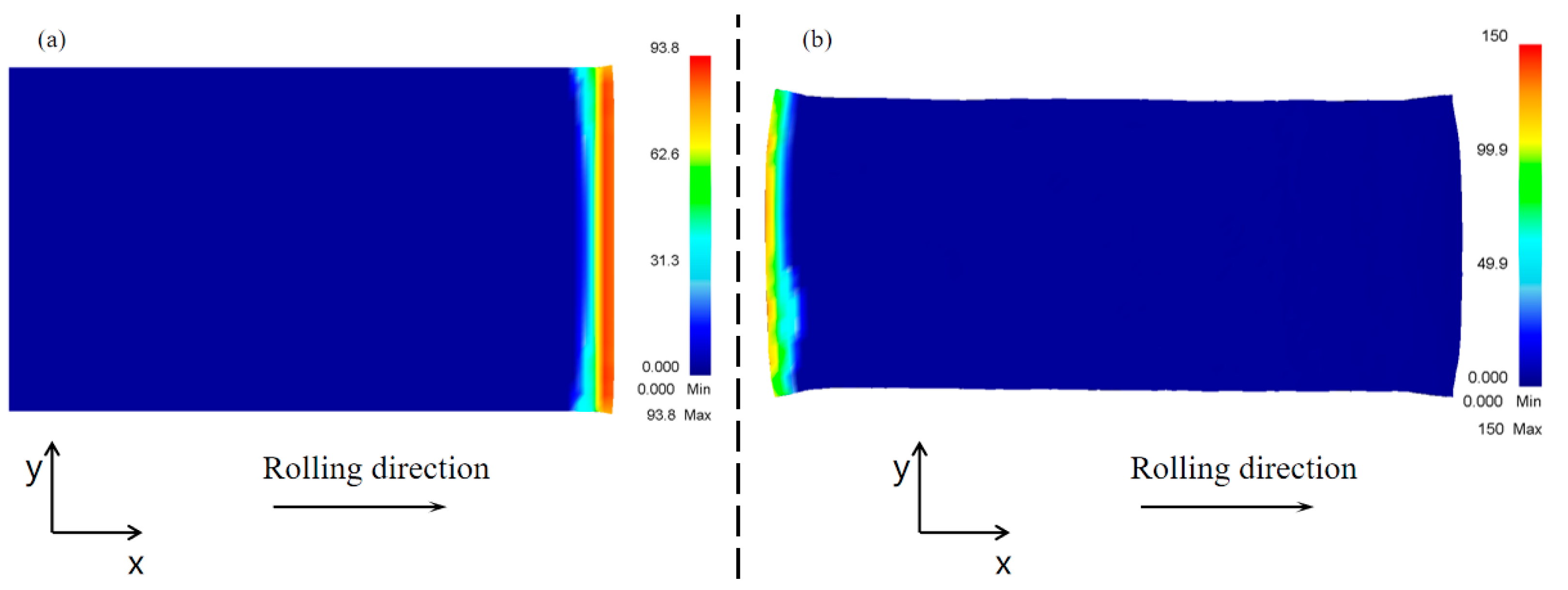
The reason for the difference between the head and tail deformation of rolled pieces after conventional rolling was analyzed through numerical simulation. Since the two bites of the two-pass angular rolling process started from two corners on the same side, the deformation difference in the rolled piece between the biting and throwing stage affected the rectangularity degree of the two-pass angular rolled plate. It was proposed to modify the two-pass angular rolling process to a four-pass angular rolling process to improve the rectangle of the angular rolled plate.
A formula to calculate the characteristic rectangular values reflecting the rectangular degree of the plate was constructed. Through this numerical simulation, the deformation of the rolled piece under the optimal rectangular process conditions of two- and four-pass angular rolling was analyzed and compared. The simulation results showed that the rectangularity degree obtained using four-pass angular rolling was better than that obtained using two-pass angular rolling.
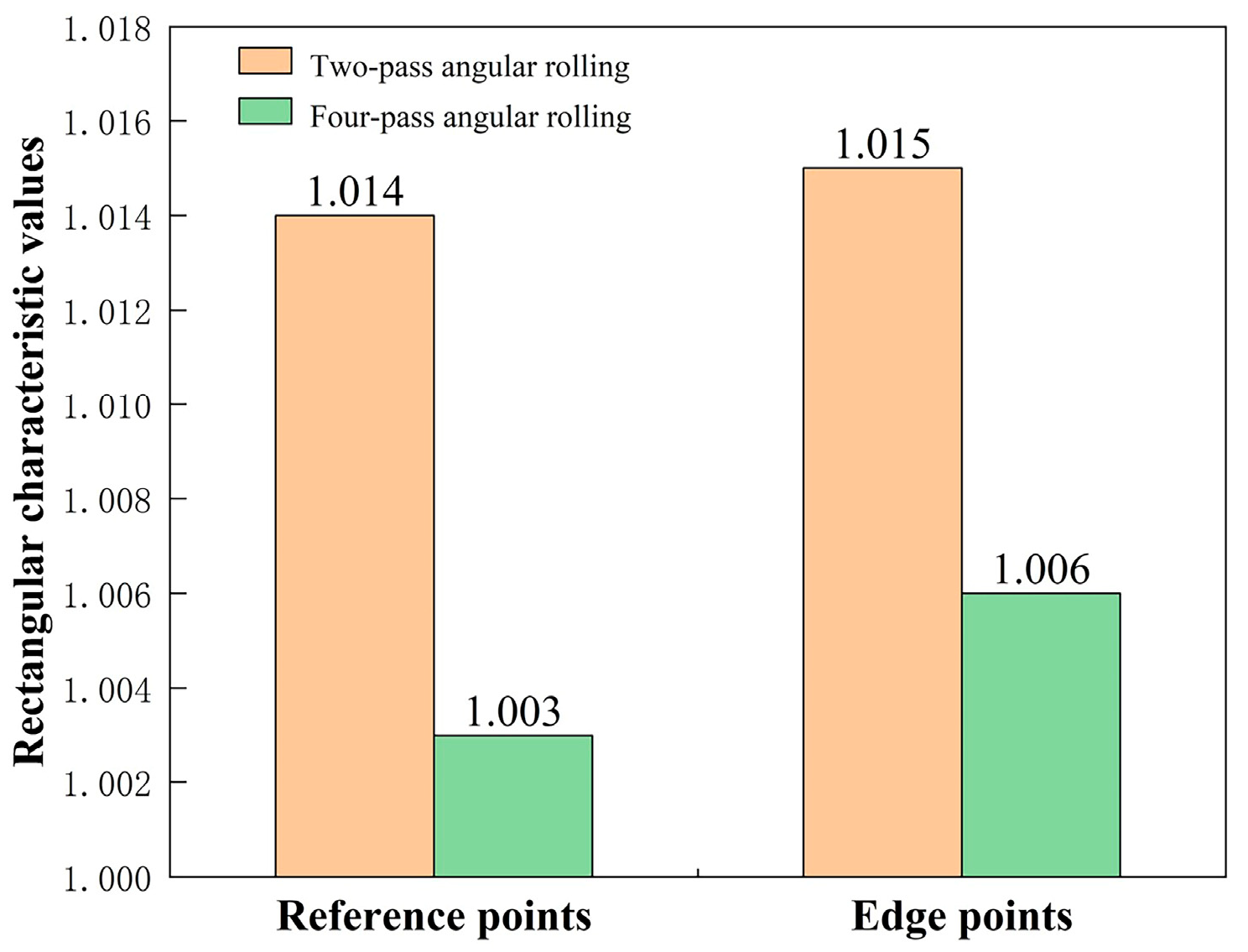
The angular rolling processes were experimentally verified. The characteristic rectangular value of the reference point of the four-pass angular rolled piece was 1.003, while that of the two-pass angular rolled piece was 1.014. The rectangle of the four-pass angular rolled piece was evidently better than that of the two-pass angular rolled piece.
The use of four-pass angular rolling can improve the degree of plate rectangularity, reduce the cutting loss, and increase the yield without increasing the turning time, as well as increase the profits of enterprises in the face of fierce competition in the plate market.
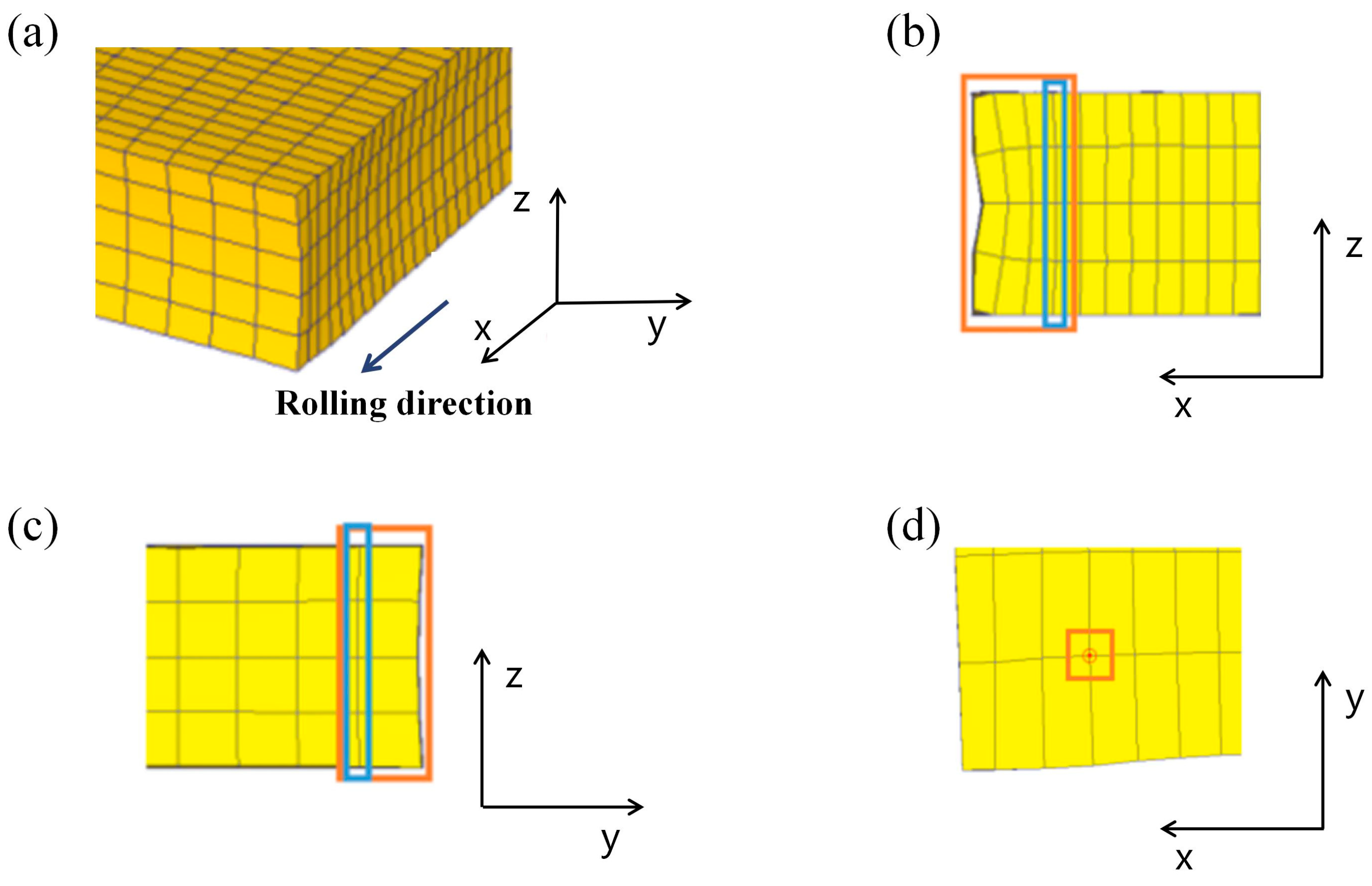
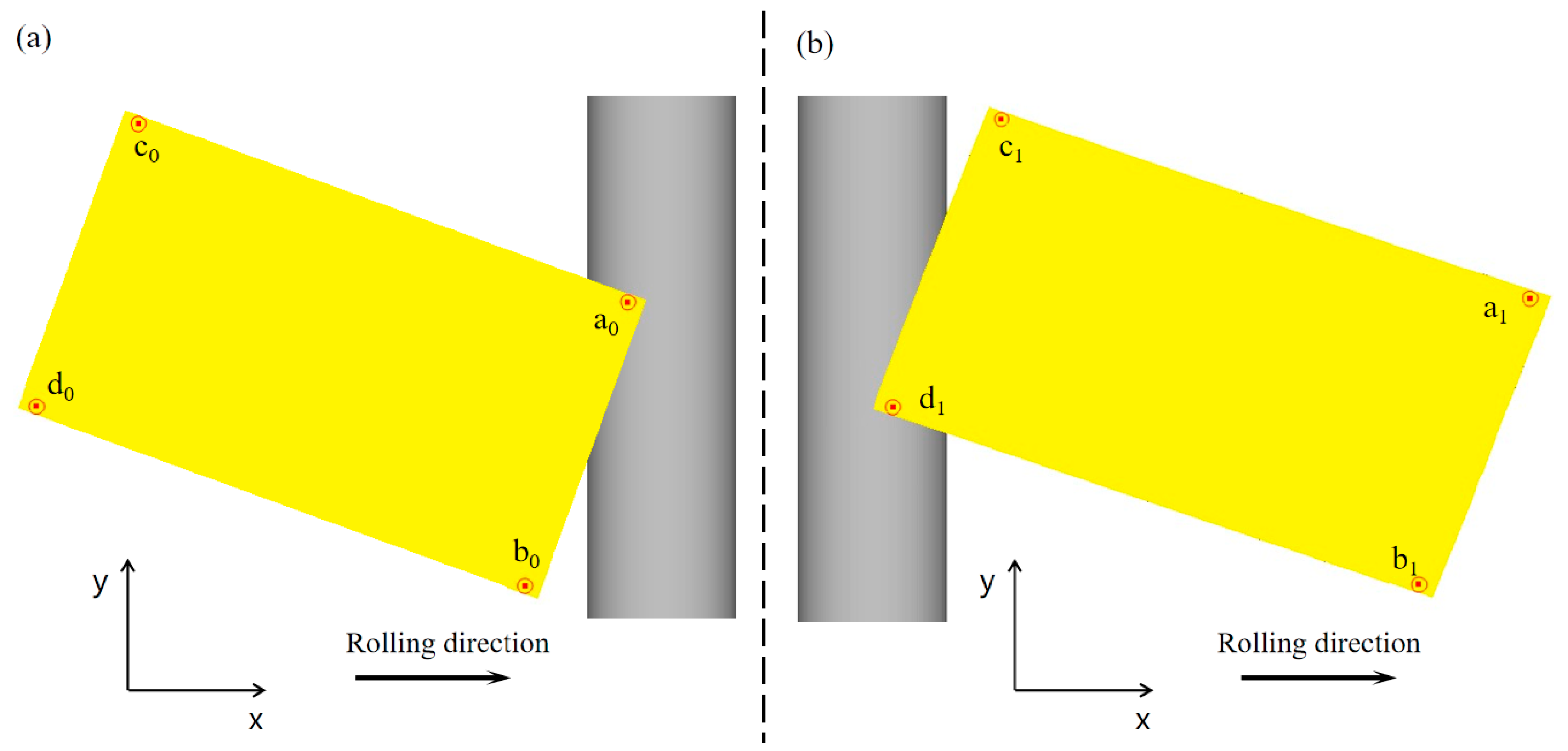


 –reference points,
–reference points,  –edge points): (a) two-pass angular rolling and (b) four-pass angular rolling.
–edge points): (a) two-pass angular rolling and (b) four-pass angular rolling.
 –reference points,
–reference points,  –edge points): (a) two-pass angular rolling and (b) four-pass angular rolling.
–edge points): (a) two-pass angular rolling and (b) four-pass angular rolling.