Bearing Characteristics of Screw-Groove Piles: Model Test and Numerical Analysis
Abstract
1. Introduction
2. Materials and Methods
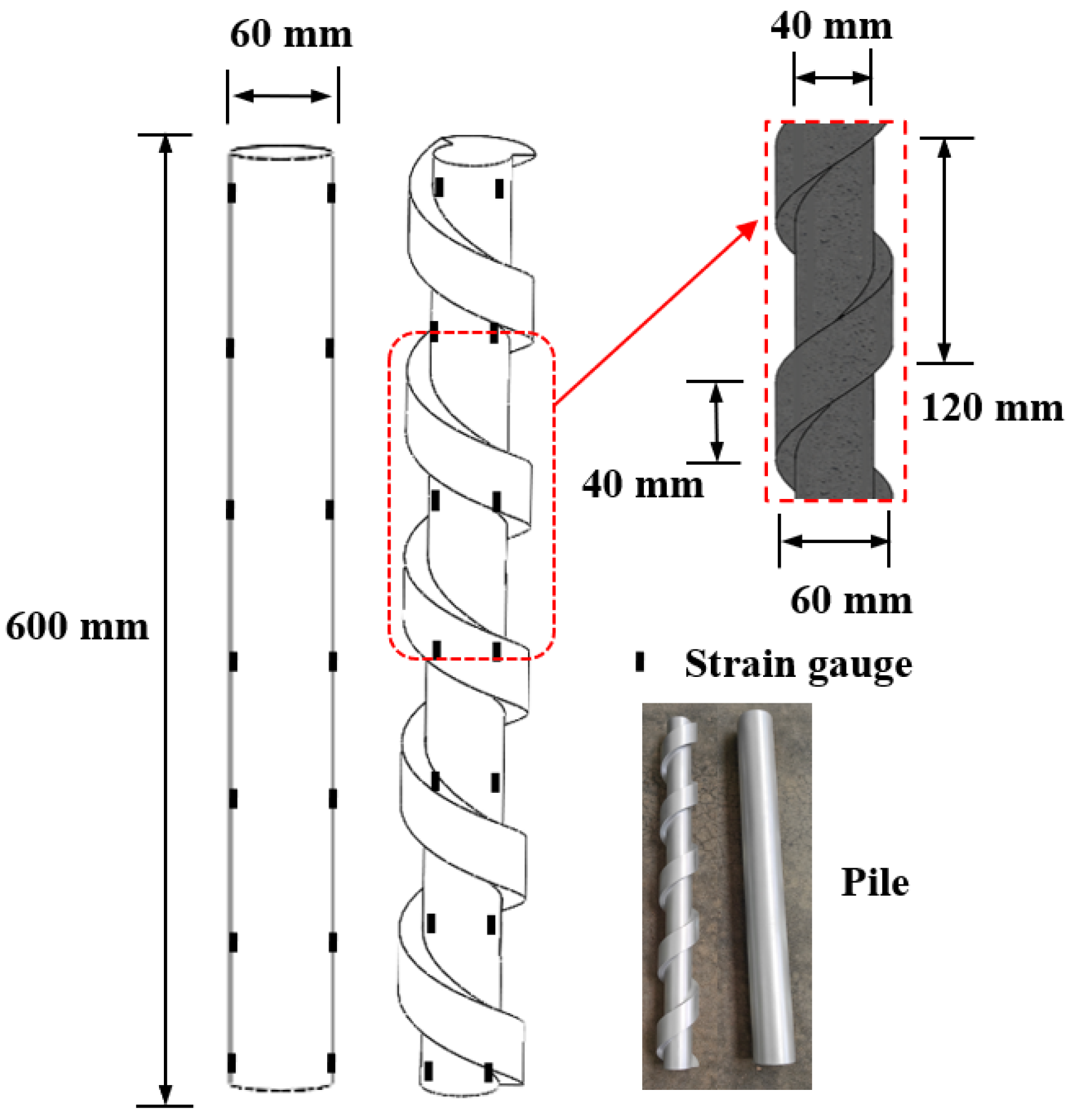
2.1. Specimen Setup and Materials
2.2. Testing Procedures
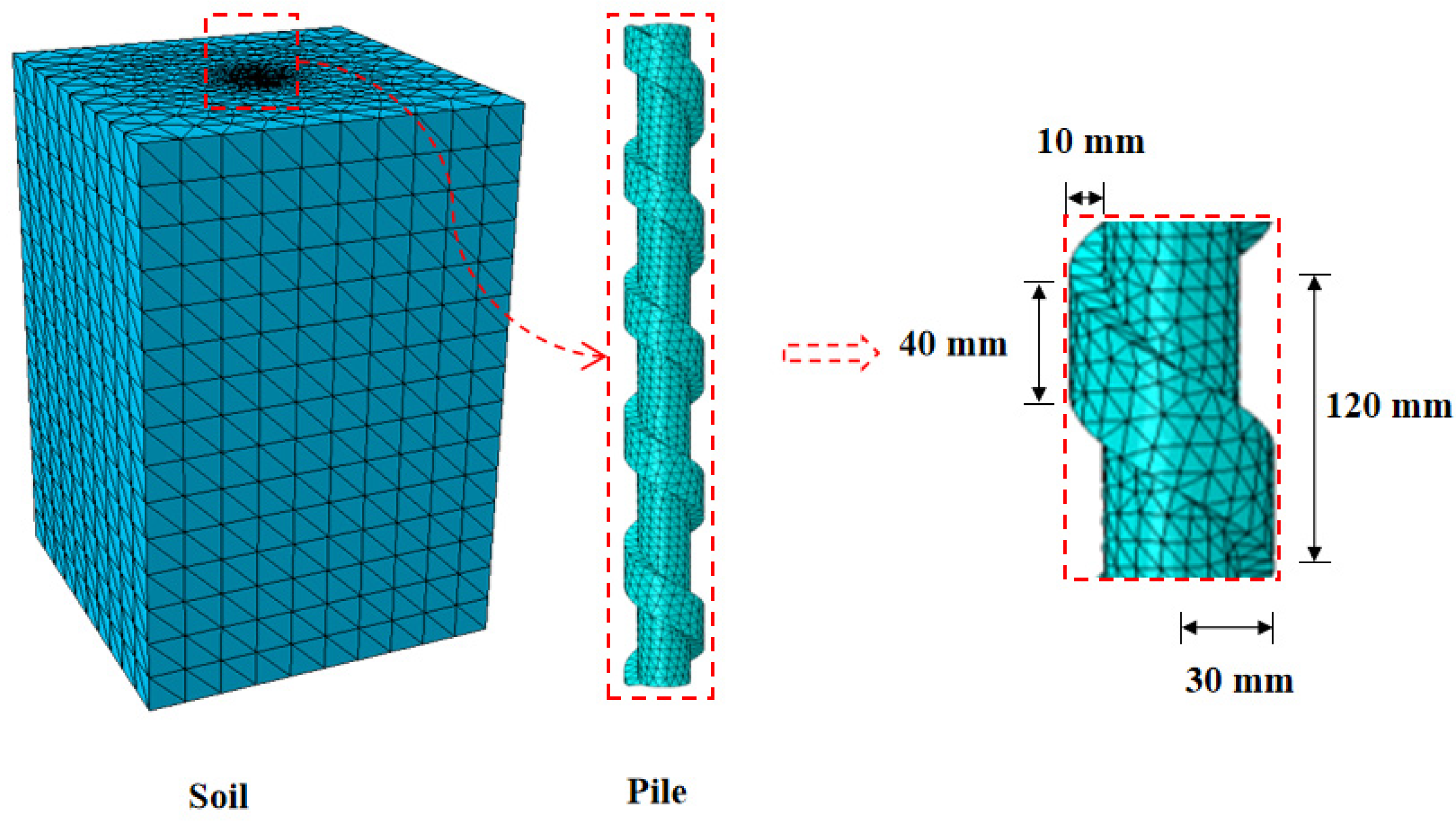
2.3. Numerical Simulation Models
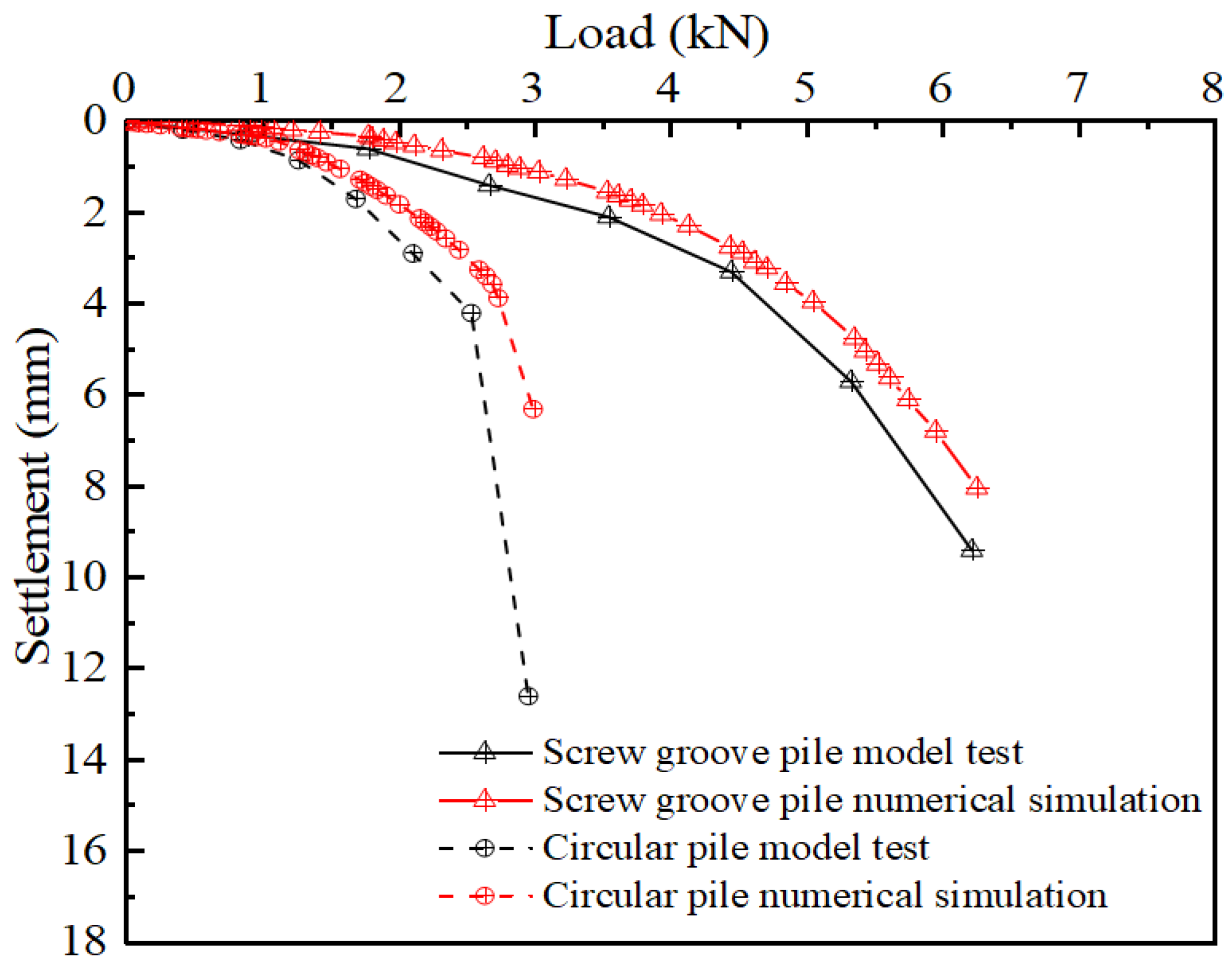
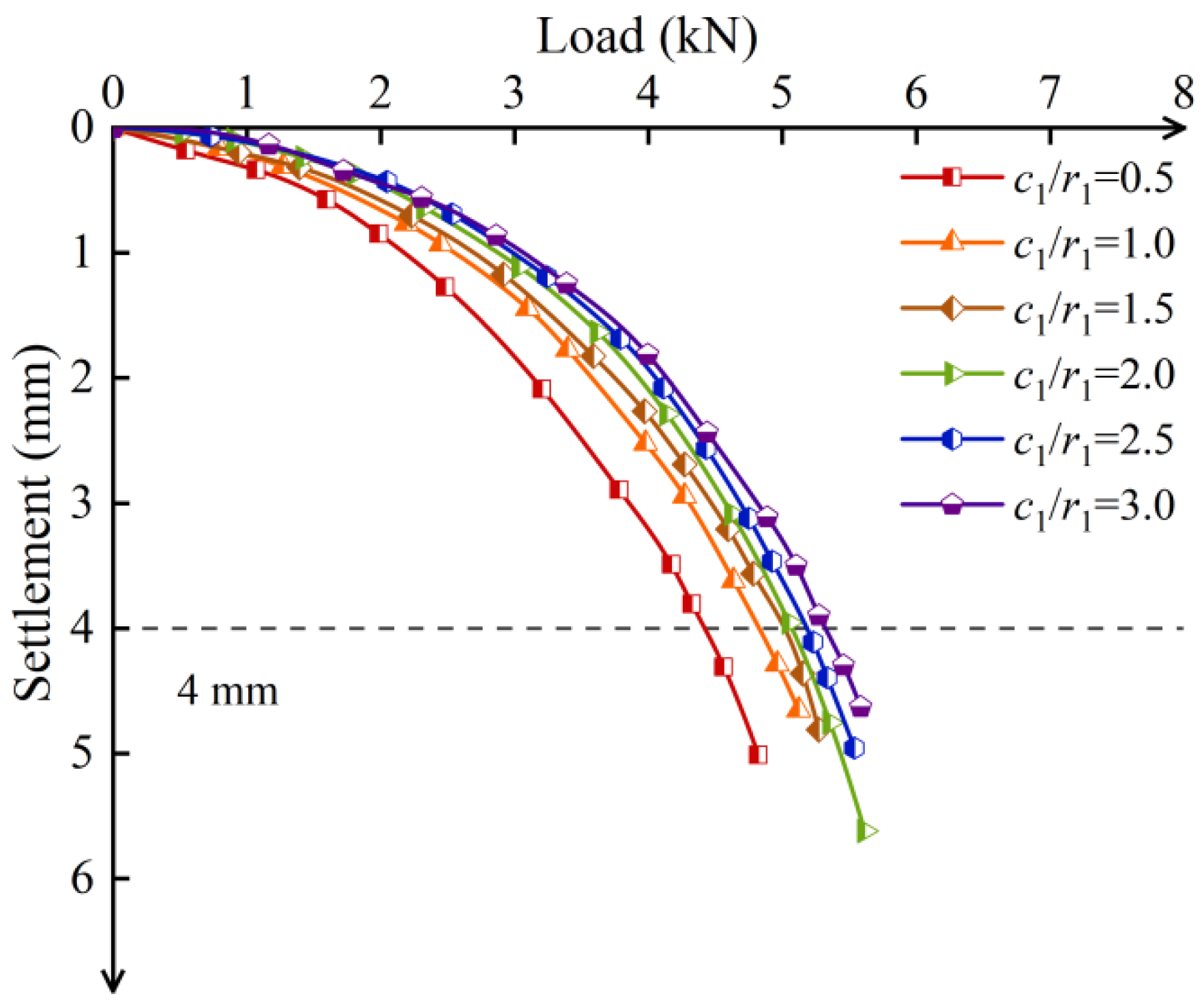
3. Results and Discussion
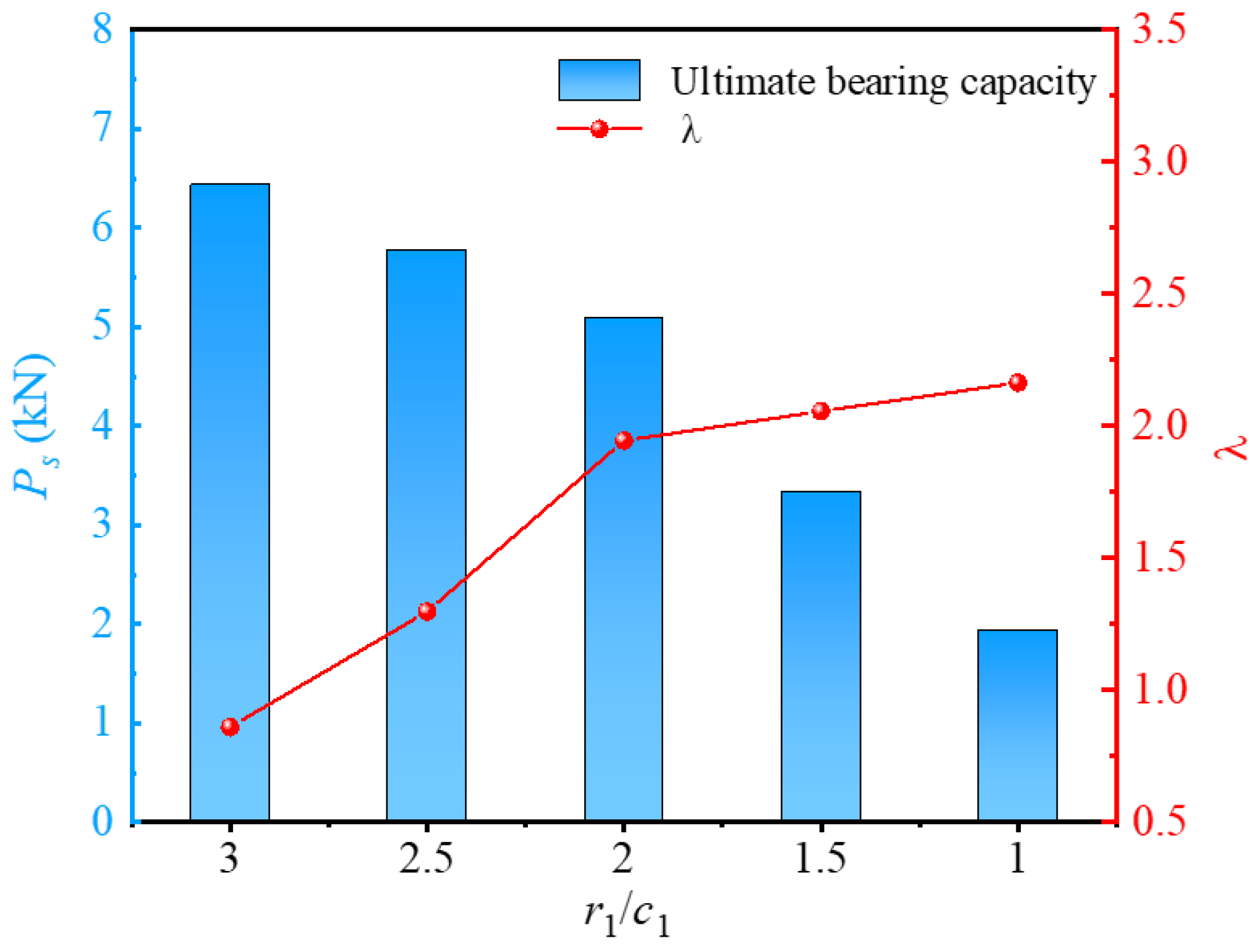
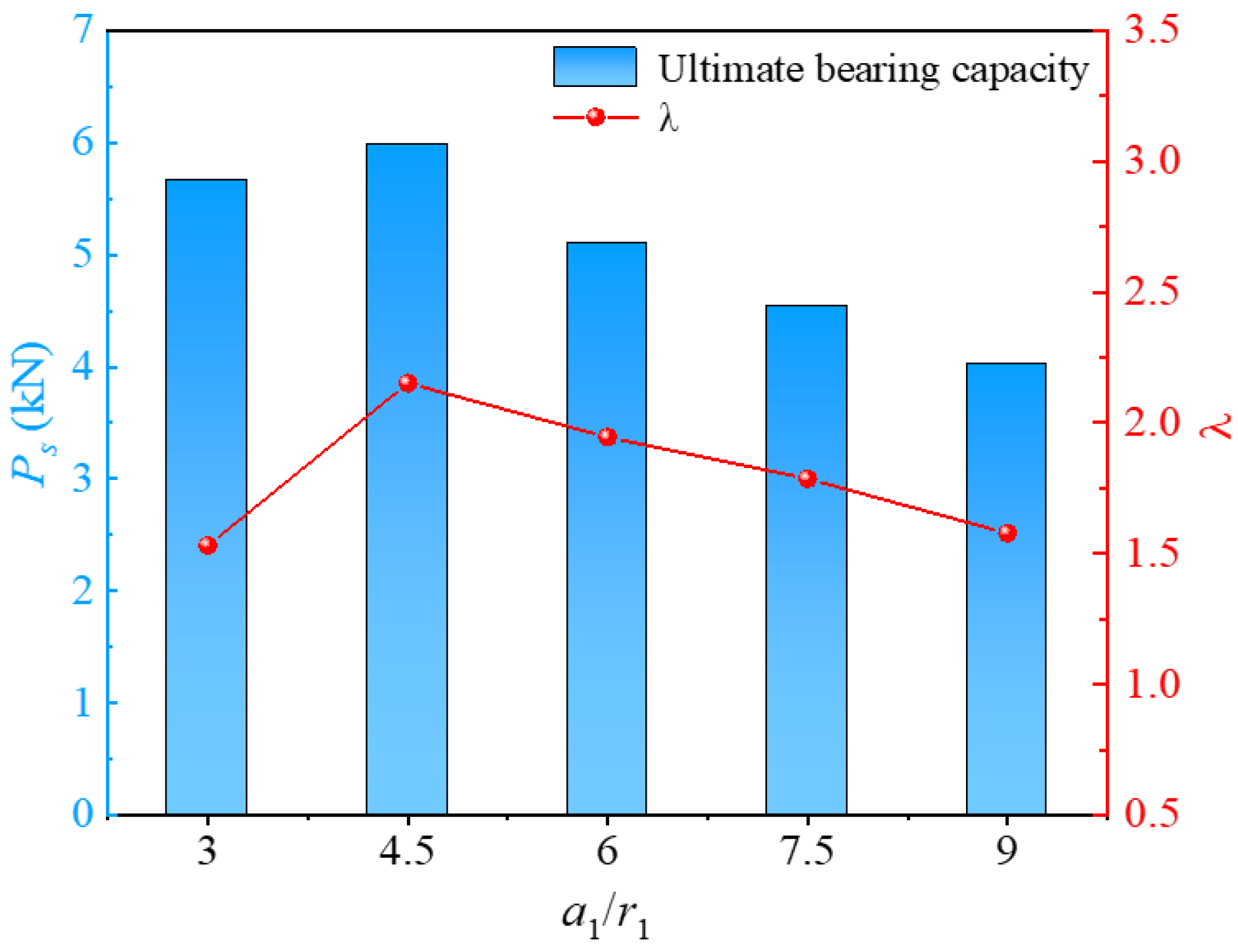
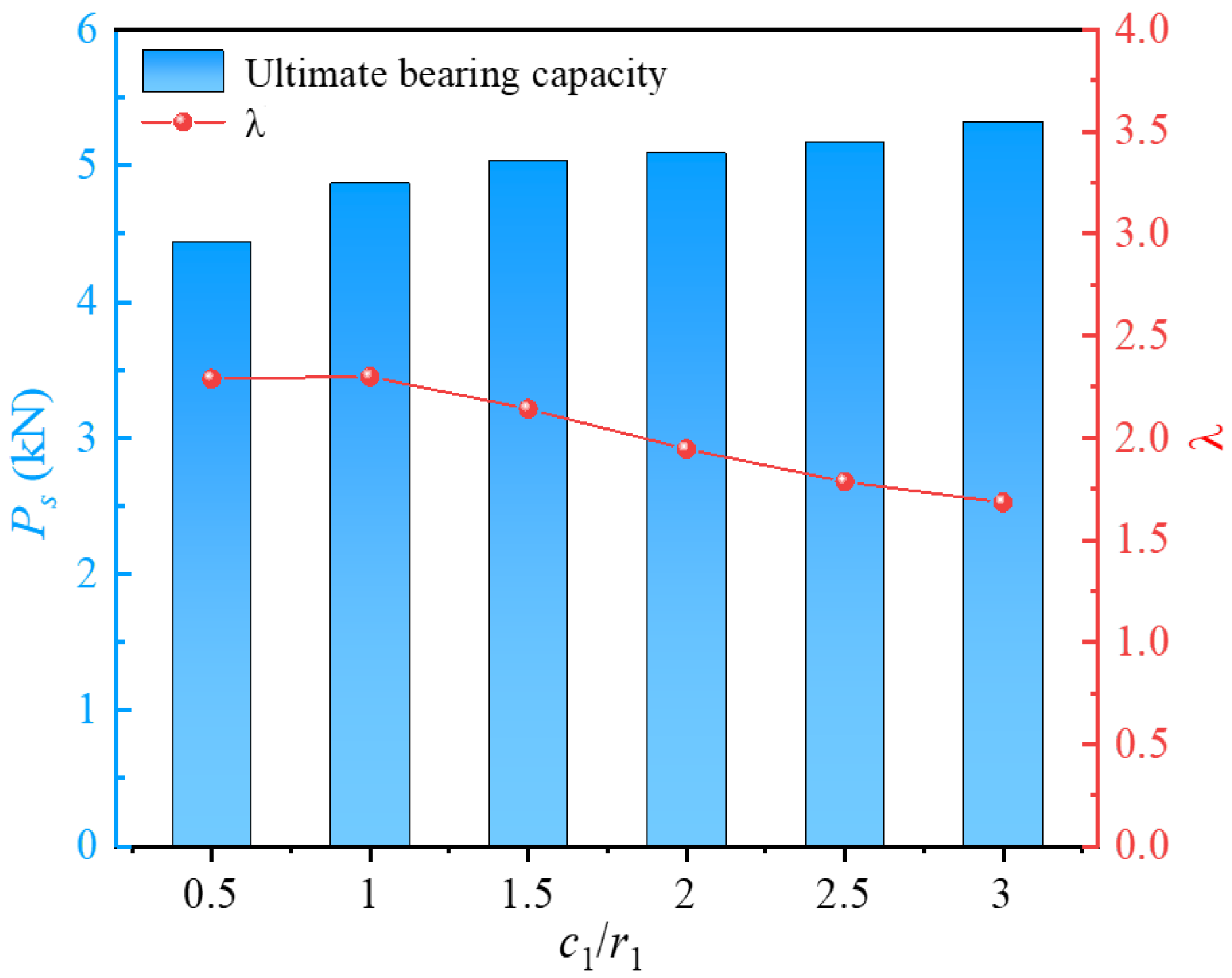
3.1. Material Utilization Ratio
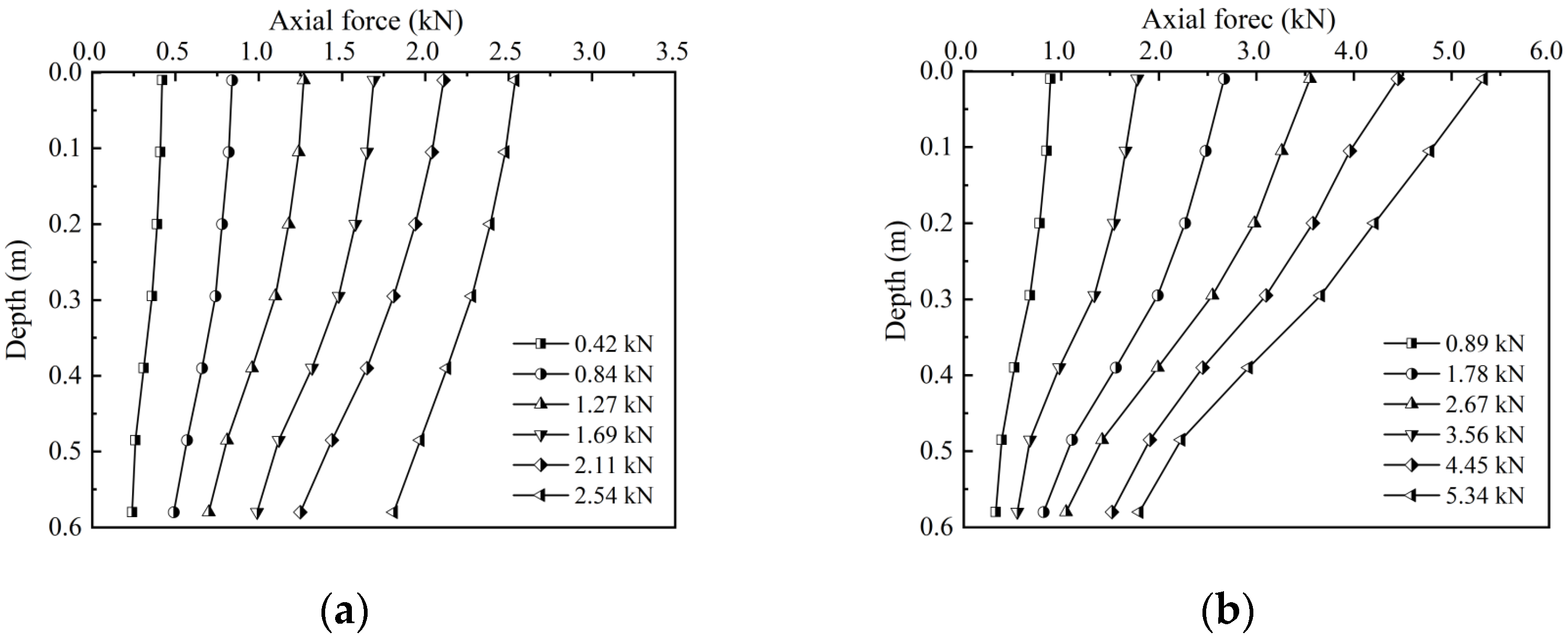
3.2. Axial Force and Skin Friction
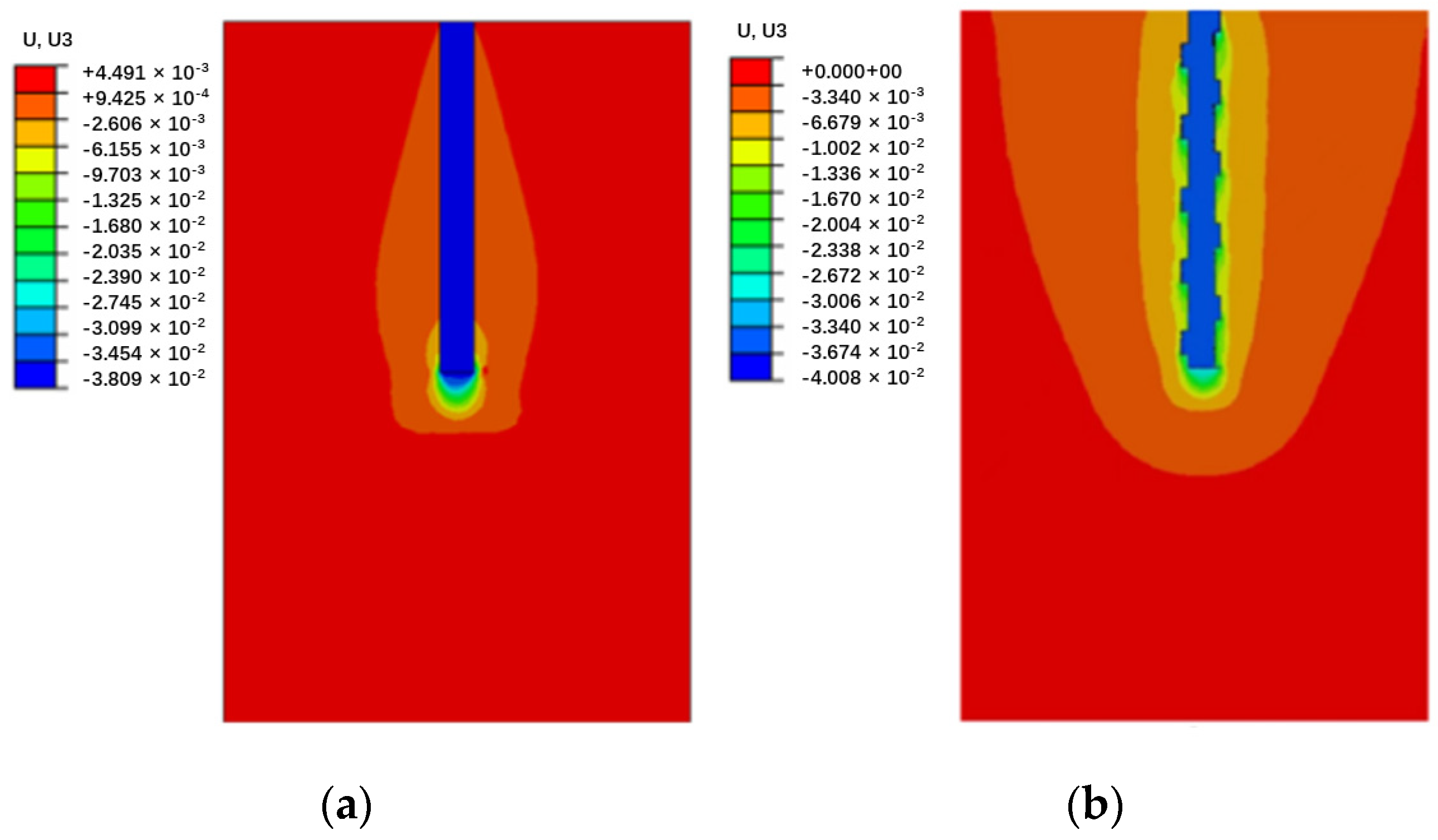
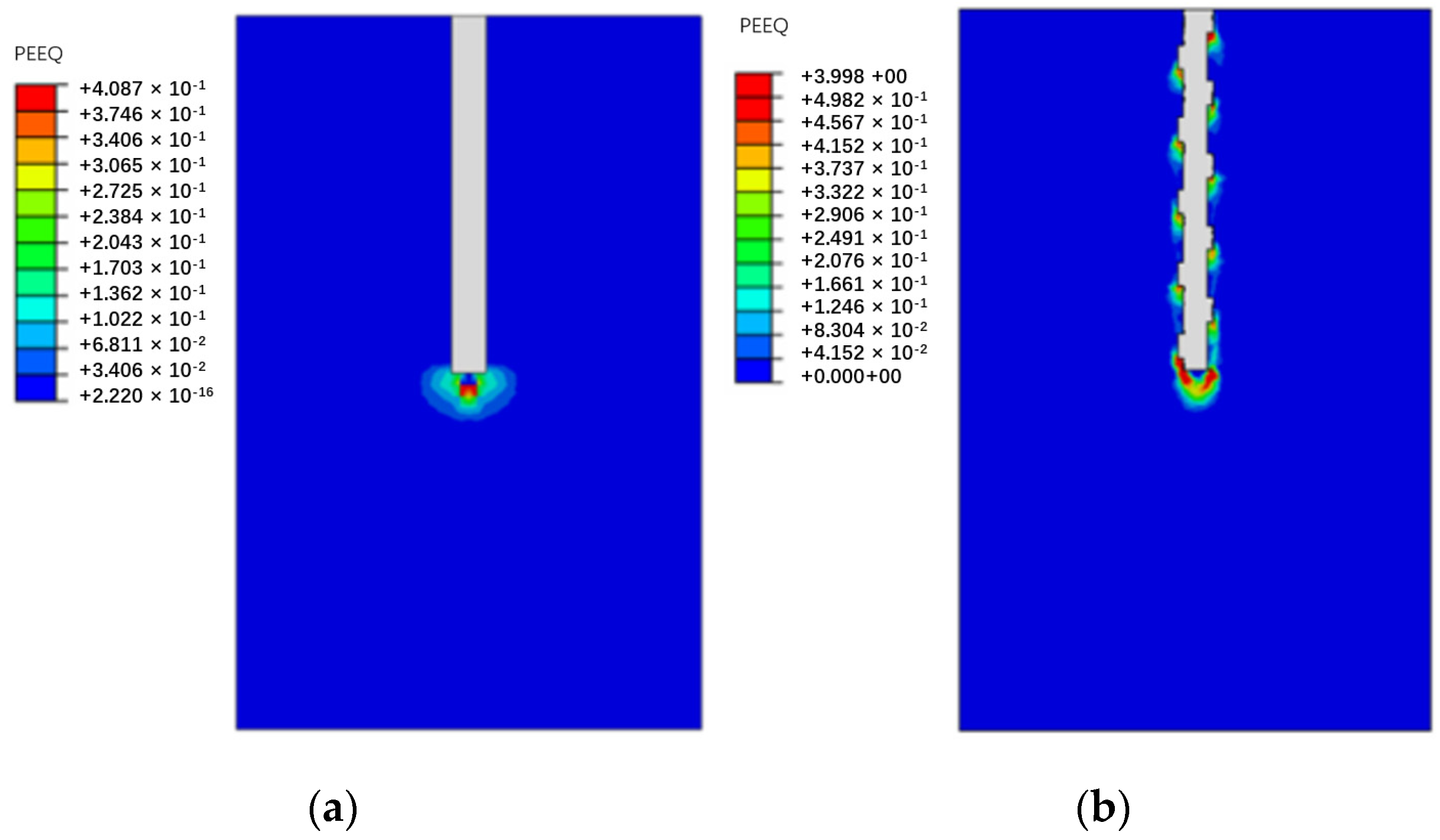
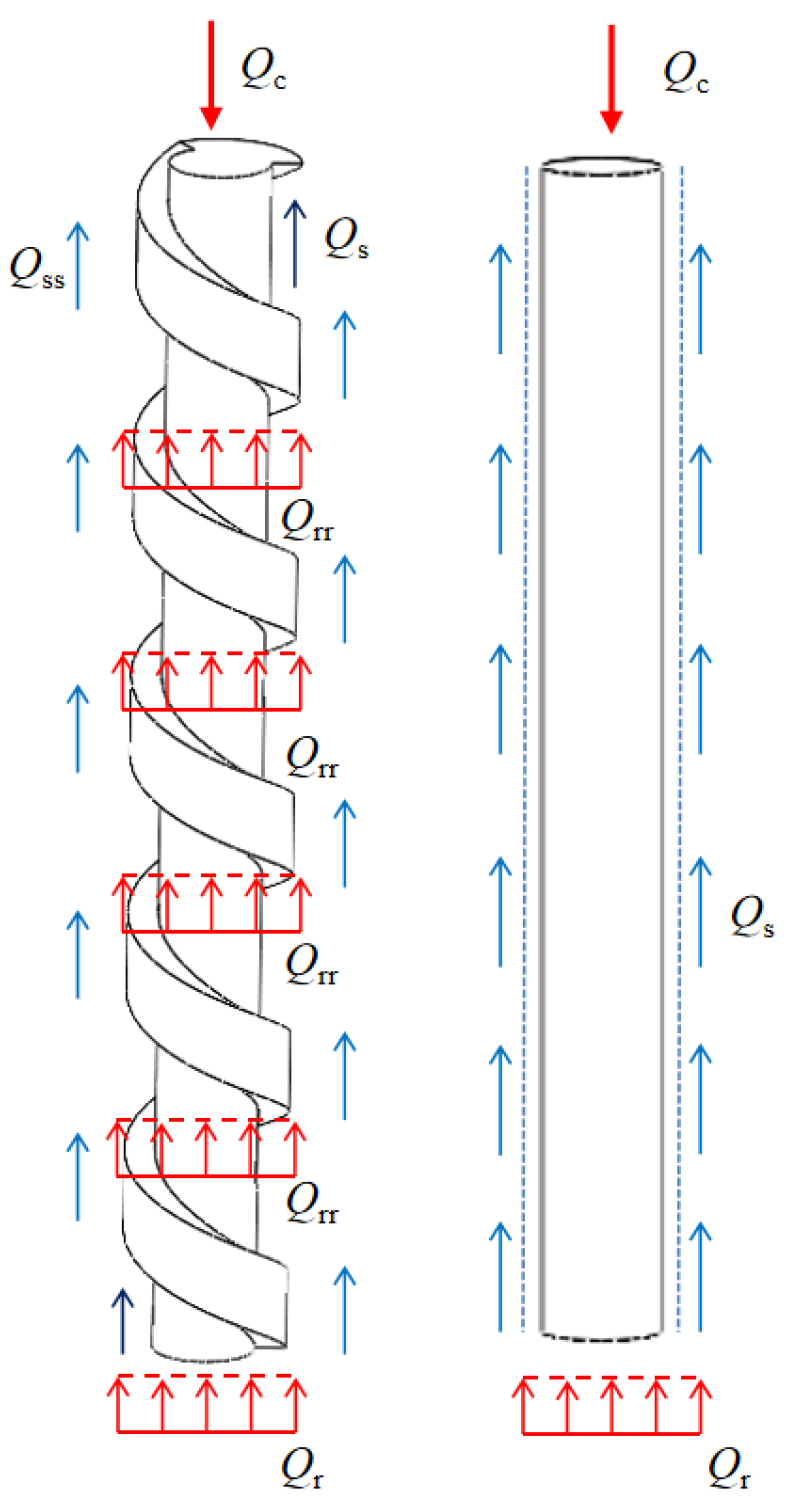
3.3. Load-Transfer Mechanism
3.4. Parameter Analysis
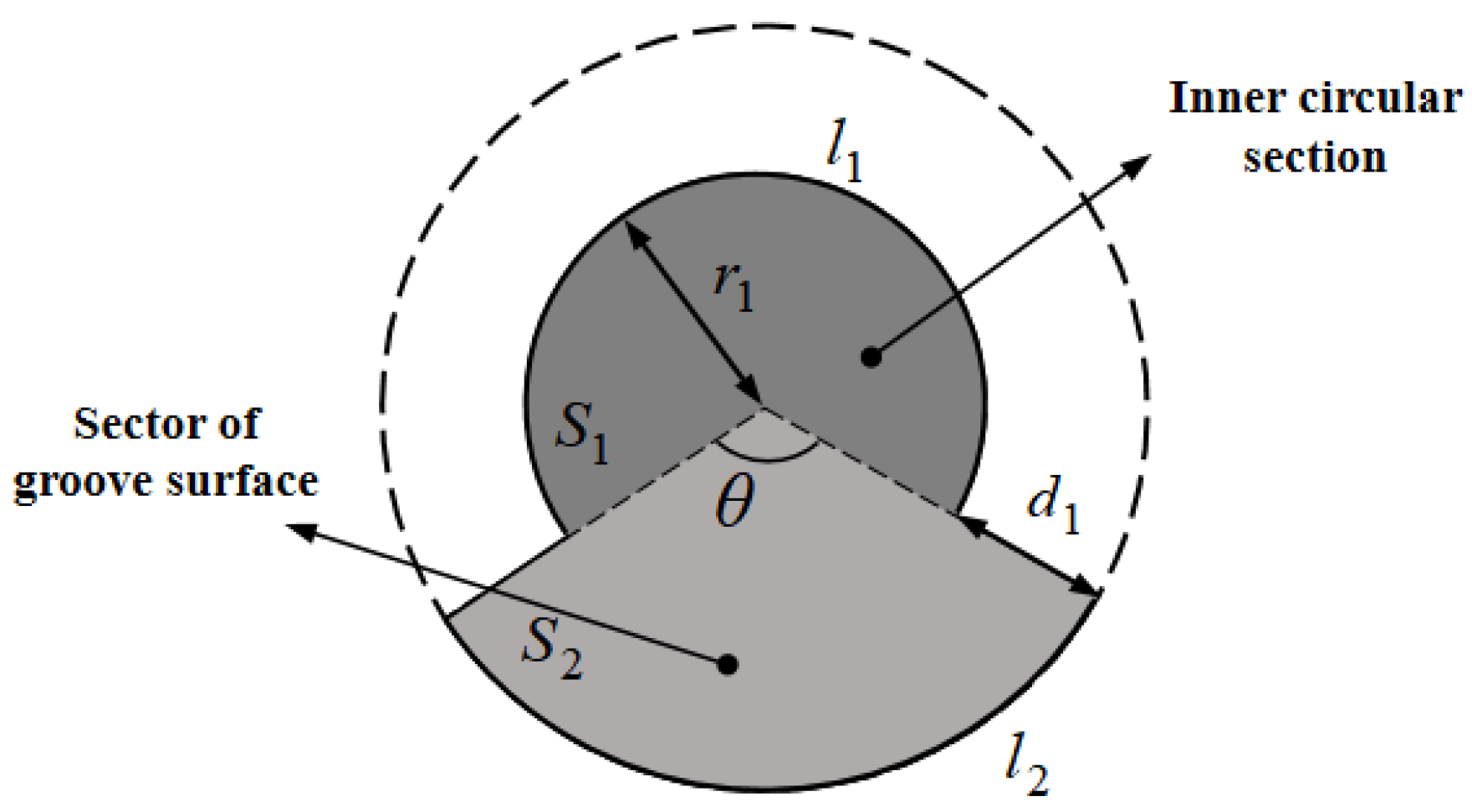
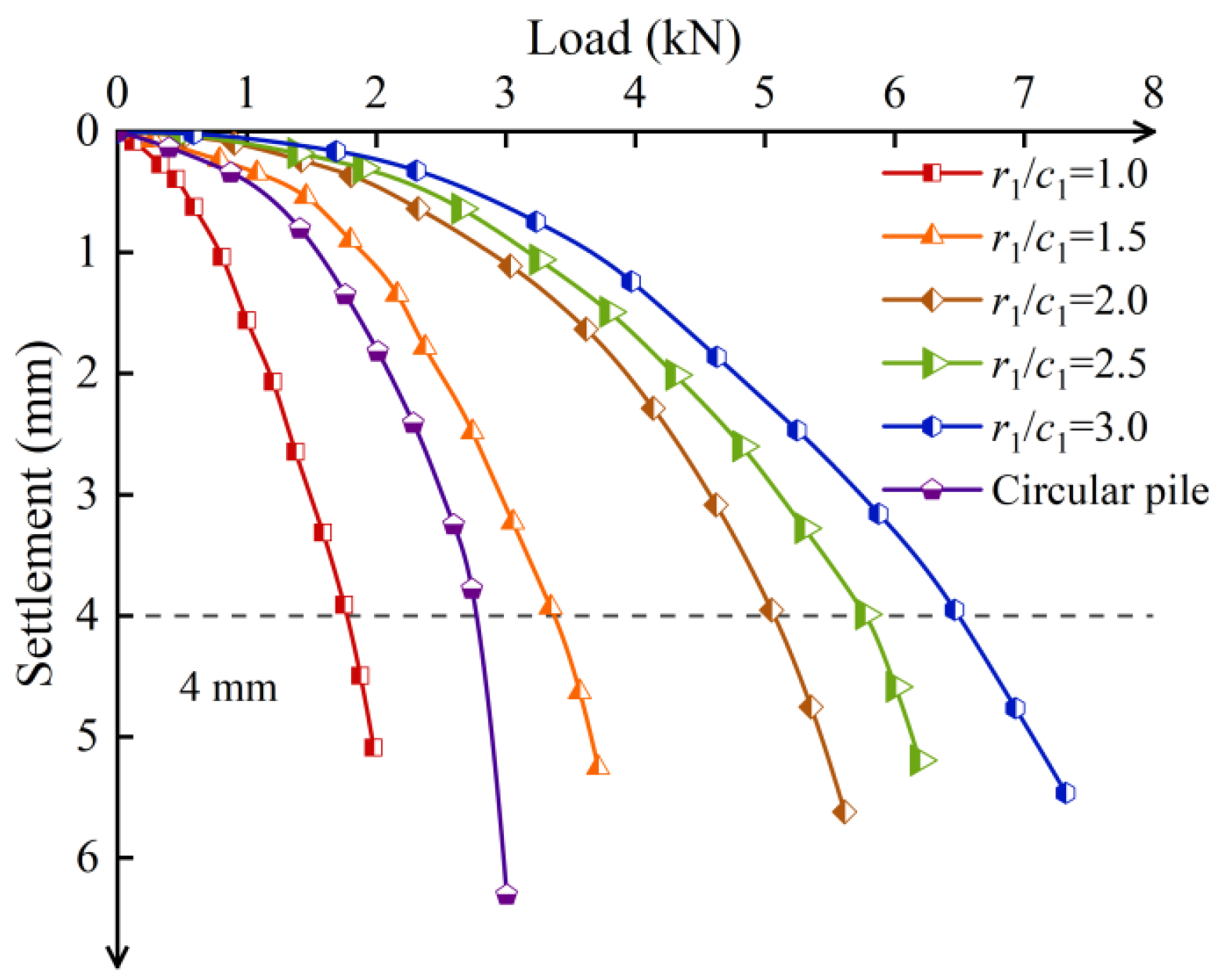
3.4.1. Inner Radius of the Screw Groove
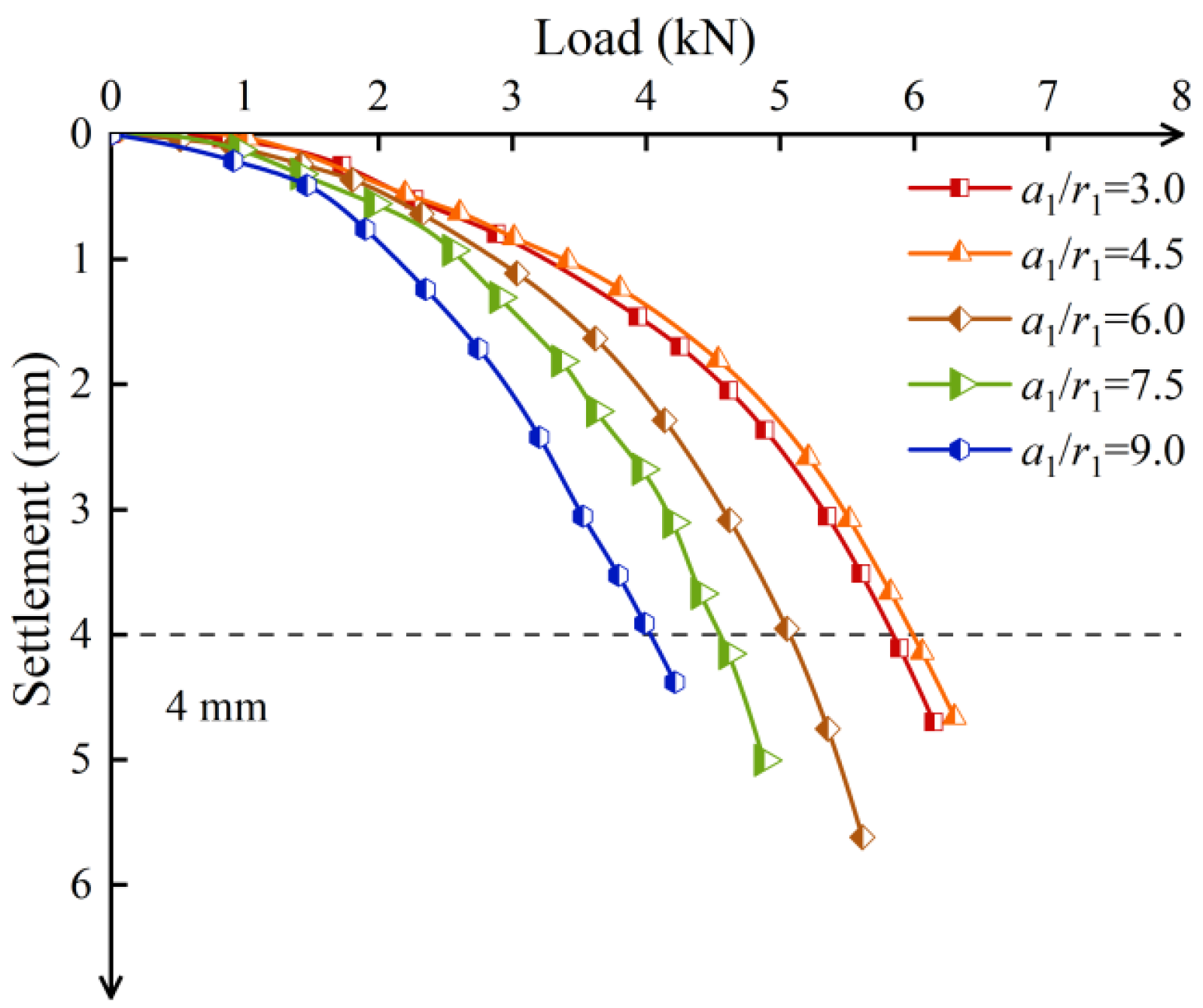
3.4.2. Screw-Groove Spacings
3.4.3. Thickness of Screw Grooves
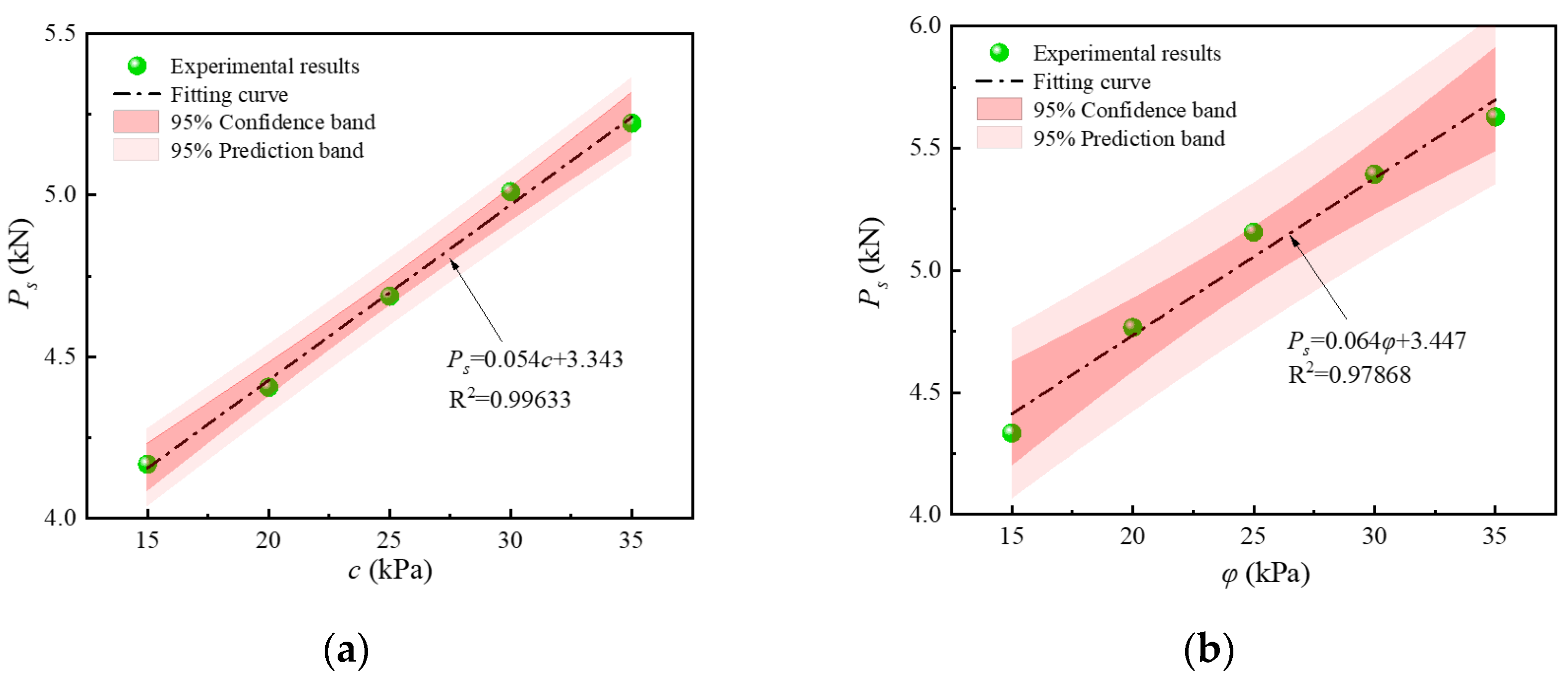
3.4.4. Soil Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| θ | Angle of sector of groove surface (°) |
| a1 | Screw-groove spacing (m) |
| b1 | Thickness of screw groove (m) |
| r1 | Inner radius of screw groove (m) |
| c1 | Width of screw groove (m) |
| d1 | Distance of screw groove (m) |
| S0 | Cross-sectional area of screw-groove pile (m2) |
| l1 | Arc length of inner circular cross-section (rad) |
| l2 | Arc length of sector of groove surface (rad) |
| l0 | Perimeter of screw-groove pile (m) |
| σ | Stress (kPa) |
| E | Modulus of elasticity (kPa) |
| ε | Strain (dimensionless) |
| P | Axial force (kPa) |
| Ac | Cross-sectional area of circular pile (m2) |
| qs | Skin friction resistance of circular pile (kPa) |
| D | Diameter of circular pile (m) |
| qss | Skin friction resistance of screw-groove pile (kPa) |
| λ | Material utilization factor |
| La | Material utilization rate of circular piles |
| Lb | Material utilization rate of screw-groove piles |
| Ps | Ultimate bearing capacity (kN) |
| τn | Shear stress (kPa) |
| c | Cohesion (kPa) |
| σn | Normal stress (kPa) |
| φ | Internal friction angle (°) |
| List of abbreviations: | |
| FEM | Finite element method |
References
- Boulifa, R.; Goudjil, K.; Samai, M.L. A new simplified approach for predicting the bearing capacity of rectangular concrete four-pile caps. Eng. Struct. 2023, 293, 116635. [Google Scholar] [CrossRef]
- Sadeghi, H.; Singh, R. Driven precast concrete geothermal energy piles: Current state of knowledge. Build. Environ. 2023, 228, 109790. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, J.; Gong, X.; Yan, T. Field tests on behavior of pre-bored grouted planted pile and bored pile embedded in deep soft clay. Soils Found. 2020, 60, 551–561. [Google Scholar] [CrossRef]
- Thusoo, S.; Obara, T.; Kono, S.; Miyahara, K. Design models for steel encased high-strength precast concrete piles under axial-flexural loads. Eng. Struct. 2021, 228, 111465. [Google Scholar] [CrossRef]
- Chen, M.; De, C.W.; Jiang, H.; Taerwe, L. Experimental study on direct-shear behaviour of narrow joints in socket connections for precast pier-to-pile footing systems. Structures 2024, 61, 106006. [Google Scholar] [CrossRef]
- Lyu, F.; Shao, H.; Zhang, W. Comparative analysis about carbon emission of precast pile and cast-in-situ pile. Energy Rep. 2022, 8, 514–525. [Google Scholar] [CrossRef]
- Ellis, L.D.; Badel, A.F.; Chiang, M.L.; Park, R.J.Y.; Chiang, Y.M. Toward electrochemical synthesis of cement-an electrolyzer-based process for decarbonating CaCO3 while producing useful gas streams. Proc. Natl. Acad. Sci. USA 2020, 117, 12584–12591. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, K.; Zhang, J.; Guo, Z. A review on low carbon emissions projects of steel industry in the world. J. Clean. Prod. 2021, 306, 127259. [Google Scholar] [CrossRef]
- Imbabi, M.S.; Carrigan, C.; McKenna, S. Trends and developments in green cement and concrete technology. Int. J. Sustain. 2012, 1, 194–216. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, A.; Wang, A.; Sun, H. Performance of screw–shaft pile in sand: Model test and DEM Simulation. Comput. Geotech. 2018, 104, 118–130. [Google Scholar] [CrossRef]
- Abushama, K.; Hawkins, W.; Pelecanos, L.; Ibell, T. Embodied carbon optimisation of concrete pile foundations and comparison of the performance of different pile geometries. Eng. Struct. 2024, 310, 118109. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, H.; Ng, C.W.; Gunawan, A.; Ding, X. A modified analytical solution of soil stress distribution for XCC pile foundations. Acta Geotech. 2014, 9, 529–546. [Google Scholar] [CrossRef]
- Wang, X.Q.; Ren, L.W.; Yang, Q.W.; Cui, Y.L. Comparative model tests on bearing behavior between Y-section pile and circular pile. China J. Highw. Transp. 2016, 29, 11–18. [Google Scholar]
- Li, L.; Deng, Y. Strengthening mechanism of Plum Blossom Pile Composite Foundation. Acta Geotech. 2024, 19, 4791–4808. [Google Scholar] [CrossRef]
- Hataf, N.; Shafaghat, A. Optimizing the bearing capacity of tapered piles in realistic scale using 3D finite element method. Geotech. Geol. Eng. 2015, 33, 1465–1473. [Google Scholar] [CrossRef]
- Aamer, F.; Azzam, W.; Farouk, A.; Nasr, A.; Nazir, A. Utilization of blade anchor for improving the uplift capacity of pile in sand: Model Study. Ocean Eng. 2023, 278, 114435. [Google Scholar] [CrossRef]
- Bak, H.M.; Halabian, A.M.; Hashemolhosseini, H.; Rowshanzamir, M. Axial response and material efficiency of tapered helical piles. J. Rock Mech. Geotech. 2021, 13, 176–187. [Google Scholar] [CrossRef]
- Chen, L.; Zhuang, Y.Z.; Song, K.S.; Easa, S.M.; Zhu, H.J. Novel HS-RC stepped pile foundation: Experimental and numerical evaluation. Ocean Eng. 2024, 299, 117196. [Google Scholar] [CrossRef]
- Hassan, I.; Mohamedelhassan, E. Enhancing the load-bearing capacity of H-pile foundation by using electrokinetic treatment. Int. J. Civ. Eng. 2023, 21, 991–1005. [Google Scholar] [CrossRef]
- Alekseev, A.G.; Bezvolev, S.G.; Sazonov, P.M. Experience of using multi-blade screw piles in silt-loam soil foundation. Soil Mech. Found. Eng. 2019, 55, 387–393. [Google Scholar] [CrossRef]
- Zhong, W.; Liu, H.; Wang, Q.; Zhang, W.; Li, Y.; Ding, X.; Chen, L. Investigation of the penetration characteristics of snake skin-inspired pile using DEM. Acta Geotech. 2021, 16, 1849–1865. [Google Scholar] [CrossRef]
- Yu, Y.C.; Ren, W.X.; Yin, Y.G.; Luo, X.G. Numerical simulation and field tests on vertical load bearing behaviour of bored root piles. Comput. Geotech. 2023, 159, 105453. [Google Scholar] [CrossRef]
- Lin, C.; Liu, Q.; Deng, T.; Yue, C.; Cui, P. Prediction of single pile response to lateral soil movement in model test. Comput. Geotech. 2023, 161, 105608. [Google Scholar] [CrossRef]
- Zhou, P.; Li, J.; Dai, K.; Vogt, S.; Miraei, S. Theoretical investigation on axial cyclic performance of monopile in sands using interface constitutive models. J. Rock Mech. Geotech. 2024, 16, 1674–7755. [Google Scholar] [CrossRef]
- Gao, F.; Cheng, X.; Wang, W.; Lv, Q.; Cheng, X. Experimental study on the bearing characteristics of rigid-flexible long-short pile composite foundations in thick collapsible loess areas. KSCE J. Civ. Eng. 2024, 28, 1690–1701. [Google Scholar] [CrossRef]
- Wang, G.H.; Chen, W.H.; Nie, Q.K.; Chen, J.H.; Fan, H.H.; Zhang, C. Impacts of pit excavation on foundation piles in deep silty soil by centrifugal model tests. Rock Soil Mech. 2020, 41, 399–407. [Google Scholar]
- JGJ106-2014; Building Pile Testing Technology Code. China Building Industry Press: Beijing, China, 2014.
- Deng, Y.; Zhang, K.; Yao, Z.; Zhao, H.; Li, L. Parametric analysis and multi-objective optimization of the coupling beam pile structure foundation. Ocean Eng. 2023, 280, 114724. [Google Scholar] [CrossRef]
- Randolph, M.F.; Worth, C.P. Application of the Failure State in Undrained Simple Shear to the Shaft Capacity of Driven Piles. Geotechnique 1981, 31, 143–157. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, S.G.; Xu, J.; Hu, Y.Y. Model test on vertical bearing capacity of variable cross-section thread piles. Rock Soil Mech. 2017, 38, 747–754, 783. [Google Scholar]
- Jäntschi, L.; Bolboacă, S.D. Computation of Probability Associated with Anderson–Darling Statistic. Mathematics 2018, 6, 88. [Google Scholar] [CrossRef]
- Cho, J.; Gong, S.; Choi, K. A Study on High-Speed Outlier Detection Method of Network Abnormal Behavior Data Using Heterogeneous Multiple Classifiers. Appl. Sci. 2022, 12, 1011. [Google Scholar] [CrossRef]
- Markovich, N.; Vaičiulis, M. Extreme Value Statistics for Evolving Random Networks. Mathematics 2023, 11, 2171. [Google Scholar] [CrossRef]



| Modulus of Elasticity [MPa] | Density [g/cm3] | Poisson Ratio | Cohesion [kPa] | Friction Angle [°] | |
|---|---|---|---|---|---|
| Pile | 7.2 × 104 | 2.70 | 0.33 | - | - |
| Soil | 8.0 | 1.81 | 0.30 | 33.3 | 23.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Deng, Y.; Zhuang, Z.; Yao, Z. Bearing Characteristics of Screw-Groove Piles: Model Test and Numerical Analysis. Materials 2024, 17, 5791. https://doi.org/10.3390/ma17235791
Zhao H, Deng Y, Zhuang Z, Yao Z. Bearing Characteristics of Screw-Groove Piles: Model Test and Numerical Analysis. Materials. 2024; 17(23):5791. https://doi.org/10.3390/ma17235791
Chicago/Turabian StyleZhao, Huiling, Yousheng Deng, Ziying Zhuang, and Zhigang Yao. 2024. "Bearing Characteristics of Screw-Groove Piles: Model Test and Numerical Analysis" Materials 17, no. 23: 5791. https://doi.org/10.3390/ma17235791
APA StyleZhao, H., Deng, Y., Zhuang, Z., & Yao, Z. (2024). Bearing Characteristics of Screw-Groove Piles: Model Test and Numerical Analysis. Materials, 17(23), 5791. https://doi.org/10.3390/ma17235791







