Optimization of the Thickness Ratio and Roll-Bonding Parameters of Bimetallic Ti/Al Rod for Bending-Dominated Negative Thermal Expansion Metamaterials
Abstract
1. Introduction
2. Material and Methods
2.1. Materials
2.2. Rolling and Heat Treatment
2.3. Microstructure and Properties Characterization
2.4. Preparation of “Cross-Shaped” Node Bending-Dominated NTEMs
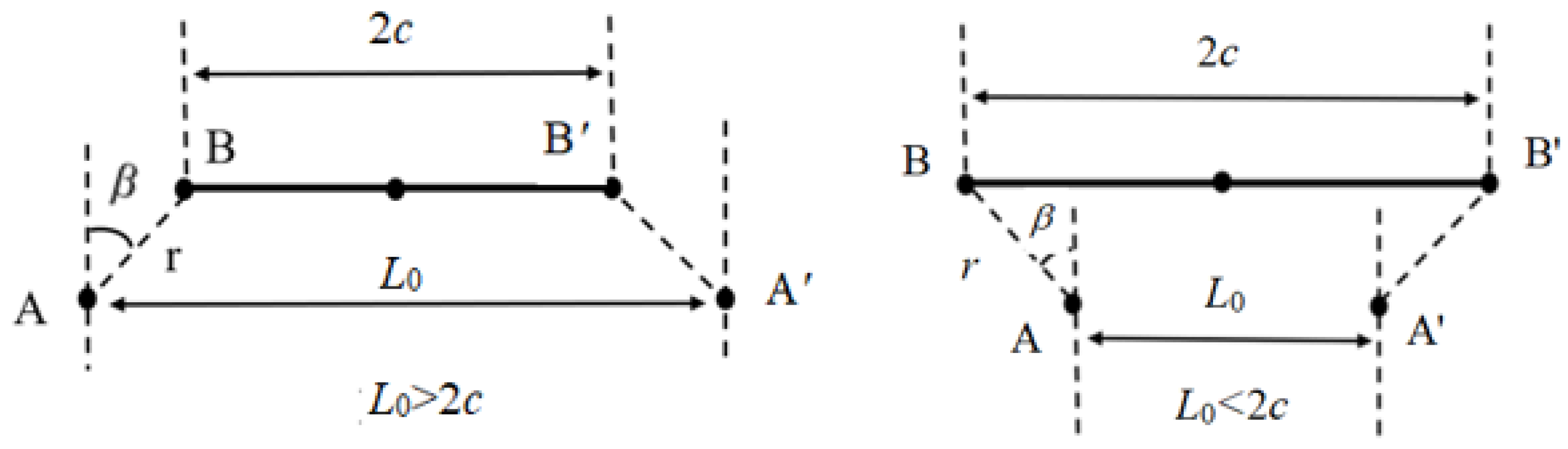
2.5. Optimization of the Thickness Ratio of Bimetallic Rods in “Cross-Shaped” Node Bending-Dominated NTEMs
2.6. Optimization Methods of Ti/Al Roll Bonding Process
3. Results
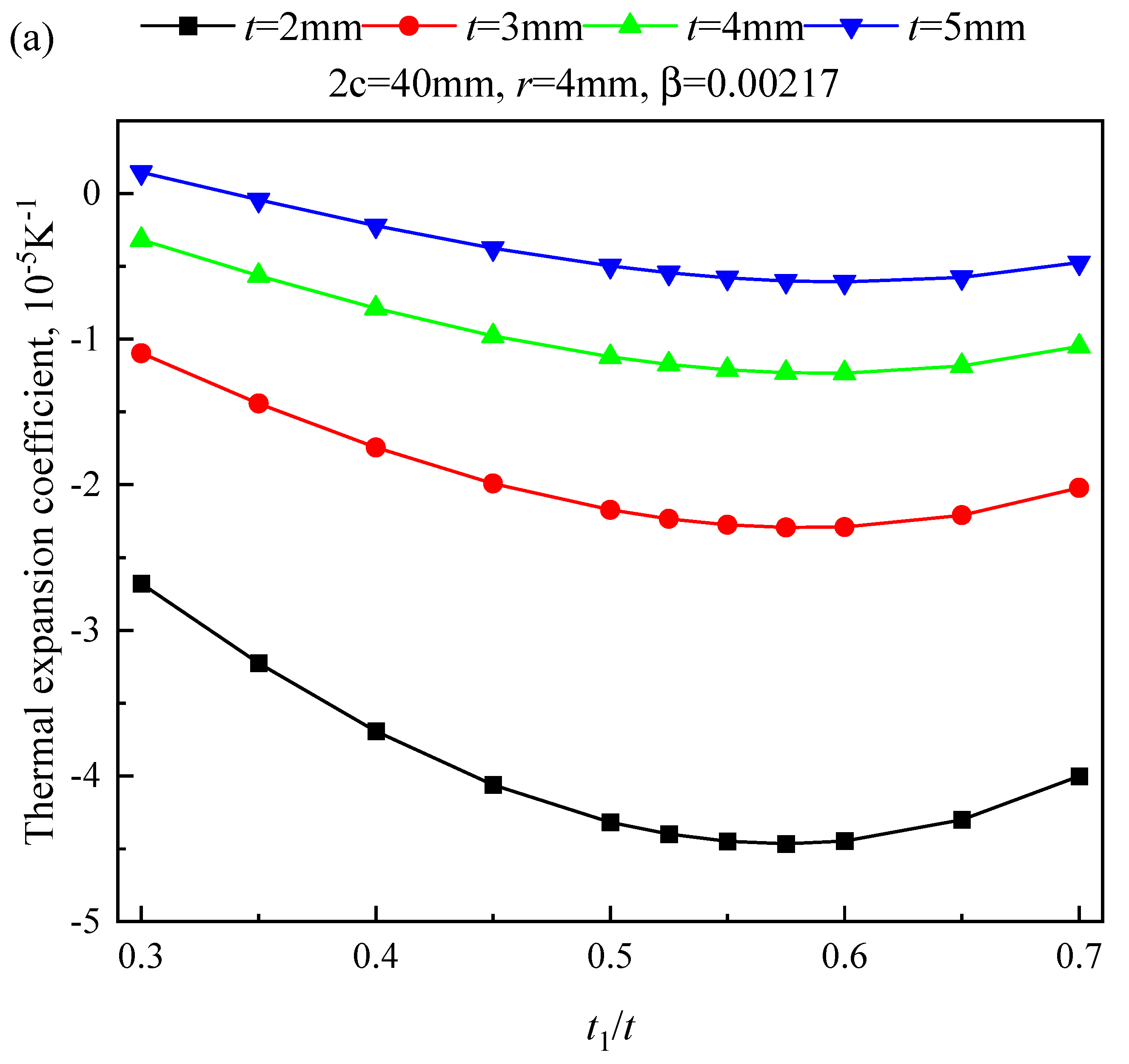
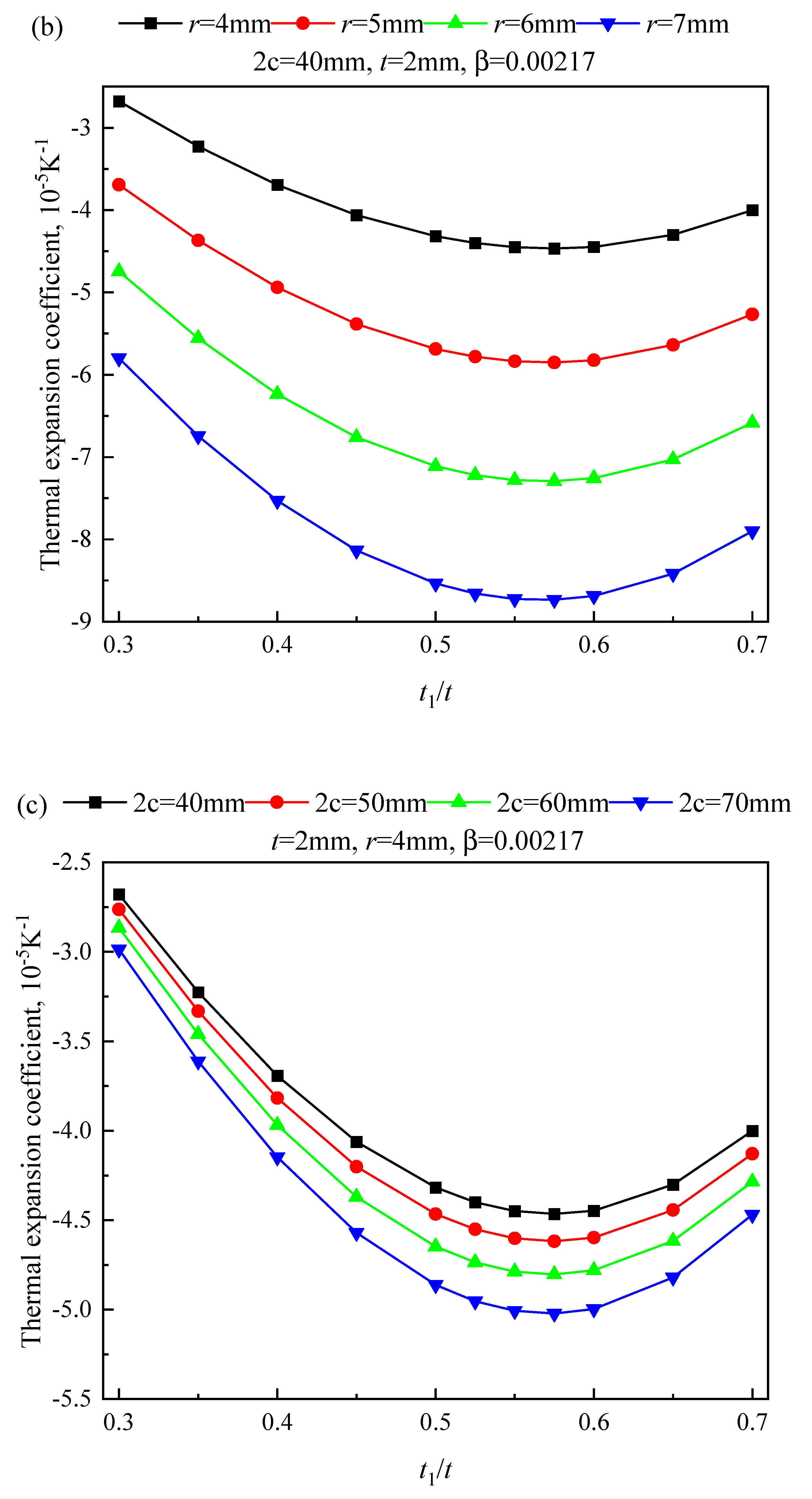
3.1. Optimization of the Thickness Ratio of Bimetallic
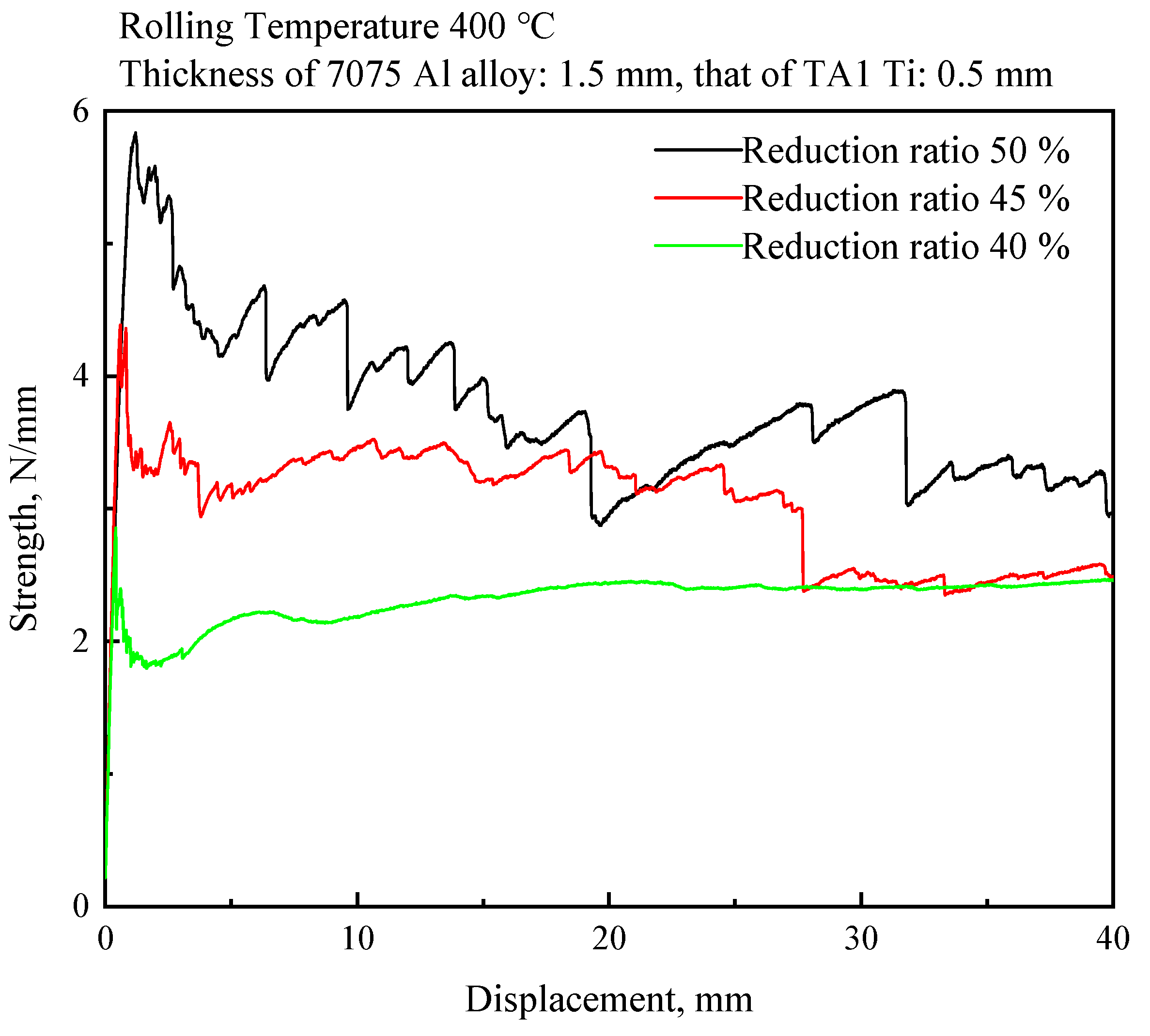
3.2. Optimization of Ti/Al Roll Bonding Process
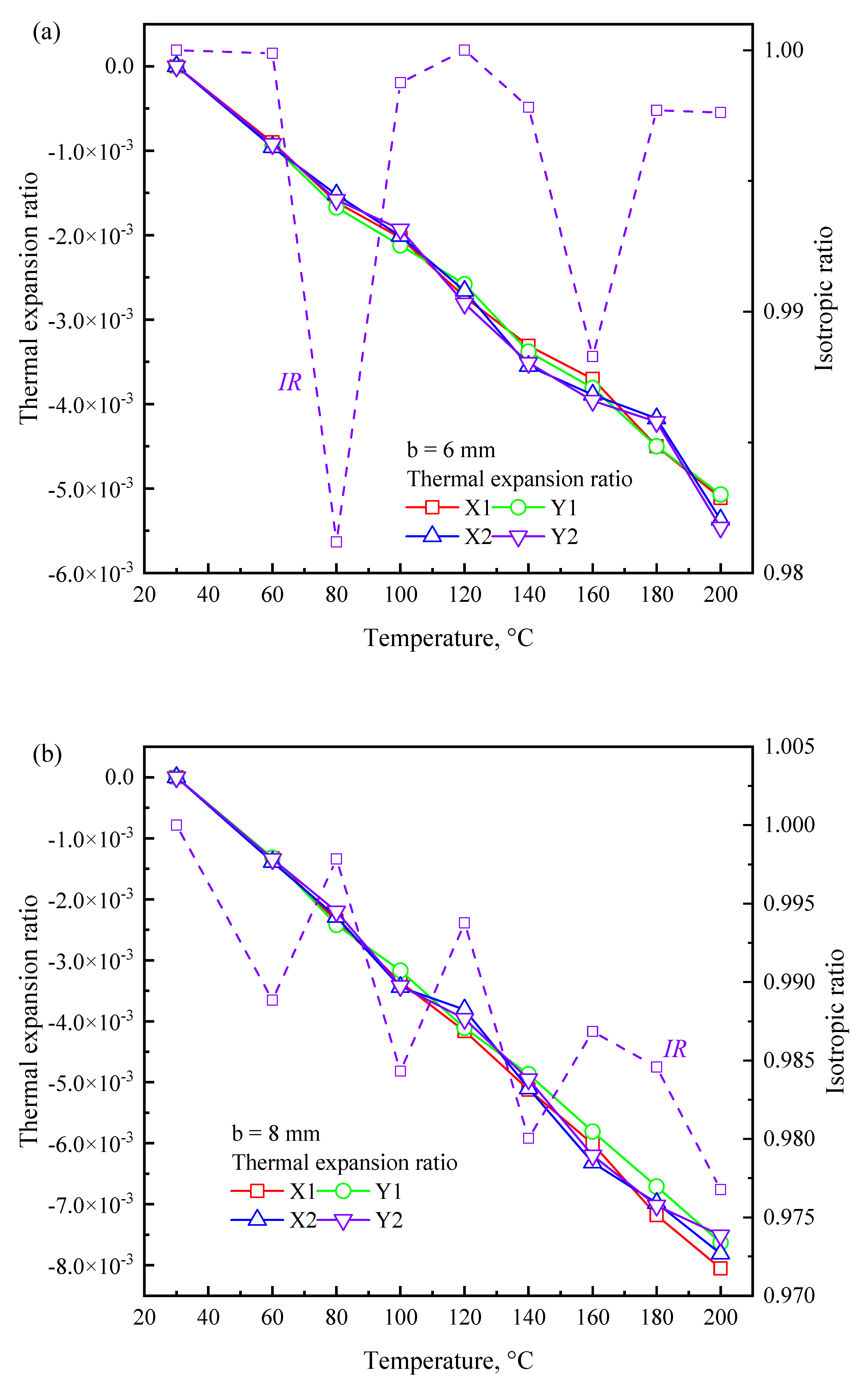
3.3. Thermal Expansion Coefficients of the NTEMs
4. Discussion
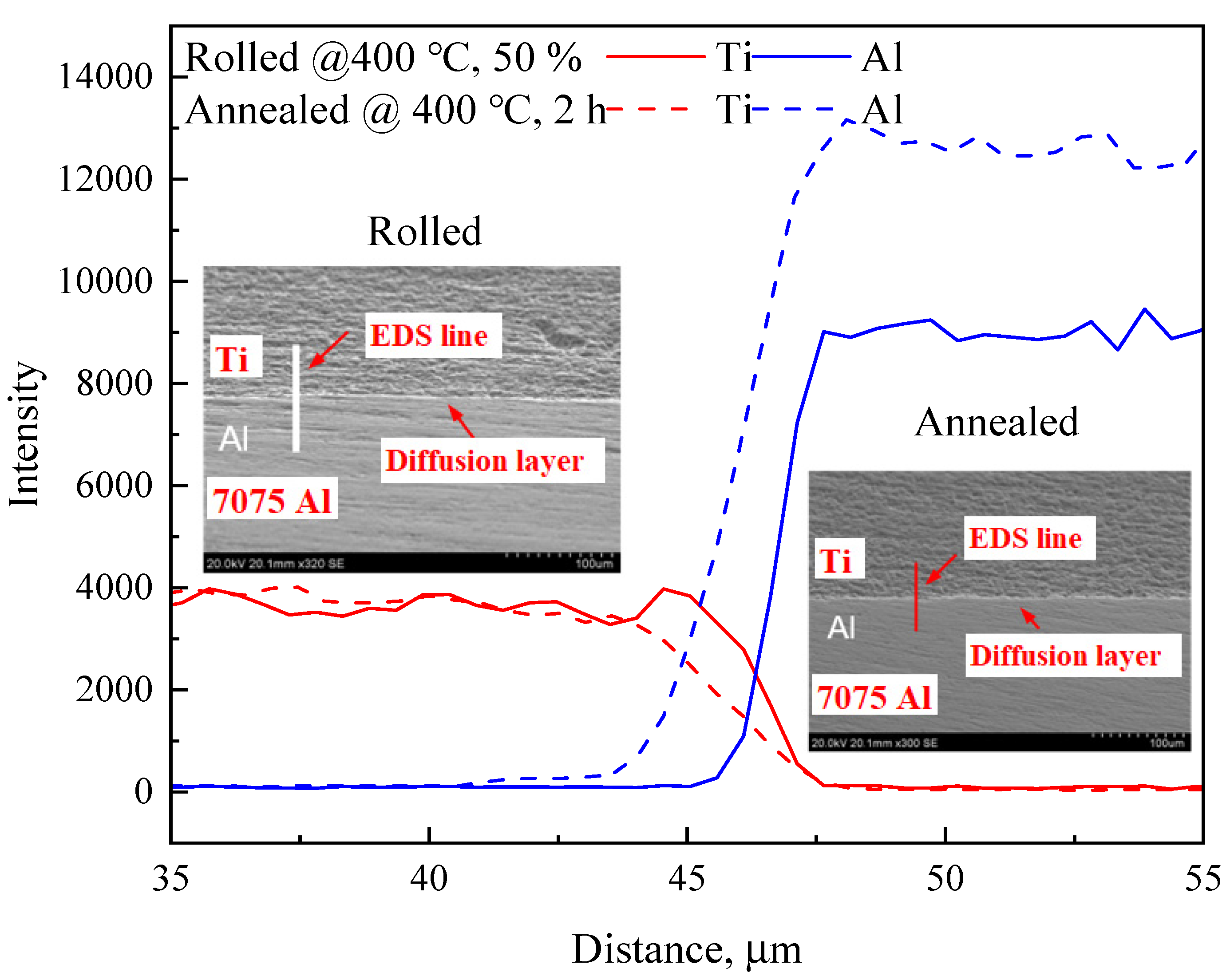
4.1. Bonding Strength of Ti/Al Bimaterial Rods for NTEMs
4.2. Isotropic Negative Thermal Expansion Properties of the TA1 Ti/7075 Al NTEMs
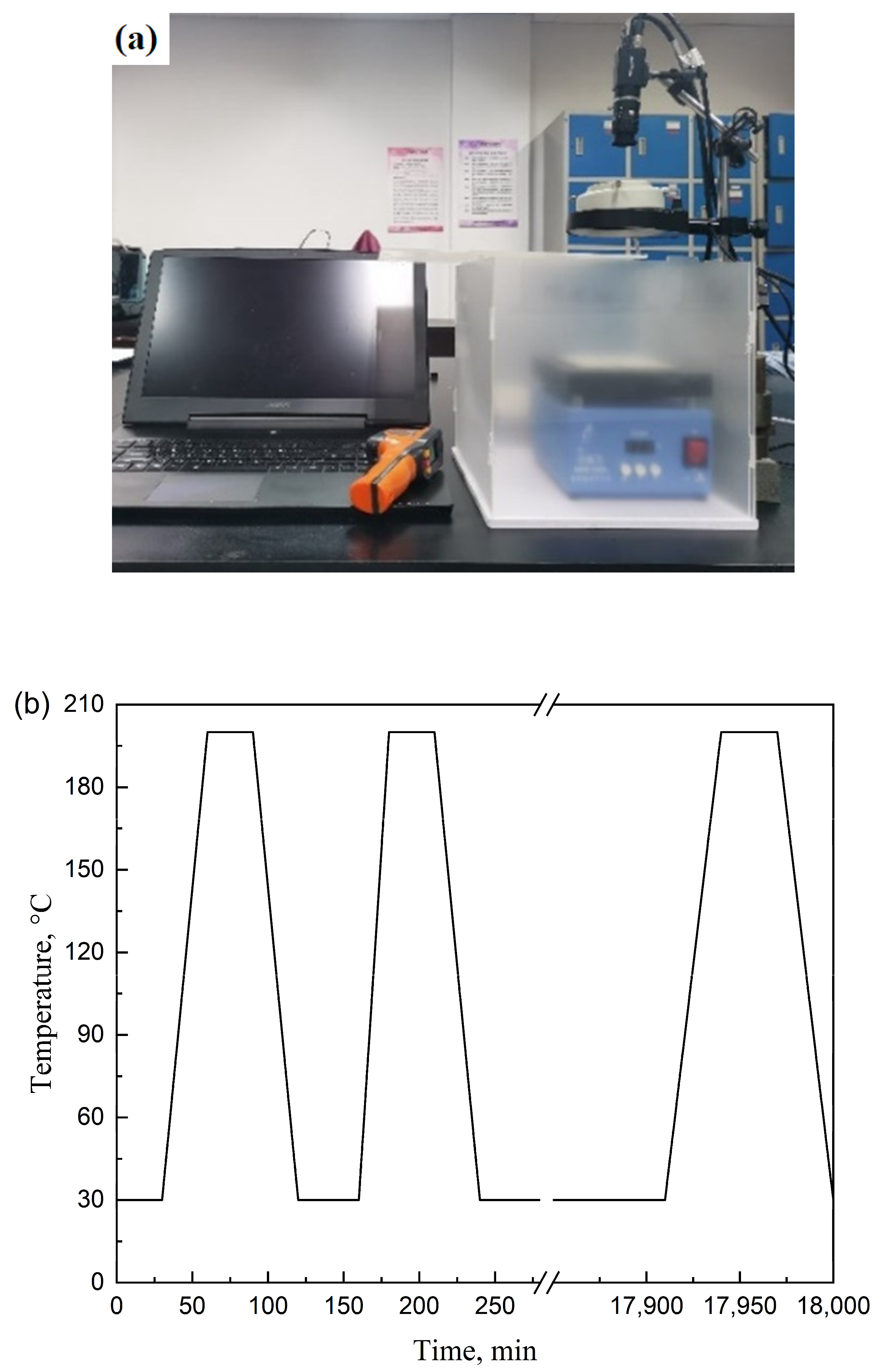
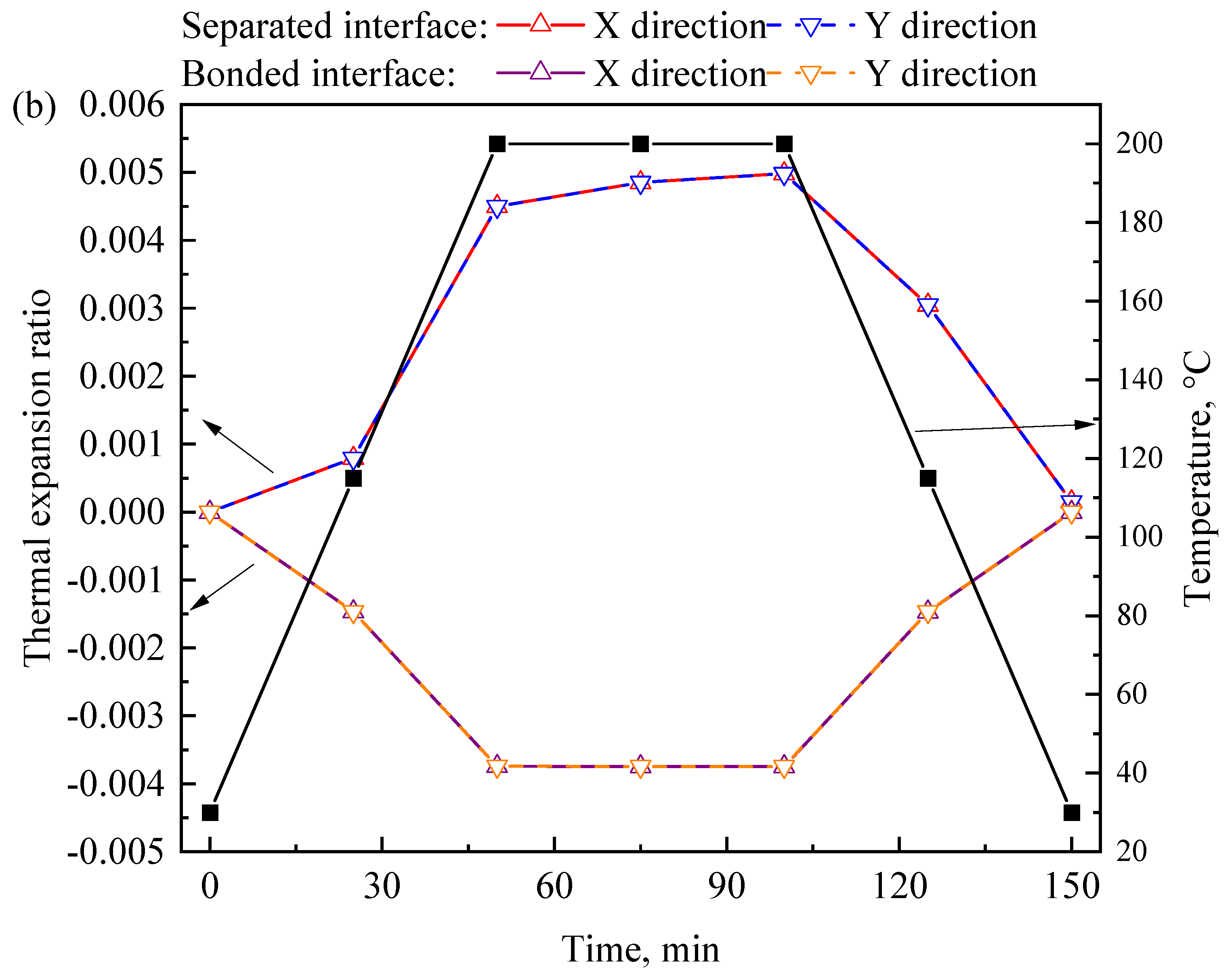
4.3. Cyclic Thermal Stability of Ti/Al NTEMs
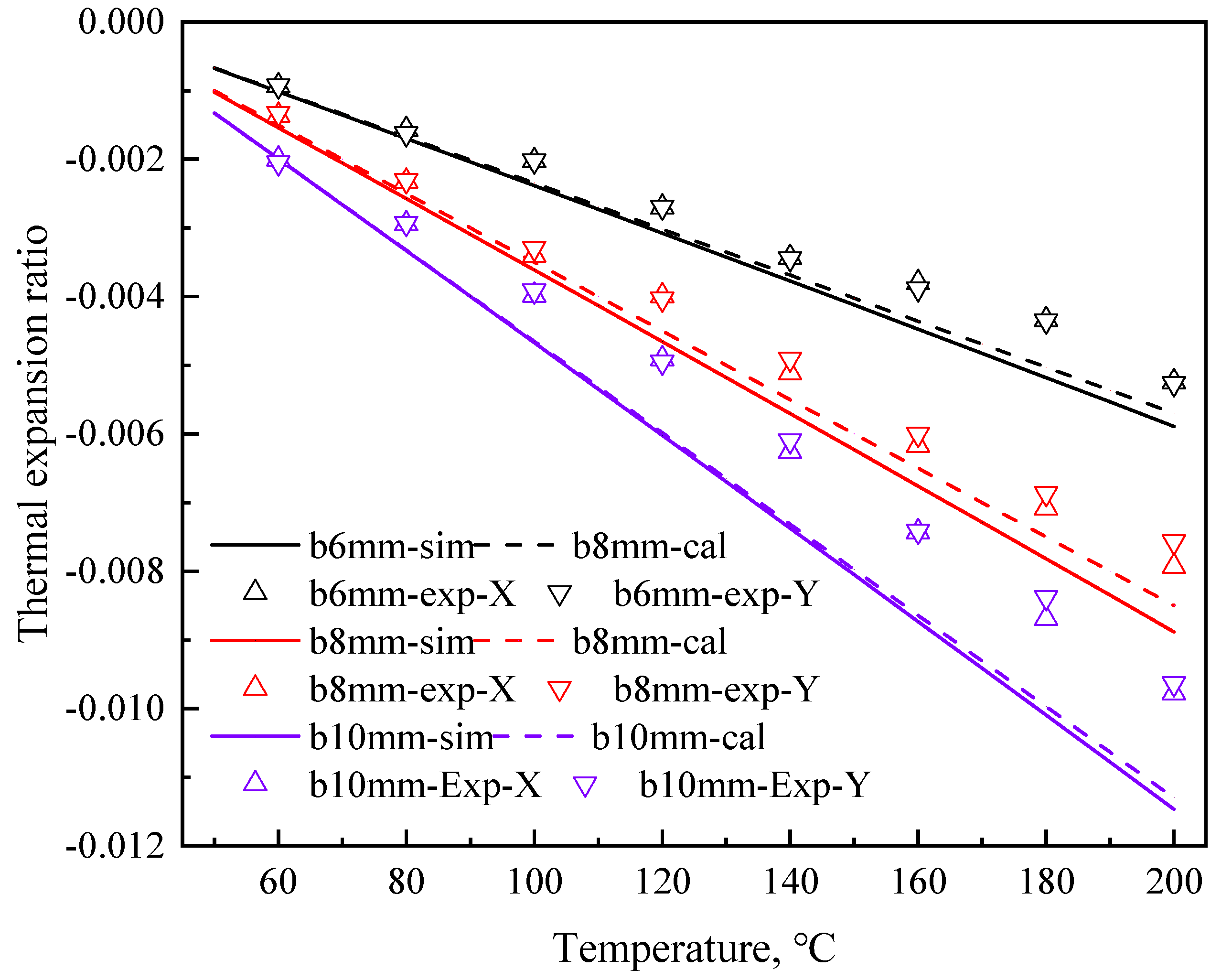
4.4. Errors Between the Modeled and Experimental Results of the αT of the TA1 Ti/7075 Al NTEMs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atifeh, S.M.; Hashemi, R.; Sedighi, M. Investigation and optimization on the formability of aluminum 1050/stainless steel 304L bilayer sheets fabricated by cold roll bonding considering the Box–Behnken method. J. Mater. Res. Technol. 2024, 31, 3453–3465. [Google Scholar] [CrossRef]
- Niu, H.; Gao, X.Y.; Jiang, L.; Han, J.C.; Liu, P.T.; Wang, T. Research on bonding mechanism of Cu/Al corrugated composite plates rolled by flat finish roll bonding. Mater. Today Commun. 2024, 40, 109303. [Google Scholar] [CrossRef]
- Yan, H.; Lenard, J.G. A study of warm and cold roll–bonding of an aluminium alloy. Mater. Sci. Eng. A 2004, 385, 419–428. [Google Scholar] [CrossRef]
- Han, J.; Niu, H.; Li, S.; Ren, Z.; Jia, Y.; Wang, T.; Plokhikh, A.I.; Huang, Q. Effect of mechanical surface treatment on the bonding mechanism and properties of cold rolled Cu/Al clad plate. Chin. J. Mech. Eng. 2022, 33, 222–234. [Google Scholar] [CrossRef]
- Zhang, X.P.; Yang, T.H.; Castagne, S.; Wang, J.T. Microstructure; bonding strength and thickness ratio of Al/Mg/Al alloy laminated composites prepared by hot rolling. Mater. Sci. Eng. A 2011, 528, 1954–1960. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Zhou, W.; Wang, Y.; Lu, Y. Novel 2D metamaterials with negative Poisson’s ratio and negative thermal expansion. Extrem. Mech. Lett. 2019, 30, 100498. [Google Scholar] [CrossRef]
- Ha, C.S.; Hestekin, E.; Li, J.; Plesha, M.E.; Lakes, R.S. Controllable thermal expansion of large magnitude in chiral negative Poisson’s ratio lattices. Phys. Status Solidi B 2015, 252, 1431–1434. [Google Scholar] [CrossRef]
- Lehman, J.; Lakes, R. Stiff lattices with zero thermal expansion and enhanced stiffness via rib cross section optimization. Int. J. Mech. Mater. Des. 2013, 9, 213–225. [Google Scholar] [CrossRef]
- Wu, L.; Li, B.; Zhou, J. Isotropic negative thermal expansion metamaterials. Appl. Mater. Interfaces 2016, 8, 17721–17727. [Google Scholar] [CrossRef]
- Wei, K.; Xiao, Y.J.; Chen, J.X.; Wu, Y.Z.; Li, M.J.; Wang, Z.G. Additively manufactured bi-material metamaterial to program a wide range of thermal expansion. Mater. Des. 2021, 198, 109343. [Google Scholar] [CrossRef]
- Lu, F.C.; Lin, B.C.; Ling, X.Y.; Zhang, C.B.; Zhu, Y.L. Controllable design of bi-material metamaterials with programmable thermal expansion and Poisson’s ratio. Compos. Struct. 2023, 322, 117417. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.T.; Zhang, Z.Y. Stiffness characteristics for bi-directional tunable thermal expansion metamaterial based on bi-material triangular unit. Int. J. Mech. Sci. 2023, 241, 107983. [Google Scholar] [CrossRef]
- Meng, Z.Q.; Qin, W.K.; Mei, T.; Chen, C.Q. Bi-material sinusoidal beam-based temperature responsive multistable metamaterials. Int. J. Solids Struct. 2023, 277–278, 112343. [Google Scholar] [CrossRef]
- Zhi, Q.; Li, D.S.; Sun, H.L.; Zhu, W.J. Adjustment of multi-directional elastic properties of chiral metamaterial via a 3D printing-based soft-hard bi-material strategy. Compos. Struct. 2023, 307, 116646. [Google Scholar] [CrossRef]
- Wei, K.; Chen, H.; Pei, Y.; Fang, D. Planar lattices with tailorable thermal expansion coefficient and high stiffness based on dual-material triangle unit. J. Mech. Phys. Solids 2016, 86, 173–191. [Google Scholar] [CrossRef]
- Fronczek, D.M.; Wojewoda, J.; Chulist, R.; Sypien, A.; Korneva, A. Structural properties of Ti/Al clads manufactured by explosive welding and annealing. Mater. Des. 2016, 91, 80–89. [Google Scholar] [CrossRef]
- Fronczek, D.M.; Saksl, K.; Chulist, R.; Michalik, S.; Wojewoda, J.; Sniezek, L.; Wachowski, M.; Torzewski, J.; Sulikova, M.; Kušnírová, K.; et al. Residual stresses distribution, correlated with bending tests, within explosively welded Ti gr. 2/A1050 bimetals. Mater. Charact. 2018, 144, 461–468. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Yu, M.; Jiang, Z.H.; Li, Z.; Song, X.G. Interfacial microstructure and mechanical properties of Al/Ti dissimilar joints fabricated via friction stir welding. J. Alloys Compd. 2019, 789, 139–149. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, R. Research on interfacial layer of laser welded aluminum to titanium. Mater. Charact. 2019, 154, 264–268. [Google Scholar] [CrossRef]
- Lazurenko, D.V.; Bataev, I.A.; Mall, V.I.; Bataev, A.A.; Maliutina, N.I. Explosively welded multilayer Ti-Al composites: Structure and transformation during heat treatment. Mater. Des. 2016, 102, 122–130. [Google Scholar] [CrossRef]
- Salikhyanov, D.; Michurov, N. Joining of dissimilar aluminum alloys AA5154 and AA2024 by cold roll bonding. Int. J. Adv. Manuf. Tech. 2023, 129, 255–277. [Google Scholar] [CrossRef]
- Ren, Z.K.; Gao, X.Y.; Hou, J.X.; Huang, Z.; Wang, T.; Huang, Q.; Liu, X. Achieving excellent strength-elongation synergy in corrugated Cu/Al laminated composites by flat finish roll bonding. J. Alloys Compd. 2024, 982, 173782. [Google Scholar] [CrossRef]
- Liu, S.C.; Li, F.Y.; Peng, J.S.; Ma, S.J.; Dong, X.H.; Zhang, X.P. Universal model describing the negative thermal expansion coefficients of bending-type two-dimensional metamaterials with chiral/anti-chiral structures. Compos. Commun. 2023, 39, 101559. [Google Scholar] [CrossRef]
- Gajanan, P.C.; Viola, A. Cold roll bonding of multi-layered bi-metal laminate composites. Compos. Sci. Technol. 2009, 69, 1667–1675. [Google Scholar] [CrossRef]
- Cabras, L.; Brun, M.; Misseroni, D. Micro-structured medium with large isotropic negative thermal expansion. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 2232. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.L.; Bargmann, S. Tunable auxeticity and isotropic negative thermal expansion in three-dimensional lattice structures of cubic symmetry. Extrem. Mech. Lett. 2021, 43, 101201. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.X. Anisotropic thermal expansion based on a novel metamaterial. Int. J. Mech. Sci. 2024, 268, 109024. [Google Scholar] [CrossRef]
- Tian, J.Y.; Yang, J.Y.; Zhao, Y. Metamaterial with synergistically controllable Poisson’s ratio and thermal expansion coefficient. Int. J. Mech. Sci. 2023, 23, 108488. [Google Scholar] [CrossRef]
- Klein, J.T.; Karpov, E.G. Bistability in thermomechanical metamaterials structured as three-dimensional composite tetrahedra. Extrem. Mech. Lett. 2019, 29, 100459. [Google Scholar] [CrossRef]
- ASTM D1876-08; Standard Test Method for Peel Resistance of Adhesives (T-Peel Test). American Society of Testing Materials: West Conshohocken, PA, USA, 2023.
- Lee, K.S.; Bae, S.J.; Lee, H.W.; Kang, S.H. Interface-correlated bonding properties for a roll-bonded Ti/Al 2-ply sheet. Mater. Charact. 2017, 134, 163–171. [Google Scholar] [CrossRef]








| Material | H | C | O | Fe | Ti | Cr | Mn | Si | Cu | Mg | Zn | Al |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TA1 | 0.014 | 0.08 | 0.15 | 0.03 | Bal. | - | - | - | - | - | - | - |
| 7075 | - | - | - | 0.5 | 0.2 | 0.23 | 0.3 | 0.4 | 1.6 | 2.5 | 5.6 | Bal. |
| Reduction ratio, % | |||
|---|---|---|---|
| 40 | 45 | 50 | |
| Simulated | 0.61 | 0.59 | 0.56 |
| Experimental | 0.62 | 0.58 | 0.55 |
| Data source: | ||||||
|---|---|---|---|---|---|---|
| Temperature, °C | b = 6 mm | b = 8 mm | b = 10 mm | |||
| X | Y | X | Y | X | Y | |
| 60 | −0.0009 | −0.0009 | −0.0013 | −0.0013 | −0.002 | −0.0020 |
| 80 | −0.0015 | −0.0016 | −0.0023 | −0.0023 | −0.0029 | −0.0029 |
| 100 | −0.0020 | −0.0020 | −0.0034 | −0.0033 | −0.0039 | −0.0039 |
| 120 | −0.0027 | −0.0027 | −0.0039 | −0.0040 | −0.0049 | −0.0049 |
| 140 | −0.0034 | −0.0034 | −0.0051 | −0.0049 | −0.0062 | −0.0061 |
| 160 | −0.0038 | −0.0038 | −0.0061 | −0.0060 | −0.0074 | −0.0074 |
| 180 | −0.0043 | −0.0043 | −0.0070 | −0.0068 | −0.0086 | −0.0083 |
| 200 | −0.0052 | −0.0052 | −0.0079 | −0.0075 | −0.0097 | −0.0096 |
| t-Test: two samples assuming unequal variance | ||||||
| Variable 1 | Variable 2 | Variable 1 | Variable 2 | Variable 1 | Variable 2 | |
| Mean | −0.00267 | −0.00269 | −0.0041 | −0.0040 | −0.0051 | −0.0050 |
| Variance | 2.88 × 10−6 | 2.91 × 10−6 | 7.1 × 10−6 | 6.53 × 10−6 | 1.04 × 10−6 | 9.89 × 10−6 |
| Observations | 9 | 9 | 9 | 9 | 9 | 9 |
| Pooled Variance | 0 | 0 | 0 | |||
| df | 16 | 16 | 16 | |||
| t Stat | 0.02974 | −0.0929 | −0.0429 | |||
| P(T ≤t) one-tail | 0.48831 | 0.46353 | 0.48313 | |||
| t Critical one-tail | 1.74588 | 1.74588 | 1.74588 | |||
| P(T ≤t) two-tail | 0.97663 | 0.92707 | 0.96627 | |||
| t Critical one-tail | 2.11990 | 2.11990 | 2.11990 | |||
| Cycle | SR for X Direction | SR for X Direction | IR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| b, mm | b, mm | b, mm | |||||||
| 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | |
| 1 | - | - | - | - | - | - | 0.997 | 0.999 | 0.986 |
| 20 | 0.0284 | 0.0128 | 0.0282 | 0.0156 | 0.0154 | 0.0029 | 0.991 | 0.998 | 0.999 |
| 40 | 0.0178 | 0.0167 | 0.0136 | 0.0254 | 0.0154 | 0.0150 | 0.999 | 1 | 1 |
| 60 | 0.0039 | 0.0065 | 0.0379 | 0.0019 | 0 | 0.0010 | 1 | 0.997 | 0.994 |
| 80 | 0.0318 | 0.0102 | 0.0214 | 0.0156 | 0.0050 | 0.0150 | 0.989 | 0.993 | 0.996 |
| 100 | 0.0178 | 0.0154 | 0.0409 | 0.0078 | 0.0230 | 0.0051 | 0.984 | 0.996 | 0.996 |
| 120 | 0.0208 | 0.0133 | 0.0442 | 0.0019 | 0.0152 | 0.0032 | 0.986 | 0.998 | 0.99 |
| Source | SS | df | MS | F | p-Value | F Crit |
|---|---|---|---|---|---|---|
| SR along X direction | ||||||
| Cycle | 0.00027 | 5 | 5.56 × 10−5 | 0.55873 | 0.72974 | 3.3258 |
| b | 0.00104 | 2 | 0.000521 | 5.23555 | 0.02781 | 4.1028 |
| Error | 0.00099 | 10 | 9.95 × 10−5 | |||
| SR along Y direction | ||||||
| Cycle | 0.00052 | 5 | 0.000105 | 2.3410 | 0.1182 | 3.3258 |
| b | 9.63 × 10−5 | 2 | 4.82 × 10−5 | 1.0744 | 0.3778 | 4.1028 |
| Error | 0.00044 | 10 | 4.48 × 10−5 | |||
| IR | ||||||
| Cycle | 0.00067 | 5 | 0.00011 | 1.2599 | 0.3442 | 2.9961 |
| b | 0.00037 | 2 | 0.00018 | 2.0784 | 0.1678 | 3.8852 |
| Error | 0.00107 | 10 | 8.98 × 10−5 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Liu, S.; Ma, S.; Zhang, X. Optimization of the Thickness Ratio and Roll-Bonding Parameters of Bimetallic Ti/Al Rod for Bending-Dominated Negative Thermal Expansion Metamaterials. Materials 2024, 17, 5738. https://doi.org/10.3390/ma17235738
Li F, Liu S, Ma S, Zhang X. Optimization of the Thickness Ratio and Roll-Bonding Parameters of Bimetallic Ti/Al Rod for Bending-Dominated Negative Thermal Expansion Metamaterials. Materials. 2024; 17(23):5738. https://doi.org/10.3390/ma17235738
Chicago/Turabian StyleLi, Feiyin, Sicong Liu, Shaojie Ma, and Xinping Zhang. 2024. "Optimization of the Thickness Ratio and Roll-Bonding Parameters of Bimetallic Ti/Al Rod for Bending-Dominated Negative Thermal Expansion Metamaterials" Materials 17, no. 23: 5738. https://doi.org/10.3390/ma17235738
APA StyleLi, F., Liu, S., Ma, S., & Zhang, X. (2024). Optimization of the Thickness Ratio and Roll-Bonding Parameters of Bimetallic Ti/Al Rod for Bending-Dominated Negative Thermal Expansion Metamaterials. Materials, 17(23), 5738. https://doi.org/10.3390/ma17235738






