A Multi-Scale Model for Predicting Physically Short Crack and Long Crack Behavior in Metals
Abstract
1. Introduction
2. Model Derivation
3. Model Validation and Discussion
4. Conclusions
- (1)
- The proposed multi-scale model avoids the curve fittings of different stress ratios in the PSC and LC stages, exhibiting predictive capabilities comparable to the fitting curves.
- (2)
- In the multi-scale model, parameter C is predominantly influenced by the transition crack growth rate Vt, and m is independent of stress ratio R, and related to the Burgers vector, elasticity modulus, and threshold SIF range.
- (3)
- By integrating the theory of normal distribution with Equation (9), a probabilistic model with 96% reliability for assessing the FCG rate was developed, which reflects the inevitability of fatigue scatter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Burgers vector |
| ν | Poisson’s ratio |
| h | Slip band width |
| l | Transition length between PSC and LC |
| a | Crack length |
| a0 | Notch depth |
| ρ | Notch root radius |
| β | Nondimensional parameter |
| μβ | Mean value of β |
| γβ | Standard deviation of β |
| σa | Stress amplitude |
| σmax | Maximum stress |
| σeR | Plain fatigue limit at stress ratio R |
| Y | Geometry factor |
| R | Stress ratio |
| E | Elasticity modulus |
| D | Grain size |
| Δσ | Stress range |
| ΔK | Stress intensity factor range |
| ∆KT | Stress intensity factor range for physically short crack to long crack |
| ∆Kth,sc | Fatigue threshold stress intensity factor range for short crack |
| ∆KTth,sc | Fatigue threshold stress intensity factor range for physically short crack to long crack |
Abbreviations
| MSC | Microstructurally short crack |
| PSC | Physically short crack |
| SC | Short crack |
| LC | Long crack |
| FCG | Fatigue crack growth |
| LEFM | Linear elastic fracture mechanics |
| SIF | Stress intensity factor |
| AX | Axial loading |
| SENT | Single edge notch tension |
References
- Salvati, E. Evaluating fatigue onset in metallic materials: Problem, current focus and future perspectives. Int. J. Fatigue 2024, 188, 108487. [Google Scholar] [CrossRef]
- Wanhill, R.J.H.; Stanzl-Tschegg, S.E. Short/small fatigue crack growth, thresholds and environmental effects: A tale of two engineering paradigms. Corros. Rev. 2021, 39, 165–175. [Google Scholar] [CrossRef]
- Hou, J.; Tang, K.; Wu, H. Short review on multiscale short fatigue crack growth model. Mater. Des. Process. Commun. 2019, 2, e93. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhan, M.; Fu, M. Microstructural and geometrical size effects on the fatigue of metallic materials. Int. J. Mech. Sci. 2022, 218, 107058. [Google Scholar] [CrossRef]
- Wang, T.; Bin, J.; Renaud, G.; Liao, M. Probabilistic method for fatigue crack growth prediction with hybrid prior. Int. J. Fatigue 2022, 157, 106686. [Google Scholar] [CrossRef]
- Zerbst, U.; Vormwald, M.; Pippan, R.; Gänser, H.-P.; Sarrazin-Baudoux, C.; Madia, M. About the fatigue crack propagation threshold of metals as a design criterion—A review. Eng. Fract. Mech. 2016, 153, 190–243. [Google Scholar] [CrossRef]
- Natkowski, E.; Durmaz, A.R.; Sonnweber-Ribic, P.; Münstermann, S. Fatigue lifetime prediction with a validated micromechanical short crack model for the ferritic steel EN 1.4003. Int. J. Fatigue 2021, 152, 106418. [Google Scholar] [CrossRef]
- Nishikawa, H.; Furuya, Y.; Kasuya, T.; Enoki, M. Microstructurally small fatigue crack initiation behavior of fine and coarse grain simulated heat-affected zone microstructures in low carbon steel. Mater. Sci. Eng. A 2021, 832, 142363. [Google Scholar] [CrossRef]
- Mao, J.; Xu, Y.; Hu, D.; Liu, X.; Pan, J.; Sun, H.; Wang, R. Microstructurally short crack growth simulation combining crystal plasticity with extended finite element method. Eng. Fract. Mech. 2022, 275, 108786. [Google Scholar] [CrossRef]
- Wilson, D.; Zheng, Z.; Dunne, F.P. A microstructure-sensitive driving force for crack growth. J. Mech. Phys. Solids 2018, 121, 147–174. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Chan, K.; Lankford, J. The role of microstructural dissimilitude in fatigue and fracture of small cracks. Acta Met. 1988, 36, 193–206. [Google Scholar] [CrossRef]
- Chapetti, M.D. Fatigue propagation threshold of short cracks under constant amplitude loading. Int. J. Fatigue 2003, 25, 1319–1326. [Google Scholar] [CrossRef]
- Chapetti, M.D. Fracture mechanics for fatigue design of metallic components and small defect assessment. Int. J. Fatigue 2022, 154, 106550. [Google Scholar] [CrossRef]
- Bang, D.; Ince, A. A short and long crack growth model based on 2-parameter driving force and crack growth thresholds. Int. J. Fatigue 2020, 141, 105870. [Google Scholar] [CrossRef]
- Chow, C.; Lu, T. Cyclic J-integral in relation to fatigue crack initiation and propagation. Eng. Fract. Mech. 1991, 39, 1–20. [Google Scholar] [CrossRef]
- Xing, S.; Pei, X.; Mei, J.; Dong, P.; Zhen, C.; Li, X.; Lu, F.; Liu, P. A novel elastic strain energy density approach for fatigue evaluation of welded components. Eng. Fract. Mech. 2023, 293, 109713. [Google Scholar] [CrossRef]
- Antunes, F.; Ferreira, M.; Branco, R.; Prates, P.; Gardin, C.; Sarrazin-Baudoux, C. Fatigue crack growth versus plastic CTOD in the 304L stainless steel. Eng. Fract. Mech. 2019, 214, 487–503. [Google Scholar] [CrossRef]
- Qi, J.; Deng, C.; Liu, Y.; Gong, B.; Wang, D. A short and long crack growth model with mean stress correction based on cyclic resistance curve. Theor. Appl. Fract. Mech. 2023, 124, 103785. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, C.-C.; Zhang, P.-Y.; Zhang, X.-C.; Tu, S.-T.; Wang, R.-Z. Fatigue life prediction of nickel-based GH4169 alloy on the basis of a multi-scale crack propagation approach. Eng. Fract. Mech. 2018, 199, 29–40. [Google Scholar] [CrossRef]
- Tang, K.; Du, Z.; Ferro, P.; Berto, F. Crack initiation and propagation from geometric microdefects: Experiment and transition fatigue behavior. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2323–2336. [Google Scholar] [CrossRef]
- Santus, C.; Taylor, D. Physically short crack propagation in metals during high cycle fatigue. Int. J. Fatigue 2009, 31, 1356–1365. [Google Scholar] [CrossRef]
- Tang, K.; Du, Z.; Wu, B.; Hou, J. Fatigue behavior prediction of metal alloys based on a unified multiscale crack growth model. Eng. Fract. Mech. 2020, 235, 107132. [Google Scholar] [CrossRef]
- Tanaka, K.; Nakai, Y. Prediction of Fatigue Threshold of Notched Components. J. Eng. Mater. Technol. 1984, 106, 192–199. [Google Scholar] [CrossRef]
- Herasymchuk, O. Microstructurally-dependent model for predicting the kinetics of physically small and long fatigue crack growth. Int. J. Fatigue 2015, 81, 148–161. [Google Scholar] [CrossRef]
- Chan, K.S. Variability of large-crack fatigue-crack-growth thresholds in structural alloys. Met. Mater. Trans. A 2004, 35, 3721–3735. [Google Scholar] [CrossRef]
- Fukumura, N.; Li, B.; Koyama, M.; Suzuki, T.; Hamada, S.; Tsuzaki, K.; Noguchi, H. Material property controlling non-propagating fatigue crack length of mechanically and physically short-crack based on Dugdale-model analysis. Theor. Appl. Fract. Mech. 2017, 90, 193–202. [Google Scholar] [CrossRef]
- Li, H.; Zhang, P.; Wang, B.; Zhang, Z. Predictive fatigue crack growth law of high-strength steels. J. Mater. Sci. Technol. 2021, 100, 46–50. [Google Scholar] [CrossRef]
- Zhu, M.-L.; Xuan, F.-Z.; Tu, S.-T. Effect of load ratio on fatigue crack growth in the near-threshold regime: A literature review, and a combined crack closure and driving force approach. Eng. Fract. Mech. 2015, 141, 57–77. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, P.; Wang, B.; Zhang, Z. A practical model for efficient anti-fatigue design and selection of metallic materials: II. Parameter analysis and fatigue strength improvement. J. Mater. Sci. Technol. 2021, 70, 250–267. [Google Scholar] [CrossRef]
- Newman, J.C.; Wu, X.R.; Venneri, S.L.; Li, C.G. Small-Crack Effects in High-Strength Aluminum Alloys. Available online: https://ntrs.nasa.gov/citations/19940029793 (accessed on 29 March 2023).
- Newman, I.; Edwards, P.R. Short Crack Growth Behavior in an Aluminium Alloy an AGARD Cooperative test Program. Available online: https://ntrs.nasa.gov/citations/19890007917 (accessed on 29 March 2023).
- Akiniwa, Y.; Tanaka, K.; Matsui, E. Statistical characteristics of propagation of small fatigue cracks in smooth specimens of aluminium alloy 2024-T3. Mater. Sci. Eng. A 1988, 104, 105–115. [Google Scholar] [CrossRef]
- Chong-Myong, P.; Ji-Ho, S. Crack growth and closure behavior of short fatigue cracks. Eng. Fract. Mech. 1994, 47, 327–343. [Google Scholar] [CrossRef]
- Ding, C.; Hui, Y.; Wu, R. Growth behaviour of small fatigue crack and fatigue-life prediction for high-strength steel 30CrMnSiNi2A. Acta Metall. Sin. 1997, 33, 277–286. Available online: https://www.ams.org.cn/CN/Y1997/V33/I3/277 (accessed on 1 October 2023).
- Edwards, P.R.; Newmann, J.C. Short-Crack Growth Behaviour in Various Aircraft Materials. Available online: https://ntrs.nasa.gov/citations/19910001927 (accessed on 29 March 2023).
- Mann, T. The influence of mean stress on fatigue crack propagation in aluminium alloys. Int. J. Fatigue 2007, 29, 1393–1401. [Google Scholar] [CrossRef]
- Marines-Garcia, I.; Paris, P.C.; Tada, H.; Bathias, C.; Lados, D. Fatigue crack growth from small to large cracks on very high cycle fatigue with fish-eye failures. Eng. Fract. Mech. 2007, 75, 1657–1665. [Google Scholar] [CrossRef]

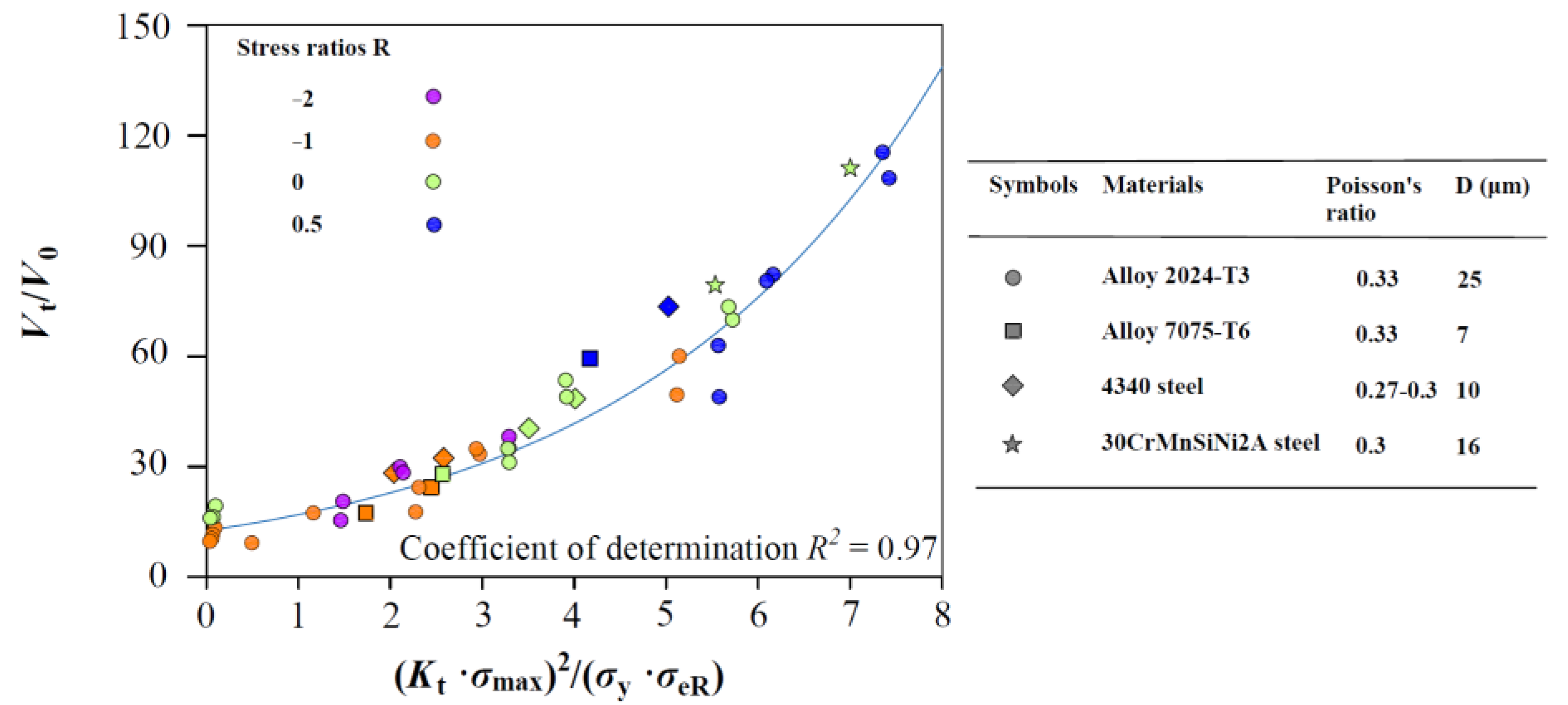
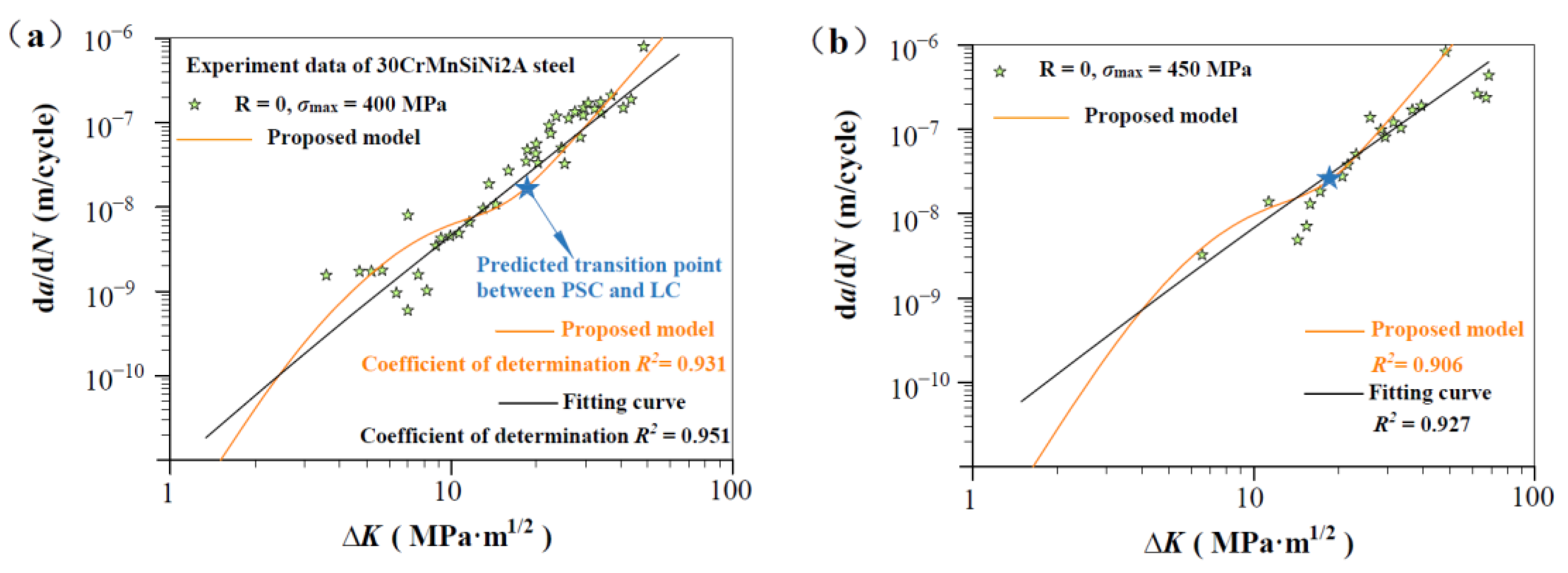

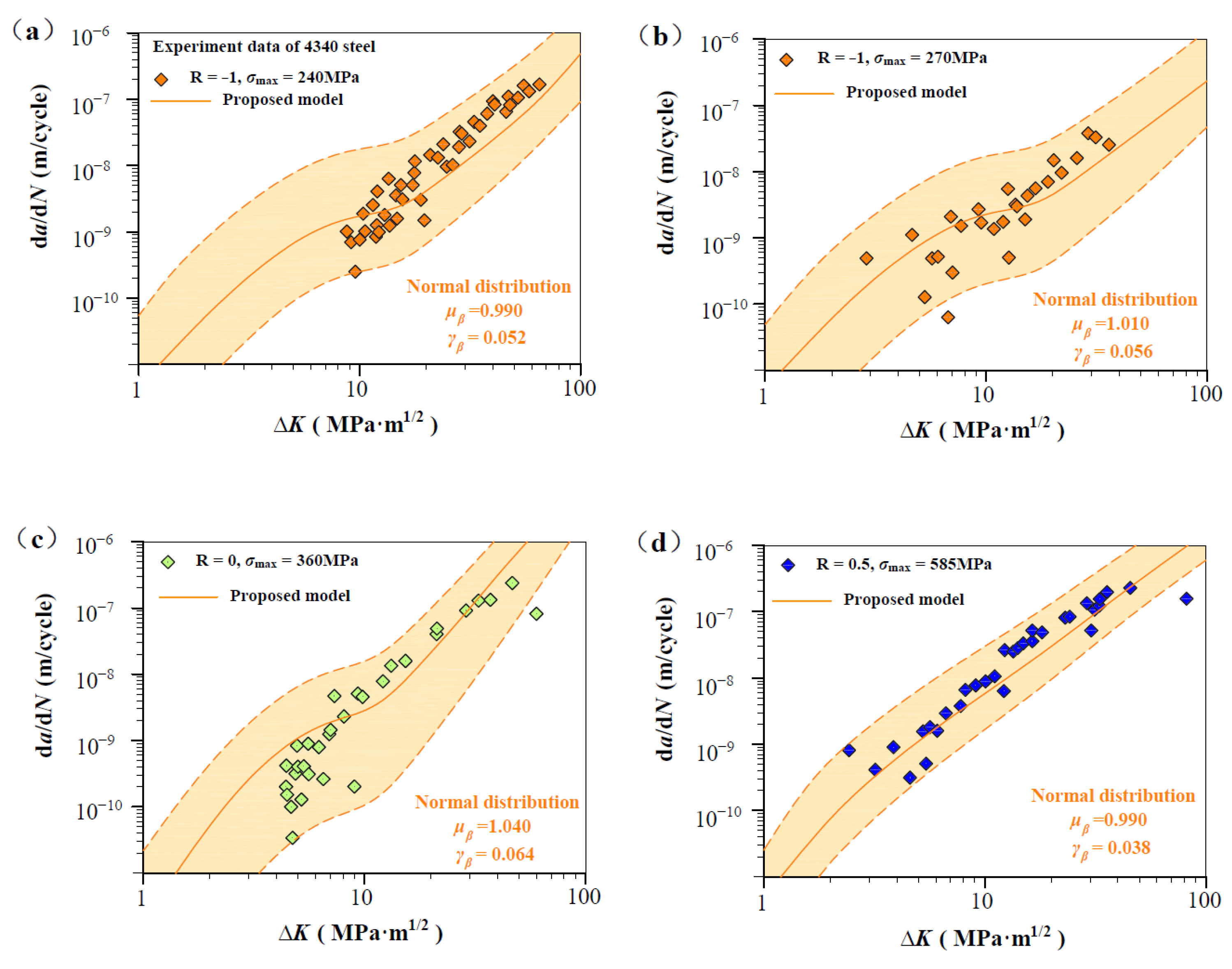
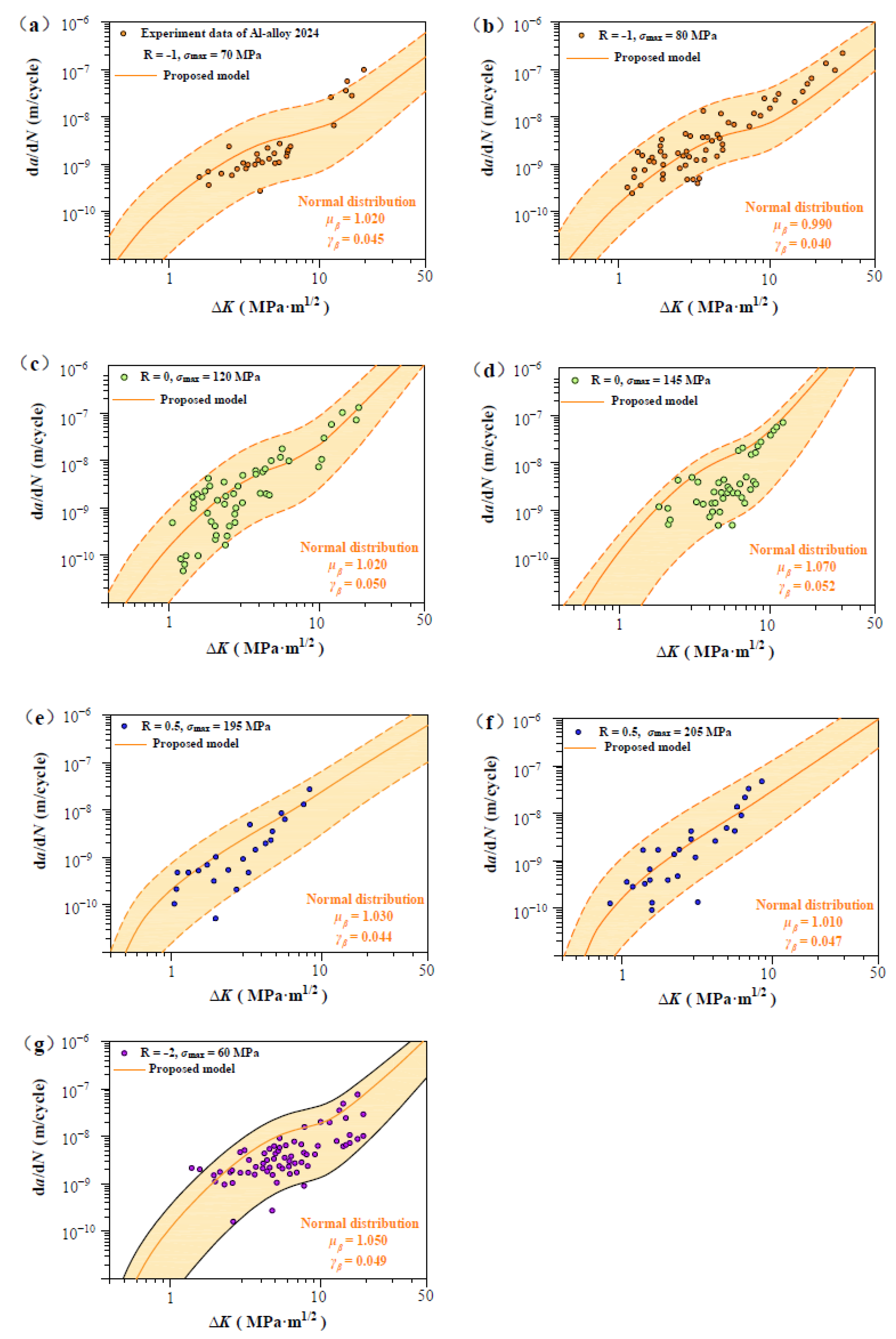
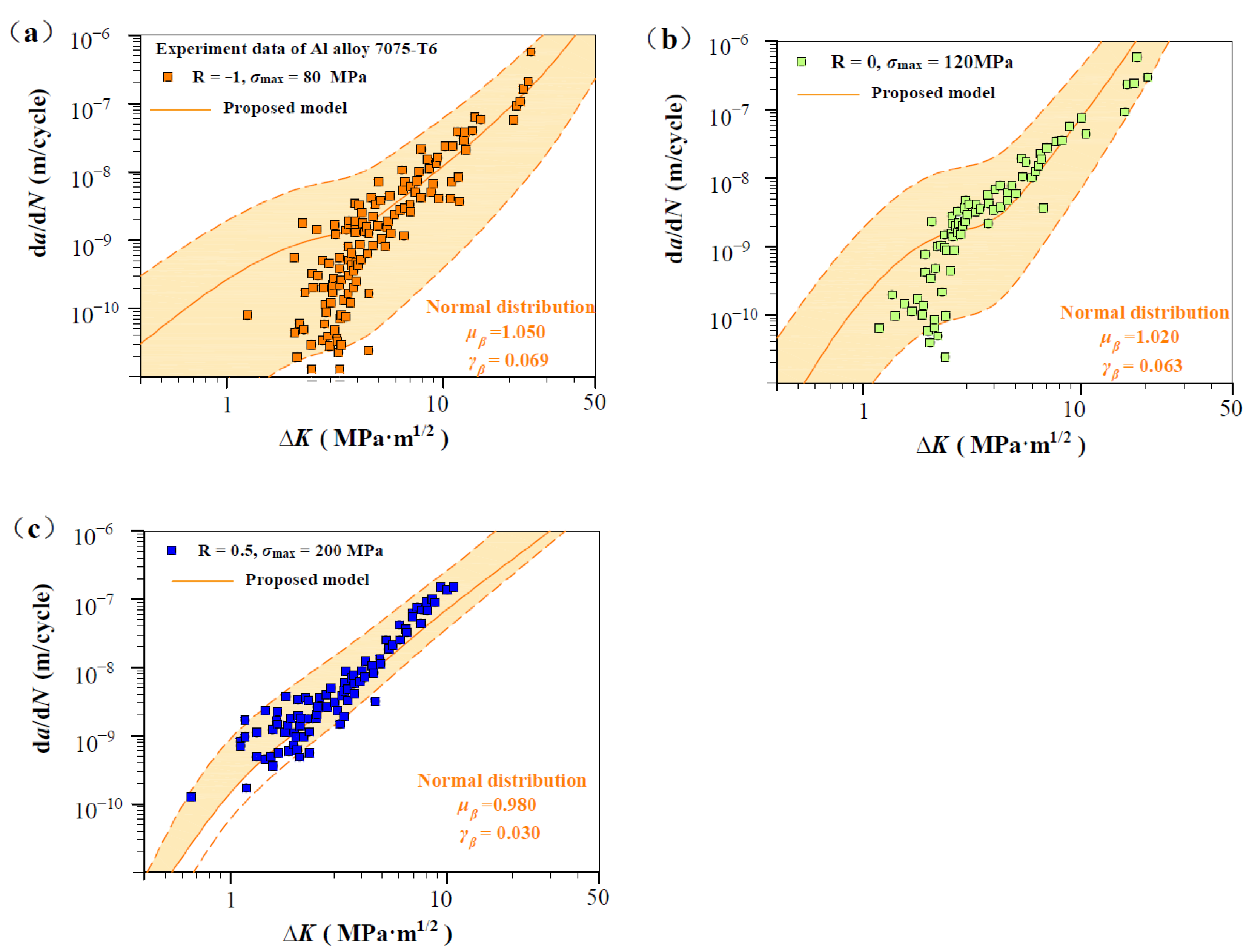
| Materials | Grain Size (μm) | Burgers Vector b (m) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|---|
| Al alloy 2024 [32] | 25 | 2.86 × 10−10 | 0.33 | 355 |
| Al alloy 7075 [31] | 7 | 2.86 × 10−10 | 0.33 | 520 |
| AISI 4340 Steel [36] | 16 | 2.48 × 10−10 | 0.27–0.3 | 1413 |
| 30CrMnSiNi2A steel [35] | 10 | 2.52 × 10−10 | 0.3 | 1189 |
| Materials | R | Load Type | σmax (MPa) | a0 (mm) | ρ (mm) | Kt | σeR (MPa) | Notch Geometry |
|---|---|---|---|---|---|---|---|---|
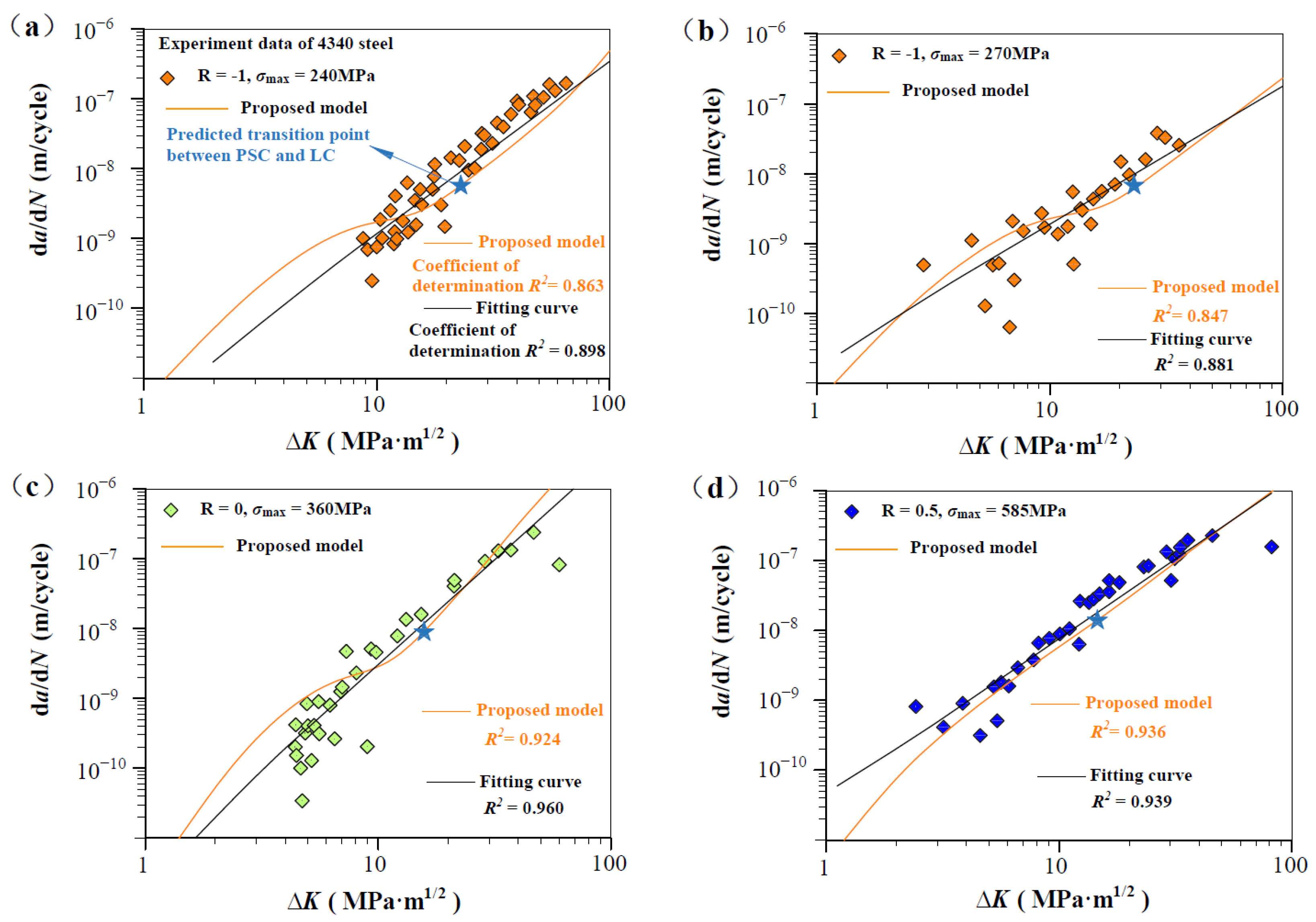
| AISI4340 [36] | −1 | AX | 240 | 3.18 | 3.18 | 3.3 | 218 | SENT |
| 270 | 3.18 | 3.18 | 3.3 | |||||
| 0 | AX | 360 | 3.18 | 3.18 | 3.3 | 285 | ||
| 0.5 | AX | 585 | 3.18 | 3.18 | 3.3 | 526 | ||
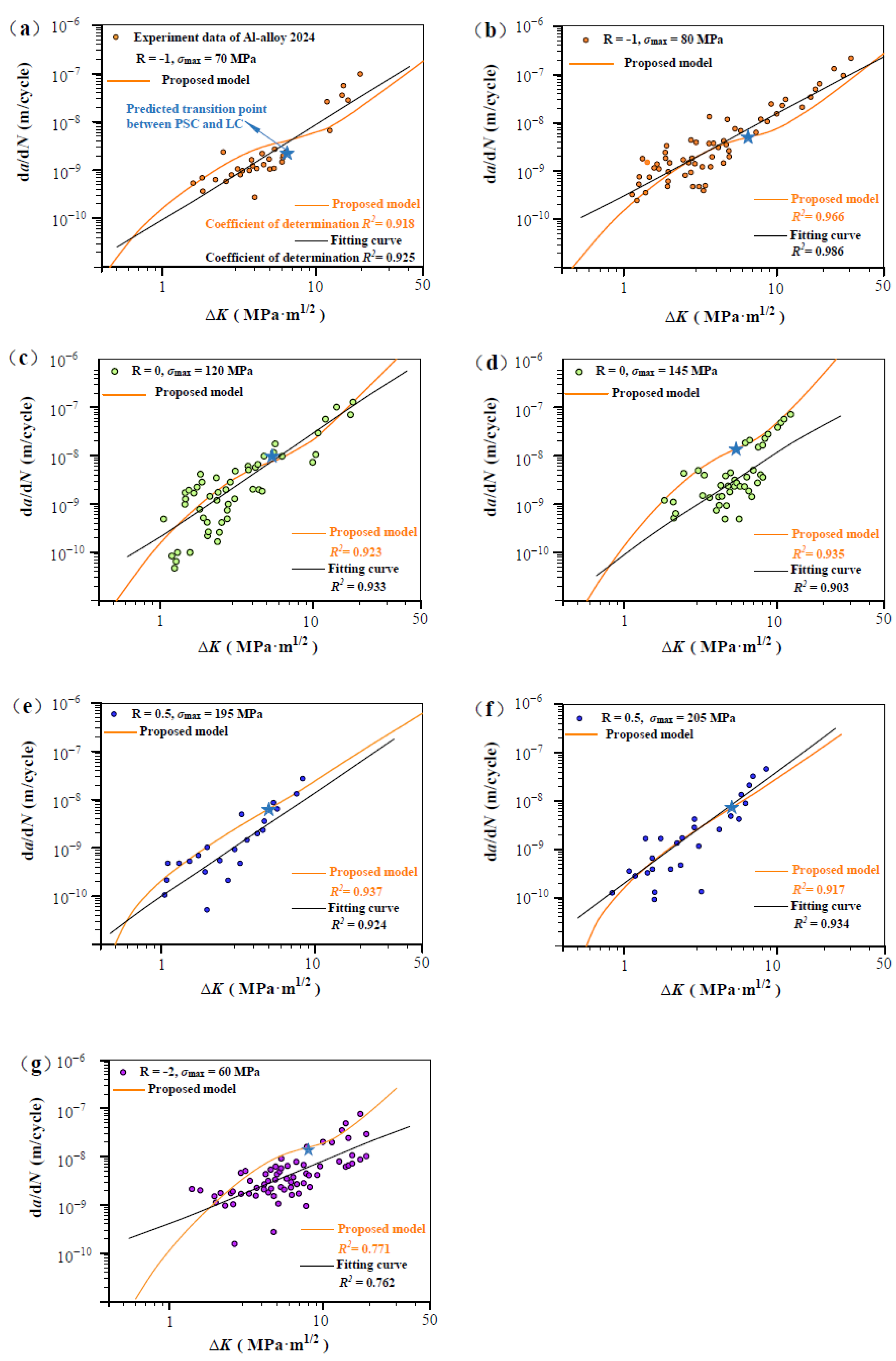
| Al alloy 2024 [32] | −1 | AX | 70 | 3.18 | 3.18 | 3.17 | 62.5 | SENT |
| 80 | 3.18 | 3.18 | 3.17 | |||||
| 0 | AX | 120 | 3.18 | 3.18 | 3.17 | 104 | ||
| 145 | 3.18 | 3.18 | 3.17 | |||||
| 0.5 | AX | 195 | 3.18 | 3.18 | 3.17 | 193 | ||
| 205 | 3.18 | 3.18 | 3.17 | |||||
| −2 | AX | 60 | 3.18 | 3.18 | 3.17 | 48.4 | ||
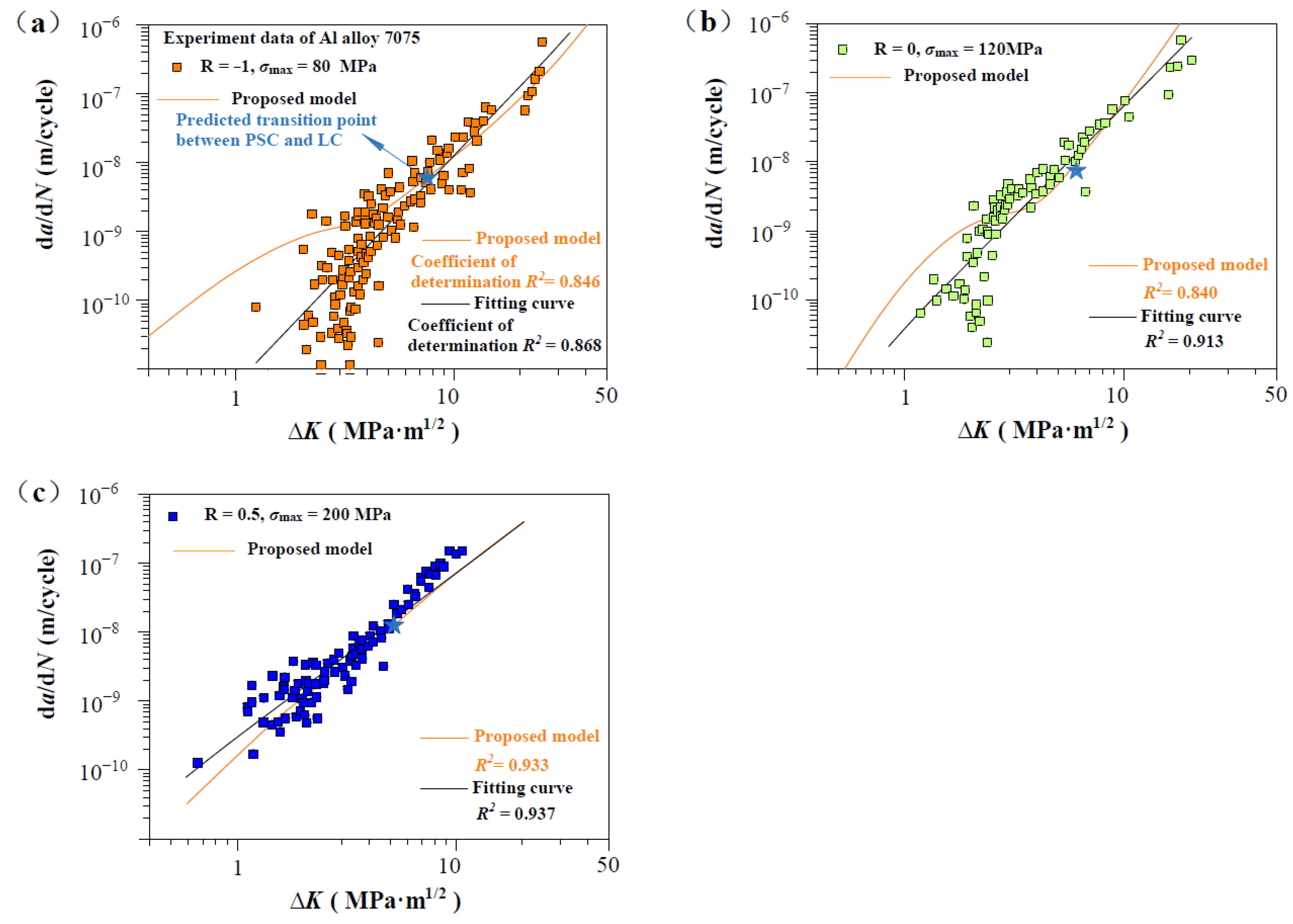
| Al alloy 7075 [31] | −1 | AX | 80 | 3.2 | 3.2 | 3.15 | 70.4 | SENT |
| 0 | AX | 120 | 3.2 | 3.2 | 3.15 | 107 | ||
| 0.5 | AX | 200 | 3.2 | 3.2 | 3.15 | 183 | ||
| 30CrMnSiNi2A steel [35] | 0 | AX | 400 | 3.2 | 3.2 | 3.3 | 265 | SENT |
| 450 | 3.2 | 3.2 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, C.; Wu, P.; Xu, A.; Ju, P.; Yang, D.; Dong, Z. A Multi-Scale Model for Predicting Physically Short Crack and Long Crack Behavior in Metals. Materials 2024, 17, 5163. https://doi.org/10.3390/ma17215163
Yang X, Zhang C, Wu P, Xu A, Ju P, Yang D, Dong Z. A Multi-Scale Model for Predicting Physically Short Crack and Long Crack Behavior in Metals. Materials. 2024; 17(21):5163. https://doi.org/10.3390/ma17215163
Chicago/Turabian StyleYang, Xing, Chunguo Zhang, Panpan Wu, Anye Xu, Pengfei Ju, Dandan Yang, and Zhonghong Dong. 2024. "A Multi-Scale Model for Predicting Physically Short Crack and Long Crack Behavior in Metals" Materials 17, no. 21: 5163. https://doi.org/10.3390/ma17215163
APA StyleYang, X., Zhang, C., Wu, P., Xu, A., Ju, P., Yang, D., & Dong, Z. (2024). A Multi-Scale Model for Predicting Physically Short Crack and Long Crack Behavior in Metals. Materials, 17(21), 5163. https://doi.org/10.3390/ma17215163






