Damage Evolution Mechanism of Railway Wagon Bogie Adapter 1035 Steel and Damage Parameter Calibration Based on Gursone–Tvergaarde–Needleman Model
Abstract
1. Introduction
2. Experimental Methods
2.1. Materials
2.2. Experimental Study
3. Results and Discussion
3.1. Introduction to GTN Model
3.2. Material Parameters in the GTN Model
3.3. Establishment of Finite Element Model
3.4. Calibration of , and
3.5. Calibration of and
3.6. Calibration of and
3.7. Damage Evolution Analysis
3.8. Establishment of Response Surface Method
3.8.1. Response Surface Model Fitting and Significance Analysis Test
3.8.2. Response Surface Analysis
3.9. Finite Element Simulation Analysis
4. Conclusions
- (1)
- The method of fitting the stress–strain curve of AISI 1035 steel with the Ramberg–Osgood hardening model is used to calibrate = 1.78, = 0.833, = 3.17 in the GTN model. The inflection point of the curve slope obtained by the finite element method and experimental method is used to determine = 0.144, and the deviation parameter is 0.1. The GTN model parameters which can characterize the damage of AISI 1035 steel were determined by combining the macroscopic mechanical properties with the microscopic morphology. By comparing the damage parameters obtained by the two methods, it is proved that the fracture parameters obtained can better simulate the fracture of materials, and the GTN fracture model exhibits strong applicability to the fracture of AISI 1035 steel. The error of the damage parameters obtained by the two methods is less than 10%, confirming the GTN damage model’s effectiveness in predicting the evolution of damage behavior in AISI 1035 steel.
- (2)
- By observing the fracture morphology of AISI 1035 steel, it is found that the size and depth of the dimples of the sample at 1100 °C are larger and deeper, which reveals that AISI 1035 steel has good plastic deformation ability and shows typical ductile fracture characteristics.
- (3)
- By studying the effects of different damage parameters on fractures, it is found that the effect of on fractures is relatively small, while the effects of , and on fractures are larger. The larger is, the earlier the fracture point is; conversely, the larger and are, the later the fracture occurs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Li, Y.; Cheng, Z.; Li, F.; Li, J.; Ghafoor, S. Sustainability assessment of incremental sheet forming: A review. Int. J. Adv. Manuf. Technol. 2022, 119, 1385–1405. [Google Scholar] [CrossRef]
- Kumar, G.; Maji, K. Forming limit analysis of friction stir tailor welded AA5083 and AA7075 sheets in single point incremental forming. Int. J. Mater. Form. 2022, 15, 20. [Google Scholar] [CrossRef]
- Wu, S.; Gao, L.; Matsuoka, Y.; Rashed, S.; Zhao, Y.; Ma, N. Multi-step toolpath approach of improving the dimensional accuracy of a non-axisymmetric part in incremental sheet forming and its mechanism analysis. J. Mech. Sci. Technol. 2022, 36, 1975–1985. [Google Scholar] [CrossRef]
- Li, G.; Cui, S. Meso-mechanics and damage evolution of AA5182-O aluminum alloy sheet Based on the GTN model. Eng. Fract. Mech. 2020, 235, 107162. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, W.; Han, K.; Liu, X.; Zhu, Y.; Xing, R.; Hou, C. Microscopic damage in eutectic SnPb alloy: First-principles calculations and experiments. Eng. Fail. Anal. 2024, 164, 108638. [Google Scholar] [CrossRef]
- Pei, C.; Zeng, W.; Yuan, H. A damage evolution model based on micro-structural characteristics for an additive manufactured superalloy under monotonic and cyclic loading conditions. Int. J. Fatigue 2020, 131, 105279. [Google Scholar] [CrossRef]
- Jianbing, C.; Yudong, R.; Guangda, L. Damage of quasi-brittle materials from a two-scale perspective: From geometric discontinuity to free energy reduction. Chin. J. Mech. Mech. 2024, 56, 1–11. [Google Scholar]
- Hou, L. Study on High Temperature Failure of Stainless Steel Spring Based on GTN Model; Xi’an University of Technology: Xi’an, China, 2023. [Google Scholar]
- Bergo, S.; Morin, D.; Hopperstad, O.S. Numerical implementation of a non-local GTN model for explicit FE simulation of ductile damage and fracture. Int. J. Solids Struct. 2021, 219, 134–150. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–18. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. An analysis of ductile rupture modes at a crack tip. J. Mech. Phys. Solids 1987, 35, 151–183. [Google Scholar] [CrossRef]
- Chu, C.C.; Needleman, A. Void nucleation effects in biaxially stretched sheets. J. Eng. Mater. Technol. 1980, 102, 249–256. [Google Scholar] [CrossRef]
- Sun, X.; Mo, X.; Liu, Y.; Shen, W.; Li, C.; Li, Y.; Hu, X.; Xue, F. GTN Poroplastic Damage Model Construction and Forming limit prediction of Magnesium Alloy Based on BP-GA Neural Network. Mater. Today Commun. 2024, 41, 110295. [Google Scholar] [CrossRef]
- He, Z.; Zhu, H.; Hu, Y. Anisotropic mechanical behavior prediction of aluminum alloy sheet based on an anisotropic GTN model: Modeling, simulation and experimental investigation. Mech. Adv. Mater. Struct. 2024, 31, 314–331. [Google Scholar] [CrossRef]
- Khademi, M.; Mirnia, M.J.; Naeini, H.M. Numerical analysis of ductile fracture in stretch bending of AA6061-T6 aluminum alloy sheet using GTN damage model. Int. J. Solids Struct. 2024, 301, 112947. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, T.; Luo, Z.; Zheng, E.; Wang, Z.; Jiang, S.; Chen, J. Numerical simulation and defect prediction of forming process for aluminum alloy sheets considering the effect of both anisotropy and lode parameter. Eng. Fract. Mech. 2024, 299, 109940. [Google Scholar] [CrossRef]
- Yin, Y.; Yang, T.; Qin, W.; Lu, Y.; Gu, Y. Calibration of GTN model for fracture analysis of steel plates with holes. J. Constr. Steel Res. 2024, 215, 108506. [Google Scholar] [CrossRef]
- Yoshida, S.; Ogawa, T.; Hayashi, T.; Saito, T.; Hattori, Y.; Sasaki, S. Study on fracture assessment by GTN model for BWR reactor internals based on material properties of simulated irradiated stainless steels. Int. J. Press. Vessel. Pip. 2024, 208, 105147. [Google Scholar] [CrossRef]
- Wu, H. Research on Strong Spinning Damage Model and Ductile Fracture Behavior of Cylindrical Parts; Harbin Institute of Technology: Harbin, China, 2021. [Google Scholar]
- Yan, R.; Xin, H.; Veljkovic, M. Ductile fracture simulation of cold-formed high strength steel using GTN damage model. J. Constr. Steel Res. 2021, 184, 106832. [Google Scholar] [CrossRef]
- Brahim, A.O.; Capozucca, R.; Khatir, S.; Magagnini, E.; Benaissa, B.; Wahab, M.A.; Cuong-Le, T. Artificial neural network and YUKI algorithm for notch depth prediction in X70 steel specimens. Theor. Appl. Fract. Mech. 2024, 129, 104227. [Google Scholar] [CrossRef]
- Yildiz, R.A.; Yilmaz, S. Influence of heat treatments on the formability of the 6061 Al alloy sheets: Experiments and GTN damage model. Int. J. Adv. Manuf. Technol. 2021, 113, 2277–2299. [Google Scholar] [CrossRef]
- Sun, Q.; Lu, Y.; Chen, J. Identification of material parameters of a shear modified GTN damage model by small punch test. Int. J. Fract. 2020, 222, 25–35. [Google Scholar] [CrossRef]
- Li, X.; Xu, M.; Zhang, Z. Hot damage evolution in a high strength aluminum alloy during hot forming: A study using the Gurson–Tvergaard–Needleman model. J. Mater. Res. Technol. 2021, 14, 1366–1376. [Google Scholar] [CrossRef]
- Gao, T.; Ying, L.; Hu, P.; Han, X.; Rong, H.; Wu, Y.; Sun, J. Investigation on mechanical behavior and plastic damage of AA7075 aluminum alloy by thermal small punch test: Experimental trials, numerical analysis. J. Manuf. Process. 2020, 50, 1–16. [Google Scholar] [CrossRef]
- Kiran, R.; Khandelwal, K. Gurson model parameters for ductile fracture simulation in ASTM A992 steels. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 171–183. [Google Scholar] [CrossRef]
- Faleskog, J.; Gao, X.; Shih, C.F. Cell model for nonlinear fracture analysis–I. Micromechanics calibration. Int. J. Fract. 1998, 89, 355–373. [Google Scholar] [CrossRef]
- Yin, Y.; Li, S.; Han, Q.; Li, M. Material parameters in void growth model for G20Mn5QT cast steel at low temperatures. Constr. Build. Mater. 2020, 243, 118123. [Google Scholar] [CrossRef]
- Yin, Y.; Ma, T.; Han, Q.; Lu, Y.; Zhang, Y. Material parameters in the GTN model for ductile fracture simulation of G20Mn5QT cast steels. J. Mater. Civ. Eng. 2022, 34, 04021412. [Google Scholar] [CrossRef]
- Jia, Z. Research and Application of Ductile Fracture Model of Aluminum Alloy Based on Pore Evolution Behavior; University of Science and Technology Beijing: Beijing, China, 2022. [Google Scholar]
- Yin, Q. Atomic Simulation of Pore Damage Evolution Behavior of Nanocrystalline Materials Under Three-Dimensional Stress; Huazhong University of Science and Technology: Wuhan, China, 2023. [Google Scholar]
- Jiang, Y.Q.; Lin, Y.C.; Jiang, X.Y.; He, D.G.; Zhang, X.Y.; Kotkunde, N. Hot tensile properties, microstructure evolution and fracture mechanisms of Ti-6Al-4V alloy with initial coarse equiaxed phases. Mater. Charact. 2020, 163, 110272. [Google Scholar] [CrossRef]
- Lin, Y.C.; Zhu, X.H.; Dong, W.Y.; Yang, H.; Xiao, Y.W.; Kotkunde, N. Effects of deformation parameters and stress triaxiality on the fracture behaviors and microstructural evolution of an Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2020, 832, 154988. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Wang, L.; Yang, Y.; Yao, L.; Wang, X.; Meng, J.; Zhou, Y.; Sun, X. Effect of hot isostatic pressing on stress-rupture crack growth of a single-crystal nickel-based superalloy. J. Mater. Res. Technol. 2024, 32, 59–66. [Google Scholar] [CrossRef]
- Tian, Y. Optimization of the Hot Stamping Forming Process for High Strength Steel Laser Tailored Welding Plate B-pillar Based on Response Surface Methodology; Changchun University of Technology: Changchun, China, 2023. [Google Scholar]
- Ji, H.; Ma, Z.; Huang, X.; Xiao, W.; Wang, B. Damage evolution of 7075 aluminum alloy basing the Gurson Tvergaard Needleman model under high temperature conditions. J. Mater. Res. Technol. 2022, 16, 398–415. [Google Scholar] [CrossRef]
- Sasani, F.; Taheri, A.K.; Bahrami, H.; Pouranvari, M. Plastic Deformation and Fracture of AlMg6/CNT Composite: A Damage Evolution Model Coupled with a Dislocation-Based Deformation Model. J. Mater. Res. Technol. 2024, 31, 187–204. [Google Scholar] [CrossRef]
- Ji, H.; Yao, R.; Huang, X.; Wang, B.; Tang, X.; Liu, Y.; Pei, W. Damage evolution of 6005A aluminum alloy sheet based on Gurson-Tvagaard-Needleman model: Experiment and finite element simulation. J. Mater. Eng. Perform. 2022, 31, 3902–3917. [Google Scholar] [CrossRef]
- Wu, D.; Wang, K.; Liu, B.; Qu, H.; Wang, X.; Liu, G. Damage evolution of titanium alloy laser-welded joint during hot deformation: Experiment and modeling. J. Mater. Res. Technol. 2023, 26, 6375–6388. [Google Scholar] [CrossRef]
- Lee, J.; Bong, H.J.; Ha, J.; Kim, D. Inter-void shearing effect on damage evolution under plane strain deformation in high-strength aluminum alloy sheet. J. Mater. Res. Technol. 2023, 26, 7547–7565. [Google Scholar] [CrossRef]
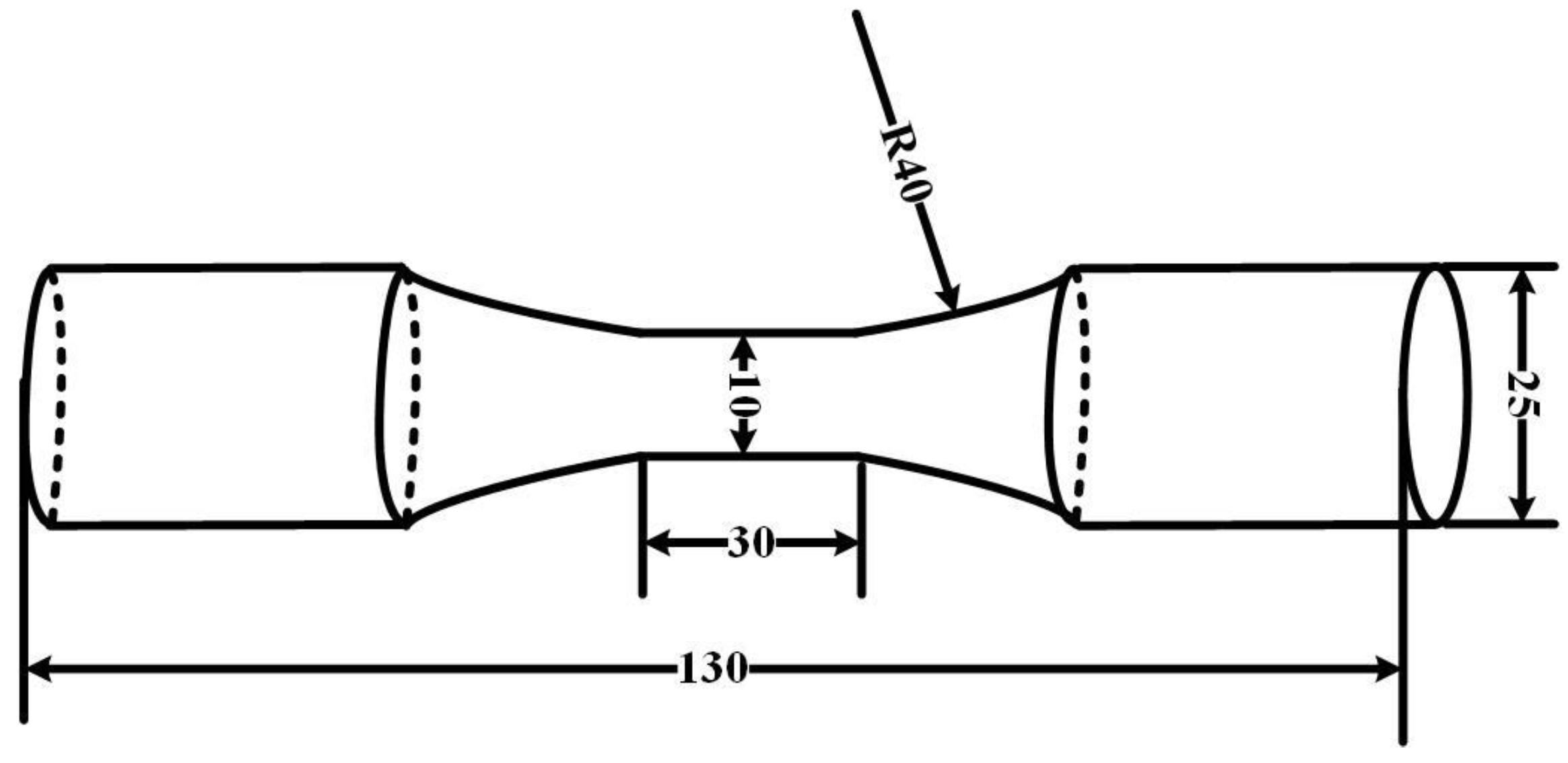
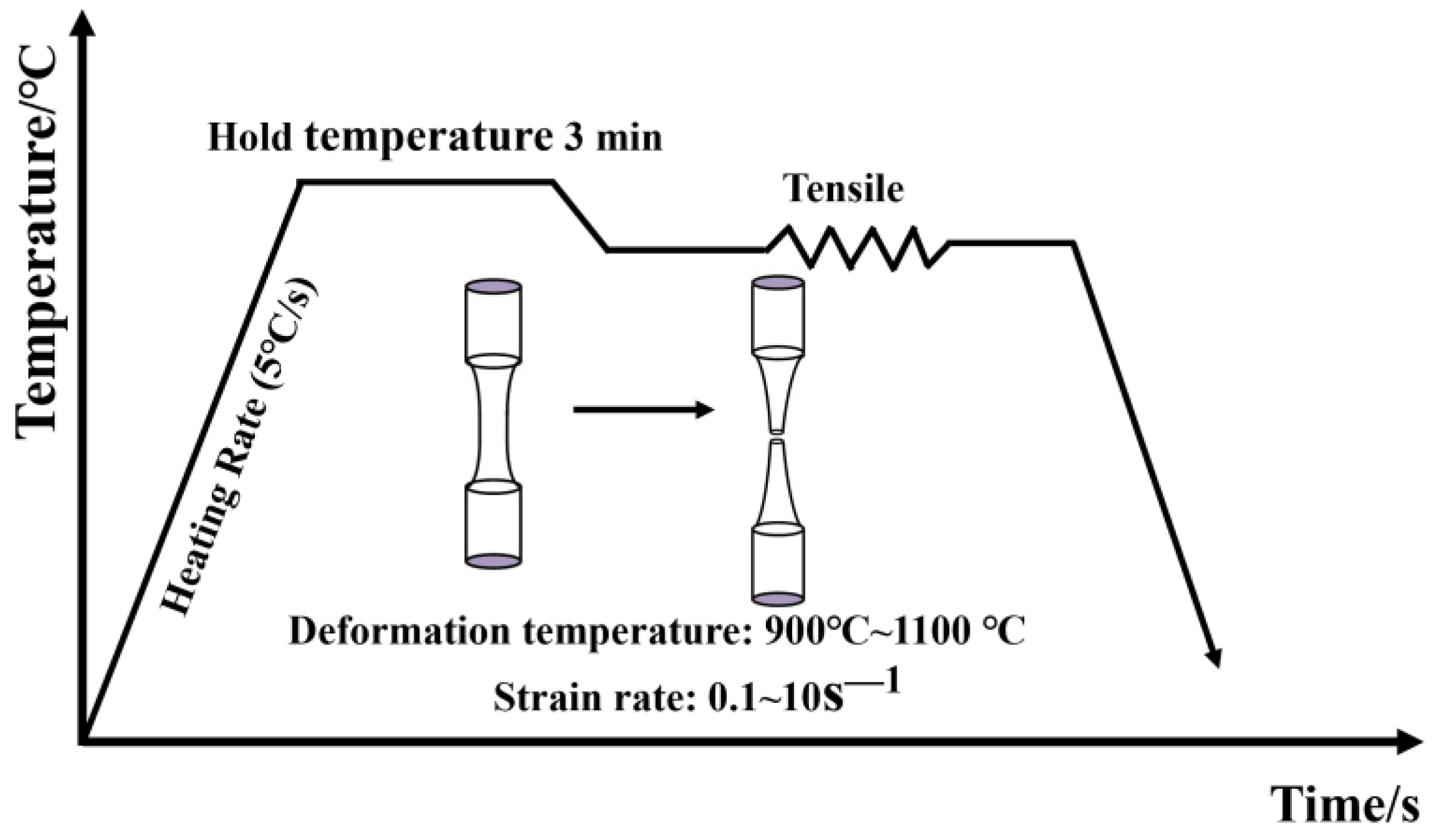
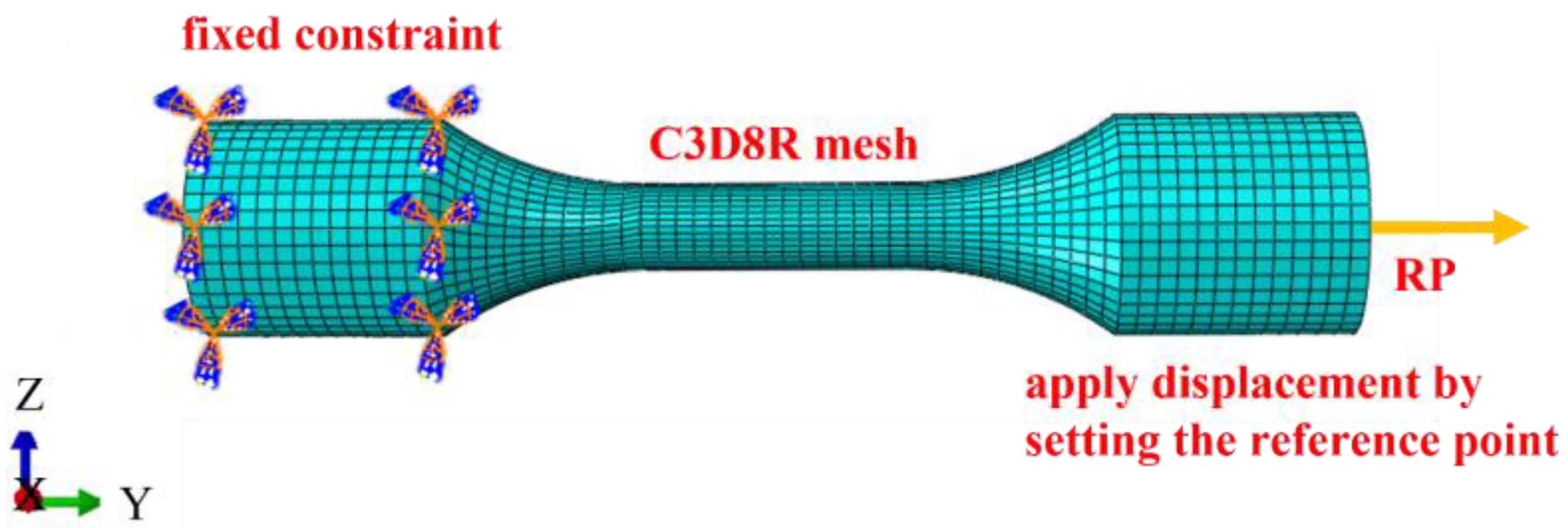

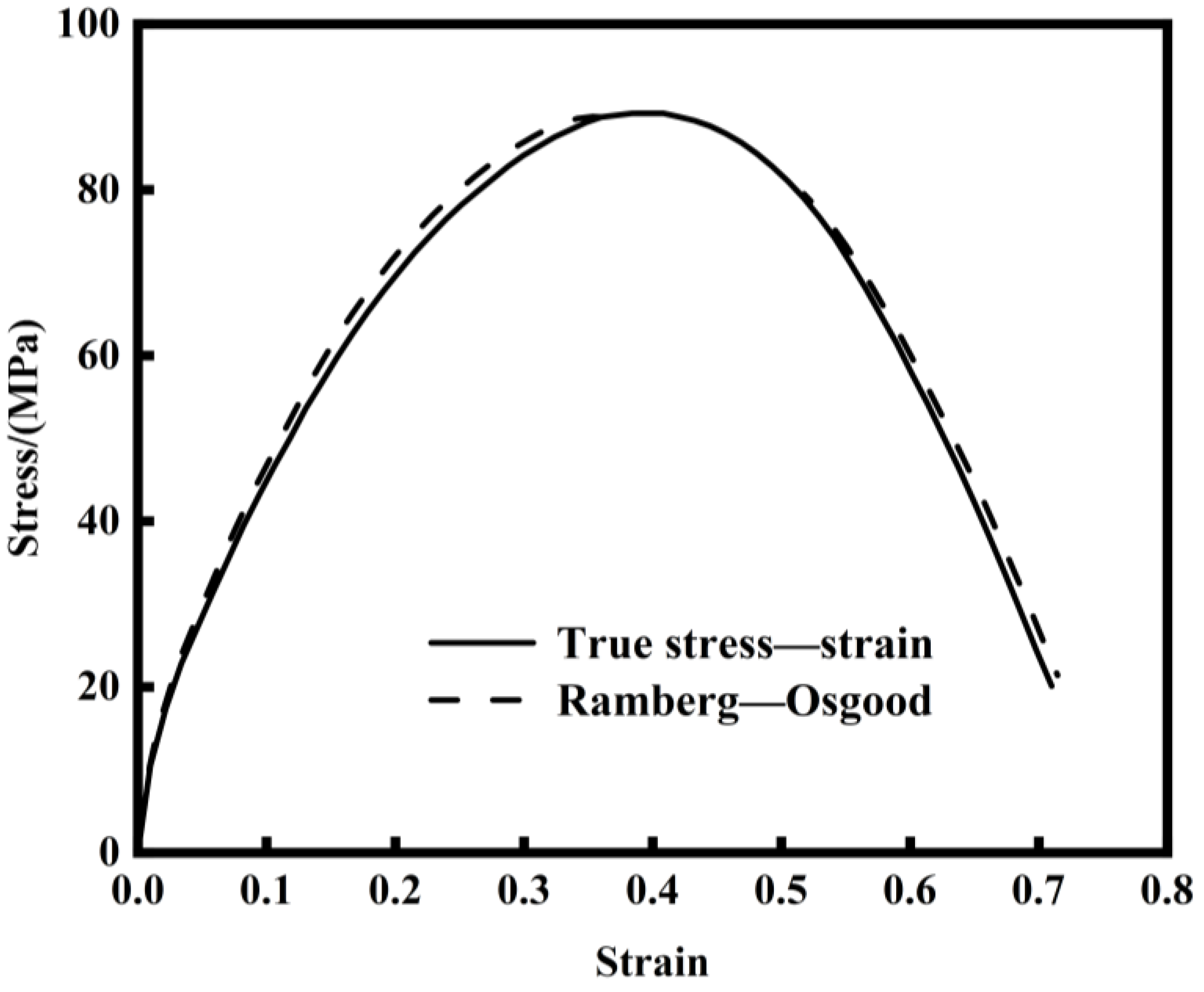



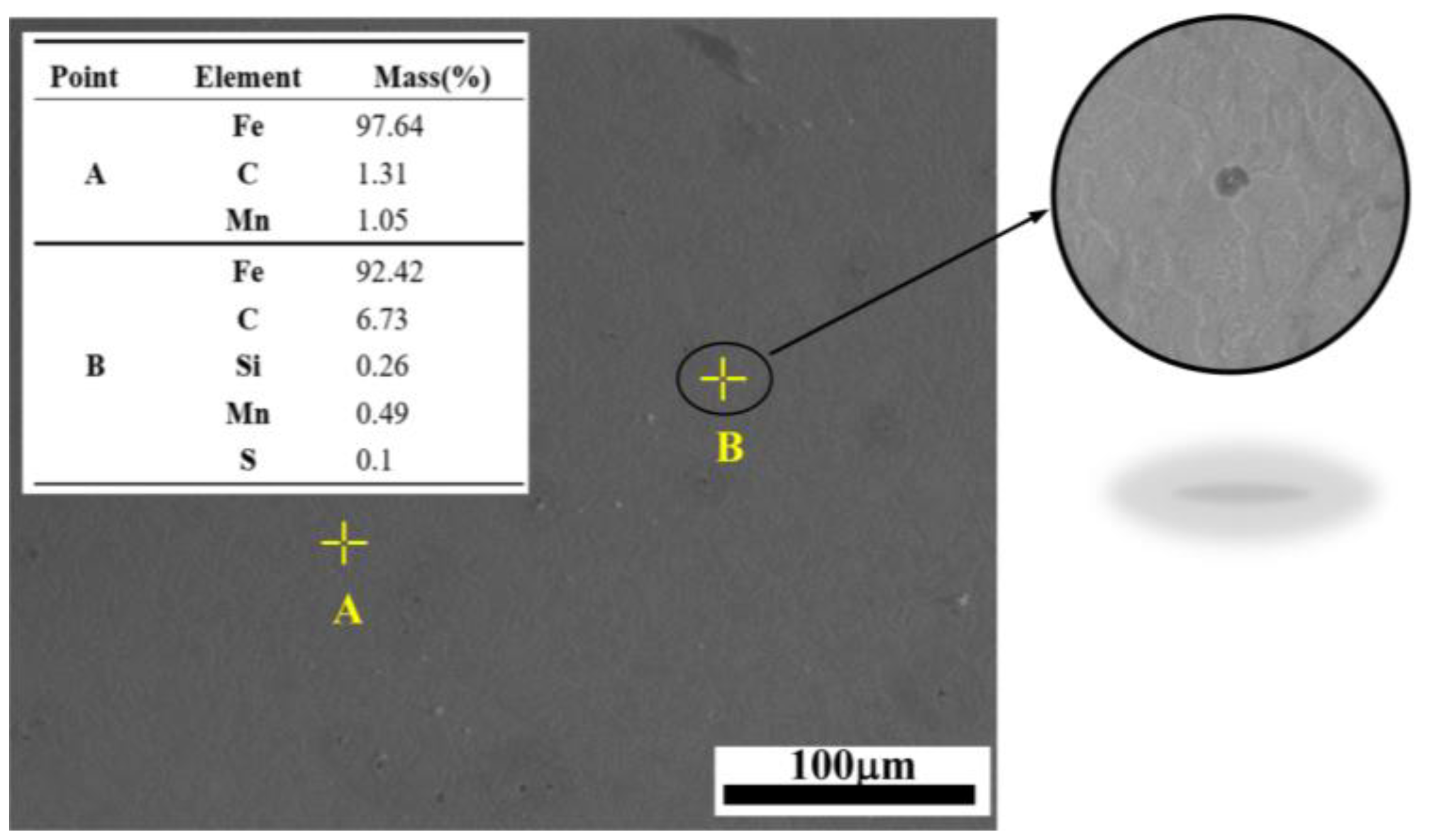





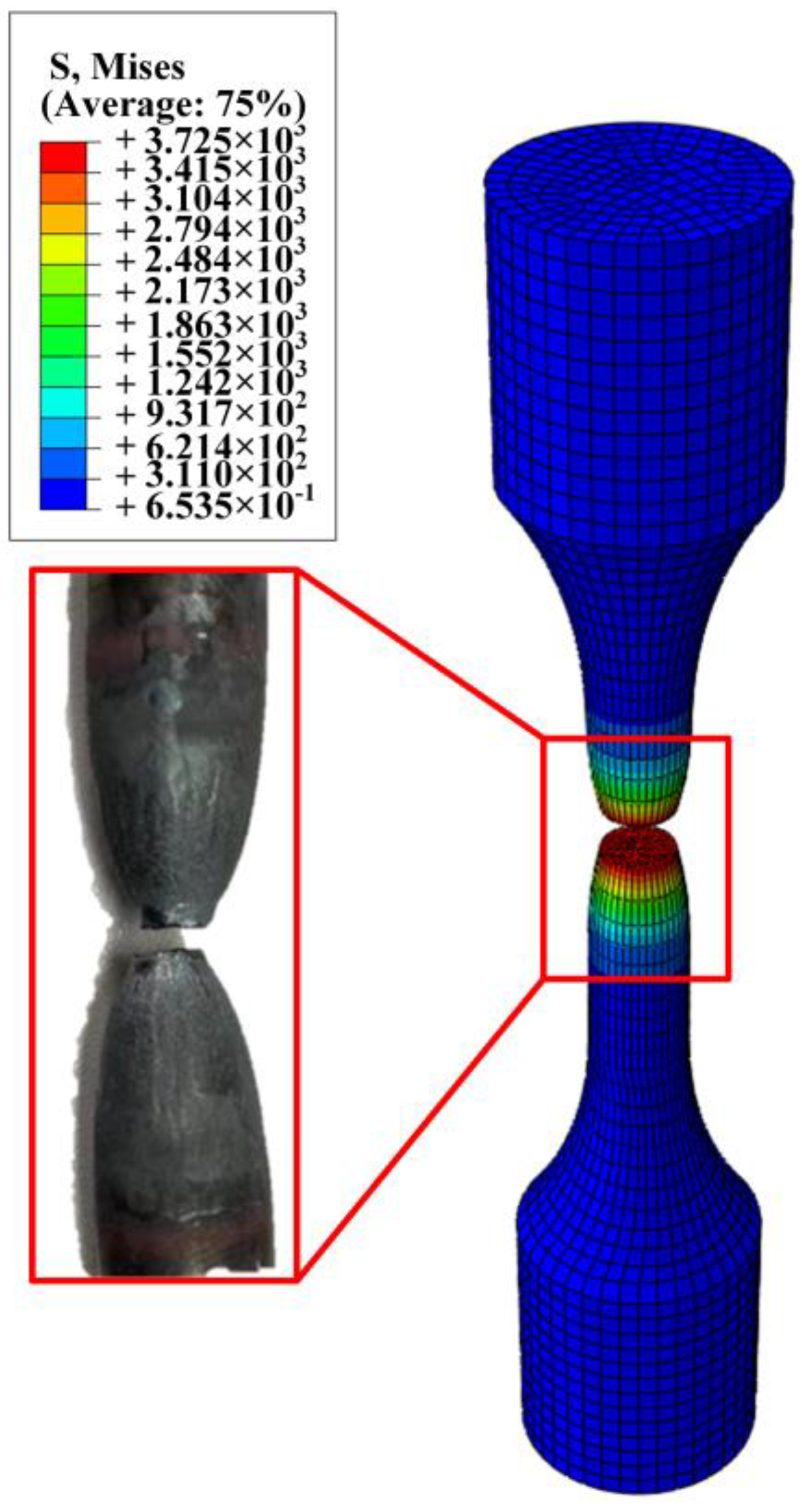
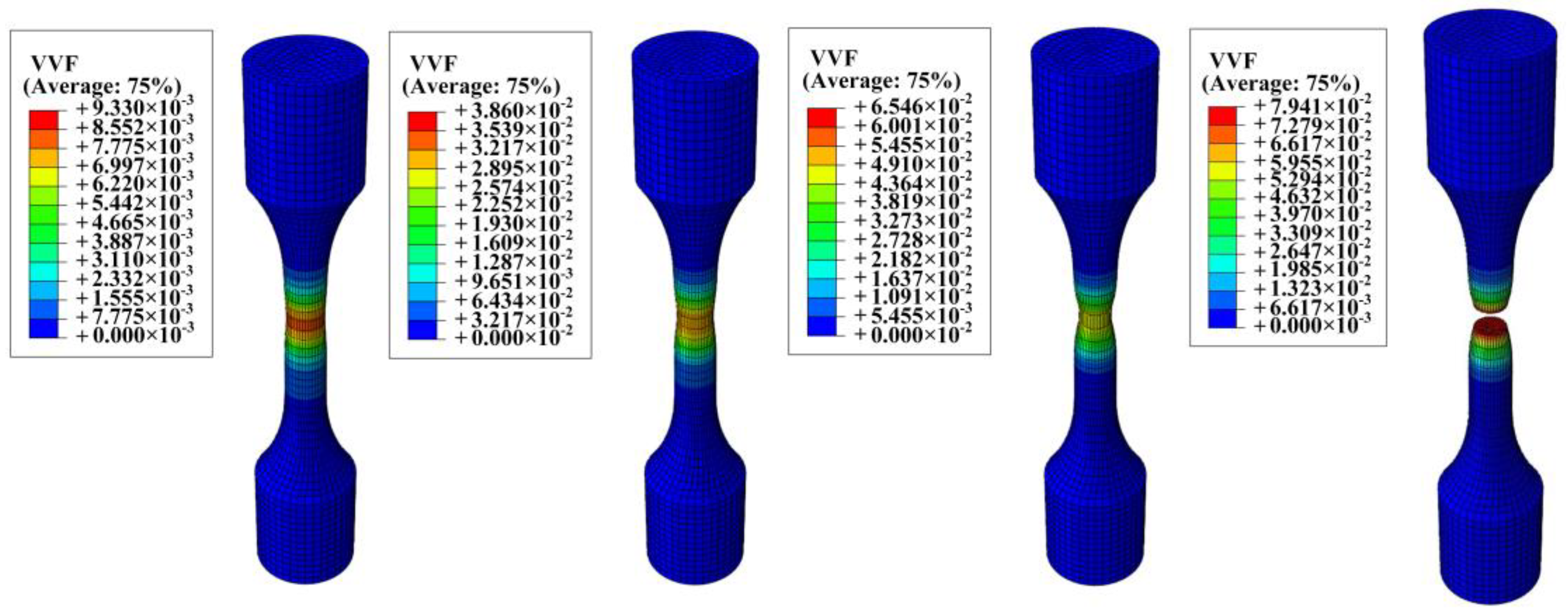
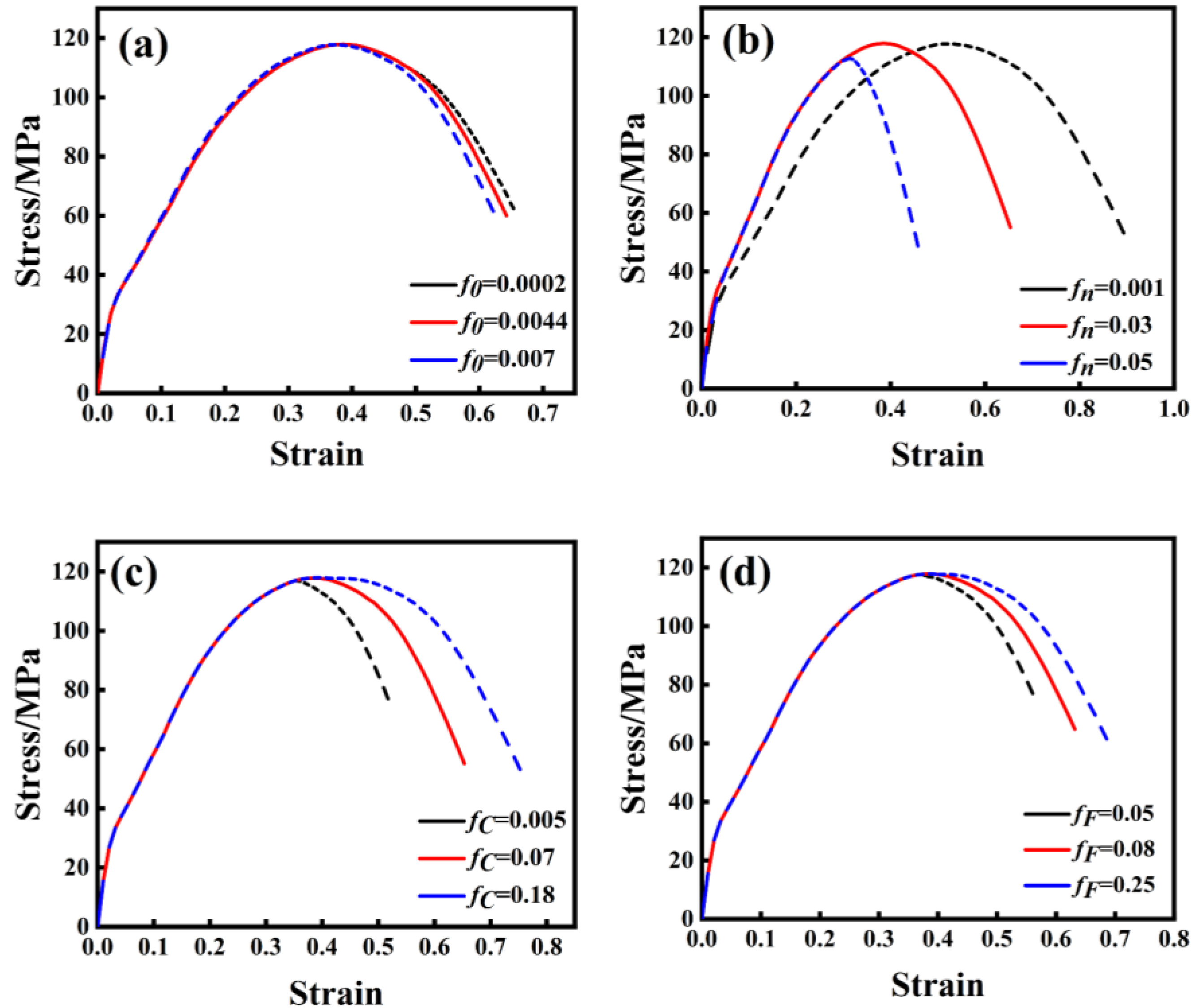
| Element | C | Mn | Si | S | P |
|---|---|---|---|---|---|
| Wt.% | 0.32 | 0.79 | 0.89 | 0.01 | 0.021 |
| Hardening N(1/n) | σy/E = 1 × 10−3 | σy/E = 2 × 10−3 | σy/E = 4 × 10−3 | |||
|---|---|---|---|---|---|---|
| q1 | q2 | q1 | q2 | q1 | q2 | |
| 0.025 | 1.88 | 0.956 | 1.84 | 0.977 | 1.74 | 1.013 |
| 0.05 | 1.63 | 0.95 | 1.57 | 0.974 | 1.48 | 1.013 |
| 0.075 | 1.52 | 0.937 | 1.45 | 0.96 | 1.33 | 1.004 |
| 0.1 | 1.58 | 0.902 | 1.46 | 0.931 | 1.29 | 0.982 |
| 0.15 | 1.78 | 0.833 | 1.68 | 0.856 | 1.49 | 0.901 |
| 0.2 | 1.96 | 0.781 | 1.87 | 0.8 | 1.71 | 0.836 |
| Mechanical Properties | Test Results |
|---|---|
| Elastic modulus E | 212,000 MPa |
| Yield strength σy | 341 MPa |
| Tensile strength σu | 587 MPa |
| Elongation δ | 29.3% |
| α | 0.21 |
| n | 7 |
| Level | f0 | fn | fc | fF |
|---|---|---|---|---|
| 1 | 0.002 | 0.001 | 0.005 | 0.05 |
| 2 | 0.00325 | 0.023 | 0.0275 | 0.125 |
| 3 | 0.0045 | 0.045 | 0.05 | 0.2 |
| No. | f0 | fn | fc | fF | R1 | R2 | R3 | R4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.002 | 0.045 | 0.0275 | 0.125 | 0.479965 | 123.024 | 0.685369 | 30.6241 |
| 2 | 0.002 | 0.023 | 0.05 | 0.125 | 0.479404 | 121.281 | 0.68642 | 30.6601 |
| 3 | 0.0045 | 0.023 | 0.05 | 0.125 | 0.478994 | 121.014 | 0.686072 | 30.3251 |
| 4 | 0.002 | 0.001 | 0.0275 | 0.125 | 0.478415 | 119.872 | 0.690461 | 30.5728 |
| 5 | 0.00325 | 0.045 | 0.05 | 0.125 | 0.479066 | 122.728 | 0.68706 | 30.6726 |
| 6 | 0.002 | 0.023 | 0.0275 | 0.2 | 0.47769 | 120.898 | 0.685855 | 30.3273 |
| 7 | 0.0045 | 0.045 | 0.0275 | 0.125 | 0.479289 | 122.757 | 0.689301 | 30.4502 |
| 8 | 0.00325 | 0.001 | 0.05 | 0.125 | 0.479304 | 119.572 | 0.686447 | 30.3121 |
| 9 | 0.002 | 0.023 | 0.0275 | 0.05 | 0.480702 | 122.99 | 0.688677 | 30.8763 |
| 10 | 0.00325 | 0.045 | 0.0275 | 0.05 | 0.479888 | 123.445 | 0.691153 | 30.5225 |
| 11 | 0.00325 | 0.045 | 0.0275 | 0.2 | 0.479372 | 122.333 | 0.68332 | 30.5486 |
| 12 | 0.00325 | 0.023 | 0.005 | 0.05 | 0.478582 | 122.024 | 0.687645 | 30.5271 |
| 13 | 0.0045 | 0.001 | 0.0275 | 0.125 | 0.479016 | 119.604 | 0.684457 | 30.2938 |
| 14 | 0.00325 | 0.023 | 0.0275 | 0.125 | 0.479599 | 121.391 | 0.682919 | 30.4796 |
| 15 | 0.00325 | 0.001 | 0.0275 | 0.05 | 0.479021 | 120.291 | 0.686677 | 30.3994 |
| 16 | 0.00325 | 0.023 | 0.0275 | 0.125 | 0.479204 | 121.326 | 0.682955 | 30.4869 |
| 17 | 0.0045 | 0.023 | 0.005 | 0.125 | 0.479447 | 121.34 | 0.685402 | 30.4182 |
| 18 | 0.0045 | 0.023 | 0.0275 | 0.05 | 0.478164 | 121.737 | 0.688163 | 30.0432 |
| 19 | 0.002 | 0.023 | 0.005 | 0.125 | 0.478925 | 121.614 | 0.687057 | 30.5307 |
| 20 | 0.00325 | 0.023 | 0.05 | 0.05 | 0.480348 | 121.703 | 0.687878 | 30.3942 |
| 21 | 0.00325 | 0.023 | 0.0275 | 0.125 | 0.479246 | 120.99 | 0.682962 | 30.4528 |
| 22 | 0.00325 | 0.023 | 0.0275 | 0.125 | 0.479944 | 121.302 | 0.683 | 30.5087 |
| 23 | 0.00325 | 0.001 | 0.0275 | 0.2 | 0.478492 | 119.185 | 0.687829 | 30.4733 |
| 24 | 0.00325 | 0.001 | 0.005 | 0.125 | 0.478289 | 119.903 | 0.687167 | 30.5539 |
| 25 | 0.00325 | 0.045 | 0.005 | 0.125 | 0.48015 | 123.052 | 0.686427 | 30.3925 |
| 26 | 0.00325 | 0.023 | 0.0275 | 0.125 | 0.479035 | 121.356 | 0.682964 | 30.4445 |
| 27 | 0.00325 | 0.023 | 0.05 | 0.2 | 0.477947 | 120.596 | 0.684295 | 30.5989 |
| 28 | 0.0045 | 0.023 | 0.0275 | 0.2 | 0.480159 | 120.629 | 0.684317 | 30.7039 |
| 29 | 0.00325 | 0.023 | 0.005 | 0.2 | 0.478998 | 120.924 | 0.684568 | 30.4269 |
| Temperature | R1 | R2 | R3 | R4 | R1 | R2 | R3 | R4 |
|---|---|---|---|---|---|---|---|---|
| R2 (%) | p-Value | |||||||
| 900 °C | 98.36 | 97.49 | 98.74 | 96.55 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| 1000 °C | 96.24 | 96.48 | 96.48 | 98.14 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| 1100 °C | 96.88 | 98.66 | 97.41 | 99.17 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Lack of Fit p-Value | ||||||||
| 900 °C | 0.363 | 0.625 | 0.065 | 0.079 | ||||
| 1000 °C | 0.064 | 0.241 | 0.215 | 0.625 | ||||
| 1100 °C | 0.099 | 0.957 | 0.278 | 0.815 | ||||
| Rate, s−1 Temp, °C | 0.1 | 1 | 10 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 900 | 1000 | 1100 | 900 | 1000 | 1100 | 900 | 1000 | 1100 | |
| 0.003 | 0.0035 | 0.0042 | 0.003 | 0.0032 | 0.00425 | 0.0033 | 0.00365 | 0.0045 | |
| 0.013 | 0.0524 | 0.0381 | 0.0082 | 0.0496 | 0.03496 | 0.0023 | 0.04633 | 0.0312 | |
| 0.028 | 0.0152 | 0.0321 | 0.0424 | 0.0249 | 0.04588 | 0.0432 | 0.03156 | 0.0752 | |
| 0.121 | 0.1852 | 0.0994 | 0.0983 | 0.1813 | 0.08195 | 0.0823 | 0.17915 | 0.0782 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Huang, X.; Ma, G.; Song, C.; Tang, X.; Ji, H. Damage Evolution Mechanism of Railway Wagon Bogie Adapter 1035 Steel and Damage Parameter Calibration Based on Gursone–Tvergaarde–Needleman Model. Materials 2024, 17, 5070. https://doi.org/10.3390/ma17205070
Yin J, Huang X, Ma G, Song C, Tang X, Ji H. Damage Evolution Mechanism of Railway Wagon Bogie Adapter 1035 Steel and Damage Parameter Calibration Based on Gursone–Tvergaarde–Needleman Model. Materials. 2024; 17(20):5070. https://doi.org/10.3390/ma17205070
Chicago/Turabian StyleYin, Jiachuan, Xiaomin Huang, Guangzhi Ma, Changzhe Song, Xuefeng Tang, and Hongchao Ji. 2024. "Damage Evolution Mechanism of Railway Wagon Bogie Adapter 1035 Steel and Damage Parameter Calibration Based on Gursone–Tvergaarde–Needleman Model" Materials 17, no. 20: 5070. https://doi.org/10.3390/ma17205070
APA StyleYin, J., Huang, X., Ma, G., Song, C., Tang, X., & Ji, H. (2024). Damage Evolution Mechanism of Railway Wagon Bogie Adapter 1035 Steel and Damage Parameter Calibration Based on Gursone–Tvergaarde–Needleman Model. Materials, 17(20), 5070. https://doi.org/10.3390/ma17205070








