Leveraging Bayesian Optimization Software for Atomic Layer Deposition: Single-Objective Optimization of TiO2 Layers
Abstract
1. Introduction
2. Materials and Methods
2.1. Bayesian Optimization
2.2. Process Optimization
2.3. Search Space
3. Experiment
3.1. Sample Preparation and Cleaning
3.2. Atomic Layer Deposition
3.3. Lifetime Measurement and Optical Characterization
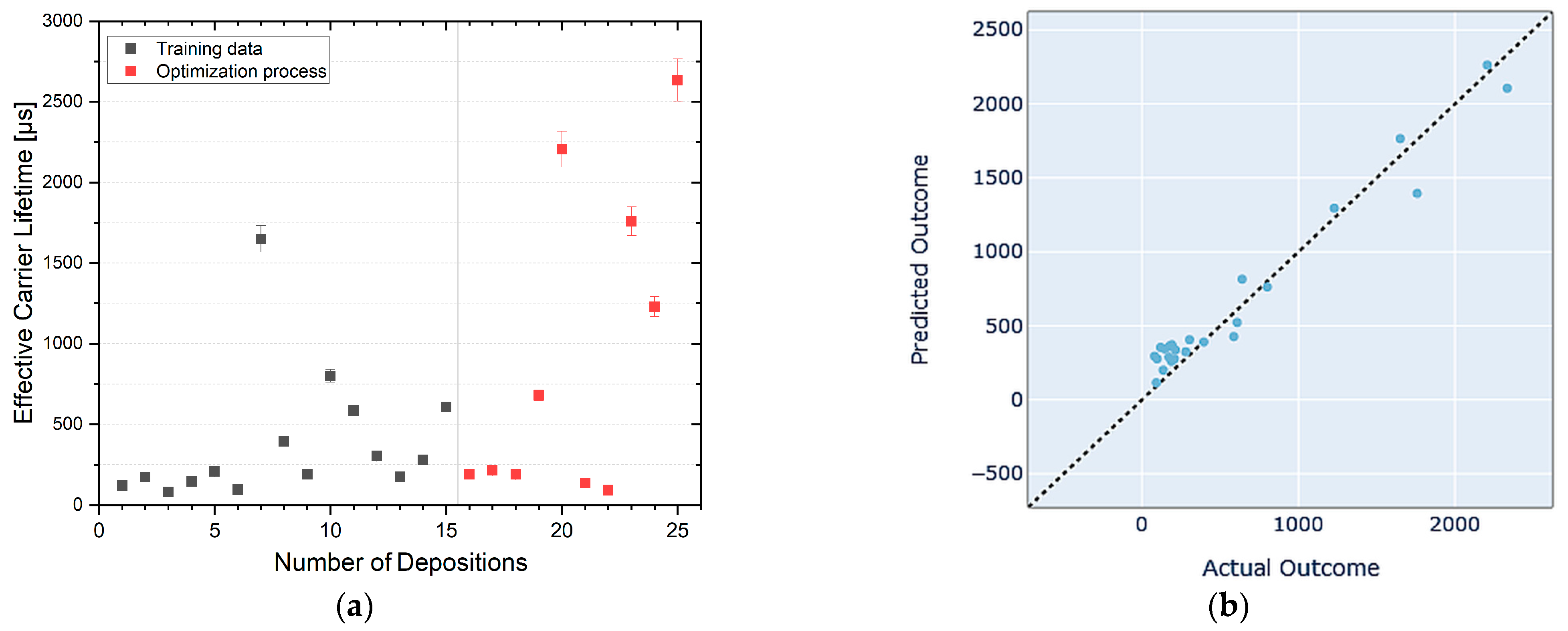
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Miikkulainen, V.; Leskelä, M.; Ritala, M.; Puurunen, R.L. Crystallinity of inorganic films grown by atomic layer deposition: Overview and general trends. J. Appl. Phys. 2013, 113, 21301. [Google Scholar] [CrossRef]
- Mikko, R.; Markku, L. Chapter 2—Atomic layer deposition. In Handbook of Thin Films; Hari, S.N., Ed.; Academic Press: Burlington, NJ, USA, 2002; pp. 103–159. ISBN 978-0-12-512908-4. [Google Scholar]
- Johnson, R.W.; Hultqvist, A.; Bent, S.F. A brief review of atomic layer deposition: From fundamentals to applications. Mater. Today 2014, 17, 236–246. [Google Scholar] [CrossRef]
- van Delft, J.A.; Garcia-Alonso, D.; Kessels, W.M.M. Atomic layer deposition for photovoltaics: Applications and prospects for solar cell manufacturing. Prog. Photovolt. Res. Appl. 2012, 27, 74002. [Google Scholar] [CrossRef]
- Gupta, B.; Hossain, M.A.; Riaz, A.; Sharma, A.; Zhang, D.; Tan, H.H.; Jagadish, C.; Catchpole, K.; Hoex, B.; Karuturi, S. Recent Advances in Materials Design Using Atomic Layer Deposition for Energy Applications. Adv. Funct. Mater. 2022, 32, 2109105. [Google Scholar] [CrossRef]
- Zardetto, V.; Williams, B.L.; Perrotta, A.; Di Giacomo, F.; Verheijen, M.A.; Andriessen, R.; Kessels, W.M.M.; Creatore, M. Atomic layer deposition for perovskite solar cells: Research status, opportunities and challenges. Sustain. Energy Fuels 2017, 1, 30–55. [Google Scholar] [CrossRef]
- Matsui, T.; Bivour, M.; Hermle, M.; Sai, H. Atomic-Layer-Deposited TiOx Nanolayers Function as Efficient Hole-Selective Passivating Contacts in Silicon Solar Cells. ACS Appl. Mater. Interfaces 2020, 12, 49777–49785. [Google Scholar] [CrossRef]
- Adaptive Experimentation Platform. Available online: https://ax.dev/ (accessed on 10 August 2024).
- Jensen, W.A. Response Surface Methodology: Process and Product Optimization Using Designed Experiments 4th edition. J. Qual. Technol. 2017, 49, 186–188. [Google Scholar] [CrossRef]
- Iwundu, M.P.; Cosmos, J. The Efficiency of Seven-Variable Box-Behnken Experimental Design with Varying Center Runs on Full and Reduced Model Types. J. Math. Stat. 2022, 18, 196–207. [Google Scholar] [CrossRef]
- Calandra, R.; Seyfarth, A.; Peters, J.; Deisenroth, M.P. Bayesian optimization for learning gaits under uncertainty. Ann. Math. Artif. Intell. 2016, 76, 5–23. [Google Scholar] [CrossRef]
- Marchant, R.; Ramos, F. Bayesian optimisation for Intelligent Environmental Monitoring. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2012), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2242–2249, ISBN 978-1-4673-1736-8. [Google Scholar]
- Mathern, A.; Steinholtz, O.S.; Sjöberg, A.; Önnheim, M.; Ek, K.; Rempling, R.; Gustavsson, E.; Jirstrand, M. Multi-objective constrained Bayesian optimization for structural design. Struct. Multidisc Optim. 2021, 63, 689–701. [Google Scholar] [CrossRef]
- Osada, K.; Kutsukake, K.; Yamamoto, J.; Yamashita, S.; Kodera, T.; Nagai, Y.; Horikawa, T.; Matsui, K.; Takeuchi, I.; Ujihara, T. Adaptive Bayesian optimization for epitaxial growth of Si thin films under various constraints. Mater. Today Commun. 2020, 25, 101538. [Google Scholar] [CrossRef]
- Paulson, N.H.; Yanguas-Gil, A.; Abuomar, O.Y.; Elam, J.W. Intelligent Agents for the Optimization of Atomic Layer Deposition. ACS Appl. Mater. Interfaces 2021, 13, 17022–17033. [Google Scholar] [CrossRef]
- Dogan, G.; Demir, S.O.; Gutzler, R.; Gruhn, H.; Dayan, C.B.; Sanli, U.T.; Silber, C.; Culha, U.; Sitti, M.; Schütz, G.; et al. Bayesian Machine Learning for Efficient Minimization of Defects in ALD Passivation Layers. ACS Appl. Mater. Interfaces 2021, 13, 54503–54515. [Google Scholar] [CrossRef]
- Miyagawa, S.; Gotoh, K.; Kutsukake, K.; Kurokawa, Y.; Usami, N. Application of Bayesian optimization for high-performance TiO /SiO /c-Si passivating contact. Sol. Energy Mater. Sol. Cells 2021, 230, 111251. [Google Scholar] [CrossRef]
- Hiller, D.; Julin, J.; Chnani, A.; Strehle, S. Silicon Surface Passivation by ALD-Ga2O3: Thermal vs. Plasma-Enhanced Atomic Layer Deposition. IEEE J. Photovolt. 2020, 10, 959–968. [Google Scholar] [CrossRef]
- Li, M.-Y.; Chang, Y.-Y.; Wu, H.-C.; Huang, C.-S.; Chen, J.-C.; Lue, J.-L.; Chang, S.-M. Effect of Process Pressure on Atomic Layer Deposition of Al2O3. J. Electrochem. Soc. 2007, 154, H967. [Google Scholar] [CrossRef]
- Wei, D.; Hossain, T.; Garces, N.Y.; Nepal, N.; Meyer, H.M.; Kirkham, M.J.; Eddy, C.R.; Edgar, J.H. Influence of Atomic Layer Deposition Temperatures on TiO2 /n-Si MOS Capacitor. ECS J. Solid. State Sci. Technol. 2013, 2, N110–N114. [Google Scholar] [CrossRef]
- Chiappim, W.; Testoni, G.E.; Doria, A.C.O.C.; Pessoa, R.S.; Fraga, M.A.; Galvão, N.K.A.M.; Grigorov, K.G.; Vieira, L.; Maciel, H.S. Relationships among growth mechanism, structure and morphology of PEALD TiO2 films: The influence of O2 plasma power, precursor chemistry and plasma exposure mode. Nanotechnology 2016, 27, 305701. [Google Scholar] [CrossRef] [PubMed]
- Chiappim, W.; Testoni, G.E.; de Lima, J.S.B.; Medeiros, H.S.; Pessoa, R.S.; Grigorov, K.G.; Vieira, L.; Maciel, H.S. Effect of Process Temperature and Reaction Cycle Number on Atomic Layer Deposition of TiO2 Thin Films Using TiCl4 and H2O Precursors: Correlation Between Material Properties and Process Environment. Braz. J. Phys. 2016, 46, 56–69. [Google Scholar] [CrossRef]
- Chiappim, W.; Fraga, M.A.; Maciel, H.S.; Pessoa, R.S. An Experimental and Theoretical Study of the Impact of the Precursor Pulse Time on the Growth Per Cycle and Crystallinity Quality of TiO2 Thin Films Grown by ALD and PEALD Technique. Front. Mech. Eng. 2020, 6, 551085. [Google Scholar] [CrossRef]
- Blum, A.L.; Swirhun, J.S.; Sinton, R.A.; Yan, F.; Herasimenka, S.; Roth, T.; Lauer, K.; Haunschild, J.; Lim, B.; Bothe, K.; et al. Interlaboratory Study of Eddy-Current Measurement of Excess-Carrier Recombination Lifetime. IEEE J. Photovolt. 2014, 4, 525–531. [Google Scholar] [CrossRef]
- Dewancker, I.; McCourt, M.; Clark, S. Bayesian Optimization for Machine Learning: A Practical Guidebook. arXiv 2016, arXiv:1612.04858. [Google Scholar] [CrossRef]
- Niemelä, J.-P.; Marin, G.; Karppinen, M. Titanium dioxide thin films by atomic layer deposition: A review. Semicond. Sci. Technol. 2017, 32, 93005. [Google Scholar] [CrossRef]
- Bronneberg, A.C.; Höhn, C.; van de Krol, R. Probing the Interfacial Chemistry of Ultrathin ALD-Grown TiO2 Films: An In-Line XPS Study. J. Phys. Chem. C 2017, 121, 5531–5538. [Google Scholar] [CrossRef]
- Biesinger, M.C.; Lau, L.W.; Gerson, A.R.; Smart, R.S. Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Sc, Ti, V, Cu and Zn. Appl. Surf. Sci. 2010, 257, 887–898. [Google Scholar] [CrossRef]
- Methaapanon, R.; Bent, S.F. Comparative Study of Titanium Dioxide Atomic Layer Deposition on Silicon Dioxide and Hydrogen-Terminated Silicon. J. Phys. Chem. C 2010, 114, 10498–10504. [Google Scholar] [CrossRef]
- Walle, L.E.; Borg, A.; Johansson, E.M.J.; Plogmaker, S.; Rensmo, H.; Uvdal, P.; Sandell, A. Mixed Dissociative and Molecular Water Adsorption on Anatase TiO2 (101). J. Phys. Chem. C 2011, 115, 9545–9550. [Google Scholar] [CrossRef]
- Chaukulkar, R.P.; Agarwal, S. Atomic layer deposition of titanium dioxide using titanium tetrachloride and titanium tetraisopropoxide as precursors. J. Vac. Sci. Technol. A Vac. Surf. Film. 2013, 31, 031509. [Google Scholar] [CrossRef]
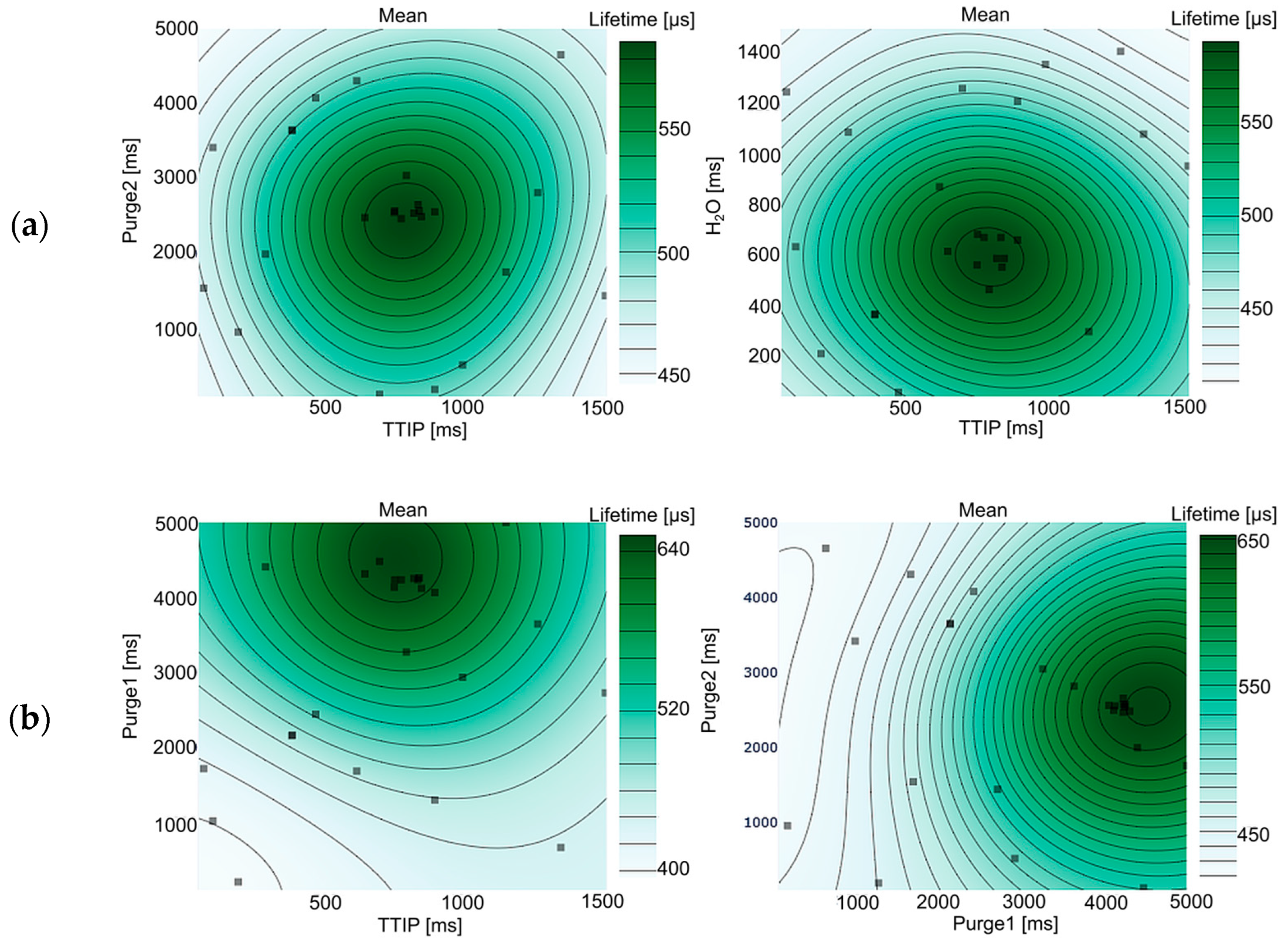
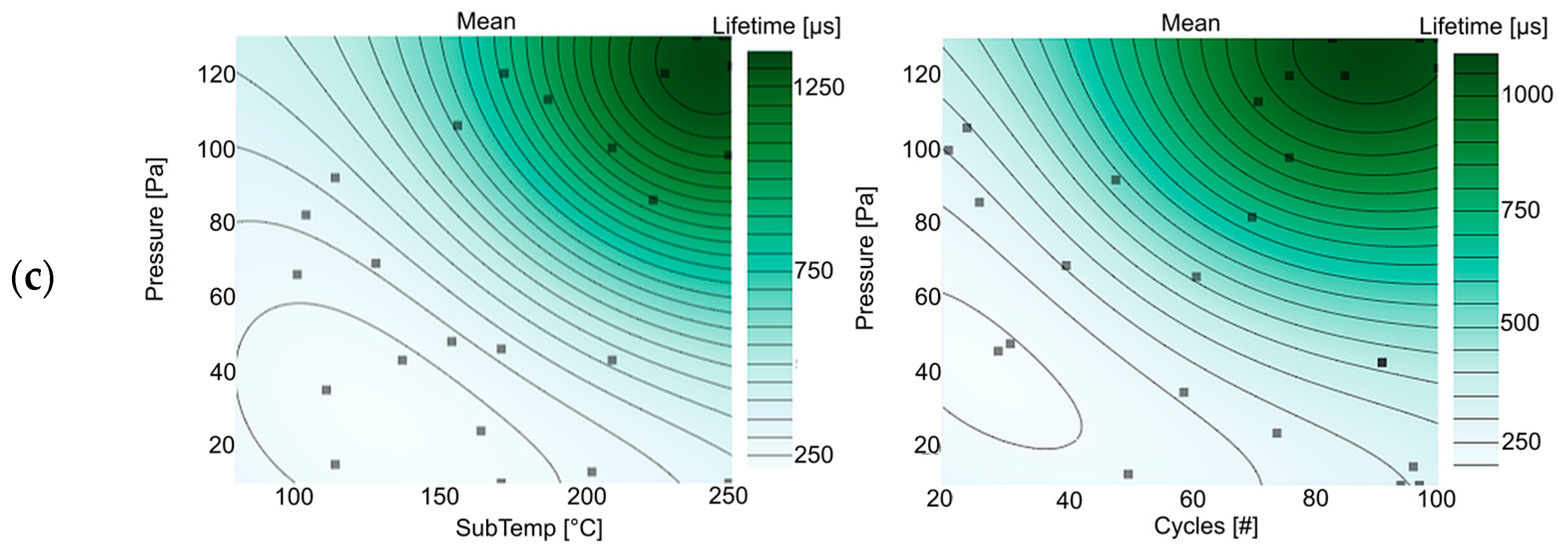
| Search Space | Lower Bound | Upper Bound |
|---|---|---|
| Process Pressure [Pa] | 10 | 130 |
| Process Temperature [°C] | 90 | 250 |
| TTIP Pulse [ms] | 50 | 1500 |
| Purge1 Pulse [ms] | 50 | 5000 |
| H2O Pulse [ms] | 50 | 1500 |
| Purge2 Pulse [ms] | 50 | 5000 |
| Cycle Count [#] | 5 | 100 |
| Processing Parameter | Upper Bound | Best Parameterization |
|---|---|---|
| Process Pressure [Pa] | 130 | 130 |
| Process Temperature [°C] | 250 | 250 |
| TTIP Pulse [ms] | 1500 | 810 |
| Purge1 Pulse [ms] | 5000 | 4250 |
| H2O Pulse [ms] | 1500 | 490 |
| Purge2 Pulse [ms] | 5000 | 2540 |
| Cycle Count [#] | 100 | 100 |
| Sample | Deposited Cycles [#] | Layer Thickness [nm] | Calculated GPC [Å/cycle] | Effective Carrier Lifetime [µs] |
|---|---|---|---|---|
| 25 * | 100 | 6.51 ± 0.037 | 0.65 | 2634 ± 132 |
| 23 | 76 | 6.26 ± 2.797 | 0.82 | 1759 ± 88 |
| 20 | 76 | 4.13 ± 0.01 | 0.54 | 2206 ± 110 |
| 19 | 94 | 5.56 ± 0.505 | 0.59 | 640 ± 32 |
| 16 | 96 | 4.82 ± 0.332 | 0.50 | 190 ± 10 |
| Relative Atom % | |||||
|---|---|---|---|---|---|
| Sample | O 1s | Si 2p | C 1s | N 1s | Ti 2p |
| 25 * | 56.96 | 2.95 | 17.16 | 0.55 | 22.38 |
| 23 | 50.25 | 12.84 | 17.75 | 0.89 | 18.27 |
| 20 | 47.75 | 10.98 | 21.55 | 2.52 | 17.20 |
| 19 | 46.48 | 18.25 | 19.87 | 0.60 | 14.80 |
| 16 | 36.41 | 25.99 | 27.74 | 1.85 | 8.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Häussermann, P.; Joseph, N.B.; Hiller, D. Leveraging Bayesian Optimization Software for Atomic Layer Deposition: Single-Objective Optimization of TiO2 Layers. Materials 2024, 17, 5019. https://doi.org/10.3390/ma17205019
Häussermann P, Joseph NB, Hiller D. Leveraging Bayesian Optimization Software for Atomic Layer Deposition: Single-Objective Optimization of TiO2 Layers. Materials. 2024; 17(20):5019. https://doi.org/10.3390/ma17205019
Chicago/Turabian StyleHäussermann, Philipp, Nikhil Biju Joseph, and Daniel Hiller. 2024. "Leveraging Bayesian Optimization Software for Atomic Layer Deposition: Single-Objective Optimization of TiO2 Layers" Materials 17, no. 20: 5019. https://doi.org/10.3390/ma17205019
APA StyleHäussermann, P., Joseph, N. B., & Hiller, D. (2024). Leveraging Bayesian Optimization Software for Atomic Layer Deposition: Single-Objective Optimization of TiO2 Layers. Materials, 17(20), 5019. https://doi.org/10.3390/ma17205019







