Calibration of Discrete Element Method Parameters for a High-Fidelity Lunar Regolith Simulant Considering the Effects of Realistic Particle Shape
Abstract
1. Introduction
2. Materials and Methods
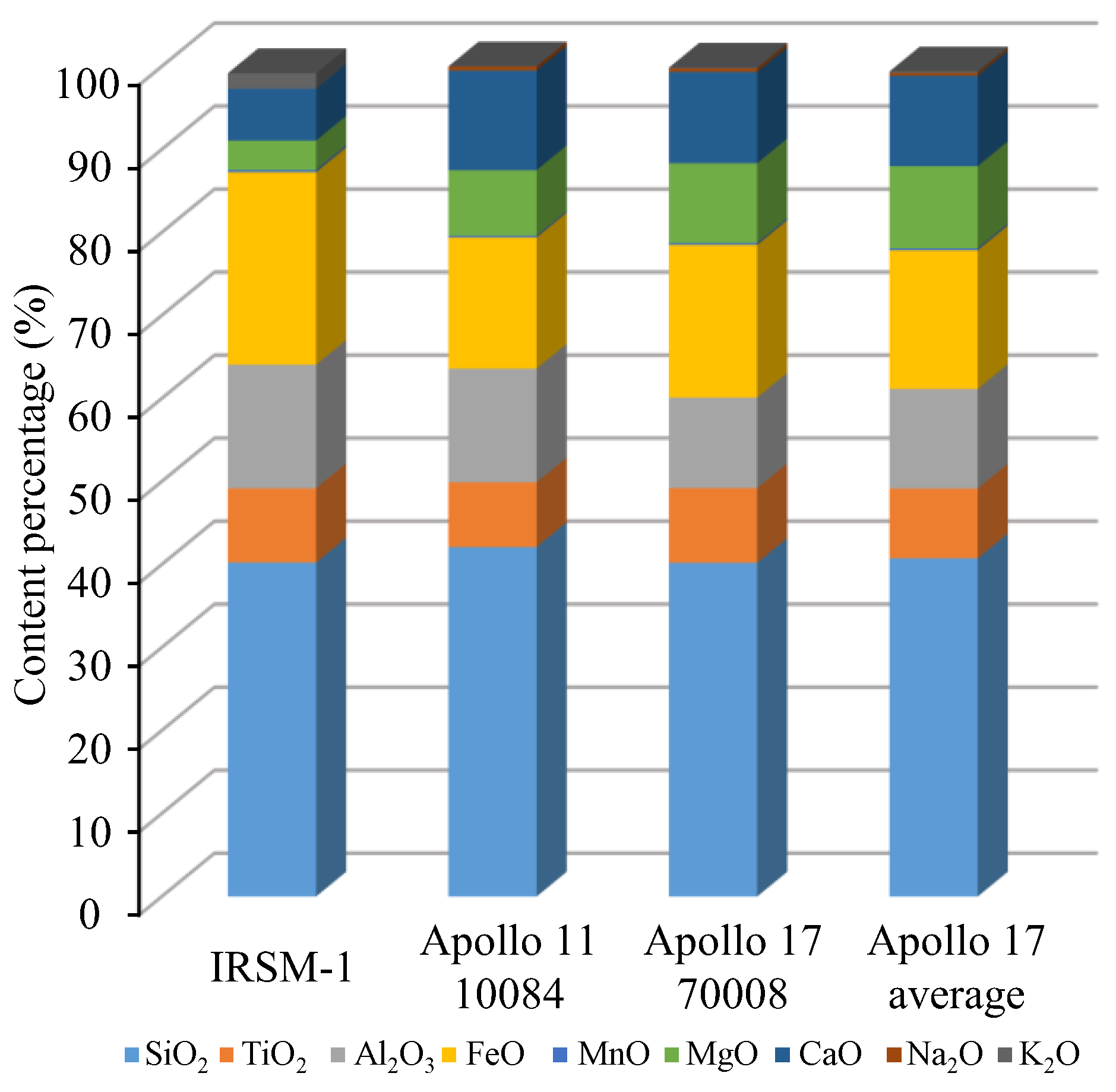
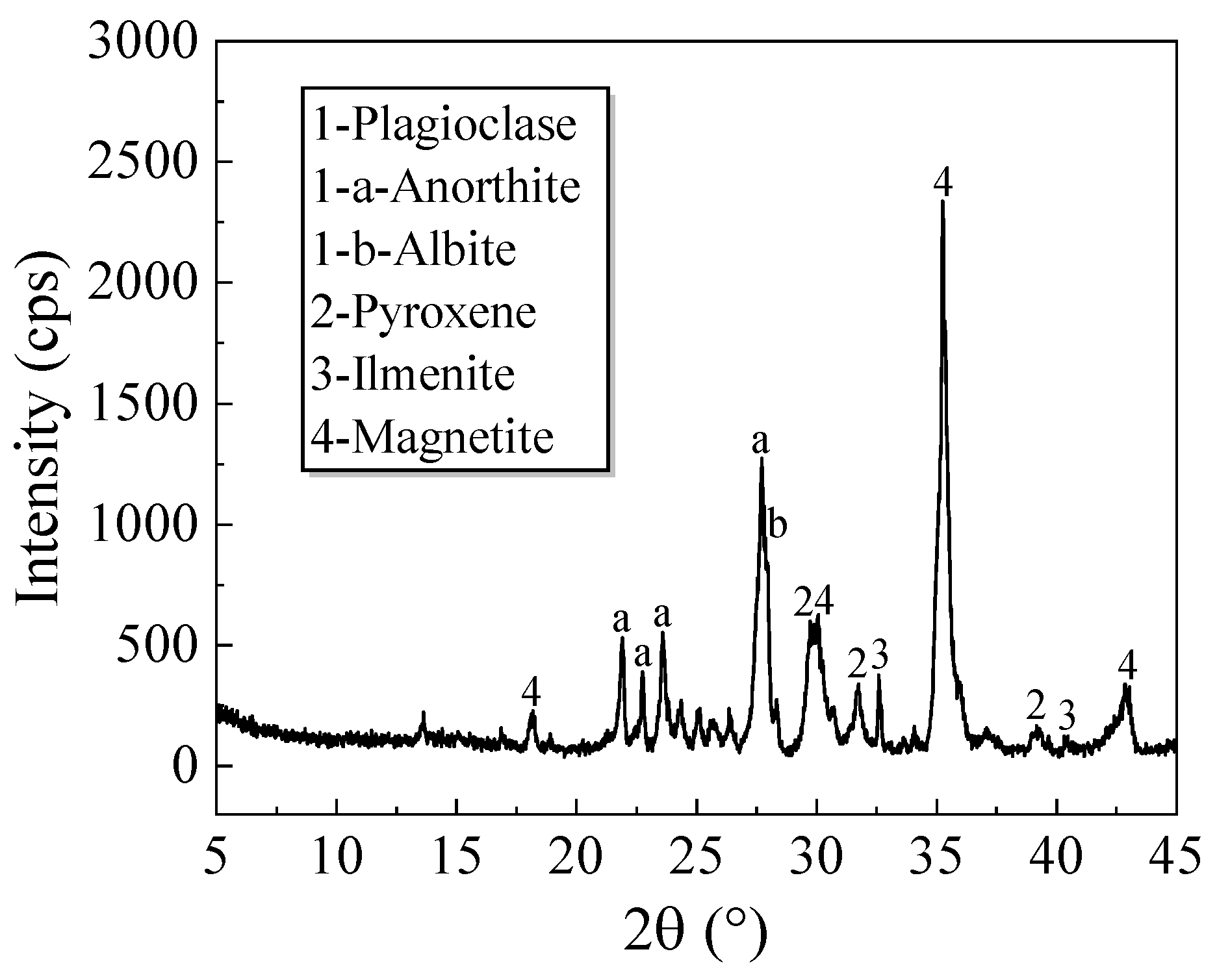
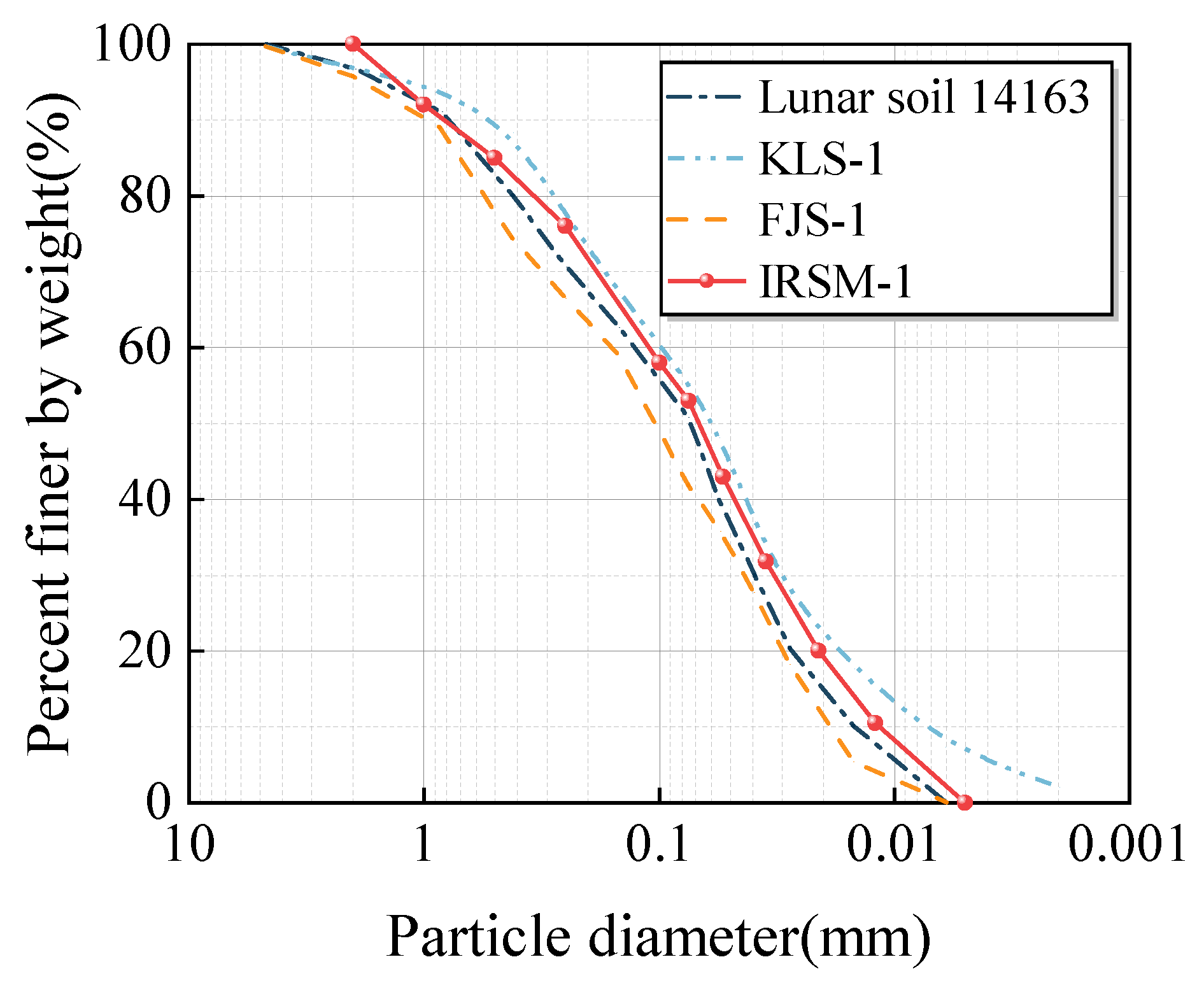
2.1. IRSM-1 Lunar Regolith Simulant
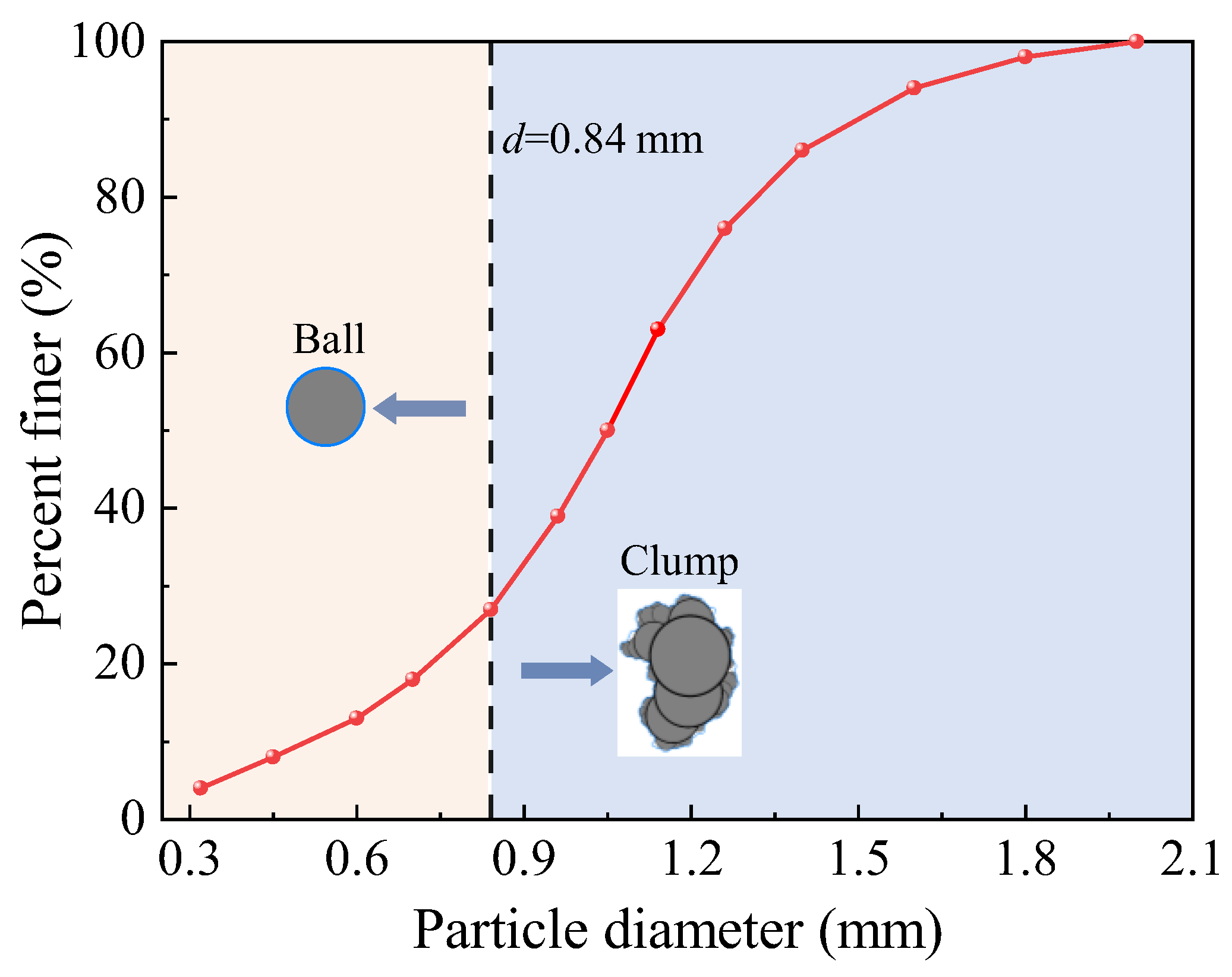
2.1.1. Image Processing
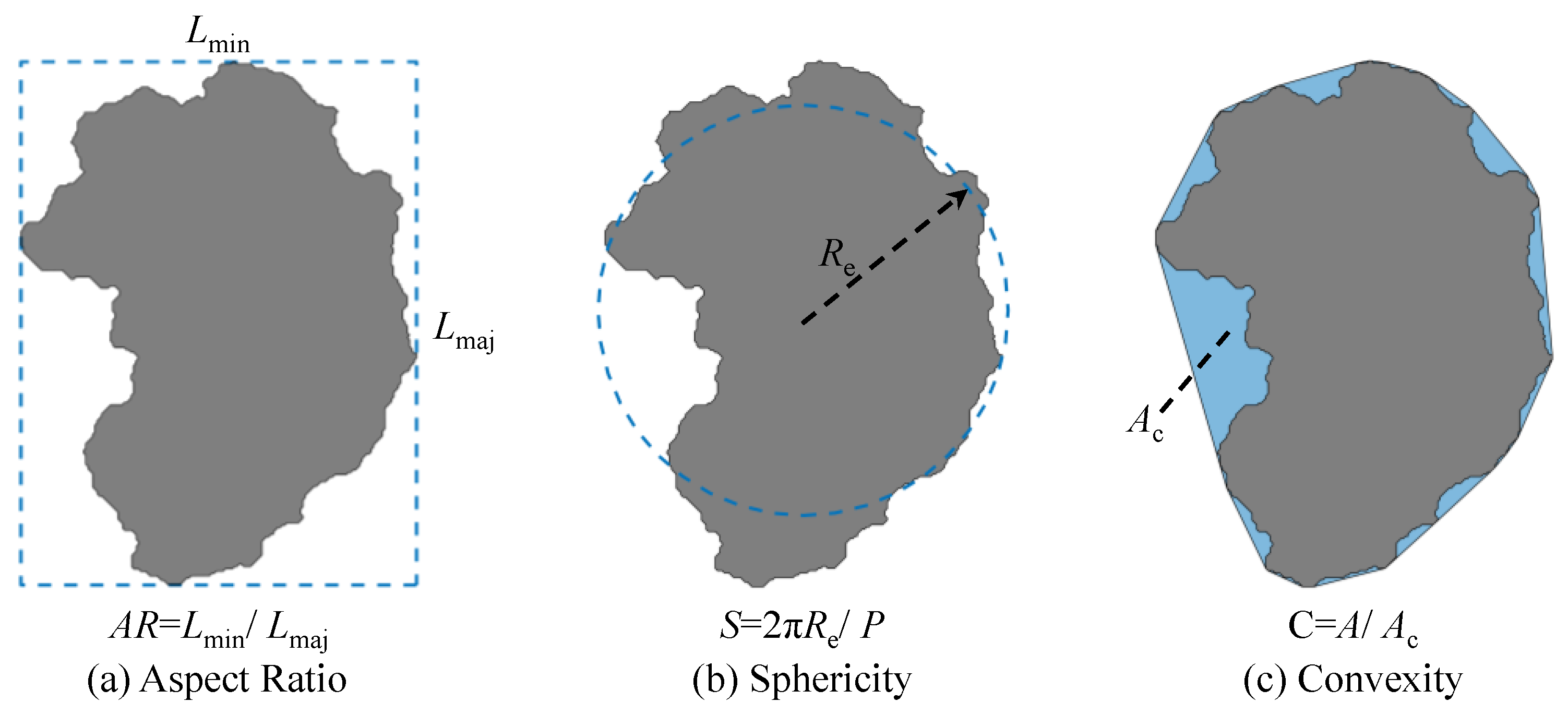
2.1.2. Particle Shape Analysis
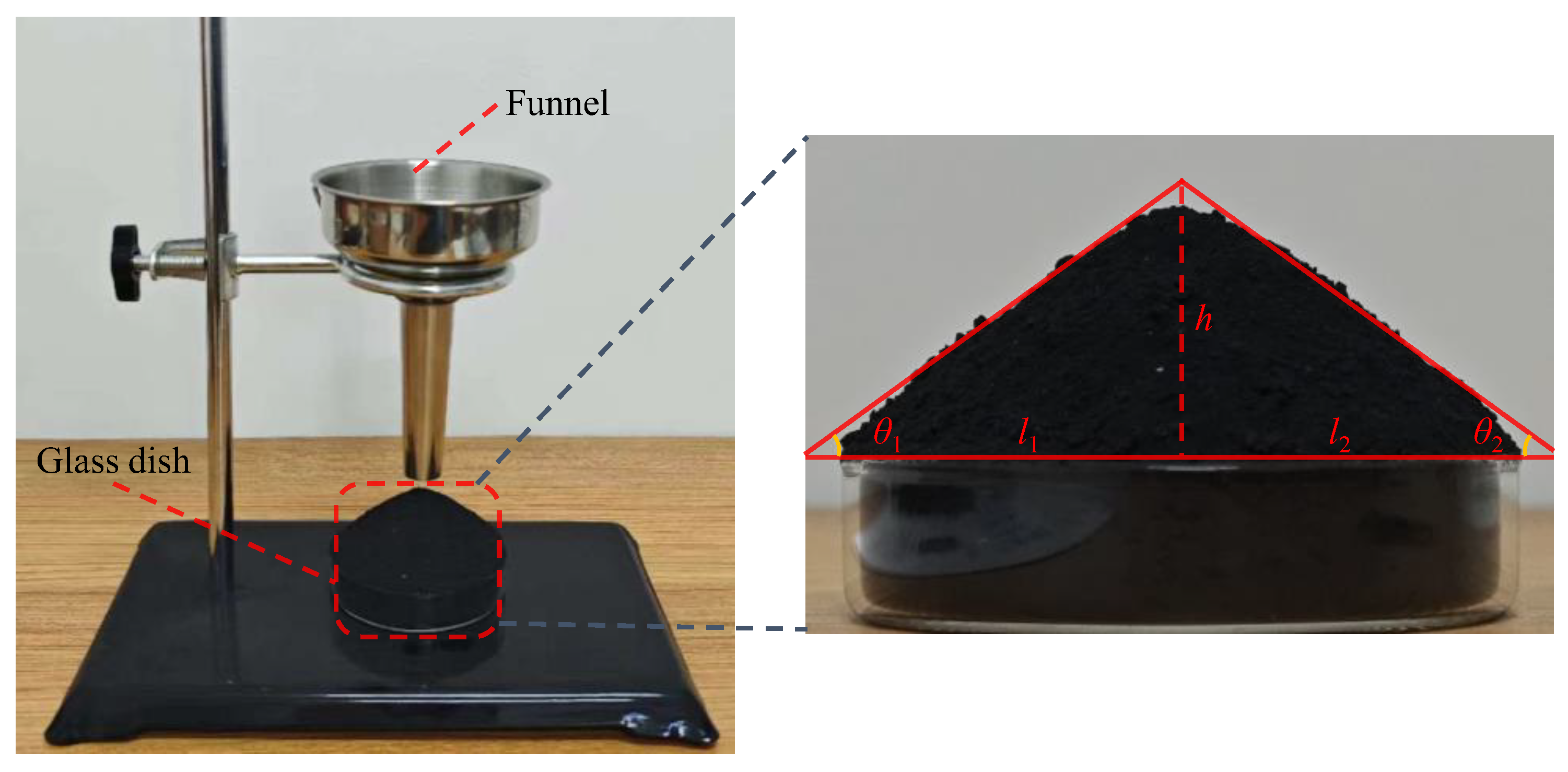
2.1.3. Angle of Repose Experiment
2.2. The DEM Simulation
2.2.1. JKR Contact Model
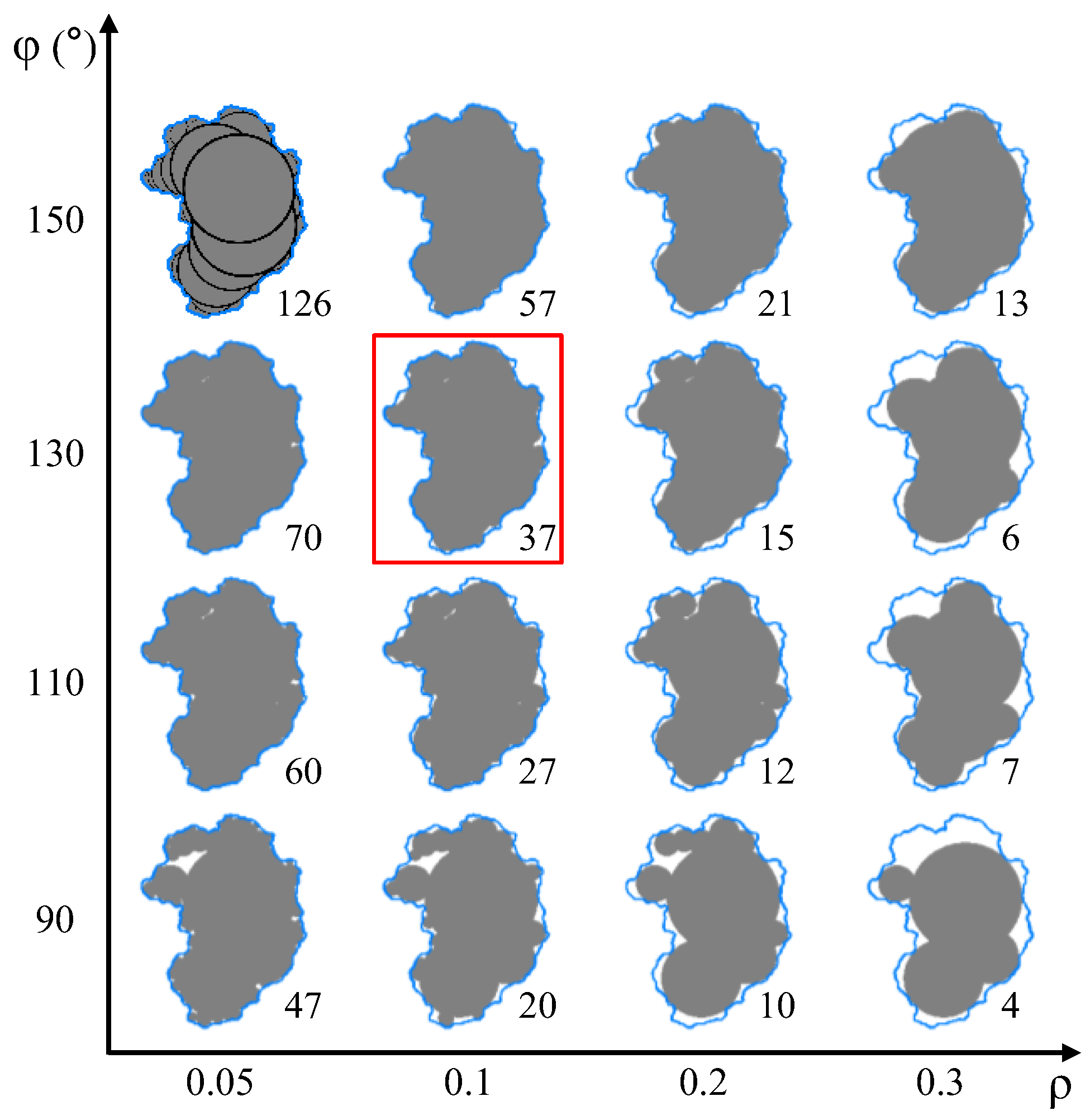
2.2.2. Particle Shape Rebuilding
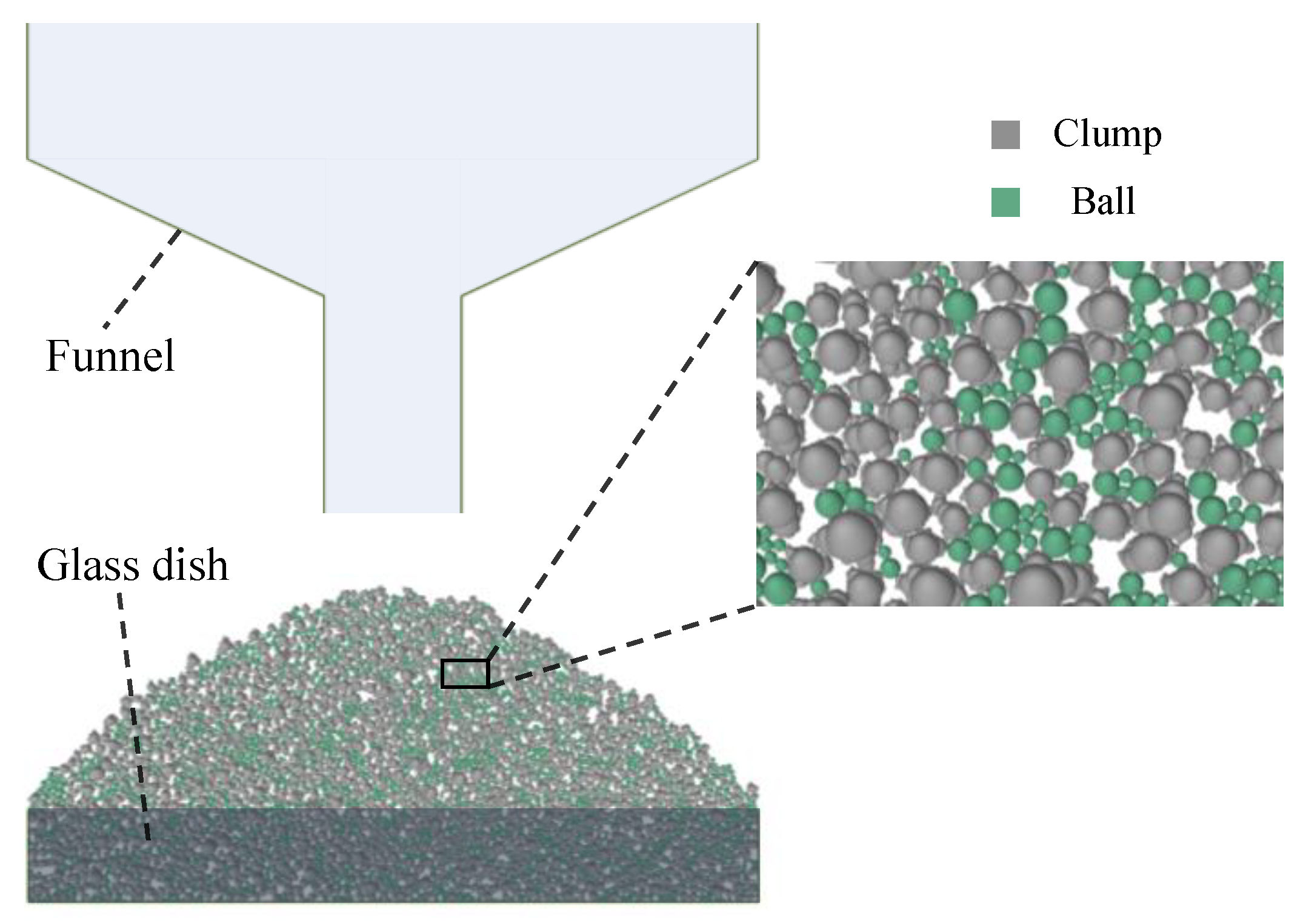
2.2.3. DEM Model of Repose Angle
2.3. The Response Surface Methodology
2.3.1. Plackett–Burman Test
2.3.2. Steepest Ascent Test
2.3.3. Box Behnken Design
3. Results and Discussion
3.1. Properties of IRSM-1 Simulant
3.1.1. Particle Morphology Characteristics
3.1.2. Results of Repose Angle Experiment
3.2. The Calibration Procedure of DEM Parameters
3.2.1. Design and Results of P-B Test
3.2.2. Design and Results Analysis of Steepest Ascent Test
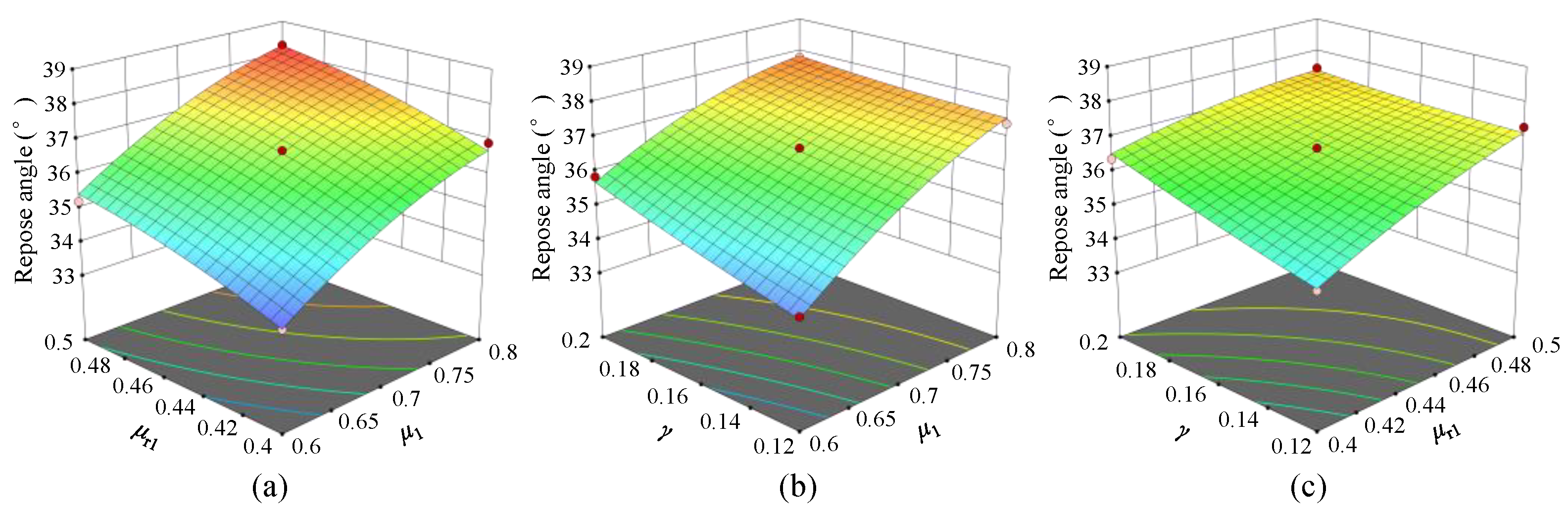
3.2.3. Box–Behnken Design and Regression Model
3.3. Optimal DEM Parameter Determination and Validation
3.3.1. Parameter Determination by the Regression Model
3.3.2. Parameter Validation by the Lifting Cylinder Test
4. Conclusions
- (1)
- The IRSM-1 lunar regolith simulant exhibits composition, physical, and mechanical properties that closely resemble those of real lunar regolith, making it a suitable substitute for lunar regolith research. The morphology of the IRSM-1 particles is complex, with median values of aspect ratio, sphericity, and concavity being 0.743, 0.755, and 0.902, respectively. A discrete element model was constructed for 1250 IRSM-1 particles utilizing the bubble packing algorithm, enabling the AoR simulation based on realistic IRSM-1 particle shapes.
- (2)
- The Plackett–Burman design was employed to quickly identify the three parameters with the most significant impact on the AoR of IRSM-1 particles: sliding friction coefficient μ1, rolling resistance coefficient μr1, and surface energy γ. The steepest ascent test was then employed to determine the optimal parameter ranges. Finally, a quadratic regression equation relating the AoR to these three significant parameters was developed using the Box–Behnken test. The optimal parameters were determined to be 0.633, 0.401, and 0.2, respectively, with the physical AoR (θ = 35.66°) as the optimization target.
- (3)
- The simulation AoR was 34.94° using the optimal parameter combination, with a deviation of only 2.1% from the physical test result. Additionally, the lifting cylinder test was conducted, where the AoR results of the simulation and physical test were 31.89° and 34.03°, respectively, leading to an error of 6.3%. The high similarity in both angles and shapes of the AoR from the tests confirms the reliability and accuracy of the parameter calibration for the IRSM-1 lunar regolith simulant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crawford, I.A. Lunar resources: A review. Prog. Phys. Geog. 2015, 39, 137–167. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Yang, M.; Pei, Z.; Zhou, Q.; Ren, X.; Liu, B.; Liu, D.; Zeng, X.; Zhang, G.; et al. Characteristics of the lunar samples returned by the Chang’E-5 mission. Natl. Sci. Rev. 2022, 9, nwab188. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Pan, P.; Tang, X.; Wang, Z.; Li, Y.; Hussain, A. A comprehensive review of lunar lava tube base construction and field research on a potential Earth test site. Int. J. Min. Sci. Technol. 2024, in press. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Wei, Y.; Lin, Y. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef]
- Jayathilake, B.A.C.S.; Ilankoon, I.M.S.K.; Dushyantha, M.N.P. Assessment of significant geotechnical parameters for lunar regolith excavations. Acta Astronaut. 2022, 196, 107–122. [Google Scholar] [CrossRef]
- Heiken, G.; Vaniman, D.; French, B.M. Lunar Sourcebook: A User’s Guide to the Moon; Cup Archive: Cambridge, UK, 1991. [Google Scholar]
- Li, R.; Zhou, G.; Yan, K.; Chen, J.; Chen, D.; Cai, S.; Mo, P. Preparation and characterization of a specialized lunar regolith simulant for use in lunar low gravity simulation. Int. J. Min. Sci. Technol. 2022, 32, 1–15. [Google Scholar] [CrossRef]
- Kalapodis, N.; Kampas, G.; Ktenidou, O. A review towards the design of extraterrestrial structures: From regolith to human outposts. Acta Astronaut. 2020, 175, 540–569. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Akpinar, P. Lunar soils, simulants and lunar construction materials: An overview. Adv. Space Res. 2022, 70, 762–779. [Google Scholar] [CrossRef]
- Hill, E.; Mellin, M.; Deane, B.; Liu, Y.; Taylor, L. Apollo sample 70051 and high- and low-Ti lunar soil simulants MLS-1A and JSC-1A: Implications for future lunar exploration. J. Geophys. Res. Planets 2007, 112, 1–11. [Google Scholar] [CrossRef]
- Arslan, H.; Sture, S.; Batiste, S. Experimental simulation of tensile behavior of lunar soil simulant JSC-1. Mater. Sci. Eng. A 2008, 478, 201–207. [Google Scholar] [CrossRef]
- Oravec, H.A.; Zeng, X.; Asnani, V.M. Design and characterization of GRC-1: A soil for lunar terramechanics testing in Earth-ambient conditions. J. Terramechanics 2010, 47, 361–377. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, S.; Ouyang, Z.; Zou, Y.; Liu, J.; Li, C.; Li, X.; Feng, J. CAS-1 lunar soil simulant. Adv. Space Res. 2009, 43, 448–454. [Google Scholar] [CrossRef]
- Jiang, M.; Li, L.; Sun, Y. Properties of TJ-1 Lunar Soil Simulant. J. Aerosp. Eng. 2012, 25, 463–469. [Google Scholar] [CrossRef]
- Zou, W.; Li, Y.; Chen, L.; Zhang, J.; Wang, X. Mechanical Properties of QH-E Lunar Soil Simulant at Low Confining Stresses. J. Aerosp. Eng. 2016, 29, 04015036. [Google Scholar] [CrossRef]
- Ryu, B.; Wang, C.; Chang, I. Development and geotechnical engineering properties of KLS-1 lunar simulant. J. Aerosp. Eng. 2018, 31, 4017083. [Google Scholar] [CrossRef]
- Engelschiøn, V.S.; Eriksson, S.R.; Cowley, A.; Fateri, M.; Meurisse, A.; Kueppers, U.; Sperl, M. EAC-1A: A novel large-volume lunar regolith simulant. Sci. Rep. 2020, 10, 5473. [Google Scholar] [CrossRef]
- Just, G.H.; Joy, K.H.; Roy, M.J.; Smith, K.L. Geotechnical characterisation of two new low-fidelity lunar regolith analogues (UoM-B and UoM-W) for use in large-scale engineering experiments. Acta Astronaut. 2020, 173, 414–424. [Google Scholar] [CrossRef]
- Jiang, M.; Yin, Z.; Shen, Z. Shear band formation in lunar regolith by discrete element analyses. Granul. Matter 2016, 18, 32. [Google Scholar] [CrossRef]
- Hou, X.; Ding, T.; Chen, T.; Liu, Y.; Li, M.; Deng, Z. Constitutive properties of irregularly shaped lunar soil simulant particles. Powder Technol. 2019, 346, 137–149. [Google Scholar] [CrossRef]
- Zhang, R.; Pang, H.; Dong, W.; Li, T.; Liu, F.; Zhang, H.; Hu, Z.; Li, J. Three-dimensional Discrete Element Method simulation system of the interaction between irregular structure wheel and lunar soil simulant. Adv. Eng. Softw. 2020, 148, 102873. [Google Scholar] [CrossRef]
- Pelech, T.; Barnett, N.; Dello-Iacovo, M.; Oh, J.; Saydam, S. Analysis of the stability of micro-tunnels in lunar regolith with the Discrete Element Method. Acta Astronaut. 2022, 196, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Wu, W.; Chu, X.; Zou, W. Effects of stress paths on triaxial compression mechanical properties of QH-E lunar soil simulant studied by DEM simulation. Granul. Matter 2020, 22, 32. [Google Scholar] [CrossRef]
- Wu, Q.; Jia, Y.; Wu, H.; Yuan, Z.; Tang, X.; Zheng, Y.; Zhao, H. Macro- and micro-mechanical behavior of CSU-LRS-1 lunar soil simulant under true triaxial loading path. Granul. Matter 2024, 26, 63. [Google Scholar] [CrossRef]
- Hasan, A.; Alshibli, K.A. Discrete Element Modeling of Strength Properties of Johnson Space Center (JSC-1A) Lunar Regolith Simulant. J. Aerosp. Eng. 2010, 23, 157–165. [Google Scholar] [CrossRef]
- Jiang, M.; Shen, Z.; Thornton, C. Microscopic contact model of lunar regolith for high efficiency discrete element analyses. Comput. Geotech. 2013, 54, 104–116. [Google Scholar] [CrossRef]
- Jiang, M.; Shen, Z.; Wang, J. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances. Comput. Geotech. 2015, 65, 147–163. [Google Scholar] [CrossRef]
- Katagiri, J.; Matsushima, T.; Yamada, Y.; Tsuchiyama, A.; Nakano, T.; Uesugi, K.; Ohtake, M.; Saiki, K. Investigation of 3D grain shape characteristics of lunar soil retrieved in Apollo 16 using image-based discrete-element modeling. J. Aerosp. Eng. 2015, 28, 4014092. [Google Scholar] [CrossRef]
- Khademian, Z.; Kim, E.; Nakagawa, M. Simulation of Lunar Soil with Irregularly Shaped, Crushable Grains: Effects of Grain Shapes on the Mechanical Behaviors. J. Geophys. Res. Planets 2019, 124, 1157–1176. [Google Scholar] [CrossRef]
- Yang, J.; Luo, X.D. Exploring the relationship between critical state and particle shape for granular materials. J. Mech. Phys. Solids 2015, 84, 196–213. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J.; Russell, A.; Cheng, Z. DEM modelling of mini-triaxial test based on one-to-one mapping of sand particles. Géotechnique 2021, 71, 714–727. [Google Scholar] [CrossRef]
- Nie, J.; Shi, X.; Cui, Y.; Yang, Z. Numerical evaluation of particle shape effect on small strain properties of granular soils. Eng. Geol. 2022, 303, 106652. [Google Scholar] [CrossRef]
- Müller, P.; Tomas, J. Simulation and calibration of granules using the discrete element method. Particuology 2014, 12, 40–43. [Google Scholar] [CrossRef]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Wang, M.; Lu, Z.; Wan, W.; Zhao, Y. A calibration framework for the microparameters of the DEM model using the improved PSO algorithm. Adv. Powder Technol. 2021, 32, 358–369. [Google Scholar] [CrossRef]
- Irazábal, J.; Salazar, F.; Vicente, D. A methodology for calibrating parameters in discrete element models based on machine learning surrogates. Comput. Part. Mech. 2023, 10, 1031–1047. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, H.; Xu, L.; Song, S.; Zhang, C.; Yu, Q. Parameter calibration of coconut bran substrate simulation model based on discrete element and response surface methodology. Powder Technol. 2022, 395, 183–194. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Xiao, X.; Li, Y.; Peng, R.; Gao, J.; Hu, C. Parameter calibration and mixing uniformity of irregular gravel materials in a rotating drum. Powder Technol. 2023, 414, 118074. [Google Scholar] [CrossRef]
- Zhou, N.; Chen, J. Preparation and Characterization of a Novel Magnetic High-Titanium Lunar Regolith Simulant for Geotechnical Engineering Application. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023; ARMA: Atlanta, GA, USA, 2023; p. 2023. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Perko, H.; Nelson, J.; Sadeh, W. Surface cleanliness effect on lunar soil shear strength. J. Geotech. Geoenviron. Eng. 2001, 127, 371–383. [Google Scholar] [CrossRef]
- Modenese, C. Numerical Study of the Mechanical Properties of Lunar Soil by the Discrete Element Method; Oxford University: Oxford, UK, 2013. [Google Scholar]
- Taghavi, R. Automatic clump generation based on mid-surface. In Proceedings of the 2nd International FLAC/DEM Symposium, Minneapolis, MN, USA, 14–16 February 2011; Itasca Consulting Group Inc: Minneapolis, MN, USA, 2011; pp. 791–797. [Google Scholar]
- Roessler, T.; Katterfeld, A. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]






| Material | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|
| IRSM-1 | 0.81–1.63 | 44.1–52.8 |
| Lunar regolith | 0.44–3.8 | 41–55 |
| TJ-1 | 0.86 | 47.6 |
| JSC-1 | 6.2 | 49.5 |
| FJS-1 | 3–8 | 32.5–39.4 |
| MLS-1 | 0.9 | 37 |
| KLS-1 | 1.85 | 44.91 |
| Parameters | Radius Ratio ρ | |||
|---|---|---|---|---|
| 0.05 | 0.1 | 0.2 | 0.3 | |
| The distance φ: degrees | ||||
| 90 | 94.41 | 90.76 | 86.34 | 75.71 |
| 110 | 97.22 | 94.13 | 90.05 | 82.53 |
| 130 | 97.82 | 96.00 | 90.92 | 81.66 |
| 150 | 98.47 | 97.12 | 93.52 | 89.70 |
| Symbol | DEM Parameters | Levels | |
|---|---|---|---|
| −1 | +1 | ||
| G | Shear modulus (MPa) | 40 | 80 |
| ν | Poisson’s ratio | 0.1 | 0.3 |
| μ1 | Sliding friction coefficient of particle | 0.4 | 0.9 |
| μr1 | Rolling friction coefficient of particle | 0.2 | 0.7 |
| β | Critical damping ratio | 0.3 | 0.7 |
| γ | Surface adhesion energy (J/m2) | 0.02 | 0.12 |
| μ2 | Sliding friction coefficient between particle and wall | 0.3 | 0.6 |
| μr2 | Rolling friction coefficient between particle and wall | 0.15 | 0.55 |
| Number | G | ν | μ1 | μr1 | β | γ | μ2 | μr2 | Repose Angle (◦) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 34.04 |
| 2 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 34.35 |
| 3 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 37.60 |
| 4 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 30.59 |
| 5 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 35.02 |
| 6 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 33.63 |
| 7 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 27.52 |
| 8 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 30.68 |
| 9 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 33.13 |
| 10 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | 35.62 |
| 11 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 35.74 |
| 12 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 27.25 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 32.99 |
| Sources | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance Ranking |
|---|---|---|---|---|---|---|
| Model | 116.11 | 8 | 14.51 | 39.06 | 0.006 ** | |
| G-G | 0.42 | 1 | 0.42 | 1.12 | 0.3678 | 4 |
| ν-ν | 0.23 | 1 | 0.227 | 0.61 | 0.4915 | 5 |
| μ1-μ1 | 64.27 | 1 | 64.27 | 172.96 | 0.0009 ** | 1 |
| μr1-μr1 | 30.90 | 1 | 30.90 | 83.15 | 0.0028 ** | 2 |
| β-β | 0.04 | 1 | 0.04 | 0.10 | 0.7773 | 8 |
| γ-γ | 19.96 | 1 | 19.96 | 53.70 | 0.0052 ** | 3 |
| μ2-μ2 | 0.19 | 1 | 0.19 | 0.52 | 0.5216 | 6 |
| μr2-μr2 | 0.10 | 1 | 0.10 | 0.28 | 0.6321 | 7 |
| Number | μ1 | μr1 | γ | Repose Angle (◦) | Relative Error (%) |
|---|---|---|---|---|---|
| 1 | 0.4 | 0.30 | 0.04 | 30.07 | 15.68 |
| 2 | 0.5 | 0.35 | 0.08 | 31.99 | 10.29 |
| 3 | 0.6 | 0.40 | 0.12 | 33.65 | 5.64 |
| 4 | 0.7 | 0.45 | 0.16 | 36.48 | 2.30 |
| 5 | 0.8 | 0.50 | 0.20 | 38.58 | 8.20 |
| 6 | 0.9 | 0.55 | 0.24 | 40.28 | 12.97 |
| Number | μ1 | μr1 | γ | Repose Angle (◦) |
|---|---|---|---|---|
| 1 | −1(0.6) | −1(0.4) | 0(0.16) | 33.89 |
| 2 | 1(0.8) | −1 | 0 | 36.91 |
| 3 | −1 | 1(0.5) | 0 | 35.20 |
| 4 | 1 | 1 | 0 | 38.26 |
| 5 | −1 | 0(0.45) | −1(0.12) | 34.17 |
| 6 | 1 | 0 | −1 | 37.39 |
| 7 | −1 | 0 | 1(0.20) | 35.86 |
| 8 | 1 | 0 | 1 | 37.79 |
| 9 | 0(0.7) | −1 | −1 | 34.86 |
| 10 | 0 | 1 | −1 | 37.29 |
| 11 | 0 | −1 | 1 | 36.38 |
| 12 | 0 | 1 | 1 | 37.46 |
| 13 | 0 | 0 | 0 | 36.70 |
| 14 | 0 | 0 | 0 | 36.54 |
| 15 | 0 | 0 | 0 | 36.61 |
| Sources | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 23.86 | 9 | 2.65 | 57.48 | 0.0002 ** |
| μ1 | 15.77 | 1 | 15.77 | 342.01 | <0.0001 ** |
| μr1 | 4.78 | 1 | 4.78 | 103.72 | 0.0002 ** |
| γ | 1.79 | 1 | 1.79 | 38.81 | 0.0016 ** |
| μ1μr1 | 0.0003 | 1 | 0.0003 | 0.0063 | 0.94 |
| μ1γ | 0.4198 | 1 | 0.4198 | 9.1 | 0.0295 * |
| μr1γ | 0.4591 | 1 | 0.4591 | 9.96 | 0.0252 * |
| μ12 | 0.5103 | 1 | 0.5103 | 11.07 | 0.0209 * |
| μr12 | 0.1191 | 1 | 0.1191 | 2.58 | 0.1689 |
| γ2 | 0.0129 | 1 | 0.0129 | 0.2792 | 0.6198 |
| Residual | 0.2306 | 5 | 0.0461 | ||
| Lack of Fit | 0.2191 | 3 | 0.073 | 12.67 | 0.074 |
| Pure Error | 0.0115 | 2 | 0.0058 | ||
| Cor Total | 24.09 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, N.; Chen, J.; Tian, N.; Tian, K.; Huang, J.; Wu, P. Calibration of Discrete Element Method Parameters for a High-Fidelity Lunar Regolith Simulant Considering the Effects of Realistic Particle Shape. Materials 2024, 17, 4789. https://doi.org/10.3390/ma17194789
Zhou N, Chen J, Tian N, Tian K, Huang J, Wu P. Calibration of Discrete Element Method Parameters for a High-Fidelity Lunar Regolith Simulant Considering the Effects of Realistic Particle Shape. Materials. 2024; 17(19):4789. https://doi.org/10.3390/ma17194789
Chicago/Turabian StyleZhou, Ningxi, Jian Chen, Ning Tian, Kaiwei Tian, Juehao Huang, and Peng Wu. 2024. "Calibration of Discrete Element Method Parameters for a High-Fidelity Lunar Regolith Simulant Considering the Effects of Realistic Particle Shape" Materials 17, no. 19: 4789. https://doi.org/10.3390/ma17194789
APA StyleZhou, N., Chen, J., Tian, N., Tian, K., Huang, J., & Wu, P. (2024). Calibration of Discrete Element Method Parameters for a High-Fidelity Lunar Regolith Simulant Considering the Effects of Realistic Particle Shape. Materials, 17(19), 4789. https://doi.org/10.3390/ma17194789






