Numerical Simulation of Failure Behavior of Reinforced Concrete Shear Walls by a Micropolar Peridynamic Model
Abstract
1. Introduction
2. Basic Theory of Peridynamics
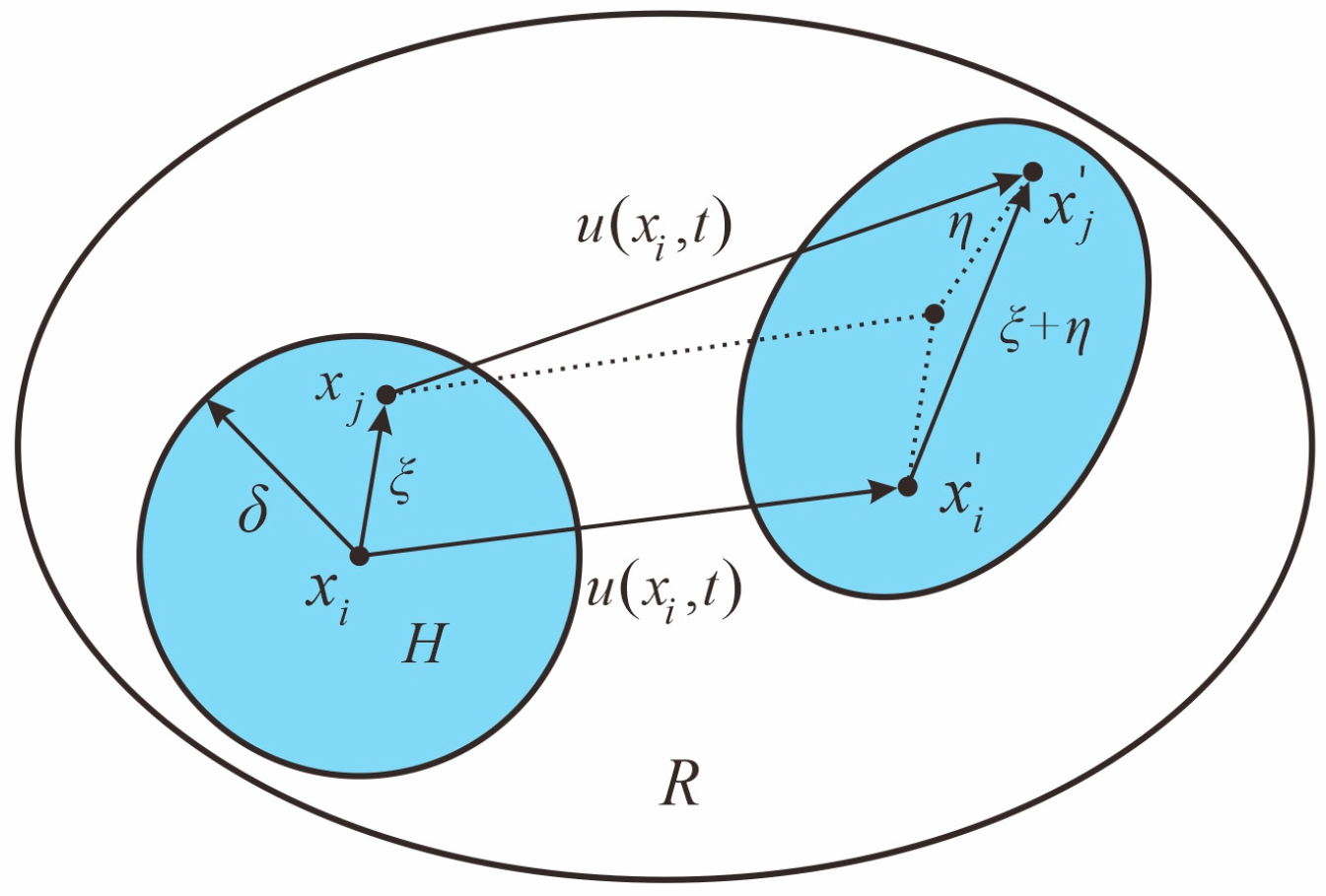
2.1. Basic Ideas
2.2. Micropolar Peridynamics
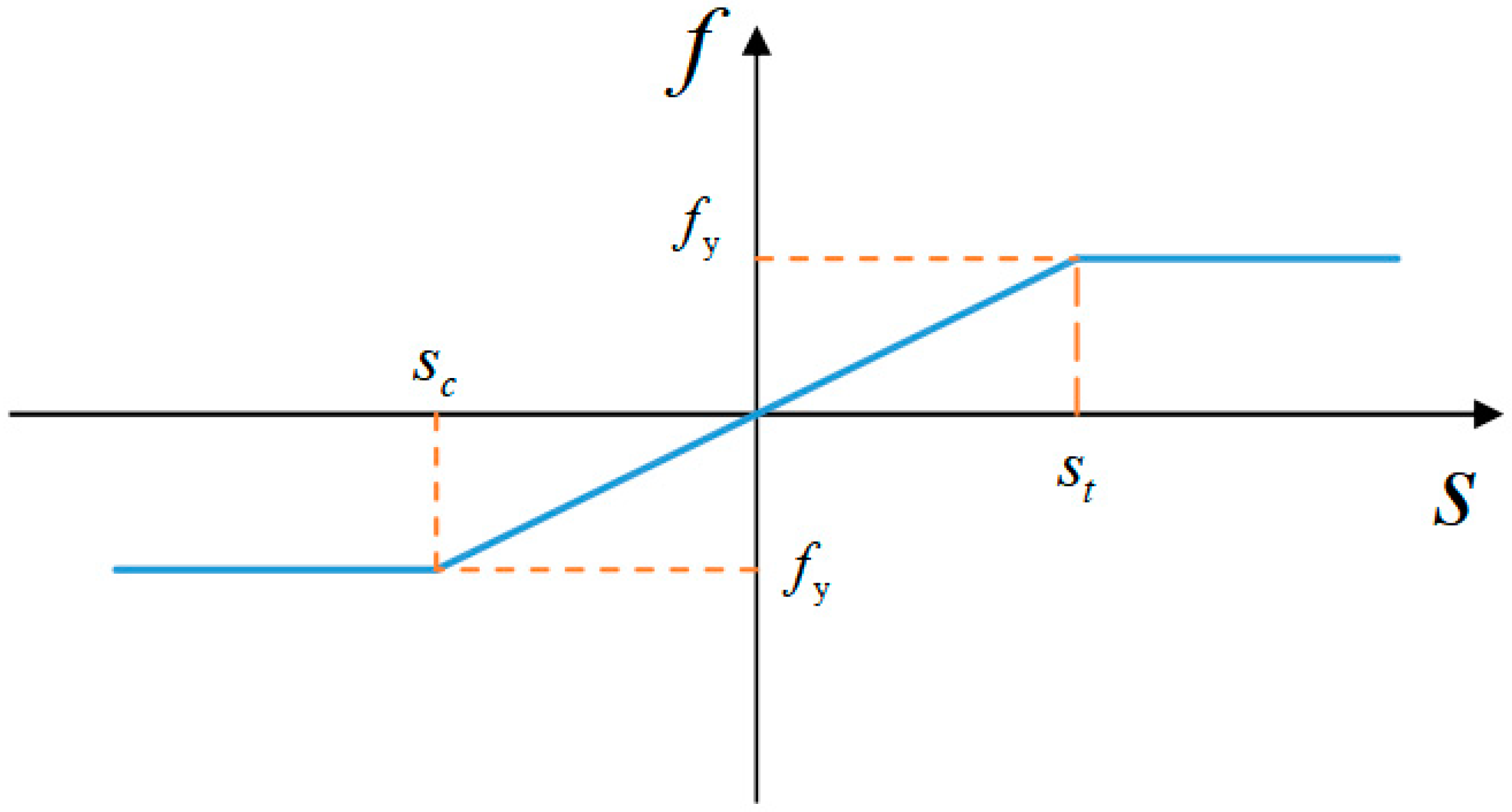
2.3. Rebar Constitutive Model
2.4. Concrete Constitutive Model
2.5. Interface Processing
3. Numerical Implementation
3.1. Artificial Damping
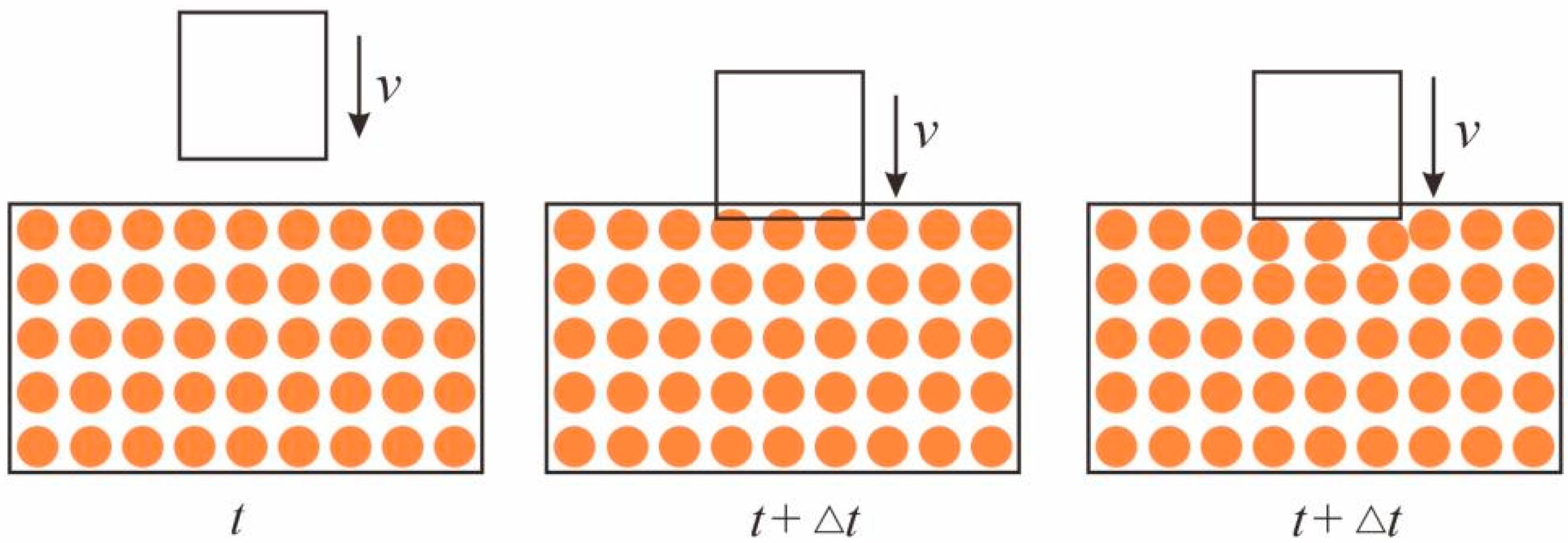
3.2. Impact Contact Algorithm
4. Numerical Examples
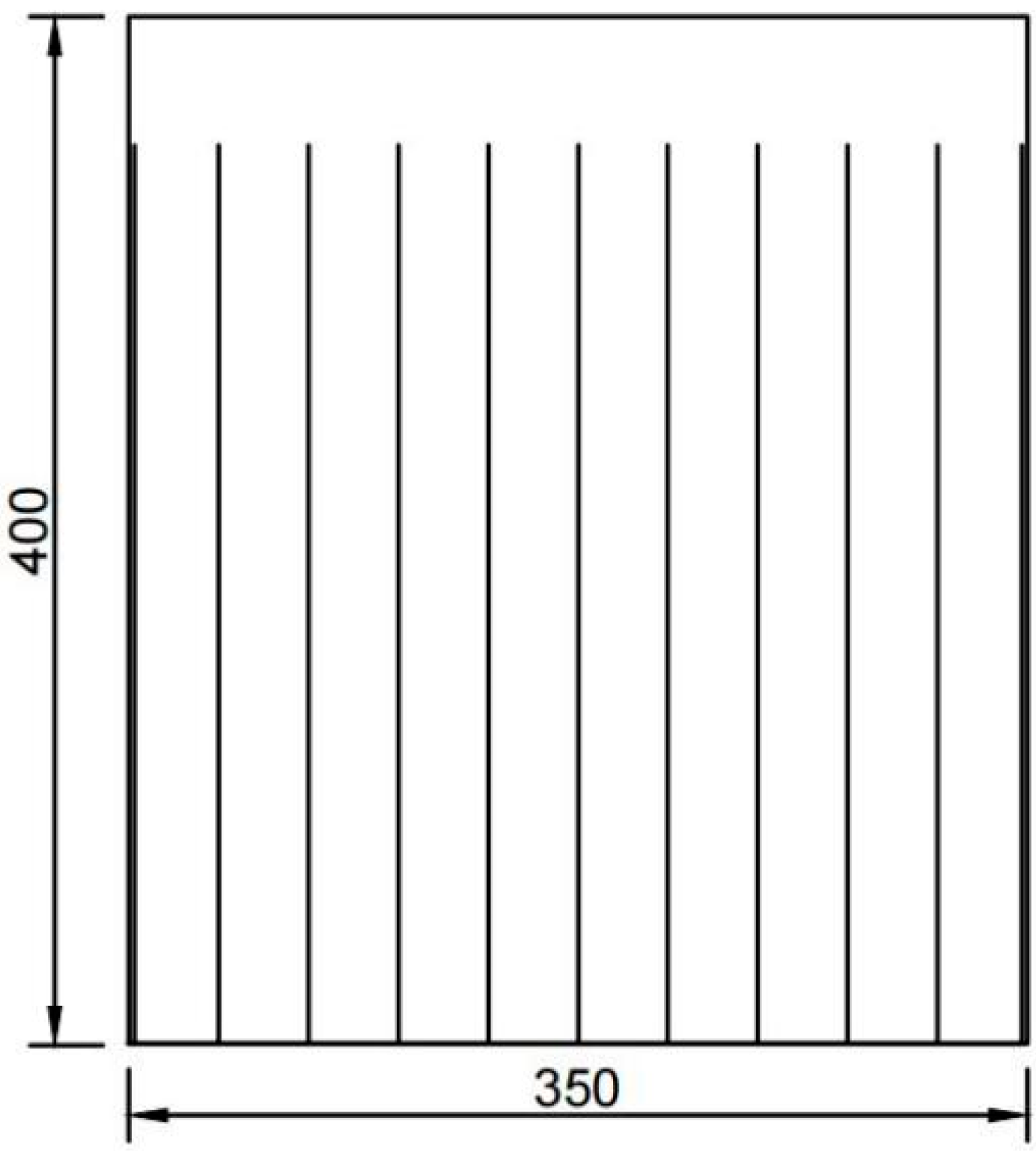
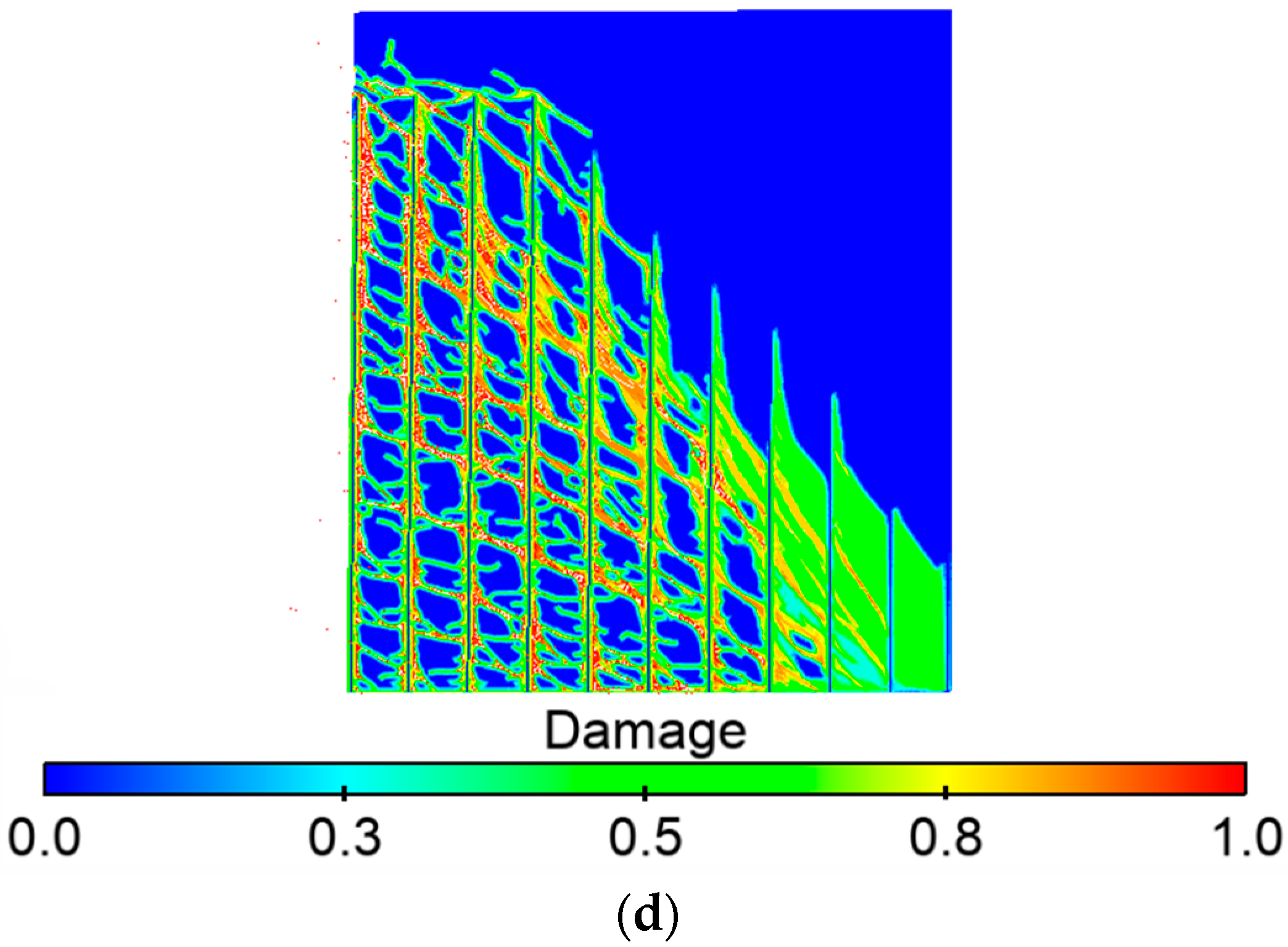
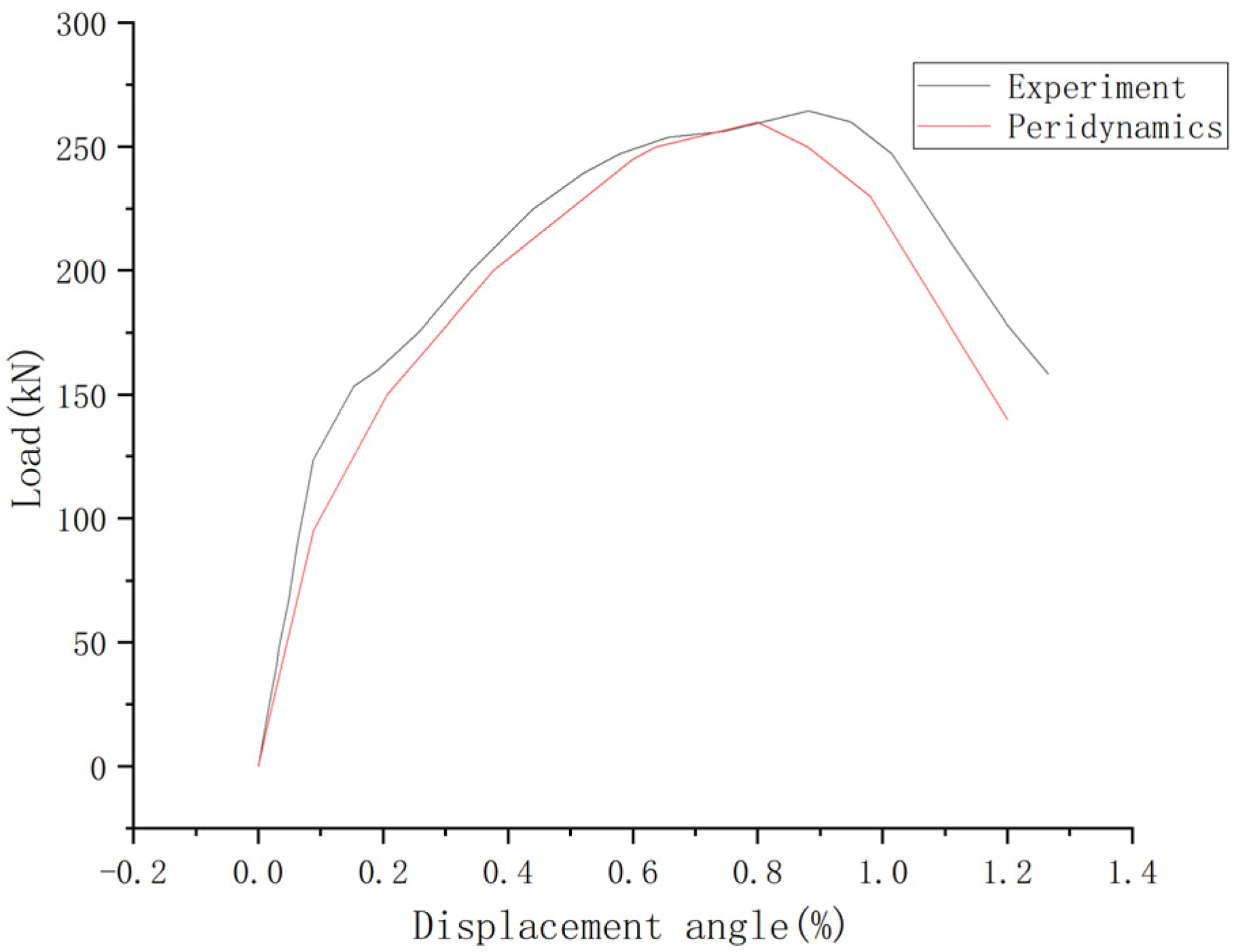
4.1. Quasi-Static Damage of RC Shear Walls
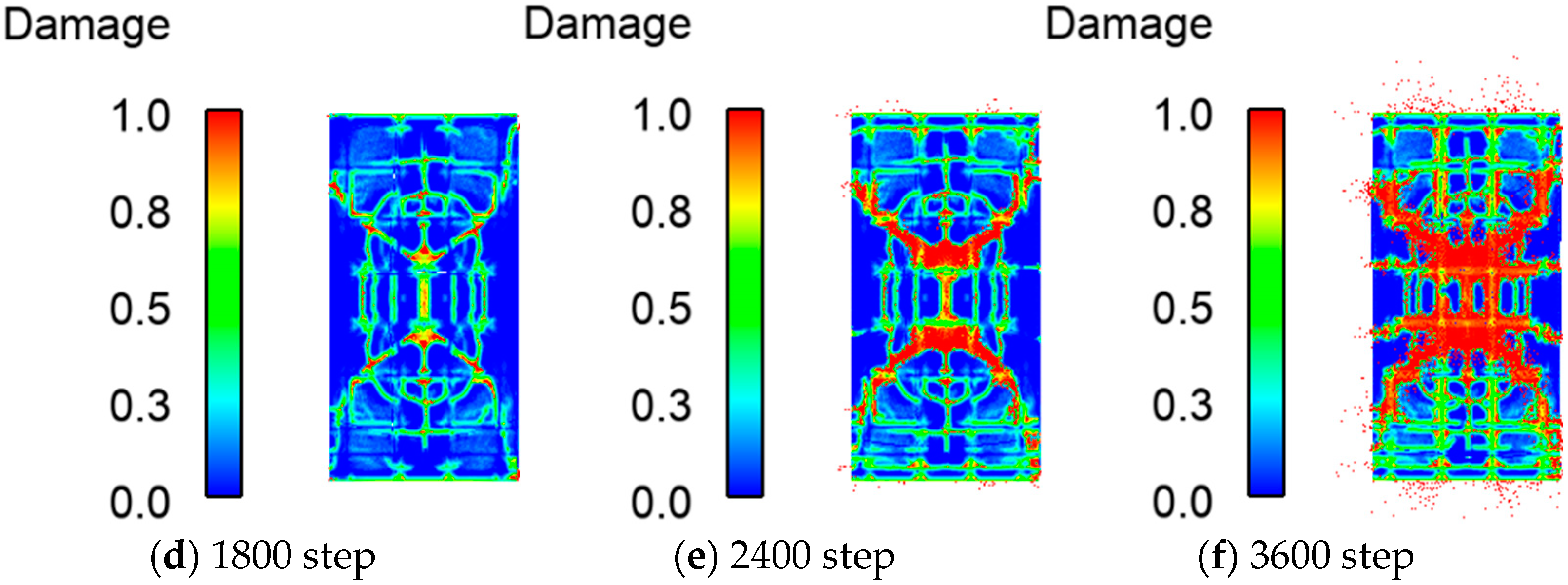
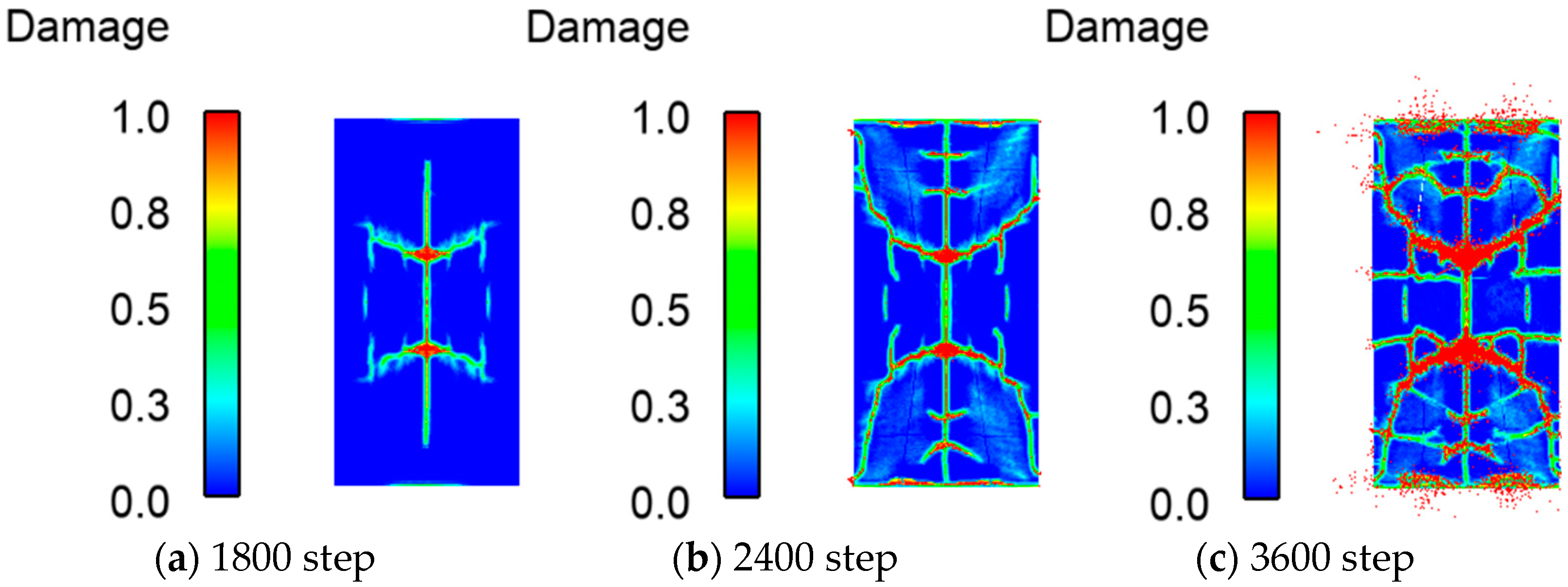
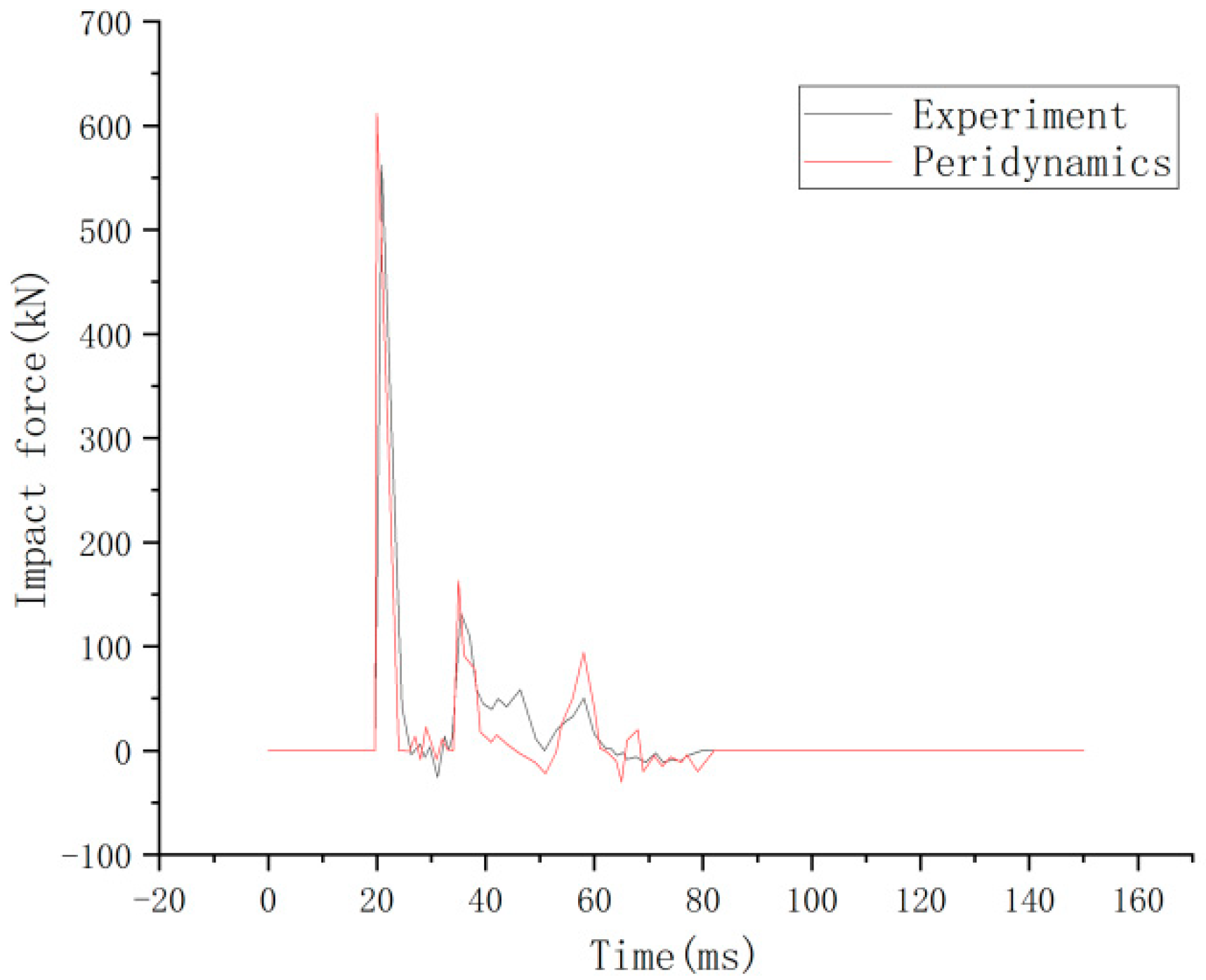
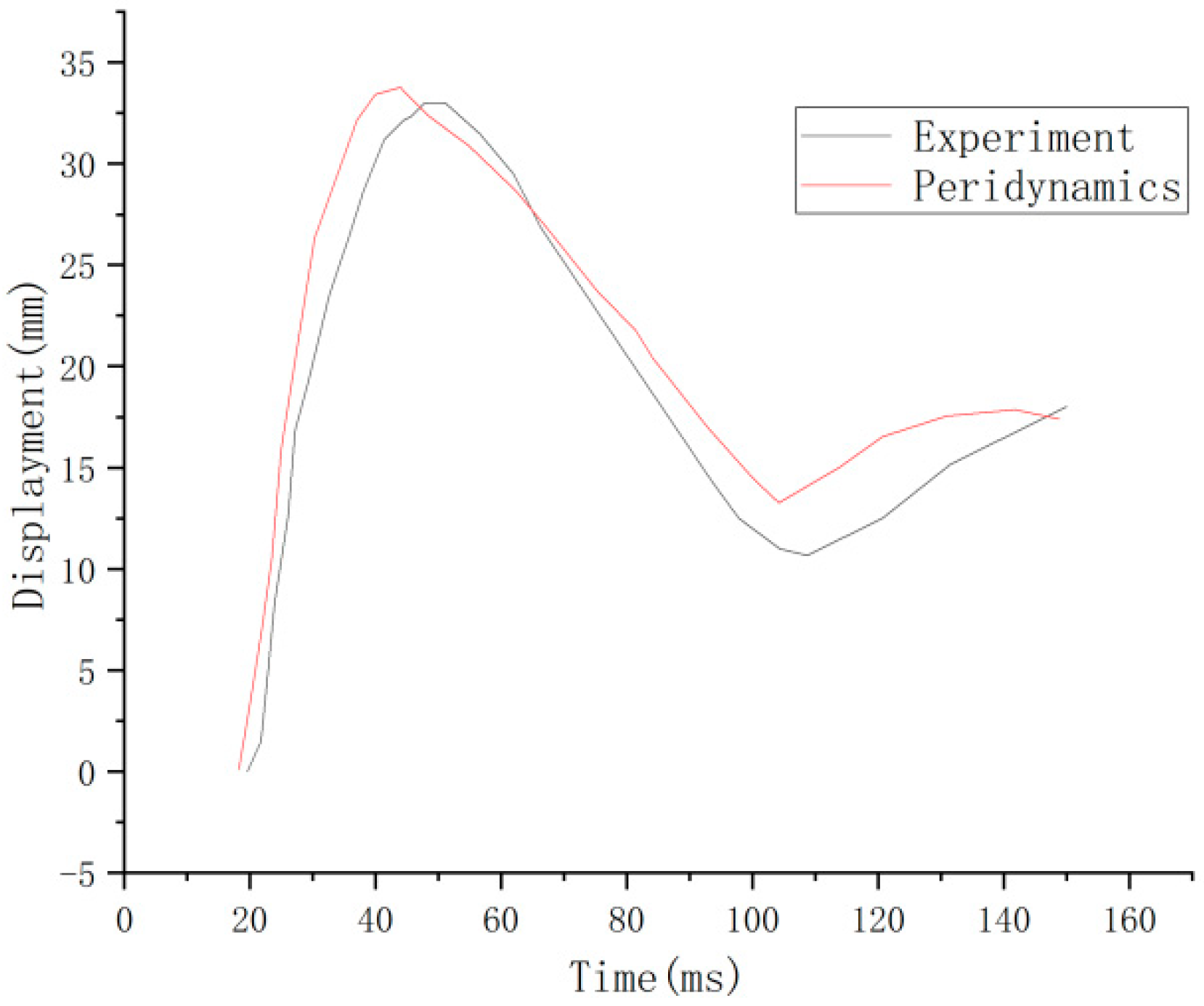
4.2. Failure Behavior of the RC Shear Walls under Impact Loading
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, H.J.; Ying, Y.; Wang, B.; Zhang, Y.X. Experiment on seismic damage behavior of RC shear walls. Build. Struct. 2012, 42, 113–117. (In Chinese) [Google Scholar]
- Cao, R.J. Seismic Damage Analysis of Reinforced Concrete Shear Walls. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2016. (In Chinese). [Google Scholar]
- Lopes, M.S. Experimental shear-dominated response of RC walls: Part I: Objectives, methodology and results. Eng. Struct. 2001, 23, 229–239. [Google Scholar] [CrossRef]
- Lopes, M.S. Experimental shear-dominated response of RC walls. Part II: Discussion of results and design implications. Eng. Struct. 2001, 23, 564–574. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M.J.N.; Synge, A.J. Ductility in earthquake resisting squat shearwalls. J. Proc. 1982, 79, 257–269. [Google Scholar]
- Lefas, I.D.; Kotsovos, M.D.; Ambraseys, N.N. Behavior of reinforced concrete structural walls: Strength, deformation characteristics, and failure mechanism. Struct. J. 1990, 87, 23–31. [Google Scholar]
- Sittipunt, C.; Wood, S.L. Influence of web reinforcement on the cyclic response of structural walls. Struct. J. 1995, 92, 745–756. [Google Scholar]
- Vallenas, J.M.; Bertero, V.V.; Popov, E.P. Hysteric behavior of reinforced concrete structural walls. Recon. Tech. Rep. N 1979, 80, 27533. [Google Scholar]
- Terzioglu, T.; Orakcal, K.; Massone, L.M. Cyclic lateral load behavior of squat reinforced concrete walls. Eng. Struct. 2018, 160, 147–160. [Google Scholar] [CrossRef]
- Salonikios, T.N. Shear strength and deformation patterns of R/C walls with aspect ratio 1.0 and 1.5 designed to Eurocode 8 (EC8). Eng. Struct. 2002, 24, 39–49. [Google Scholar] [CrossRef]
- Salonikios, T.N. Analytical prediction of the inelastic response of RC walls with low aspect ratio. J. Struct. Eng. 2007, 133, 844–854. [Google Scholar] [CrossRef]
- Looi, D.T.W.; Su, R.K.L.; Cheng, B.; Tsang, H.H. Effects of axial load on seismic performance of reinforced concrete walls with short shear span. Eng. Struct. 2017, 151, 312–326. [Google Scholar] [CrossRef]
- Houshmand-Sarvestani, A.; Totonchi, A.; Shahmohammadi, M.A. Numerical assessment of the effects of ADAS yielding metallic dampers on the structural behavior of steel shear walls (SSWs). Mech. Based Des. Struc. 2023, 51, 1626–1644. [Google Scholar] [CrossRef]
- Yi, J.W.; Shi, X.D. Numerical simulation analysis for RC shear walls under impact load. Vibr. Shock 2019, 38, 102–110. (In Chinese) [Google Scholar]
- Tan, J.K.; Su, M.N.; Wang, Y.H. Experimental study on cyclic shear performance of steel plate shear wall with different buckling restraints. Structures. 2022, 35, 469–482. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, X.; Li, Y. Prediction of failure modes, strength, and deformation capacity of RC shear walls through machine learning. J. Build. Eng. 2022, 50, 104145. [Google Scholar] [CrossRef]
- Grégoire, D.; Maigre, H.; Rethore, J.; Combescure, A. Dynamic crack propagation under mixed-mode loading–comparison between experiments and X-FEM simulations. Int. J. Solid Struct. 2007, 44, 6517–6534. [Google Scholar] [CrossRef]
- Meng, Q.; Xue, H.; Song, H.; Zhuang, X.; Rabczuk, T. Rigid-Block DEM Modeling of Mesoscale Fracture Behavior of Concrete with Random Aggregates. J. Eng. Mech. 2023, 149, 2. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Gerstle, W.; Sau, N.; Silling, S. Peridynamic modeling of concrete structures. Nuclear Eng. Design 2007, 237, 1250–1258. [Google Scholar] [CrossRef]
- Gerstle, W.; Sau, N.; Aguilera, E. Micropolar peridynamic constitutive model for concrete 2007. In Proceedings of the 19th International Conference on Structural Mechanics in Reactor Technology, Toronto, Japan, 7 August 2007. [Google Scholar]
- Zhang, N.; Gu, Q.; Huang, S.; Xue, X.; Li, S. A practical bond-based peridynamic modeling of reinforced concrete structures. Eng. Struct. 2021, 244, 112748. [Google Scholar] [CrossRef]
- Yaghoobi, A.; Chorzepa, M.G. Fracture analysis of fiber reinforced concrete structures in the micropolar peridynamic analysis framework. Eng. Fract. Mech. 2017, 169, 238–250. [Google Scholar] [CrossRef]
- Yaghoobi, A.; Chorzepa, M.G. Meshless modeling framework for fiber reinforced concrete structures. Comput. Struct. 2015, 161, 43–54. [Google Scholar] [CrossRef]
- Shi, H.S.; Qian, S.R.; Xu, T. Study on reinforced concrete structure failure based on peridynamic theories. Guizhou Sci. 2016, 34, 64–68. (In Chinese) [Google Scholar]
- Zheng, J.; Shen, F.; Gu, X.; Zhang, Q. Simulating failure behavior of reinforced concrete T-beam under impact loading by using peridynamics. Int. J. Impact Eng. 2022, 165, 104231. [Google Scholar] [CrossRef]
- Zhang, J.; Han, F.; Yang, Z.; Cui, J. Coupling of an atomistic model and bond-based peridynamic model using an extended Arlequin framework. Comput. Methods Appl. Mech. Eng. 2023, 403, 115663. [Google Scholar] [CrossRef]
- Zheng, G.; Li, L.; Han, F.; Xia, Y.; Shen, G.; Hu, P. Coupled peridynamic model for geometrically nonlinear deformation and fracture analysis of slender beam structures. Int. J. Numer. Methods Eng. 2022, 123, 3658–3680. [Google Scholar] [CrossRef]
- Shen, F.; Yu, Y.; Zhang, Q.; Gu, X. Hybrid model of peridynamics and finite element method for static elastic deformation and brittle fracture analysis. Eng. Anal. Bound. Elements. 2020, 113, 17–25. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Liu, L.S.; Liu, Q.W.; Lai, X. Application of an Improved Bond-based Peridynamic Method to Analysis of Flow around a Cylinder. Saf. Environ. Eng. 2018, 5, 174–180. (In Chinese) [Google Scholar]
- Bai, Y.L.; Wang, H.Y.; Xia, M.F.; Ke, J.F. Statistical mesomechanics of solid, linking coupled multiple space and time scales. Appl. Mech. Rev. 2005, 58, 372–388. [Google Scholar] [CrossRef]
- Guo, Z.H.; Shi, X.D. Reinforced Concrete Theory and Analysis; Tsinghua University Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Madenci, E.; Oterkus, E. Peridynamic Theory and its Applications; Springer: New York, NY, USA, 2013. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, F.; Chen, Z.; Zheng, J.; Zhang, Q. Numerical Simulation of Failure Behavior of Reinforced Concrete Shear Walls by a Micropolar Peridynamic Model. Materials 2023, 16, 3199. https://doi.org/10.3390/ma16083199
Shen F, Chen Z, Zheng J, Zhang Q. Numerical Simulation of Failure Behavior of Reinforced Concrete Shear Walls by a Micropolar Peridynamic Model. Materials. 2023; 16(8):3199. https://doi.org/10.3390/ma16083199
Chicago/Turabian StyleShen, Feng, Zihan Chen, Jia Zheng, and Qing Zhang. 2023. "Numerical Simulation of Failure Behavior of Reinforced Concrete Shear Walls by a Micropolar Peridynamic Model" Materials 16, no. 8: 3199. https://doi.org/10.3390/ma16083199
APA StyleShen, F., Chen, Z., Zheng, J., & Zhang, Q. (2023). Numerical Simulation of Failure Behavior of Reinforced Concrete Shear Walls by a Micropolar Peridynamic Model. Materials, 16(8), 3199. https://doi.org/10.3390/ma16083199





