Measurement and Classification Criteria of Strength Decrease Rate and Brittleness Indicator Index for Rockburst Proneness Evaluation of Hard Rocks
Abstract
1. Introduction
2. Definitions of B and SDR
| Indicators | Formula | Parameter | |
|---|---|---|---|
| represent the uniaxial compressive strength and dynamic failure time after peak strength, respectively | |||
| B | 1 | represent the uniaxial compressive strength and Brazilian tensile strength, respectively | |
| represent the strain corresponding to the stress at the unloading point and the terminal strain at the unloading stage, respectively | |||
| represent the pre-peak elastic modulus and post-peak elastic modulus, respectively | |||
- None;
- Weak;
- Medium;
- Strong.
- None;
- Weak;
- Medium;
- Strong.
3. Loading Mode and Rate Effect on B and SDR
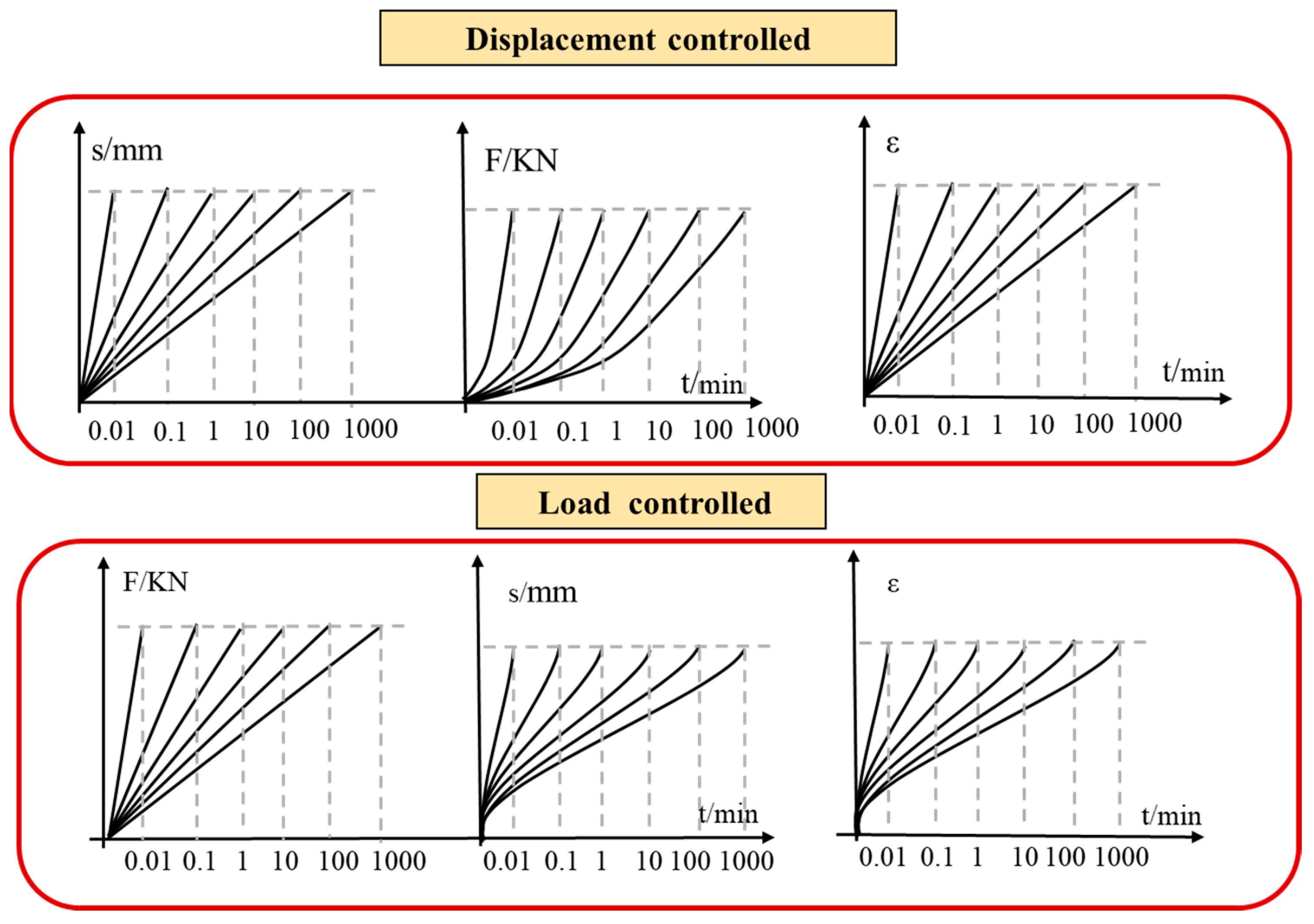
3.1. Testing Design
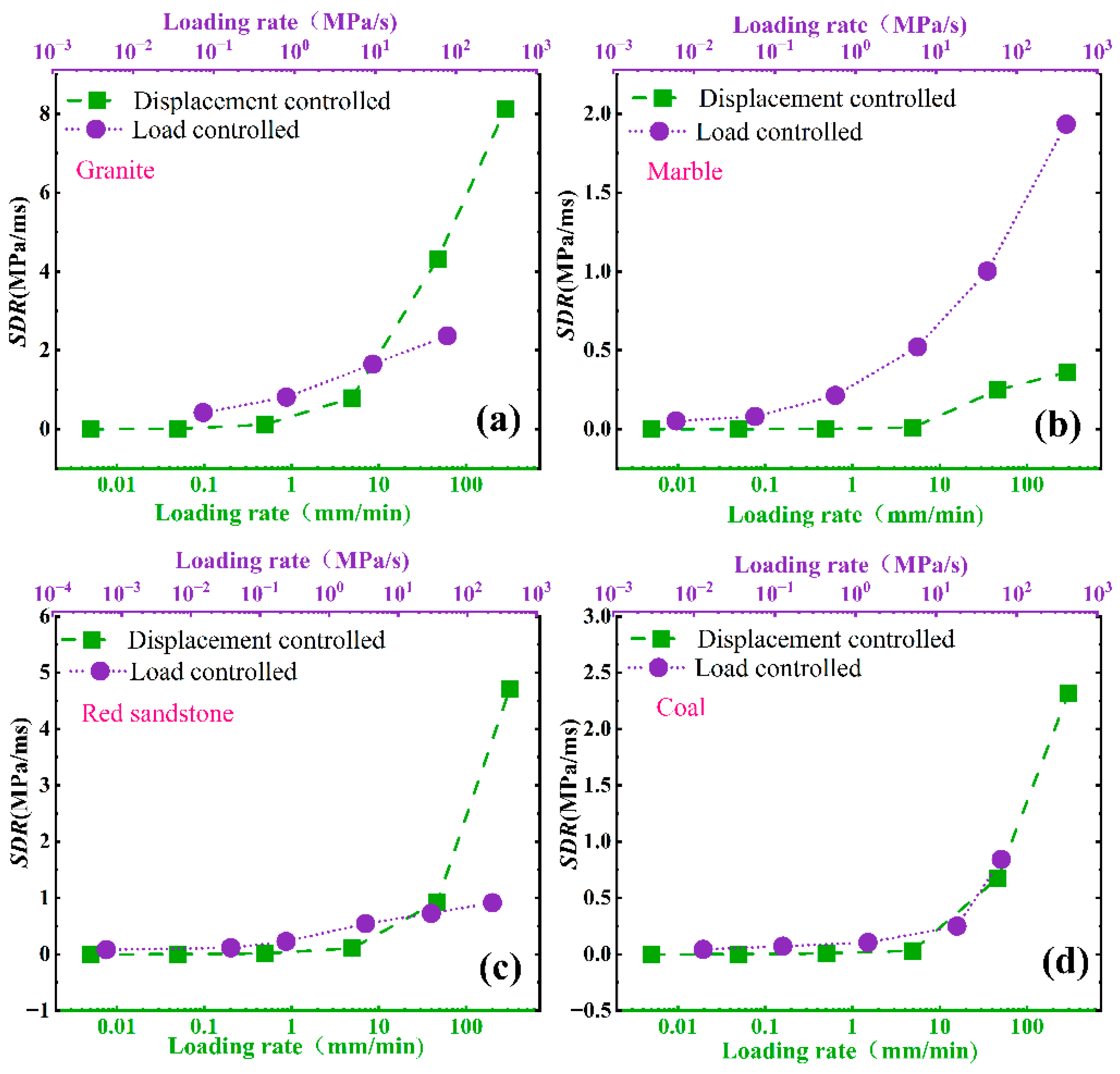
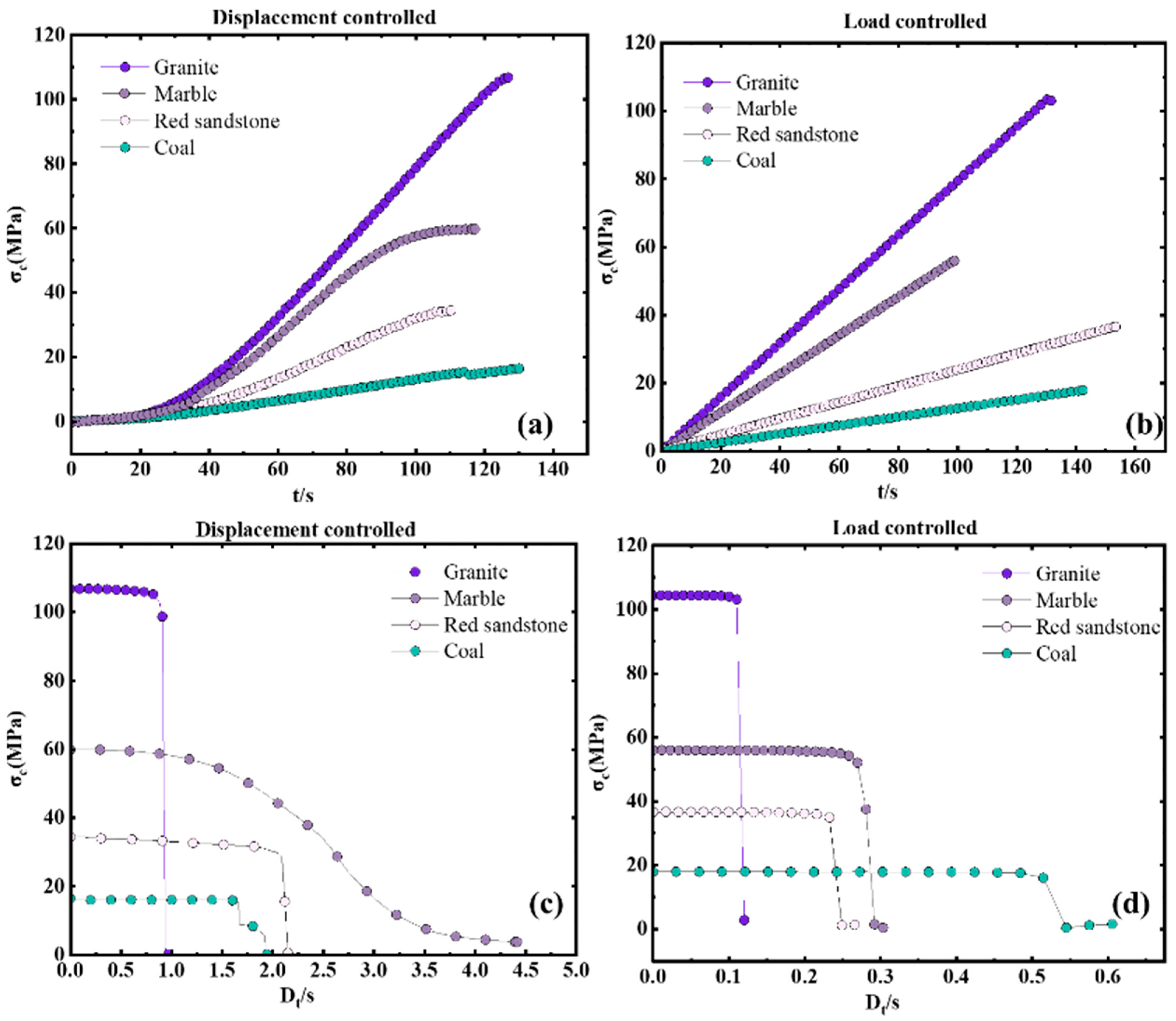
3.2. Determination of SDR
3.3. Determination of B
3.4. Data Processing
3.5. Influence of Loading Terms on B and SDR
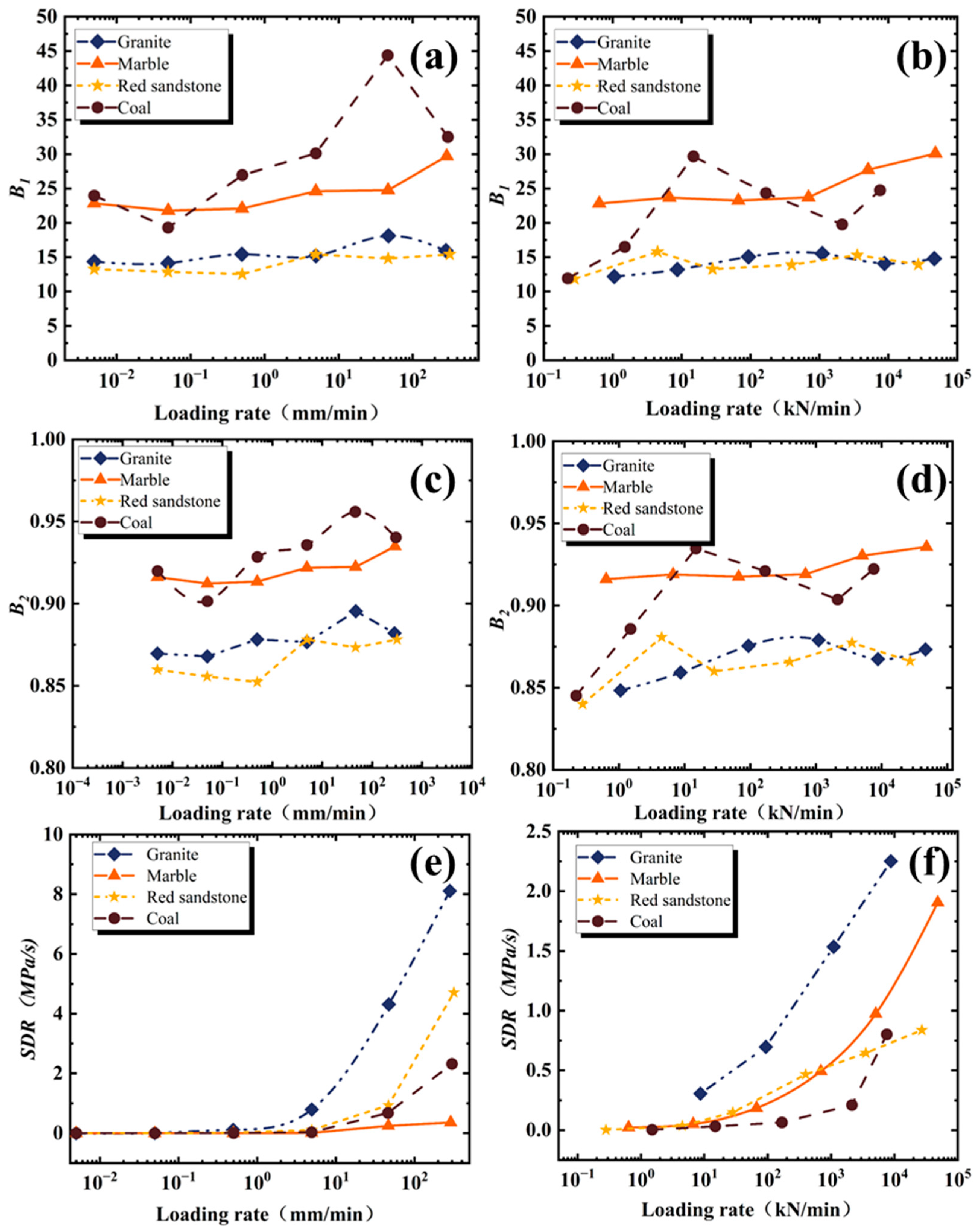
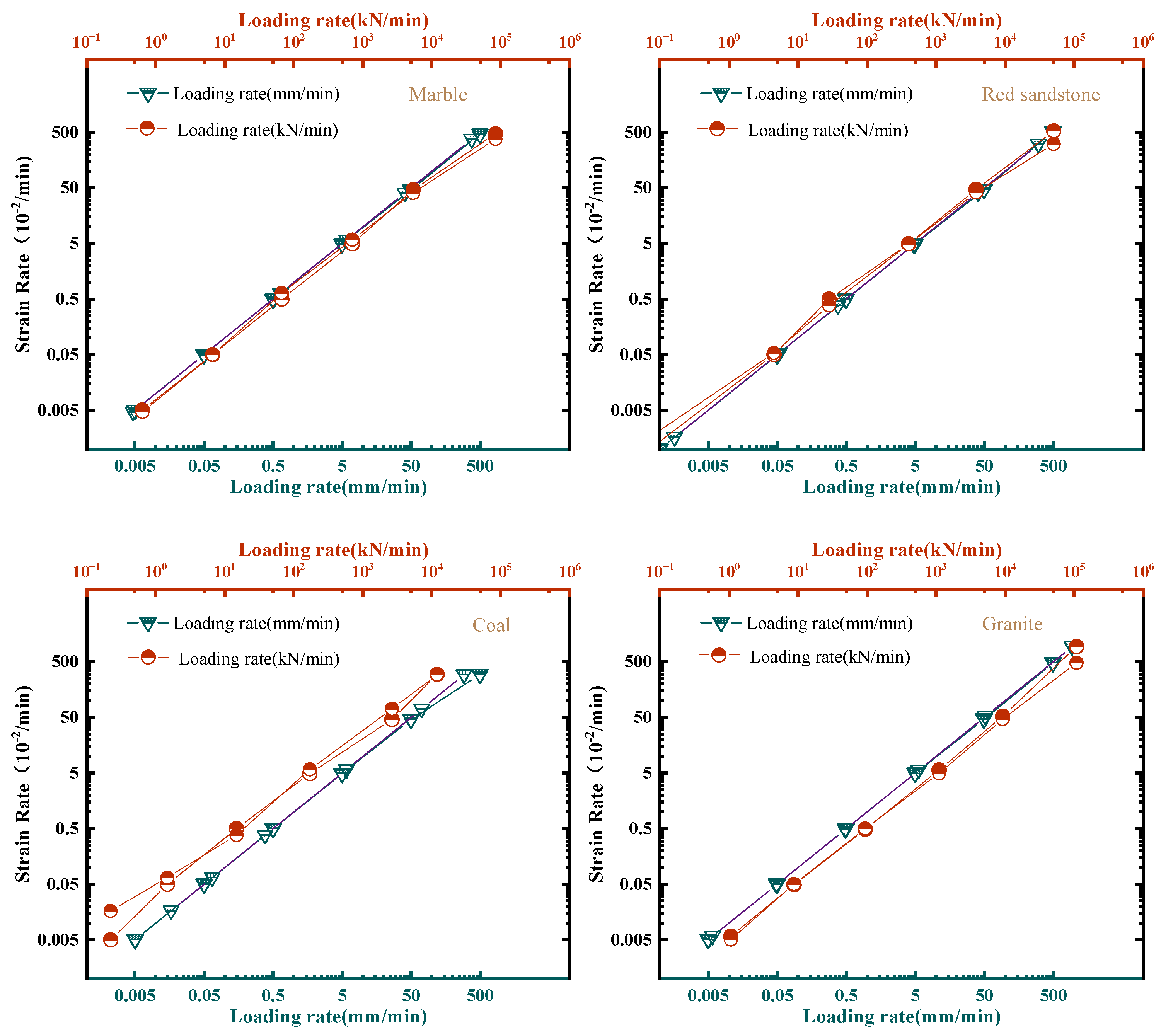
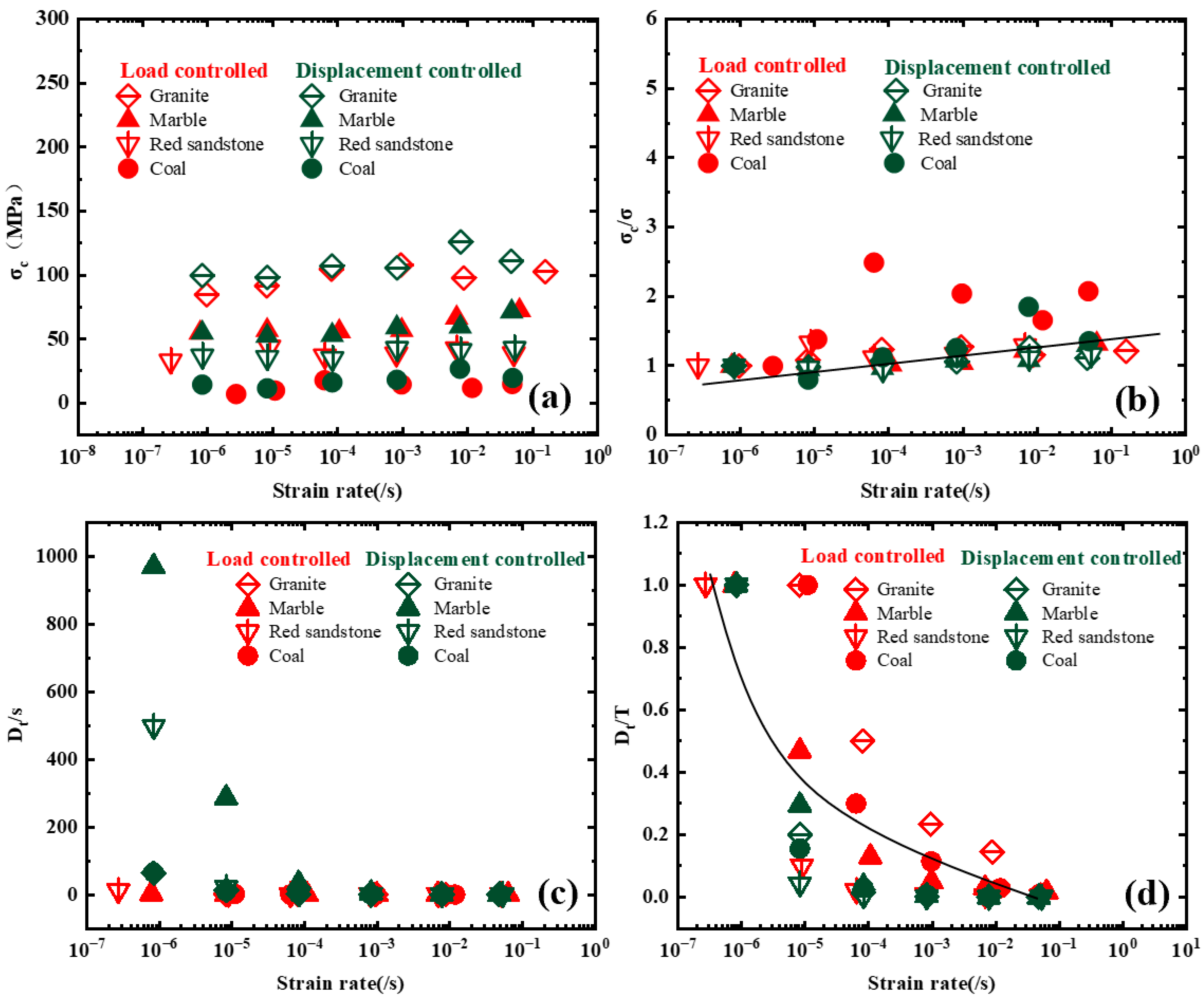
3.5.1. Impact of Loading Rate
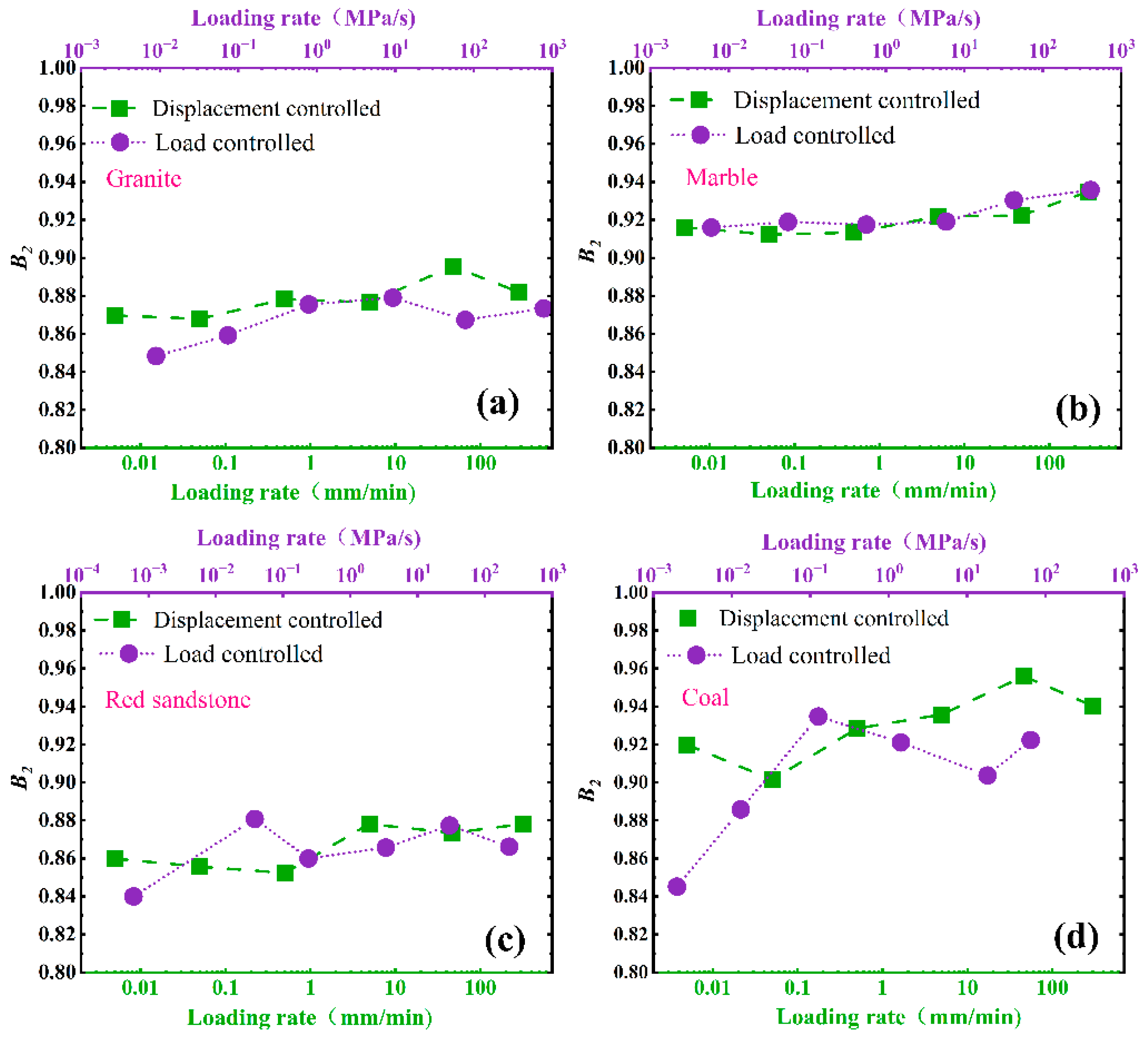
3.5.2. Effect of Loading Mode
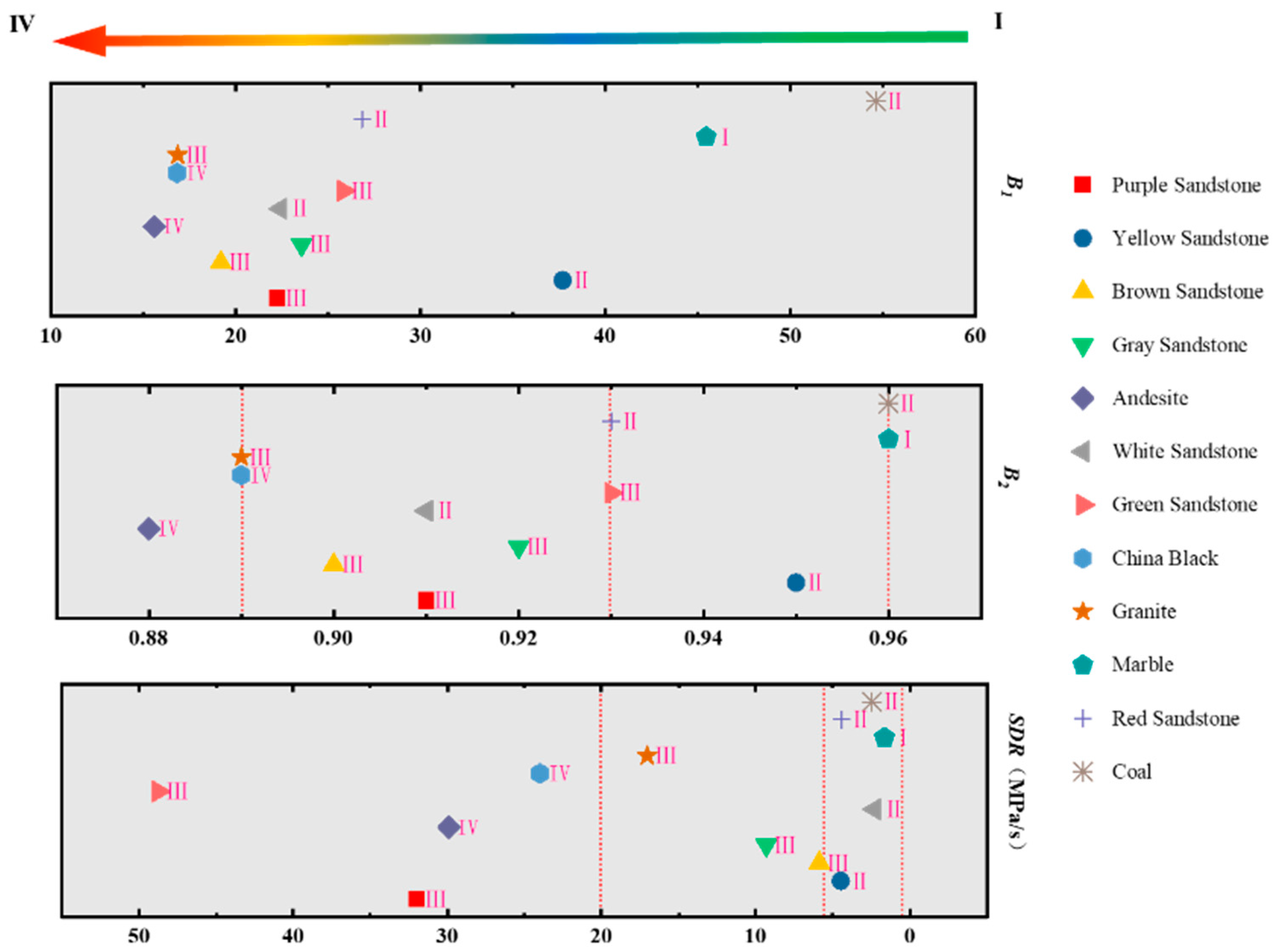
4. Classification Criteria of B and SDR
- None;
- Weak;
- Medium;
- Strong;
- None;
- Weak;
- Medium;
- Strong.
5. Discussion
5.1. Rationality of Classification Criteria
5.2. Strain Rate Effect on Rockburst Index
6. Conclusions
- The B2 and SDR were selected as the basic indexes for the rockburst tendency evaluation of hard rocks. It is considered that the strength decrease rate reflects the speed of stress drop speed and energy release rate in rock failure stage, and the brittleness indicator index value reflects the fundamental properties of rocks. The combination of the two indexes can describe rockburst tendency more comprehensively.
- The reasonable loading mode and rate in rockburst tendency tests were determined. After studying the influence of loading rate and loading mode on rockburst tendency, it is suggested to adopt the displacement control mode of 0.1–0.7 mm/min for rockburst tendency assessment for B2 and SDR.
- The classification criteria of B2 and SDR were put forward. According to the results in this study, and were divided into four grades. It was found that there is a strong consistency between the B2 index and SDR, which proves a rationality of the classification criteria based on the failure phenomena of rocks in uniaxial compression tests.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, K.; Yang, C.; Su, R.; Tao, M.; Wang, S. Failure properties of cubic granite, marble, and sandstone specimens under true triaxial stress. Int. J. Rock Mech. Min. Sci. 2020, 130, 104309. [Google Scholar] [CrossRef]
- Li, X.B.; Gong, F.Q.; Tao, M.; Dong, L.J.; Du, K.; Ma, C.D.; Zhou, Z.L.; Yin, T.B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Cai, M.; Brown, E.T. Challenges in the Mining and Utilization of Deep Mineral Resources. Engineering 2017, 3, 432–433. [Google Scholar] [CrossRef]
- Wu, M.; Ye, Y.; Wang, Q.; Hu, N. Development of Rockburst Research: A Comprehensive Review. Appl. Sci. 2022, 12, 974. [Google Scholar] [CrossRef]
- Solak, T. Ground behavior evaluation for tunnels in blocky rock masses. Tunn. Undergr. Space Technol. 2009, 24, 323–330. [Google Scholar] [CrossRef]
- Farhadian, H. A new empirical chart for rockburst analysis in tunnelling: Tunnel rockburst classification (TRC). Int. J. Min. Sci. Technol. 2021, 31, 603–610. [Google Scholar] [CrossRef]
- Keneti, A.; Sainsbury, B.-A. Review of published rockburst events and their contributing factors. Eng. Geol. 2018, 246, 361–373. [Google Scholar] [CrossRef]
- Malan, D.; Napier, J. A limit equilibrium fracture zone model to investigate seismicity in coal mines. Int. J. Min. Sci. Technol. 2018, 28, 745–753. [Google Scholar] [CrossRef]
- Li, X.; Jian, Z.; Wang, S.; Bing, L. Review and practice of deep mining for solid mineral resources. Zhongguo Youse Jinshu Xuebao/Chin. J. Nonferr. Met. 2017, 27, 1236–1262. [Google Scholar]
- Ma, T.-H.; Tang, C.-A.; Liu, F.; Zhang, S.-C.; Feng, Z.-Q. Microseismic monitoring, analysis and early warning of rockburst. Geomatics, Nat. Hazards Risk 2021, 12, 2956–2983. [Google Scholar] [CrossRef]
- Li, S.; Feng, X.-T.; Li, Z.; Chen, B.; Zhang, C.; Zhou, H. In situ monitoring of rockburst nucleation and evolution in the deeply buried tunnels of Jinping II hydropower station. Eng. Geol. 2012, 137–138, 85–96. [Google Scholar] [CrossRef]
- Voza, A.; Valguarnera, L.; Marrazzo, R.; Ascari, G.; Boldini, D. A New In Situ Test for the Assessment of the Rock-Burst Alarm Threshold During Tunnelling. Rock Mech. Rock Eng. 2022, 56, 1645–1661. [Google Scholar] [CrossRef]
- Wang, W.W. Testing study on rockburst pronounces of serpentine under a deep mine. J. Wuhan Polytech. Univ. 2017, 36, 55–58. [Google Scholar]
- Wang, S.-F.; Sun, L.-C.; Tang, Y.; Jing, Y.; Li, X.-B.; Yao, J.-R. Field application of non-blasting mechanized mining using high-frequency impact hammer in deep hard rock mine. Trans. Nonferr. Met. Soc. China 2022, 32, 3051–3064. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Sun, Y.; Tian, B.; Liu, X.; Chen, D.; Wu, Y. A Kind of Prediction Based on SOM Neural Clustering and Combination Weighting Evaluation Method. In Proceedings of the WWW’21: Companion Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 90–96. [Google Scholar]
- Zhou, J.; Li, X.; Shi, X. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines. Saf. Sci. 2012, 50, 629–644. [Google Scholar] [CrossRef]
- Tang, C.; Wang, J.; Zhang, J. Preliminary engineering application of microseismic monitoring technique to rockburst prediction in tunneling of Jinping II project. J. Rock Mech. Geotech. Eng. 2010, 2, 193–208. [Google Scholar] [CrossRef]
- Liu, H. Classified prediction model of rockburst using rough sets-normal cloud. Neur. Comput. Appl. 2019, 31, 8185–8193. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, G.; Hao, W.; Bing, D. Risk assessment of rockburst via an extended MABAC method under fuzzy environment. Tunn. Undergr Space Technol. 2019, 83, 533–544. [Google Scholar] [CrossRef]
- Xuan, Z.; Bu, X. The Forecasting of Rockburst in Deep-buried Tunnel with Adaptive Neural Network. In Proceedings of the 2009 International Conference on Industrial and Information Systems, Haikou, China, 24–25 April 2009; pp. 3–6. [Google Scholar]
- Chen, J.; Chen, Y.; Yang, S.; Zhong, X.; Han, X. A prediction model on rockburst intensity grade based on variable weight and matter-element extension. PLoS ONE 2019, 14, e0218525. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Wu, J.; Zhao, D.; Fu, H. Rockburst prediction model based on comprehensive weight and extension methods and its engineering application. Bull. Eng. Geol. Environ. 2020, 79, 4891–4903. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel ensemble intelligence methodologies for rockburst assessment in complex and variable environments. Sci. Rep. 2022, 12, 1844. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Taheri, A.; Ribeiro e Sousa, L.; Karakus, M. Rockburst assessment in deep geotechnical conditions using true-triaxial tests and data-driven approaches. Int. J. Rock Mech. Min. Sci. 2020, 128, 104279. [Google Scholar] [CrossRef]
- Cui, Z.G. Rock burst tendency evaluation and analysis based on laboratory test. Northeast Water Resour. Hydropower 2019, 37, 3. [Google Scholar]
- Gong, F.; Luo, S.; Jiang, Q.; Xu, L. Theoretical verification of the rationality of strain energy storage index as rockburst criterion based on linear energy storage law. J. Rock Mech. Geotech. Eng. 2022, 14, 1737–1746. [Google Scholar] [CrossRef]
- Liu, S.; Xiao, F.; Li, T.; Zhang, B. Analysis of Impact Tendency and Sensitivity of Fractured Rock with Different Crack Arrest Measures. Sustainability 2022, 14, 13833. [Google Scholar] [CrossRef]
- Gong, F.; Yan, J.; Li, X.; Luo, S. A peak-strength strain energy storage index for rock burst proneness of rock materials. Int. J. Rock Mech. Min. Sci. 2019, 117, 76–89. [Google Scholar] [CrossRef]
- Gong, F.Q.; Yan, J.Y.; Li, X.B. A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index. Chin. J. Rock Mech. Eng. 2018, 37, 1993–2014. [Google Scholar]
- Kang, Q.; Xia, Y.; Shi, M.; Zhang, W.; Wang, W.; Kong, D.; Wang, Y. Evaluation of Rock Burst Propensity and Rock Burst Mechanism in Deep Phosphate Mines: A Case Study of Sujiapo Phosphate Mine, Hubei Province, China. Adv. Mater. Sci. Eng. 2022, 2022, 7874016. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y. Long and short term rockburst risk assessment of deep hard rock. Chin. J. Rock Mech. Eng. 2022, 41, 21. [Google Scholar]
- Xia, Y.; Zhou, H.; Zhang, C.; He, S.; Gao, Y.; Wang, P. The evaluation of rock brittleness and its application: A review study. Eur. J. Environ. Civ. Eng. 2019, 26, 239–279. [Google Scholar] [CrossRef]
- Du, K.; Sun, Y.; Yang, S.; Lv, S.; Wang, S. Differences of Mechanical Parameters and Rockburst Tendency Indices between Coal and Non-Coal Rocks and Modified Rockburst Tendency Classification Criteria for Non-Coal Rocks. Appl. Sci. 2021, 11, 2641. [Google Scholar] [CrossRef]
- Methods for Determination, Monitoring and Control of Rock Burst—Part 2: Classification and Index Determination of Coal Bursting Liability. 2010. Available online: https://kns.cnki.net/kcms2/article/abstract?v=kxaUMs6x75KB1kF296ShrYo_9ZoYIWW4VfT4bfQP25xUu13oQ_hU9IEAfQx8mV-5auDdJFuN3RSHbQ9f9FWvw%3d%3d&uniplatform=NZKPT (accessed on 10 April 2023).
- Jian, M.X.; Lin, Y.; Ma, C.D.; Xu, M.S.; He, Z.G.; Wang, Y.Q. Evaluation and prevention of rockburst tendency in deep mining of Malu Ping Mine. Min. Technol. 2011, 11, 52–54. [Google Scholar]
- Qin, M.; Liu, C. Application of Comprehensive Analysis of Rockburst Tendency in Deep Mining of Ashele Copper Mine. Min. Metall. Eng. 2015, 35, 39–45. [Google Scholar]
- Huang, B.; Li, S.L.; Gao, Z.P.; Hu, G.Y.; Wu, X.H.; Xu, G. Comprehensive Evaluation of Rockburst on Deep and Large-scale Mining in Dahongshan Iron Mine. Ment. Mine 2016, 45, 19–25. [Google Scholar]
- Zhou, H.; Chen, S.K.; Zhang, G.Z.; Wang, H.L.; He, H.D.; Feng, J. Rockburst Prediction in Deep Lying and Long Tunnel Based on Efficiency Coefficient Method and Ground Stress Field Inversion. J. Eng. Geol. 2019. [Google Scholar] [CrossRef]
- Yi, Y.L.; Cao, P.; Pu, C.Z. Multi-factorial Comprehensive Estimation for Jinchuan’s Deep Typical Rockburst Tendency. Sci. Technol. Rev. 2010, 28, 76–80. [Google Scholar]
- Qiao, C.S.; Tian, Z.Y. Study on the possibility of rock burst in Dongguashan Copper Deposit. Chin. J. Rock Mech. Eng. 1998, 17, 917–921. [Google Scholar]
- Liu, R.T.; Zhang, X.M.; Liu, J.X. Experimental study on rock burst tendency of granite in Linglong Gold Deposit. ShanXi Archit. 2014, 40, 57–59. [Google Scholar]
- Jiang, C.L.; Jiang, Z.Q.; Zhang, R. Experimental Study of Impact Proneness of Deep Coal Seam and Roof Rock. Coal Technol. 2010, 29, 108–110. [Google Scholar]
- Guo, D.M.; Zhang, T.; Li, Y.; Wang, G.D.; Li, G.E.; Guo, A.M. Research on rockburst tendency and its preventive measures of 800m deep surrounding-rock in Huxi coal mine. China Min. Mag. 2008, 17, 50–63. [Google Scholar]
- Chen, S.J.; Guo, W.J.; Yang, Y.J.; Zou, J. Experimental study on bursting liability of coal seam. Min. Saf. Environ. Prot. 2007, 34, 10–15. [Google Scholar]
- Guo, D.M.; Hou, J.F.; Yan, H.X.; Wang, J.; Cheng, H.Y.; Wang, Y.X. Study on bursting liability of deep surrounding rock of Suncun Coal Mine -1 300 m and countermeasures. J. Jiaozuo Inst. Technol. (Nat. Sci.) 2003, 22, 9–11. [Google Scholar]
- Tian, S.F. The Risk Assessment and Prediction-Prevention of Rockburst in PengZhuang Mine. 2011. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C475KOm_zrgu4lQARvep2SAkWGEmc0QetxDh64Dt3veMp_smSqBMOO34GtmQPt4ZcHD-metONYmBhxwPqQEl0d7S&uniplatform=NZKPT&src=copy (accessed on 10 April 2023).
- Wang, G.F.; Li, Q.; Zhao, Z.L.; Pang, Y.H. The Impact Tendentiousness Testing of Working Faces and Roadways with Strong Rock burst and Fore Support System. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2011, 30, 1–8. [Google Scholar]
- Sun, Q.J. Experimental study on bursting liability of Longjiabao No. 2 coal seam. Shanxi Coking Coal Sci. Technol. 2010, 23–26. [Google Scholar] [CrossRef]
- Guan, W. The Risk Assessment and Prediction of Rock Burst in the No. 9 District of No. 2 Jining Coal Mine. 2014. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C475KOm_zrgu4lQARvep2SAkkyu7xrzFWukWIylgpWWcEnphZzgD0g6QolGV8xVCW1j7aGuBkkqKhZFS6E685Xmi&uniplatform=NZKPT&src=copy (accessed on 10 April 2023).
- Liu, Z.P.; Liu, W.B.; Wu, L.Q.; Lu, S.B. Experiment Study of Burst Tendency of Coal and Rock Layers at Tangkou Coal Mine. Saf. Coal Min. 2009, 40, 8–10. [Google Scholar]
- Li, Y.S.; Hu, Y.C. A study on the coal seam pressure bump tendency in Ding6 coal seam in Pingdingshan Coal Group No. 1 Coal Mine. Saf. Coal Min. 2009, 36, 99–101. [Google Scholar]
- Meng, H.D.; Hou, X.Z.; Li, H.Y.; Zhao, Q. Monitoring and Prevention Research of Working Face Rock Burst in Deep Coal Well with Large Dip Angle. Coal Technol. 2014, 33, 63–65. [Google Scholar]
- Wang, H.W.; Jiang, Y.D.; Deng, D.X.; Zhang, D.Q.; Lv, J.G. Investigation on the inducing factors of coal bursts under complicated geological environment in Yima mining area. Chin. J. Rock Mech. Eng. 2017, 36, 4085–4092. [Google Scholar]
- Zhang, P.D.; Cui, J.S.; Wang, H.; Cai, F.; Gao, C. Experimental study on bursting liability of No.7 coal and roof in Yaoqiao Coal Mine. Coal Sci. Technol. Mag. 2015, 47–50. [Google Scholar]
- Zheng, S.D. Exploration on comprehensive control technology of rock burst in Gengcun Coal Mine. Inn. Mong. Coal Econ. 2014, 2. [Google Scholar]
- Wang, J.; Cui, J.S.; Hao, Y.X.; Zhang, Y.L.; Meng, Z.G.; Wang, H. Experement study on bursting Liability of 12# coal and roof rock of Hongyang coal mine. China Min. Mag. 2016, 25, 70–101. [Google Scholar]
- Hu, S.Y.; Zhang, H. Research on rockburst risk assessment and prevention techniques in Changcun Coal Mine. China Energy Environ. Prot. 2019, 41, 15–23. [Google Scholar]
- Wang, L.F.; Zhong, Z.L.; Liu, Y.L.; Xin, C.R. Evaluation and Control of Rock Burst Hazard of 2315 Working Face of Anju Coal Mine. Coal Min. Technol. 2019, 24, 120–123. [Google Scholar]
- Su, C.D.; Yuan, R.F.; Zhai, X.X. Experimental Research on Bursting Liability Index of Coal Samples of ChengJiao Coal Mine. Chin. J. Rock Mech. Eng. 2013, 32, 3696–3704. [Google Scholar]
- Jiang, F.X.; Zhu, S.T.; Wang, X.Y.; Jiang, Y.W.; Ning, T.Z.; Sun, S.H. Energy accumulation characteristics and rockburst mechanism of surrounding rock at heading face of extra-thick coal seam. Chin. J. Geotech. Eng. 2019, 41, 2071–2078. [Google Scholar]
- Pan, J.F.; Jian, F.J.; Liu, S.H.; Zhao, W.G.; Yuan, D.S.; Wang, H.T.; Liu, H. Geological Characteristic and Control of Rock Burst of Huanglong Jurassic Coal Mine Field. Coal Min. Technol. 2019, 24, 110–115. [Google Scholar]
- Kim, J.; Moridis, G.J. Numerical analysis of fracture propagation during hydraulic fracturing operations in shale gas systems. Int. J. Rock Mech. Min. Sci. 2015, 76, 127–137. [Google Scholar] [CrossRef]
- Hajiabdolmajid, V.; Kaiser, P. Brittleness of rock and stability assessment in hard rock tunneling. Tunn. Undergr. Space Technol. 2003, 18, 35–48. [Google Scholar] [CrossRef]
- Kahraman, S. Correlation of TBM and drilling machine performances with rock brittleness. Eng. Geol. 2002, 65, 269–283. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, D.; Su, J.; Niu, X. Experimental study of influences of confining pressures and ground water on residual strength and post-peak volumetric change of soft rock. Chin. J. Rock Mech. Eng. 2009, 28, 2644–2650. [Google Scholar]
- Jing, H.W. Experimental study on dilatancy nature of the rock post-peak behavior. Rock Soil Mech. 2003, 24, 93–96. [Google Scholar]
- Wong, L.N.Y.; Meng, F.; Guo, T.; Shi, X. The Role of Load Control Modes in Determination of Mechanical Properties of Granite. Rock Mech. Rock Eng. 2019, 53, 539–552. [Google Scholar] [CrossRef]
- Gong, F.-q.; Wang, Y.-l.; Luo, S. Rockburst proneness criteria for rock materials: Review and new insights. J. Cent. South Univ. 2020, 27, 2793–2821. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, Y.H.; Li, T.J. Griffith theory and criterion of rockburst. J. Rock Mech. Eng. 1996, 15, 491–495. [Google Scholar]
- Zhang, J.; Fu, B.; Li, Z.; Song, S.; Shang, Y. Criterion and classification for strain mode rockbursts based on five-factor comprehensive method. Harmonis. Rock Eng. Environ. 2012, 1435–1440. [Google Scholar]
- Singh, S.P. The influence of rock properties on the occurrence and control of rockbursts. Min. Sci. Technol. 1987, 5, 11–18. [Google Scholar] [CrossRef]
- Du, K.; Li, X.; Su, R.; Tao, M.; Lv, S.; Luo, J.; Zhou, J. Shape ratio effects on the mechanical characteristics of rectangular prism rocks and isolated pillars under uniaxial compression. Int. J. Min. Sci. Technol. 2022, 32, 347–362. [Google Scholar] [CrossRef]
- Du, K.; Sun, Y.; Zhou, J.; Khandelwal, M.; Gong, F. Mineral Composition and Grain Size Effects on the Fracture and Acoustic Emission (AE) Characteristics of Rocks Under Compressive and Tensile Stress. Rock Mech. Rock Eng. 2022, 55, 6445–6474. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. State Administration for Market Regulation, Standard for Test Methods of Engineering Rock Mass. 2013. Available online: https://kns.cnki.net/kcms2/article/abstract?v=kxaUMs6x75KB1kF296ShrYo_9ZoYIWW4VfT4bfQP25xUu13oQ_hU422dDazkYSspThIUfafUZKejgo7g1IOMg%3d%3d&uniplatform=NZKPT&src=copy (accessed on 10 April 2023).
- Cheng, Y.; Zhang, Y.L.; Ma, Y.L. The Mechanism of Rockburst and the Control Countermeasure in Deep-Well Tough Rock, Controlling Seismic Hazard and Sustainable Development of Deep Mines. In Proceedings of the 7th International Symposium on Rockburst and Seismicity in Mines (Rasim7), Dalian, China, 21–23 August 2009; Volume 1 and 2, pp. 313–318. [Google Scholar]
- Si, X.F.; Huang, L.Q.; Gong, F.Q.; Liu, X.L.; Li, X.B. Experimental investigation on influence of loading rate on rockburst in deep circular tunnel under true-triaxial stress condition. J. Cent. South Univ. 2020, 27, 2914–2929. [Google Scholar] [CrossRef]
- Hu, F.; Cheng, J.Z.; Li, C.Y. Experiment study on rock burst of granite roadway under the loading rate effect. Min. Metall. 2019, 28. [Google Scholar]
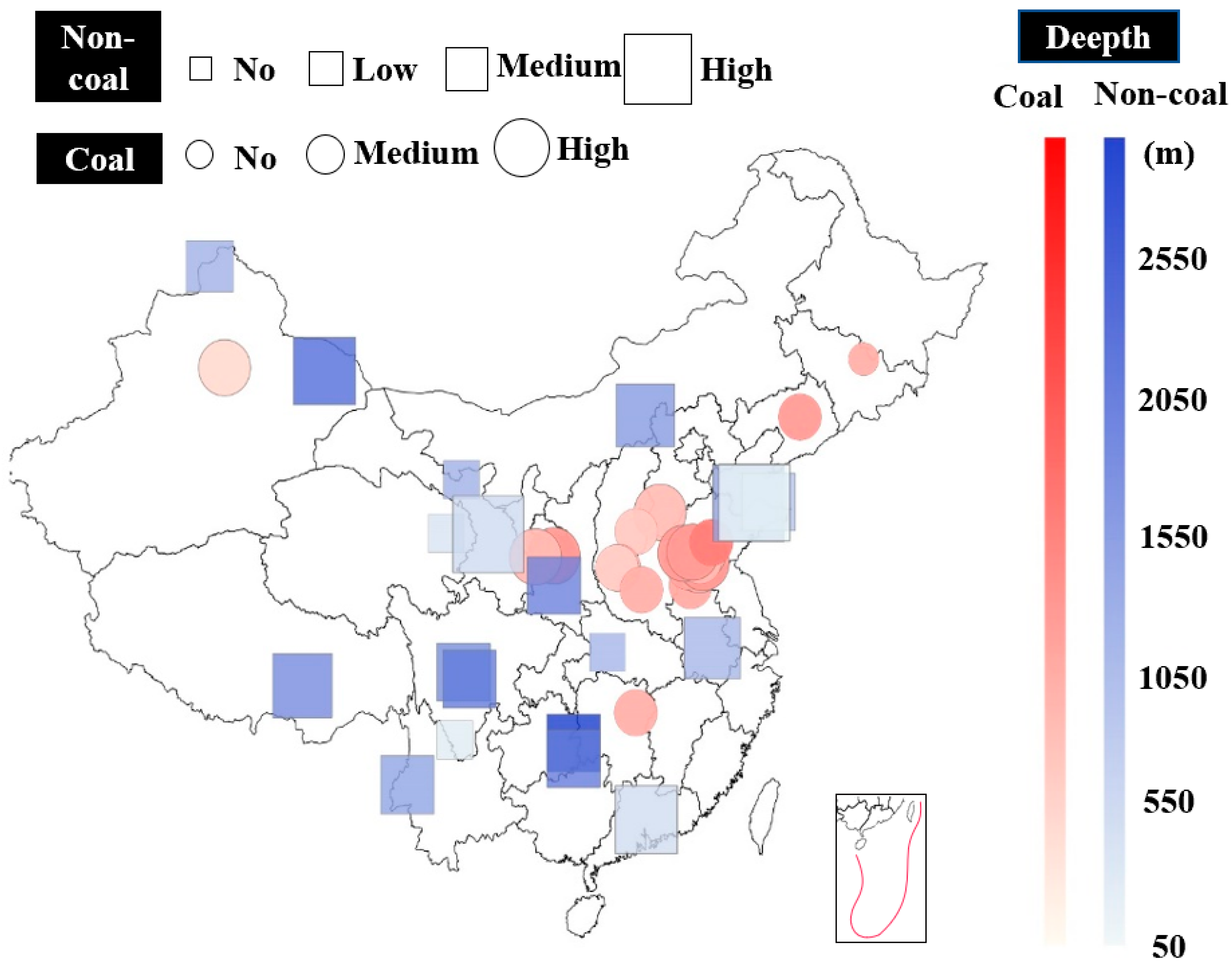
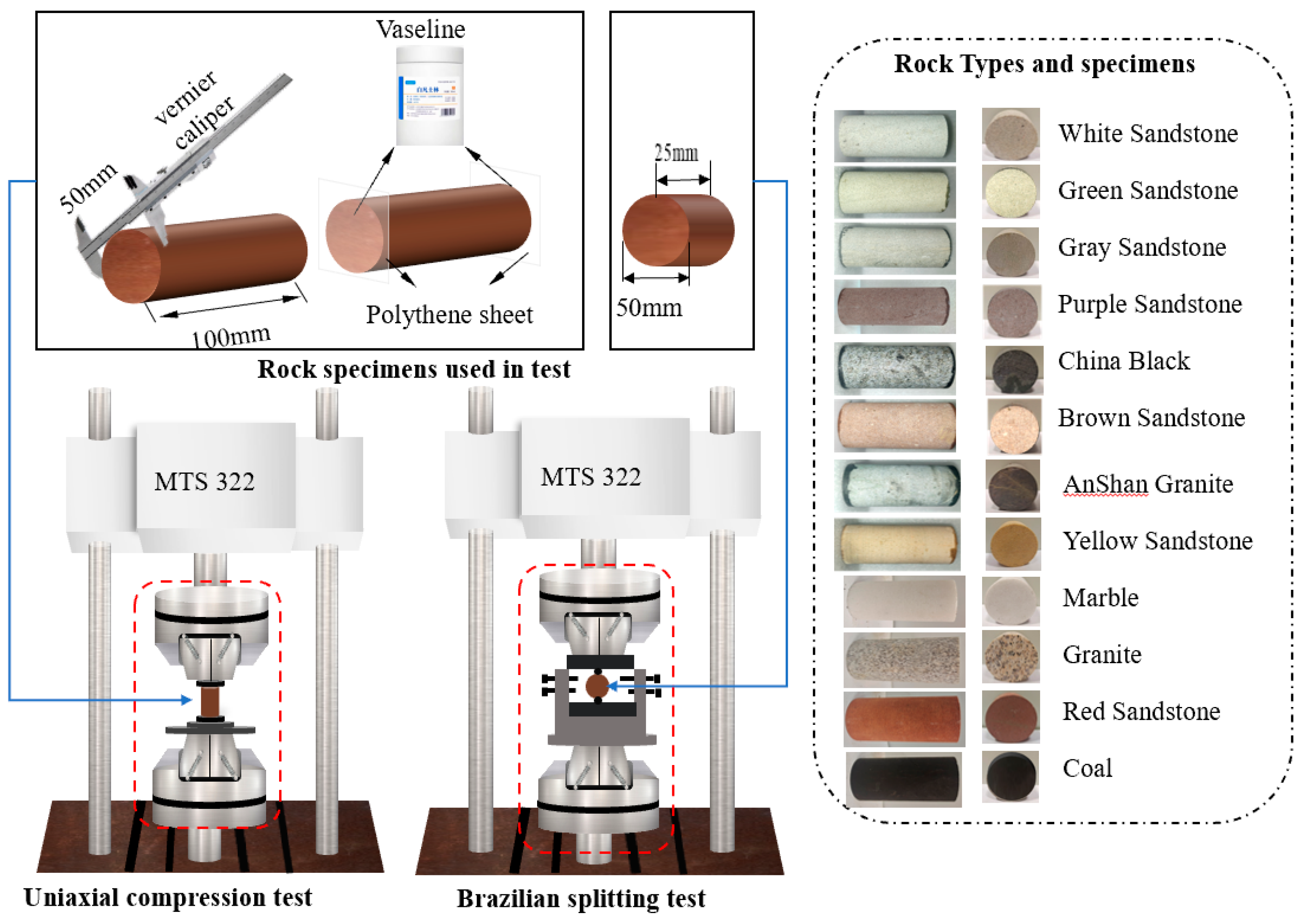
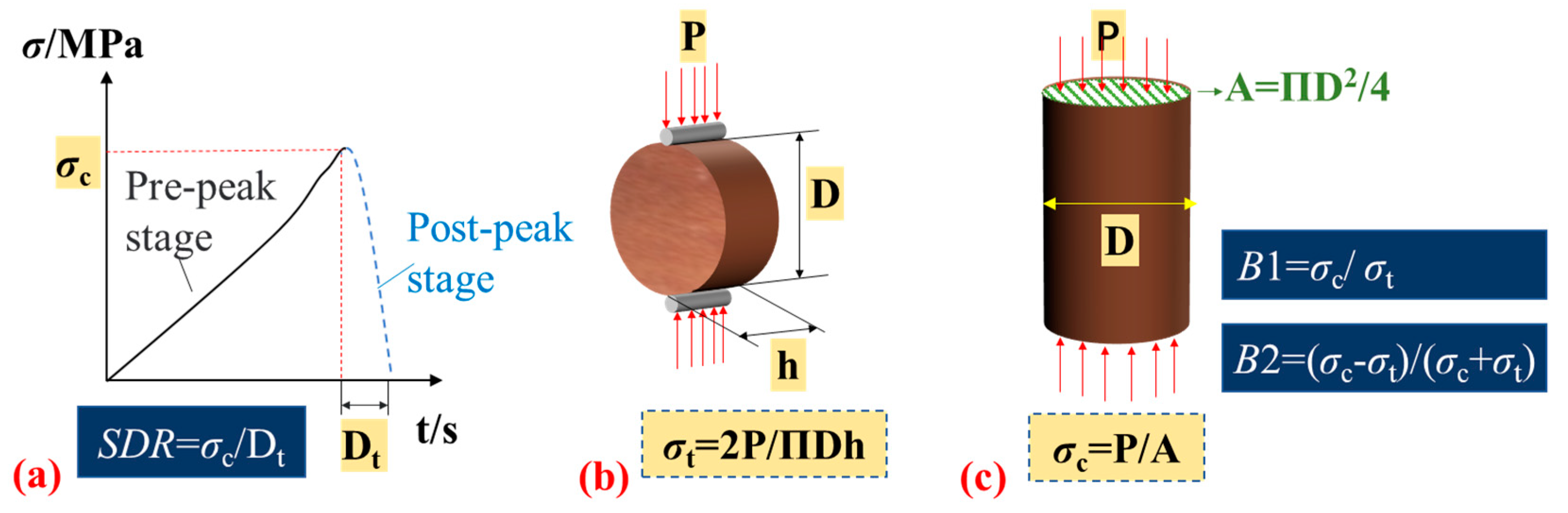
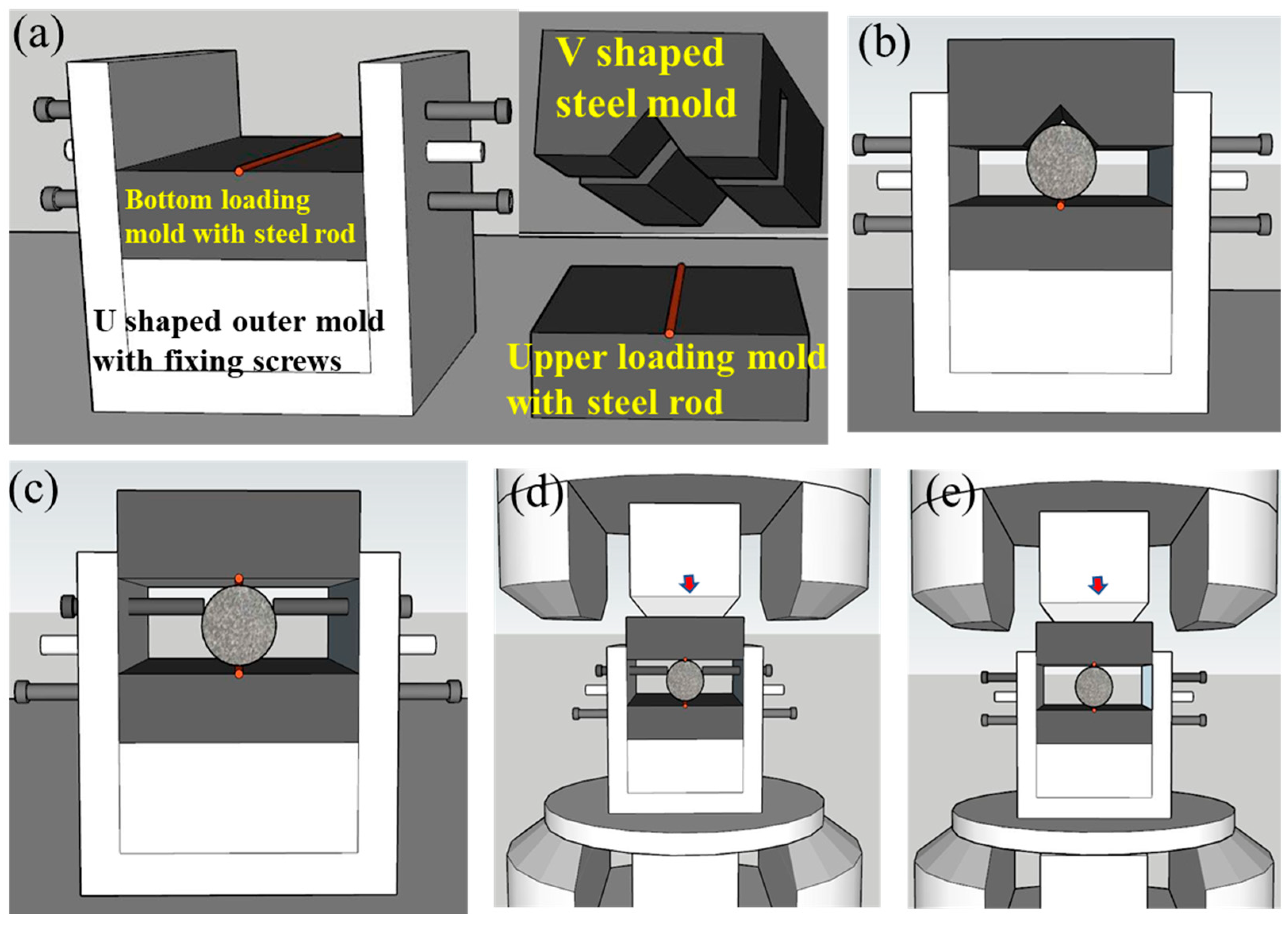

| Rock Lithology | Loading Rate of Each Group | ||||||||
| Group 1 | Group 2 | Group 3 | |||||||
| kN/min | MPa/s | Sample Number | kN/min | MPa/s | Sample Number | kN/min | MPa/s | Sample Number | |
| Granite | 1.06 | 0.009 | 1 | 8.72 | 0.074 | 1 | 93.48 | 0.7935 | 1 |
| Marble | 0.64 | 0.006 | 1 | 6.66 | 0.057 | 1 | 66.67 | 0.5659 | 1 |
| Red sandstone | 0.07 | 0.0006 | 1 | 4.49 | 0.038 | 1 | 28.17 | 0.2391 | 1 |
| Coal | 0.22 | 0.002 | 1 | 1.50 | 0.013 | 1 | 14.87 | 0.1262 | 1 |
| Rock Lithology | Group 4 | Group 5 | Group 6 | ||||||
| kN/min | MPa/s | kN/min | MPa/s | kN/min | MPa/s | ||||
| Granite | 1101.60 | 9.3507 | 1 | 8799.93 | 78.383 | 1 | 46,683.47 | 778.0578 | 1 |
| Marble | 693.32 | 5.8857 | 1 | 5082.66 | 43.1430 | 1 | 48,380.29 | 410.6647 | 1 |
| Red sandstone | 397.46 | 3.37377 | 1 | 3540.87 | 30.0558 | 1 | 27,172.56 | 230.6478 | 1 |
| Coal | 168.14 | 1.4273 | 1 | 2135.74 | 18.1287 | 1 | 7590.34 | 64.4288 | 1 |
| Rock Lithology | Loading Rate (mm/min) | Formula (1) | Formula (2) | SDR (MPa/s) |
|---|---|---|---|---|
| Granite | 0.005 | 14.35 | 0.87 | 1.57 |
| Granite | 0.05 | 14.14 | 0.87 | 7.72 |
| Granite | 0.49 | 15.42 | 0.88 | 114.25 |
| Granite | 4.94 | 15.20 | 0.88 | 795.80 |
| Granite | 47.18 | 18.12 | 0.90 | 4299.82 |
| Granite | 281.23 | 15.95 | 0.88 | 8109.59 |
| Marble | 0.005 | 22.83 | 0.92 | 0.06 |
| Marble | 0.05 | 21.78 | 0.91 | 0.18 |
| Marble | 0.50 | 22.08 | 0.91 | 1.61 |
| Marble | 4.93 | 24.59 | 0.92 | 11.08 |
| Marble | 46.52 | 24.75 | 0.92 | 250.26 |
| Marble | 288.25 | 29.69 | 0.93 | 362.04 |
| Red sandstone | 0.001 | 13.27 | 0.86 | 0.07 |
| Red sandstone | 0.05 | 12.86 | 0.86 | 1.69 |
| Red sandstone | 0.50 | 12.54 | 0.85 | 16.25 |
| Red sandstone | 4.94 | 15.41 | 0.88 | 108.82 |
| Red sandstone | 46.63 | 14.80 | 0.87 | 932.70 |
| Red sandstone | 316.67 | 15.41 | 0.88 | 4627.39 |
| Coal | 0.005 | 23.95 | 0.92 | 0.22 |
| Coal | 0.05 | 19.30 | 0.90 | 1.16 |
| Coal | 0.50 | 26.95 | 0.93 | 8.47 |
| Coal | 4.93 | 30.12 | 0.94 | 32.00 |
| Coal | 46.04 | 44.38 | 0.96 | 676.21 |
| Coal | 298.95 | 32.50 | 0.94 | 2320.13 |
| Rock Type | Loading Rate (kN/min) | Formula (1) | Formula (2) | SDR (MPa/s) |
|---|---|---|---|---|
| Granite | 1.06 | 12.19 | 0.85 | / |
| Granite | 8.72 | 13.20 | 0.86 | 305.62 |
| Granite | 93.48 | 15.06 | 0.88 | 697.20 |
| Granite | 1101.60 | 15.53 | 0.88 | 1534.98 |
| Granite | 8799.93 | 14.08 | 0.87 | 2251.52 |
| Granite | 46,683.47 | 14.78 | 0.87 | -- |
| Marble | 0.64 | 22.81 | 0.92 | 23.38 |
| Marble | 6.66 | 23.66 | 0.92 | 51.82 |
| Marble | 66.67 | 23.24 | 0.92 | 184.78 |
| Marble | 693.32 | 23.71 | 0.92 | 492.96 |
| Marble | 5082.66 | 27.70 | 0.93 | 973.80 |
| Marble | 48,380.29 | 30.08 | 0.94 | 1904.80 |
| Red sandstone | 0.28 | 11.84 | 0.84 | 2.75 |
| Red sandstone | 4.49 | 15.77 | 0.88 | 36.57 |
| Red sandstone | 28.17 | 13.28 | 0.86 | 148.54 |
| Red sandstone | 397.46 | 13.89 | 0.87 | 466.09 |
| Red sandstone | 3540.87 | 15.31 | 0.88 | 646.69 |
| Red sandstone | 27,172.56 | 13.94 | 0.87 | 837.16 |
| Coal | 0.22 | 11.91 | 0.85 | -- |
| Coal | 1.50 | 16.51 | 0.89 | 5.54 |
| Coal | 14.87 | 29.66 | 0.93 | 33.20 |
| Coal | 168.14 | 24.33 | 0.92 | 71.36 |
| Coal | 2135.74 | 19.77 | 0.90 | 230.81 |
| Coal | 7590.34 | 24.74 | 0.92 | 835.25 |
| Rock Lithology | Sample Number | Brazilian Tensile Strength (MPa) | Uniaxial Compressive Strength (MPa) | |||
|---|---|---|---|---|---|---|
| Purple sandstone | 1 | 4.27 | 95.04 | 22.26 | 0.91 | 31.98 |
| Yellow sandstone | 1 | 1.16 | 43.72 | 37.69 | 0.95 | 4.48 |
| Brown sandstone | 1 | 3.38 | 64.92 | 19.21 | 0.90 | 5.86 |
| Grey sandstone | 1 | 2.99 | 70.45 | 23.56 | 0.92 | 9.3 |
| Andesite | 1 | 12.85 | 200.59 | 15.61 | 0.88 | 29.91 |
| White sandstone | 1 | 1.64 | 36.80 | 22.44 | 0.91 | 2.29 |
| Green sandstone | 1 | 2.60 | 67.15 | 25.83 | 0.93 | 48.77 |
| Chinese black granite | 1 | 8.97 | 150.98 | 16.83 | 0.89 | 24 |
| Granite | 1 | 6.68 | 112.65 | 16.86 | 0.89 | 17.03 |
| Marble | 1 | 2.41 | 109.54 | 45.45 | 0.96 | 1.63 |
| Red sandstone | 1 | 2.79 | 74.90 | 26.85 | 0.93 | 4.41 |
| Coal | 1 | 0.61 | 33.33 | 54.64 | 0.96 | 2.45 |
| Category | I (None) | II (Weak) | III (Medium) | IV (Strong) |
|---|---|---|---|---|
| Phenomenon | One or two penetrating cracks appeared on the specimen surface after failure. Few fragments formed with slight sound. | Multiple cracks appeared on the specimen surface after failure. A small number of fragments dropped slowly with a slight sound. | Multiple cracks appeared on the specimen surface after failure. Several fragments ejected with a clear failure sound. | Multiple cracks appeared on the specimen surface after failure. A large number of fragments ejected with great failure sound. |
| Classification results |  Marble |  Yellow sandstone Other rocks: Red sandstone, White sandstone, Coal |  Grey sandstone Other rocks: Brown sandstone, Green sandstone Purple sandstone Granite |  Chinese black granite Other rocks: Andesite |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Yang, S.; Zhou, J.; Wang, L. Measurement and Classification Criteria of Strength Decrease Rate and Brittleness Indicator Index for Rockburst Proneness Evaluation of Hard Rocks. Materials 2023, 16, 3101. https://doi.org/10.3390/ma16083101
Du K, Yang S, Zhou J, Wang L. Measurement and Classification Criteria of Strength Decrease Rate and Brittleness Indicator Index for Rockburst Proneness Evaluation of Hard Rocks. Materials. 2023; 16(8):3101. https://doi.org/10.3390/ma16083101
Chicago/Turabian StyleDu, Kun, Songge Yang, Jian Zhou, and Lichang Wang. 2023. "Measurement and Classification Criteria of Strength Decrease Rate and Brittleness Indicator Index for Rockburst Proneness Evaluation of Hard Rocks" Materials 16, no. 8: 3101. https://doi.org/10.3390/ma16083101
APA StyleDu, K., Yang, S., Zhou, J., & Wang, L. (2023). Measurement and Classification Criteria of Strength Decrease Rate and Brittleness Indicator Index for Rockburst Proneness Evaluation of Hard Rocks. Materials, 16(8), 3101. https://doi.org/10.3390/ma16083101








