Quantum Oscillations of the Energy Loss Rate of Hot Electrons in Graphene at Strong Magnetic Fields
Abstract
1. Introduction
2. Theoretical Method
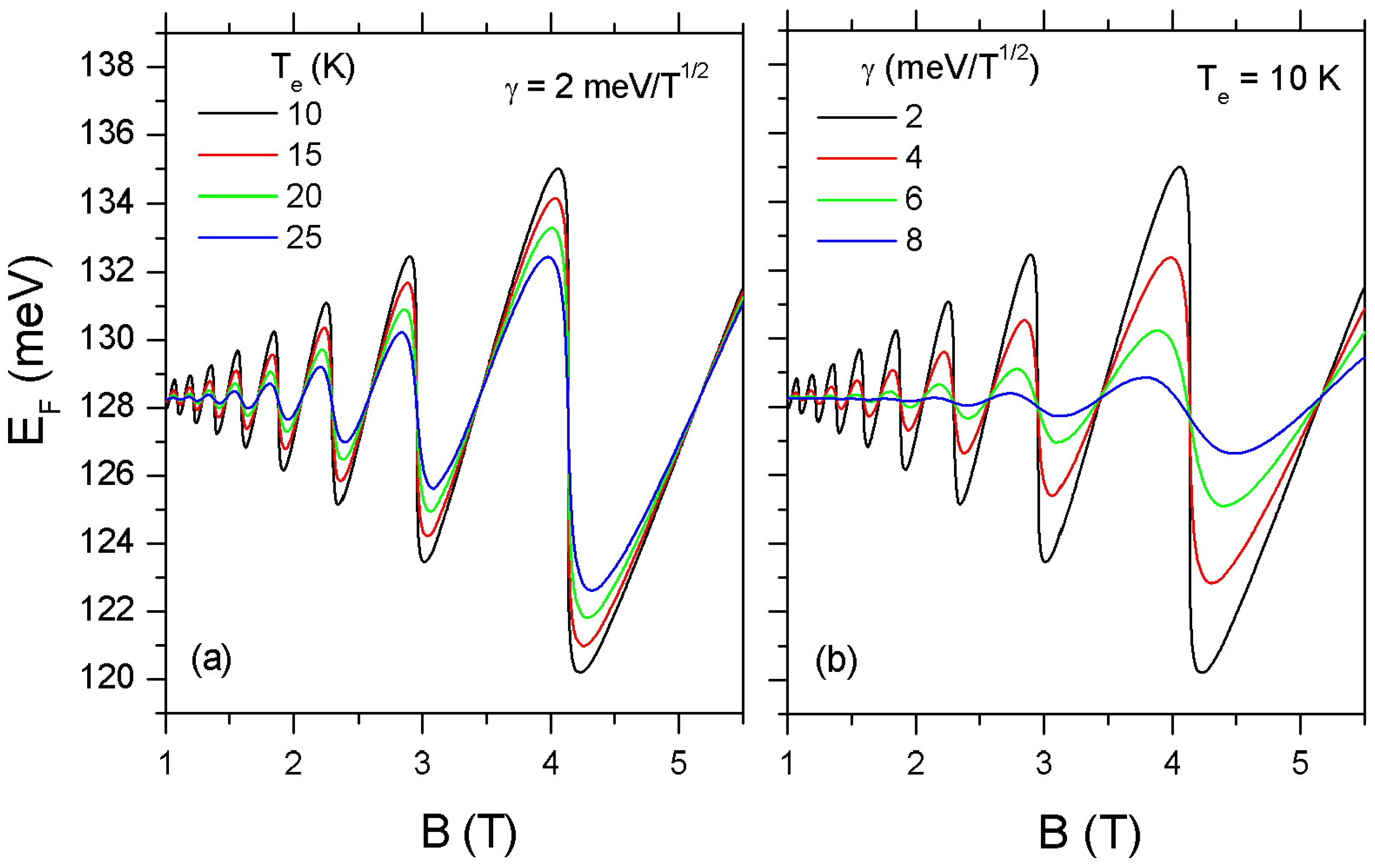
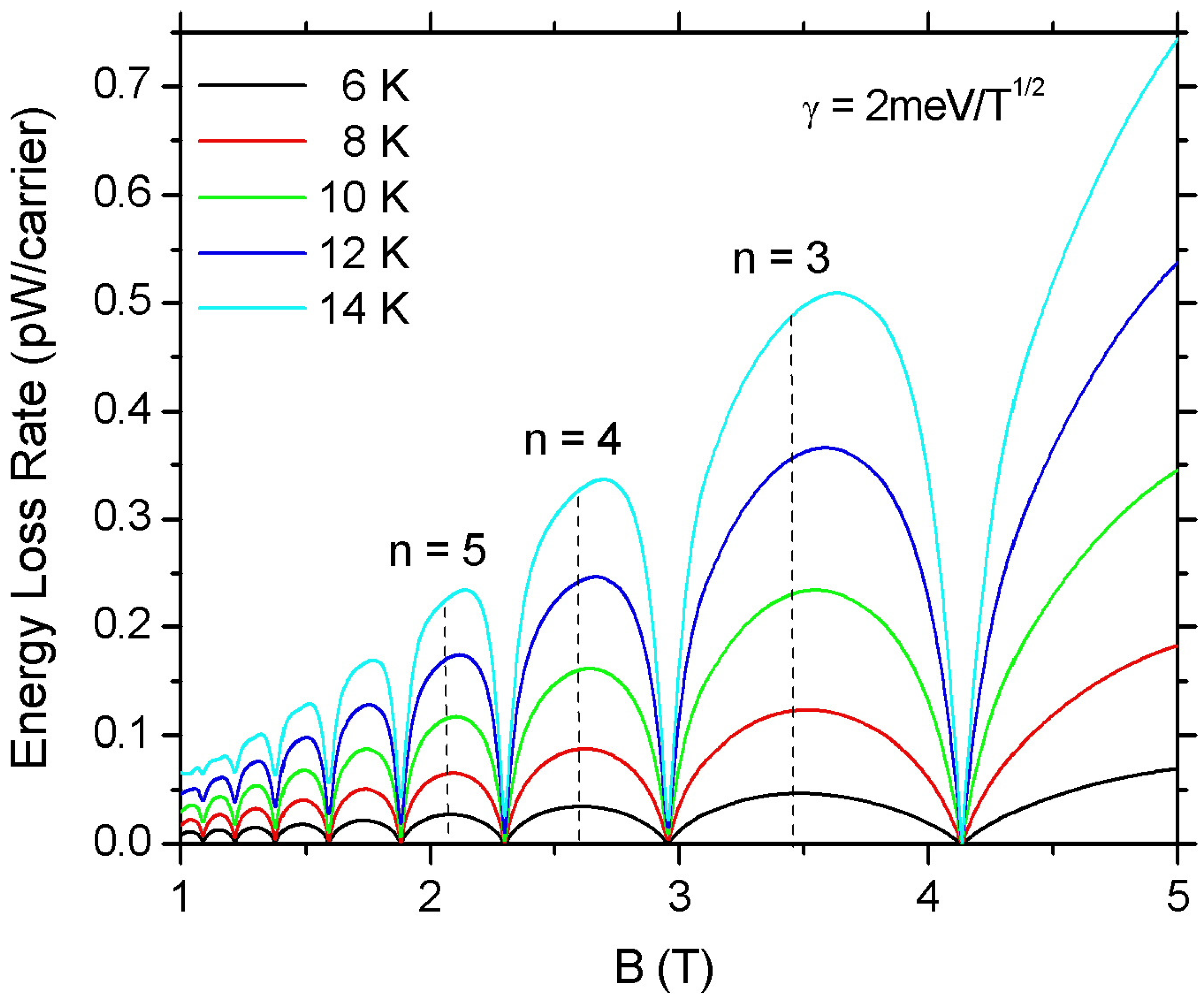
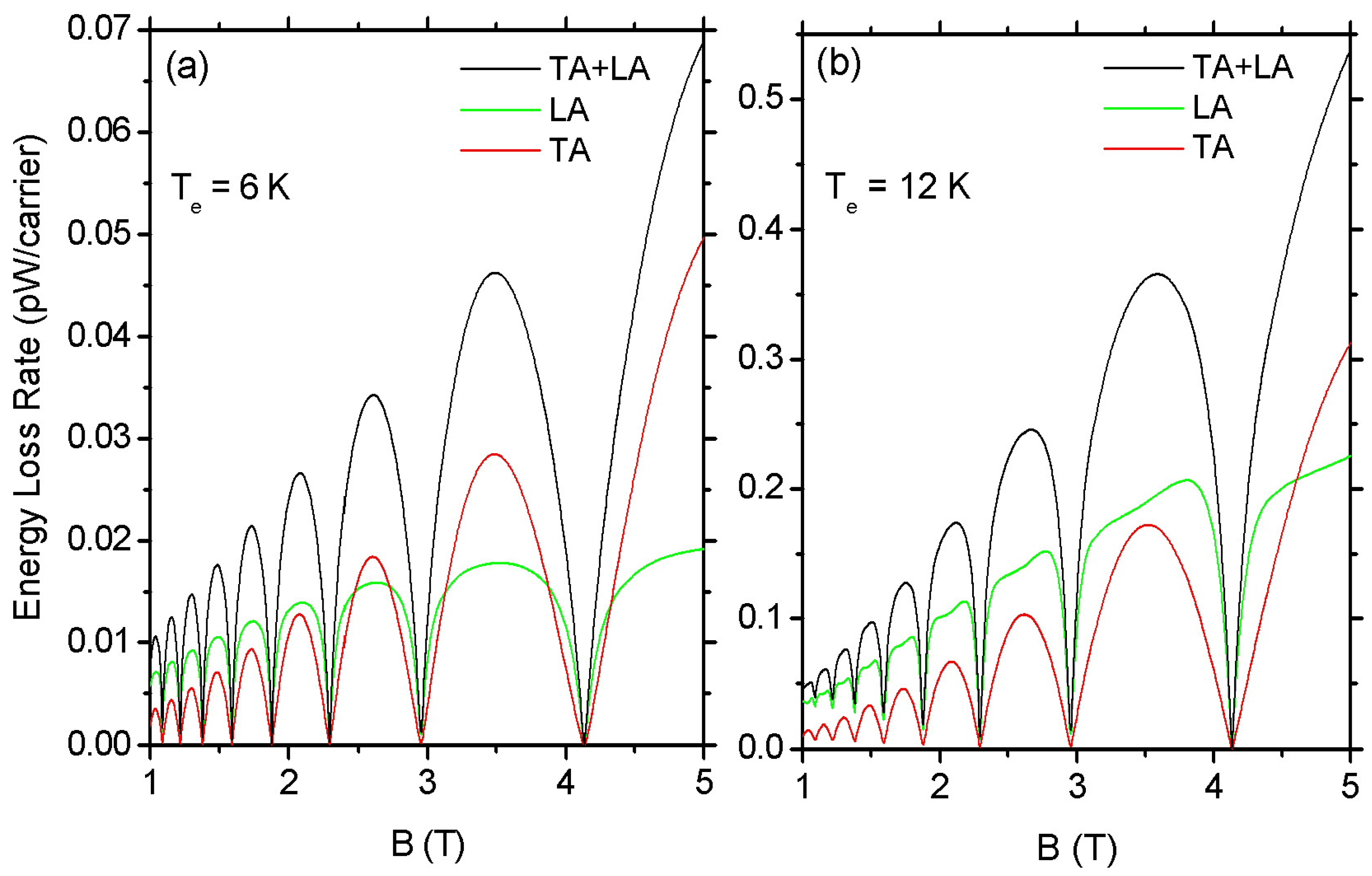
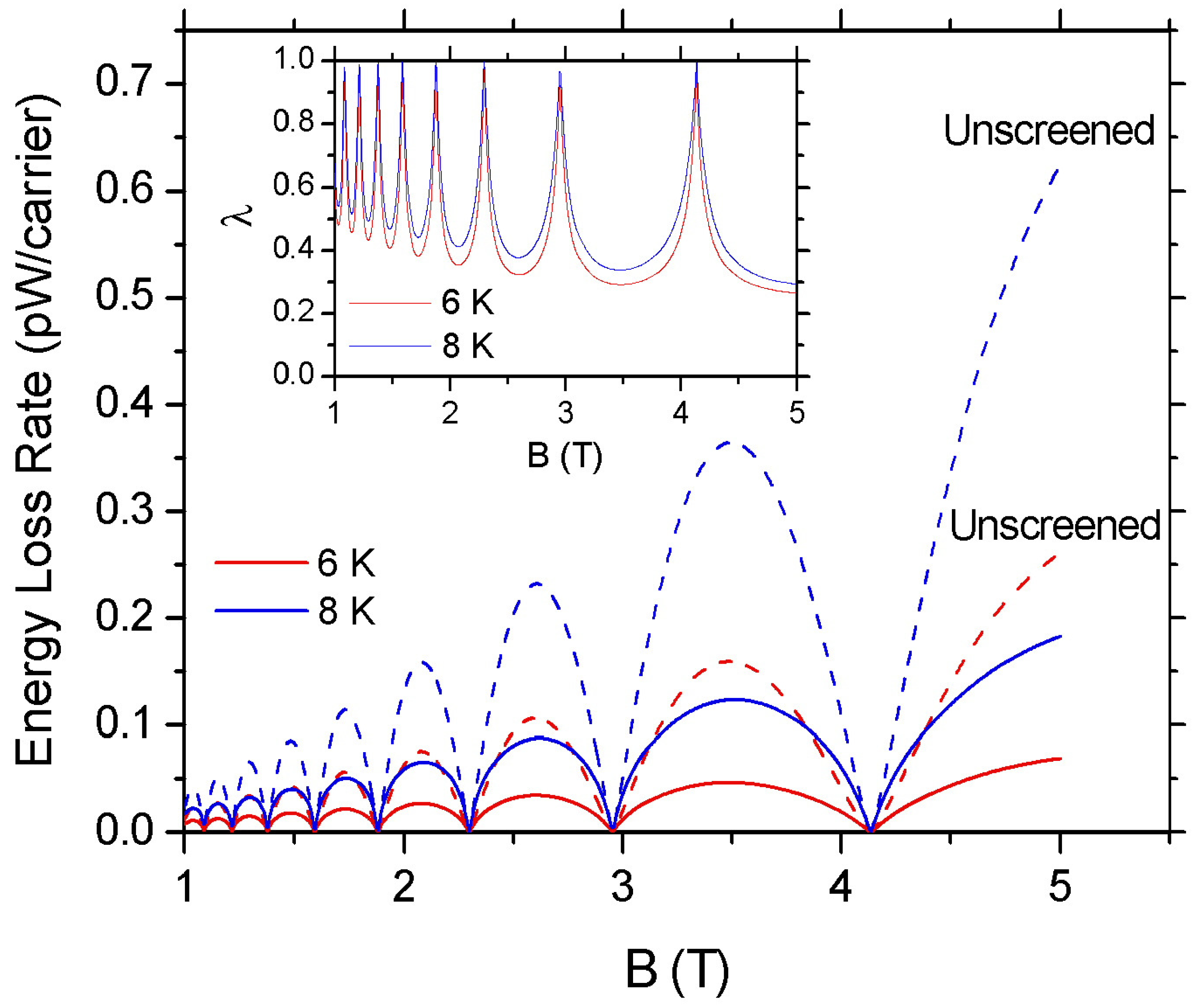
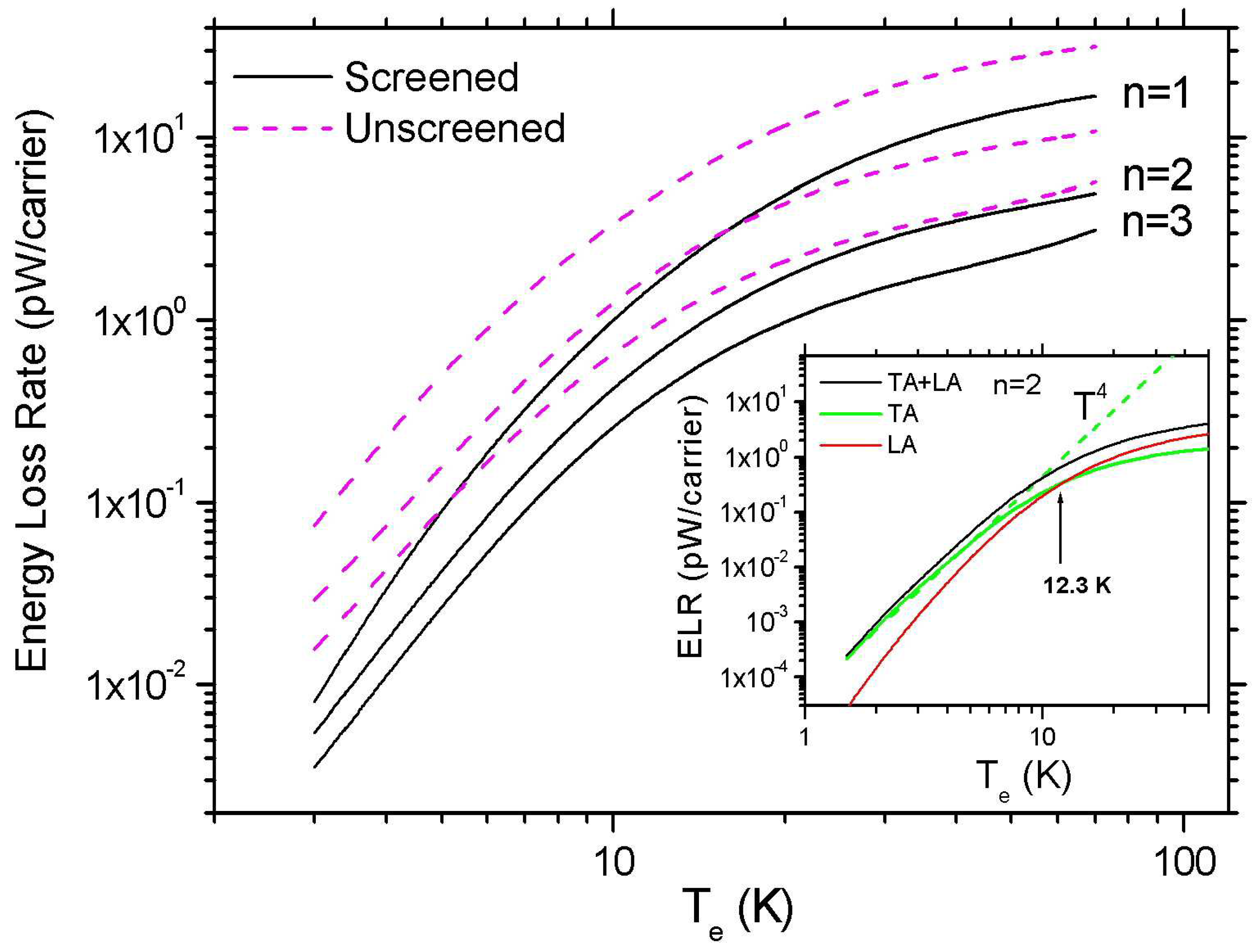
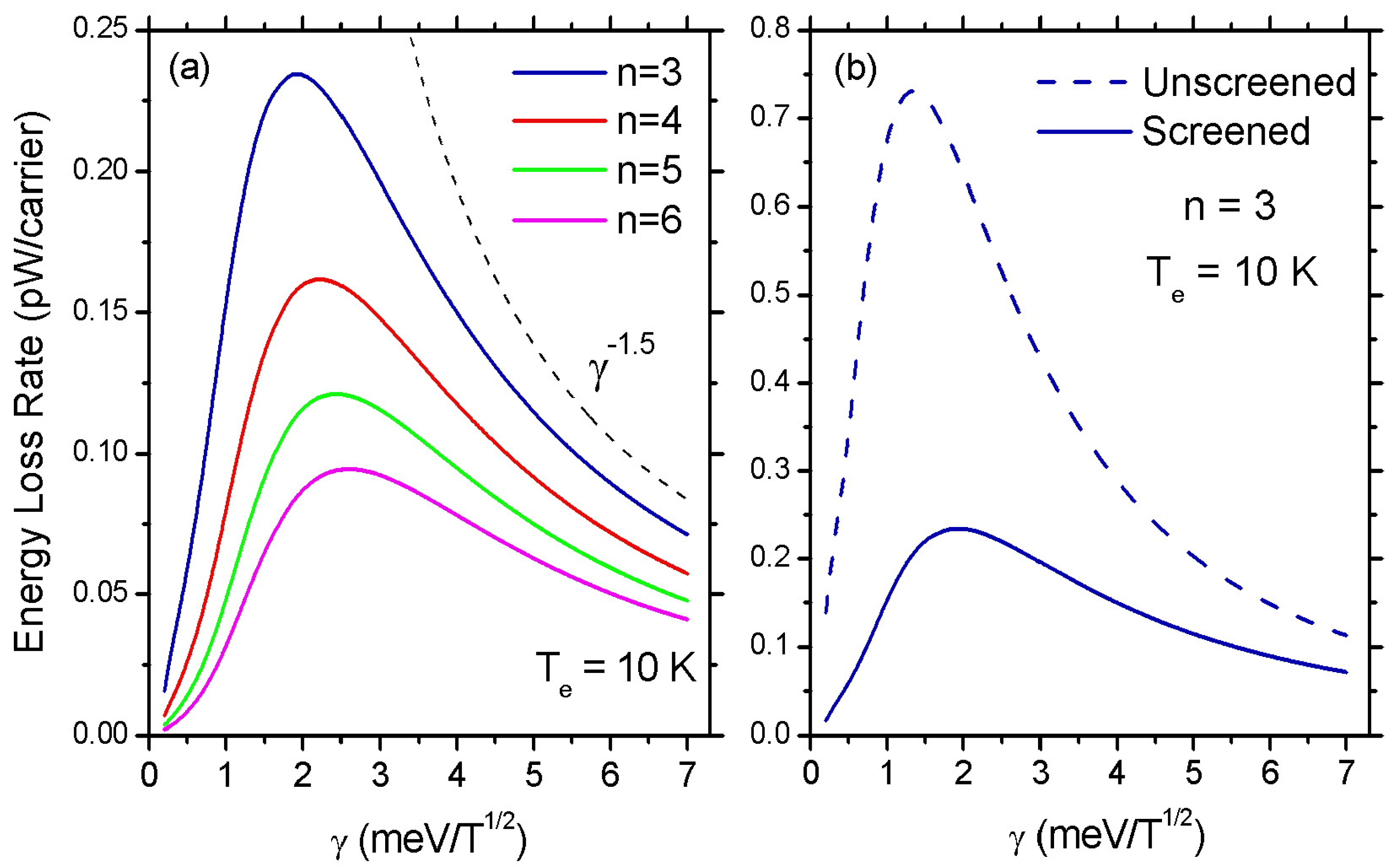
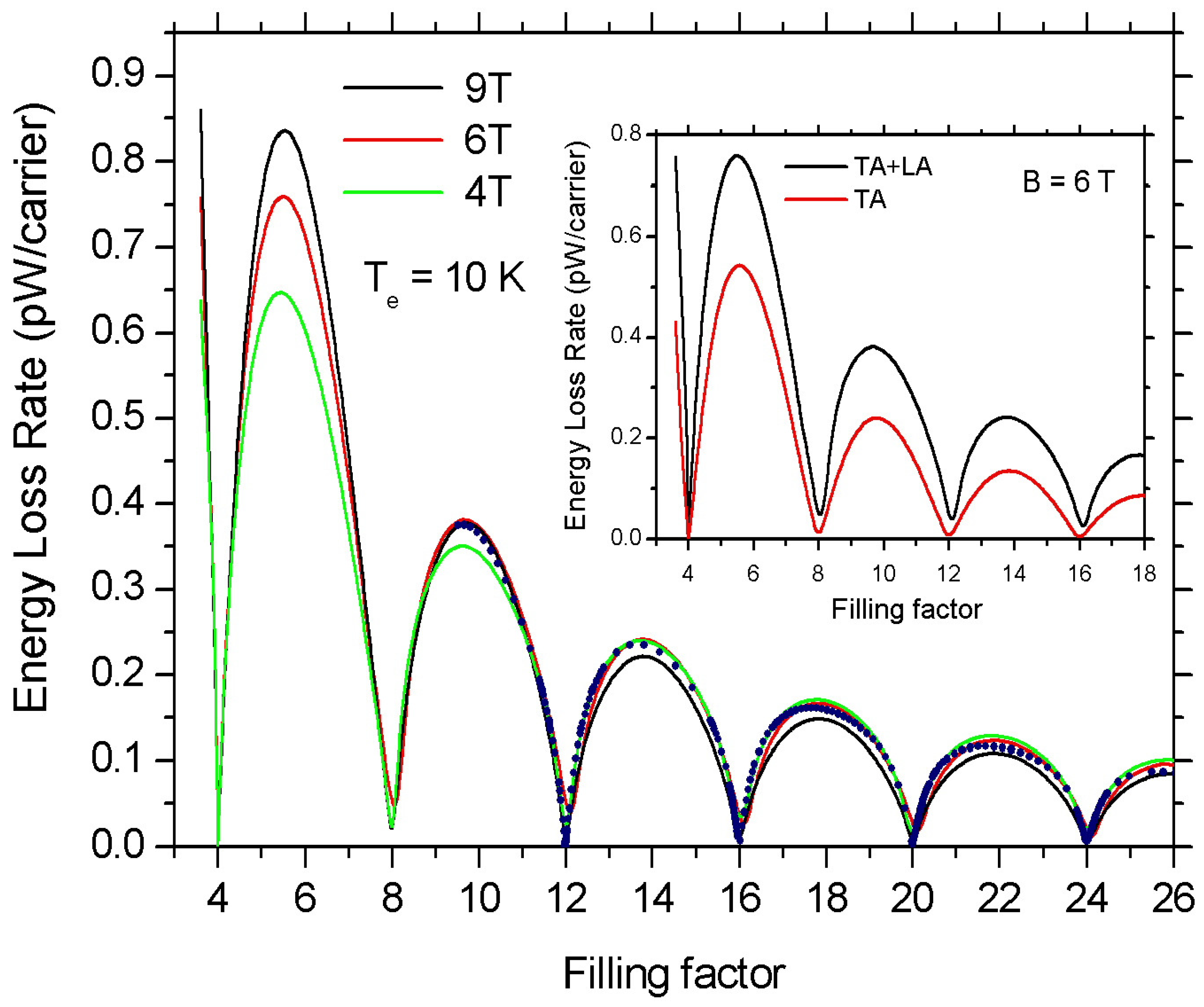
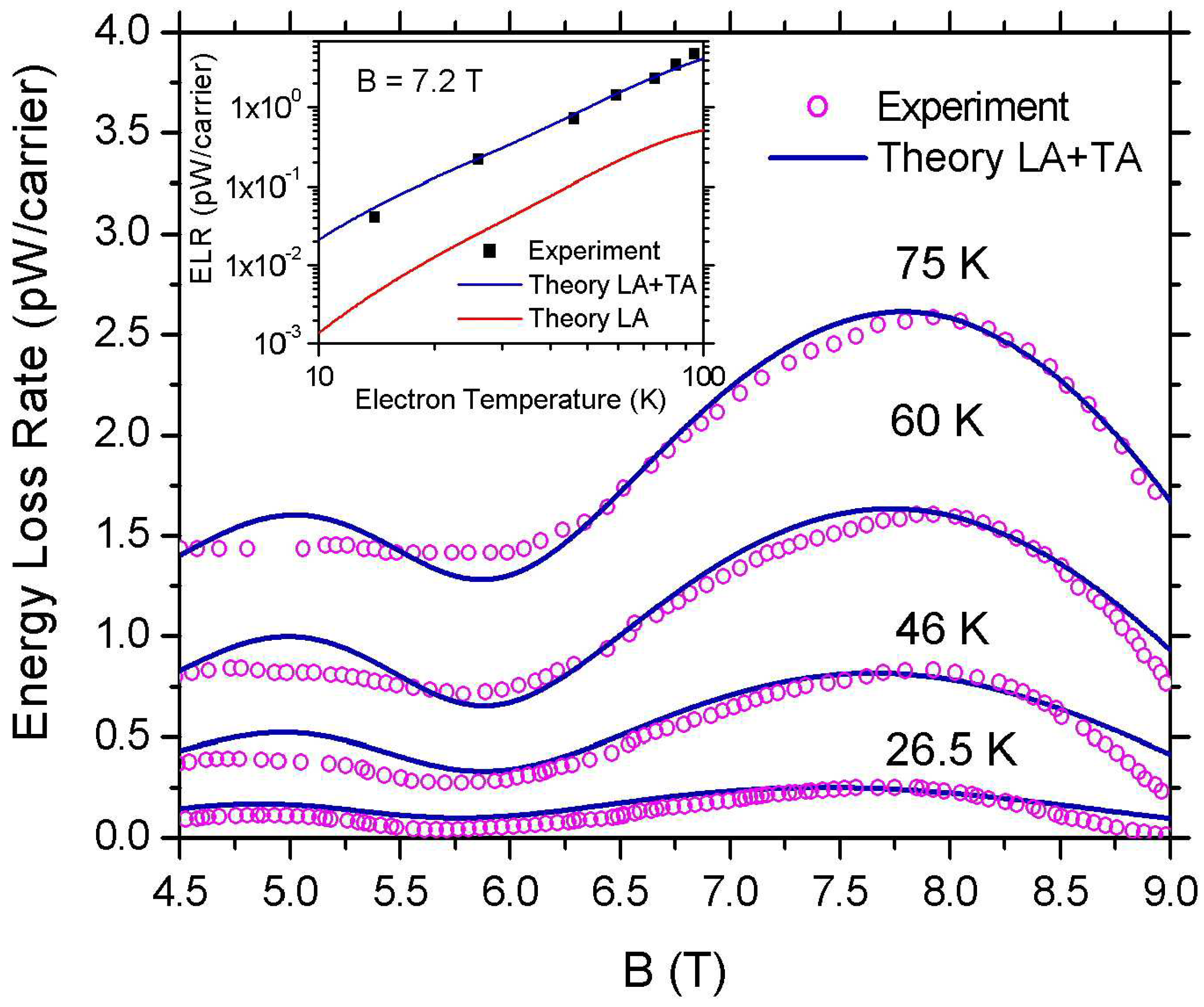
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407. [Google Scholar] [CrossRef]
- Morozov, S.V.; Novoselov, K.S.; Katsnelson, M.I.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A.K. Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Hone, J.; Stormer, H.L.; Kim, P. Temperature-Dependent Transport in Suspended Graphene. Phys. Rev. Lett. 2008, 101, 096802. [Google Scholar] [CrossRef] [PubMed]
- Kubakaddi, S.S. Interaction of massless Dirac electrons with acoustic phonons in graphene at low temperatures. Phys. Rev. B 2009, 79, 075417. [Google Scholar] [CrossRef]
- Bistritzer, R.; MacDonald, A.H. Electronic Cooling in Graphene. Phys. Rev. Lett. 2009, 102, 206410. [Google Scholar] [CrossRef]
- Tse, W.-K.; Das Sarma, S. Energy relaxation of hot Dirac fermions in graphene. Phys. Rev. B 2009, 79, 235406. [Google Scholar] [CrossRef]
- Viljas, J.K.; Heikkilä, T.T. Electron–phonon heat transfer in monolayer and bilayer graphene. Phys. Rev. B 2010, 81, 245404. [Google Scholar] [CrossRef]
- Song, J.C.W.; Rudner, M.S.; Marcus, C.M.; Levitov, L.S. Hot Carrier Transport and Photocurrent Response in Graphene. Nano Lett. 2011, 11, 4688. [Google Scholar] [CrossRef] [PubMed]
- Song, J.C.W.; Reizer, M.Y.; Levitov, L.S. Disorder-Assisted electron–phonon Scattering and Cooling Pathways in Graphene. Phys. Rev. Lett. 2012, 109, 106602. [Google Scholar] [CrossRef]
- Low, T.; Perebeinos, V.; Kim, R.; Freitag, M.; Avouris, P. Cooling of photoexcited carriers in graphene by internal and substrate phonons. Phys. Rev. B 2012, 86, 045413. [Google Scholar] [CrossRef]
- Chen, W.; Clerk, A.A. Electron–phonon mediated heat flow in disordered graphene. Phys. Rev. B 2012, 86, 125443. [Google Scholar] [CrossRef]
- Plochocka, P.; Kossacki, P.; Golnik, A.; Kazimierczuk, T.; Berger, C.; de Heer, W.A.; Potemski, M. Slowing hot-carrier relaxation in graphene using a magnetic field. Phys. Rev. B 2009, 80, 245415. [Google Scholar] [CrossRef]
- DaSilva, A.M.; Zou, K.; Jain, J.K.; Zhu, J. Mechanism for Current Saturation and Energy Dissipation in Graphene Transistors. Phys. Rev. Lett. 2010, 104, 236601. [Google Scholar] [CrossRef]
- Voutilainen, J.; Fay, A.; Häkkinen, P.; Viljas, J.K.; Heikkilxax, T.T.; Hakonen, P.J. Energy relaxation in graphene and its measurement with supercurrent. Phys. Rev. B 2011, 84, 045419. [Google Scholar] [CrossRef]
- Gabor, N.M.; Song, J.C.W.; Ma, Q.; Nair, N.L.; Taychatanapat, T.; Watanabe, K.; Taniguchi, T.; Levitov, L.S.; Jarillo-Herrero, P. Hot Carrier–Assisted Intrinsic Photoresponse in Graphene. Science 2011, 334, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.; Tan, C.; Ma, L.; Liu, G.T.; Lu, L.; Yang, C.L. Shubnikov-de Haas oscillations of a single layer graphene under dc current bias. Phys. Rev. B 2011, 84, 115429. [Google Scholar] [CrossRef]
- Sun, D.; Aivazian, G.; Jones, A.M.; Ross, J.S.; Yao, W.; Cobden, D.; Xu, X. Ultrafast hot-carrier-dominated photocurrent in graphene. Nat. Nanotechnol. 2012, 7, 114–118. [Google Scholar] [CrossRef]
- Baker, A.M.R.; Alexaner-Webber, J.A.; Altebaeumer, T.; Nicholas, R.J. Energy relaxation for hot Dirac fermions in graphene and breakdown of the quantum Hall effect. Phys. Rev. B 2012, 85, 115403. [Google Scholar] [CrossRef]
- Price, A.S.; Hornett, S.M.; Shytov, A.V.; Hendry, E.; Horsell, D.W. Nonlinear resistivity and heat dissipation in monolayer graphene. Phys. Rev. B 2012, 85, 161411(R). [Google Scholar] [CrossRef]
- Betz, A.C.; Vialla, F.; Brunel, D.; Voisin, C.; Picher, M.; Cavanna, A.; Madouri, A.; Fève, G.; Berroir, J.-M.; Plaçais, B.; et al. Hot Electron Cooling by Acoustic Phonons in Graphene. Phys. Rev. Lett. 2013, 109, 056805. [Google Scholar] [CrossRef]
- Baker, A.M.R.; Alexer-Webber, J.A.; Altebaeumer, T.; McMullan, S.D.; Janssen, T.J.B.M.; Tzalenchuk, A.; Lara-Avila, S.; Kubatkin, S.; Yakimova, R.; Lin, C.-T.; et al. Energy loss rates of hot Dirac fermions in epitaxial, exfoliated, and CVD graphene. Phys. Rev. B 2013, 87, 045414. [Google Scholar] [CrossRef]
- Graham, M.W.; Shi, S.-F.; Ralph, D.C.; Park, J.; McEuen, P.L. Photocurrent measurements of supercollision cooling in graphene. Nat. Phys. 2012, 9, 103–108. [Google Scholar] [CrossRef]
- Graham, M.W.; Shi, S.-F.; Wang, Z.; Ralph, D.C.; Park, J.; McEuen, P.L. Transient Absorption and Photocurrent Microscopy Show That Hot Electron Supercollisions Describe the Rate-Limiting Relaxation Step in Graphene. Nano Lett. 2013, 13, 5497–5502. [Google Scholar] [CrossRef] [PubMed]
- Fong, K.C.; Wollman, E.E.; Ravi, H.; Chen, W.; Clerk, A.A.; MDShaw, M.D.; Leduc, H.G.; Schwab, K.C. Measurement of the Electronic Thermal Conductance Channels and Heat Capacity of Graphene at Low Temperature. Phys. Rev. X 2013, 3, 041008. [Google Scholar] [CrossRef]
- Betz, A.C.; Jhang, S.H.; Pallecchi, E.; Ferreira, R.; Fève, G.; Berroir, J.-M.; Plaçais, B. Supercollision cooling in undoped graphene. Nat. Phys. 2012, 9, 109–112. [Google Scholar] [CrossRef]
- Somphonsane, R.; Ramamoorthy, H.; Bohra, G.; He, G.; Ferry, D.K.; Ochiai, Y.; Aoki, N.; Bird, J.P. Fast Energy Relaxation of Hot Carriers Near the Dirac Point of Graphene. Nano Lett. 2013, 13, 4305–4310. [Google Scholar] [CrossRef] [PubMed]
- Laitinen, A.; Oksanen, M.; Fay, A.; Cox, D.; Tomi, M.; Virtanen, P.; Hakonen, P.J. Electron–Phonon Coupling in Suspended Graphene: Supercollisions by Ripples. Nano Lett. 2014, 14, 3009–3013. [Google Scholar] [CrossRef]
- Ramamoorthy, H.; Somphonsane, R.; He, G.; Ferry, D.K.; Ochiai, Y.; Aoki, N.; Bird, J.P. Reversing hot-carrier energy-relaxation in graphene with a magnetic field. Appl. Phys. Lett. 2014, 104, 193115. [Google Scholar] [CrossRef]
- Das Sarma, S.; Campos, V.B. Low-temperature thermal relaxation of electrons in one-dimensional nanometer-size structures. Phys. Rev. B 1993, 47, 3728. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.H.; Peeters, F.M.; Xu, W. Landau-level broadening due to electron-impurity interaction in graphene in strong magnetic fields. Phys. Rev. B 2010, 82, 075401. [Google Scholar] [CrossRef]
- Manion, S.J.; Artaki, M.; Emanuel, M.A.; Coleman, J.J.; Hess, K. Electron-energy-loss rates in AlxGa1-xAs/GaAs heterostructures at low temperatures. Phys. Rev. B 1987, 35, 9203. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Fletcher, R.; Zaremba, E.; D’Iorio, M.; Foxon, C.T.; Harris, J.J. Energy-loss rates of two-dimensional electrons at a GaAs/AlxGa1-xAs interface. Phys. Rev. B 1991, 43, 9033. [Google Scholar] [CrossRef] [PubMed]
- Fromhold, T.M.; Butcher, P.N.; Qin, G.; Mulimani, B.G.; Oxley, J.P.; Gallagher, B.L. Phonon-drag magnetothermopower oscillations in GaAs/AsxGa1-xAs heterojunctions. Phys. Rev. B 1993, 48, 5326. [Google Scholar] [CrossRef]
- Ando, T.; Fowler, A.B.; Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 1982, 54, 437. [Google Scholar] [CrossRef]
- Tsaousidou, M.; Kubakaddi, S.S. Materials Science Department, University of Patras, Patras, Greece, 2023; manuscript in preperation.
- Kumaravadivel, P.; Greenaway, M.T.; Perello, D.; Berdyugin, A.; Birkbeck, J.; Wengraf, J.; Liu, S.; Edgar, J.H.; Geim, A.K.; Eaves, L.; et al. Strong magnetophonon oscillations in extra-large graphene. Nat. Commun. 2019, 10, 3334. [Google Scholar] [CrossRef]
- Greenaway, M.T.; Kumar, R.K.; Kumaravadivel, P.; Geim, A.K.; Eaves, L. Magnetophonon spectroscopy of Dirac fermion scattering by transverse and longitudinal acoustic phonons in graphene. Phys. Rev. B 2019, 100, 155120. [Google Scholar] [CrossRef]
- Murayama, Y.; Ando, T. Theory of magnetoconductivity in a two-dimensional electron-gas system: Self-consistent screening model. Phys. Rev. B 1987, 35, 2252. [Google Scholar] [CrossRef]
- Ando, T.; Murayama, Y. Landau-Level Broadening in GaAs/AlGaAs Heterojunctions. Phys. Soc. Jpn. 1985, 54, 1519–1527. [Google Scholar] [CrossRef]
- Nguyen, K.V.; Chang, Y.-C. Full consideration of acoustic phonon scatterings in two-dimensional Dirac materials. Phys. Chem. Chem. Phys. 2020, 22, 3999–4009. [Google Scholar] [CrossRef] [PubMed]
- Suzuura, H.; Ando, T. Phonons and electron–phonon scattering in carbon nanotubes. Phys. Rev. B 2002, 65, 235412. [Google Scholar] [CrossRef]
- Reinen, H.A.J.M.; Berendschot, T.T.J.M.; Kappert, R.J.H.; Bluyssen, H.J.A. Electron–phonon interaction of a two-dimensional electron gas in a strong magnetic field. Solid State Commun. 1988, 65, 1495–1499. [Google Scholar] [CrossRef]
- Bich, T.N.; Kubakaddi, S.S.; Dinh, L.; Hieu, N.N.; Phuc, H.V. Oscillations of the electron energy loss rate in two-dimensional transition-metal dichalcogenides in the presence of a quantizing magnetic field. Phys. Rev. B 2021, 103, 235417. [Google Scholar] [CrossRef]
- Fletcher, R.; D’Iorio, M.; Moore, W.T.; Stoner, R. A search for trends in the thermopower of GaAs-Ga1-xAlxAs heterojunctions. J. Phys. C Solid State Phys. 1988, 21, 2681. [Google Scholar] [CrossRef]
- Lyo, S.K. Magnetoquantum oscillations of the phonon-drag thermoelectric power in heterojunctions. Phys. Rev. B 1989, 40, 6458(R). [Google Scholar] [CrossRef]
- Fletcher, R.; Pudalov, V.M.; Feng, Y.; Tsaousidou, M.; Butcher, P.N. Thermoelectric and hot-electron properties of a silicon inversion layer. Phys. Rev. B 1997, 56, 12422. [Google Scholar] [CrossRef]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 205418. [Google Scholar] [CrossRef]
- Goerbig, M.O. Electronic properties of graphene in a strong magnetic field. Rev. Mod. Phys. 2011, 83, 1193. [Google Scholar] [CrossRef]
- Sobol, O.O.; Pyatkovskiy, P.K.; Gorbar, E.V.; Gusynin, V.P. Screening of a charged impurity in graphene in a magnetic field. Phys. Rev. B 2016, 94, 115409. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsaousidou, M.; Kubakaddi, S.S. Quantum Oscillations of the Energy Loss Rate of Hot Electrons in Graphene at Strong Magnetic Fields. Materials 2023, 16, 2274. https://doi.org/10.3390/ma16062274
Tsaousidou M, Kubakaddi SS. Quantum Oscillations of the Energy Loss Rate of Hot Electrons in Graphene at Strong Magnetic Fields. Materials. 2023; 16(6):2274. https://doi.org/10.3390/ma16062274
Chicago/Turabian StyleTsaousidou, Margarita, and Shrishail S. Kubakaddi. 2023. "Quantum Oscillations of the Energy Loss Rate of Hot Electrons in Graphene at Strong Magnetic Fields" Materials 16, no. 6: 2274. https://doi.org/10.3390/ma16062274
APA StyleTsaousidou, M., & Kubakaddi, S. S. (2023). Quantum Oscillations of the Energy Loss Rate of Hot Electrons in Graphene at Strong Magnetic Fields. Materials, 16(6), 2274. https://doi.org/10.3390/ma16062274





