A Gradient Microstructure Improves the Barrier Properties of Flake-Filled Composite Films: A Computational Study
Abstract
1. Introduction
2. A Model for the Effective Barrier Improvement Factor (BIF) of a Graded Composite Film
- (i)
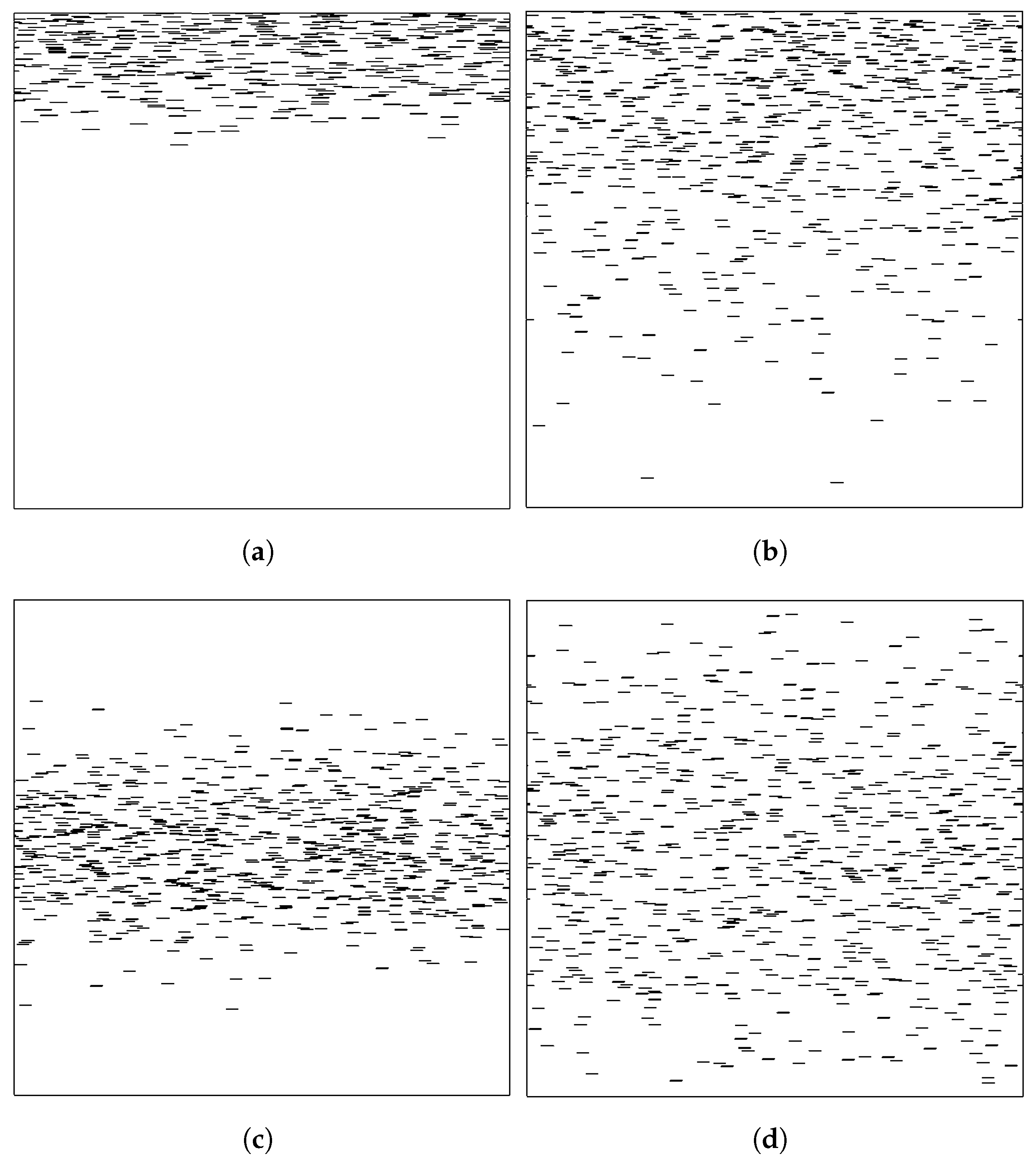
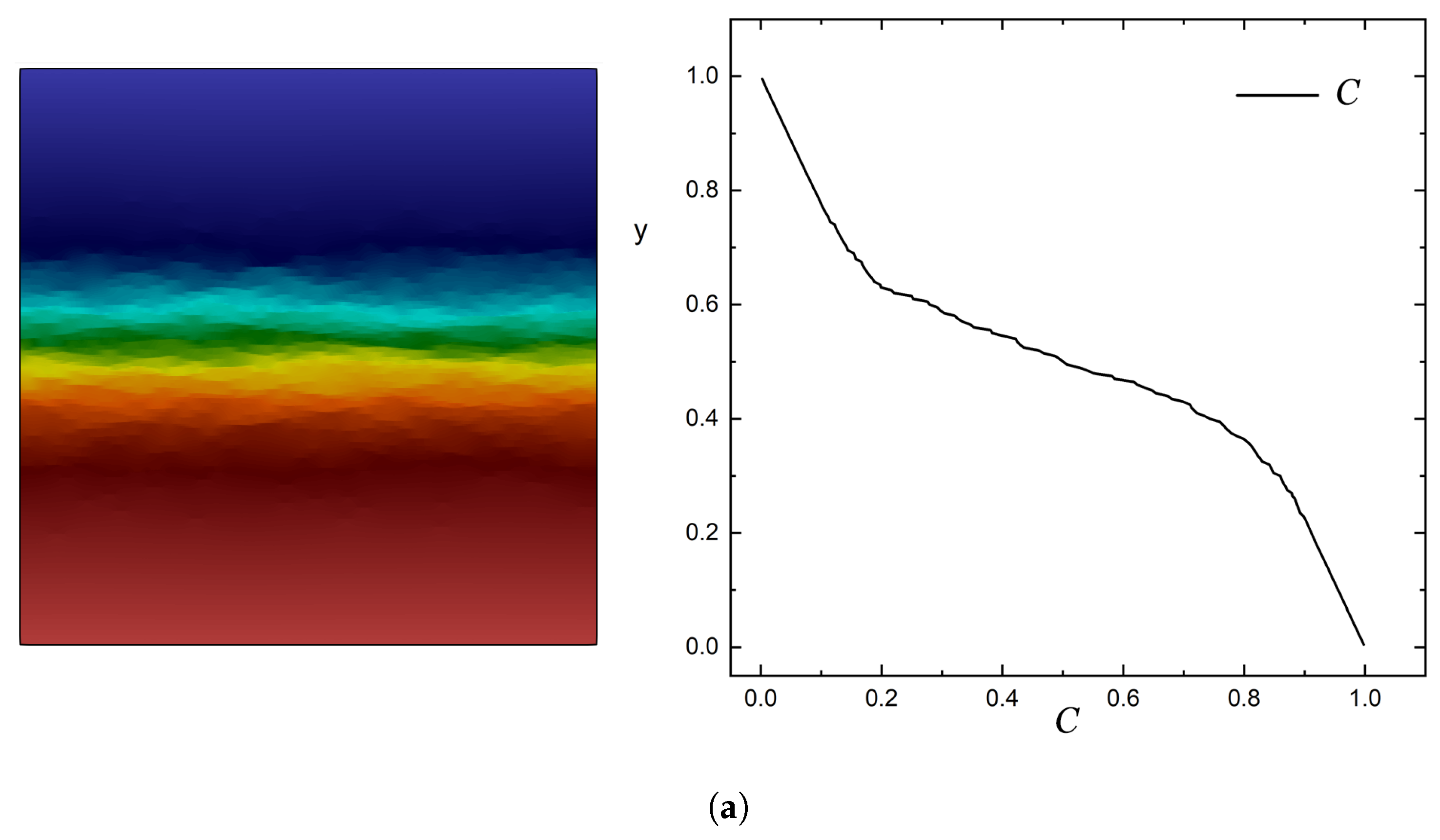
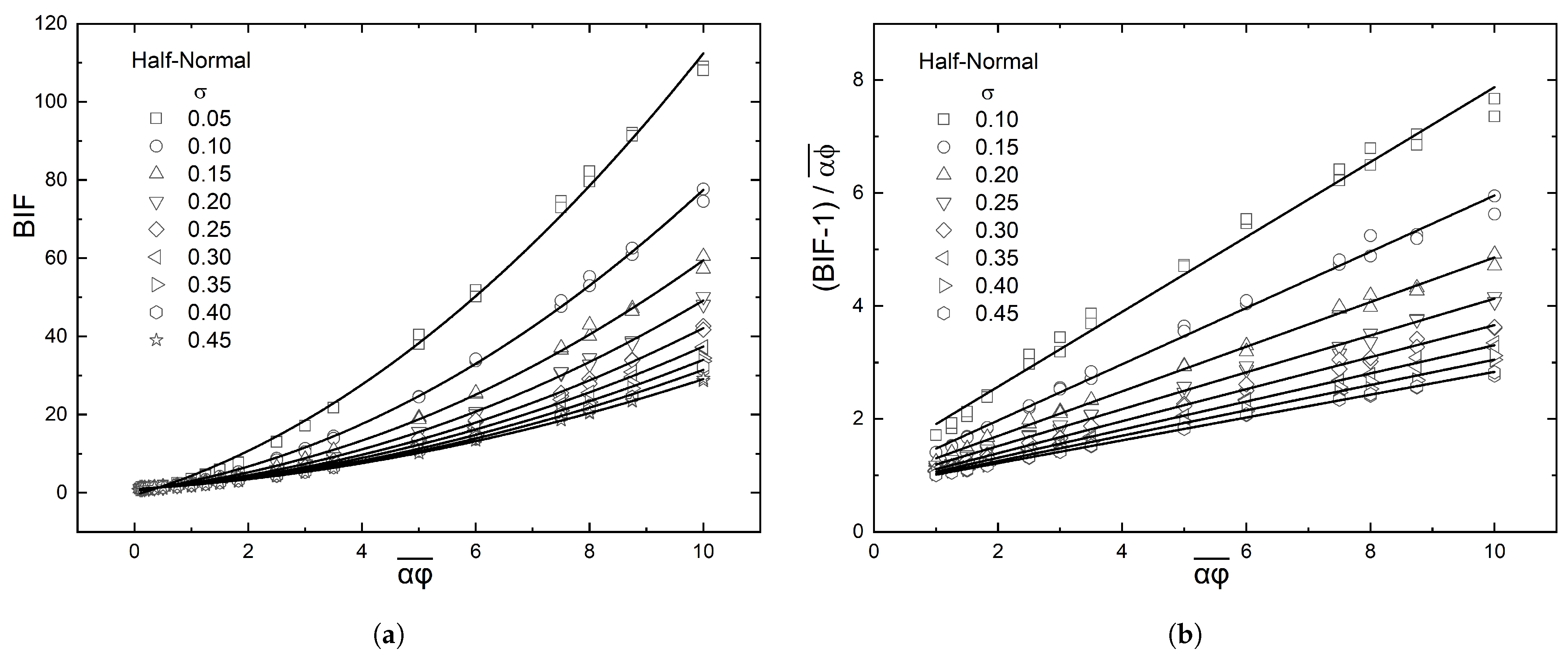
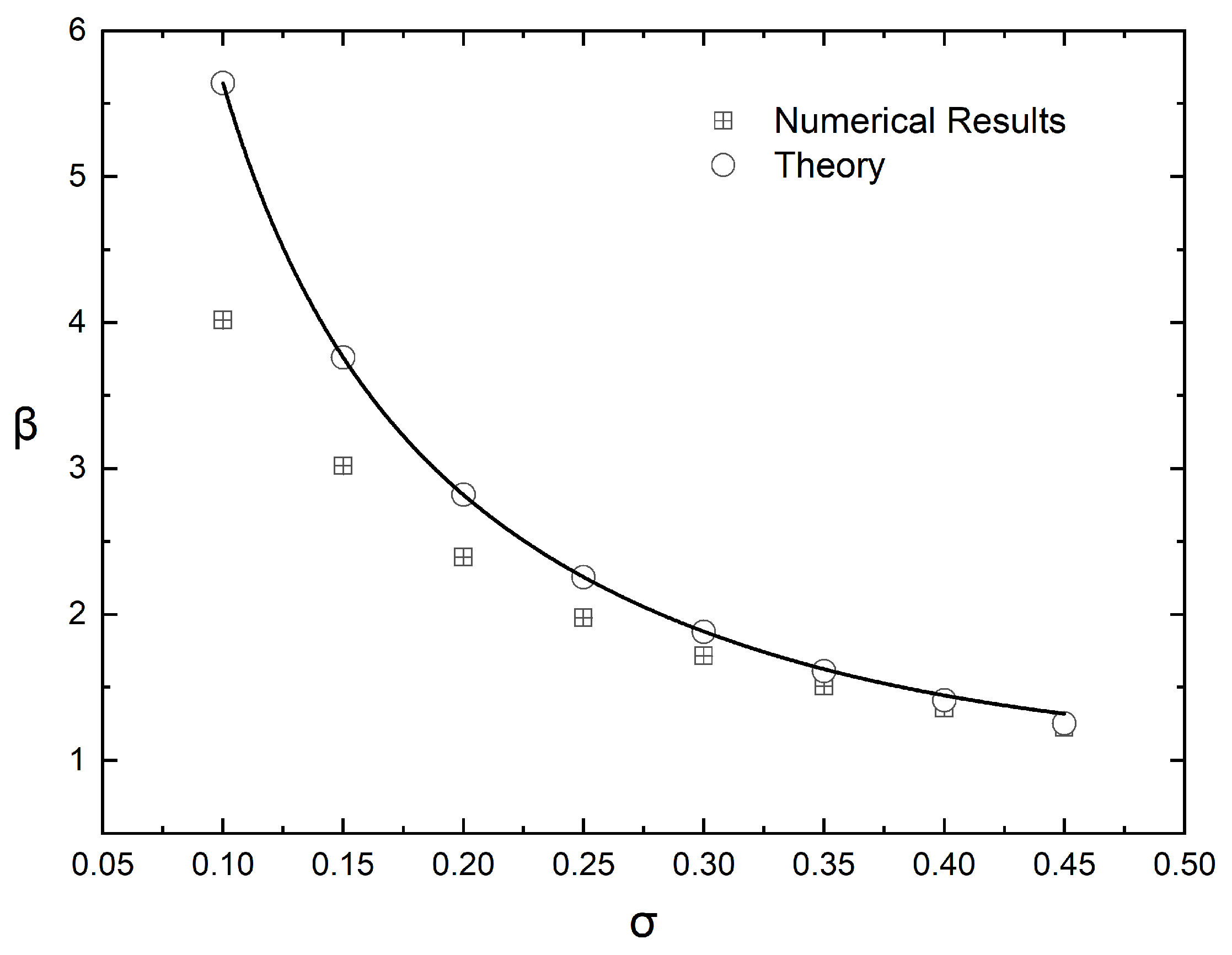
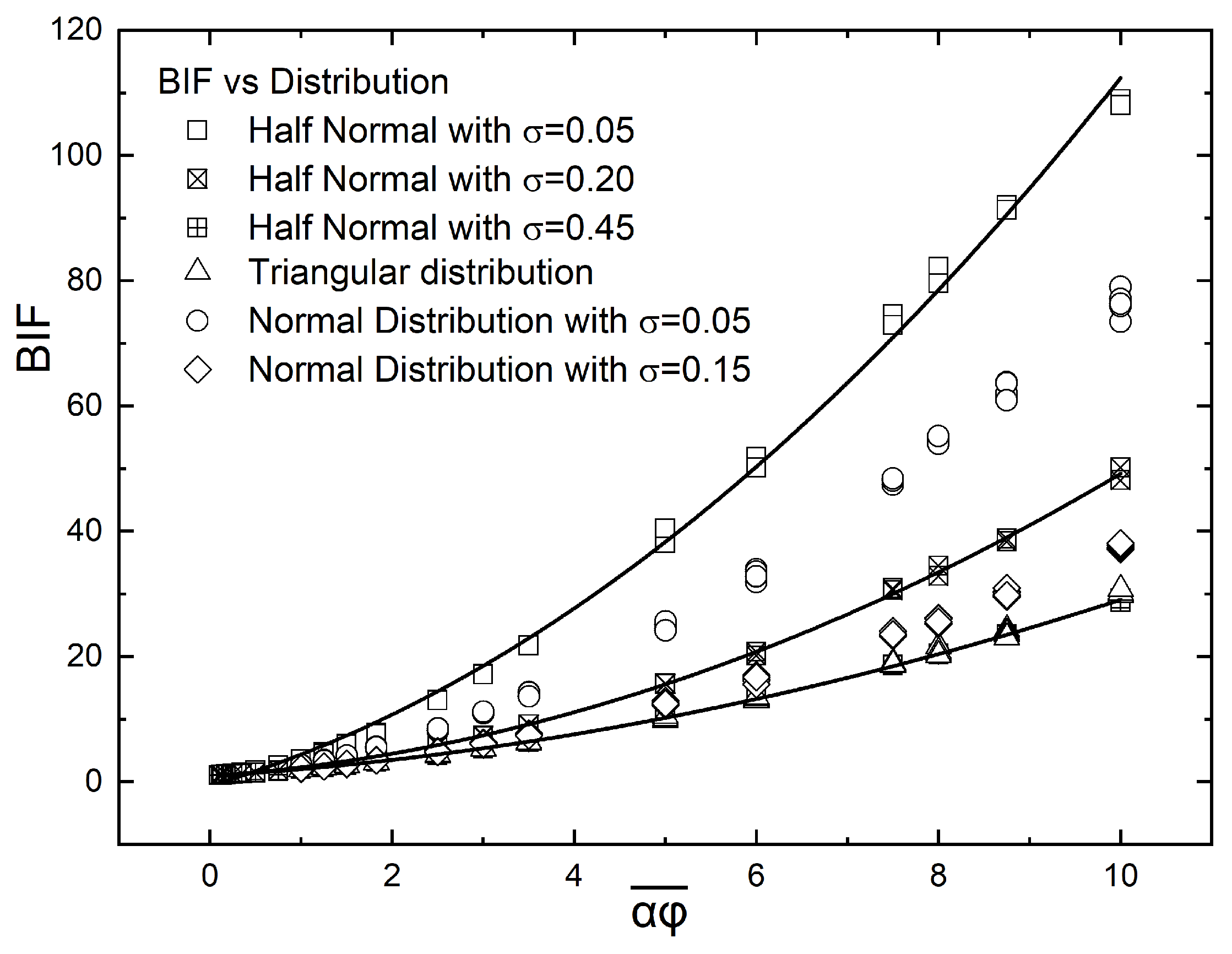
- A half-normal distribution, according to which the flake concentration is maximum on the surface () and minimum at the bottom () of the film.In this case, the number-density of the flakes is given bywhere the constant A is related to the total number of flakes through a total balance: . From Equation (5), it can be shown that in this case the enhancement factor is a function of the steepness of the distribution (expressed by the parameter ). The relation between and is:It can be formally shown that as , then . This result has also been verified with numerical computations, as will be shown later in this paper.
- (ii)
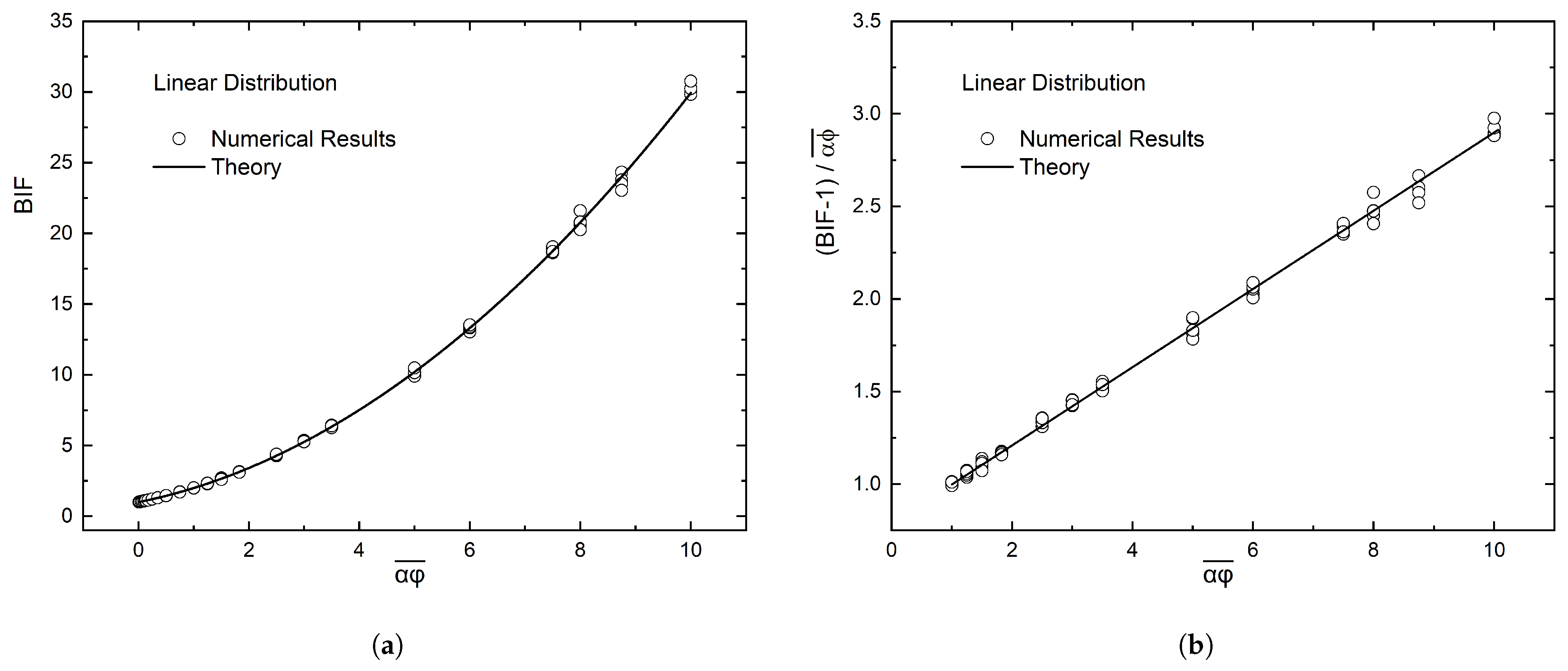
- A linear distribution between the two sides of the film. In this case, it is , where k is a constant. Since , it follows that , and therefore . Taking into account that and introducing this in Equation (5), we derive
- (iii)
- A triangular distribution in which the flake concentration is maximum at the center and drops linearly towards the two edges of the film. It can be shown that in this case it is also .
- (iv)
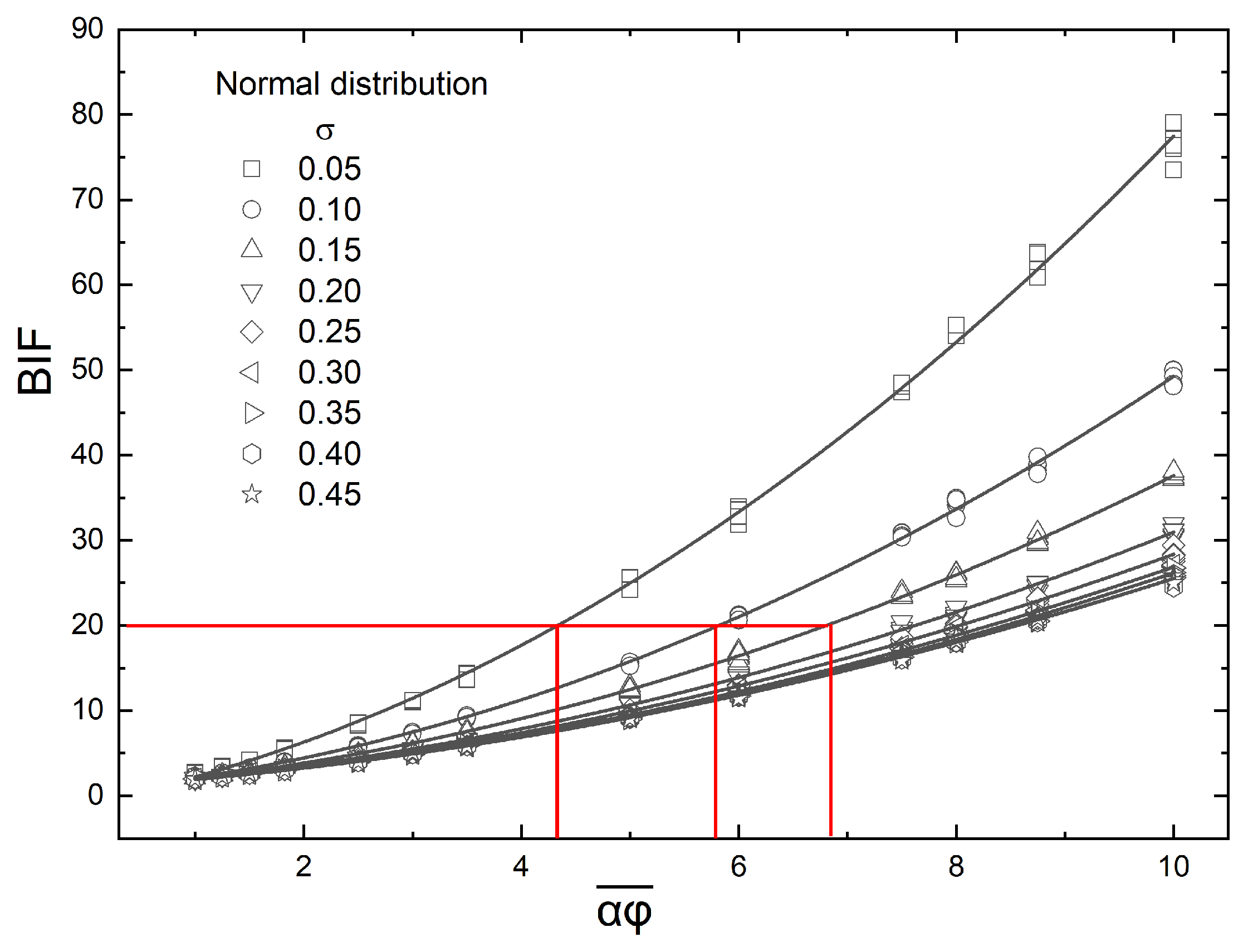
- A normal distribution, with the maximum flake density occurring at the center of the film (). In this case, the number-density of the flakes varies asIn a manner similar to the one used in the case of the half-normal distribution, the enhancement factor can be shown to depend only on the variance () of the distribution; the result is:It can be shown that as the variance of the distribution increases, the enhancement factor approaches 1 asymptotically.
3. Computational
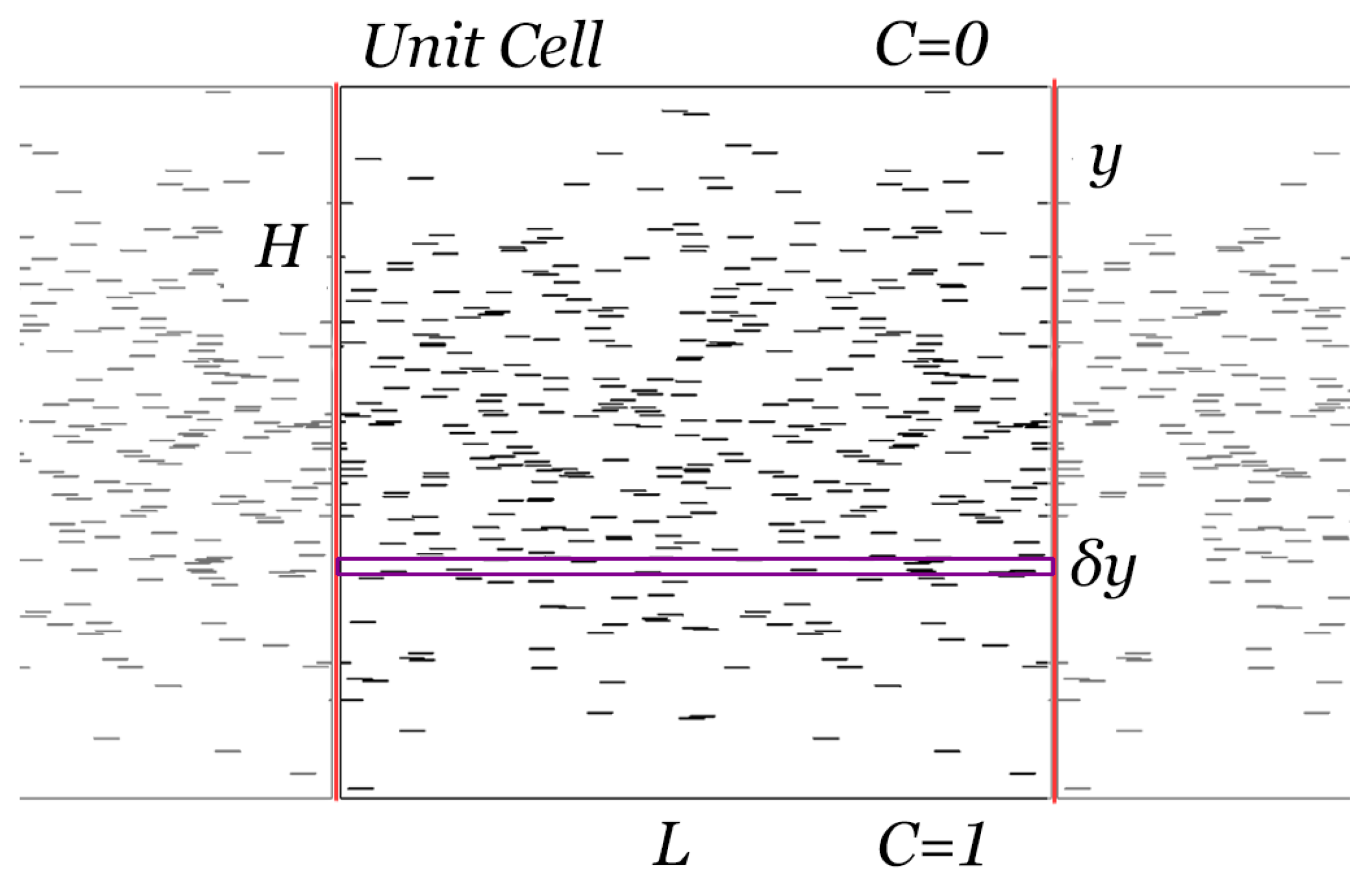
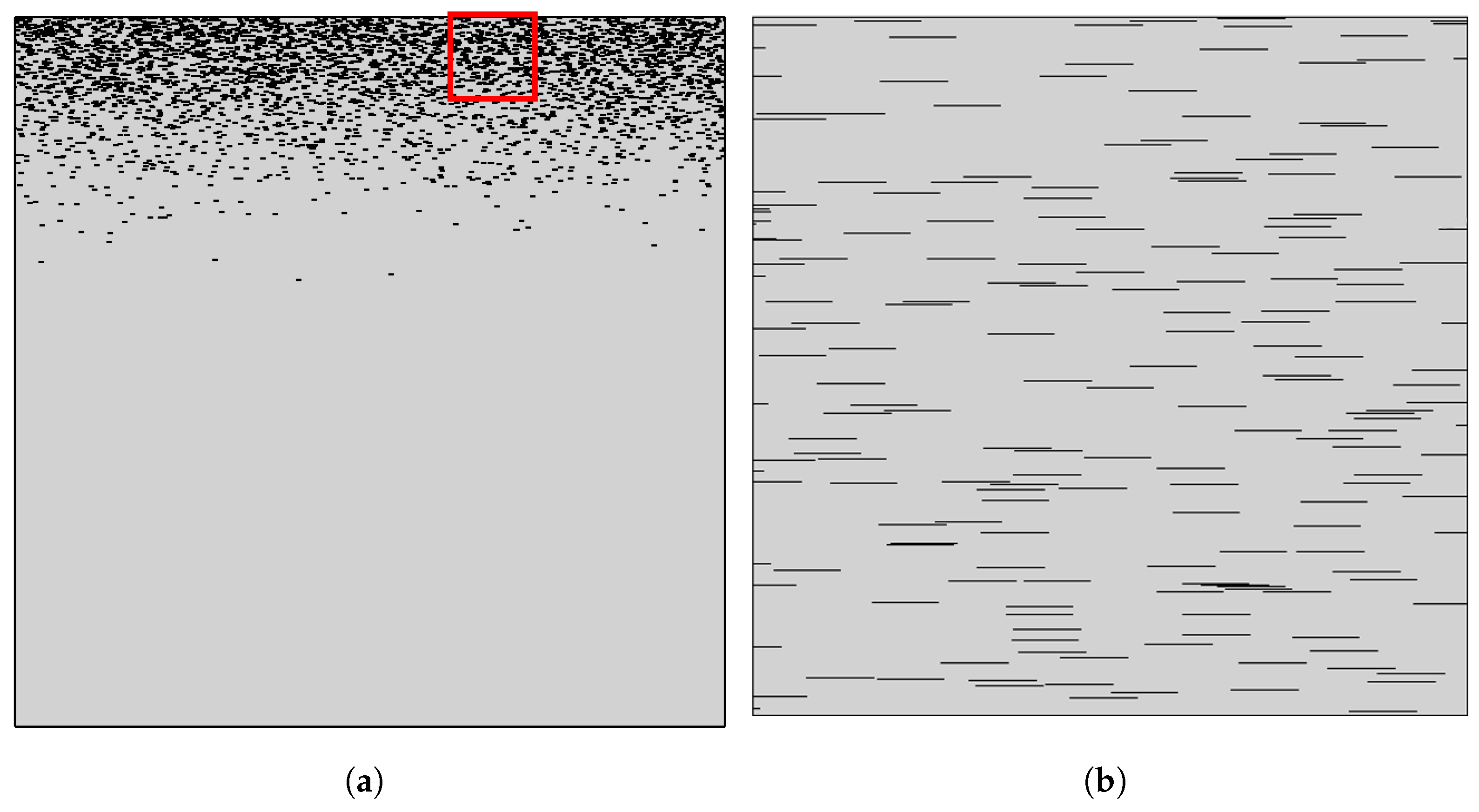
- A set of parameters is determined, and the in-house application generates the appropriate geometry files. A unit cell is created with the desired dimensions, and for each set of and distribution the number of flakes is calculated. Then, the flakes are placed using a random sequential addition algorithm [33], according to which random numbers define the coordinates of the center of each line. The RSA algorithm performs checks to ensure no flake overlap occurs, and to ensure that a minimum separation distance between neighboring flakes is maintained. The latter is essential so that a computational mesh can be generated in the narrow gaps separating adjacent flakes. After the completion of the unit cell calculation, the case directories are created with the appropriate scripts for execution. A master script is created that will run in the main node and coordinate the execution at the various nodes.
- The master script is executed; it uses a greedy strategy to assign the cases to each computational node. According to this strategy, each node in the computational cluster sequentially scans the case directories until an ‘unsolved’ case is found. In this case, the actions in step 3 are executed. If all of the cases are scanned and no other ‘unsolved’ cases are found, the script terminates its execution.
- The nodes are searching for the existence of status files inside each directory that indicate the state of the case. If the status is ‘unsolved’, it is flagged as ‘running’ and the node starts the execution of a sub-script that runs the simulation. If a different node accesses that case folder, it will read the status and will skip it if its status is any other than ‘unsolved’. If a case is ‘unsolved’, then the actions of step 4 are executed.
- A sub script is run in each case directory that executes the commands for running the simulation. The first step is the creation of the mesh. Then the mesh is converted using OpenFOAM utilities, and the boundary conditions are applied. The flakes are being simulated as being one dimensional entities that have only length or ‘baffles’, as referenced in the boundary conditions settings. In the case of baffles, boundary conditions are applied to the internal faces of both cells that lie on each side of the geometrical entity, effectively creating an internal boundary inside the mesh. The simulation is split in order to run in parallel using the the public domain openMPI implementation of the standard message passing interface (MPI). After a solution is achieved, the results are written in a file and the case is flagged as ‘solved’.
- The in-house application is used to scan the case directories and is retrieving the simulation results. Here, it is interesting to note that there is no need to finish all of the simulations before the results are obtained. The results that have been obtained at any time can be collected as needed.
4. Results and Discussion
4.1. Half-Normal Distribution of Flakes
4.2. Linear Distribution
4.3. Triangular Linear Distribution
4.4. Normal Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
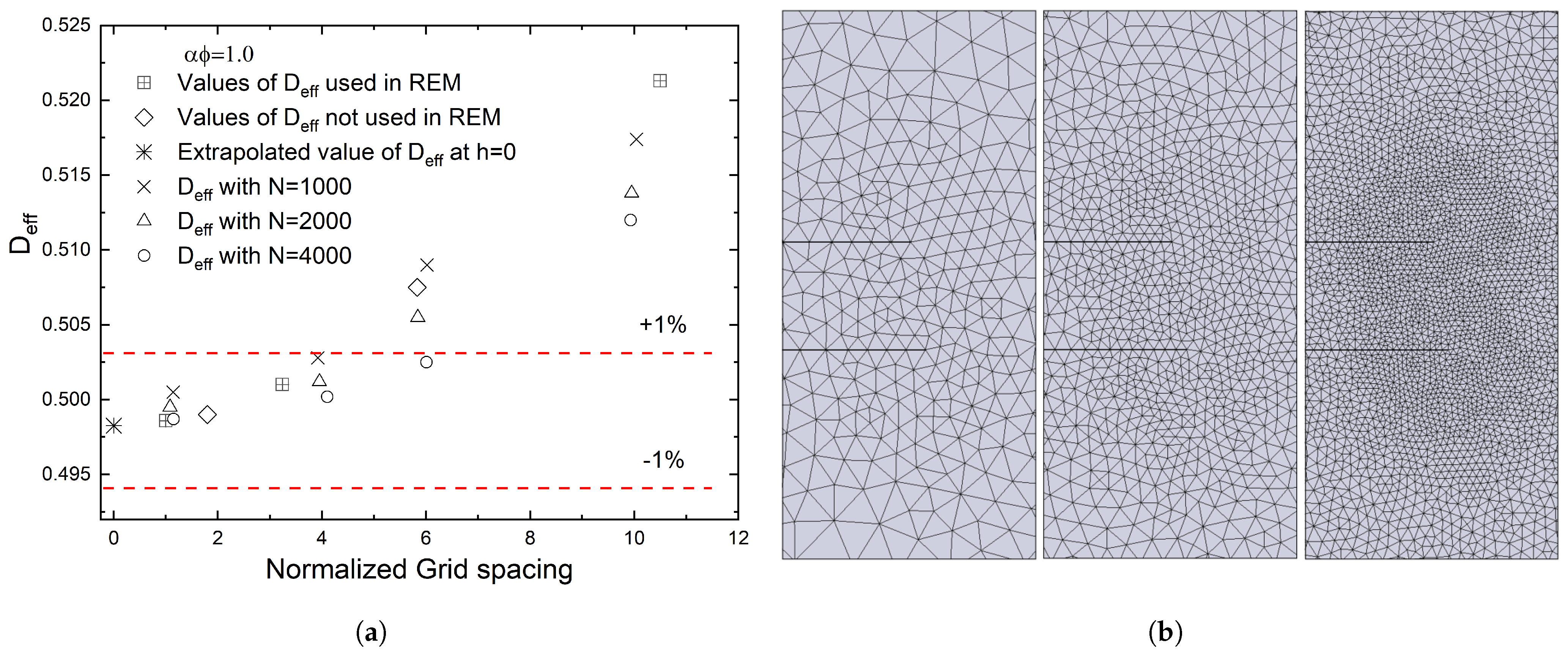
Appendix A. Spatial Mesh Convergence
References
- Aboudi, J.; Arnold, S.; Pindera, M.J. Response of functionally graded composites to thermal gradients. Compos. Eng. 1994, 4, 1–18. [Google Scholar] [CrossRef]
- Rajan, T.; Pillai, R.; Pai, B. Characterization of centrifugal cast functionally graded aluminum-silicon carbide metal matrix composites. Mater. Charact. 2010, 61, 923–928. [Google Scholar] [CrossRef]
- Gannon, A.; Nagel, T.; Kelly, D. The role of the superficial region in determining the dynamic properties of articular cartilage. Osteoarthr. Cartil. 2012, 20, 1417–1425. [Google Scholar] [CrossRef]
- Farquhar, T.; Dawson, P.; Torzilli, P. A microstructural model for the anisotropic drained stiffness of articular cartilage. J. Biomech. Eng. 1990, 112, 414–425. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Kawasaki, A.; Watanabe, R. Concept and P/M fabrication of functionally gradient materials. Ceram. Int. 1997, 23, 73–83. [Google Scholar] [CrossRef]
- Roop Kumar, R.; Wang, M. Functionally graded bioactive coatings of hydroxyapatite/titanium oxide composite system. Mater. Lett. 2002, 55, 133–137. [Google Scholar] [CrossRef]
- Khor, K.; Gu, Y.; Quek, C.; Cheang, P. Plasma spraying of functionally graded hydroxyapatite/Ti-6Al-4V coatings. Surf. Coatings Technol. 2003, 168, 195–201. [Google Scholar] [CrossRef]
- Chu, C.; Zhu, J.; Yin, Z.; Lin, P. Structure optimization and properties of hydroxyapatite-Ti symmetrical functionally graded biomaterial. Mater. Sci. Eng. A 2001, 316, 205–210. [Google Scholar] [CrossRef]
- Choi, K.H.; Kim, H.S.; Park, C.H.; Kim, G.H.; Baik, K.H.; Lee, S.H.; Kim, T.; Kim, H.S. High-temperature thermo-mechanical behavior of functionally graded materials produced by plasma sprayed coating: Experimental and modeling results. Met. Mater. Int. 2016, 22, 817–824. [Google Scholar] [CrossRef]
- Watanabe, Y.; Inaguma, Y.; Sato, H. Cold model for process of a Ni-aluminide/steel clad pipe by a reactive centrifugal casting method. Mater. Lett. 2011, 65, 467–470. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Z.; Hao, L.; Huang, L.; Xin, C.; Wang, Y.; Bilotti, E.; Essa, K.; Zhang, H.; Li, Z.; et al. A Review on Functionally Graded Materials and Structures via Additive Manufacturing: From Multi-Scale Design to Versatile Functional Properties. Adv. Mater. Technol. 2020, 5, 1900981. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Dondero, M.; Cisilino, A.; Carella, J.; Tomba, J. Effective thermal conductivity of functionally graded random micro-heterogeneous materials using representative volume element and BEM. Int. J. Heat Mass Transf. 2011, 54, 3874–3881. [Google Scholar] [CrossRef]
- Chen, X.; Papathanasiou, T. Barrier properties of flake-filled membranes: Review and numerical evaluation. J. Plast. Film. Sheeting 2007, 23, 319–345. [Google Scholar] [CrossRef]
- Xia, L.; Wu, H.; Guo, S.; Sun, X.; Liang, W. Enhanced sound insulation and mechanical properties of LDPE/mica composites through multilayered distribution and orientation of the mica. Compos. Part A Appl. Sci. Manuf. 2016, 81, 225–233. [Google Scholar] [CrossRef]
- Idris, A.; Muntean, A.; Mesic, B. A review on predictive tortuosity models for composite films in gas barrier applications. J. Coatings Technol. Res. 2022, 19, 699–716. [Google Scholar] [CrossRef]
- Pajarito, B.; Kubouchi, M. Flake-filled polymers for corrosion protection. J. Chem. Eng. Jpn. 2013, 46, 18–26. [Google Scholar] [CrossRef]
- Dasari, A.; Yu, Z.Z.; Cai, G.P.; Mai, Y.W. Recent developments in the fire retardancy of polymeric materials. Prog. Polym. Sci. 2013, 38, 1357–1387. [Google Scholar] [CrossRef]
- Lagaron, J.; Núñez, E. Nanocomposites of moisture-sensitive polymers and biopolymers with enhanced performance for flexible packaging applications. J. Plast. Film. Sheeting 2012, 28, 79–89. [Google Scholar] [CrossRef]
- Greco, A. Simulation and modeling of diffusion in oriented lamellar nanocomposites. Comput. Mater. Sci. 2014, 83, 164–170. [Google Scholar] [CrossRef]
- Moggridge, G.; Lape, N.; Yang, C.; Cussler, E. Barrier films using flakes and reactive additives. Prog. Org. Coatings 2003, 46, 231–240. [Google Scholar] [CrossRef]
- Dondero, M.; Tomba, J.; Cisilino, A. The effect of flake orientational order on the permeability of barrier membranes: Numerical simulations and predictive models. J. Membr. Sci. 2016, 514, 95–104. [Google Scholar] [CrossRef]
- Nagy, T.; Duxbury, P. Permeability and conductivity of platelet-reinforced membranes and composites. Phys. Rev. Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 66, 020802. [Google Scholar] [CrossRef]
- Lape, N.; Nuxoll, E.; Cussler, E. Polydisperse flakes in barrier films. J. Membr. Sci. 2004, 236, 29–37. [Google Scholar] [CrossRef]
- Cussler, E.; Hughes, S.; Ward, W., III; Aris, R. Barrier membranes. J. Membr. Sci. 1988, 38, 161–174. [Google Scholar] [CrossRef]
- Zid, S.; Zinet, M.; Espuche, E. 3D Mass diffusion in ordered nanocomposite systems: Finite element simulation and phenomenological modeling. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 51–61. [Google Scholar] [CrossRef]
- Minelli, M.; Baschetti, M.; Doghieri, F. Analysis of modeling results for barrier properties in ordered nanocomposite systems. J. Membr. Sci. 2009, 327, 208–215. [Google Scholar] [CrossRef]
- Tsiantis, A.; Papathanasiou, T. A closed-form solution for the barrier properties of randomly oriented high aspect ratio flake composites. J. Compos. Mater. 2019, 53, 2239–2247. [Google Scholar] [CrossRef]
- Tsiantis, A.; Papathanasiou, T. The Barrier Properties of Flake-Filled Composites with Precise Control of Flake Orientation. Mater. Sci. Appl. 2017, 8, 234–246. [Google Scholar] [CrossRef]
- Tsiantis, A.; Papathanasiou, T. An evaluation of models and computational approaches for the barrier properties of coatings containing flakes of high aspect ratio. J. Coatings Technol. Res. 2019, 16, 521–530. [Google Scholar] [CrossRef]
- Papathanasiou, T.D.; Bénard, A. Flow-Induced Alignment in Composite Materials; Woodhead Publishing: Sawston, UK, 2022; pp. 1–385. [Google Scholar]
- Tsiantis, A.; Papathanasiou, T. A novel FastRSA algorithm: Statistical properties and evolution of microstructure. Phys. A Stat. Mech. Its Appl. 2019, 534, 122083. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- OpenFOAM-The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 10 December 2022).
- Ganß, M.; Staudinger, U.; Satapathy, B.K.; Leuteritz, A.; Weidisch, R. Mechanism of strengthening and toughening of a nanostructured styrene-butadiene based block copolymer by oligostyrene-modified montmorillonites. Polymer 2021, 213, 123328. [Google Scholar] [CrossRef]
- Navarro Oliva, F.S.; Sahihi, M.; Lenglet, L.; Ospina, A.; Guenin, E.; Jaramillo-Botero, A.; Goddard, W.A.I.; Bedoui, F. Nanoparticle size and surface chemistry effects on mechanical and physical properties of nano-reinforced polymers: The case of PVDF-Fe3O4 nano-composites. Polym. Test. 2023, 117, 107851. [Google Scholar] [CrossRef]
- Papathanasiou, T.D.; Tsiantis, A. Orientational randomness and its influence on the barrier properties of flake-filled composite films. J. Plast. Film. Sheeting 2017, 33, 438–456. [Google Scholar] [CrossRef]
- Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa Publishers: Socorro, NM, USA, 1998. [Google Scholar]
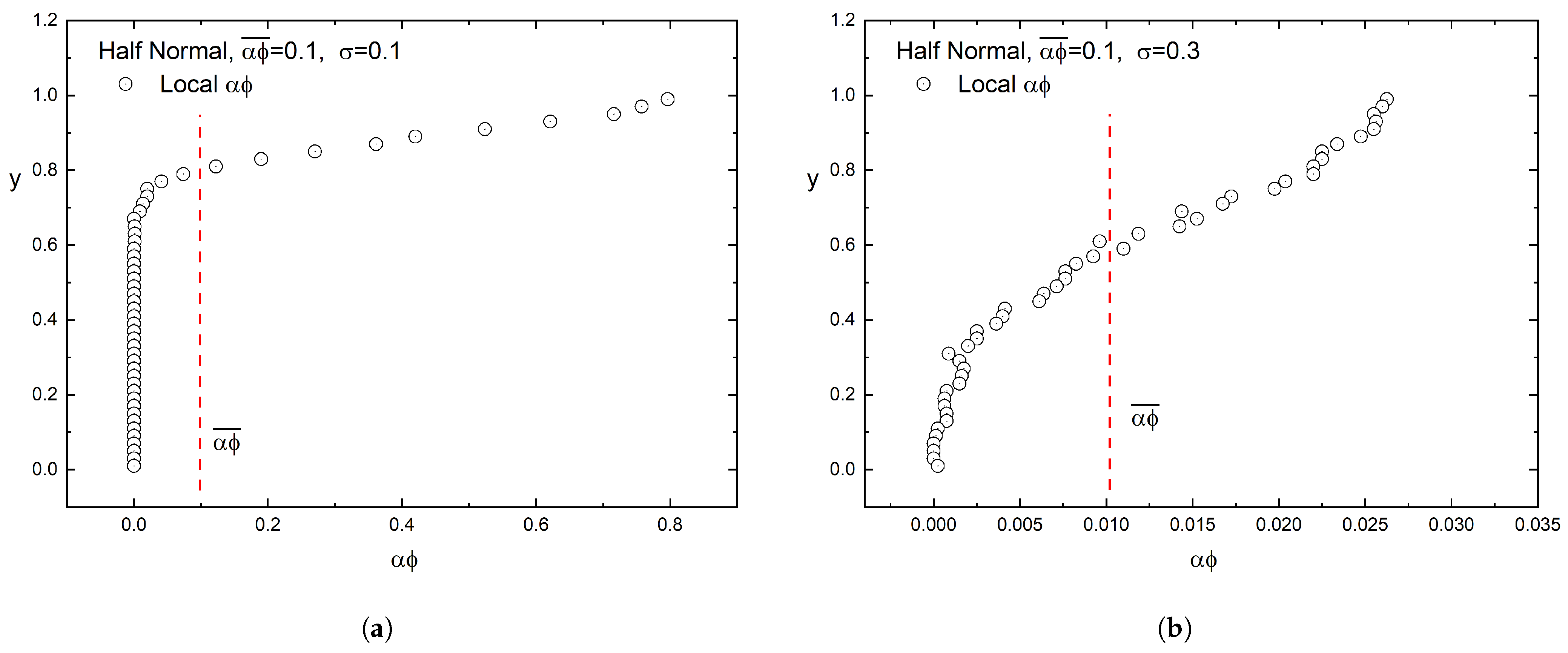


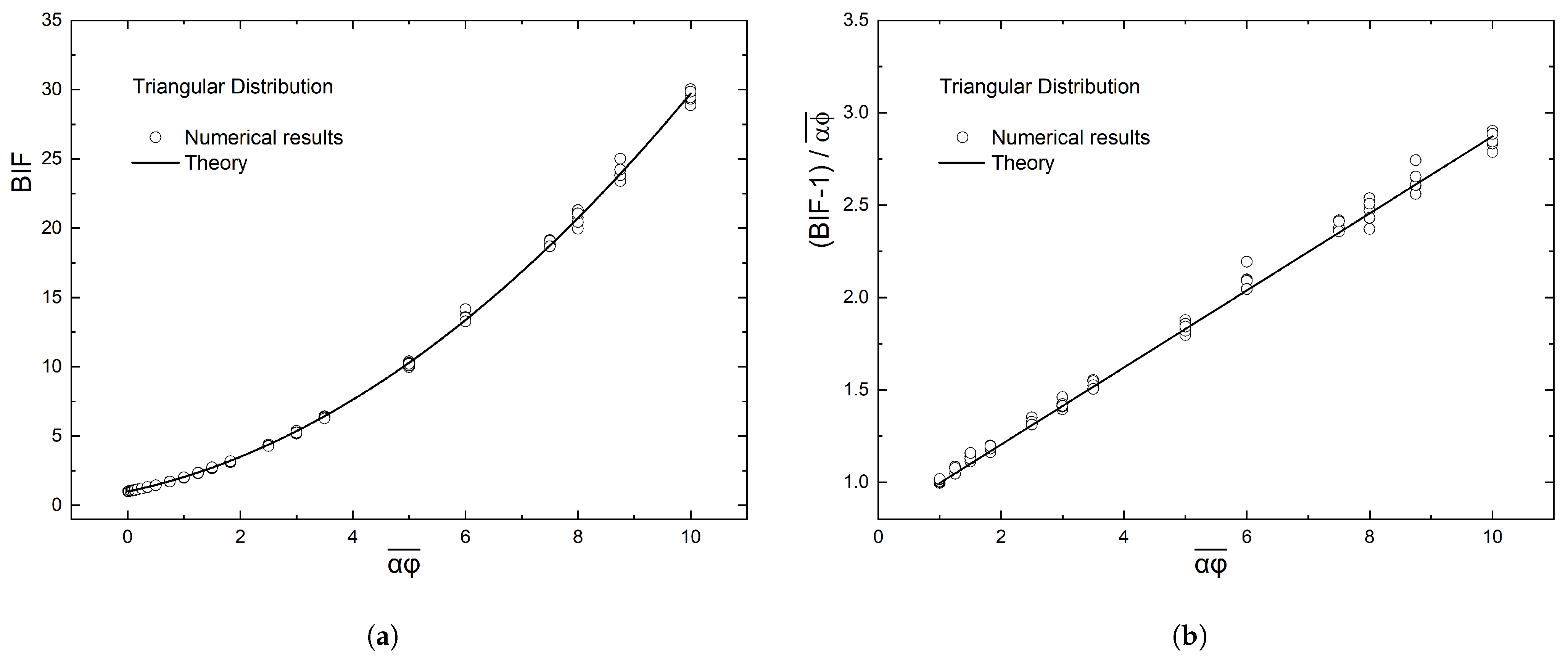


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papathanasiou, T.D.; Diakonikolis, M.; Tsiantis, A. A Gradient Microstructure Improves the Barrier Properties of Flake-Filled Composite Films: A Computational Study. Materials 2023, 16, 1691. https://doi.org/10.3390/ma16041691
Papathanasiou TD, Diakonikolis M, Tsiantis A. A Gradient Microstructure Improves the Barrier Properties of Flake-Filled Composite Films: A Computational Study. Materials. 2023; 16(4):1691. https://doi.org/10.3390/ma16041691
Chicago/Turabian StylePapathanasiou, Thanasis D., Michalis Diakonikolis, and Andreas Tsiantis. 2023. "A Gradient Microstructure Improves the Barrier Properties of Flake-Filled Composite Films: A Computational Study" Materials 16, no. 4: 1691. https://doi.org/10.3390/ma16041691
APA StylePapathanasiou, T. D., Diakonikolis, M., & Tsiantis, A. (2023). A Gradient Microstructure Improves the Barrier Properties of Flake-Filled Composite Films: A Computational Study. Materials, 16(4), 1691. https://doi.org/10.3390/ma16041691






