The Impact of Electron Phonon Scattering, Finite Size and Lateral Electric Field on Transport Properties of Topological Insulators: A First Principles Quantum Transport Study
Abstract
1. Introduction
2. Materials and Methods
3. Results
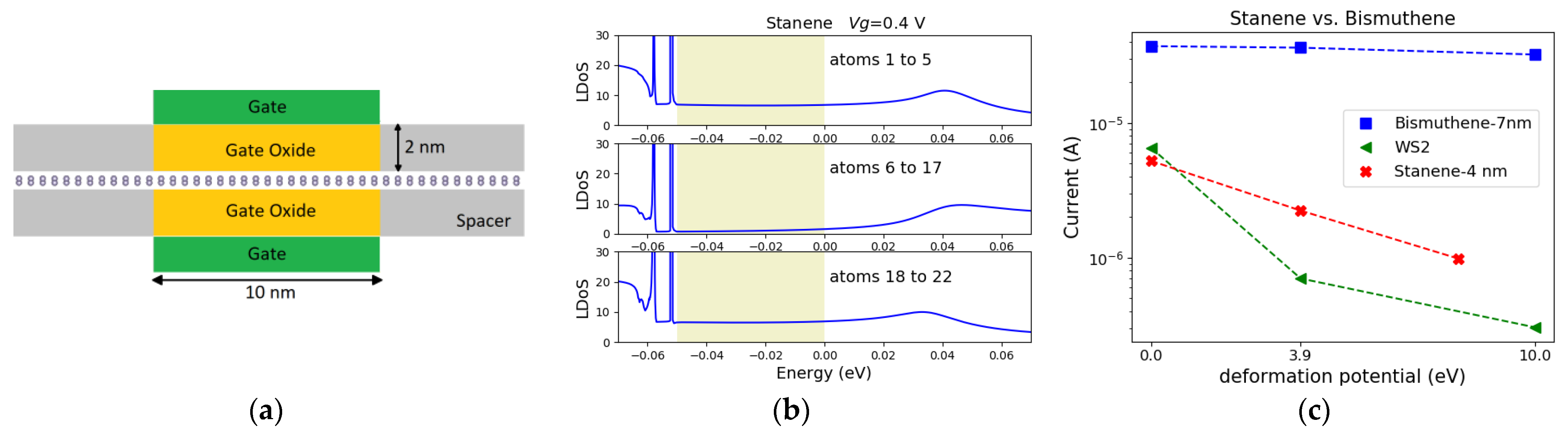
3.1. Zigzag Nanoribbons of Stanene and Bismuthene
3.1.1. Mode Space Basis
3.1.2. The Effects of Electron–Phonon Coupling
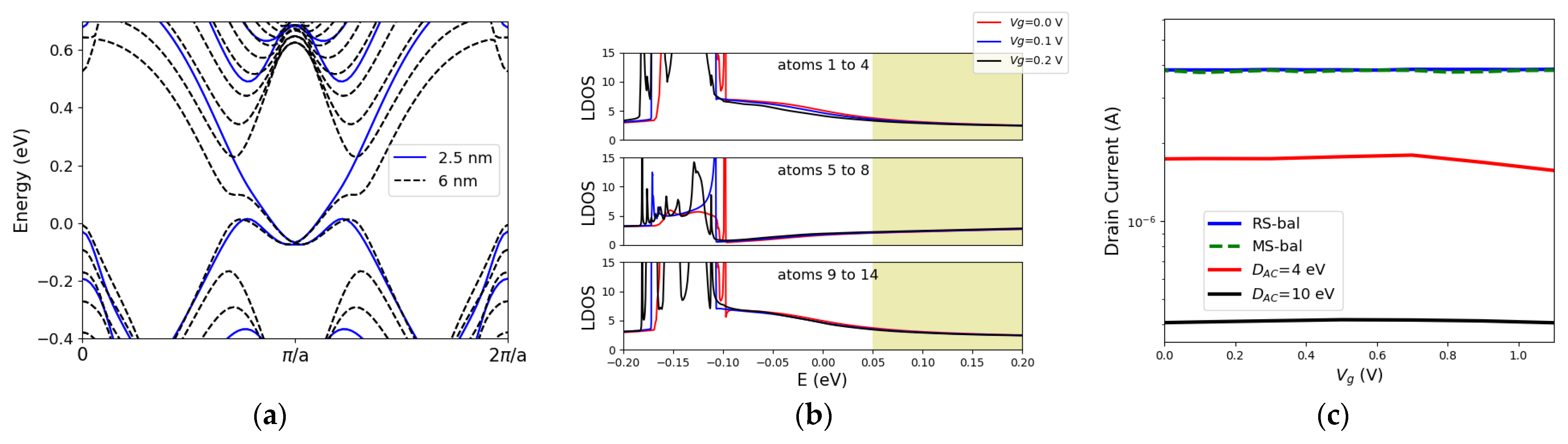
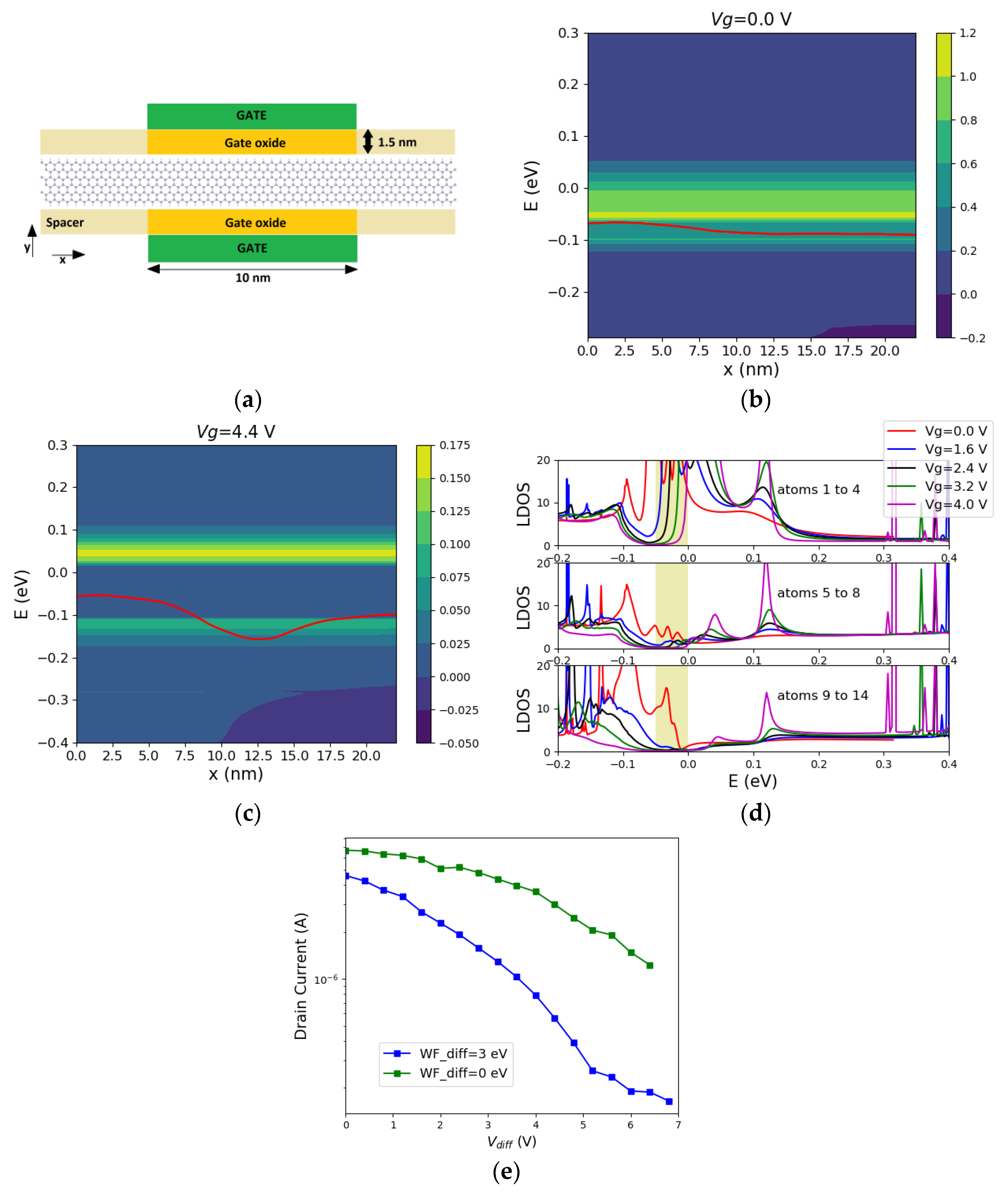
3.2. Ultra-Narrow Ribbons
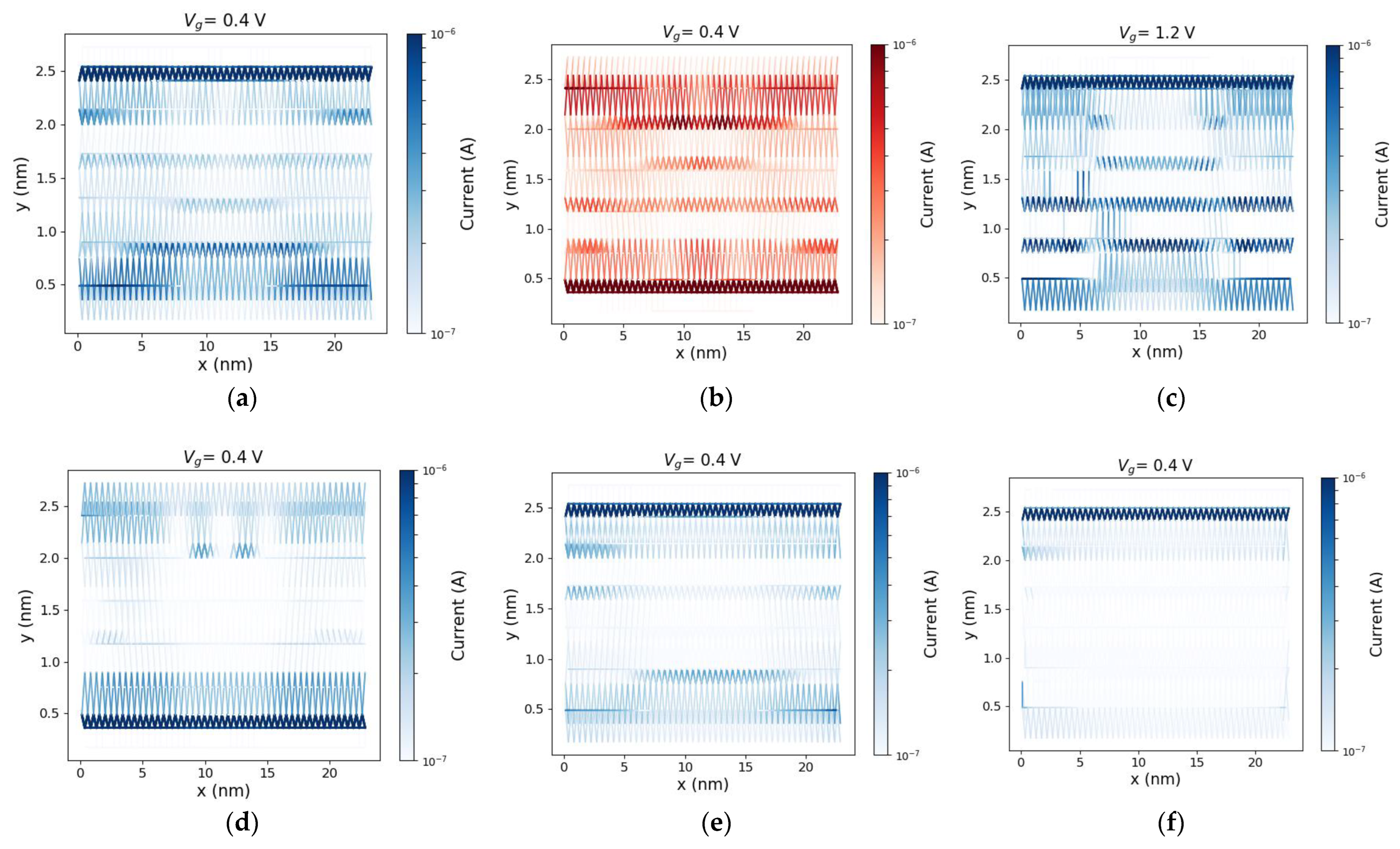
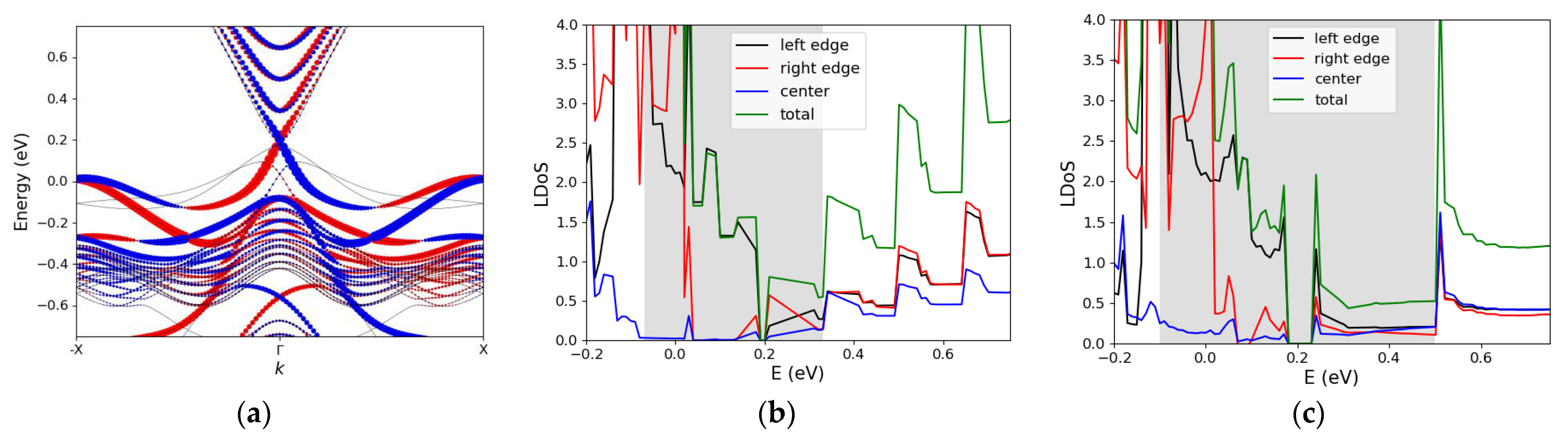
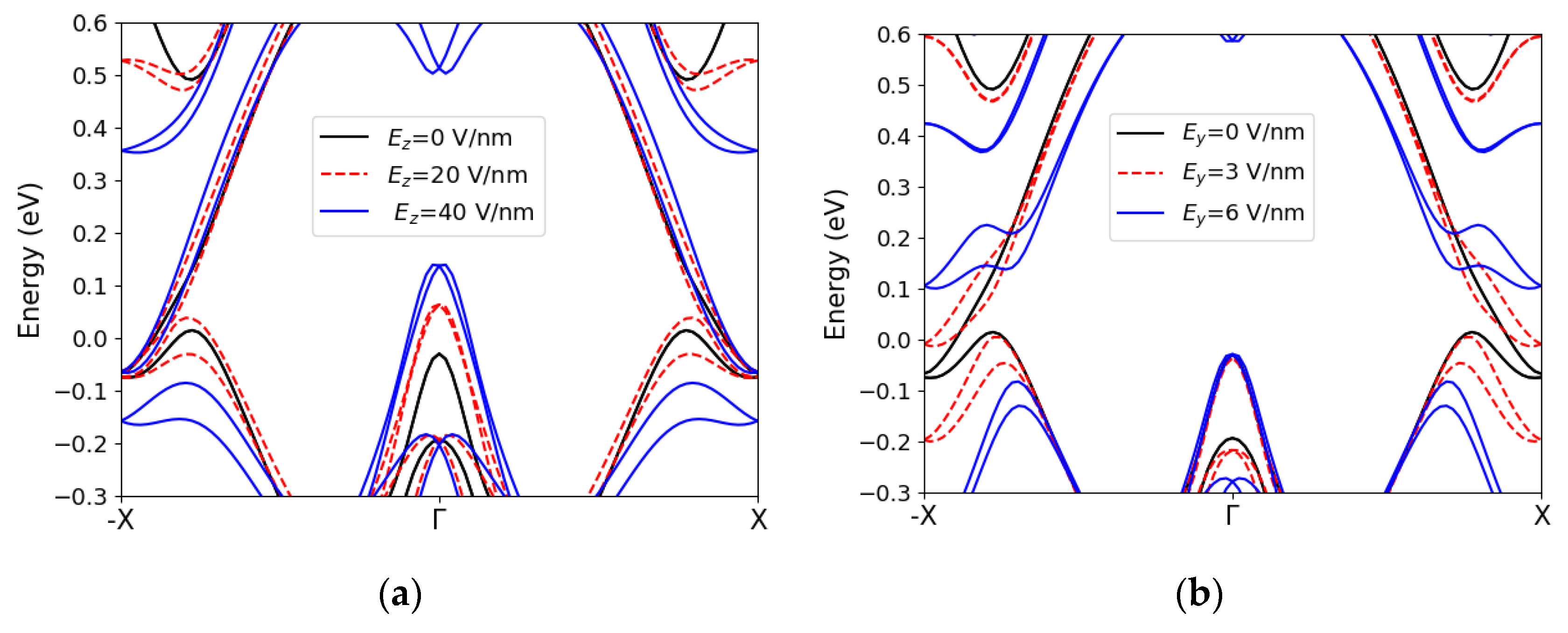
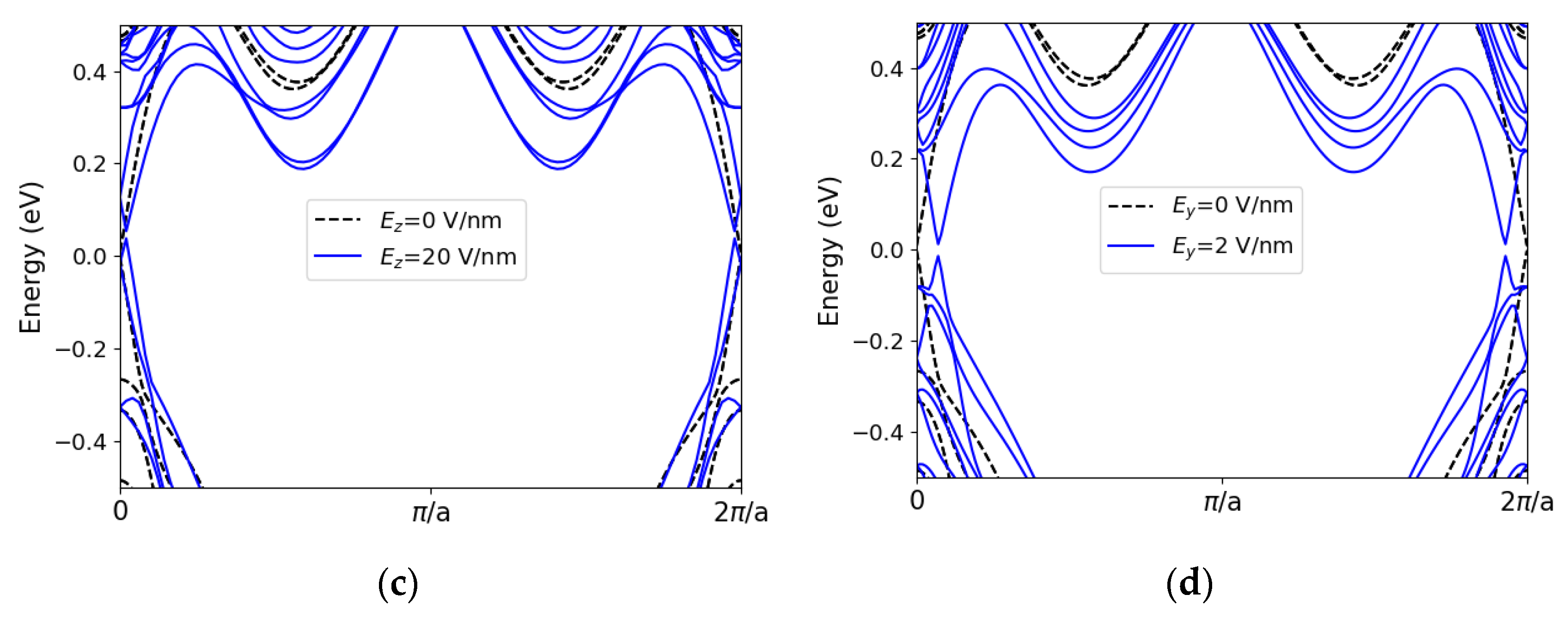
3.3. Electric Field-Induced Topological Phase Transition in Xenes
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef]
- Tiwari, S.; Van de Put, M.L.; Sorée, B.; Vandenberghe, W.G. Carrier transport in two-dimensional topological insulator nanoribbons in the presence of vacancy defects. 2D Mater. 2019, 6, 025011. [Google Scholar] [CrossRef]
- Pezo, A.; Focassio, B.; Schleder, G.R.; Costa, M.; Lewenkopf, C.; Fazzio, A. Disorder effects of vacancies on the electronic transport properties of realistic topological insulator nanoribbons: The case of bismuthene. Phys. Rev. Mater. 2021, 5, 014204. [Google Scholar] [CrossRef]
- Konig, M.; Wiedmann, S.; Brune, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Fatemi, V.; Gibson, Q.D.; Watanabe, K.; Taniguchi, T.; Cava, R.J.; Jarillo-Herrero, P. Observation of the quantum spin Hall effect up to 100 Kelvin in a monolayer crystal. Science 2018, 359, 76–79. [Google Scholar] [CrossRef]
- Lima, L.R.; Lewenkopf, C. Breakdown of topological protection due to nonmagnetic edge disorder in two-dimensional materials in the quantum spin Hall phase. Phys. Rev. B 2022, 106, 245408. [Google Scholar] [CrossRef]
- Nguyen, N.M.; Cuono, G.; Islam, R.; Autieri, C.; Hyart, T.; Brzezicki, W. Unprotected edge modes in quantum spin Hall insulator candidate materials. arXiv 2022, arXiv:2209.06912. [Google Scholar] [CrossRef]
- Paul, T.; Becerra, V.F.; Hyart, T. Interplay of quantum spin Hall effect and spontaneous time-reversal symmetry breaking in electron-hole bilayers I: Transport properties. arXiv 2022, arXiv:2205.12790. [Google Scholar] [CrossRef]
- Väyrynen, J.I.; Goldstein, M.; Gefen, Y.; Glazman, L.I. Resistance of helical edges formed in a semiconductor heterostructure. Phys. Rev. B 2014, 90, 115309. [Google Scholar] [CrossRef]
- Dietl, T. Charge dopants control quantum spin Hall materials. arXiv 2022, arXiv:2206.01613. [Google Scholar]
- Vannucci, L.; Olsen, T.; Thygesen, K.S. Conductance of quantum spin Hall edge states from first principles: The critical role of magnetic impurities and inter-edge scattering. Phys. Rev. B 2020, 101, 155404. [Google Scholar] [CrossRef]
- Ezawa, M.; Nagaosa, N. Interference of topologically protected edge states in silicene nanoribbons. Phys. Rev. B 2013, 88, 121401. [Google Scholar] [CrossRef]
- Das, B.; Sen, D.; Mahapatra, S. Tuneable quantum spin Hall states in confined 1T’transition metal dichalcogenides. Sci. Rep. 2020, 10, 6670. [Google Scholar] [CrossRef]
- Nadeem, M.; Zhang, C.; Culcer, D.; Hamilton, A.R.; Fuhrer, M.S.; Wang, X. Optimizing topological switching in confined 2D-Xene nanoribbons via finite-size effects. Appl. Phys. Rev. 2022, 9, 011411. [Google Scholar] [CrossRef]
- Shi, B.; Tang, H.; Song, Z.; Li, J.; Xu, L.; Liu, S.; Yang, J.; Sun, X.; Quhe, R.; Yang, J.; et al. Phase transition and topological transistors based on monolayer Na3Bi nanoribbons. Nanoscale 2021, 13, 15048–15057. [Google Scholar] [CrossRef]
- Vandenberghe, W.G.; Fischetti, M.V. Imperfect two-dimensional topological insulator field-effect transistors. Nat. Commun. 2017, 8, 14184. [Google Scholar] [CrossRef]
- Molle, A.; Goldberger, J.; Houssa, M.; Xu, Y.; Zhang, S.C.; Akinwande, D. Buckled two-dimensional Xene sheets. Nat. Mater. 2017, 16, 163–169. [Google Scholar] [CrossRef]
- Qian, X.; Liu, J.; Fu, L.; Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 2014, 346, 1344–1347. [Google Scholar] [CrossRef]
- Collins, J.L.; Tadich, A.; Wu, W.; Gomes, L.C.; Rodrigues, J.N.; Liu, C.; Hellerstedt, J.; Ryu, H.; Tang, S.; Mo, S.K.; et al. Electric-field-tuned topological phase transition in ultrathin Na3Bi. Nature 2018, 564, 390–394. [Google Scholar] [CrossRef]
- Focassio, B.; Schleder, G.R.; Pezo, A.; Costa, M.; Fazzio, A. Dual topological insulator device with disorder robustness. Phys. Rev. B 2020, 102, 045414. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Y.R.; Wang, J.; Liu, J.F.; Ma, Z. Quantized field-effect tunneling between topological edge or interface states. Phys. Rev. Lett. 2019, 123, 206801. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar] [CrossRef]
- Afzalian, A.; Pourtois, G. Atomos: An atomistic modelling solver for dissipative dft transport in ultra-scaled hfs2 and black phosphorus mosfets. In Proceedings of the 2019 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Udine, Italy, 4–6 September 2019; pp. 1–4. [Google Scholar]
- Afzalian, A. Ab initio perspective of ultra-scaled CMOS from 2d material fundamentals to dynamically doped transistors. NPJ 2D Mater. Appl. 2021, 5, 5. [Google Scholar] [CrossRef]
- Afzalian, A.; Huang, J.; Ilatikhameneh, H.; Charles, J.; Lemus, D.; Lopez, J.B.; Rubiano, S.P.; Kubis, T.; Povolotskyi, M.; Klimeck, G.; et al. Mode space tight binding model for ultra-fast simulations of III-V nanowire MOSFETs and heterojunction TFETs. In Proceedings of the 2015 International Workshop on Computational Electronics (IWCE), West Lafayette, IN, USA, 2–4 September 2015; pp. 1–3. [Google Scholar]
- Afzalian, A.; Vasen, T.; Ramvall, P.; Passlack, M. Physics and performance of III-V nanowire broken-gap heterojunction TFETs using an efficient tight-binding mode-space NEGF model enabling million-atom nanowire simulations. J. Phys. Condens. Matter 2018, 30, 254002. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.; Jeong, W.J.; Lee, J. Density functional theory based simulations of silicon nanowire field effect transistors. J. Appl. Phys. 2016, 119, 154505. [Google Scholar] [CrossRef]
- Taisuke, O. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar]
- Kotaka, H.; Ishii, F.; Saito, M. Rashba effect on the structure of the Bi one-bilayer film: Fully relativistic first-principles calculation. Jpn. J. Appl. Phys. 2013, 52, 035204. [Google Scholar] [CrossRef]
- Afzalian, A.; Akhoundi, E.; Gaddemane, G.; Duflou, R.; Houssa, M. Advanced DFT–NEGF Transport Techniques for Novel 2-D Material and Device Exploration Including HfS2/WSe2 van der Waals Heterojunction TFET and WTe2/WS2 Metal/Semiconductor Contact. IEEE Trans. Electron Devices 2021, 68, 5372–5379. [Google Scholar] [CrossRef]
- Afzalian, A. Computationally efficient self-consistent born approximation treatments of phonon scattering for coupled-mode space non-equilibrium Green’s function. J. Appl. Phys. 2011, 110, 094517. [Google Scholar] [CrossRef]
- Afzalian, A.; Doornbos, G.; Shen, T.M.; Passlack, M.; Wu, J. A High-Performance InAs/GaSb Core-Shell Nanowire Line-Tunneling TFET: An Atomistic Mode-Space NEGF Study. IEEE J. Electron Dev. Soc. 2018, 7, 88–99. [Google Scholar] [CrossRef]
- Vandenberghe, W.; Massimo, V. Calculation of room temperature conductivity and mobility in tin-based topological insulator nanoribbons. J. Appl. Phys. 2014, 116, 173707. [Google Scholar] [CrossRef]
- Akhoundi, E.; Houssa, M.; Afzalian, A. The impact of electron phonon scattering on transport properties of topological insulators: A first principles quantum transport study. Solid-State Electron. 2023, 201, 108587. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhoundi, E.; Houssa, M.; Afzalian, A. The Impact of Electron Phonon Scattering, Finite Size and Lateral Electric Field on Transport Properties of Topological Insulators: A First Principles Quantum Transport Study. Materials 2023, 16, 1603. https://doi.org/10.3390/ma16041603
Akhoundi E, Houssa M, Afzalian A. The Impact of Electron Phonon Scattering, Finite Size and Lateral Electric Field on Transport Properties of Topological Insulators: A First Principles Quantum Transport Study. Materials. 2023; 16(4):1603. https://doi.org/10.3390/ma16041603
Chicago/Turabian StyleAkhoundi, Elaheh, Michel Houssa, and Aryan Afzalian. 2023. "The Impact of Electron Phonon Scattering, Finite Size and Lateral Electric Field on Transport Properties of Topological Insulators: A First Principles Quantum Transport Study" Materials 16, no. 4: 1603. https://doi.org/10.3390/ma16041603
APA StyleAkhoundi, E., Houssa, M., & Afzalian, A. (2023). The Impact of Electron Phonon Scattering, Finite Size and Lateral Electric Field on Transport Properties of Topological Insulators: A First Principles Quantum Transport Study. Materials, 16(4), 1603. https://doi.org/10.3390/ma16041603






