A Novel 3D-Printed Negative-Stiffness Lattice Structure with Internal Resonance Characteristics and Tunable Bandgap Properties
Abstract
:1. Introduction
2. Structural Design
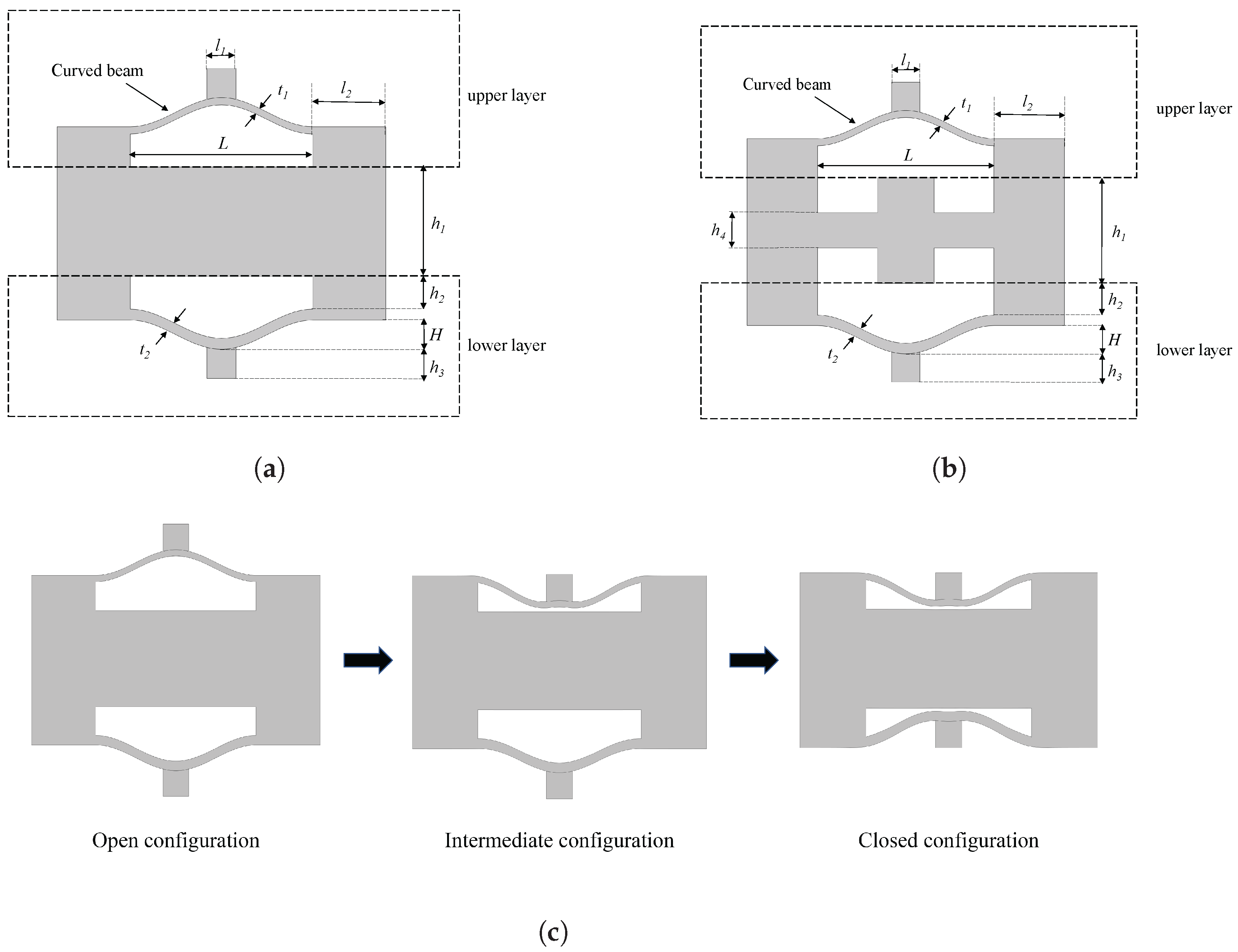
2.1. Normal NSLS and Meta-NSLS
2.2. Selection of Geometric Parameters
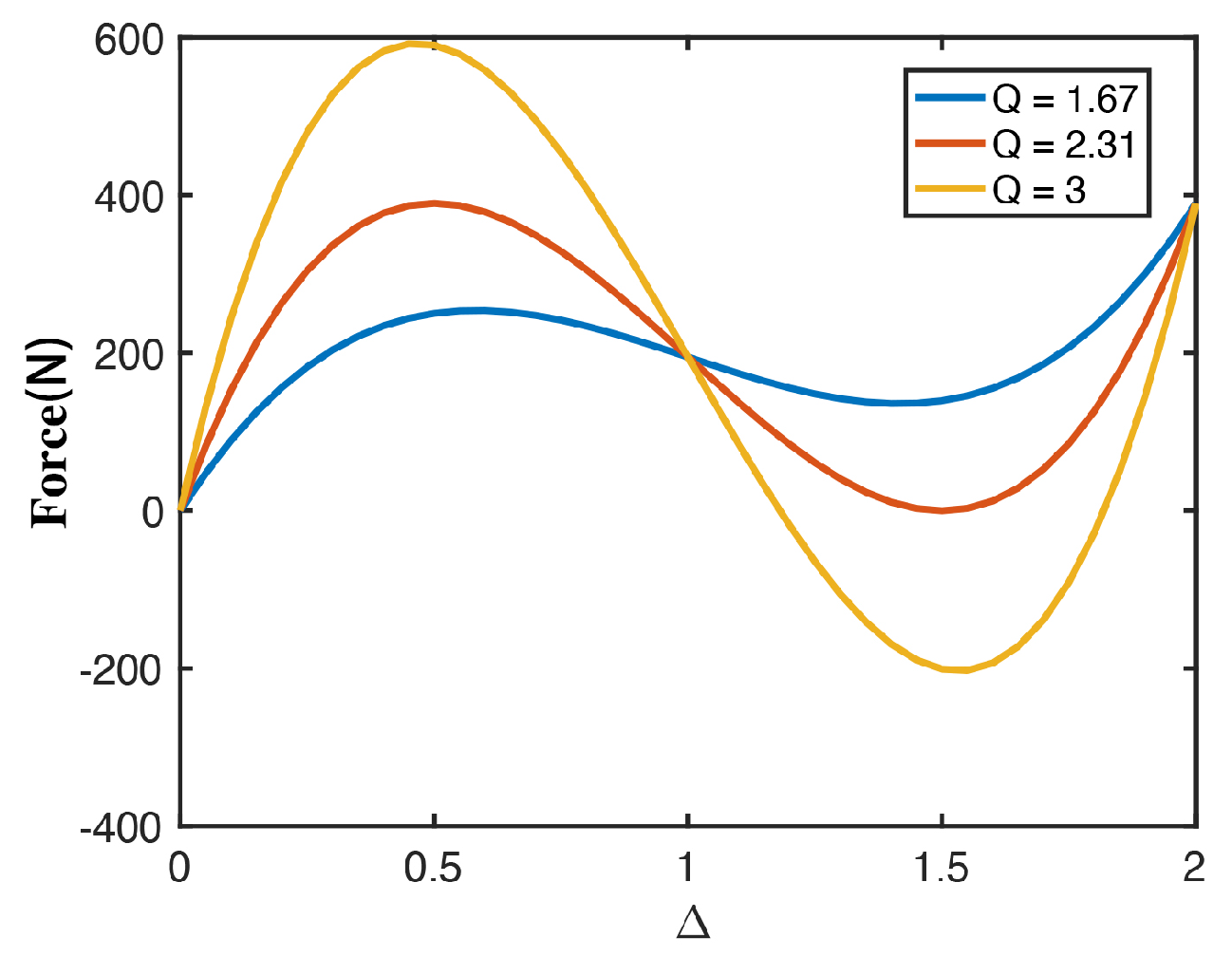
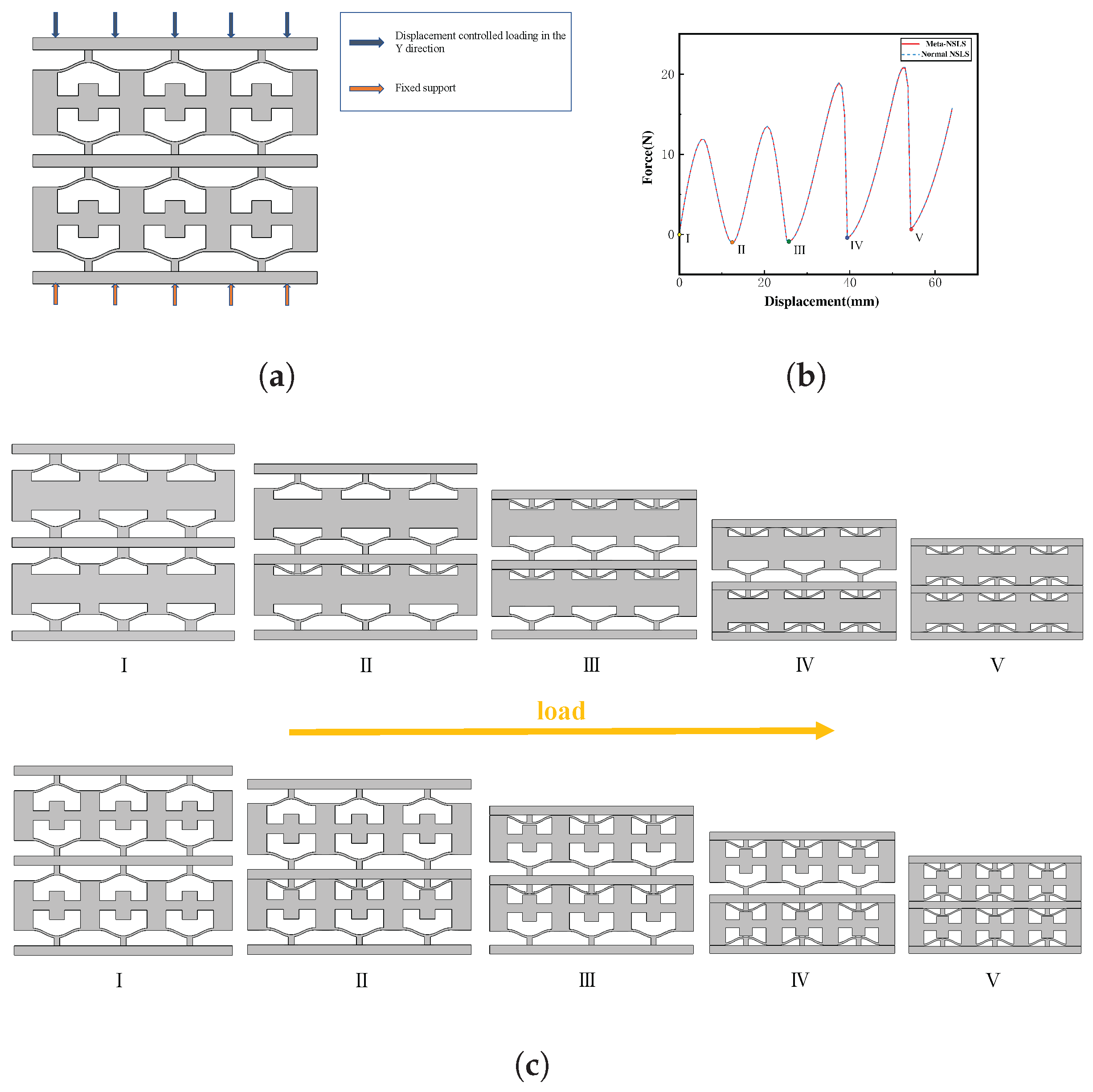
2.3. Compression Performance Analysis
3. Bandgap Analysis
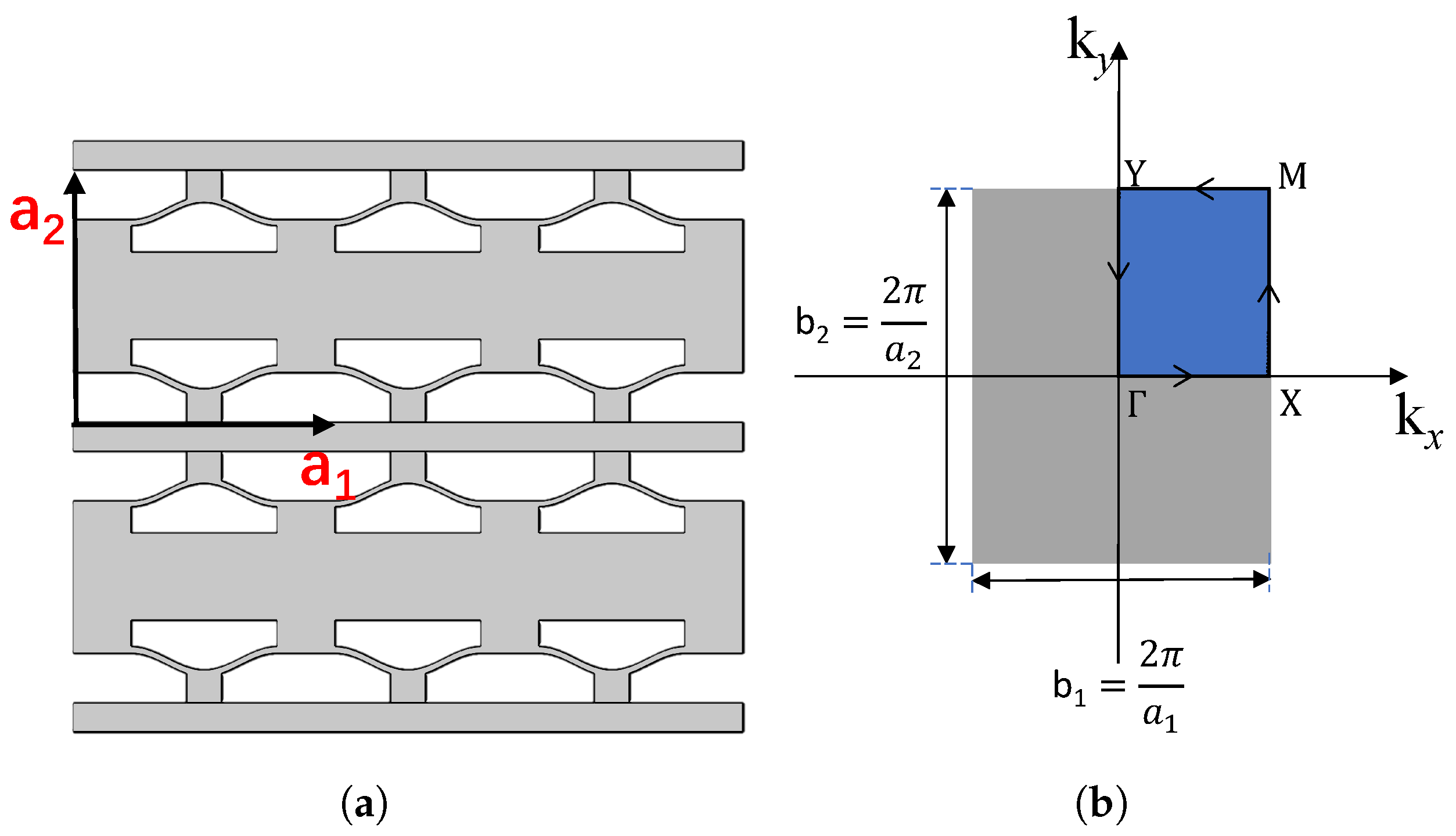
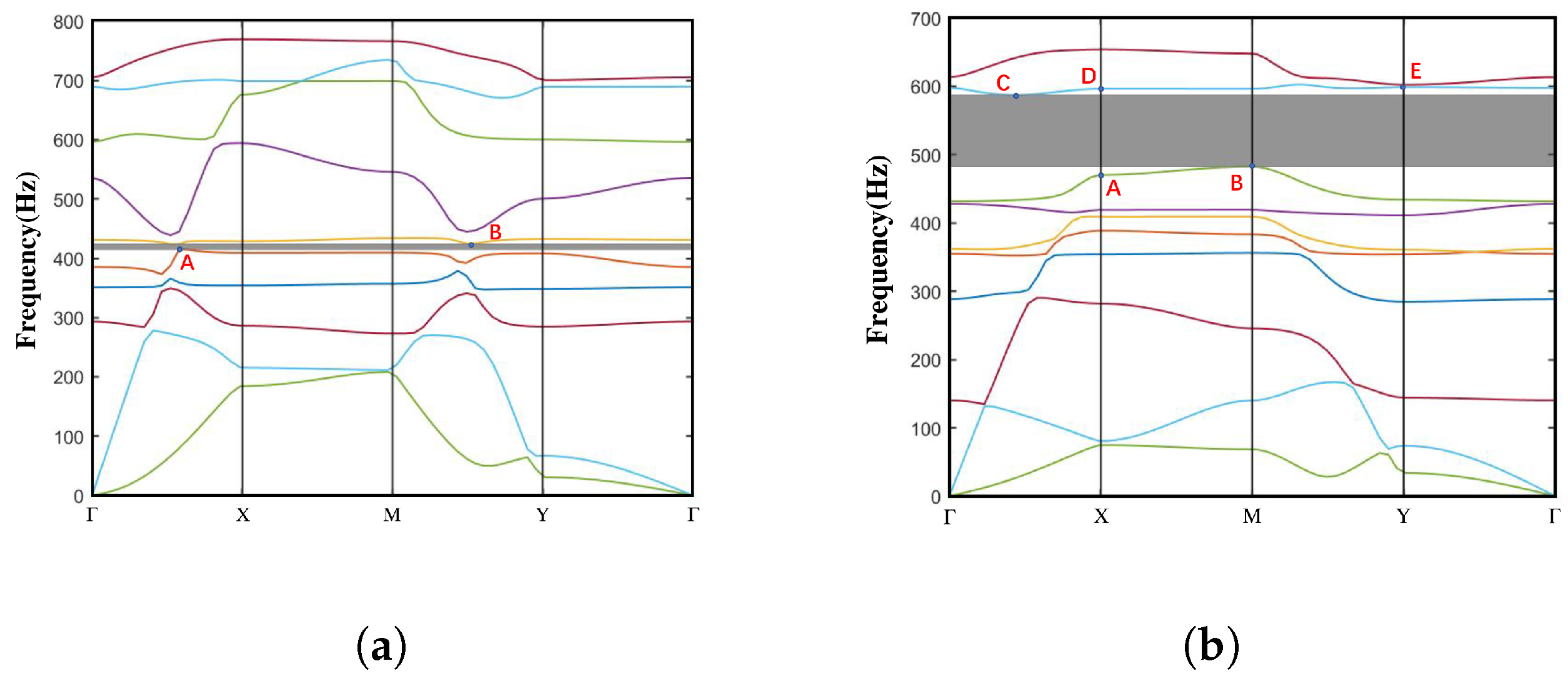
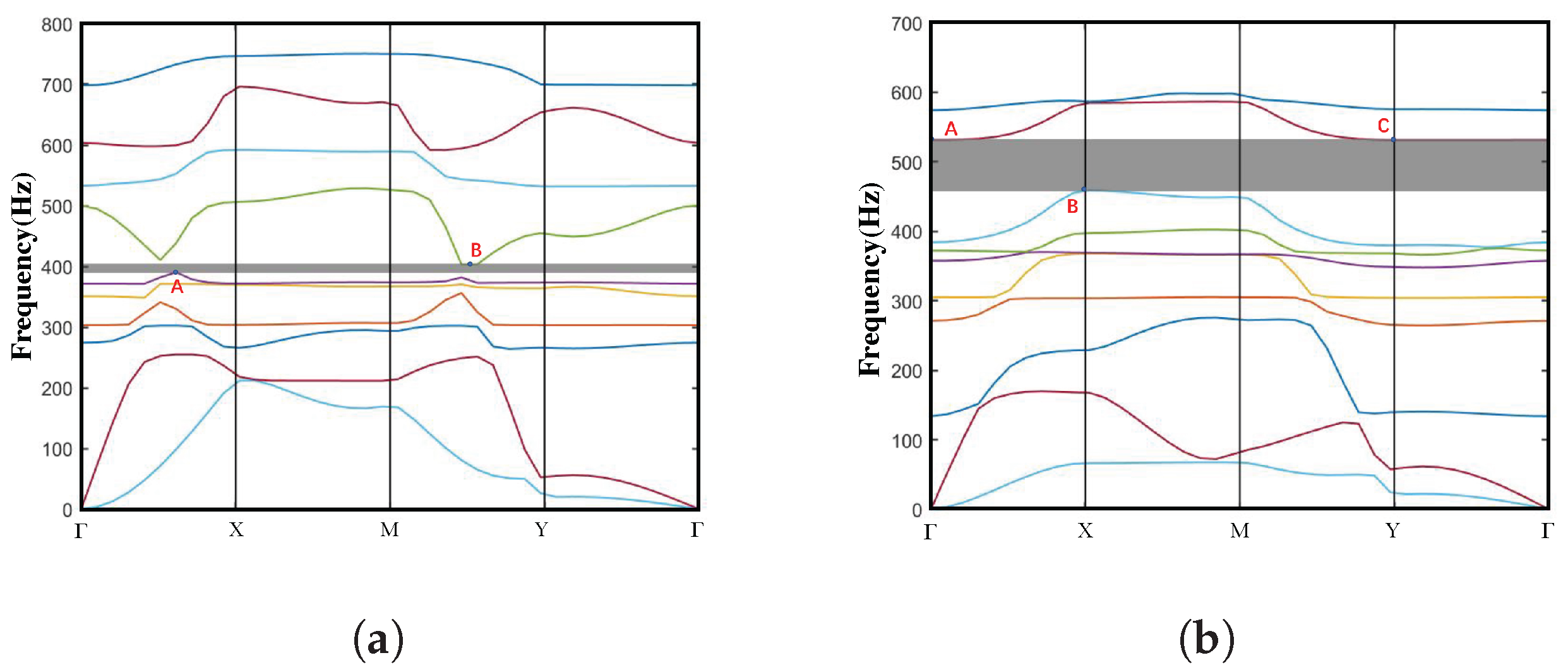
3.1. Dispersion Spectra and Bandgaps
3.1.1. Open Configuration
3.1.2. Intermediate Configuration
3.1.3. Closed Configuration
3.2. Parametrical Analysis and Discussion
4. Vibration Transmission
5. Conclusions
- (1).
- Analysis of the mechanical properties of the proposed normal NSLS and meta-NSLS reveals their capacity to provide excellent energy absorption characteristics once suitable geometric parameters for the curved beams are determined. These configurations effectively reach various stable states during the compression process. Moreover, due to the complete identity of the curved beam sections in normal NSLS and meta-NSLS, there are minimal differences in their mechanical properties. Both models exhibit a fixed bending sequence during compressive deformation due to the differing thicknesses of the upper and lower curved beams. This enables rapid and efficient controllable and locally selectable deformations.
- (2).
- Both configurations exhibit three stable states under the influence of external loads, namely the open configuration, intermediate configuration, and closed configuration, as proposed in this study. The selection of design parameters ensures that the stable deformation modes of each unit cell closely approach the elastic stability limit. Consequently, transitions between stable structures can be employed to adjust the frequency range of elastic wave attenuation. Notably, the bandgap distribution and effective bandgap width differ between different configurations. Importantly, meta-NSLS demonstrates superior bandgap capabilities compared to normal NSLS, offering significant deformability, reconfigurability, multi-directional bandgap tunability, and an extended range of tunable bandgaps. This suggests its potential for vibration isolation in practical applications.
- (3).
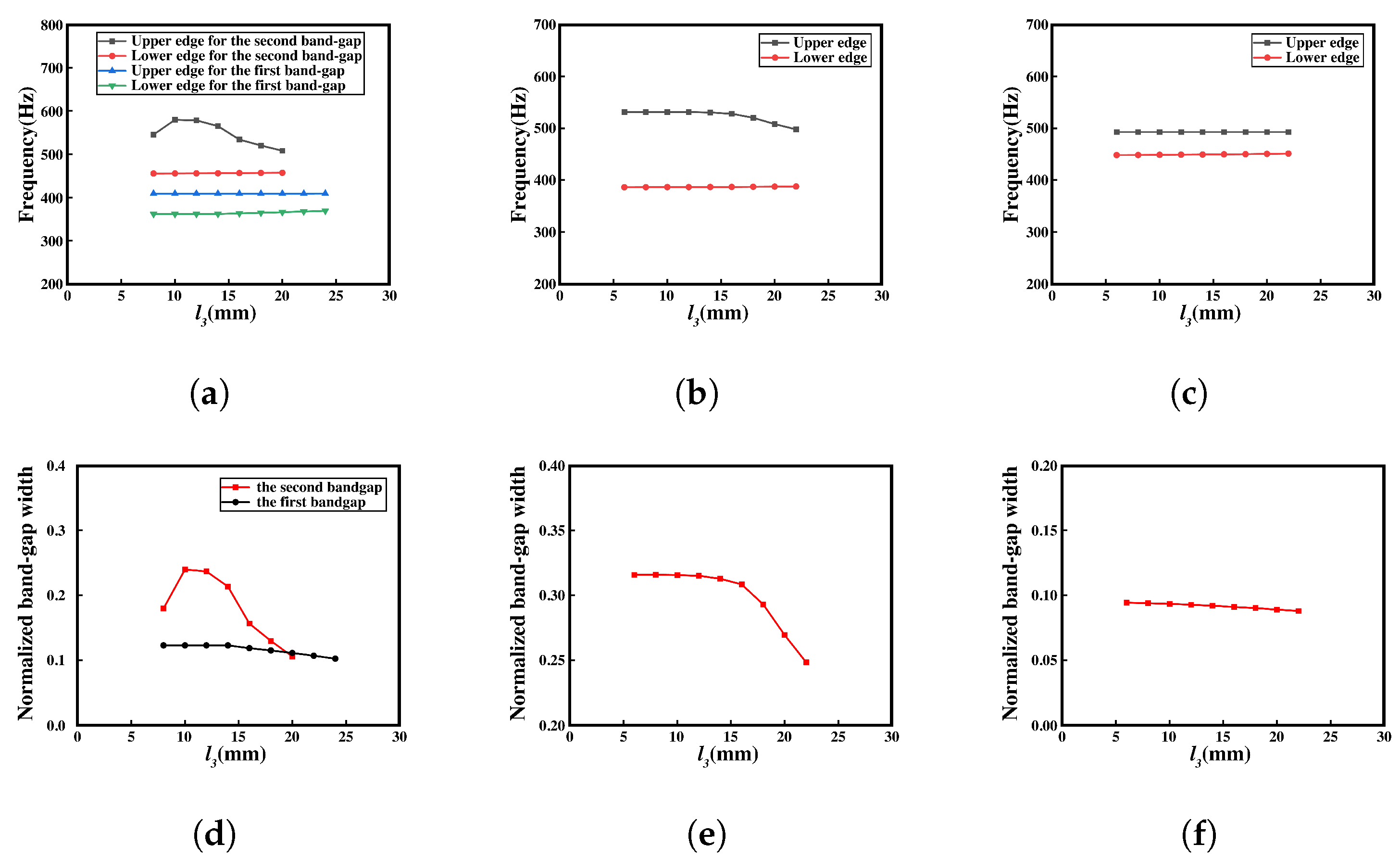
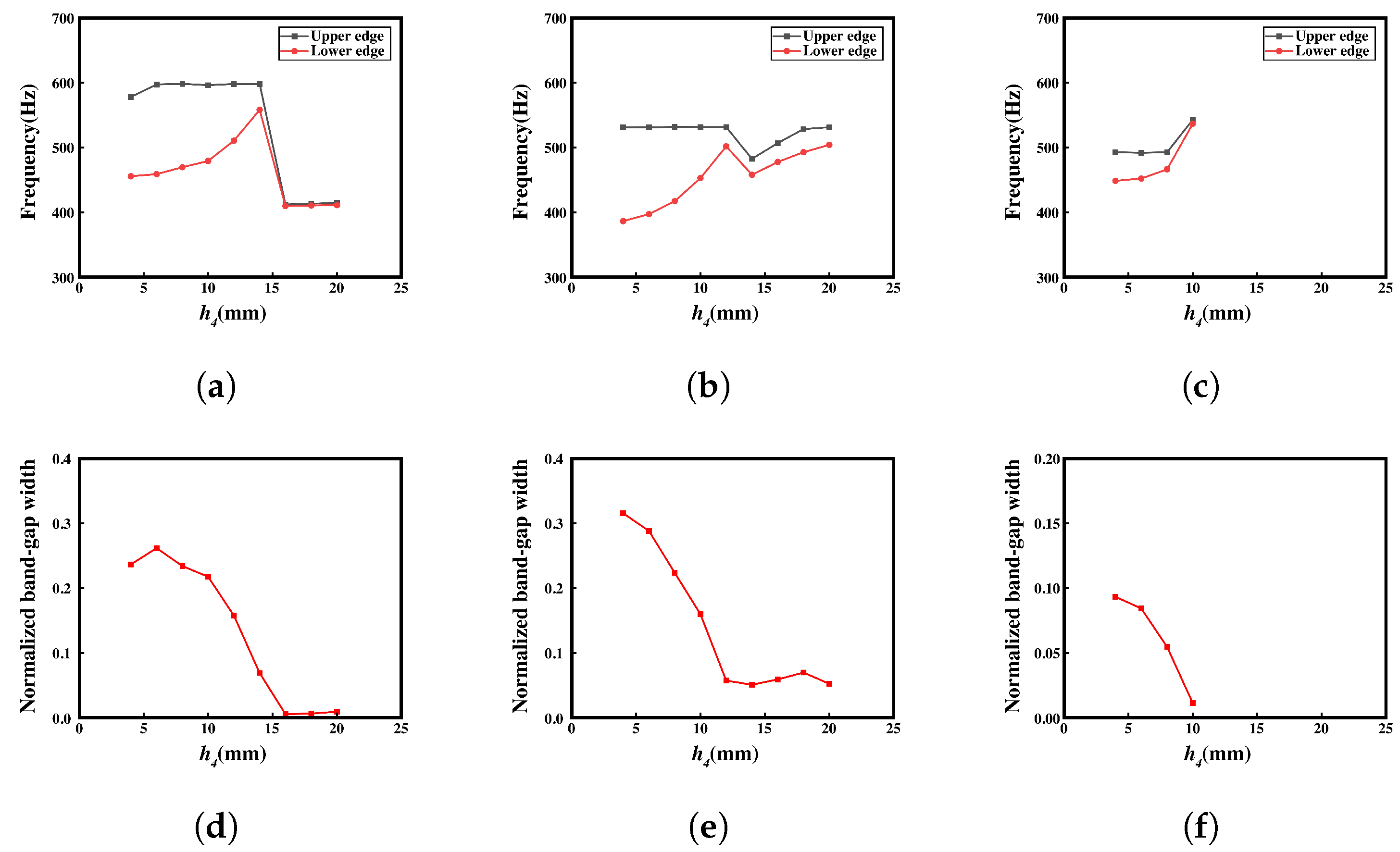
- The study provides a detailed discussion of the influence of geometric parameters on the bandgap of meta-NSLS. The band structure under different deformation conditions and the influence of parameters on the bandgap are analyzed by numerical simulations. As the primary parameters (, , ) vary within reasonable ranges, the bandgap widths in the three configurations exhibit systematic changes. This observation underscores the sensitivity of bandgap properties to alterations in these key parameters, highlighting the crucial role of geometric adjustments in tailoring the bandgap characteristics of NS mechanical metamaterials.
- 4).
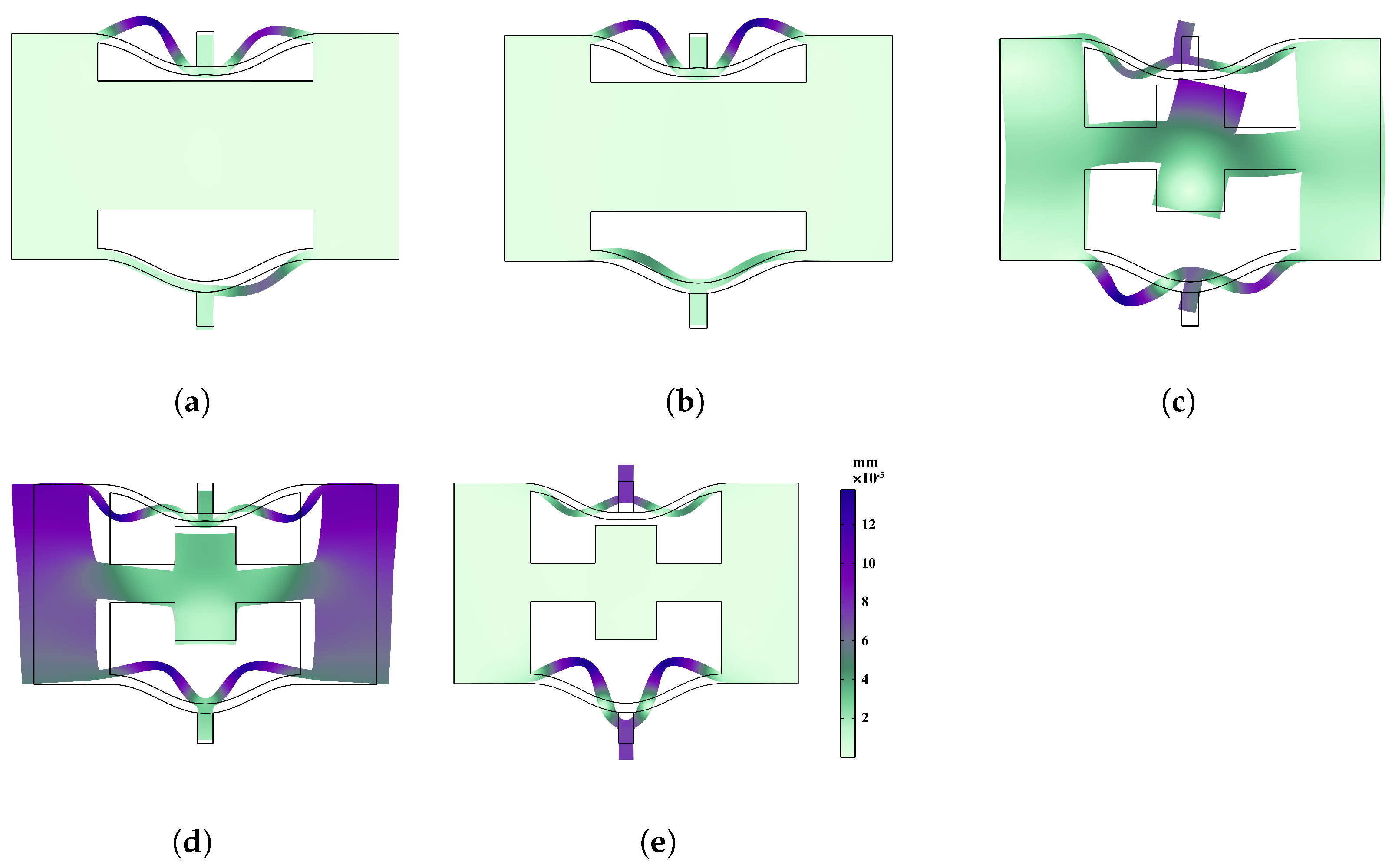
- Through the implementation of transmittance analysis and the presentation of dynamic response visualizations, the distinctions in vibration damping performance between the two structures are effectively elucidated. This serves to validate the precision of the bandgap mechanism delineated in the preceding section while substantiating that the local resonance of meta-NSLS is the primary factor in vibration suppression. These discoveries underscore the potency of meta-NSLS in delivering robust vibration suppression capabilities. Additionally, the variations in bandgap features among stable configurations ensure the adaptability of meta-NSLS to cater to precise engineering demands.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
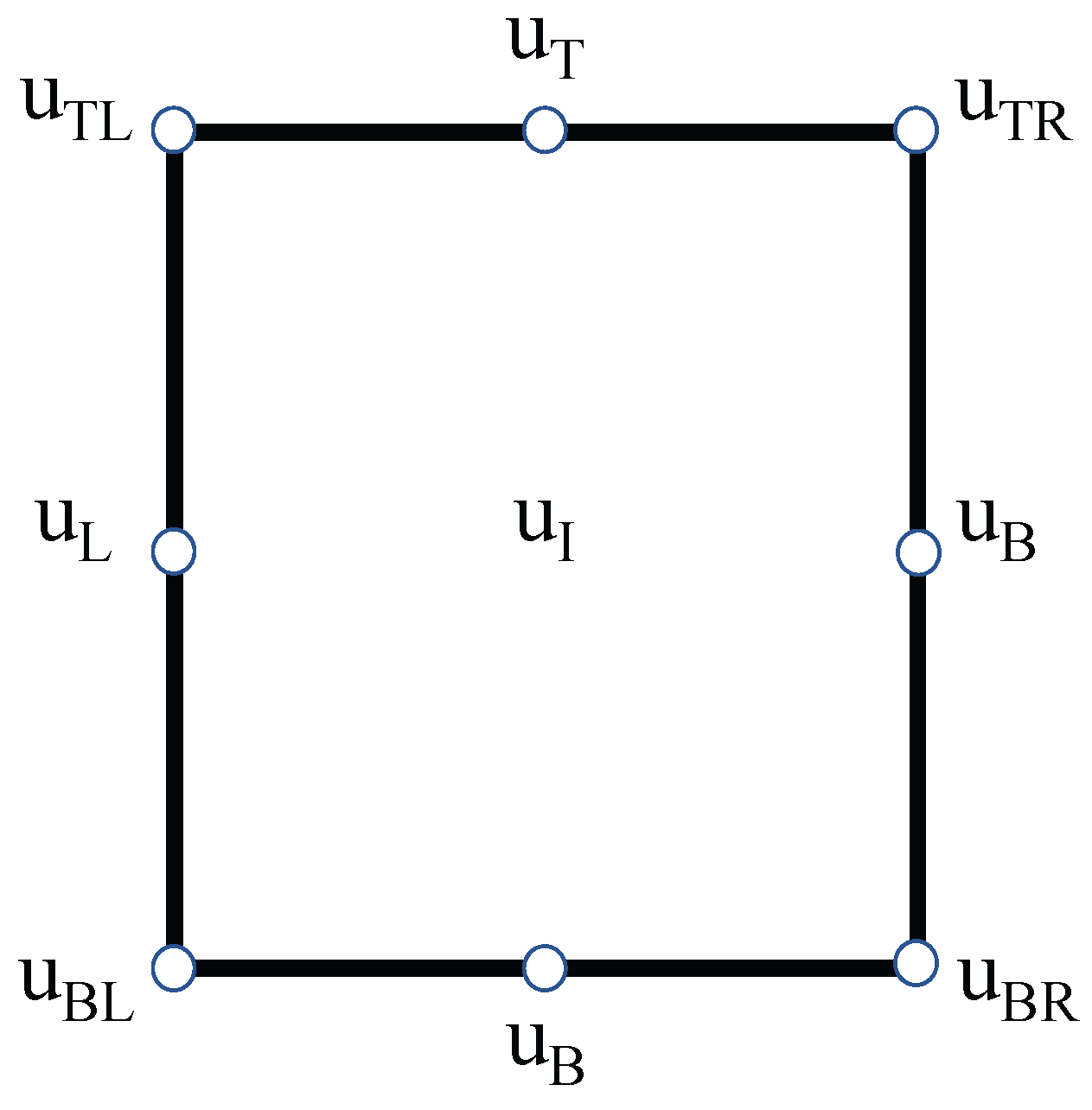
Appendix A. Dispersion Analysis
References
- Niknam, H.; Akbarzadeh, A. Graded lattice structures: Simultaneous enhancement in stiffness and energy absorption. Mater. Des. 2020, 196, 109129. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.; Liu, G.; Zong, H.; Zhang, C. Stiffness and energy absorption of additive manufactured hybrid lattice structures. Virtual Phys. Prototyp. 2021, 16, 428–443. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight Metamaterials for energy absorption. Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Gungor, O.U.; Yıldız, S.; Erem, E. Energy absorption behavior of stiffness optimized graded lattice structures fabricated by material extrusion. Meccanica 2021, 56, 2825–2841. [Google Scholar] [CrossRef]
- Köhnen, P.; Haase, C.; Bültmann, J.; Ziegler, S.; Schleifenbaum, J.H.; Bleck, W. Mechanical properties and deformation behavior of additively manufactured lattice structures of stainless steel. Mater. Des. 2018, 145, 205–217. [Google Scholar] [CrossRef]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D soft metamaterials with negative Poisson’s ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef]
- Duoss, E.B.; Weisgraber, T.H.; Hearon, K.; Zhu, C.; Small, W., IV; Metz, T.R.; Vericella, J.J.; Barth, H.D.; Kuntz, J.D.; Maxwell, R.S.; et al. Three-dimensional printing of elastomeric, cellular architectures with negative stiffness. Adv. Funct. Mater. 2014, 24, 4905–4913. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Caruana-Gauci, R.; Gatt, R. Negative linear compressibility of hexagonal honeycombs and related systems. Scr. Mater. 2011, 65, 565–568. [Google Scholar] [CrossRef]
- Wang, Q.; Jackson, J.A.; Ge, Q.; Hopkins, J.B.; Spadaccini, C.M.; Fang, N.X. Lightweight mechanical metamaterials with tunable negative thermal expansion. Phys. Rev. Lett. 2016, 117, 175901. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef]
- Sigalas, M.M. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Villeneuve, P.R.; Piche, M. Photonic band gaps in two-dimensional square and hexagonal lattices. Phys. Rev. B 1992, 46, 4969. [Google Scholar] [CrossRef]
- Qiu, M.; He, S. Large complete band gap in two-dimensional photonic crystals with elliptic air holes. Phys. Rev. B 1999, 60, 10610. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef]
- Wagner, M.R.; Graczykowski, B.; Reparaz, J.S.; El Sachat, A.; Sledzinska, M.; Alzina, F.; Sotomayor Torres, C.M. Two-dimensional phononic crystals: Disorder matters. Nano Lett. 2016, 16, 5661–5668. [Google Scholar] [CrossRef]
- Placidi, L.; El Sherbiny, M.G.; Baragatti, P. Experimental investigation for the existence of frequency band gap in a microstructure model. Math. Mech. Complex Syst. 2022, 9, 413–421. [Google Scholar] [CrossRef]
- Hosseinkhani, A.; Younesian, D.; Ranjbar, M.; Scarpa, F. Enhancement of the vibro-acoustic performance of anti-tetra-chiral auxetic sandwich panels using topologically optimized local resonators. Appl. Acoust. 2021, 177, 107930. [Google Scholar] [CrossRef]
- Arjunan, A.; Baroutaji, A.; Robinson, J. Advances in Acoustic Metamaterials; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Gasparetto, V.E.; ElSayed, M.S. Shape transformers for phononic band gaps tuning in two-dimensional Bloch-periodic lattice structures. Eur. J. Mech.-A/Solids 2021, 89, 104278. [Google Scholar] [CrossRef]
- Gao, N.; Huang, Y.L.; Bao, R.H.; Chen, W.Q. Robustly tuning bandgaps in two-dimensional soft phononic crystals with criss-crossed elliptical holes. Acta Mech. Solida Sin. 2018, 31, 573–588. [Google Scholar] [CrossRef]
- Pal, R.K.; Rimoli, J.; Ruzzene, M. Effect of large deformation pre-loads on the wave properties of hexagonal lattices. Smart Mater. Struct. 2016, 25, 054010. [Google Scholar] [CrossRef]
- Casadei, F.; Delpero, T.; Bergamini, A.; Ermanni, P.; Ruzzene, M. Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials. J. Appl. Phys. 2012, 112, 064902. [Google Scholar] [CrossRef]
- Schaeffer, M.; Ruzzene, M. Wave propagation in multistable magneto-elastic lattices. Int. J. Solids Struct. 2015, 56, 78–95. [Google Scholar] [CrossRef]
- Kashdan, L.; Seepersad, C.C.; Haberman, M.; Wilson, P.S. Design, fabrication, and evaluation of negative stiffness elements using SLS. Rapid Prototyp. J. 2012, 18, 194–200. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Hua, H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 2013, 332, 3359–3376. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Conner Seepersad, C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Huang, D.; Li, W.; Yang, G.; He, M.; Dang, H. Vibration analysis of a piecewise-smooth system with negative stiffness under delayed feedback control. Shock Vib. 2017, 2017, 3502475. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Xie, S.; Zhang, Y. Theoretical and experimental study of a vibration isolator using a negative stiffness magnetic spring. In Proceedings of the 24th International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
- Meaud, J.; Che, K. Tuning elastic wave propagation in multistable architected materials. Int. J. Solids Struct. 2017, 122, 69–80. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Antoniadis, I.; Ampatzidis, T. Enhanced acoustic insulation properties of composite metamaterials having embedded negative stiffness inclusions. Extrem. Mech. Lett. 2017, 12, 48–54. [Google Scholar] [CrossRef]
- Katz, S.; Givli, S. Solitary waves in a bistable lattice. Extrem. Mech. Lett. 2018, 22, 106–111. [Google Scholar] [CrossRef]
- Goldsberry, B.M.; Haberman, M.R. Negative stiffness honeycombs as tunable elastic metamaterials. J. Appl. Phys. 2018, 123, 091711. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef]
- Correa, D.M.; Klatt, T.; Cortes, S.; Haberman, M.; Kovar, D.; Seepersad, C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyp. J. 2015, 21, 193–200. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Akbarzadeh, A.; Pasini, D. Snapping mechanical metamaterials under tension. Adv. Mater. 2015, 27, 5931–5935. [Google Scholar] [CrossRef] [PubMed]
- Shan, S.; Kang, S.H.; Raney, J.R.; Wang, P.; Fang, L.; Candido, F.; Lewis, J.A.; Bertoldi, K. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 2015, 27, 4296–4301. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, D.; Mankame, N.D.; Zavattieri, P.D. Phase transforming cellular materials. Extrem. Mech. Lett. 2015, 4, 52–60. [Google Scholar] [CrossRef]
- Haghpanah, B.; Salari-Sharif, L.; Pourrajab, P.; Hopkins, J.; Valdevit, L. Multistable shape-reconfigurable architected materials. Adv. Mater. 2016, 28, 7915–7920. [Google Scholar] [CrossRef] [PubMed]
- Frenzel, T.; Findeisen, C.; Kadic, M.; Gumbsch, P.; Wegener, M. Tailored buckling microlattices as reusable light-weight shock absorbers. Adv. Mater. 2016, 28, 5865–5870. [Google Scholar] [CrossRef] [PubMed]
- Cortes, S.; Allison, J.; Morris, C.; Haberman, M.; Seepersad, C.; Kovar, D. Design, manufacture, and quasi-static testing of metallic negative stiffness structures within a polymer matrix. Exp. Mech. 2017, 57, 1183–1191. [Google Scholar] [CrossRef]
- Ha, C.S.; Lakes, R.S.; Plesha, M.E. Design, fabrication, and analysis of lattice exhibiting energy absorption via snap-through behavior. Mater. Des. 2018, 141, 426–437. [Google Scholar] [CrossRef]
- Debeau, D.A.; Seepersad, C.C.; Haberman, M.R. Impact behavior of negative stiffness honeycomb materials. J. Mater. Res. 2018, 33, 290–299. [Google Scholar] [CrossRef]
- Chen, T.; Mueller, J.; Shea, K. Integrated design and simulation of tunable, multi-state structures fabricated monolithically with multi-material 3D printing. Sci. Rep. 2017, 7, 45671. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zeng, H.; Peng, X.; Zhao, Z.; Liu, J. A stiffness adjustment mechanism based on negative work for high-efficient propulsion of robotic fish. J. Bionic Eng. 2018, 15, 270–282. [Google Scholar] [CrossRef]
- Ando, B.; Baglio, S.; L’Episcopo, G.; Trigona, C. Investigation on mechanically bistable MEMS devices for energy harvesting from vibrations. J. Microelectromechanical Syst. 2012, 21, 779–790. [Google Scholar] [CrossRef]
- Li, Y.; Baker, E.; Reissman, T.; Sun, C.; Liu, W.K. Design of mechanical metamaterials for simultaneous vibration isolation and energy harvesting. Appl. Phys. Lett. 2017, 111, 251903. [Google Scholar] [CrossRef]
- Brinkmeyer, A.; Santer, M.; Pirrera, A.; Weaver, P. Pseudo-bistable self-actuated domes for morphing applications. Int. J. Solids Struct. 2012, 49, 1077–1087. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extrem. Mech. Lett. 2016, 9, 291–296. [Google Scholar] [CrossRef]
- Hewage, T.A.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson’s Ratio Properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef]
- Reda, H.; Elnady, K.; Ganghoffer, J.; Lakiss, H. Wave propagation in pre-deformed periodic network materials based on large strains homogenization. Compos. Struct. 2018, 184, 860–871. [Google Scholar] [CrossRef]
- Reda, H.; El Nady, K.; Ganghoffer, J.F.; Lakiss, H. Nonlinear wave propagation analysis in hyperelastic 1D microstructured materials constructed by homogenization. Mech. Res. Commun. 2017, 84, 136–141. [Google Scholar] [CrossRef]
- ElNady, K.; Goda, I.; Ganghoffer, J.F. Computation of the effective nonlinear mechanical response of lattice materials considering geometrical nonlinearities. Comput. Mech. 2016, 58, 957–979. [Google Scholar] [CrossRef]
- Che, K.; Yuan, C.; Wu, J.; Jerry Qi, H.; Meaud, J. Three-dimensional-printed multistable mechanical metamaterials with a deterministic deformation sequence. J. Appl. Mech. 2017, 84, 011004. [Google Scholar] [CrossRef]
- Zhang, K.; Qi, L.; Zhao, P.; Zhao, C.; Deng, Z. Buckling induced negative stiffness mechanical metamaterial for bandgap tuning. Compos. Struct. 2023, 304, 116421. [Google Scholar] [CrossRef]
- Valencia, C.; Restrepo, D.; Mankame, N.D.; Zavattieri, P.D.; Gomez, J. Computational characterization of the wave propagation behavior of multi-stable periodic cellular materials. Extrem. Mech. Lett. 2019, 33, 100565. [Google Scholar] [CrossRef]
- Gan, J.; Li, F.; Li, K.; Li, E.; Li, B. Dynamic failure of 3D printed negative-stiffness meta-sandwich structures under repeated impact loadings. Compos. Sci. Technol. 2023, 234, 109928. [Google Scholar] [CrossRef]









| Parameters | NSLS | Meta-NSLS |
|---|---|---|
| L | 50 | 50 |
| 4 | 4 | |
| 20 | 20 | |
| 2 | 2 | |
| 2.5 | 2.5 | |
| H | 8 | 8 |
| 30 | 30 | |
| 9 | 9 | |
| 8 | 8 | |
| 10 |
| Mass Density (kg/m) | Young’s Modulus (MPa) | Poisson’s Ratio | |
|---|---|---|---|
| TPU | 1280 | 24.4 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, S. A Novel 3D-Printed Negative-Stiffness Lattice Structure with Internal Resonance Characteristics and Tunable Bandgap Properties. Materials 2023, 16, 7669. https://doi.org/10.3390/ma16247669
Liu J, Li S. A Novel 3D-Printed Negative-Stiffness Lattice Structure with Internal Resonance Characteristics and Tunable Bandgap Properties. Materials. 2023; 16(24):7669. https://doi.org/10.3390/ma16247669
Chicago/Turabian StyleLiu, Jiayang, and Shu Li. 2023. "A Novel 3D-Printed Negative-Stiffness Lattice Structure with Internal Resonance Characteristics and Tunable Bandgap Properties" Materials 16, no. 24: 7669. https://doi.org/10.3390/ma16247669
APA StyleLiu, J., & Li, S. (2023). A Novel 3D-Printed Negative-Stiffness Lattice Structure with Internal Resonance Characteristics and Tunable Bandgap Properties. Materials, 16(24), 7669. https://doi.org/10.3390/ma16247669






