Numerical Study on the Impact of Locked-In Stress on Rock Failure Processes and Energy Evolutions
Abstract
:1. Introduction
2. Stress Distribution of Rock Fracture
2.1. Rock Load Model without Locked-In Stress
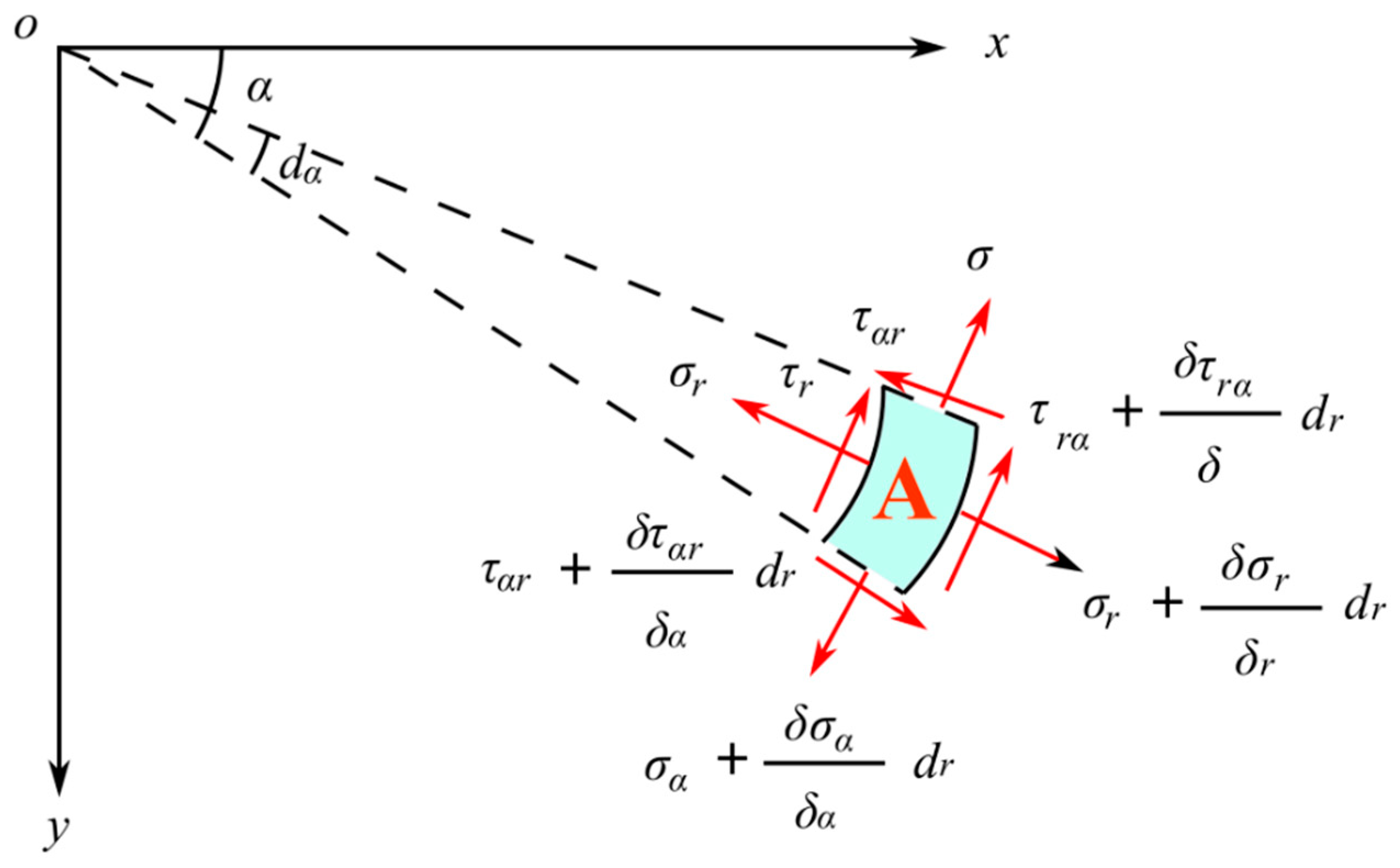
2.1.1. Mechanical Model
2.1.2. Analytical Solution of Stress Distribution without Locked-In Stress
2.2. Rock Load Model with Locked-In Stress
2.2.1. Mechanical Model
2.2.2. Analytical Solution of Stress Distribution with Locked-In Stress
3. The Impact of Stress Inclusions on Rock Deformation and Failure
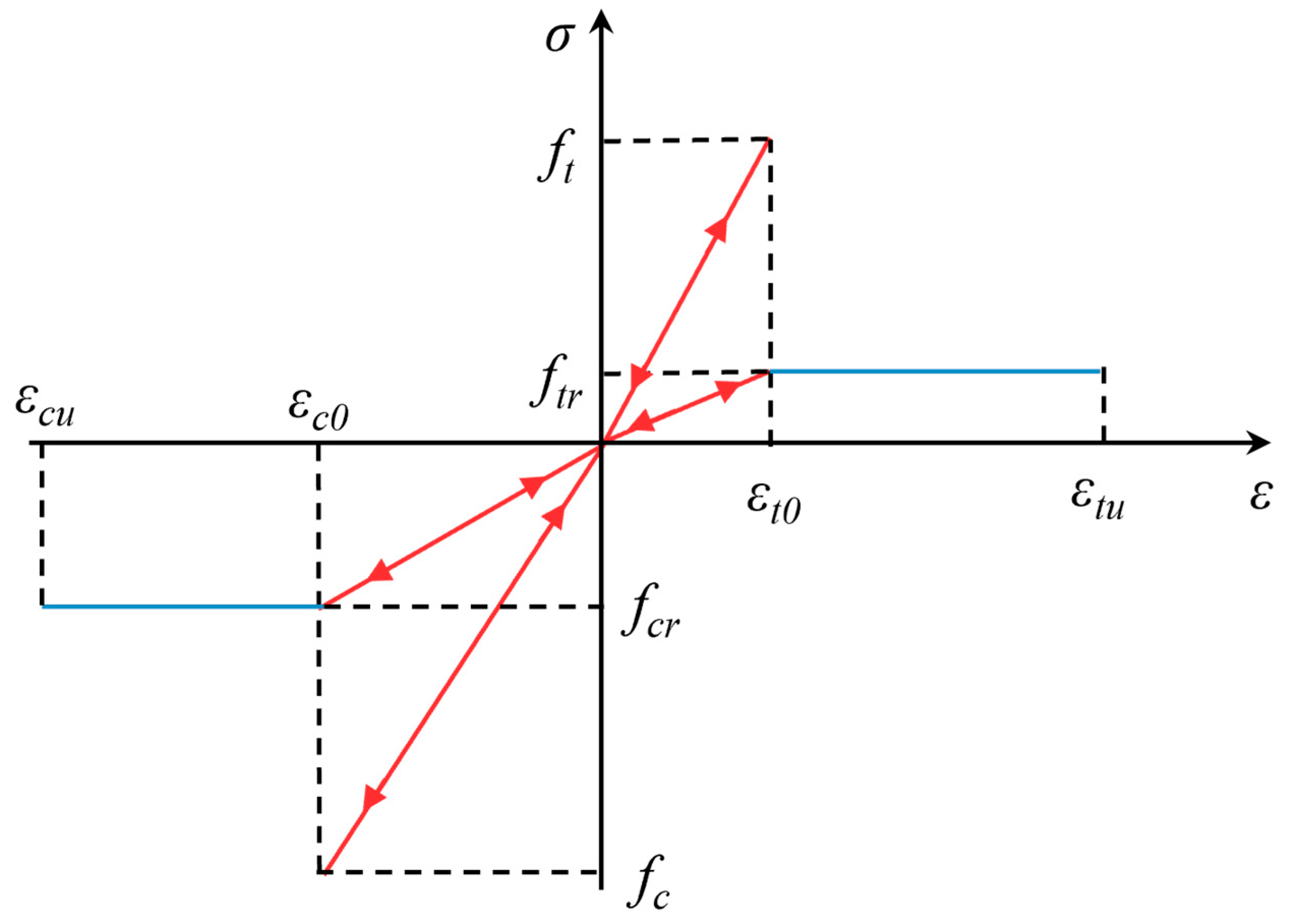
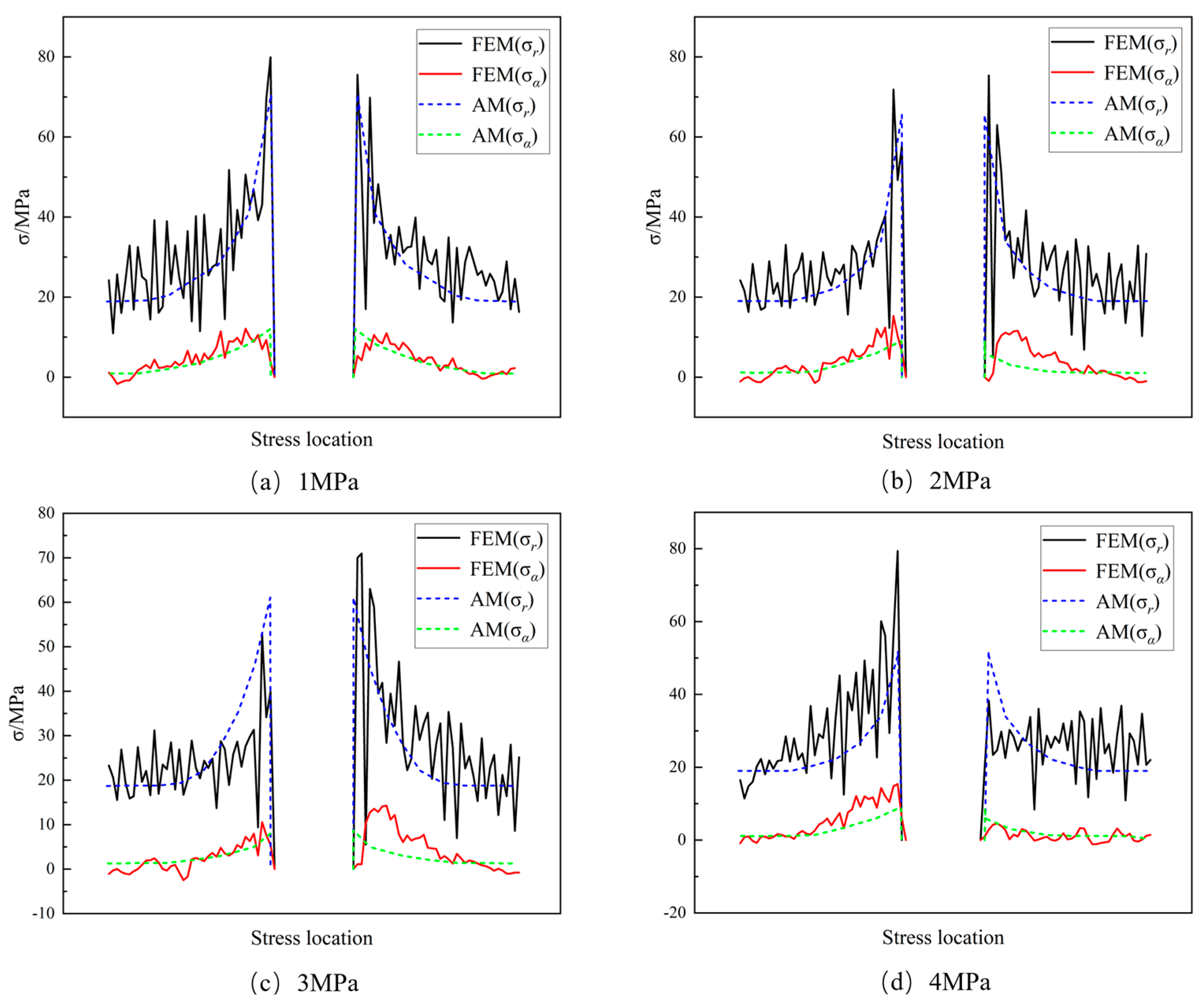
3.1. Analytical Method and Finite Element Method for Stress Inclusions Exist
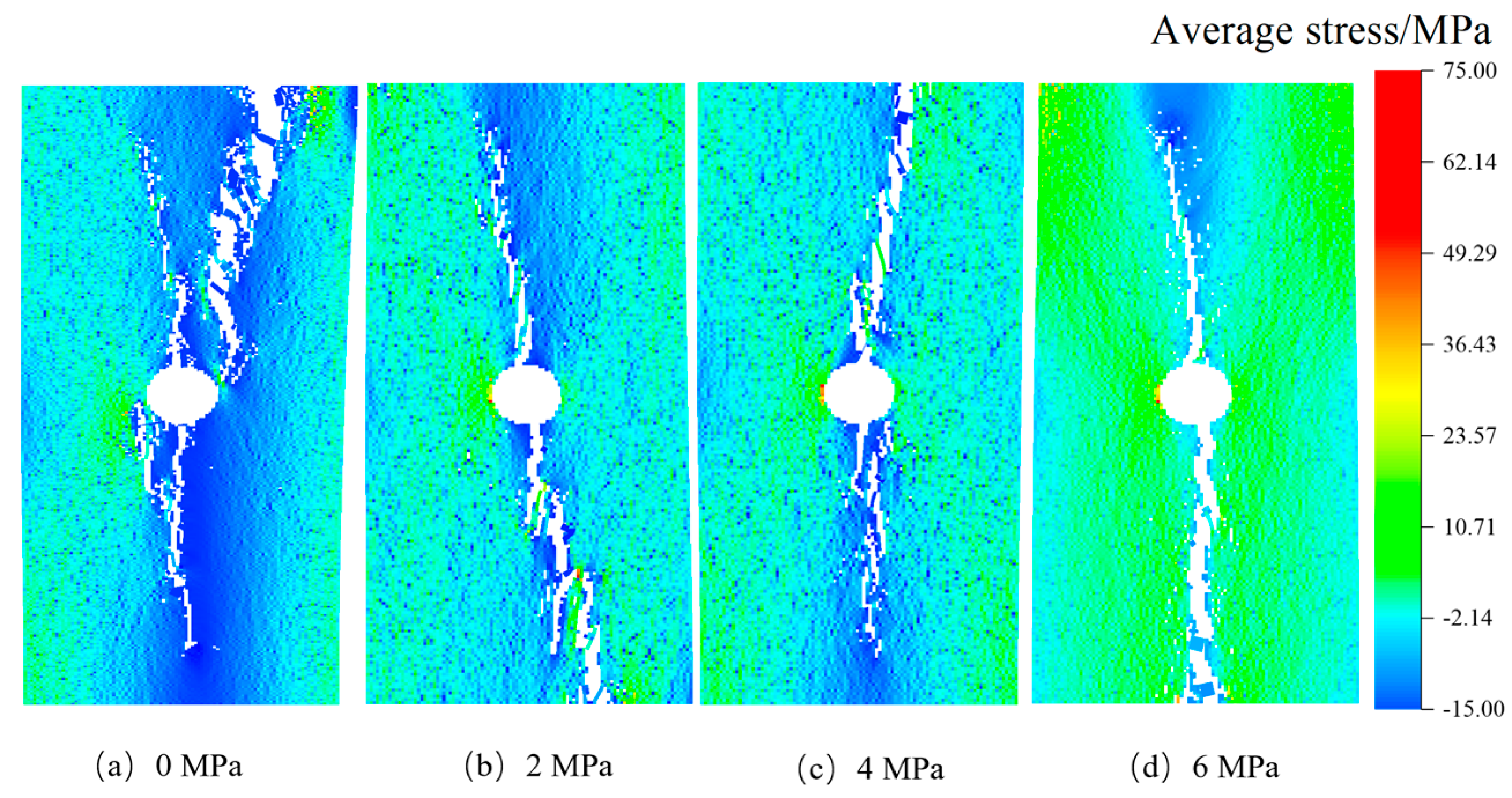
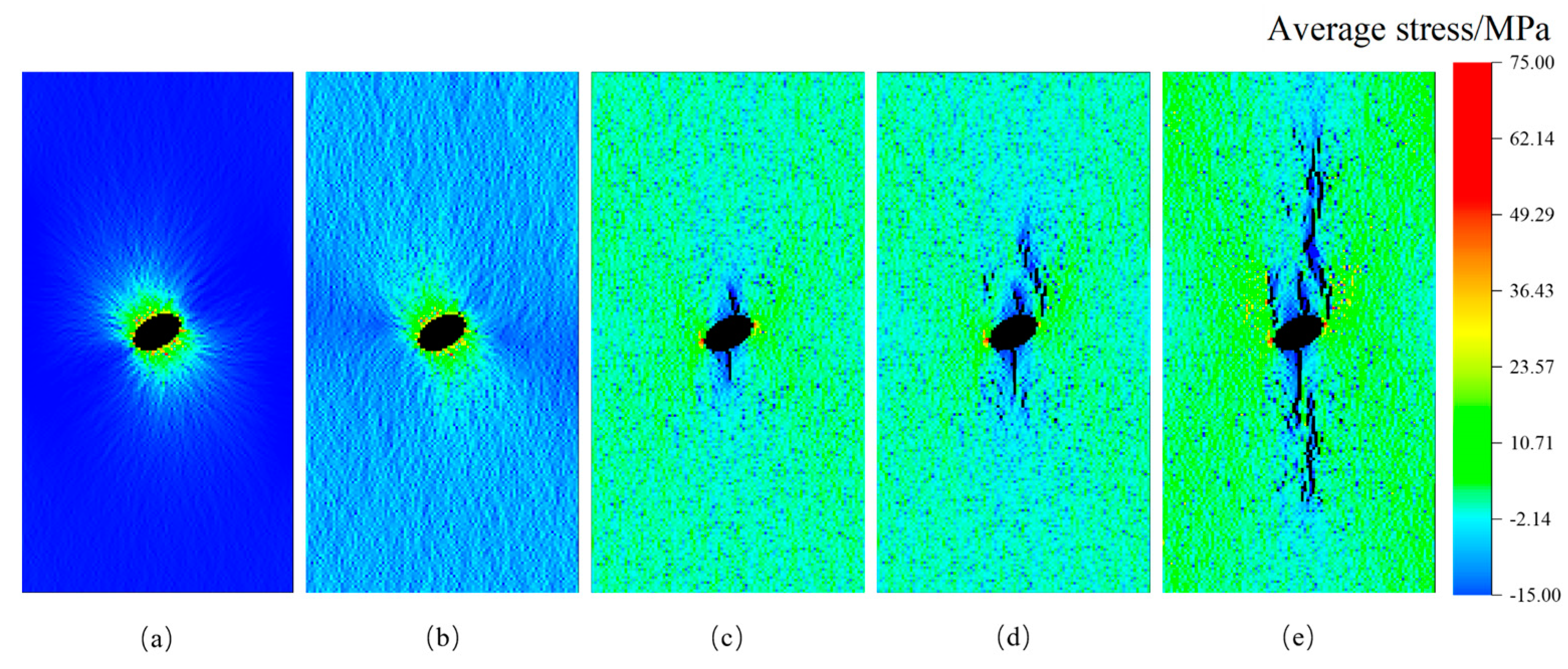
3.2. Rock Failure Processes According to Different Stress Inclusions Geometry
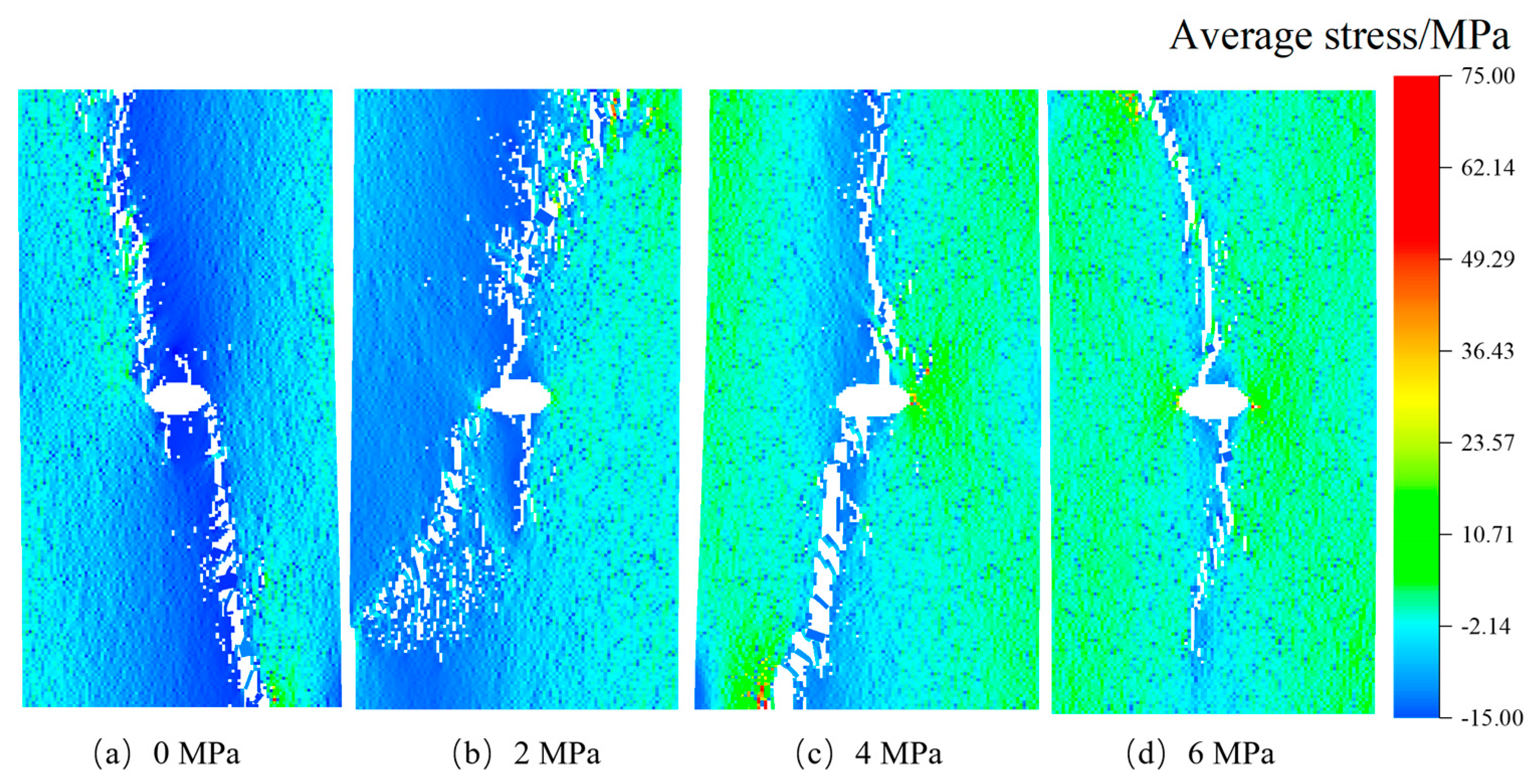
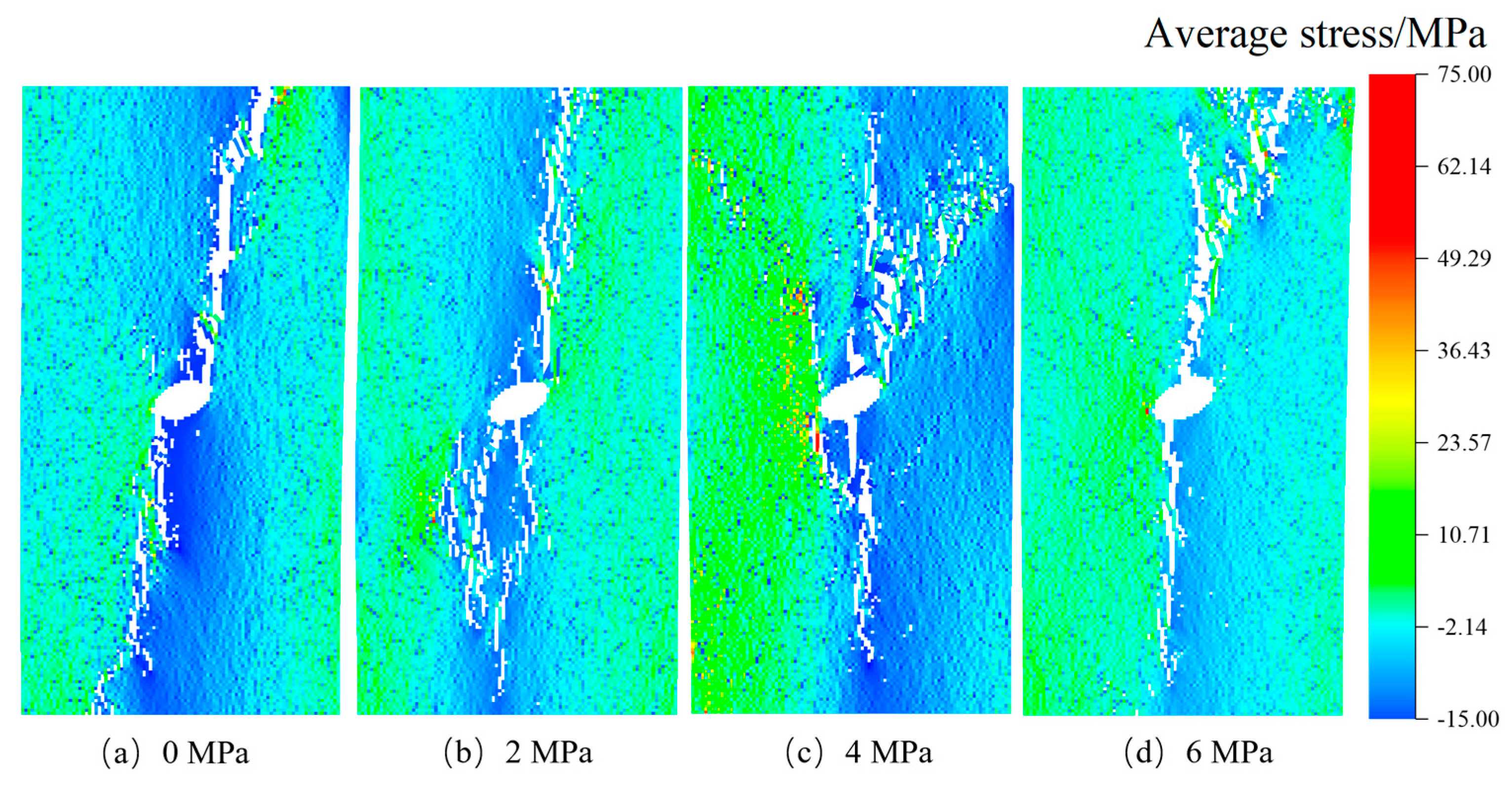
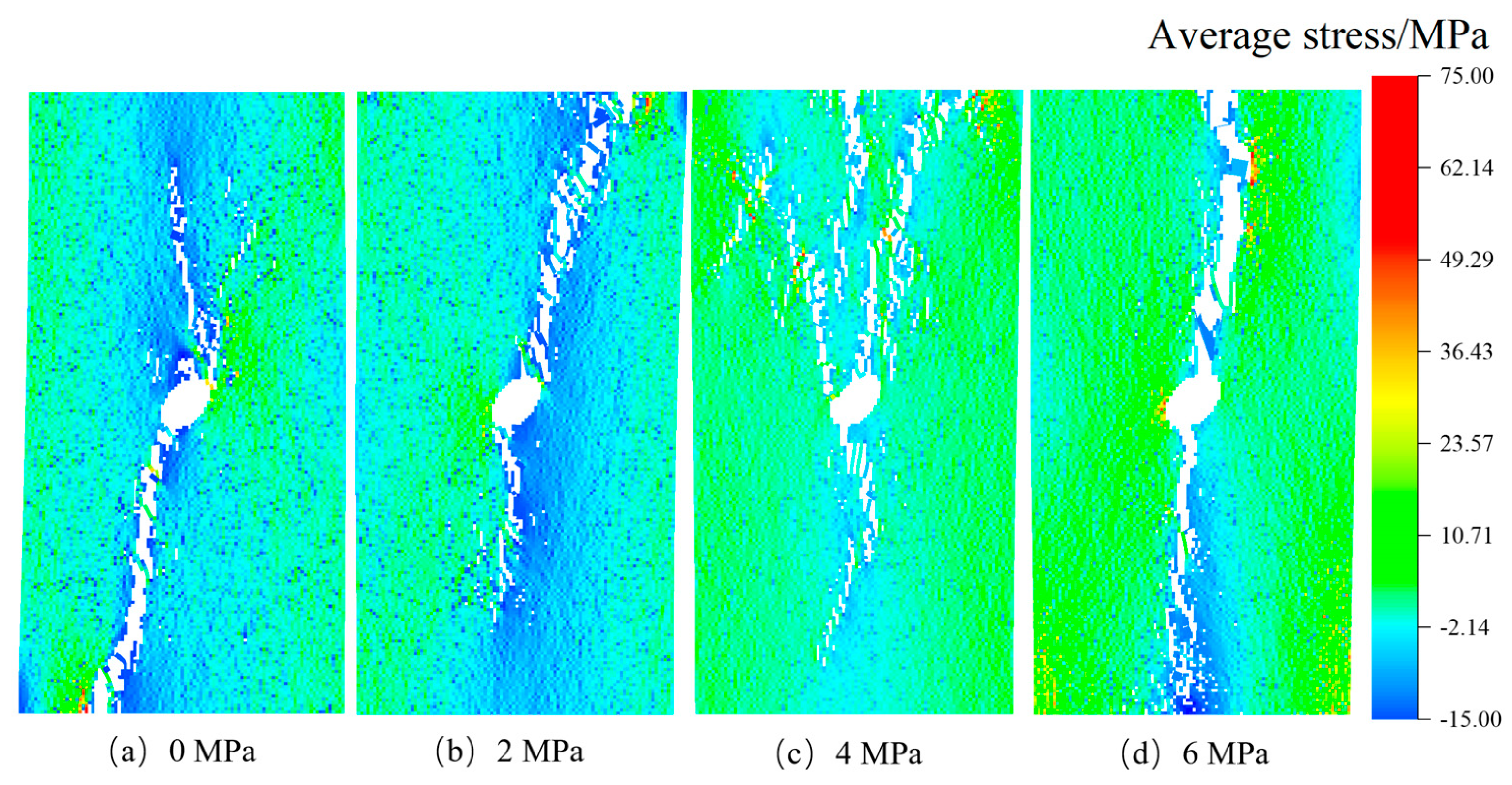
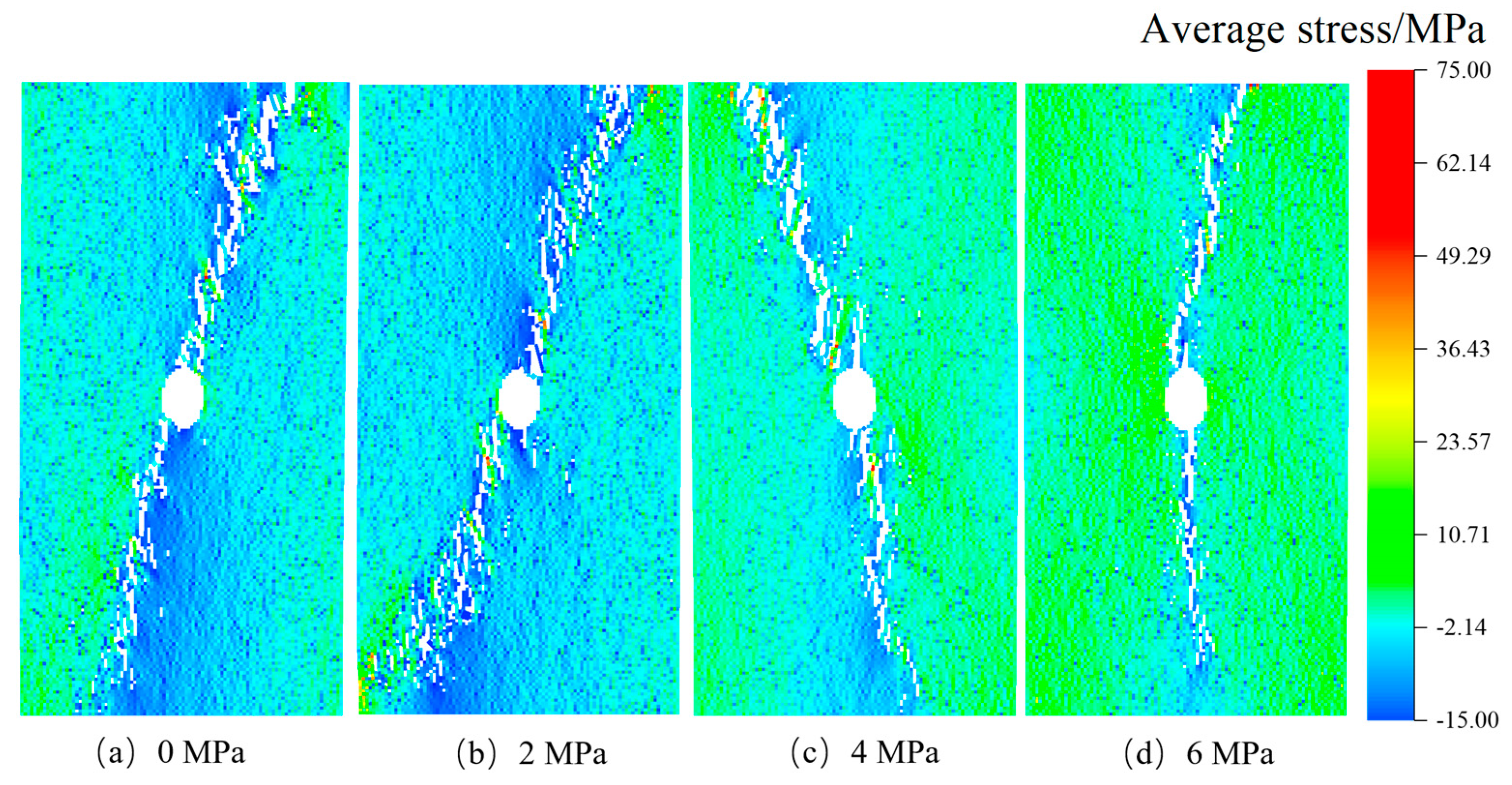
3.2.1. Influence of Geometric Shapes of Stress Inclusions
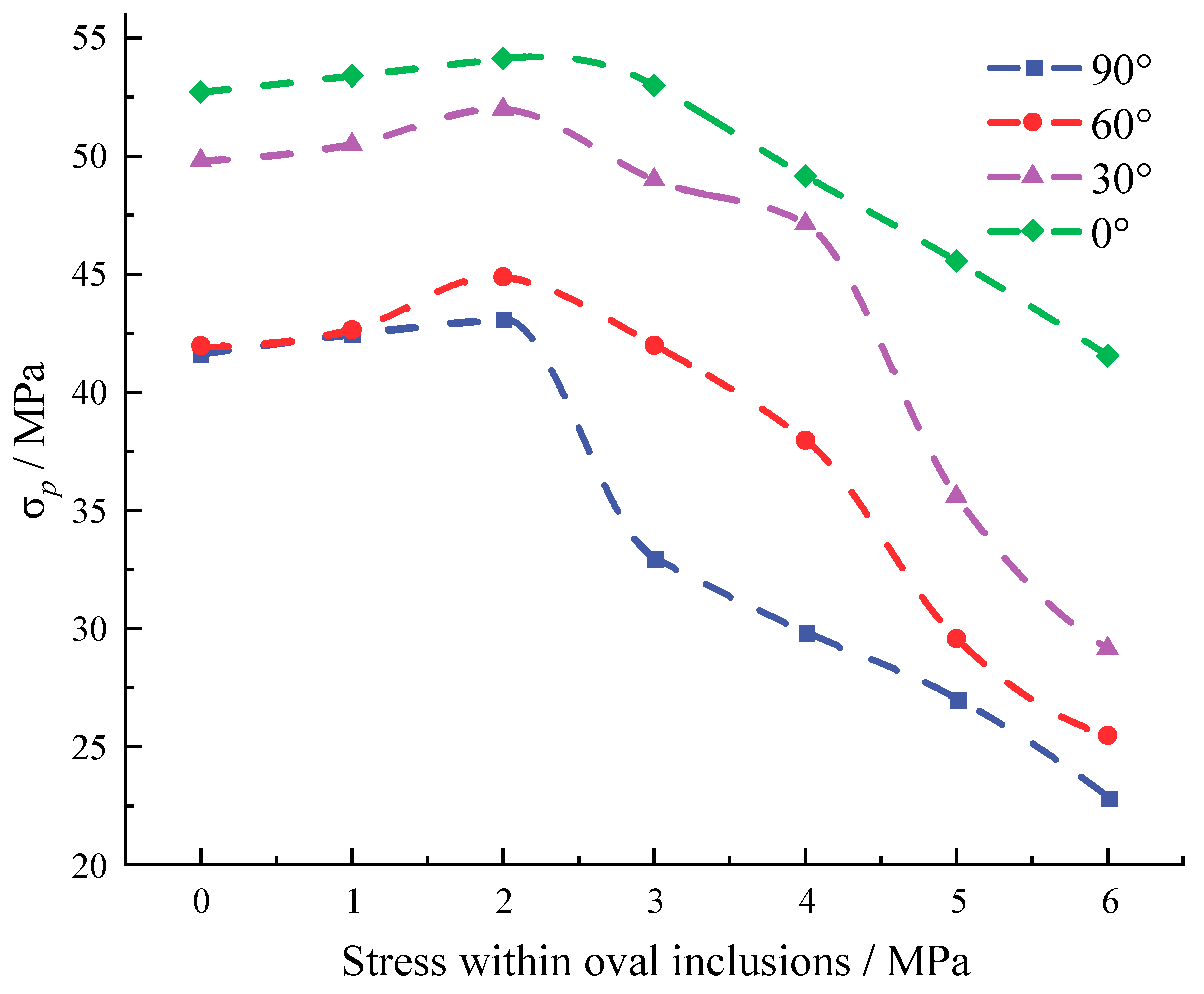
3.2.2. Influence of Stress Confinement Angle
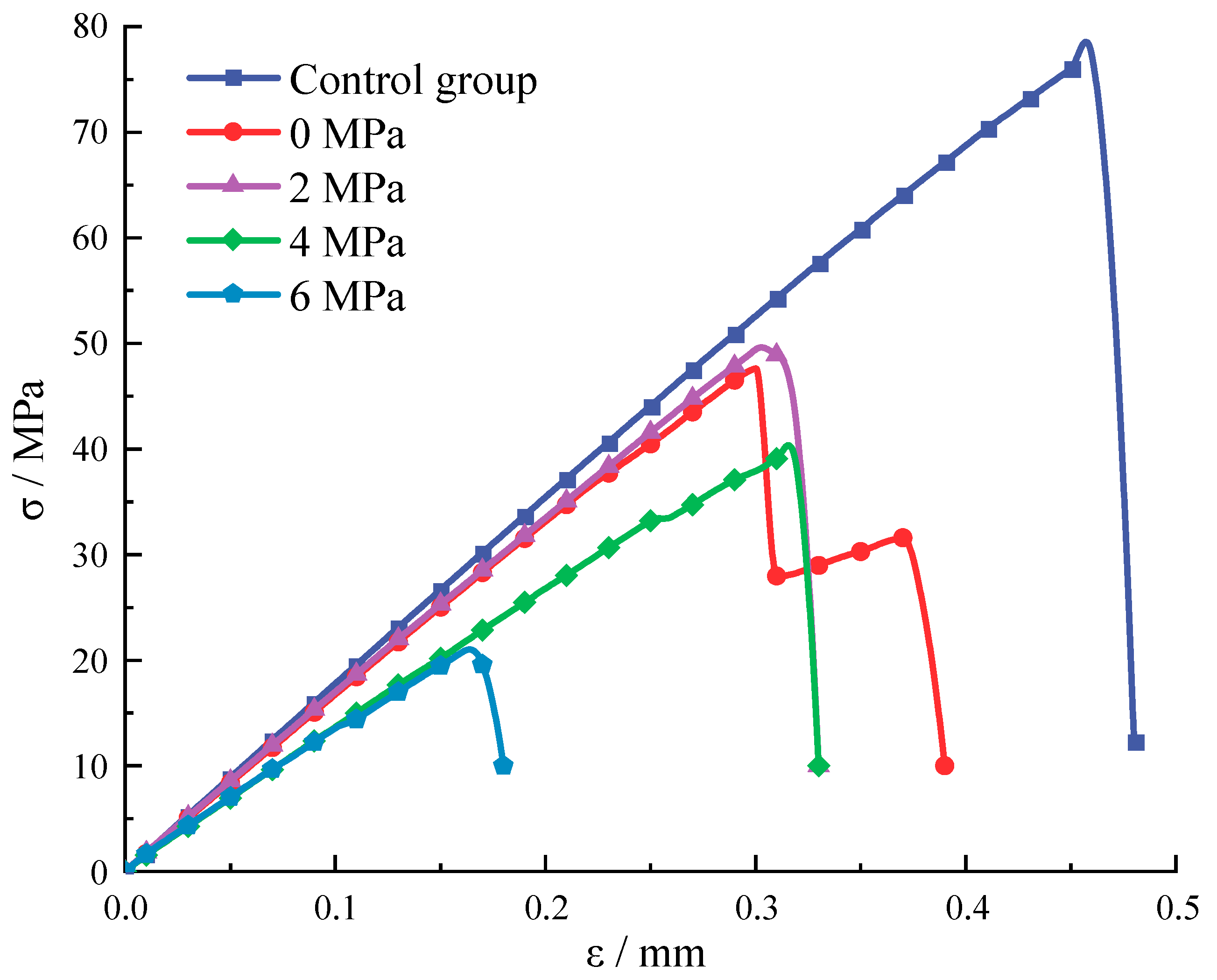
3.3. The Impact of Stress Inclusions on Rock Peak Stress and Peak Strain
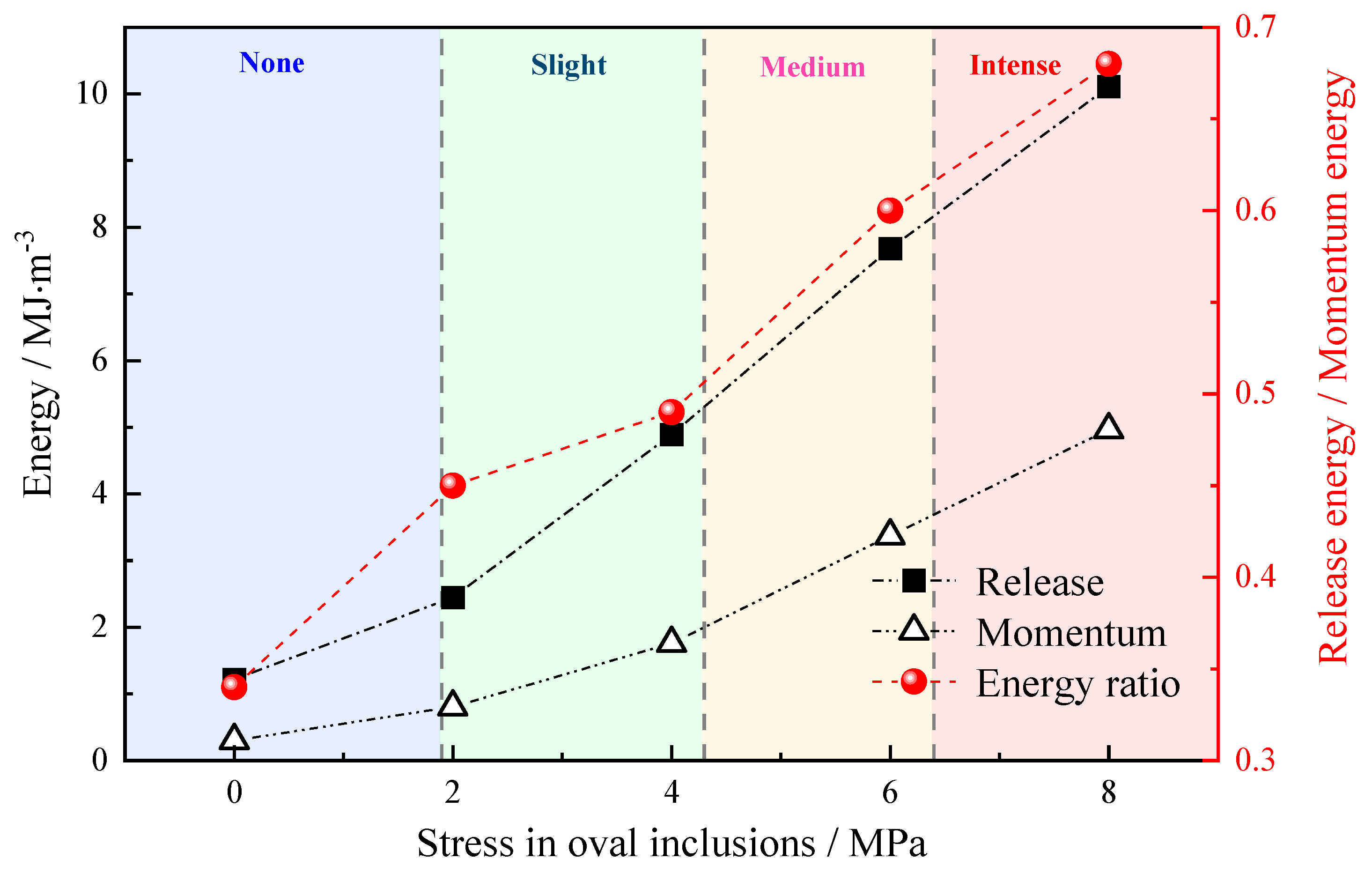
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, Y. Introduce a new classification of rocks. Geol. Rev. 1937, 3, 273–284. [Google Scholar]
- Müller, L. Rock Mechanics; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Voyiadjis, G.; Kiousis, P.; Hartley, C. Analysis of residual stresses in cylindrically anisotropic materials. Exp. Mech. 1985, 25, 145–147. [Google Scholar] [CrossRef]
- Voyiadjis, G.; Hartley, C. Residual-stress determination of concentric layers of cylindrically orthotropic materials. Exp. Mech. 1987, 27, 290–297. [Google Scholar] [CrossRef]
- Zhang, T. Comprehensive Treatment of Gas in High-Gas Comprehensive Mining Face. 1999. Available online: https://kns.cnki.net/kcms2/article/abstract?v=AnuRcxOpZiGfsafXMq6h1QLX1zYr109CKXUs1Lbb_ibic9UwellPPoT9dSBZ-67Xb9bhCdhz9vZfP7LKEV6HF5dPis9kmCNXrPPuns1Wsjw8Po82o53coVk-WRyLWLu1kCkDXMPP9eA=&uniplatform=NZKPT&language=CHS (accessed on 20 October 2023).
- Yang, B.; Sui, W.; Duan, L. Risk assessment of water inrush in an underground coal mine based on GIS and fuzzy set theory. Mine Water Environ. 2017, 36, 617–627. [Google Scholar] [CrossRef]
- Song, Z.; Yuan, C.; Du, Y.; Wang, Y. The Characteristics and Formation Mechanism of Rock-burst for a Long and Deep Tunnel of Chengdu-Lanzhou Railway. J. Railw. Eng. Soc. 2017, 34, 66–72. [Google Scholar]
- Zhao, T.-B.; Guo, W.-Y.; Tan, Y.-L.; Lu, C.-P.; Wang, C.-W. Case histories of rock bursts under complicated geological conditions. Bull. Eng. Geol. Environ. 2018, 77, 1529–1545. [Google Scholar] [CrossRef]
- Zhou, X.P.; Qian, Q.H.; Yang, H.Q. Rock burst of deep circular tunnels surrounded by weakened rock mass with cracks. Theor. Appl. Fract. Mech. 2011, 56, 79–88. [Google Scholar] [CrossRef]
- Chen, Z.; Kang, W.; Huang, J. On the locked instress, creep and dilatation of rocks, and the constitutive equations. Chin. J. Rock Mech. Eng. 1991, 10, 299–312. [Google Scholar]
- Kie, T.T. Vice-president address note. In Proceedings of the Congress on Rock Mechanics of International Society for Rock Mechanics, Montreux, Switzerland, 2–8 September 1979; pp. S253–S254. [Google Scholar]
- Tan, T.-K.; Kang, W.-F. Locked in stresses, creep and dilatancy of rocks, and constitutive equations. Rock Mech. 1980, 13, 5–22. [Google Scholar] [CrossRef]
- An, O.; Gao, G.; Li, Z. Measuremeat of paleotectonic residual stress field by X-ray diffractometry. North China Earthq. Sci. 1991, 3, 1–17. [Google Scholar]
- Sijing, H.; Zhongjian, H. Spatio-temporal variation of subsurface porosity and permeability and its influential factors. Acta Sedimentol. Sin. 2001, 19, 224–232. [Google Scholar]
- Wang, M.; Li, J.; Li, K. A nonlinear mechanical energy theory in deep rock mass engineering and its application. Chin. J. Rock Mech. Eng. 2015, 34, 659–667. [Google Scholar]
- Yue, Z. Gas inclusions and their expansion power as foundation ofrock “locked in” stress hypothesis. J. Eng. Geol. 2014, 22, 739–756. [Google Scholar]
- Yue, Z. Expansion power of compressed micro fluid inclusions as the cause of rockburst. Mech. Eng. 2015, 37, 287–294. [Google Scholar]
- He, J.; Dou, L.; Gong, S.; Li, J.; Ma, Z. Rock burst assessment and prediction by dynamic and static stress analysis based on micro-seismic monitoring. Int. J. Rock Mech. Min. Sci. 2017, 93, 46–53. [Google Scholar] [CrossRef]
- Geng, H.; Xu, H.; Chen, X.; Bai, Z. Research progress of locked-in stress in rocks. Mech. Eng. 2018, 40, 613–624. [Google Scholar]
- Xu, H.; Li, K.; Geng, H.; Chen, X. Similar simulation technique for the rock containing locked-in stress. In Proceedings of the Exchange Meeting on New Materials, New Technologies and Their Engineering Applications in Civil Engineering, Beijing, China, 28–31 October 2019; pp. 1174–1178. [Google Scholar] [CrossRef]
- Liu, X.; Geng, H.S.; Xu, H.F.; Yang, Y.H.; Ma, L.J.; Dong, L. Experimental study on the influence of locked-in stress on the uniaxial compressive strength and elastic modulus of rocks. Sci. Rep. 2020, 10, 1744. [Google Scholar] [CrossRef]
- Wang, T.; Ye, W.; Tong, Y.; Jiang, N.; Liu, L. Residual stress measurement and analysis of siliceous slate-containing quartz veins. Int. J. Miner. Metall. Mater. 2023; in press. [Google Scholar] [CrossRef]
- Zhou, X.; Qian, Q. Non-euclidean model of failure of deep rock masses under incompatible deformation. Chin. J. Rock Mech. Eng. 2013, 32, 767–774. [Google Scholar]
- Geng, H.; Xu, H.; Gao, L.; Chen, L.; Wang, B.; Zhao, X. Elastic modulus and strength of rock-like material with locked-in stress. Math. Probl. Eng. 2018, 2018, 5320906. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X.P. Numerical simulation of zonal disintegration of the surrounding rock masses around a deep circular tunnel under dynamic unloading. Int. J. Comput. Methods 2015, 12, 1550020. [Google Scholar] [CrossRef]
- Geng, H.; Xu, H.; Ma, L.; Yang, Y.; Dong, L.; Liu, X. Experimental study of similar simulation of locked-in stress in rock based on simplified mechanical model. Arab. J. Geosci. 2020, 13, 733. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Ji, H. Mechanism analysis of rock damage and failure based on relation between deep cavern axial variation and in situ stress filed. Chin. J. Eng. 2022, 44, 516–525. [Google Scholar]
- Qiu, L.; Zhu, Y.; Liu, Q.; Ming, G. Response law and indicator selection of seismic wave velocity for coal seam outburst risk. Adv. Geo-Energy Res. 2023, 9, 198–210. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, W.; Wei, C.; Elsworth, D.; Wang, J. Microcrack-based geomechanical modeling of rock-gas interaction during supercritical CO2 fracturing. J. Pet. Sci. Eng. 2018, 164, 91–102. [Google Scholar] [CrossRef]
- Hondros, G. The evaluation of Poisson’s ratio and the modulus of materials of a low tensile resistance by the Brazilian (indirect tensile) test with particular reference to concrete. Aust. J. Appl. Sci. 1959, 10, 243–264. [Google Scholar]
- Chen, Y.; Lin, H.; Xie, S.; Cao, R.; Sun, S.; Zha, W.; Wang, Y.; Zhao, Y.; Hu, H. Fracture Closure Empirical Model and Theoretical Failure Model of Rock under Compression. Materials 2023, 16, 589. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Y.; Mei, C. Numerical modeling of cracking behaviors for the rock-inclusion composite under dynamic tensile loading. Comput. Geotech. 2023, 157, 105325. [Google Scholar] [CrossRef]
- Zhu, W.; Tang, C. Micromechanical model for simulating the fracture process of rock. Rock Mech. Rock Eng. 2004, 37, 25–56. [Google Scholar] [CrossRef]
- Mishra, D.; Yoo, S.; Park, C.; Pak, Y. Elliptical inclusion problem in antiplane piezoelectricity: Stress concentrations and energy release rates. Int. J. Fract. 2013, 179, 213–220. [Google Scholar] [CrossRef]
- Amstutz, H.; Vormwald, M. Analysis of an elastic elliptical inclusion in an infinite elastic plate under uniform remote tension based on the solution of the corresponding cavity problem. J. Strain Anal. Eng. Des. 2017, 52, 515–527. [Google Scholar] [CrossRef]
- Liu, L.; Ji, H.; Elsworth, D.; Zhi, S.; Lv, X.; Wang, T. Dual-failure constitutive model to define thermal failure in rock. Int. J. Rock Mech. Min. Sci. 2020, 126, 104185. [Google Scholar] [CrossRef]
- Li, B.Q.; Casanova, M.; Einstein, H.H. Laboratory study of fracture initiation and propagation in Barre granite under fluid pressure at stress state close to failure. J. Rock Mech. Geotech. Eng. 2023, 15, 538–550. [Google Scholar] [CrossRef]
- Xie, H.; Kwasniewski, M. Fractals in Rock Mechanics; Geomechanics Research Series; Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Zheng, B.; Qi, S. A new index to describe joint roughness coefficient (JRC) under cyclic shear. Eng. Geol. 2016, 212, 72–85. [Google Scholar] [CrossRef]
- Qian, Q. Definition, mechanism, classification and quantitative forecast model for rockburst and pressure bump. Rock Soil Mech. 2014, 35, 1–6. [Google Scholar]
- Linkov, A.M. New Geomechanical Approaches to Develop Quantitative Seismicity, Rockbursts and Seismicity in Mines. 1997, pp. 151–166. Available online: http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=6251031 (accessed on 20 October 2023).
- Ji, P.Q.; Zhang, X.P.; Zhang, Q. A new method to model the non-linear crack closure behavior of rocks under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2018, 112, 171–183. [Google Scholar] [CrossRef]
- Liu, L.; Ji, H.; Wang, T.; Pei, F.; Quan, D. Mechanism of country rock damage and failure in deep shaft excavation under high pore pressure and asymmetric geostress. Chin. J. Eng. 2020, 42, 715–722. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Liu, Z.; Liu, L.; Feng, X. Numerical Study on the Impact of Locked-In Stress on Rock Failure Processes and Energy Evolutions. Materials 2023, 16, 7519. https://doi.org/10.3390/ma16247519
Wang T, Liu Z, Liu L, Feng X. Numerical Study on the Impact of Locked-In Stress on Rock Failure Processes and Energy Evolutions. Materials. 2023; 16(24):7519. https://doi.org/10.3390/ma16247519
Chicago/Turabian StyleWang, Tao, Zishuo Liu, Liyuan Liu, and Xianhui Feng. 2023. "Numerical Study on the Impact of Locked-In Stress on Rock Failure Processes and Energy Evolutions" Materials 16, no. 24: 7519. https://doi.org/10.3390/ma16247519
APA StyleWang, T., Liu, Z., Liu, L., & Feng, X. (2023). Numerical Study on the Impact of Locked-In Stress on Rock Failure Processes and Energy Evolutions. Materials, 16(24), 7519. https://doi.org/10.3390/ma16247519




