Predictive Modeling of Tensile Strength in Aluminum Alloys via Machine Learning
Abstract
:1. Introduction
2. Data Preparation and Analysis
2.1. Data Collection and Preprocessing
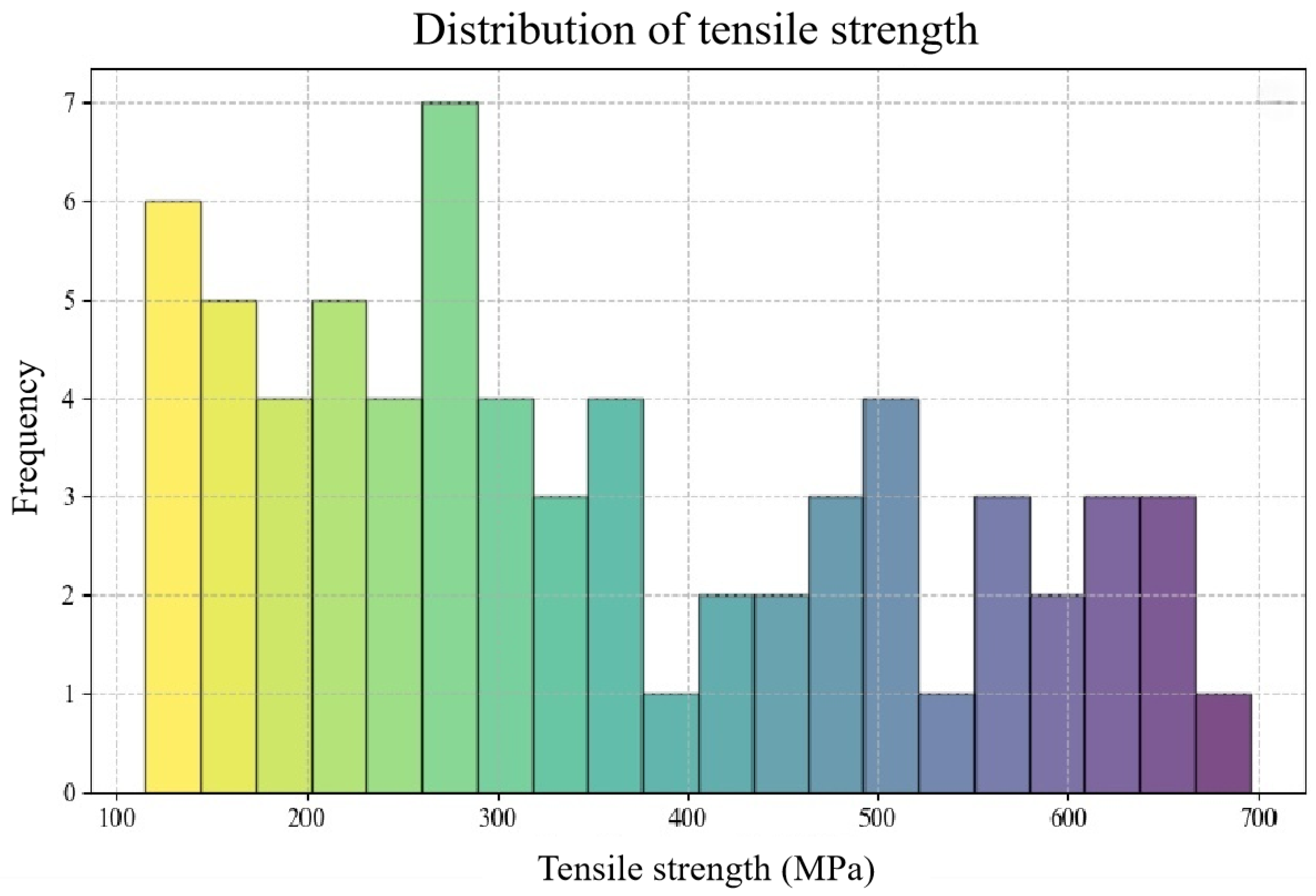
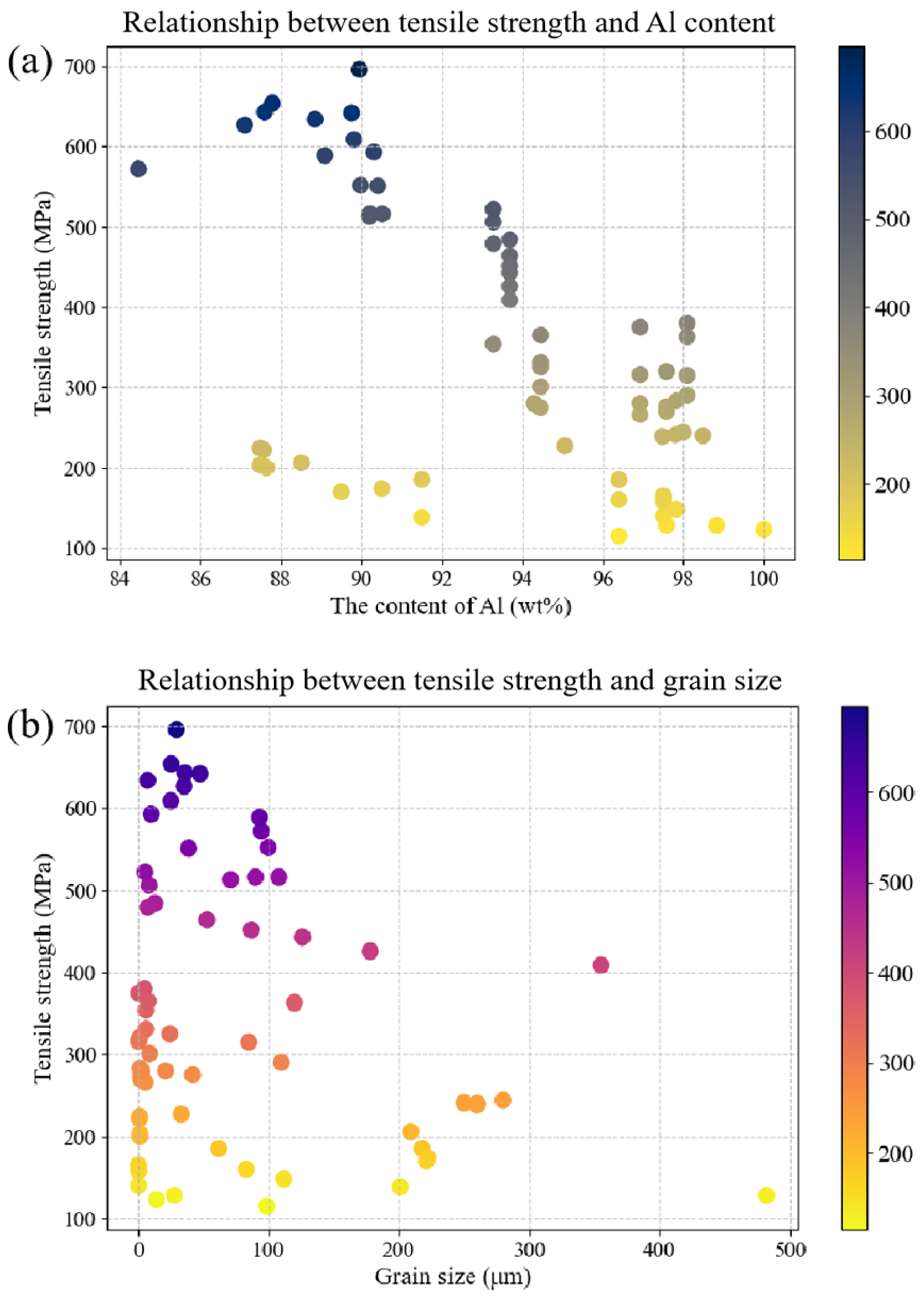
2.2. Data Analysis
3. Machine Learning Algorithms and Evaluation Methods
3.1. Machine Learning Algorithm and Parameter Settings
3.2. Model Evaluation Methods and Evaluation Indicators
4. Results and Discussion
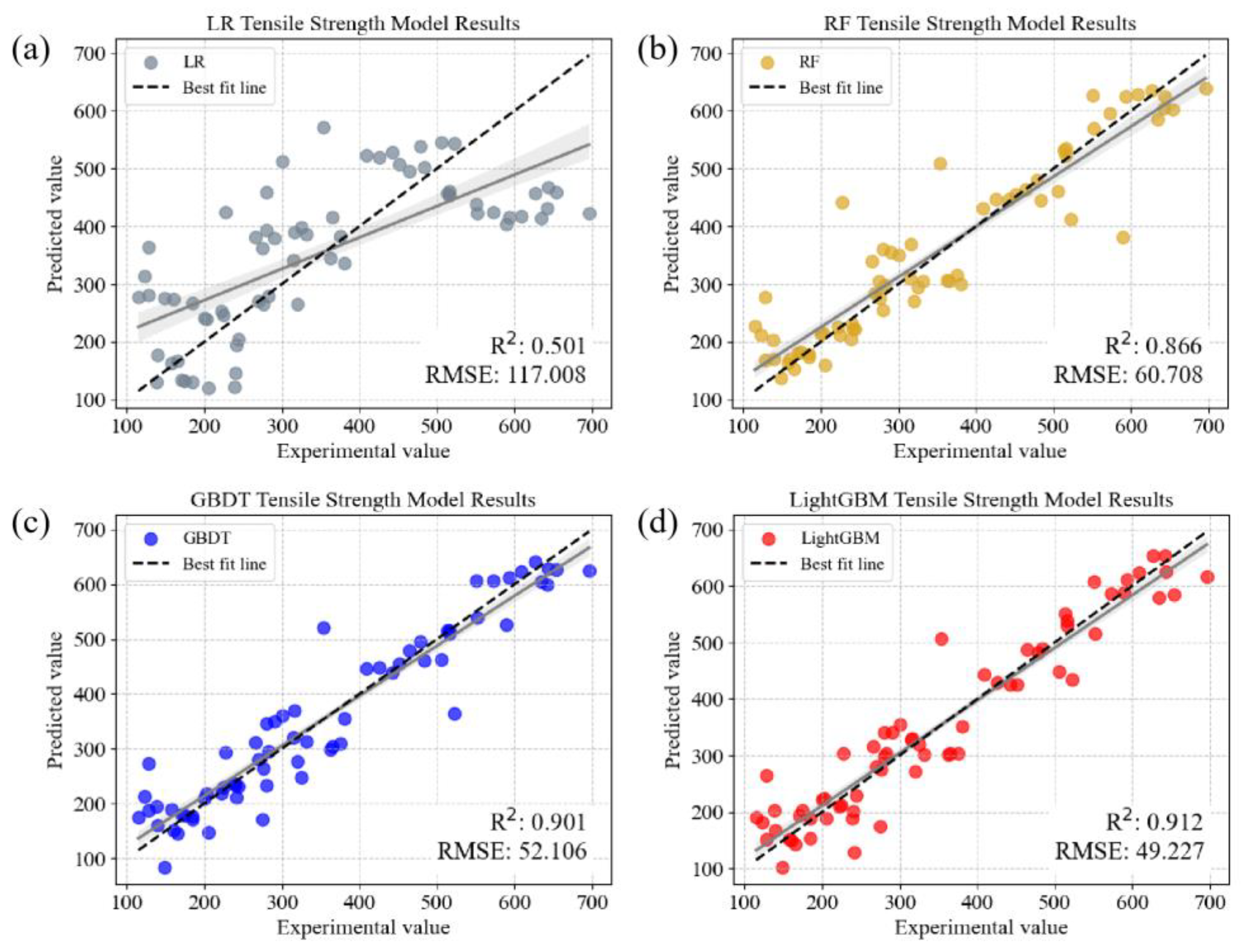
4.1. Modeling Based on Aluminum Alloy Composition and Grain Size
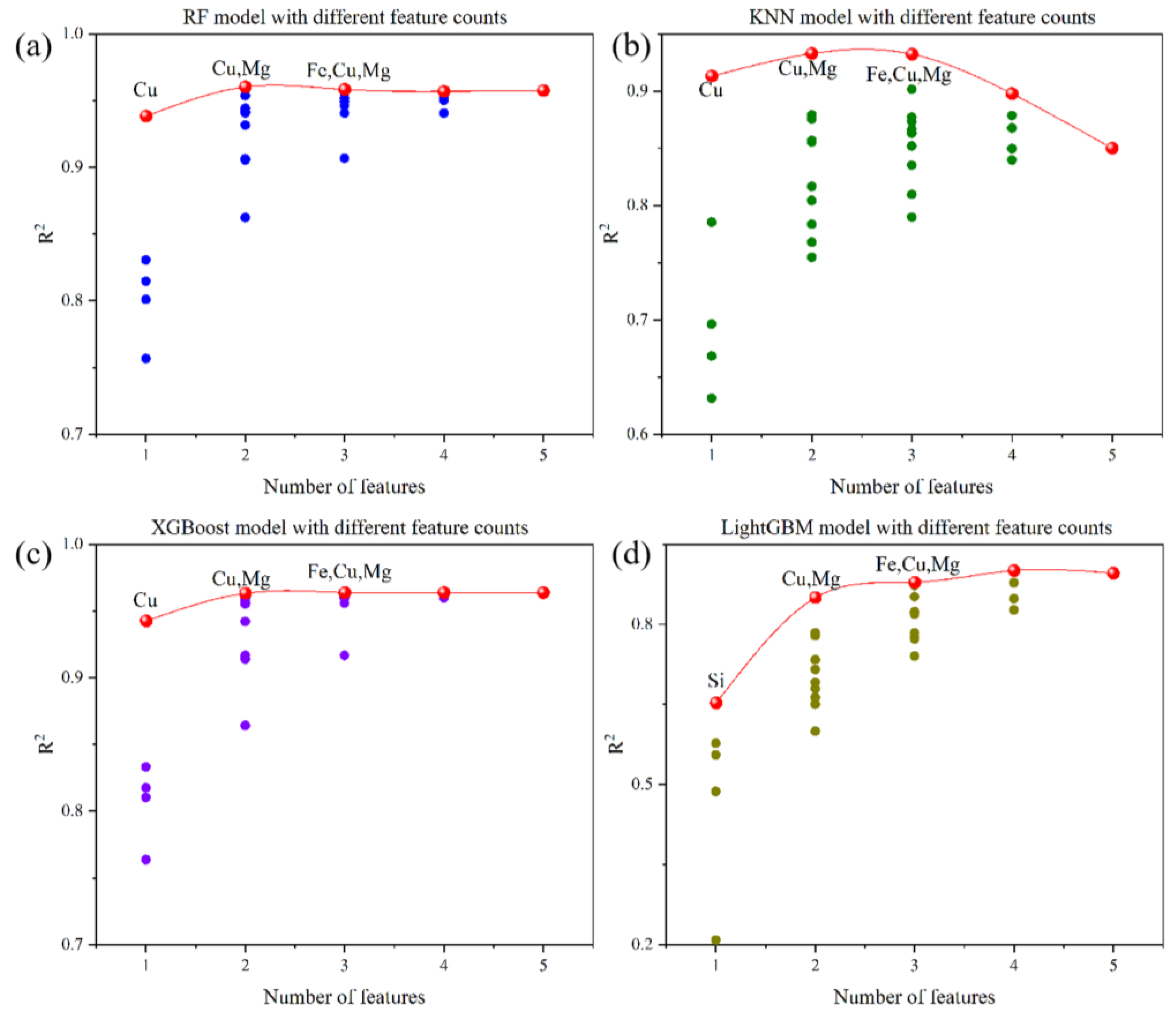
4.2. Feature Selection and Modeling
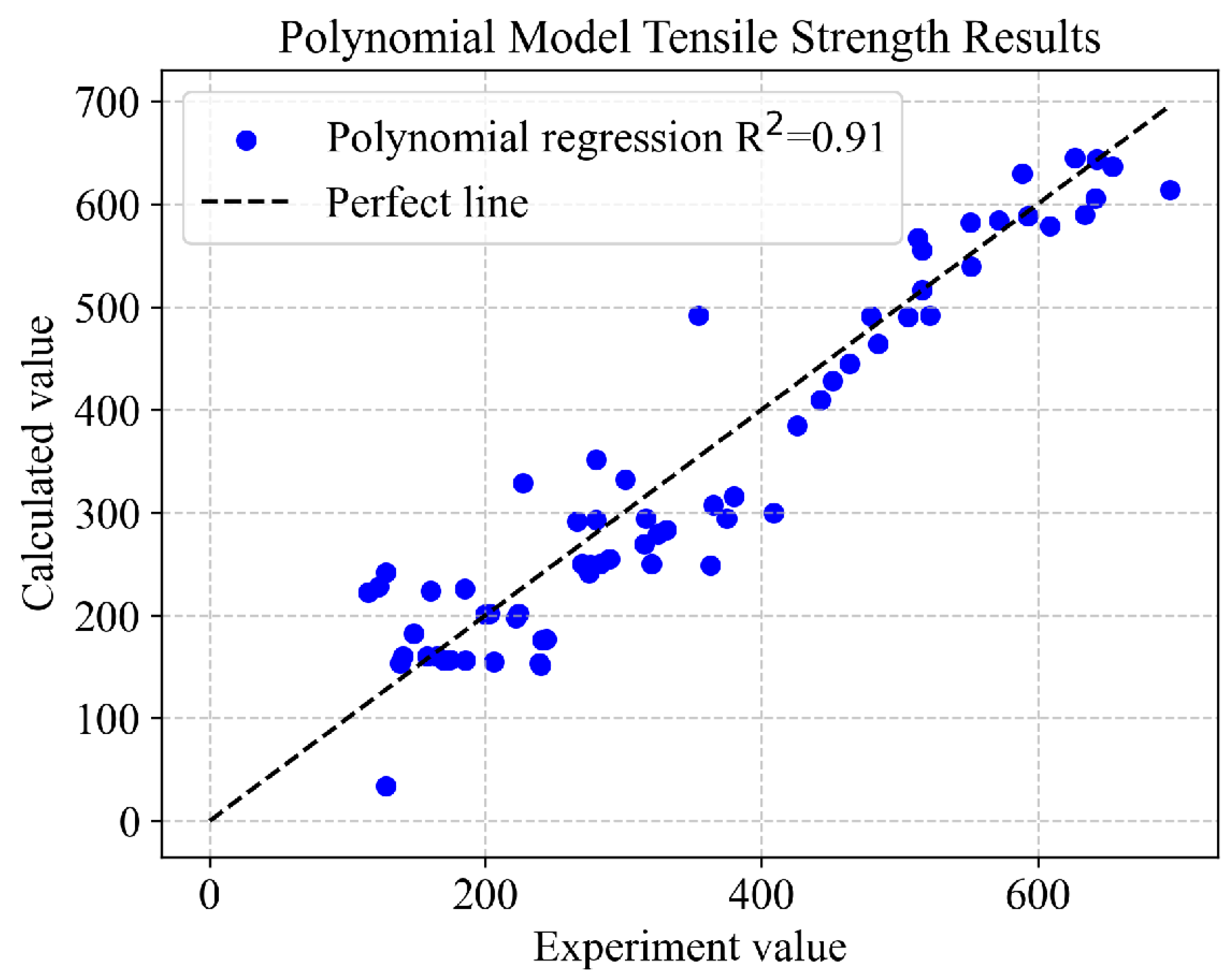
4.3. Polynomial Regression and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Li, M.; Han, Q.; Yun, X.; Zhou, K.; Gardner, L.; Mazzolani, F.M. Structural fire behaviour of aluminium alloy structures: Review and outlook. Eng. Struct. 2022, 268, 114746. [Google Scholar] [CrossRef]
- Bayoumy, D.; Kan, W.; Wu, X.; Zhu, Y.; Huang, A. The latest development of Sc-strengthened aluminum alloys by laser powder bed fusion. J. Mater. Sci. Technol. 2023, 149, 1–17. [Google Scholar] [CrossRef]
- Yun, X.; Wang, Z.; Gardner, L. Full-Range Stress–Strain Curves for Aluminum Alloys. J. Struct. Eng. 2021, 147, 04021060. [Google Scholar] [CrossRef]
- Xiong, Z.; Guo, X.; Luo, Y.; Zhu, S.; Liu, Y. Experimental and numerical studies on single-layer reticulated shells with aluminium alloy gusset joints. Thin-Walled Struct. 2017, 118, 124–136. [Google Scholar] [CrossRef]
- Yang, L.; Chen, C.; Yu, F.; Chen, C.; Liu, J.; Wang, Z.; Wang, X.; Cui, J. Coordinated deformation and high formability mechanisms of 7A36 aluminum alloy by Sc micro-alloying and low-frequency electromagnetic casting. J. Mater. Res. Technol. 2023, 24, 5186–5201. [Google Scholar] [CrossRef]
- Leng, J.F.; Ren, B.H.; Dong, Y.F.; Wu, H. Grain Refinement and Strengthening Mechanism Analysis of an Ultrahigh Strength Sc(Er)-Zr-7075 Aluminum Alloy. Phys. Met. Metallogr. 2021, 122, 1597–1604. [Google Scholar] [CrossRef]
- Guo, Y.; Wei, W.; Shi, W.; Zhang, B.; Zhou, X.; Wen, S.; Wu, X.; Gao, K.; Rong, L.; Huang, H.; et al. Effect of Er and Zr additions and aging treatment on grain refinement of aluminum alloy fabricated by laser powder bed fusion. J. Alloys Compd. 2022, 912, 165237. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, J.; Yang, S.; Song, B.; Zhang, L.; Lu, J.; Shi, Y. Breaking the strength-ductility trade-off in additively manufactured aluminum alloys through grain structure control by duplex nucleation. J. Mater. Sci. Technol. 2023, 152, 201–211. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Li, M.V.; Bu, H.; Zhu, Z.; Cai, C. Porosity suppressing and grain refining of narrow-gap rotating laser-MIG hybrid welding of 5A06 aluminum alloy. J. Manuf. Process. 2021, 68, 1100–1113. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Kawasaki, M.; Langdon, T.G. Seventy years of Hall-Petch, ninety years of superplasticity and a generalized approach to the effect of grain size on flow stress. Prog. Mater. Sci. 2023, 137, 101131. [Google Scholar] [CrossRef]
- Chen, G.Q.; Fu, G.S.; Wei, T.Y.; Cheng, C.Z.; Wang, H.S.; Song, L.L. Establishment of Prediction Model of Microstructure and Properties of 3003 Aluminum Alloy during Hot Deformation. Mater. Sci.-Medzg. 2019, 25, 369–375. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, Z.; Huang, Z.; Song, D.; Jia, Y.; Zhou, N.; Wang, K.; Zheng, K.; Du, H. Prediction of Grain Size in Cast Aluminum Alloys. Crystals 2022, 12, 474. [Google Scholar] [CrossRef]
- Easton, M.A.; StJohn, D.H. Improved prediction of the grain size of aluminum alloys that includes the effect of cooling rate. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2008, 486, 8–13. [Google Scholar] [CrossRef]
- Nadella, R.; Eskin, D.; Katgerman, L. Effect of Grain Refining on Defect Formation in DC Cast Al-Zn-Mg-Cu Alloy Billet. In Grandfield, Eskin. Essential Readings in Light Metals: Volume 3 Cast Shop for Aluminum Production; Springer International Publishing: Cham, Switzerland, 2016; pp. 842–847. [Google Scholar]
- Lu, Z.Y.; Huang, X.Q.; Huang, J.Z. Role of Grain Size and Shape in Superplasticity of Metals. Front. Mater. 2021, 8, 641928. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, L.; Zhao, G.; Yu, J.; Liu, F.; Sun, X.; Lv, Z.; Cao, S. Abnormal grain growth behavior and mechanism of 6005A aluminum alloy extrusion profile. J. Mater. Sci. Technol. 2023, 157, 42–59. [Google Scholar] [CrossRef]
- Liu, R.; Li, K.; Zhou, G.W.; Tang, W.Q.; Shen, Y.; Tang, D.; Li, D.Y. Simulation of strain induced abnormal grain growth in aluminum alloy by coupling crystal plasticity and phase field methods. Trans. Nonferrous Met. Soc. China 2022, 32, 3873–3886. [Google Scholar] [CrossRef]
- Kalinenko, A.; Mishin, V.; Shishov, I.; Malopheyev, S.; Zuiko, I.; Novikov, V.; Mironov, S.; Kaibyshev, R.; Semiatin, S.L. Mechanisms of abnormal grain growth in friction-stir-welded aluminum alloy 6061-T6. Mater. Charact. 2022, 194, 112473. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- Busby, J.T.; Hash, M.C.; Was, G.S. The relationship between hardness and yield stress in irradiated austenitic and ferritic steels. J. Nucl. Mater. 2005, 336, 267–278. [Google Scholar] [CrossRef]
- Chen, G.; Fu, G.; Lin, S.; Cheng, C.; Yan, W.; Chen, H. Simulation of flow of aluminum alloy 3003 under hot compressive deformation. Met. Sci. Heat Treat. 2013, 54, 623–627. [Google Scholar] [CrossRef]
- Chen, G.Q.; Clelland, J.; Slemrod, M.; Wang, D.H.; Yang, D. Isometric embedding via strongly symmetric positive systems. Asian J. Math. 2018, 22, 1–40. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.Y.; Wu, H.H.; Dong, L.S.; Pan, G.F.; Zhou, X.Y.; Wang, S.Z.; Guo, R.Q.; Wu, G.L.; Gao, J.H.; Dai, F.Z. Atomic-scale simulations in multi-component alloys and compounds: A review on advances in interatomic potential. J. Mater. Sci. Technol. 2023, 165, 49–65. [Google Scholar] [CrossRef]
- Pan, G.; Wang, F.; Shang, C.; Wu, H.; Wu, G.; Gao, J.; Mao, X. Advances in machine learning-and artificial intelligence-assisted material design of steels. Int. J. Miner. Metall. Mater. 2023, 30, 1003–1024. [Google Scholar] [CrossRef]
- Zhu, D.; Pan, K.; Wu, H.H.; Wu, Y.; Xiong, J.; Yang, X.S.; Lookman, T. Identifying intrinsic factors for ductile-to-brittle transition temperatures in Fe-Al intermetallics via machine learning. J. Mater. Res. Technol. 2023, 26, 8836–8845. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Xiong, J.; Wu, G.; Gao, J.; Wu, Y.; Mao, X. Identifying facile material descriptors for Charpy impact toughness in low-alloy steel via machine learning. J. Mater. Sci. Technol. 2023, 132, 213–222. [Google Scholar] [CrossRef]
- Lookman, T.; Balachandran, P.V.; Xue, D.; Yuan, R. Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design. NPJ Comput. Mater. 2019, 5, 21. [Google Scholar] [CrossRef]
- Wei, Q.; Xiong, J.; Sun, S.; Zhang, T.Y. Multi-objective machine learning of four mechanical properties of steels. Sci. China Technol. Sci. 2021, 51. [Google Scholar] [CrossRef]
- Zhu, D.X.; Pan, K.M.; Wu, Y.; Zhou, X.Y.; Li, X.Y.; Ren, Y.P.; Yang, X.S. Improved material descriptors for bulk modulus in intermetallic compounds via machine learning. Rare Met. 2023, 42, 2396–2405. [Google Scholar] [CrossRef]
- Sui, X.; Zhang, X.; Wei, J. Effects of cold rolling deformation rate and annealing temperature on microstructure and properties of automobile 5182 Aluminum alloy. Nonferrous Met. Process. 2023, 52, 40–43. [Google Scholar]
- Huang, K.; Guo, L.; Yang, F.; Ma, K.; Liu, P.; Liu, G. Effects of extrusion ratio on microstructure and tensile properties of an extruded Al-Fe-Cu alloy. Mater. Mech. Eng. 2015, 39, 6. [Google Scholar]
- Qin, J.; Zhi, L.; Yi, D.; Bin, W. Diversity of intergranular corrosion and stress corrosion cracking for 5083 Al alloy with different grain sizes. Trans. Nonferrous Met. Soc. China 2022, 32, 765–777. [Google Scholar] [CrossRef]
- Tsai, T.C.; Chuang, T.H. Role of grain size on the stress corrosion cracking of 7475 aluminum alloys. Mater. Sci. Eng. A 1997, 225, 135–144. [Google Scholar] [CrossRef]
- Ludtka, G.M.; Laughlin, D.E. The influence of microstructure and strength on the fracture mode and toughness of 7XXX series aluminum alloys. Metall. Trans. A 1982, 13, 411–425. [Google Scholar] [CrossRef]
- Ma, K.; Wen, H.; Hu, T.; Topping, T.D.; Isheim, D.; Seidman, D.N.; Schoenung, J.M. Mechanical behavior and strengthening mechanisms in ultrafine grain precipitation-strengthened aluminum alloy. Acta Mater. 2014, 62, 141–155. [Google Scholar] [CrossRef]
- Suresh, S.; Vasudévan, A.K.; Bretz, P.E. Mechanisms of Slow Fatigue Crack Growth in High Strength Aluminum Alloys: Role of Microstructure and Environment. Metall. Trans. A 1984, 15, 369–379. [Google Scholar] [CrossRef]
- Curle, U.A.; Govender, G. Semi-solid rheocasting of grain refined aluminum alloy 7075. Trans. Nonferrous Met. Soc. China 2010, 20, s832–s836. [Google Scholar] [CrossRef]
- Shou, W.B.; Yi, D.Q.; Liu, H.Q.; Tang, C.; Shen, F.H.; Wang, B. Effect of grain size on the fatigue crack growth behavior of 2524-T3 aluminum alloy. Arch. Civ. Mech. Eng. 2016, 16, 304–312. [Google Scholar] [CrossRef]
- Mobasherpour, I.; Tofigh, A.A.; Ebrahimi, M. Effect of nano-size Al2O3 reinforcement on the mechanical behavior of synthesis 7075 aluminum alloy composites by mechanical alloying. Mater. Chem. Phys. 2013, 138, 535–541. [Google Scholar] [CrossRef]
- Woo, W.; Balogh, L.; Ungar, T.; Choo, H.; Feng, Z. Grain structure and dislocation density measurements in a friction-stir welded aluminum alloy using X-ray peak profile analysis. Mater. Sci. Eng. A 2008, 498, 308–313. [Google Scholar] [CrossRef]
- Ram, G.D.J.; Murugesan, R.; Sundaresan, S. Fusion zone grain refinement in aluminum alloy welds through magnetic arc oscillation and its effect on tensile behavior. J. Mater. Eng. Perform. 1999, 8, 513–520. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, M.; Zhang, X.; Yang, G. Microstructural characteristics and mechanical properties of bobbin tool friction stir welded 2A14-T6 aluminum alloy. Mater. Des. 2015, 65, 559–566. [Google Scholar] [CrossRef]
- Li, Z.; Yi, D.; Tan, C.; Wang, B. Investigation of the stress corrosion cracking behavior in annealed 5083 aluminum alloy sheets with different texture types. J. Alloys Compd. Interdiscip. J. Mater. Sci. Solid-State Chem. Phys. 2020, 817, 152690. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Zhang, Q.; Zhang, S.; Shi, Q.; Qi, H. Research on Grain Refinement Mechanism of 6061 Aluminum Alloy Processed by Combined SPD Methods of ECAP and MAC. Materials 2018, 11, 1246. [Google Scholar] [CrossRef]
- Tan, Y.B.; Wang, X.M.; Ma, M.; Zhang, J.X.; Liu, W.C.; Fu, R.D.; Xiang, S. A study on microstructure and mechanical properties of AA 3003 aluminum alloy joints by underwater friction stir welding. Mater. Charact. 2017, 127, 41–52. [Google Scholar] [CrossRef]
- Gupta, M.; Srivatsan, T.S. Interrelationship between matrix microhardness and ultimate tensile strength of discontinuous particulate-reinforced aluminum alloy composites. Mater. Lett. 2001, 51, 255–261. [Google Scholar] [CrossRef]
- Hosseinifar, M.; Malakhov, D.V. Effect of Ce and La on microstructure and properties of a 6xxx series type aluminum alloy. J. Mater. Sci. 2008, 43, 7157–7164. [Google Scholar] [CrossRef]
- Howeyze, M.; Eivani, A.R.; Arabi, H.; Jafarian, H.R. Effects of deformation routes on the evolution of microstructure, texture and tensile properties of AA5052 aluminum alloy. Mater. Sci. Eng. A 2018, 732, 120–128. [Google Scholar] [CrossRef]
- Pattnaik, A.B.; Das, S.; Jha, B.B.; Prasanth, N. Effect of Al–5Ti–1B grain refiner on the microstructure, mechanical properties and acoustic emission characteristics of Al5052 aluminium alloy. J. Mater. Res. Technol. 2015, 4, 171–179. [Google Scholar] [CrossRef]
- Zhao, K.; Gao, T.; Yang, H.; Hu, K.; Liu, G.; Sun, Q.; Liu, X. Enhanced grain refinement and mechanical properties of a high–strength Al–Zn–Mg–Cu–Zr alloy induced by TiC nano–particles. Mater. Sci. Eng. A 2021, 806, 140852. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, N.; Le, Y. Mechanical properties and damping capacity after grain refinement in A356 alloy. Mater. Lett. 2005, 59, 2174–2177. [Google Scholar] [CrossRef]
- Mehmood, A.; Shah, M.; Sheikh, N.A.; Qayyum, J.A.; Khushnood, S. Grain refinement of ASTM A356 aluminum alloy using sloping plate process through gravity die casting. Alex. Eng. J. 2016, 55, 2431–2438. [Google Scholar] [CrossRef]
- Camicia, G.; Timelli, G. Grain refinement of gravity die cast secondary AlSi7Cu3Mg alloys for automotive cylinder heads. Trans. Nonferrous Met. Soc. China 2016, 26, 1211–1221. [Google Scholar] [CrossRef]
- Ding, W.; Zhao, X.; Chen, T.; Zhang, H.; Liu, X.; Cheng, Y.; Lei, D. Effect of rare earth Y and Al–Ti–B master alloy on the microstructure and mechanical properties of 6063 aluminum alloy. J. Alloys Compd. 2020, 830, 154685. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, É. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Jablonka, K.M.; Jothiappan, G.M.; Wang, S.; Smit, B.; Yoo, B. Bias free multiobjective active learning for materials design and discovery. Nat. Commun. 2021, 12, 2312. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, A.K. Chemical hardness-driven interpretable machine learning approach for rapid search of photocatalysts. npj Comput. Mater. 2021, 7, 197. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Sarram, M.A.; Gharaghani, S.; Chahooki, M.A.Z. A survey on semi-supervised feature selection methods. Pattern Recognit. 2017, 64, 141–158. [Google Scholar] [CrossRef]
- Shang, C.; Wang, C.; Wu, H.; Liu, W.; Chen, Y.; Pan, G.; Mao, X. Improved data-driven performance of Charpy impact toughness via literature-assisted production data in pipeline steel. Sci. China Technol. Sci. 2023, 66, 2069–2079. [Google Scholar] [CrossRef]
- Eva, O. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar]

| Input/Output | Abb. | Description | Min | Max | Mean |
|---|---|---|---|---|---|
| Inputs | Al | Mass fraction of Al/% | 84.450 | 100.00 | 93.626 |
| Si | Mass fraction of Si/% | 0.000 | 7.270 | 1.114 | |
| Fe | Mass fraction of Fe/% | 0.000 | 0.634 | 0.209 | |
| Cu | Mass fraction of Cu/% | 0.000 | 4.420 | 1.297 | |
| Mn | Mass fraction of Mn/% | 0.000 | 5.420 | 0.480 | |
| Mg | Mass fraction of Mg/% | 0.000 | 6.380 | 1.628 | |
| Cr | Mass fraction of Cr/% | 0.000 | 5.600 | 0.135 | |
| Zn | Mass fraction of Zn/% | 0.000 | 7.840 | 1.460 | |
| Ti | Mass fraction of Ti/% | 0.000 | 1.010 | 0.073 | |
| Sc | Mass fraction of Sc/% | 0.000 | 0.100 | 0.001 | |
| Er | Mass fraction of Er/% | 0.000 | 0.100 | 0.001 | |
| Zr | Mass fraction of Zr/% | 0.000 | 0.200 | 0.011 | |
| Ni | Mass fraction of Ni/% | 0.000 | 0.035 | 0.003 | |
| B | Mass fraction of B/% | 0.000 | 0.042 | 0.002 | |
| Be | Mass fraction of Be/% | 0.000 | 0.001 | 0.000 | |
| Li | Mass fraction of Li/% | 0.000 | 2.200 | 0.033 | |
| Ce | Mass fraction of Ce/% | 0.000 | 0.100 | 0.001 | |
| La | Mass fraction of La/% | 0.000 | 0.210 | 0.003 | |
| Sr | Mass fraction of Sr/% | 0.000 | 0.011 | 0.001 | |
| Gs | Grain size/um | 0.360 | 482.000 | 76.713 | |
| Hardness | Hardness/Hv | 48.000 | 302.030 | 108.838 | |
| Output | Ts | Tensile strength/MPa | 115.000 | 696.000 | 349.528 |
| ML Models | R2 | RMSE (MPa) | MSE (MPa) | MAE (MPa) |
|---|---|---|---|---|
| KNN | 0.393 | 129.044 | 16,652.275 | 99.490 |
| LR | 0.550 | 171.507 | 29,414.598 | 85.920 |
| ANN | 0.732 | 85.691 | 33,282.024 | 145.833 |
| LightGBM | 0.766 | 80.062 | 6409.911 | 63.933 |
| RF | 0.858 | 62.424 | 3688.174 | 43.259 |
| XGBoost | 0.878 | 57.721 | 3331.768 | 39.267 |
| ML Models | R2 | RMSE (MPa) | MAE (MPa) | MSE (MPa) |
|---|---|---|---|---|
| LR | 0.501 | 117.008 | 93.539 | 13,690.907 |
| XGBoost | 0.884 | 56.452 | 40.034 | 3186.835 |
| RF | 0.891 | 54.689 | 37.897 | 2990.903 |
| LightGBM | 0.912 | 49.227 | 37.675 | 2423.319 |
| ML Models | R2 | RMSE (MPa) | MAE (MPa) | MSE (MPa) |
|---|---|---|---|---|
| RF | 0.854 | 54.447 | 40.573 | 2964.502 |
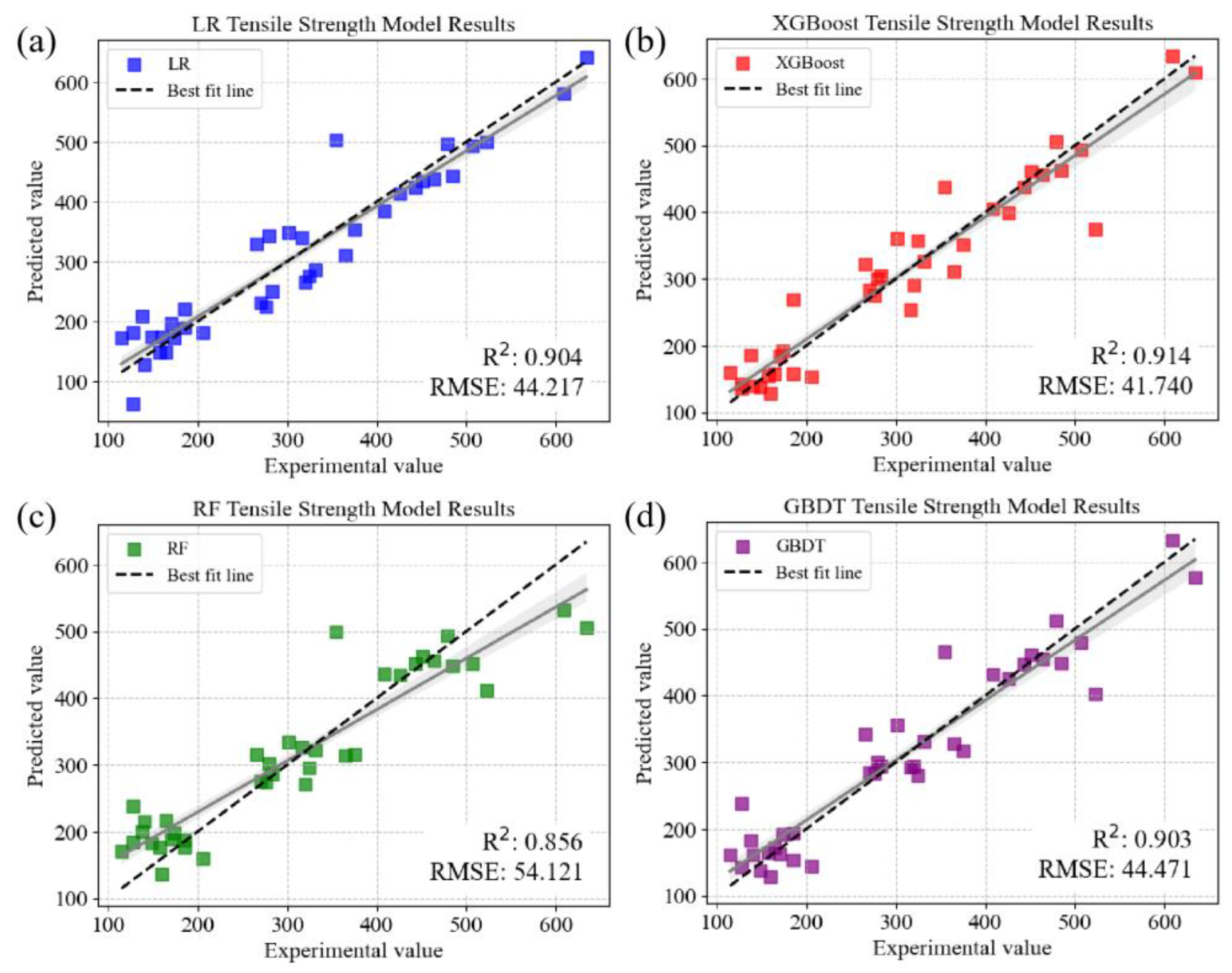
| LR | 0.904 | 44.217 | 35.324 | 1955.187 |
| GBDT | 0.907 | 43.470 | 31.785 | 1889.660 |
| XGBoost | 0.914 | 41.740 | 29.910 | 1742.203 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, K.; Zhu, D.; Zhang, Y.; Zhang, C.; Wang, X.; Wang, C.; Jiang, T.; Mao, F.; Zhang, C.; Meng, X.; et al. Predictive Modeling of Tensile Strength in Aluminum Alloys via Machine Learning. Materials 2023, 16, 7236. https://doi.org/10.3390/ma16227236
Fu K, Zhu D, Zhang Y, Zhang C, Wang X, Wang C, Jiang T, Mao F, Zhang C, Meng X, et al. Predictive Modeling of Tensile Strength in Aluminum Alloys via Machine Learning. Materials. 2023; 16(22):7236. https://doi.org/10.3390/ma16227236
Chicago/Turabian StyleFu, Keya, Dexin Zhu, Yuqi Zhang, Cheng Zhang, Xiaodong Wang, Changji Wang, Tao Jiang, Feng Mao, Cheng Zhang, Xiaobo Meng, and et al. 2023. "Predictive Modeling of Tensile Strength in Aluminum Alloys via Machine Learning" Materials 16, no. 22: 7236. https://doi.org/10.3390/ma16227236
APA StyleFu, K., Zhu, D., Zhang, Y., Zhang, C., Wang, X., Wang, C., Jiang, T., Mao, F., Zhang, C., Meng, X., & Yu, H. (2023). Predictive Modeling of Tensile Strength in Aluminum Alloys via Machine Learning. Materials, 16(22), 7236. https://doi.org/10.3390/ma16227236







